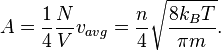From Wikipedia, the free encyclopedia
Solar irradiance (also Insolation, from Latin insolare, to expose to the sun)[1][2] is the power per unit area produced by the Sun in the form of electromagnetic radiation. Irradiance may be measured in space or at the Earth's surface after atmospheric absorption and scattering. Total solar irradiance (TSI), is a measure of the solar radiative power per unit area normal to the rays, incident on the Earth's upper atmosphere. The solar constant is a conventional measure of mean TSI at a distance of one Astronomical Unit (AU). Irradiance is a function of distance from the Sun, the solar cycle, and cross-cycle changes.[3] Irradiance on Earth is most intense at points directly facing (normal to) the Sun.
An alternate unit of measure is the Langley (1 thermochemical calorie per square centimeter or 41,840 J/m2) or irradiance per unit time.
The solar energy business uses watt-hour per square metre (Wh/m2). Divided by the recording time, this measure becomes insolation, another unit of irradiance.
Insolation can be measured in space, at the edge of the atmosphere or at a terrestrial object.
Insolation can also be expressed in Suns, where one Sun equals 1000 W/m2 at the point of arrival, with kWh/m2/day expressed as hours/day.[5]
Reaching an object, part of the irradiance is absorbed and the remainder reflected. Usually the absorbed radiation is converted to thermal energy, increasing the object's temperature. Manmade or natural systems, however, can convert part of the absorbed radiation into another form such as electricity or chemical bonds, as in the case of photovoltaic cells or plants. The proportion of reflected radiation is the object's reflectivity or albedo.
Projection effect
Insolation onto a surface is largest when the surface directly faces (is normal to) the sun. As the angle between the surface and the Sun moves from normal, the insolation is reduced in proportion to the angle's Cosine; see Effect of sun angle on climate.
In the figure, the angle shown is between the ground and the sunbeam rather than between the vertical direction and the sunbeam; hence the sine rather than the cosine is appropriate. A sunbeam one mile (1.6 km) wide arrives from directly overhead, and another at a 30° angle to the horizontal. The Sine of a 30° angle is 1/2, whereas the sine of a 90° angle is 1. Therefore, the angled sunbeam spreads the light over twice the area. Consequently, half as much light falls on each square mile.
This 'projection effect' is the main reason why Earth's polar regions are much colder than equatorial regions. On an annual average the poles receive less insolation than does the equator, because the poles are always angled more away from the sun than the tropics. At a lower angle the light must travel through more atmosphere. This attenuates it (by absorption and scattering) further reducing insolation.
Categories
Direct insolation is measured at a given location with a surface element perpendicular to the Sun. It excludes diffuse insolation (radiation that is scattered or reflected by atmospheric components). Direct insolation is equal to the Solar constant minus the atmospheric losses due to absorption and scattering. While the solar constant varies, losses depend on time of day (length of light's path through the atmosphere depending on the Solar elevation angle), Cloud cover, Moisture content and other contents. Insolation affects plant metabolism and animal behavior.[6]
Diffuse insolation is the contribution of light scattered by the atmosphere to total insolation.
Earth
Average annual solar radiation arriving at the top of the Earth's atmosphere is roughly 1366 W/m2.[7][8] The radiation is distributed across the Electromagnetic spectrum, although most is Visible light. The Sun's rays are attenuated as they pass through the Atmosphere, leaving maximum normal surface irradiance at approximately 1000 W /m2 at Sealevel on a clear day.[clarification needed]

The actual figure varies with the Sun's angle and atmospheric circumstances. Ignoring clouds, the daily average irradiance for the Earth is approximately 6 kWh/m2 = 21.6 MJ/m2. The output of, for example, a photovoltaic panel, partly depends on the angle of the sun relative to the panel. One Sun is a unit of power flux, not a standard value for actual insolation. Sometimes this unit is referred to as a Sol, not to be confused with a sol, meaning one solar day.[9]
Solar potential maps
Top of the atmosphere

 , the theoretical daily-average insolation at the top of the atmosphere, where θ is the polar angle of the Earth's orbit, and θ = 0 at the vernal equinox, and θ = 90° at the summer solstice; φ is the latitude of the Earth. The calculation assumed conditions appropriate for 2000 A.D.: a solar constant of S0 = 1367 W m−2, obliquity of ε = 23.4398°, longitude of perihelion of ϖ = 282.895°, eccentricity e = 0.016704. Contour labels (green) are in units of W m−2.
, the theoretical daily-average insolation at the top of the atmosphere, where θ is the polar angle of the Earth's orbit, and θ = 0 at the vernal equinox, and θ = 90° at the summer solstice; φ is the latitude of the Earth. The calculation assumed conditions appropriate for 2000 A.D.: a solar constant of S0 = 1367 W m−2, obliquity of ε = 23.4398°, longitude of perihelion of ϖ = 282.895°, eccentricity e = 0.016704. Contour labels (green) are in units of W m−2.
The distribution of solar radiation at the top of the atmosphere is determined by Earth's sphericity and orbital parameters. This applies to any unidirectional beam incident to a rotating sphere. Insolation is essential for numerical weather prediction and understanding seasons and climate change. Application to ice ages is known as Milankovitch cycles.
Distribution is based on a fundamental identity from Spherical trigonometry, the spherical law of cosines:
 , or for h0 as a solution of
, or for h0 as a solution of
 .
.

is nearly constant over the course of a day, and can be taken outside the integral
 can be calculated for any latitude φ and θ. Because of the elliptical orbit, and as a consequence of Kepler's second law, θ does not progress uniformly with time. Nevertheless, θ = 0° is exactly the time of the vernal equinox, θ = 90° is exactly the time of the summer solstice, θ = 180° is exactly the time of the autumnal equinox and θ = 270° is exactly the time of the winter solstice.
can be calculated for any latitude φ and θ. Because of the elliptical orbit, and as a consequence of Kepler's second law, θ does not progress uniformly with time. Nevertheless, θ = 0° is exactly the time of the vernal equinox, θ = 90° is exactly the time of the summer solstice, θ = 180° is exactly the time of the autumnal equinox and θ = 270° is exactly the time of the winter solstice.
Variation
Ultraviolet irradiance
Ultraviolet irradiance (EUV) varies by approximately 1.5 percent from solar maxima to minima, for 200 to 300 nm wavelengths.[17] However, a proxy study estimated that UV has increased by 3.0% since the Maunder Minimum.[18]
Milankovitch cycles
Some variations in insolation are not due to solar changes but rather due to the Earth moving between its perigee and apogee, or changes in the latitudinal distribution of radiation. These orbital changes or Milankovitch cycles have caused radiance variations of as much as 25% (locally; global average changes are much smaller) over long periods. The most recent significant event was an axial tilt of 24° during boreal summer near the Holocene climatic optimum.
Obtaining a time series for a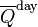 for a particular time of year, and particular latitude, is a useful application in the theory of Milankovitch cycles. For example, at the summer solstice, the declination δ is equal to the obliquity ε. The distance from the sun is
for a particular time of year, and particular latitude, is a useful application in the theory of Milankovitch cycles. For example, at the summer solstice, the declination δ is equal to the obliquity ε. The distance from the sun is
 , the precession index, whose variation dominates the variations in insolation at 65° N when eccentricity is large. For the next 100,000 years, with variations in eccentricity being relatively small, variations in obliquity dominate.
, the precession index, whose variation dominates the variations in insolation at 65° N when eccentricity is large. For the next 100,000 years, with variations in eccentricity being relatively small, variations in obliquity dominate.
Measurement
The space-based TSI record comprises measurements from more than ten radiometers spanning three solar cycles.
Technique
All modern TSI satellite instruments employ active cavity electrical substitution radiometry. This technique applies measured electrical heating to maintain an absorptive blackened cavity in thermal equilibrium while incident sunlight passes through a precision aperture of calibrated area. The aperture is modulated via a shutter. Accuracy uncertainties of <0.01% are required to detect long term solar irradiance variations, because expected changes are in the range 0.05 to 0.15 W m−2 per century.[19]
Intertemporal calibration
In orbit, radiometric calibrations drift for reasons including solar degradation of the cavity, electronic degradation of the heater, surface degradation of the precision aperture and varying surface emissions and temperatures that alter thermal backgrounds. These calibrations require compensation to preserve consistent measurements.[19]
For various reasons, the sources do not always agree. The Solar Radiation and Climate Experiment/Total Irradiance Measurement (SORCE/TIM) TSI values are lower than prior measurements by the Earth Radiometer Budget Experiment (ERBE) on the Earth Radiation Budget Satellite (ERBS), VIRGO on the Solar Heliospheric Observatory (SoHO) and the ACRIM instruments on the Solar Maximum Mission (SMM), Upper Atmosphere Research Satellite (UARS) and ACRIMSat. Pre-launch ground calibrations relied on component rather than system level measurements, since irradiance standards lacked absolute accuracies.[19]
Measurement stability involves exposing different radiometer cavities to different accumulations of solar radiation to quantify exposure-dependent degradation effects. These effects are then compensated for in final data. Observation overlaps permits corrections for both absolute offsets and validation of instrumental drifts.[19]
Uncertainties of individual observations exceed irradiance variability (∼0.1%). Thus, instrument stability and measurement continuity are relied upon to compute real variations.
Long-term radiometer drifts can be mistaken for irradiance variations that can be misinterpreted as affecting climate. Examples include the issue of the irradiance increase between cycle minima in 1986 and 1996, evident only in the ACRIM composite (and not the model) and the low irradiance levels in the PMOD composite during the 2008 minimum.
Despite the fact that ACRIM I, ACRIM II, ACRIM III, VIRGO and TIM all track degradation with redundant cavities, notable and unexplained differences remain in irradiance and the modeled influences of sunspots and faculae.
Persistent inconsistencies
Disagreement among overlapping observations indicates unresolved drifts that suggest the TSI record is not sufficiently stable to discern solar changes on decadal time scales. Only the ACRIM composite shows irradiance increasing by ∼1 W m−2 between 1986 and 1996; this change is also absent in the model.[19]
Recommendations to resolve the instrument discrepancies include validating optical measurement accuracy by comparing ground-based instruments to laboratory references, such as those at National Institute of Science and Technology (NIST); NIST validation of aperture area calibrations uses spares from each instrument; and applying diffraction corrections from the view-limiting aperture.[19]
For ACRIM, NIST determined that diffraction from the view-limiting aperture contributes a 0.13% signal not accounted for in the three ACRIM instruments. This correction lowers the reported ACRIM values, bringing ACRIM closer to TIM. In ACRIM and all other instruments, the aperture is deep inside the instrument, with a larger view-limiting aperture at the front. Depending on edge imperfections this can directly scatter light into the cavity. This design admits two to three times the amount of light intended to be measured; if not completely absorbed or scattered, this additional light produces erroneously high signals. In contrast, TIM's design places the precision aperture at the front so that only desired light enters.[19]
Variations from other sources likely include an annual cycle that is nearly in phase with the Sun-Earth distance in ACRIM III data and 90-day spikes in the VIRGO data coincident with SoHO spacecraft maneuvers that were most apparent during the 2008 solar minimum.
TSI Radiometer Facility
TIM's high absolute accuracy creates new opportunities for measuring climate variables. TSI Radiometer Facility (TRF) is a cryogenic radiometer that operates in a vacuum with controlled light sources. L-1 Standards and Technology (LASP) designed and built the system, completed in 2008. It was calibrated for optical power against the NIST Primary Optical Watt Radiometer, a cryogenic radiometer that maintains the NIST radiant power scale to an uncertainty of 0.02% (1σ). As of 2011 TRF was the only facility that approached the desired <0.01% uncertainty for pre-launch validation of solar radiometers measuring irradiance (rather than merely optical power) at solar power levels and under vacuum conditions.[19]
TRF encloses both the reference radiometer and the instrument under test in a common vacuum system that contains a stationary, spatially uniform illuminating beam. A precision aperture with area calibrated to 0.0031% (1σ) determines the beam's measured portion. The test instrument's precision aperture is positioned in the same location, without optically altering the beam, for direct comparison to the reference. Variable beam power provides linearity diagnostics, and variable beam diameter diagnoses scattering from different instrument components.[19]
The Glory/TIM and PICARD/PREMOS flight instrument absolute scales are now traceable to the TRF in both optical power and irradiance. The resulting high accuracy reduces the consequences of any future gap in the solar irradiance record.[19]
2011 reassessment
The most probable value of TSI representative of solar minimum is 1360.8 ± 0.5 W m−2, lower than the earlier accepted value of 1365.4 ± 1.3 W m−2, established in the 1990s. The new value came from SORCE/TIM and radiometric laboratory tests. Scattered light is a primary cause of the higher irradiance values measured by earlier satellites in which the precision aperture is located behind a larger, view-limiting aperture. The TIM uses a view-limiting aperture that is smaller than precision aperture that precludes this spurious signal. The new estimate is from better measurement rather than a change in solar output.[19]
A regression model-based split of the relative proportion of sunspot and facular influences from SORCE/TIM data accounts for 92% of observed variance and tracks the observed trends to within TIM's stability band. This agreement provides further evidence that TSI variations are primarily due to solar surface magnetic activity.[19]
Instrument inaccuracies add a significant uncertainty in determining Earth's energy balance. The energy imbalance has been variously measured (during a deep solar minimum of 2005–2010) to be +0.58 ± 0.15 W/m²),[20] +0.60 ± 0.17 W/m²[21] and +0.85 W m−2. Estimates from space-based measurements range from +3 to 7 W m−2. SORCE/TIM's lower TSI value reduces this discrepancy by 1 W m−2. This difference between the new lower TIM value and earlier TSI measurements corresponds to a climate forcing of −0.8 W m−2, which is comparable to the energy imbalance.[19]
2014 reassessment
In 2014 a new ACRIM composite was developed using the updated ACRIM3 record. It added corrections for scattering and diffraction revealed during recent testing at TRF and two algorithm updates. The algorithm updates more accurately account for instrument thermal behavior and parsing of shutter cycle data. These corrected a component of the quasi-annual signal and increased the signal to noise ratio, respectively. The net effect of these corrections decreased the average ACRIM3 TSI value without affecting the trending in the ACRIM Composite TSI.[22]
Differences between ACRIM and PMOD TSI composites are evident, but the most significant is the solar minimum-to-minimum trends during solar cycles 21-23. ACRIM established an increase of +0.037%/decade from 1980 to 2000 and a decrease thereafter. PMOD instead presents a steady decrease since 1978. Significant differences can also be seen during the peak of solar cycles 21 and 22. These arise from the fact that ACRIM uses the original TSI results published by the satellite experiment teams while PMOD significantly modifies some results to conform them to specific TSI proxy models. The implications of increasing TSI during the global warming of the last two decades of the 20th century are that solar forcing may be a significantly larger factor in climate change than represented in the CMIP5 general circulation climate models.[22]
Applications
Buildings
In construction, insolation is an important consideration when designing a building for a particular site.[23]
The projection effect can be used to design buildings that are cool in summer and warm in winter, by providing vertical windows on the equator-facing side of the building (the south face in the northern hemisphere, or the north face in the southern hemisphere): this maximizes insolation in the winter months when the Sun is low in the sky and minimizes it in the summer when the Sun is high. (The Sun's north/south path through the sky spans 47 degrees through the year).
Solar power
Insolation figures are used as an input to worksheets to size solar power systems.[24] Because (except for asphalt solar collectors)[25] panels are almost always mounted at an angle[26] towards the sun, insolation must be adjusted to prevent estimates that are inaccurately low for winter and inaccurately high for summer.[27] In many countries the figures can be obtained from an insolation map or from insolation tables that reflect data over the prior 30–50 years. Photovoltaic panels are rated under standard conditions to determine the Wp rating (watts peak),[28] which can then be used with insolation to determine the expected output, adjusted by factors such as tilt, tracking and shading (which can be included to create the installed Wp rating).[29] Insolation values range from 800 to 950 kWh/(kWp·y) in Norway to up to 2,900 in Australia.
Climate research
Irradiance plays a part in climate modeling and weather forecasting. A non-zero average global net radiation at the top of the atmosphere is indicative of Earth's thermal disequilibrium as imposed by climate forcing.
The impact of the lower 2014 TSI value on climate models is unknown. A few tenths of a percent change in the absolute TSI level is typically considered to be of minimal consequence for climate simulations. The new measurements require climate model parameter adjustments.
Experiments with GISS Model 3 investigated the sensitivity of model performance to the TSI absolute value during present and pre-industrial epochs, and describe, for example, how the irradiance reduction is partitioned between the atmosphere and surface and the effects on outgoing radiation.[19]
Assessing the impact of long-term irradiance changes on climate requires greater instrument stability[19] combined with reliable global surface temperature observations to quantify climate response processes to radiative forcing on decadal time scales. The observed 0.1% irradiance increase imparts 0.22 W m−2 climate forcing, which suggests a transient climate response of 0.6 °C per W m−2. This response is larger by a factor of 2 or more than in the IPCC-assessed 2008 models, possibly appearing in the models' heat uptake by the ocean.[19]
Space travel
Insolation is the primary variable affecting equilibrium temperature in spacecraft design and planetology.
Solar activity and irradiance measurement is a concern for space travel. For example, the American space agency, NASA, launched its Solar Radiation and Climate Experiment (SORCE) satellite with Solar Irradiance Monitors.[3]
Civil engineering
In civil engineering and hydrology, numerical models of snowmelt runoff use observations of insolation. This permits estimation of the rate at which water is released from a melting snowpack. Field measurement is accomplished using a pyranometer.
Units
The unit recommended by the World Meteorological Organization is the megajoule per square metre (MJ/m2) or joule per square millimetre (J/mm2).[4]An alternate unit of measure is the Langley (1 thermochemical calorie per square centimeter or 41,840 J/m2) or irradiance per unit time.
The solar energy business uses watt-hour per square metre (Wh/m2). Divided by the recording time, this measure becomes insolation, another unit of irradiance.
Insolation can be measured in space, at the edge of the atmosphere or at a terrestrial object.
Insolation can also be expressed in Suns, where one Sun equals 1000 W/m2 at the point of arrival, with kWh/m2/day expressed as hours/day.[5]
Absorption and reflection[edit source | edit]
Reaching an object, part of the irradiance is absorbed and the remainder reflected. Usually the absorbed radiation is converted to thermal energy, increasing the object's temperature. Manmade or natural systems, however, can convert part of the absorbed radiation into another form such as electricity or chemical bonds, as in the case of photovoltaic cells or plants. The proportion of reflected radiation is the object's reflectivity or albedo.
Projection effect
Insolation onto a surface is largest when the surface directly faces (is normal to) the sun. As the angle between the surface and the Sun moves from normal, the insolation is reduced in proportion to the angle's Cosine; see Effect of sun angle on climate.
In the figure, the angle shown is between the ground and the sunbeam rather than between the vertical direction and the sunbeam; hence the sine rather than the cosine is appropriate. A sunbeam one mile (1.6 km) wide arrives from directly overhead, and another at a 30° angle to the horizontal. The Sine of a 30° angle is 1/2, whereas the sine of a 90° angle is 1. Therefore, the angled sunbeam spreads the light over twice the area. Consequently, half as much light falls on each square mile.
This 'projection effect' is the main reason why Earth's polar regions are much colder than equatorial regions. On an annual average the poles receive less insolation than does the equator, because the poles are always angled more away from the sun than the tropics. At a lower angle the light must travel through more atmosphere. This attenuates it (by absorption and scattering) further reducing insolation.
Categories
Direct insolation is measured at a given location with a surface element perpendicular to the Sun. It excludes diffuse insolation (radiation that is scattered or reflected by atmospheric components). Direct insolation is equal to the Solar constant minus the atmospheric losses due to absorption and scattering. While the solar constant varies, losses depend on time of day (length of light's path through the atmosphere depending on the Solar elevation angle), Cloud cover, Moisture content and other contents. Insolation affects plant metabolism and animal behavior.[6]
Diffuse insolation is the contribution of light scattered by the atmosphere to total insolation.
Earth
Average annual solar radiation arriving at the top of the Earth's atmosphere is roughly 1366 W/m2.[7][8] The radiation is distributed across the Electromagnetic spectrum, although most is Visible light. The Sun's rays are attenuated as they pass through the Atmosphere, leaving maximum normal surface irradiance at approximately 1000 W /m2 at Sealevel on a clear day.[clarification needed]
A Pyranometer, a component of a temporary remote meteorological station, measures insolation on Skagit Bay, Washington.
The actual figure varies with the Sun's angle and atmospheric circumstances. Ignoring clouds, the daily average irradiance for the Earth is approximately 6 kWh/m2 = 21.6 MJ/m2. The output of, for example, a photovoltaic panel, partly depends on the angle of the sun relative to the panel. One Sun is a unit of power flux, not a standard value for actual insolation. Sometimes this unit is referred to as a Sol, not to be confused with a sol, meaning one solar day.[9]
Solar potential maps
Top of the atmosphere

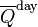 , the theoretical daily-average insolation at the top of the atmosphere, where θ is the polar angle of the Earth's orbit, and θ = 0 at the vernal equinox, and θ = 90° at the summer solstice; φ is the latitude of the Earth. The calculation assumed conditions appropriate for 2000 A.D.: a solar constant of S0 = 1367 W m−2, obliquity of ε = 23.4398°, longitude of perihelion of ϖ = 282.895°, eccentricity e = 0.016704. Contour labels (green) are in units of W m−2.
, the theoretical daily-average insolation at the top of the atmosphere, where θ is the polar angle of the Earth's orbit, and θ = 0 at the vernal equinox, and θ = 90° at the summer solstice; φ is the latitude of the Earth. The calculation assumed conditions appropriate for 2000 A.D.: a solar constant of S0 = 1367 W m−2, obliquity of ε = 23.4398°, longitude of perihelion of ϖ = 282.895°, eccentricity e = 0.016704. Contour labels (green) are in units of W m−2.The distribution of solar radiation at the top of the atmosphere is determined by Earth's sphericity and orbital parameters. This applies to any unidirectional beam incident to a rotating sphere. Insolation is essential for numerical weather prediction and understanding seasons and climate change. Application to ice ages is known as Milankovitch cycles.
Distribution is based on a fundamental identity from Spherical trigonometry, the spherical law of cosines:

- where a, b and c are arc lengths, in radians, of the sides of a spherical triangle. C is the angle in the vertex opposite the side which has arc length c. Applied to the calculation of Solar zenith angle Θ, the following applies to the Spherical law of cosines:
 , or for h0 as a solution of
, or for h0 as a solution of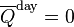 .
.
is nearly constant over the course of a day, and can be taken outside the integral
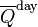 can be calculated for any latitude φ and θ. Because of the elliptical orbit, and as a consequence of Kepler's second law, θ does not progress uniformly with time. Nevertheless, θ = 0° is exactly the time of the vernal equinox, θ = 90° is exactly the time of the summer solstice, θ = 180° is exactly the time of the autumnal equinox and θ = 270° is exactly the time of the winter solstice.
can be calculated for any latitude φ and θ. Because of the elliptical orbit, and as a consequence of Kepler's second law, θ does not progress uniformly with time. Nevertheless, θ = 0° is exactly the time of the vernal equinox, θ = 90° is exactly the time of the summer solstice, θ = 180° is exactly the time of the autumnal equinox and θ = 270° is exactly the time of the winter solstice.
Variation
Total irradiance
Total solar irradiance (TSI)[11] changes slowly on decadal and longer timescales. The variation during solar cycle 21 was about 0.1% (peak-to-peak).[12] In contrast to older reconstructions,[13] most recent TSI reconstructions point to an increase of only about 0.05% to 0.1% between the Maunder Minimum and the present.[14][15][16]
Ultraviolet irradiance
Ultraviolet irradiance (EUV) varies by approximately 1.5 percent from solar maxima to minima, for 200 to 300 nm wavelengths.[17] However, a proxy study estimated that UV has increased by 3.0% since the Maunder Minimum.[18]
Milankovitch cycles
Some variations in insolation are not due to solar changes but rather due to the Earth moving between its perigee and apogee, or changes in the latitudinal distribution of radiation. These orbital changes or Milankovitch cycles have caused radiance variations of as much as 25% (locally; global average changes are much smaller) over long periods. The most recent significant event was an axial tilt of 24° during boreal summer near the Holocene climatic optimum.
Obtaining a time series for a
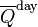 for a particular time of year, and particular latitude, is a useful application in the theory of Milankovitch cycles. For example, at the summer solstice, the declination δ is equal to the obliquity ε. The distance from the sun is
for a particular time of year, and particular latitude, is a useful application in the theory of Milankovitch cycles. For example, at the summer solstice, the declination δ is equal to the obliquity ε. The distance from the sun is , the precession index, whose variation dominates the variations in insolation at 65° N when eccentricity is large. For the next 100,000 years, with variations in eccentricity being relatively small, variations in obliquity dominate.
, the precession index, whose variation dominates the variations in insolation at 65° N when eccentricity is large. For the next 100,000 years, with variations in eccentricity being relatively small, variations in obliquity dominate.
Measurement
The space-based TSI record comprises measurements from more than ten radiometers spanning three solar cycles.
Technique
All modern TSI satellite instruments employ active cavity electrical substitution radiometry. This technique applies measured electrical heating to maintain an absorptive blackened cavity in thermal equilibrium while incident sunlight passes through a precision aperture of calibrated area. The aperture is modulated via a shutter. Accuracy uncertainties of <0.01% are required to detect long term solar irradiance variations, because expected changes are in the range 0.05 to 0.15 W m−2 per century.[19]
Intertemporal calibration
In orbit, radiometric calibrations drift for reasons including solar degradation of the cavity, electronic degradation of the heater, surface degradation of the precision aperture and varying surface emissions and temperatures that alter thermal backgrounds. These calibrations require compensation to preserve consistent measurements.[19]For various reasons, the sources do not always agree. The Solar Radiation and Climate Experiment/Total Irradiance Measurement (SORCE/TIM) TSI values are lower than prior measurements by the Earth Radiometer Budget Experiment (ERBE) on the Earth Radiation Budget Satellite (ERBS), VIRGO on the Solar Heliospheric Observatory (SoHO) and the ACRIM instruments on the Solar Maximum Mission (SMM), Upper Atmosphere Research Satellite (UARS) and ACRIMSat. Pre-launch ground calibrations relied on component rather than system level measurements, since irradiance standards lacked absolute accuracies.[19]
Measurement stability involves exposing different radiometer cavities to different accumulations of solar radiation to quantify exposure-dependent degradation effects. These effects are then compensated for in final data. Observation overlaps permits corrections for both absolute offsets and validation of instrumental drifts.[19]
Uncertainties of individual observations exceed irradiance variability (∼0.1%). Thus, instrument stability and measurement continuity are relied upon to compute real variations.
Long-term radiometer drifts can be mistaken for irradiance variations that can be misinterpreted as affecting climate. Examples include the issue of the irradiance increase between cycle minima in 1986 and 1996, evident only in the ACRIM composite (and not the model) and the low irradiance levels in the PMOD composite during the 2008 minimum.
Despite the fact that ACRIM I, ACRIM II, ACRIM III, VIRGO and TIM all track degradation with redundant cavities, notable and unexplained differences remain in irradiance and the modeled influences of sunspots and faculae.
Persistent inconsistencies
Disagreement among overlapping observations indicates unresolved drifts that suggest the TSI record is not sufficiently stable to discern solar changes on decadal time scales. Only the ACRIM composite shows irradiance increasing by ∼1 W m−2 between 1986 and 1996; this change is also absent in the model.[19]Recommendations to resolve the instrument discrepancies include validating optical measurement accuracy by comparing ground-based instruments to laboratory references, such as those at National Institute of Science and Technology (NIST); NIST validation of aperture area calibrations uses spares from each instrument; and applying diffraction corrections from the view-limiting aperture.[19]
For ACRIM, NIST determined that diffraction from the view-limiting aperture contributes a 0.13% signal not accounted for in the three ACRIM instruments. This correction lowers the reported ACRIM values, bringing ACRIM closer to TIM. In ACRIM and all other instruments, the aperture is deep inside the instrument, with a larger view-limiting aperture at the front. Depending on edge imperfections this can directly scatter light into the cavity. This design admits two to three times the amount of light intended to be measured; if not completely absorbed or scattered, this additional light produces erroneously high signals. In contrast, TIM's design places the precision aperture at the front so that only desired light enters.[19]
Variations from other sources likely include an annual cycle that is nearly in phase with the Sun-Earth distance in ACRIM III data and 90-day spikes in the VIRGO data coincident with SoHO spacecraft maneuvers that were most apparent during the 2008 solar minimum.
TSI Radiometer Facility
TIM's high absolute accuracy creates new opportunities for measuring climate variables. TSI Radiometer Facility (TRF) is a cryogenic radiometer that operates in a vacuum with controlled light sources. L-1 Standards and Technology (LASP) designed and built the system, completed in 2008. It was calibrated for optical power against the NIST Primary Optical Watt Radiometer, a cryogenic radiometer that maintains the NIST radiant power scale to an uncertainty of 0.02% (1σ). As of 2011 TRF was the only facility that approached the desired <0.01% uncertainty for pre-launch validation of solar radiometers measuring irradiance (rather than merely optical power) at solar power levels and under vacuum conditions.[19]TRF encloses both the reference radiometer and the instrument under test in a common vacuum system that contains a stationary, spatially uniform illuminating beam. A precision aperture with area calibrated to 0.0031% (1σ) determines the beam's measured portion. The test instrument's precision aperture is positioned in the same location, without optically altering the beam, for direct comparison to the reference. Variable beam power provides linearity diagnostics, and variable beam diameter diagnoses scattering from different instrument components.[19]
The Glory/TIM and PICARD/PREMOS flight instrument absolute scales are now traceable to the TRF in both optical power and irradiance. The resulting high accuracy reduces the consequences of any future gap in the solar irradiance record.[19]
| Instrument | Irradiance: View-Limiting Aperture Overfilled | Irradiance: Precision Aperture Overfilled | Difference Attributable To Scatter Error | Measured Optical Power Error | Residual Irradiance Agreement | Uncertainty |
|---|---|---|---|---|---|---|
| SORCE/TIM ground | NA | −0.037% | NA | −0.037% | 0.000% | 0.032% |
| Glory/TIM flight | NA | −0.012% | NA | −0.029% | 0.017% | 0.020% |
| PREMOS-1 ground | −0.005% | −0.104% | 0.098% | −0.049% | −0.104% | ∼0.038% |
| PREMOS-3 flight | 0.642% | 0.605% | 0.037% | 0.631% | −0.026% | ∼0.027% |
| VIRGO-2 ground | 0.897% | 0.743% | 0.154% | 0.730% | 0.013% | ∼0.025% |
2011 reassessment
The most probable value of TSI representative of solar minimum is 1360.8 ± 0.5 W m−2, lower than the earlier accepted value of 1365.4 ± 1.3 W m−2, established in the 1990s. The new value came from SORCE/TIM and radiometric laboratory tests. Scattered light is a primary cause of the higher irradiance values measured by earlier satellites in which the precision aperture is located behind a larger, view-limiting aperture. The TIM uses a view-limiting aperture that is smaller than precision aperture that precludes this spurious signal. The new estimate is from better measurement rather than a change in solar output.[19]A regression model-based split of the relative proportion of sunspot and facular influences from SORCE/TIM data accounts for 92% of observed variance and tracks the observed trends to within TIM's stability band. This agreement provides further evidence that TSI variations are primarily due to solar surface magnetic activity.[19]
Instrument inaccuracies add a significant uncertainty in determining Earth's energy balance. The energy imbalance has been variously measured (during a deep solar minimum of 2005–2010) to be +0.58 ± 0.15 W/m²),[20] +0.60 ± 0.17 W/m²[21] and +0.85 W m−2. Estimates from space-based measurements range from +3 to 7 W m−2. SORCE/TIM's lower TSI value reduces this discrepancy by 1 W m−2. This difference between the new lower TIM value and earlier TSI measurements corresponds to a climate forcing of −0.8 W m−2, which is comparable to the energy imbalance.[19]
2014 reassessment
In 2014 a new ACRIM composite was developed using the updated ACRIM3 record. It added corrections for scattering and diffraction revealed during recent testing at TRF and two algorithm updates. The algorithm updates more accurately account for instrument thermal behavior and parsing of shutter cycle data. These corrected a component of the quasi-annual signal and increased the signal to noise ratio, respectively. The net effect of these corrections decreased the average ACRIM3 TSI value without affecting the trending in the ACRIM Composite TSI.[22]Differences between ACRIM and PMOD TSI composites are evident, but the most significant is the solar minimum-to-minimum trends during solar cycles 21-23. ACRIM established an increase of +0.037%/decade from 1980 to 2000 and a decrease thereafter. PMOD instead presents a steady decrease since 1978. Significant differences can also be seen during the peak of solar cycles 21 and 22. These arise from the fact that ACRIM uses the original TSI results published by the satellite experiment teams while PMOD significantly modifies some results to conform them to specific TSI proxy models. The implications of increasing TSI during the global warming of the last two decades of the 20th century are that solar forcing may be a significantly larger factor in climate change than represented in the CMIP5 general circulation climate models.[22]
Applications
Buildings
In construction, insolation is an important consideration when designing a building for a particular site.[23]The projection effect can be used to design buildings that are cool in summer and warm in winter, by providing vertical windows on the equator-facing side of the building (the south face in the northern hemisphere, or the north face in the southern hemisphere): this maximizes insolation in the winter months when the Sun is low in the sky and minimizes it in the summer when the Sun is high. (The Sun's north/south path through the sky spans 47 degrees through the year).
Solar power
Insolation figures are used as an input to worksheets to size solar power systems.[24] Because (except for asphalt solar collectors)[25] panels are almost always mounted at an angle[26] towards the sun, insolation must be adjusted to prevent estimates that are inaccurately low for winter and inaccurately high for summer.[27] In many countries the figures can be obtained from an insolation map or from insolation tables that reflect data over the prior 30–50 years. Photovoltaic panels are rated under standard conditions to determine the Wp rating (watts peak),[28] which can then be used with insolation to determine the expected output, adjusted by factors such as tilt, tracking and shading (which can be included to create the installed Wp rating).[29] Insolation values range from 800 to 950 kWh/(kWp·y) in Norway to up to 2,900 in Australia.
Climate research
Irradiance plays a part in climate modeling and weather forecasting. A non-zero average global net radiation at the top of the atmosphere is indicative of Earth's thermal disequilibrium as imposed by climate forcing.The impact of the lower 2014 TSI value on climate models is unknown. A few tenths of a percent change in the absolute TSI level is typically considered to be of minimal consequence for climate simulations. The new measurements require climate model parameter adjustments.
Experiments with GISS Model 3 investigated the sensitivity of model performance to the TSI absolute value during present and pre-industrial epochs, and describe, for example, how the irradiance reduction is partitioned between the atmosphere and surface and the effects on outgoing radiation.[19]
Assessing the impact of long-term irradiance changes on climate requires greater instrument stability[19] combined with reliable global surface temperature observations to quantify climate response processes to radiative forcing on decadal time scales. The observed 0.1% irradiance increase imparts 0.22 W m−2 climate forcing, which suggests a transient climate response of 0.6 °C per W m−2. This response is larger by a factor of 2 or more than in the IPCC-assessed 2008 models, possibly appearing in the models' heat uptake by the ocean.[19]
Space travel
Insolation is the primary variable affecting equilibrium temperature in spacecraft design and planetology.Solar activity and irradiance measurement is a concern for space travel. For example, the American space agency, NASA, launched its Solar Radiation and Climate Experiment (SORCE) satellite with Solar Irradiance Monitors.[3]
Civil engineering
In civil engineering and hydrology, numerical models of snowmelt runoff use observations of insolation. This permits estimation of the rate at which water is released from a melting snowpack. Field measurement is accomplished using a pyranometer.| Conversion factor (multiply top row by factor to obtain side column) | |||||
|---|---|---|---|---|---|
| W/m2 | kW·h/(m2·day) | sun hours/day | kWh/(m2·y) | kWh/(kWp·y) | |
| W/m2 | 1 | 41.66666 | 41.66666 | 0.1140796 | 0.1521061 |
| kW·h/(m2·day) | 0.024 | 1 | 1 | 0.0027379 | 0.0036505 |
| sun hours/day | 0.024 | 1 | 1 | 0.0027379 | 0.0036505 |
| kWh/(m2·y) | 8.765813 | 365.2422 | 365.2422 | 1 | 1.333333 |
| kWh/(kWp·y) | 6.574360 | 273.9316 | 273.9316 | 0.75 | 1 |













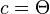



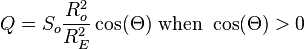


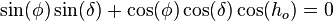


![\int_\pi^{-\pi}Q\,dh = S_o\frac{R_o^2}{R_E^2}\left[ h \sin(\phi)\sin(\delta) + \cos(\phi)\cos(\delta)\sin(h) \right]_{h=h_o}^{h=-h_o}](http://upload.wikimedia.org/math/3/d/b/3db3a6974d7cb587f2718193f2d01eb4.png)
![\int_\pi^{-\pi}Q\,dh = -2 S_o\frac{R_o^2}{R_E^2}\left[ h_o \sin(\phi) \sin(\delta) + \cos(\phi) \cos(\delta) \sin(h_o) \right]](http://upload.wikimedia.org/math/c/4/b/c4bd2db88c90b2016bc3e6b4e8fe4973.png)
![\overline{Q}^{\text{day}} = \frac{S_o}{\pi}\frac{R_o^2}{R_E^2}\left[ h_o \sin(\phi) \sin(\delta) + \cos(\phi) \cos(\delta) \sin(h_o) \right]](http://upload.wikimedia.org/math/2/7/9/2799e8169ccb6459545f50431db351b0.png)











 .
.


 which is a
which is a 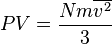 , we may combine it with the
, we may combine it with the 
 is the
is the  the
the  ,
, .
. . Then the temperature
. Then the temperature 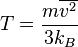



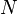 particles, the kinetic energy per degree of freedom per molecule is
particles, the kinetic energy per degree of freedom per molecule is