Newton's laws of motion

From Wikipedia, the free encyclopedia

Newton's laws of motion are three physical laws that, together, laid the foundation for classical mechanics. They describe the relationship between a body and the forces acting upon it, and its motion in response to those forces. More precisely, the first law defines the force qualitatively, the second law offers a quantitative measure of the force, and the third asserts that a single isolated force doesn't exist. These three laws have been expressed in several ways, over nearly three centuries, and can be summarised as follows:

---

First law:	In an inertial frame of reference, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a force.
Second law:	In an inertial reference frame, the vector sum of the forces F on an object is equal to the mass m of that object multiplied by the acceleration a of the object: F = ma. (It is assumed here that the mass m is constant – see below.)
Third law:	When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.

---

The three laws of motion were first compiled by Isaac Newton in his Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), first published in 1687. Newton used them to explain and investigate the motion of many physical objects and systems. For example, in the third volume of the text, Newton showed that these laws of motion, combined with his law of universal gravitation, explained Kepler's laws of planetary motion.

A fourth law is often also described in the bibliography, which states that forces add up like vectors, that is, that forces obey the principle of superposition.

Overview

Isaac Newton (1643–1727), the physicist who formulated the laws

Newton's laws are applied to objects which are idealised as single point masses, in the sense that the size and shape of the object's body are neglected to focus on its motion more easily. This can be done when the object is small compared to the distances involved in its analysis, or the deformation and rotation of the body are of no importance. In this way, even a planet can be idealised as a particle for analysis of its orbital motion around a star.

In their original form, Newton's laws of motion are not adequate to characterise the motion of rigid bodies and deformable bodies. Leonhard Euler in 1750 introduced a generalisation of Newton's laws of motion for rigid bodies called Euler's laws of motion, later applied as well for deformable bodies assumed as a continuum. If a body is represented as an assemblage of discrete particles, each governed by Newton's laws of motion, then Euler's laws can be derived from Newton's laws. Euler's laws can, however, be taken as axioms describing the laws of motion for extended bodies, independently of any particle structure.

Newton's laws hold only with respect to a certain set of frames of reference called Newtonian or inertial reference frames. Some authors interpret the first law as defining what an inertial reference frame is; from this point of view, the second law holds only when the observation is made from an inertial reference frame, and therefore the first law cannot be proved as a special case of the second. Other authors do treat the first law as a corollary of the second. The explicit concept of an inertial frame of reference was not developed until long after Newton's death.

In the given interpretation mass, acceleration, momentum, and (most importantly) force are assumed to be externally defined quantities. This is the most common, but not the only interpretation of the way one can consider the laws to be a definition of these quantities.

Newtonian mechanics has been superseded by special relativity, but it is still useful as an approximation when the speeds involved are much slower than the speed of light.

Laws

Newton's first law

The first law states that if the net force (the vector sum of all forces acting on an object) is zero, then the velocity of the object is constant. Velocity is a vector quantity which expresses both the object's speed and the direction of its motion; therefore, the statement that the object's velocity is constant is a statement that both its speed and the direction of its motion are constant.

The first law can be stated mathematically when the mass is a non-zero constant, as,

${\displaystyle \sum \mathbf {F} =0\;\Leftrightarrow \;{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}=0.}$

Consequently,

• An object that is at rest will stay at rest unless a force acts upon it.
• An object that is in motion will not change its velocity unless a force acts upon it.

This is known as uniform motion. An object continues to do whatever it happens to be doing unless a force is exerted upon it. If it is at rest, it continues in a state of rest (demonstrated when a tablecloth is skilfully whipped from under dishes on a tabletop and the dishes remain in their initial state of rest). If an object is moving, it continues to move without turning or changing its speed. This is evident in space probes that continuously move in outer space. Changes in motion must be imposed against the tendency of an object to retain its state of motion. In the absence of net forces, a moving object tends to move along a straight line path indefinitely.

Newton placed the first law of motion to establish frames of reference for which the other laws are applicable. The first law of motion postulates the existence of at least one frame of reference called a Newtonian or inertial reference frame, relative to which the motion of a particle not subject to forces is a straight line at a constant speed. Newton's first law is often referred to as the law of inertia. Thus, a condition necessary for the uniform motion of a particle relative to an inertial reference frame is that the total net force acting on it is zero. In this sense, the first law can be restated as:

In every material universe, the motion of a particle in a preferential reference frame Φ is determined by the action of forces whose total vanished for all times when and only when the velocity of the particle is constant in Φ. That is, a particle initially at rest or in uniform motion in the preferential frame Φ continues in that state unless compelled by forces to change it.

Newton's first and second laws are valid only in an inertial reference frame. Any reference frame that is in uniform motion with respect to an inertial frame is also an inertial frame, i.e. Galilean invariance or the principle of Newtonian relativity.

Newton's second law

The second law states that the rate of change of momentum of a body is directly proportional to the force applied, and this change in momentum takes place in the direction of the applied force.

${\displaystyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {\mathrm {d} (m\mathbf {v} )}{\mathrm {d} t}}.}$

The second law can also be stated in terms of an object's acceleration. Since Newton's second law is valid only for constant-mass systems, m can be taken outside the differentiation operator by the constant factor rule in differentiation. Thus,

${\displaystyle \mathbf {F} =m\,{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}=m\mathbf {a} ,}$

where F is the net force applied, m is the mass of the body, and a is the body's acceleration. Thus, the net force applied to a body produces a proportional acceleration. In other words, if a body is accelerating, then there is a force on it. An application of this notation is the derivation of G Subscript C.

Consistent with the first law, the time derivative of the momentum is non-zero when the momentum changes direction, even if there is no change in its magnitude; such is the case with uniform circular motion. The relationship also implies the conservation of momentum: when the net force on the body is zero, the momentum of the body is constant. Any net force is equal to the rate of change of the momentum.

Any mass that is gained or lost by the system will cause a change in momentum that is not the result of an external force. A different equation is necessary for variable-mass systems (see below).
Newton's second law is an approximation that is increasingly worse at high speeds because of relativistic effects.

Impulse

An impulse J occurs when a force F acts over an interval of time Δt, and it is given by

${\displaystyle \mathbf {J} =\int _{\Delta t}\mathbf {F} \,\mathrm {d} t.}$

Since force is the time derivative of momentum, it follows that

${\displaystyle \mathbf {J} =\Delta \mathbf {p} =m\Delta \mathbf {v} .}$

This relation between impulse and momentum is closer to Newton's wording of the second law.

Impulse is a concept frequently used in the analysis of collisions and impacts.

Variable-mass systems

Variable-mass systems, like a rocket burning fuel and ejecting spent gases, are not closed and cannot be directly treated by making mass a function of time in the second law;^[18] that is, the following formula is wrong:

${\displaystyle \mathbf {F} _{\mathrm {net} }={\frac {\mathrm {d} }{\mathrm {d} t}}{\big [}m(t)\mathbf {v} (t){\big ]}=m(t){\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}+\mathbf {v} (t){\frac {\mathrm {d} m}{\mathrm {d} t}}.\qquad \mathrm {(wrong)} }$

The falsehood of this formula can be seen by noting that it does not respect Galilean invariance: a variable-mass object with F = 0 in one frame will be seen to have F ≠ 0 in another frame. The correct equation of motion for a body whose mass m varies with time by either ejecting or accreting mass is obtained by applying the second law to the entire, constant-mass system consisting of the body and its ejected/accreted mass; the result is

${\displaystyle \mathbf {F} +\mathbf {u} {\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}}$

where u is the velocity of the escaping or incoming mass relative to the body. From this equation one can derive the equation of motion for a varying mass system, for example, the Tsiolkovsky rocket equation. Under some conventions, the quantity u dm/dt on the left-hand side, which represents the advection of momentum, is defined as a force (the force exerted on the body by the changing mass, such as rocket exhaust) and is included in the quantity F. Then, by substituting the definition of acceleration, the equation becomes F = ma.

Newton's third law

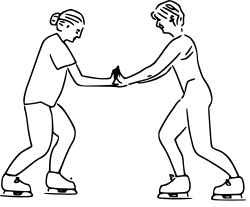
An illustration of Newton's third law in which two skaters push against each other. The first skater on the left exerts a normal force N₁₂ on the second skater directed towards the right, and the second skater exerts a normal force N₂₁ on the first skater directed towards the left.

The magnitudes of both forces are equal, but they have opposite directions, as dictated by Newton's third law.

The third law states that all forces between two objects exist in equal magnitude and opposite direction: if one object A exerts a force F_A on a second object B, then B simultaneously exerts a force F_B on A, and the two forces are equal in magnitude and opposite in direction: F_A = −F_B. The third law means that all forces are interactions between different bodies, or different regions within one body, and thus that there is no such thing as a force that is not accompanied by an equal and opposite force. In some situations, the magnitude and direction of the forces are determined entirely by one of the two bodies, say Body A; the force exerted by Body A on Body B is called the "action", and the force exerted by Body B on Body A is called the "reaction". This law is sometimes referred to as the action-reaction law, with F_A called the "action" and F_B the "reaction". In other situations the magnitude and directions of the forces are determined jointly by both bodies and it isn't necessary to identify one force as the "action" and the other as the "reaction". The action and the reaction are simultaneous, and it does not matter which is called the action and which is called reaction; both forces are part of a single interaction, and neither force exists without the other.

The two forces in Newton's third law are of the same type (e.g., if the road exerts a forward frictional force on an accelerating car's tires, then it is also a frictional force that Newton's third law predicts for the tires pushing backward on the road).

From a conceptual standpoint, Newton's third law is seen when a person walks: they push against the floor, and the floor pushes against the person. Similarly, the tires of a car push against the road while the road pushes back on the tires—the tires and road simultaneously push against each other. In swimming, a person interacts with the water, pushing the water backward, while the water simultaneously pushes the person forward—both the person and the water push against each other. The reaction forces account for the motion in these examples. These forces depend on friction; a person or car on ice, for example, may be unable to exert the action force to produce the needed reaction force.

History

Newton's First and Second laws, in Latin, from the original 1687 Principia Mathematica

Newton's 1st Law

From the original Latin of Newton's Principia:

“

Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.

”

Translated to English, this reads:

“

Law I: Every body persists in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by force impressed.

”

The ancient Greek philosopher Aristotle had the view that all objects have a natural place in the universe: that heavy objects (such as rocks) wanted to be at rest on the Earth and that light objects like smoke wanted to be at rest in the sky and the stars wanted to remain in the heavens. He thought that a body was in its natural state when it was at rest, and for the body to move in a straight line at a constant speed an external agent was needed continually to propel it, otherwise it would stop moving. Galileo Galilei, however, realised that a force is necessary to change the velocity of a body, i.e., acceleration, but no force is needed to maintain its velocity. In other words, Galileo stated that, in the absence of a force, a moving object will continue moving. (The tendency of objects to resist changes in motion was what Johannes Kepler had called inertia.) This insight was refined by Newton, who made it into his first law, also known as the "law of inertia"—no force means no acceleration, and hence the body will maintain its velocity. As Newton's first law is a restatement of the law of inertia which Galileo had already described, Newton appropriately gave credit to Galileo.

The law of inertia apparently occurred to several different natural philosophers and scientists independently, including Thomas Hobbes in his Leviathan. The 17th-century philosopher and mathematician René Descartes also formulated the law, although he did not perform any experiments to confirm it.

Newton's 2nd Law

Newton's original Latin reads:

“

Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.

”

This was translated quite closely in Motte's 1729 translation as:

“

Law II: The alteration of motion is ever proportional to the motive force impress'd; and is made in the direction of the right line in which that force is impress'd.

”

According to modern ideas of how Newton was using his terminology, this is understood, in modern terms, as an equivalent of:

The change of momentum of a body is proportional to the impulse impressed on the body, and happens along the straight line on which that impulse is impressed.

This may be expressed by the formula F = p', where p' is the time derivative of the momentum p. This equation can be seen clearly in the Wren Library of Trinity College, Cambridge, in a glass case in which Newton's manuscript is open to the relevant page.

Motte's 1729 translation of Newton's Latin continued with Newton's commentary on the second law of motion, reading:

If a force generates a motion, a double force will generate double the motion, a triple force triple the motion, whether that force be impressed altogether and at once, or gradually and successively. And this motion (being always directed the same way with the generating force), if the body moved before, is added to or subtracted from the former motion, according as they directly conspire with or are directly contrary to each other; or obliquely joined, when they are oblique, so as to produce a new motion compounded from the determination of both.

The sense or senses in which Newton used his terminology, and how he understood the second law and intended it to be understood, have been extensively discussed by historians of science, along with the relations between Newton's formulation and modern formulations.

Newton's 3rd Law

“

Lex III: Actioni contrariam semper et æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales et in partes contrarias dirigi.

”

Translated to English, this reads:

“

Law III: To every action there is always opposed an equal reaction: or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.

”

Newton's Scholium (explanatory comment) to this law:

Whatever draws or presses another is as much drawn or pressed by that other. If you press a stone with your finger, the finger is also pressed by the stone. If a horse draws a stone tied to a rope, the horse (if I may so say) will be equally drawn back towards the stone: for the distended rope, by the same endeavour to relax or unbend itself, will draw the horse as much towards the stone, as it does the stone towards the horse, and will obstruct the progress of the one as much as it advances that of the other. If a body impinges upon another, and by its force changes the motion of the other, that body also (because of the equality of the mutual pressure) will undergo an equal change, in its own motion, toward the contrary part. The changes made by these actions are equal, not in the velocities but in the motions of the bodies; that is to say, if the bodies are not hindered by any other impediments. For, as the motions are equally changed, the changes of the velocities made toward contrary parts are reciprocally proportional to the bodies. This law takes place also in attractions, as will be proved in the next scholium.

In the above, as usual, motion is Newton's name for momentum, hence his careful distinction between motion and velocity.

Newton used the third law to derive the law of conservation of momentum; from a deeper perspective, however, conservation of momentum is the more fundamental idea (derived via Noether's theorem from Galilean invariance), and holds in cases where Newton's third law appears to fail, for instance when force fields as well as particles carry momentum, and in quantum mechanics.

Importance and range of validity

Newton's laws were verified by experiment and observation for over 200 years, and they are excellent approximations at the scales and speeds of everyday life. Newton's laws of motion, together with his law of universal gravitation and the mathematical techniques of calculus, provided for the first time a unified quantitative explanation for a wide range of physical phenomena.

These three laws hold to a good approximation for macroscopic objects under everyday conditions. However, Newton's laws (combined with universal gravitation and classical electrodynamics) are inappropriate for use in certain circumstances, most notably at very small scales, very high speeds (in special relativity, the Lorentz factor must be included in the expression for momentum along with the rest mass and velocity) or very strong gravitational fields. Therefore, the laws cannot be used to explain phenomena such as conduction of electricity in a semiconductor, optical properties of substances, errors in non-relativistically corrected GPS systems and superconductivity. Explanation of these phenomena requires more sophisticated physical theories, including general relativity and quantum field theory.

In quantum mechanics, concepts such as force, momentum, and position are defined by linear operators that operate on the quantum state; at speeds that are much lower than the speed of light, Newton's laws are just as exact for these operators as they are for classical objects. At speeds comparable to the speed of light, the second law holds in the original form F = dp/dt, where F and p are four-vectors.

Relationship to the conservation laws

In modern physics, the laws of conservation of momentum, energy, and angular momentum are of more general validity than Newton's laws, since they apply to both light and matter, and to both classical and non-classical physics.

This can be stated simply, "Momentum, energy and angular momentum cannot be created or destroyed."

Because force is the time derivative of momentum, the concept of force is redundant and subordinate to the conservation of momentum, and is not used in fundamental theories (e.g., quantum mechanics, quantum electrodynamics, general relativity, etc.). The standard model explains in detail how the three fundamental forces known as gauge forces originate out of exchange by virtual particles. Other forces, such as gravity and fermionic degeneracy pressure, also arise from the momentum conservation. Indeed, the conservation of 4-momentum in inertial motion via curved space-time results in what we call gravitational force in general relativity theory. The application of the space derivative (which is a momentum operator in quantum mechanics) to the overlapping wave functions of a pair of fermions (particles with half-integer spin) results in shifts of maxima of compound wavefunction away from each other, which is observable as the "repulsion" of the fermions.

Newton stated the third law within a world-view that assumed instantaneous action at a distance between material particles. However, he was prepared for philosophical criticism of this action at a distance, and it was in this context that he stated the famous phrase "I feign no hypotheses". In modern physics, action at a distance has been completely eliminated, except for subtle effects involving quantum entanglement. (In particular, this refers to Bell's theorem – that no local model can reproduce the predictions of quantum theory.) Despite only being an approximation, in modern engineering and all practical applications involving the motion of vehicles and satellites, the concept of action at a distance is used extensively.

The discovery of the second law of thermodynamics by Carnot in the 19th century showed that not every physical quantity is conserved over time, thus disproving the validity of inducing the opposite metaphysical view from Newton's laws. Hence, a "steady-state" worldview based solely on Newton's laws and the conservation laws does not take entropy into account.

Newton's law of universal gravitation

From Wikipedia, the free encyclopedia

Newton's law of universal gravitation states that every particle attracts every other particle in the universe with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This is a general physical law derived from empirical observations by what Isaac Newton called inductive reasoning. It is a part of classical mechanics and was formulated in Newton's work Philosophiæ Naturalis Principia Mathematica ("the Principia"), first published on 5 July 1686. When Newton's book was presented in 1686 to the Royal Society, Robert Hooke made a claim that Newton had obtained the inverse square law from him.

In today's language, the law states that every point mass attracts every other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses, and inversely proportional to the square of the distance between them.

The equation for universal gravitation thus takes the form:

${\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}\ }$

where F is the gravitational force acting between two objects, m₁ and m₂ are the masses of the objects, r is the distance between the centers of their masses, and G is the gravitational constant.

The first test of Newton's theory of gravitation between masses in the laboratory was the Cavendish experiment conducted by the British scientist Henry Cavendish in 1798. It took place 111 years after the publication of Newton's Principia and approximately 71 years after his death.

Newton's law of gravitation resembles Coulomb's law of electrical forces, which is used to calculate the magnitude of the electrical force arising between two charged bodies. Both are inverse-square laws, where force is inversely proportional to the square of the distance between the bodies. Coulomb's law has the product of two charges in place of the product of the masses, and the electrostatic constant in place of the gravitational constant.

Newton's law has since been superseded by Albert Einstein's theory of general relativity, but it continues to be used as an excellent approximation of the effects of gravity in most applications. Relativity is required only when there is a need for extreme precision, or when dealing with very strong gravitational fields, such as those found near extremely massive and dense objects, or at very close distances (such as Mercury's orbit around the Sun).

History

Early history

The relation of the distance of objects in free fall to the square of the time taken had recently been confirmed by Grimaldi and Riccioli between 1640 and 1650. They had also made a calculation of the gravitational constant by recording the oscillations of a pendulum.

A modern assessment about the early history of the inverse square law is that "by the late 1670s", the assumption of an "inverse proportion between gravity and the square of distance was rather common and had been advanced by a number of different people for different reasons".^[5] The same author credits Robert Hooke with a significant and seminal contribution, but treats Hooke's claim of priority on the inverse square point as irrelevant, as several individuals besides Newton and Hooke had suggested it. He points instead to the idea of "compounding the celestial motions" and the conversion of Newton's thinking away from "centrifugal" and towards "centripetal" force as Hooke's significant contributions.

Newton gave credit in his Principia to two people: Bullialdus (who wrote without proof that there was a force on the Earth towards the Sun), and Borelli (who wrote that all planets were attracted towards the Sun). The main influence may have been Borelli, whose book Newton had a copy of.

Hooke's work and claims

Robert Hooke published his ideas about the "System of the World" in the 1660s, when he read to the Royal Society on March 21, 1666, a paper "concerning the inflection of a direct motion into a curve by a supervening attractive principle", and he published them again in somewhat developed form in 1674, as an addition to "An Attempt to Prove the Motion of the Earth from Observations". Hooke announced in 1674 that he planned to "explain a System of the World differing in many particulars from any yet known", based on three "Suppositions": that "all Celestial Bodies whatsoever, have an attraction or gravitating power towards their own Centers" and "they do also attract all the other Celestial Bodies that are within the sphere of their activity"; that "all bodies whatsoever that are put into a direct and simple motion, will so continue to move forward in a straight line, till they are by some other effectual powers deflected and bent..."; and that "these attractive powers are so much the more powerful in operating, by how much the nearer the body wrought upon is to their own Centers". Thus Hooke clearly postulated mutual attractions between the Sun and planets, in a way that increased with nearness to the attracting body, together with a principle of linear inertia.

Hooke's statements up to 1674 made no mention, however, that an inverse square law applies or might apply to these attractions. Hooke's gravitation was also not yet universal, though it approached universality more closely than previous hypotheses. He also did not provide accompanying evidence or mathematical demonstration. On the latter two aspects, Hooke himself stated in 1674: "Now what these several degrees [of attraction] are I have not yet experimentally verified"; and as to his whole proposal: "This I only hint at present", "having my self many other things in hand which I would first compleat, and therefore cannot so well attend it" (i.e. "prosecuting this Inquiry"). It was later on, in writing on 6 January 1679|80^[12] to Newton, that Hooke communicated his "supposition ... that the Attraction always is in a duplicate proportion to the Distance from the Center Reciprocall, and Consequently that the Velocity will be in a subduplicate proportion to the Attraction and Consequently as Kepler Supposes Reciprocall to the Distance." (The inference about the velocity was incorrect.)

Hooke's correspondence with Newton during 1679–1680 not only mentioned this inverse square supposition for the decline of attraction with increasing distance, but also, in Hooke's opening letter to Newton, of 24 November 1679, an approach of "compounding the celestial motions of the planets of a direct motion by the tangent & an attractive motion towards the central body".

Newton's work and claims

Newton, faced in May 1686 with Hooke's claim on the inverse square law, denied that Hooke was to be credited as author of the idea. Among the reasons, Newton recalled that the idea had been discussed with Sir Christopher Wren previous to Hooke's 1679 letter. Newton also pointed out and acknowledged prior work of others, including Bullialdus, (who suggested, but without demonstration, that there was an attractive force from the Sun in the inverse square proportion to the distance), and Borelli (who suggested, also without demonstration, that there was a centrifugal tendency in counterbalance with a gravitational attraction towards the Sun so as to make the planets move in ellipses). D T Whiteside has described the contribution to Newton's thinking that came from Borelli's book, a copy of which was in Newton's library at his death.

Newton further defended his work by saying that had he first heard of the inverse square proportion from Hooke, he would still have some rights to it in view of his demonstrations of its accuracy. Hooke, without evidence in favor of the supposition, could only guess that the inverse square law was approximately valid at great distances from the center. According to Newton, while the 'Principia' was still at pre-publication stage, there were so many a-priori reasons to doubt the accuracy of the inverse-square law (especially close to an attracting sphere) that "without my (Newton's) Demonstrations, to which Mr Hooke is yet a stranger, it cannot believed by a judicious Philosopher to be any where accurate."

This remark refers among other things to Newton's finding, supported by mathematical demonstration, that if the inverse square law applies to tiny particles, then even a large spherically symmetrical mass also attracts masses external to its surface, even close up, exactly as if all its own mass were concentrated at its center. Thus Newton gave a justification, otherwise lacking, for applying the inverse square law to large spherical planetary masses as if they were tiny particles. In addition, Newton had formulated, in Propositions 43-45 of Book 1 and associated sections of Book 3, a sensitive test of the accuracy of the inverse square law, in which he showed that only where the law of force is calculated as the inverse square of the distance will the directions of orientation of the planets' orbital ellipses stay constant as they are observed to do apart from small effects attributable to inter-planetary perturbations.

In regard to evidence that still survives of the earlier history, manuscripts written by Newton in the 1660s show that Newton himself had, by 1669, arrived at proofs that in a circular case of planetary motion, "endeavour to recede" (what was later called centrifugal force) had an inverse-square relation with distance from the center. After his 1679-1680 correspondence with Hooke, Newton adopted the language of inward or centripetal force. According to Newton scholar J. Bruce Brackenridge, although much has been made of the change in language and difference of point of view, as between centrifugal or centripetal forces, the actual computations and proofs remained the same either way. They also involved the combination of tangential and radial displacements, which Newton was making in the 1660s. The lesson offered by Hooke to Newton here, although significant, was one of perspective and did not change the analysis. This background shows there was basis for Newton to deny deriving the inverse square law from Hooke.

Newton's acknowledgment

On the other hand, Newton did accept and acknowledge, in all editions of the Principia, that Hooke (but not exclusively Hooke) had separately appreciated the inverse square law in the solar system. Newton acknowledged Wren, Hooke and Halley in this connection in the Scholium to Proposition 4 in Book 1. Newton also acknowledged to Halley that his correspondence with Hooke in 1679-80 had reawakened his dormant interest in astronomical matters, but that did not mean, according to Newton, that Hooke had told Newton anything new or original: "yet am I not beholden to him for any light into that business but only for the diversion he gave me from my other studies to think on these things & for his dogmaticalness in writing as if he had found the motion in the Ellipsis, which inclined me to try it ..."

Modern priority controversy

Since the time of Newton and Hooke, scholarly discussion has also touched on the question of whether Hooke's 1679 mention of 'compounding the motions' provided Newton with something new and valuable, even though that was not a claim actually voiced by Hooke at the time. As described above, Newton's manuscripts of the 1660s do show him actually combining tangential motion with the effects of radially directed force or endeavour, for example in his derivation of the inverse square relation for the circular case. They also show Newton clearly expressing the concept of linear inertia—for which he was indebted to Descartes' work, published in 1644 (as Hooke probably was). These matters do not appear to have been learned by Newton from Hooke.

Nevertheless, a number of authors have had more to say about what Newton gained from Hooke and some aspects remain controversial. The fact that most of Hooke's private papers had been destroyed or have disappeared does not help to establish the truth.

Newton's role in relation to the inverse square law was not as it has sometimes been represented. He did not claim to think it up as a bare idea. What Newton did was to show how the inverse-square law of attraction had many necessary mathematical connections with observable features of the motions of bodies in the solar system; and that they were related in such a way that the observational evidence and the mathematical demonstrations, taken together, gave reason to believe that the inverse square law was not just approximately true but exactly true (to the accuracy achievable in Newton's time and for about two centuries afterwards – and with some loose ends of points that could not yet be certainly examined, where the implications of the theory had not yet been adequately identified or calculated).

Plagiarism dispute

In 1686, when the first book of Newton's Principia was presented to the Royal Society, Robert Hooke accused Newton of plagiarism by claiming that he had taken from him the "notion" of "the rule of the decrease of Gravity, being reciprocally as the squares of the distances from the Center". At the same time (according to Edmond Halley's contemporary report) Hooke agreed that "the Demonstration of the Curves generated thereby" was wholly Newton's.

In this way, the question arose as to what, if anything, Newton owed to Hooke. This is a subject extensively discussed since that time and on which some points, outlined below, continue to excite controversy.

About thirty years after Newton's death in 1727, Alexis Clairaut, a mathematical astronomer eminent in his own right in the field of gravitational studies, wrote after reviewing what Hooke published, that "One must not think that this idea ... of Hooke diminishes Newton's glory"; and that "the example of Hooke" serves "to show what a distance there is between a truth that is glimpsed and a truth that is demonstrated".

Modern form

In modern language, the law states the following:

Every point mass attracts every single other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them:
${\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}\ }$ where: F is the force between the masses; G is the gravitational constant (6.674×10−11 N · (m/kg)2); m1 is the first mass; m2 is the second mass; r is the distance between the centers of the masses.

Error plot showing experimental values for big G.

Assuming SI units, F is measured in newtons (N), m₁ and m₂ in kilograms (kg), r in meters (m), and the constant G is approximately equal to 6.674×10⁻¹¹ N m² kg⁻². The value of the constant G was first accurately determined from the results of the Cavendish experiment conducted by the British scientist Henry Cavendish in 1798, although Cavendish did not himself calculate a numerical value for G. This experiment was also the first test of Newton's theory of gravitation between masses in the laboratory. It took place 111 years after the publication of Newton's Principia and 71 years after Newton's death, so none of Newton's calculations could use the value of G; instead he could only calculate a force relative to another force.

Bodies with spatial extent

Gravitational field strength within the Earth

Gravity field near the surface of the Earth – an object is shown accelerating toward the surface

If the bodies in question have spatial extent (as opposed to being point masses), then the gravitational force between them is calculated by summing the contributions of the notional point masses which constitute the bodies. In the limit, as the component point masses become "infinitely small", this entails integrating the force (in vector form, see below) over the extents of the two bodies.

In this way, it can be shown that an object with a spherically-symmetric distribution of mass exerts the same gravitational attraction on external bodies as if all the object's mass were concentrated at a point at its centre. (This is not generally true for non-spherically-symmetrical bodies.)

For points inside a spherically-symmetric distribution of matter, Newton's Shell theorem can be used to find the gravitational force. The theorem tells us how different parts of the mass distribution affect the gravitational force measured at a point located a distance r₀ from the center of the mass distribution:

• The portion of the mass that is located at radii r < r₀ causes the same force at r₀ as if all of the mass enclosed within a sphere of radius r₀ was concentrated at the center of the mass distribution (as noted above).
• The portion of the mass that is located at radii r > r₀ exerts no net gravitational force at the distance r₀ from the center. That is, the individual gravitational forces exerted by the elements of the sphere out there, on the point at r₀, cancel each other out.

As a consequence, for example, within a shell of uniform thickness and density there is no net gravitational acceleration anywhere within the hollow sphere.

Furthermore, inside a uniform sphere the gravity increases linearly with the distance from the center; the increase due to the additional mass is 1.5 times the decrease due to the larger distance from the center. Thus, if a spherically symmetric body has a uniform core and a uniform mantle with a density that is less than 2/3 of that of the core, then the gravity initially decreases outwardly beyond the boundary, and if the sphere is large enough, further outward the gravity increases again, and eventually it exceeds the gravity at the core/mantle boundary. The gravity of the Earth may be highest at the core/mantle boundary.

Vector form

Gravity field surrounding Earth from a macroscopic perspective.

Newton's law of universal gravitation can be written as a vector equation to account for the direction of the gravitational force as well as its magnitude. In this formula, quantities in bold represent vectors.

${\displaystyle \mathbf {F} _{21}=-G{m_{1}m_{2} \over {\vert \mathbf {r} _{12}\vert }^{2}}\,\mathbf {\hat {r}} _{12}}$

where

F₂₁ is the force applied on object 2 exerted by object 1,

G is the gravitational constant,

m₁ and m₂ are respectively the masses of objects 1 and 2,

|r₁₂| = |r₂ − r₁| is the distance between objects 1 and 2, and

${\displaystyle \mathbf {\hat {r}} _{12}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathbf {r} _{2}-\mathbf {r} _{1}}{\vert \mathbf {r} _{2}-\mathbf {r} _{1}\vert }}}$ is the unit vector from object 1 to 2.

It can be seen that the vector form of the equation is the same as the scalar form given earlier, except that F is now a vector quantity, and the right hand side is multiplied by the appropriate unit vector. Also, it can be seen that F₁₂ = −F₂₁.

Gravitational field

The gravitational field is a vector field that describes the gravitational force which would be applied on an object in any given point in space, per unit mass. It is actually equal to the gravitational acceleration at that point.

It is a generalisation of the vector form, which becomes particularly useful if more than 2 objects are involved (such as a rocket between the Earth and the Moon). For 2 objects (e.g. object 2 is a rocket, object 1 the Earth), we simply write r instead of r₁₂ and m instead of m₂ and define the gravitational field g(r) as:

${\displaystyle \mathbf {g} (\mathbf {r} )=-G{m_{1} \over {{\vert \mathbf {r} \vert }^{2}}}\,\mathbf {\hat {r}} }$

so that we can write:

${\displaystyle \mathbf {F} (\mathbf {r} )=m\mathbf {g} (\mathbf {r} ).}$

This formulation is dependent on the objects causing the field. The field has units of acceleration; in SI, this is m/s².

Gravitational fields are also conservative; that is, the work done by gravity from one position to another is path-independent. This has the consequence that there exists a gravitational potential field V(r) such that

${\displaystyle \mathbf {g} (\mathbf {r} )=-\nabla V(\mathbf {r} ).}$

If m₁ is a point mass or the mass of a sphere with homogeneous mass distribution, the force field g(r) outside the sphere is isotropic, i.e., depends only on the distance r from the center of the sphere. In that case

${\displaystyle V(r)=-G{\frac {m_{1}}{r}}.}$

the gravitational field is on, inside and outside of symmetric masses.

As per Gauss Law, field in a symmetric body can be found by the mathematical equation:

${\displaystyle \partial V}$ ${\displaystyle \mathbf {g(r)} \cdot d\mathbf {A} =-4\pi GM_{\text{enc}},}$

where ${\displaystyle \partial V}$ is a closed surface and ${\displaystyle M_{\text{enc}}}$ is the mass enclosed by the surface.

Hence, for a hollow sphere of radius ${\displaystyle R}$ and total mass ${\displaystyle M}$,

${\displaystyle |\mathbf {g(r)} |={\begin{cases}0,&{\mbox{if }}r$

For a uniform solid sphere of radius ${\displaystyle R}$ and total mass ${\displaystyle M}$,

${\displaystyle |\mathbf {g(r)} |={\begin{cases}{\dfrac {GMr}{R^{3}}},&{\mbox{if }}r$

Problematic aspects

Newton's description of gravity is sufficiently accurate for many practical purposes and is therefore widely used. Deviations from it are small when the dimensionless quantities φ/c² and (v/c)² are both much less than one, where φ is the gravitational potential, v is the velocity of the objects being studied, and c is the speed of light. For example, Newtonian gravity provides an accurate description of the Earth/Sun system, since

${\displaystyle {\frac {\Phi }{c^{2}}}={\frac {GM_{\mathrm {sun} }}{r_{\mathrm {orbit} }c^{2}}}\sim 10^{-8},\quad \left({\frac {v_{\mathrm {Earth} }}{c}}\right)^{2}=\left({\frac {2\pi r_{\mathrm {orbit} }}{(1\ \mathrm {yr} )c}}\right)^{2}\sim 10^{-8}}$

where r_orbit is the radius of the Earth's orbit around the Sun.

In situations where either dimensionless parameter is large, then general relativity must be used to describe the system. General relativity reduces to Newtonian gravity in the limit of small potential and low velocities, so Newton's law of gravitation is often said to be the low-gravity limit of general relativity.

Theoretical concerns with Newton's expression

• There is no immediate prospect of identifying the mediator of gravity. Attempts by physicists to identify the relationship between the gravitational force and other known fundamental forces are not yet resolved, although considerable headway has been made over the last 50 years (See: Theory of everything and Standard Model). Newton himself felt that the concept of an inexplicable action at a distance was unsatisfactory (see "Newton's reservations" below), but that there was nothing more that he could do at the time.
• Newton's theory of gravitation requires that the gravitational force be transmitted instantaneously. Given the classical assumptions of the nature of space and time before the development of General Relativity, a significant propagation delay in gravity leads to unstable planetary and stellar orbits.

Observations conflicting with Newton's formula

• Newton's Theory does not fully explain the precession of the perihelion of the orbits of the planets, especially of planet Mercury, which was detected long after the life of Newton. There is a 43 arcsecond per century discrepancy between the Newtonian calculation, which arises only from the gravitational attractions from the other planets, and the observed precession, made with advanced telescopes during the 19th century.
• The predicted angular deflection of light rays by gravity that is calculated by using Newton's Theory is only one-half of the deflection that is actually observed by astronomers. Calculations using General Relativity are in much closer agreement with the astronomical observations.
• In spiral galaxies, the orbiting of stars around their centers seems to strongly disobey Newton's law of universal gravitation. Astrophysicists, however, explain this spectacular phenomenon in the framework of Newton's laws, with the presence of large amounts of dark matter.

Newton's reservations

While Newton was able to formulate his law of gravity in his monumental work, he was deeply uncomfortable with the notion of "action at a distance" that his equations implied. In 1692, in his third letter to Bentley, he wrote: "That one body may act upon another at a distance through a vacuum without the mediation of anything else, by and through which their action and force may be conveyed from one another, is to me so great an absurdity that, I believe, no man who has in philosophic matters a competent faculty of thinking could ever fall into it."
 
He never, in his words, "assigned the cause of this power". In all other cases, he used the phenomenon of motion to explain the origin of various forces acting on bodies, but in the case of gravity, he was unable to experimentally identify the motion that produces the force of gravity (although he invented two mechanical hypotheses in 1675 and 1717). Moreover, he refused to even offer a hypothesis as to the cause of this force on grounds that to do so was contrary to sound science. He lamented that "philosophers have hitherto attempted the search of nature in vain" for the source of the gravitational force, as he was convinced "by many reasons" that there were "causes hitherto unknown" that were fundamental to all the "phenomena of nature". These fundamental phenomena are still under investigation and, though hypotheses abound, the definitive answer has yet to be found. And in Newton's 1713 General Scholium in the second edition of Principia: "I have not yet been able to discover the cause of these properties of gravity from phenomena and I feign no hypotheses.... It is enough that gravity does really exist and acts according to the laws I have explained, and that it abundantly serves to account for all the motions of celestial bodies."

Einstein's solution

These objections were explained by Einstein's theory of general relativity, in which gravitation is an attribute of curved spacetime instead of being due to a force propagated between bodies. In Einstein's theory, energy and momentum distort spacetime in their vicinity, and other particles move in trajectories determined by the geometry of spacetime. This allowed a description of the motions of light and mass that was consistent with all available observations. In general relativity, the gravitational force is a fictitious force due to the curvature of spacetime, because the gravitational acceleration of a body in free fall is due to its world line being a geodesic of spacetime.

Extensions

Newton was the first to consider in his Principia an extended expression of his law of gravity including an inverse-cube term of the form

${\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}+B{\frac {m_{1}m_{2}}{r^{3}}}\ }$, ${\displaystyle B}$ a constant

attempting to explain the Moon's apsidal motion. Other extensions were proposed by Laplace (around 1790) and Decombes (1913):

${\displaystyle F(r)=k{\frac {m_{1}m_{2}}{r^{2}}}\exp(-\alpha r)}$ (Laplace)

${\displaystyle F(r)=k{\frac {m_{1}m_{2}}{r^{2}}}\left(1+{\alpha \over {r^{3}}}\right)}$ (Decombes)

In recent years, quests for non-inverse square terms in the law of gravity have been carried out by neutron interferometry.

Solutions of Newton's law of universal gravitation

The n-body problem is an ancient, classical problem of predicting the individual motions of a group of celestial objects interacting with each other gravitationally. Solving this problem — from the time of the Greeks and on — has been motivated by the desire to understand the motions of the Sun, planets and the visible stars. In the 20th century, understanding the dynamics of globular cluster star systems became an important n-body problem too. The n-body problem in general relativity is considerably more difficult to solve.

The classical physical problem can be informally stated as: given the quasi-steady orbital properties (instantaneous position, velocity and time) of a group of celestial bodies, predict their interactive forces; and consequently, predict their true orbital motions for all future times.

The two-body problem has been completely solved, as has the restricted three-body problem.