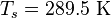From Wikipedia, the free encyclopedia
"The current prediction for Sunspot Cycle 24 gives a smoothed sunspot number maximum of about 69 in the late Summer of 2013. The smoothed sunspot number reached 68.9 in August 2013 so the official maximum will be at least this high. The smoothed sunspot number has been rising again towards this second peak over the last five months and has now surpassed the level of the first peak (66.9 in February 2012). Many cycles are double peaked but this is the first in which the second peak in sunspot number was larger than the first. We are currently over five years into Cycle 24. The current predicted and observed size makes this the smallest sunspot cycle since Cycle 14 which had a maximum of 64.2 in February of 1906."[1] The monthly sunspot number was still rising as of March 2014.[2]
They have been observed (by changes in the sun's appearance and by changes seen on Earth, such as auroras) for centuries.
The changes on the sun cause effects in space, in the atmosphere, and on Earth's surface. While it is the dominant variable in solar activity, aperiodic fluctuations also occur.
Definition
Solar cycles have an average duration of about 11 years. Solar maximum and solar minimum refer respectively to periods of maximum and minimum sunspot counts. Cycles span from one minimum to the next.Observational history
The solar cycle was discovered in 1843 by Samuel Heinrich Schwabe, who after 17 years of observations noticed a periodic variation in the average number of sunspots.[3] Rudolf Wolf compiled and studied these and other observations, reconstructing the cycle back to 1745, eventually pushing these reconstructions to the earliest observations of sunspots by Galileo and contemporaries in the early seventeenth century.
Following Wolf's numbering scheme, the 1755–1766 cycle is traditionally numbered "1". Wolf created a standard sunspot number index, the Wolf index, which continues to be used today.
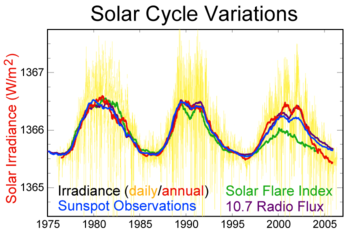
The period between 1645 and 1715, a time of few sunspots,[4] is known as the Maunder minimum, after Edward Walter Maunder, who extensively researched this peculiar event, first noted by Gustav Spörer.
In the second half of the nineteenth century Richard Carrington and by Spörer independently noted the phenomena of sunspots appearing at different latitudes at different parts of the cycle.
The cycle's physical basis was elucidated by Hale and collaborators, who in 1908 showed that sunspots were strongly magnetized (the first detection of magnetic fields beyond the Earth). In 1919 they showed that the magnetic polarity of sunspot pairs:
- Is constant throughout a cycle;
- Is opposite across the equator throughout a cycle;
- Reverses itself from one cycle to the next.
In 1961 the father-and-son team of Harold and Horace Babcock established that the solar cycle is a spatiotemporal magnetic process unfolding over the Sun as a whole. They observed that the solar surface is magnetized outside of sunspots; that this (weaker) magnetic field is to first order a dipole; and that this dipole undergoes polarity reversals with the same period as the sunspot cycle. Horace's Babcock model described the Sun's oscillatory magnetic field, with a quasi-steady periodicity of 22 years.[2] [3] It covered the oscillatory exchange of energy between poloidal and toroidal solar magnetic field ingredients. The two halves of the 22-year cycle are not identical, typically alternating cycles show higher (lower) sunspot counts (the "Gnevyshev–Ohl Rule."[5])
Cycle history
Sunspot numbers over the past 11,400 years have been reconstructed using Carbon-14-based dendroclimatology. The level of solar activity beginning in the 1940s is exceptional – the last period of similar magnitude occurred around 9,000 years ago (during the warm Boreal period).[6][7][8] The Sun was at a similarly high level of magnetic activity for only ~10% of the past 11,400 years. Almost all earlier high-activity periods were shorter than the present episode.[7]
| Event | Start | End |
|---|---|---|
| Homeric minimum[9] | 950BC | 800BC |
| Oort minimum | 1040 | 1080 |
| Medieval maximum | 1100 | 1250 |
| Wolf minimum | 1280 | 1350 |
| Spörer Minimum | 1450 | 1550 |
| Maunder Minimum | 1645 | 1715 |
| Dalton Minimum | 1790 | 1820 |
| Modern Maximum | 1900 | present |
A list of historical Grand minima of solar activity[6] came around 690 AD, 360 BC, 770 BC, 1390 BC, 2860 BC, 3340 BC, 3500 BC, 3630 BC, 3940 BC, 4230 BC, 4330 BC, 5260 BC, 5460 BC, 5620 BC, 5710 BC, 5990 BC, 6220 BC, 6400 BC, 7040 BC, 7310 BC, 7520 BC, 8220 BC and 9170 BC. Since observations began, cycles have ranged from 9–14 years. Significant amplitude variations also occur.
It was first thought that 28 cycles had spanned the 309 years between 1699 and 2008, giving an average length of 11.04 years, but recent research has showed that the longest of these (1784–1799) seems actually to have been two cycles,[10][11] meaning that one of the two had to have lasted less than 8 years.
Recent cycles
Cycle 24
The current solar cycle began on January 4, 2008, with minimal activity until early 2010.[12][13] It is on track to have the lowest recorded sunspot activity since accurate records began in 1750. The cycle featured a "double-peaked" solar maximum. The first peak was reached 99 in 2011 and the second in early 2014 at 101.[14]Cycle 23
This cycle lasted 11.6 years, beginning in May 1996 and ending in January 2008. The maximum smoothed sunspot number (monthly number of sunspots averaged over a twelve-month period) observed during the solar cycle was 120.8 (March 2000), and the minimum was 1.7.[15] A total of 805 days had no sunspots during this cycle.[16][17][18]Phenomena
Various solar phenomena follow the solar cycle, including sunspots and coronal mass ejections.Sunspots
The best information today comes from SOHO (a cooperative project of the European Space Agency and NASA), such as the MDI magnetogram, where the solar "surface" magnetic field can be seen.
As each cycle begins, sunspots appear at mid-latitudes, and then closer and closer to the equator until solar minimum is reached. This pattern is best visualized in the form of the so-called butterfly diagram. Images of the Sun are divided into latitudinal strips, and the monthly-averaged fractional surface of sunspots calculated. This is plotted vertically as a color-coded bar, and the process is repeated month after month to produce this time-series diagram. As there are peaks in sunspot number around 1955–58, James T. Struck argued for a Struck Maximum, given his discovery of the peak at this point, like Maunder and Dalton's work.[citation needed]
While magnetic field changes are concentrated at sunspots, the entire sun undergoes analogous changes, albeit of smaller magnitude.

Time vs. solar latitude diagram of the radial component of the solar magnetic field, averaged over successive solar rotation. The "butterfly" signature of sunspots is clearly visible at low latitudes. Diagram constructed (and regularly updated) by the solar group at NASA Marshall Space Flight Center.
Coronal mass ejection
The solar magnetic field structures the corona, giving it its characteristic shape visible at times of solar eclipses. Complex coronal magnetic field structures evolve in response to fluid motions at the solar surface, and emergence of magnetic flux produced by dynamo action in the solar interior. For reasons not yet understood in detail, sometimes these structures lose stability, leading to coronal mass ejections into interplanetary space, or flares, caused by sudden localized release of magnetic energy driving emission of ultraviolet and X-ray radiation as well as energetic particles. These eruptive phenomena can have a significant impact on Earth's upper atmosphere and space environment, and are the primary drivers of what is now called space weather.The occurrence frequency of coronal mass ejections and flares is strongly modulated by the cycle. Flares of any given size are some 50 times more frequent at solar maximum than at minimum. Large coronal mass ejections occur on average a few times a day at solar maximum, down to one every few days at solar minimum. The size of these events themselves does not depend sensitively on the phase of the solar cycle. A case in point are the three large X-class flares that occurred in December 2006, very near solar minimum; an X9.0 flare on Dec 5 stands as one of the brightest on record.[21]
Patterns

An overview of three solar cycles shows the relationship between the sunspot cycle, galactic cosmic rays, and the state of our near-space environment.[22]
The Waldmeier effect names the observation that cycles with larger maximum amplitudes tend to take less time to reach their maxima than cycles with smaller amplitudes;[23] maximum amplitudes are negatively correlated to the lengths of earlier cycles, aiding prediction.[24]
Solar maxima and minima also exhibit fluctuations at time scales greater than solar cycles. Increasing and decreasing trends can continue for periods of a century or more.
The 87 year (70–100 year Gleissberg cycle, named after Wolfgang Gleißberg, is thought to be an amplitude modulation of the Schwabe Cycle,[5][25][26] The Gleisberg cycle implied that the next solar cycle have a maximum smoothed sunspot number of about 145±30 in 2010 (instead 2010 was just after the cycle's solar minimum) and that the following cycle have a maximum of about 70±30 in 2023.[27]
Associated centennial variations in magnetic fields in the Corona and Heliosphere have been detected using Carbon-14 and beryllium-10 cosmogenic isotopes stored in terrestrial reservoirs such as ice sheets and tree rings[28] and by using historic observations of Geomagnetic storm activity, which bridge the time gap between the end of the usable cosmogenic isotope data and the start of modern satellite data.[29]
These variations have been successfully reproduced using models that employ magnetic flux continuity equations and observed sunspot numbers to quantify the emergence of magnetic flux from the top of the solar atmosphere and into the Heliosphere,[30] showing that sunspot observations, geomagnetic activity and cosmogenic isotopes offer a convergent understanding of solar activity variations.
Hypothesized cycles
Periodicity of solar activity with periods longer than the sunspot cycle has been proposed,[5] including:The 210 year Suess cycle (a.k.a. "de Vries cycle").[26] This cycle is recorded from radiocarbon studies, although "little evidence of the Suess Cycle" appears in the 400-year sunspot record.[5])
The Hallstatt cycle is hypothesized to extend for approximately 2,300 years.[31][32]
An as yet unnamed cycle may extend over 6,000 years.[33]
In carbon-14 cycles of 105, 131, 232, 385, 504, 805 and 2,241 years have been observed, possibly matching cycles derived from other sources.[34] Damon and Sonett[35] proposed carbon 14-based medium- and short-term variations of periods 208 and 88 years; as well as suggesting a 2300-year radiocarbon period that modulates the 208-year period.[36]
During the Upper Permian 240 million years ago, mineral layers created in the Castile Formation show cycles of 2,500 years.[citation needed]
Solar magnetic field
The Sun's magnetic field structures its atmosphere and outer layers all the way through the corona and into the solar wind. Its spatiotemporal variations lead to various measurable solar phenomena. Other solar phenomena are closely related to the cycle, which serves as the energy source and dynamical engine for the former.Effects
Solar
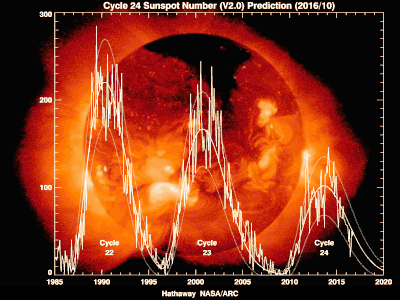
Activity cycles 21, 22 and 23 seen in sunspot number index, TSI, 10.7cm radio flux, and flare index. The vertical scales for each quantity have been adjusted to permit overplotting on the same vertical axis as TSI. Temporal variations of all quantities are tightly locked in phase, but the degree of correlation in amplitudes is variable to some degree.
Surface magnetism
Sunspots eventually decay, releasing magnetic flux in the photosphere. This flux is dispersed and churned by turbulent convection and solar large-scale flows. These transport mechanisms lead to the accumulation of magnetized decay products at high solar latitudes, eventually reversing the polarity of the polar fields (notice how the blue and yellow fields reverse in the Hathaway/NASA/MSFC graph above).The dipolar component of the solar magnetic field reverses polarity around the time of solar maximum and reaches peak strength at the solar minimum.
Space
Spacecraft
CMEs (coronal mass ejections) produce a radiation flux of high-energy protons, sometimes known as solar cosmic rays. These can cause radiation damage to electronics and solar cells in satellites. Solar proton events also can cause single-event upset (SEU) events on electronics; at the same, the reduced flux of galactic cosmic radiation during solar maximum decreases the high-energy component of particle flux.CME radiation is dangerous to astronauts on a space mission who are outside the shielding produced by the Earth's magnetic field. Future mission designs (e.g., for a Mars Mission) therefore incorporate a radiation-shielded "storm shelter" for astronauts to retreat to during such an event.
Gleißberg developed a CME forecasting method that relies on consecutive cycles.[37]
On the positive side, the increased irradiance during solar maximum expands the envelope of the Earth's atmosphere, causing low-orbiting space debris to re-enter more quickly.
Galactic cosmic ray flux
The outward expansion of solar ejecta into interplanetary space provides overdensities of plasma that are efficient at scattering high-energy cosmic rays entering the solar system from elsewhere in the galaxy. The frequency of solar eruptive events is modulated by the cycle, changing the degree of cosmic ray scattering in the outer solar system accordingly. As a consequence, the cosmic ray flux in the inner solar system is anticorrelated with the overall level of solar activity. This anticorrelation is clearly detected in cosmic ray flux measurements at the Earth's surface. The effect amounts to several percent variation over the solar cycle, greater than the typically 0.1% variation in total solar irradiance.[38][39]Some high-energy cosmic rays entering Earth's atmosphere collide hard enough with molecular atmospheric constituents to cause occasionally nuclear spallation reactions. Fission products include radionuclides such as 14C and 10Be that settle on the Earth's surface. Their concentration can be measured in ice cores, allowing a reconstruction of solar activity levels into the distant past.[40] Such reconstructions indicate that the overall level of solar activity since the middle of the twentieth century stands amongst the highest of the past 10,000 years, and that epochs of suppressed activity, of varying durations have occurred repeatedly over that time span.
Atmospheric
Solar irradiance
The total solar irradiance (TSI) is the amount of solar radiative energy incident on the Earth's upper atmosphere. TSI variations were undetectable until satellite observations began in late 1978. A series of radiometers were launched on satellites from the 1970s to the 2000s.[41] TSI measurements varied from 1360 to 1370 W/m2 across ten satellites. One of the satellites, the ACRIMSAT was launched by the ACRIM group. The controversial 1989-1991 "ACRIM gap" between non-overlapping satellites was interpolated by an ACRIM composite showing +0.037%/decade rise. Another series based on ACRIM data is produced by the PMOD group. Its series shows a -0.008%/decade downward trend.[42] This 0.045%/decade difference impacts climate models.Solar irradiance varies systematically over the cycle,[43] both in total irradiance and in its relative components (UV vs visible and other frequencies). The solar luminosity is an estimated 0.07 percent brighter during the mid-cycle solar maximum than the terminal solar minimum. Photospheric magnetism appears to be the primary cause (96%) of 1996-2013 TSI variation.[44] The ratio of ultraviolet to visible light varies.[45]
TSI varies in phase with the solar magnetic activity cycle[46] with an amplitude of about 0.1% around an average value of about 1361.5 W/m2[47] (the "solar constant"). Variations about the average of up to −0.3% are caused by large sunspot groups and of +0.05% by large faculae and the bright network on a 7-10-day timescale[48] (see TSI variation graphics).[49] Satellite-era TSI variations show small but detectable trends.[50][51]
TSI is higher at solar maximum, even though sunspots are darker (cooler) than the average photosphere. This is caused by magnetized structures other than sunspots during solar maxima, such as faculae and active elements of the "bright" network, that are brighter (hotter) than the average photosphere. They collectively overcompensate for the irradiance deficit associated with the cooler, but less numerous sunspots. The primary driver of TSI changes on solar rotational and sunspot cycle timescales is the varying photospheric coverage of these radiatively active solar magnetic structures.[citation needed]
Energy changes in UV irradiance involved in production and loss of ozone have atmospheric effects. The 30 HPa Atmospheric pressure level changed height in phase with solar activity during solar cycles 20-23. UV irradiance increase caused higher ozone production, leading to stratospheric heating and to poleward displacements in the stratospheric and tropospheric wind systems.[52]
Short-wavelength radiation
With a temperature of 5870 K, the photosphere emits a proportion of radiation in the extreme ultraviolet (EUV) and above. However, hotter upper layers of the Sun's atmosphere (chromosphere and corona) emit more short-wavelength radiation. Since the upper atmosphere is not homogeneous and contains significant magnetic structure, the solar ultraviolet (UV), EUV and X-ray flux varies markedly over the cycle.
The photo montage to the left illustrates this variation for soft X-ray, as observed by the Japanese satellite Yohkoh from after August 30, 1991, at the peak of cycle 22, to September 6, 2001, at the peak of cycle 23. Similar cycle-related variations are observed in the flux of solar UV or EUV radiation, as observed, for example, by the SOHO or TRACE satellites.
Even though it only accounts for a minuscule fraction of total solar radiation, the impact of solar UV, EUV and X-ray radiation on the Earth's upper atmosphere is profound. Solar UV flux is a major driver of stratospheric chemistry, and increases in ionizing radiation significantly affect ionosphere-influenced temperature and electrical conductivity.
Solar radio flux
Emission from the Sun at centimetric (radio) wavelength is due primarily to coronal plasma trapped in the magnetic fields overlying active regions.[53] The F10.7 index is a measure of the solar radio flux per unit frequency at a wavelength of 10.7 cm, near the peak of the observed solar radio emission. F10.7 is often expressed in SFU or solar flux units (1 SFU = 10−22 W m−2 Hz−1). It represents a measure of diffuse, nonradiative coronal plasma heating. It is an excellent indicator of overall solar activity levels and correlates well with solar UV emissions.Sunspot activity has a major effect on long distance radio communications, particularly on the shortwave bands although medium wave and low VHF frequencies are also affected. High levels of sunspot activity lead to improved signal propagation on higher frequency bands, although they also increase the levels of solar noise and ionospheric disturbances. These effects are caused by impact of the increased level of solar radiation on the ionosphere.
10.7 cm solar flux could interfere with point-to-point terrestrial communications.[54]
Clouds
The cosmic ray changes over the cycle potentially have significant atmospheric effects. Speculations about cosmic rays include:- Changes in ionization affect the aerosol abundance that serves as the condensation nucleus for cloud formation.[55] During solar minima more cosmic rays reach Earth, potentially creating ultra-small aerosol particles as precursors to Cloud condensation nuclei.[56] Clouds formed from greater amounts of condensation nuclei are brighter, longer lived and likely to produce less precipitation.
- A change in cosmic rays could cause an increase in certain types of clouds, affecting Earth's albedo.[citation needed]
- Particularly at high latitudes, with less shielding from Earth's magnetic field, cosmic ray variation may impact terrestrial low altitude cloud cover (unlike a lack of correlation with high altitude clouds), partially influenced by the solar-driven interplanetary magnetic field (as well as passage through the galactic arms over longer timeframes).[38][39][57][58] A 2002 paper rejected this hypothesis.[59]
Terrestrial
Organisms
The impact of the solar cycle on living organisms has been investigated (see chronobiology). Some researchers claim to have found connections with human health.[64][65]The amount of ultraviolet UVB light at 300 nm reaching the Earth varies by as much as 400% over the solar cycle due to variations in the protective ozone layer. In the stratosphere, ozone is continuously regenerated by the splitting of O2 molecules by ultraviolet light. During a solar minimum, the decrease in ultraviolet light received from the Sun leads to a decrease in the concentration of ozone, allowing increased UVB to reach the Earth's surface.[66]
Radio communication
Skywave modes of radio communication operate by bending (refracting) radio waves (electromagnetic radiation) through the Ionosphere. During the "peaks" of the solar cycle, the ionosphere becomes increasingly ionized by solar photons and cosmic rays. This affects the propagation of the radio wave in complex ways that can either facilitate or hinder communications. Forecasting of skywave modes is of considerable interest to commercial marine and aircraft communications, amateur radio operators and shortwave broadcasters. These users occupy frequencies within the High Frequency or 'HF' radio spectrum that are most affected by these solar and ionospheric variances. Changes in solar output affect the maximum usable frequency, a limit on the highest frequency usable for communications.Climate
Both long-term and short-term variations in solar activity are hypothesized to affect global climate, but it has proven extremely challenging to quantify the link between solar variation and climate.[67]Early research attempted to correlate weather with limited success,[68] followed by attempts to correlate solar activity with global temperature. The cycle also impacts regional climate. Measurements from the SORCE's Spectral Irradiance Monitor show that solar UV variability produces, for example, colder winters in the U.S. and southern Europe and warmer winters in Canada and northern Europe during solar minima.[69]
Three hypothetical mechanisms mediate solar variations' climate impacts:
- Total solar irradiance ("Radiative forcing").
- Ultraviolet irradiance. The UV component varies by more than the total, so if UV were for some (as yet unknown) reason having a disproportionate effect, this might affect climate.
- Solar wind-mediated galactic cosmic ray changes, which may affect cloud cover.
The current scientific consensus is that solar variations do not play a major role in driving global warming,[67] since the measured magnitude of recent solar variation is much smaller than the forcing due to greenhouse gases.[74] Also, solar activity in the 2010s was not higher than in the 1950s (see above), whereas global warming had risen markedly. Otherwise, the level of understanding of solar impacts on weather is low.[75]
Causes
The basic causes of solar cycles are debated. While the proximate cause is a solar dynamo, the forces driving its behavior are less clear. Possibilities include a link with the tidal forces due to the gas giants Jupiter and Saturn,[76][77] or due to solar inertial motion.[78][79] Another cause of sunspots may be solar jet stream "torsional oscillation".Models
Single dynamo
The 11-year sunspot cycle is half of a 22-year Babcock–Leighton solar dynamo cycle, which corresponds to an oscillatory exchange of energy between toroidal and poloidal solar magnetic fields. At solar-cycle maximum, the external poloidal dipolar magnetic field is near its dynamo-cycle minimum strength, but an internal toroidal quadrupolar field, generated through differential rotation within the tachocline, is near its maximum strength. At this point in the dynamo cycle, buoyant upwelling within the Convection zone forces emergence of the toroidal magnetic field through the photosphere, giving rise to pairs of sunspots, roughly aligned east–west with opposite magnetic polarities. The magnetic polarity of sunspot pairs alternates every solar cycle, a phenomenon known as the Hale cycle.[80][81]During the solar cycle’s declining phase, energy shifts from the internal toroidal magnetic field to the external poloidal field, and sunspots diminish in number. At solar minimum, the toroidal field is, correspondingly, at minimum strength, sunspots are relatively rare and the poloidal field is at maximum strength. During the next cycle, differential rotation converts magnetic energy back from the poloidal to the toroidal field, with a polarity that is opposite to the previous cycle. The process carries on continuously, and in an idealized, simplified scenario, each 11-year sunspot cycle corresponds to a change in the polarity of the Sun's large-scale magnetic field.[82][83]
Double dynamo
In 2015, a new model of the solar cycle was published. The model draws on dynamo effects in two layers of the Sun, one close to the surface and one deep within its Convection zone. Model predictions suggest that solar activity will fall by 60 per cent during the 2030s to conditions last seen during the 'Little ice age' that began in 1645. Prior models included only the deeper dynamo.[84]The model features paired magnetic wave components. Both components have a frequency of approximately 11 years, although their frequencies are slightly different and temporally offset. Over the cycle, the waves fluctuate between the Sun's northern and southern hemispheres.[84]
The model used principal component analysis of the Magnetic field observations from the Wilcox Solar Observatory. They examined magnetic field activity from solar cycles 21-23, covering 1976-2008. They also compared their predictions to average Sunspot numbers. The model was 97% accurate in predicting solar activity fluctuations.[84]
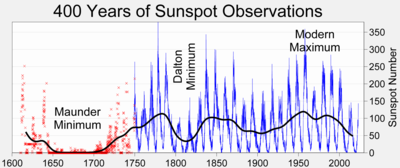











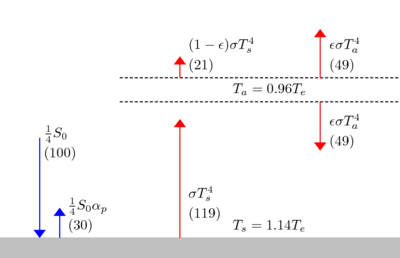

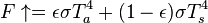

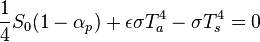


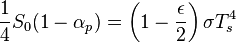
![T_s=\left[ \frac{S_0(1-\alpha_p)}{4\sigma} \frac{1}{1-{\epsilon \over 2}} \right]^{1/4}](http://upload.wikimedia.org/math/f/6/0/f60ed5667aa5d6059ec21d6d485c6e73.png)
![T_e \equiv \left[ \frac{S_0(1-\alpha_p)}{4\sigma} \right]^{1/4}](http://upload.wikimedia.org/math/a/a/8/aa849874c11f621aa0ca3c9c3cc99c2d.png)
![T_s= T_e \left[ \frac{1}{1-{\epsilon \over 2}} \right]^{1/4}](http://upload.wikimedia.org/math/a/9/a/a9aef1253eb6921fd553b60e19c8e381.png)



 .
. ,
,
 = -3.71 W m−2 with Δε=.019. Thus a change of ε from 0.78 to 0.80 is consistent with the radiative forcing from a doubling of carbon dioxide. For ε=0.80,
= -3.71 W m−2 with Δε=.019. Thus a change of ε from 0.78 to 0.80 is consistent with the radiative forcing from a doubling of carbon dioxide. For ε=0.80,