From Wikipedia, the free encyclopedia
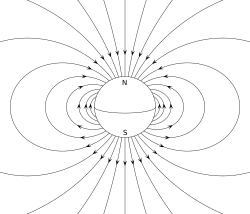
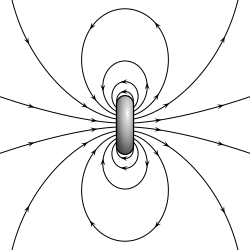
The Earth's magnetic field, approximated as a magnetic dipole. However, the "N" and "S" (north and south) poles are labeled here geographically, which is the opposite of the convention for labeling the poles of a magnetic dipole moment.
In physics, there are several kinds of dipole:
- An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some (usually small) distance. A permanent electric dipole is called an electret.
- A magnetic dipole is a closed circulation of electric current. A simple example of this is a single loop of wire with some constant current through it.[1][2]
- A current dipole is a current from a sink of current to a source of current within a (usually conducting) medium. Current dipoles are often used to model neuronal sources of electromagnetic fields that can be measured using Magnetoencephalography or Electroencephalography.
For the current loop, the magnetic dipole moment points through the loop (according to the right hand grip rule), with a magnitude equal to the current in the loop times the area of the loop.
In addition to current loops, the electron, among other fundamental particles, has a magnetic dipole moment. This is because it generates a magnetic field that is identical to that generated by a very small current loop. However, the electron's magnetic moment is not due to a current loop, but is instead an intrinsic property of the electron.[3] It is also possible that the electron has an electric dipole moment, although this has not yet been observed (see electron electric dipole moment for more information).

Contour plot of the electrostatic potential of a horizontally oriented electrical dipole of finite size. Strong colors indicate highest and lowest potential (where the opposing charges of the dipole are located).
A permanent magnet, such as a bar magnet, owes its magnetism to the intrinsic magnetic dipole moment of the electron. The two ends of a bar magnet are referred to as poles (not to be confused with monopoles), and may be labeled "north" and "south". In terms of the Earth's magnetic field, these are respectively "north-seeking" and "south-seeking" poles, that is if the magnet were freely suspended in the Earth's magnetic field, the north-seeking pole would point towards the north and the south-seeking pole would point twards the south. The dipole moment of the bar magnet points from its magnetic south to its magnetic north pole. The north pole of a bar magnet in a compass points north. However, this means that Earth's geomagnetic north pole is the south pole (south-seeking pole) of its dipole moment, and vice versa.
The only known mechanisms for the creation of magnetic dipoles are by current loops or quantum-mechanical spin since the existence of magnetic monopoles has never been experimentally demonstrated.
The term comes from the Greek δίς (dis), "twice"[4] and πόλος (pòlos), "axis".[5][6]
Classification
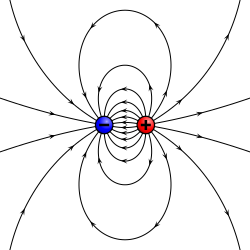
A physical dipole consists of two equal and opposite point charges: in the literal sense, two poles. Its field at large distances (i.e., distances large in comparison to the separation of the poles) depends almost entirely on the dipole moment as defined above. A point (electric) dipole is the limit obtained by letting the separation tend to 0 while keeping the dipole moment fixed. The field of a point dipole has a particularly simple form, and the order-1 term in the multipole expansion is precisely the point dipole field.
Although there are no known magnetic monopoles in nature, there are magnetic dipoles in the form of the quantum-mechanical spin associated with particles such as electrons (although the accurate description of such effects falls outside of classical electromagnetism). A theoretical magnetic point dipole has a magnetic field of exactly the same form as the electric field of an electric point dipole. A very small current-carrying loop is approximately a magnetic point dipole; the magnetic dipole moment of such a loop is the product of the current flowing in the loop and the (vector) area of the loop.
Any configuration of charges or currents has a 'dipole moment', which describes the dipole whose field is the best approximation, at large distances, to that of the given configuration. This is simply one term in the multipole expansion when the total charge ("monopole moment") is 0 — as it always is for the magnetic case, since there are no magnetic monopoles. The dipole term is the dominant one at large distances: Its field falls off in proportion to 1/r3, as compared to 1/r4 for the next (quadrupole) term and higher powers of 1/r for higher terms, or 1/r2 for the monopole term.
Molecular dipoles
Many molecules have such dipole moments due to non-uniform distributions of positive and negative charges on the various atoms. Such is the case with polar compounds like hydrogen fluoride (HF), where electron density is shared unequally between atoms. Therefore, a molecule's dipole is an electric dipole with an inherent electric field which should not be confused with a magnetic dipole which generates a magnetic field.The physical chemist Peter J. W. Debye was the first scientist to study molecular dipoles extensively, and, as a consequence, dipole moments are measured in units named debye in his honor.
For molecules there are three types of dipoles:
- Permanent dipoles: These occur when two atoms in a molecule have substantially different electronegativity: One atom attracts electrons more than another, becoming more negative, while the other atom becomes more positive. A molecule with a permanent dipole moment is called a polar molecule. See dipole-dipole attractions.
- Instantaneous dipoles: These occur due to chance when electrons happen to be more concentrated in one place than another in a molecule, creating a temporary dipole. See instantaneous dipole.
- Induced dipoles: These can occur when one molecule with a permanent dipole repels another molecule's electrons, inducing a dipole moment in that molecule. A molecule is polarized when it carries an induced dipole. See induced-dipole attraction.
Dipole moment values can be obtained from measurement of the dielectric constant. Some typical gas phase values in debye units are:[7]
- carbon dioxide: 0
- carbon monoxide: 0.112 D
- ozone: 0.53 D
- phosgene: 1.17 D
- water vapor: 1.85 D
- hydrogen cyanide: 2.98 D
- cyanamide: 4.27 D
- potassium bromide: 10.41 D
KBr has one of the highest dipole moments because it is a very ionic molecule (which only exists as a molecule in the gas phase).
The overall dipole moment of a molecule may be approximated as a vector sum of bond dipole moments. As a vector sum it depends on the relative orientation of the bonds, so that from the dipole moment information can be deduced about the molecular geometry. For example the zero dipole of CO2 implies that the two C=O bond dipole moments cancel so that the molecule must be linear. For H2O the O-H bond moments do not cancel because the molecule is bent. For ozone (O3) which is also a bent molecule, the bond dipole moments are not zero even though the O-O bonds are between similar atoms. This agrees with the Lewis structures for the resonance forms of ozone which show a positive charge on the central oxygen atom.

Another example of the role of molecular geometry is boron trifluoride, which has three polar bonds with a difference in electronegativity greater than the traditionally cited threshold of 1.7 for ionic bonding. However, due to the equilateral triangular distribution of the fluoride ions about the boron cation center, the molecule as a whole does not exhibit any identifiable pole: one cannot construct a plane that divides the molecule into a net negative part and a net positive part.
Quantum mechanical dipole operator
Consider a collection of N particles with charges qi and position vectors ri. For instance, this collection may be a molecule consisting of electrons, all with charge −e, and nuclei with charge eZi, where Zi is the atomic number of the i th nucleus. The dipole observable (physical quantity) has the quantum mechanical dipole operator:[citation needed] is the center of mass of the molecule/group of particles.[8]
is the center of mass of the molecule/group of particles.[8]
Atomic dipoles
A non-degenerate (S-state) atom can have only a zero permanent dipole. This fact follows quantum mechanically from the inversion symmetry of atoms. All 3 components of the dipole operator are antisymmetric under inversion with respect to the nucleus, is the dipole operator and
is the dipole operator and  is the inversion operator. The permanent dipole moment of an atom in a non-degenerate state (see degenerate energy level) is given as the expectation (average) value of the dipole operator,
is the inversion operator. The permanent dipole moment of an atom in a non-degenerate state (see degenerate energy level) is given as the expectation (average) value of the dipole operator, is an S-state, non-degenerate, wavefunction, which is symmetric or antisymmetric under inversion:
is an S-state, non-degenerate, wavefunction, which is symmetric or antisymmetric under inversion: 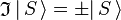 . Since the product of the wavefunction (in the ket) and its complex conjugate (in the bra) is always symmetric under inversion and its inverse,
. Since the product of the wavefunction (in the ket) and its complex conjugate (in the bra) is always symmetric under inversion and its inverse, , being a symmetry operator, is unitary:
, being a symmetry operator, is unitary:  and by definition the Hermitian adjoint
and by definition the Hermitian adjoint  may be moved from bra to ket and then becomes
may be moved from bra to ket and then becomes  . Since the only quantity that is equal to minus itself is the zero, the expectation value vanishes,
. Since the only quantity that is equal to minus itself is the zero, the expectation value vanishes,Field of a static magnetic dipole
Magnitude
The far-field strength, B, of a dipole magnetic field is given by- B is the strength of the field, measured in teslas
- r is the distance from the center, measured in metres
- λ is the magnetic latitude (equal to 90° − θ) where θ is the magnetic colatitude, measured in radians or degrees from the dipole axis[note 1]
- m is the dipole moment (VADM=virtual axial dipole moment), measured in ampere square-metres (A·m2), which equals joules per tesla
- μ0 is the permeability of free space, measured in henries per metre.
Vector form
The field itself is a vector quantity:- B is the field
- r is the vector from the position of the dipole to the position where the field is being measured
- r is the absolute value of r: the distance from the dipole
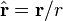 is the unit vector parallel to r;
is the unit vector parallel to r;- m is the (vector) dipole moment
- μ0 is the permeability of free space
- δ3 is the three-dimensional delta function.[note 2]
Magnetic vector potential
The vector potential A of a magnetic dipole is
Field from an electric dipole
The electrostatic potential at position r due to an electric dipole at the origin is given by: is a unit vector in the direction of r, p is the (vector) dipole moment, and ε0 is the permittivity of free space.
is a unit vector in the direction of r, p is the (vector) dipole moment, and ε0 is the permittivity of free space.
Torque on a dipole
Since the direction of an electric field is defined as the direction of the force on a positive charge, electric field lines point away from a positive charge and toward a negative charge.When placed in an electric or magnetic field, equal but opposite forces arise on each side of the dipole creating a torque τ:
The resulting torque will tend to align the dipole with the applied field, which in the case of an electric dipole, yields a potential energy of
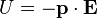 .
.
 .
.
Dipole radiation

Evolution of the magnetic field of an oscillating electric dipole. The field lines, which are horizontal rings around the axis of the vertically oriented dipole, are perpendicularly crossing the x-y-plane of the image. Shown as a colored contour plot is the z-component of the field. Cyan is zero magnitude, green–yellow–red and blue–pink–red are increasing strengths in opposing directions.
In particular, consider a harmonically oscillating electric dipole, with angular frequency ω and a dipole moment
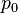 along the
along the 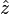 direction of the form
direction of the form
For
 , the far-field takes the simpler form of a radiating "spherical" wave, but with angular dependence embedded in the cross-product:[9]
, the far-field takes the simpler form of a radiating "spherical" wave, but with angular dependence embedded in the cross-product:[9]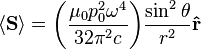
is not distributed isotropically, but concentrated around the directions lying perpendicular to the dipole moment, as a result of the non-spherical electric and magnetic waves. In fact, the spherical harmonic function (
 ) responsible for such "donut-shaped" angular distribution is precisely the
) responsible for such "donut-shaped" angular distribution is precisely the  "p" wave.
"p" wave.The total time-average power radiated by the field can then be derived from the Poynting vector as
A circular polarized dipole is described as a superposition of two linear dipoles.











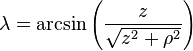


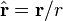 is the unit vector parallel to r;
is the unit vector parallel to r;

 is a unit vector in the direction of r, p is the (vector)
is a unit vector in the direction of r, p is the (vector) 

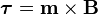
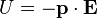 .
. .
.


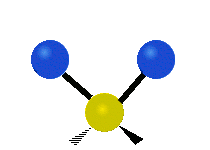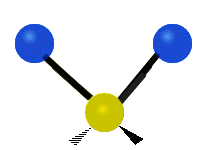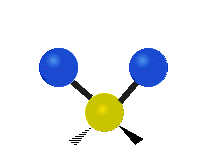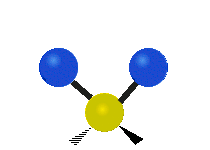
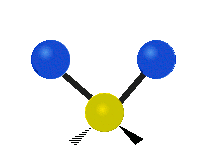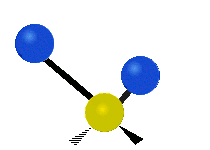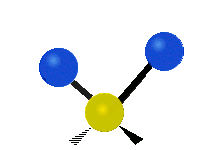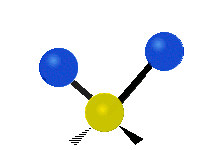






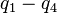 are the internal coordinates for stretching of each of the four C-H bonds.
are the internal coordinates for stretching of each of the four C-H bonds.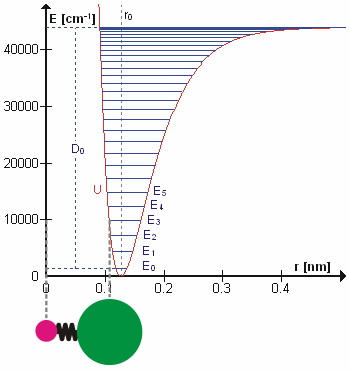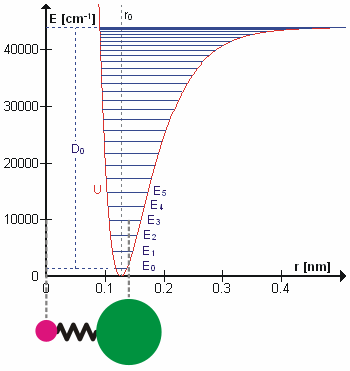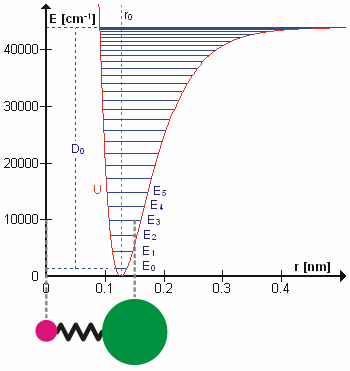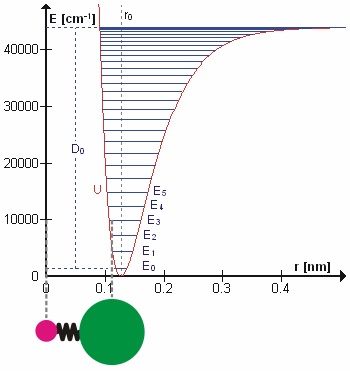






 ,
, , the product of the
, the product of the  (in the harmonic oscillator approximation).
(in the harmonic oscillator approximation).


