Neuron (updated)

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Neuron

 

Neuron
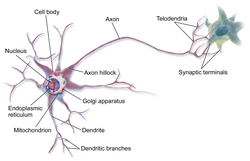
Anatomy of a multipolar neuron
Identifiers
MeSH	D009474
NeuroLex ID	sao1417703748
TA	A14.0.00.002
TH	H2.00.06.1.00002
FMA	54527
Anatomical terms of neuroanatomy

Schematic of an anatomically accurate single pyramidal neuron, the primary excitatory neuron of cerebral cortex, with a synaptic connection from an incoming axon onto a dendritic spine.

 

A neuron, neurone (old British spelling) or nerve cell, is an electrically excitable cell that communicates with other cells via specialized connections called synapses. It is the main component of nervous tissue. All animals except sponges and placozoans have neurons, but other multicellular organisms such as plants do not.

Neurons are typically classified into three types based on their function. Sensory neurons respond to stimuli such as touch, sound, or light that affect the cells of the sensory organs, and they send signals to the spinal cord or brain. Motor neurons receive signals from the brain and spinal cord to control everything from muscle contractions to glandular output. Interneurons connect neurons to other neurons within the same region of the brain or spinal cord. A group of connected neurons is called a neural circuit.

A typical neuron consists of a cell body (soma), dendrites, and a single axon. The soma is usually compact. The axon and dendrites are filaments that extrude from it. Dendrites typically branch profusely and extend a few hundred micrometers from the soma. The axon leaves the soma at a swelling called the axon hillock, and travels for as far as 1 meter in humans or more in other species. It branches but usually maintains a constant diameter. At the farthest tip of the axon's branches are axon terminals, where the neuron can transmit a signal across the synapse to another cell. Neurons may lack dendrites or have no axon. The term neurite is used to describe either a dendrite or an axon, particularly when the cell is undifferentiated.

Most neurons receive signals via the dendrites and soma and send out signals down the axon. At the majority of synapses, signals cross from the axon of one neuron to a dendrite of another. However, synapses can connect an axon to another axon or a dendrite to another dendrite.

The signaling process is partly electrical and partly chemical. Neurons are electrically excitable, due to maintenance of voltage gradients across their membranes. If the voltage changes by a large enough amount over a short interval, the neuron generates an all-or-nothing electrochemical pulse called an action potential. This potential travels rapidly along the axon, and activates synaptic connections as it reaches them. Synaptic signals may be excitatory or inhibitory, increasing or reducing the net voltage that reaches the soma.

In most cases, neurons are generated by neural stem cells during brain development and childhood. Neurogenesis largely ceases during adulthood in most areas of the brain. However, strong evidence supports generation of substantial numbers of new neurons in the hippocampus and olfactory bulb.

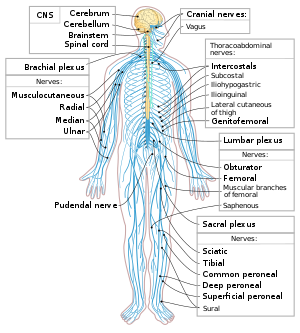
Nervous system

Diagram of the human nervous system. The relationship between the brain, spinal cord, and rest of the nerves in the body is demonstrated.

 

Neurons are the primary components of the nervous system, along with the glial cells that give them structural and metabolic support. The nervous system is made up of the central nervous system, which includes the brain and spinal cord, and the peripheral nervous system, which includes the autonomic and somatic nervous systems. In vertebrates, the majority of neurons belong to the central nervous system, but some reside in peripheral ganglia, and many sensory neurons are situated in sensory organs such as the retina and cochlea.

Axons may bundle into fascicles that make up the nerves in the peripheral nervous system (like strands of wire make up cables). Bundles of axons in the central nervous system are called tracts.

Anatomy and histology

Structure of a typical neuron

Neuron (peripheral nervous system)
Dendrite Soma Axon Nucleus Node of Ranvier Axon terminal Schwann cell Myelin sheath

Neurons are highly specialized for the processing and transmission of cellular signals. Given their diversity of functions performed in different parts of the nervous system, there is a wide variety in their shape, size, and electrochemical properties. For instance, the soma of a neuron can vary from 4 to 100 micrometers in diameter.

• The soma is the body of the neuron. As it contains the nucleus, most protein synthesis occurs here. The nucleus can range from 3 to 18 micrometers in diameter.
• The dendrites of a neuron are cellular extensions with many branches. This overall shape and structure is referred to metaphorically as a dendritic tree. This is where the majority of input to the neuron occurs via the dendritic spine.
• The axon is a finer, cable-like projection that can extend tens, hundreds, or even tens of thousands of times the diameter of the soma in length. The axon primarily carries nerve signals away from the soma, and carries some types of information back to it. Many neurons have only one axon, but this axon may—and usually will—undergo extensive branching, enabling communication with many target cells. The part of the axon where it emerges from the soma is called the axon hillock. Besides being an anatomical structure, the axon hillock also has the greatest density of voltage-dependent sodium channels. This makes it the most easily excited part of the neuron and the spike initiation zone for the axon. In electrophysiological terms, it has the most negative threshold potential.
  • While the axon and axon hillock are generally involved in information outflow, this region can also receive input from other neurons.
• The axon terminal is found at the end of the axon farthest from the soma and contains synapses. Synaptic boutons are specialized structures where neurotransmitter chemicals are released to communicate with target neurons. In addition to synaptic boutons at the axon terminal, a neuron may have en passant boutons, which are located along the length of the axon.
  

Neuron cell body

The accepted view of the neuron attributes dedicated functions to its various anatomical components; however, dendrites and axons often act in ways contrary to their so-called main function. 

Diagram of a typical myelinated vertebrate motor neuron

 

Axons and dendrites in the central nervous system are typically only about one micrometer thick, while some in the peripheral nervous system are much thicker. The soma is usually about 10–25 micrometers in diameter and often is not much larger than the cell nucleus it contains. The longest axon of a human motor neuron can be over a meter long, reaching from the base of the spine to the toes. 

Sensory neurons can have axons that run from the toes to the posterior column of the spinal cord, over 1.5 meters in adults. Giraffes have single axons several meters in length running along the entire length of their necks. Much of what is known about axonal function comes from studying the squid giant axon, an ideal experimental preparation because of its relatively immense size (0.5–1 millimeters thick, several centimeters long).

Fully differentiated neurons are permanently postmitotic; however, stem cells present in the adult brain may regenerate functional neurons throughout the life of an organism. Astrocytes are star-shaped glial cells. They have been observed to turn into neurons by virtue of their stem cell-like characteristic of pluripotency. 

Membrane

Like all animal cells, the cell body of every neuron is enclosed by a plasma membrane, a bilayer of lipid molecules with many types of protein structures embedded in it. A lipid bilayer is a powerful electrical insulator, but in neurons, many of the protein structures embedded in the membrane are electrically active. These include ion channels that permit electrically charged ions to flow across the membrane and ion pumps that chemically transport ions from one side of the membrane to the other. Most ion channels are permeable only to specific types of ions. Some ion channels are voltage gated, meaning that they can be switched between open and closed states by altering the voltage difference across the membrane. Others are chemically gated, meaning that they can be switched between open and closed states by interactions with chemicals that diffuse through the extracellular fluid. The ion materials include sodium, potassium, chloride, and calcium. The interactions between ion channels and ion pumps produce a voltage difference across the membrane, typically a bit less than 1/10 of a volt at baseline. This voltage has two functions: first, it provides a power source for an assortment of voltage-dependent protein machinery that is embedded in the membrane; second, it provides a basis for electrical signal transmission between different parts of the membrane. 

Histology and internal structure

Golgi-stained neurons in human hippocampal tissue

 

Actin filaments in a mouse Cortical Neuron in culture

Numerous microscopic clumps called Nissl bodies (or Nissl substance) are seen when nerve cell bodies are stained with a basophilic ("base-loving") dye. These structures consist of rough endoplasmic reticulum and associated ribosomal RNA. Named after German psychiatrist and neuropathologist Franz Nissl (1860–1919), they are involved in protein synthesis and their prominence can be explained by the fact that nerve cells are very metabolically active. Basophilic dyes such as aniline or (weakly) haematoxylin highlight negatively charged components, and so bind to the phosphate backbone of the ribosomal RNA.

The cell body of a neuron is supported by a complex mesh of structural proteins called neurofilaments, which together with neurotubules (neuronal microtubules) are assembled into larger neurofibrils. Some neurons also contain pigment granules, such as neuromelanin (a brownish-black pigment that is byproduct of synthesis of catecholamines), and lipofuscin (a yellowish-brown pigment), both of which accumulate with age. Other structural proteins that are important for neuronal function are actin and the tubulin of microtubules. Class III β-tubulin is found almost exclusively in neurons. Actin is predominately found at the tips of axons and dendrites during neuronal development. There the actin dynamics can be modulated via an interplay with microtubule.

There are different internal structural characteristics between axons and dendrites. Typical axons almost never contain ribosomes, except some in the initial segment. Dendrites contain granular endoplasmic reticulum or ribosomes, in diminishing amounts as the distance from the cell body increases. 

Classification

Image of pyramidal neurons in mouse cerebral cortex expressing green fluorescent protein. The red staining indicates GABAergic interneurons.

 

SMI32-stained pyramidal neurons in cerebral cortex

Neurons vary in shape and size and can be classified by their morphology and function. The anatomist Camillo Golgi grouped neurons into two types; type I with long axons used to move signals over long distances and type II with short axons, which can often be confused with dendrites. Type I cells can be further classified by the location of the soma. The basic morphology of type I neurons, represented by spinal motor neurons, consists of a cell body called the soma and a long thin axon covered by a myelin sheath. The dendritic tree wraps around the cell body and receives signals from other neurons. The end of the axon has branching terminals (axon terminal) that release neurotransmitters into a gap called the synaptic cleft between the terminals and the dendrites of the next neuron. 

Structural classification

Polarity

 

Different kinds of neurons:

1 Unipolar neuron
2 Bipolar neuron
3 Multipolar neuron
4 Pseudounipolar neuron

Most neurons can be anatomically characterized as:

• Unipolar: single process
• Bipolar: 1 axon and 1 dendrite
• Multipolar: 1 axon and 2 or more dendrites
  • Golgi I: neurons with projecting axonal processes; examples are pyramidal cells, Purkinje cells, and anterior horn cells
  • Golgi II: neurons whose axonal process projects locally; the best example is the granule cell
• Anaxonic: where the axon cannot be distinguished from the dendrite(s)
• Pseudounipolar: 1 process which then serves as both an axon and a dendrite

Other

Some unique neuronal types can be identified according to their location in the nervous system and distinct shape. Some examples are:

• Basket cells, interneurons that form a dense plexus of terminals around the soma of target cells, found in the cortex and cerebellum
• Betz cells, large motor neurons
• Lugaro cells, interneurons of the cerebellum
• Medium spiny neurons, most neurons in the corpus striatum
• Purkinje cells, huge neurons in the cerebellum, a type of Golgi I multipolar neuron
• Pyramidal cells, neurons with triangular soma, a type of Golgi I
• Renshaw cells, neurons with both ends linked to alpha motor neurons
• Unipolar brush cells, interneurons with unique dendrite ending in a brush-like tuft
• Granule cells, a type of Golgi II neuron
• Anterior horn cells, motoneurons located in the spinal cord
• Spindle cells, interneurons that connect widely separated areas of the brain

Functional classification

Direction

• Afferent neurons convey information from tissues and organs into the central nervous system and are also called sensory neurons.
• Efferent neurons (motor neurons) transmit signals from the central nervous system to the effector cells.
• Interneurons connect neurons within specific regions of the central nervous system.

Afferent and efferent also refer generally to neurons that, respectively, bring information to or send information from the brain.

Action on other neurons

A neuron affects other neurons by releasing a neurotransmitter that binds to chemical receptors. The effect upon the postsynaptic neuron is determined by the type of receptor that is activated, not by the presynaptic neuron or by the neurotransmitter. A neurotransmitter can be thought of as a key, and a receptor as a lock: the same neurotransmitter can activate multiple types of receptors. Receptors can be classified broadly as excitatory (causing an increase in firing rate), inhibitory (causing a decrease in firing rate), or modulatory (causing long-lasting effects not directly related to firing rate).

The two most common (90%+) neurotransmitters in the brain, glutamate and GABA, have largely consistent actions. Glutamate acts on several types of receptors, and has effects that are excitatory at ionotropic receptors and a modulatory effect at metabotropic receptors. Similarly, GABA acts on several types of receptors, but all of them have inhibitory effects (in adult animals, at least). Because of this consistency, it is common for neuroscientists to refer to cells that release glutamate as "excitatory neurons", and cells that release GABA as "inhibitory neurons". Some other types of neurons have consistent effects, for example, "excitatory" motor neurons in the spinal cord that release acetylcholine, and "inhibitory" spinal neurons that release glycine.

The distinction between excitatory and inhibitory neurotransmitters is not absolute. Rather, it depends on the class of chemical receptors present on the postsynaptic neuron. In principle, a single neuron, releasing a single neurotransmitter, can have excitatory effects on some targets, inhibitory effects on others, and modulatory effects on others still. For example, photoreceptor cells in the retina constantly release the neurotransmitter glutamate in the absence of light. So-called OFF bipolar cells are, like most neurons, excited by the released glutamate. However, neighboring target neurons called ON bipolar cells are instead inhibited by glutamate, because they lack typical ionotropic glutamate receptors and instead express a class of inhibitory metabotropic glutamate receptors. When light is present, the photoreceptors cease releasing glutamate, which relieves the ON bipolar cells from inhibition, activating them; this simultaneously removes the excitation from the OFF bipolar cells, silencing them. 

It is possible to identify the type of inhibitory effect a presynaptic neuron will have on a postsynaptic neuron, based on the proteins the presynaptic neuron expresses. Parvalbumin-expressing neurons typically dampen the output signal of the postsynaptic neuron in the visual cortex, whereas somatostatin-expressing neurons typically block dendritic inputs to the postsynaptic neuron.

Discharge patterns

Neurons have intrinsic electroresponsive properties like intrinsic transmembrane voltage oscillatory patterns. So neurons can be classified according to their electrophysiological characteristics:

• Tonic or regular spiking. Some neurons are typically constantly (tonically) active, typically firing at a constant frequency. Example: interneurons in neurostriatum.
• Phasic or bursting. Neurons that fire in bursts are called phasic.
• Fast spiking. Some neurons are notable for their high firing rates, for example some types of cortical inhibitory interneurons, cells in globus pallidus, retinal ganglion cells.

Neurotransmitter

• Cholinergic neurons—acetylcholine. Acetylcholine is released from presynaptic neurons into the synaptic cleft. It acts as a ligand for both ligand-gated ion channels and metabotropic (GPCRs) muscarinic receptors. Nicotinic receptors are pentameric ligand-gated ion channels composed of alpha and beta subunits that bind nicotine. Ligand binding opens the channel causing influx of Na⁺ depolarization and increases the probability of presynaptic neurotransmitter release. Acetylcholine is synthesized from choline and acetyl coenzyme A.
• GABAergic neurons—gamma aminobutyric acid. GABA is one of two neuroinhibitors in the central nervous system (CNS), along with glycine. GABA has a homologous function to ACh, gating anion channels that allow Cl⁻ ions to enter the post synaptic neuron. Cl⁻ causes hyperpolarization within the neuron, decreasing the probability of an action potential firing as the voltage becomes more negative (for an action potential to fire, a positive voltage threshold must be reached). GABA is synthesized from glutamate neurotransmitters by the enzyme glutamate decarboxylase.
• Glutamatergic neurons—glutamate. Glutamate is one of two primary excitatory amino acid neurotransmitters, along with aspartate. Glutamate receptors are one of four categories, three of which are ligand-gated ion channels and one of which is a G-protein coupled receptor (often referred to as GPCR).

1. AMPA and Kainate receptors function as cation channels permeable to Na⁺ cation channels mediating fast excitatory synaptic transmission.
2. NMDA receptors are another cation channel that is more permeable to Ca²⁺. The function of NMDA receptors depend on glycine receptor binding as a co-agonist within the channel pore. NMDA receptors do not function without both ligands present.
3. Metabotropic receptors, GPCRs modulate synaptic transmission and postsynaptic excitability.

Glutamate can cause excitotoxicity when blood flow to the brain is interrupted, resulting in brain damage. When blood flow is suppressed, glutamate is released from presynaptic neurons, causing greater NMDA and AMPA receptor activation than normal outside of stress conditions, leading to elevated Ca²⁺ and Na⁺ entering the post synaptic neuron and cell damage. Glutamate is synthesized from the amino acid glutamine by the enzyme glutamate synthase.

• Dopaminergic neurons—dopamine. Dopamine is a neurotransmitter that acts on D1 type (D1 and D5) Gs-coupled receptors, which increase cAMP and PKA, and D2 type (D2, D3, and D4) receptors, which activate Gi-coupled receptors that decrease cAMP and PKA. Dopamine is connected to mood and behavior and modulates both pre- and post-synaptic neurotransmission. Loss of dopamine neurons in the substantia nigra has been linked to Parkinson's disease. Dopamine is synthesized from the amino acid tyrosine. Tyrosine is catalyzed into levadopa (or L-DOPA) by tyrosine hydroxlase, and levadopa is then converted into dopamine by the aromatic amino acid decarboxylase.
• Serotonergic neurons—serotonin. Serotonin (5-Hydroxytryptamine, 5-HT) can act as excitatory or inhibitory. Of its four 5-HT receptor classes, 3 are GPCR and 1 is a ligand-gated cation channel. Serotonin is synthesized from tryptophan by tryptophan hydroxylase, and then further by decarboxylase. A lack of 5-HT at postsynaptic neurons has been linked to depression. Drugs that block the presynaptic serotonin transporter are used for treatment, such as Prozac and Zoloft.

Connectivity

A signal propagating down an axon to the cell body and dendrites of the next cell

 

Chemical synapse

 

Neurons communicate with each another via synapses, where either the axon terminal of one cell contacts another neuron's dendrite, soma or, less commonly, axon. Neurons such as Purkinje cells in the cerebellum can have over 1000 dendritic branches, making connections with tens of thousands of other cells; other neurons, such as the magnocellular neurons of the supraoptic nucleus, have only one or two dendrites, each of which receives thousands of synapses.

Synapses can be excitatory or inhibitory, either increasing or decreasing activity in the target neuron, respectively. Some neurons also communicate via electrical synapses, which are direct, electrically conductive junctions between cells.

When an action potential reaches the axon terminal, it opens voltage-gated calcium channels, allowing calcium ions to enter the terminal. Calcium causes synaptic vesicles filled with neurotransmitter molecules to fuse with the membrane, releasing their contents into the synaptic cleft. The neurotransmitters diffuse across the synaptic cleft and activate receptors on the postsynaptic neuron. High cytosolic calcium in the axon terminal triggers mitochondrial calcium uptake, which, in turn, activates mitochondrial energy metabolism to produce ATP to support continuous neurotransmission.

An autapse is a synapse in which a neuron's axon connects to its own dendrites.

The human brain has some 8.6 x 10¹⁰ (eighty six billion) neurons. Each neuron has on average 7,000 synaptic connections to other neurons. It has been estimated that the brain of a three-year-old child has about 10¹⁵ synapses (1 quadrillion). This number declines with age, stabilizing by adulthood. Estimates vary for an adult, ranging from 10¹⁴ to 5 x 10¹⁴ synapses (100 to 500 trillion).

An annotated diagram of the stages of an action potential propagating down an axon including the role of ion concentration and pump and channel proteins.

Mechanisms for propagating action potentials

In 1937 John Zachary Young suggested that the squid giant axon could be used to study neuronal electrical properties. It is larger than but similar to human neurons, making it easier to study. By inserting electrodes into the squid giant axons, accurate measurements were made of the membrane potential. 

The cell membrane of the axon and soma contain voltage-gated ion channels that allow the neuron to generate and propagate an electrical signal (an action potential). Some neurons also generate subthreshold membrane potential oscillations. These signals are generated and propagated by charge-carrying ions including sodium (Na⁺), potassium (K⁺), chloride (Cl⁻), and calcium (Ca²⁺).

Several stimuli can activate a neuron leading to electrical activity, including pressure, stretch, chemical transmitters, and changes of the electric potential across the cell membrane. Stimuli cause specific ion-channels within the cell membrane to open, leading to a flow of ions through the cell membrane, changing the membrane potential. Neurons must maintain the specific electrical properties that define their neuron type.

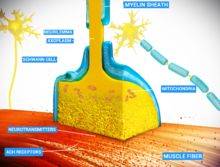
Thin neurons and axons require less metabolic expense to produce and carry action potentials, but thicker axons convey impulses more rapidly. To minimize metabolic expense while maintaining rapid conduction, many neurons have insulating sheaths of myelin around their axons. The sheaths are formed by glial cells: oligodendrocytes in the central nervous system and Schwann cells in the peripheral nervous system. The sheath enables action potentials to travel faster than in unmyelinated axons of the same diameter, whilst using less energy. The myelin sheath in peripheral nerves normally runs along the axon in sections about 1 mm long, punctuated by unsheathed nodes of Ranvier, which contain a high density of voltage-gated ion channels. Multiple sclerosis is a neurological disorder that results from demyelination of axons in the central nervous system.

Some neurons do not generate action potentials, but instead generate a graded electrical signal, which in turn causes graded neurotransmitter release. Such non-spiking neurons tend to be sensory neurons or interneurons, because they cannot carry signals long distances. 

Neural coding

Neural coding is concerned with how sensory and other information is represented in the brain by neurons. The main goal of studying neural coding is to characterize the relationship between the stimulus and the individual or ensemble neuronal responses, and the relationships among the electrical activities of the neurons within the ensemble. It is thought that neurons can encode both digital and analog information.

All-or-none principle

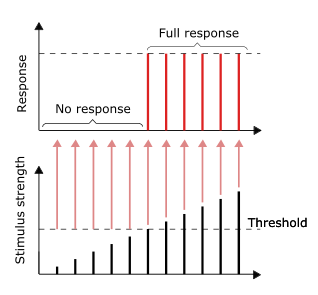
As long as the stimulus reaches the threshold, the full response would be given. Larger stimulus does not result in a larger response, vice versa.

The conduction of nerve impulses is an example of an all-or-none response. In other words, if a neuron responds at all, then it must respond completely. Greater intensity of stimulation, like brighter image/louder sound, does not produce a stronger signal, but can increase firing frequency. Receptors respond in different ways to stimuli. Slowly adapting or tonic receptors respond to steady stimulus and produce a steady rate of firing. Tonic receptors most often respond to increased intensity of stimulus by increasing their firing frequency, usually as a power function of stimulus plotted against impulses per second. This can be likened to an intrinsic property of light where greater intensity of a specific frequency (color) requires more photons, as the photons can't become "stronger" for a specific frequency.

Other receptor types include quickly adapting or phasic receptors, where firing decreases or stops with steady stimulus; examples include skin which, when touched causes neurons to fire, but if the object maintains even pressure, the neurons stop firing. The neurons of the skin and muscles that are responsive to pressure and vibration have filtering accessory structures that aid their function. 

The pacinian corpuscle is one such structure. It has concentric layers like an onion, which form around the axon terminal. When pressure is applied and the corpuscle is deformed, mechanical stimulus is transferred to the axon, which fires. If the pressure is steady, stimulus ends; thus, typically these neurons respond with a transient depolarization during the initial deformation and again when the pressure is removed, which causes the corpuscle to change shape again. Other types of adaptation are important in extending the function of a number of other neurons.

History

Drawing by Camillo Golgi of a hippocampus stained using the silver nitrate method

 

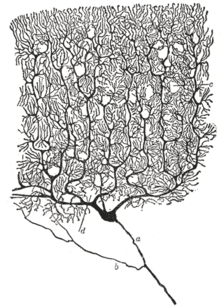
Drawing of a Purkinje cell in the cerebellar cortex done by Santiago Ramón y Cajal, demonstrating the ability of Golgi's staining method to reveal fine detail

 

The neuron's place as the primary functional unit of the nervous system was first recognized in the late 19th century through the work of the Spanish anatomist Santiago Ramón y Cajal.

To make the structure of individual neurons visible, Ramón y Cajal improved a silver staining process that had been developed by Camillo Golgi. The improved process involves a technique called "double impregnation" and is still in use.

In 1888 Ramón y Cajal published a paper about the bird cerebellum. In this paper, he stated that he could not find evidence for anastomosis between axons and dendrites and called each nervous element "an absolutely autonomous canton." This became known as the neuron doctrine, one of the central tenets of modern neuroscience.

In 1891 German anatomist Heinrich Wilhelm Waldeyer wrote a highly influential review about the neuron doctrine in which he introduced the term neuron to describe the anatomical and physiological unit of the nervous system.

The silver impregnation stains are a useful method for neuroanatomical investigations because, for reasons unknown, it stains only a small percentage of cells in a tissue, exposing the complete micro structure of individual neurons without much overlap from other cells.

Neuron doctrine

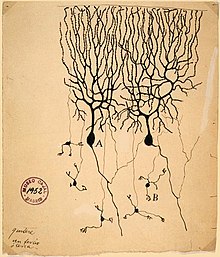
Drawing of neurons in the pigeon cerebellum, by Spanish neuroscientist Santiago Ramón y Cajal in 1899. (A) denotes Purkinje cells and (B) denotes granule cells, both of which are multipolar.

 

The neuron doctrine is the now fundamental idea that neurons are the basic structural and functional units of the nervous system. The theory was put forward by Santiago Ramón y Cajal in the late 19th century. It held that neurons are discrete cells (not connected in a meshwork), acting as metabolically distinct units. 

Later discoveries yielded refinements to the doctrine. For example, glial cells, which are not considered neurons, play an essential role in information processing. Also, electrical synapses are more common than previously thought, comprising direct, cytoplasmic connections between neurons. In fact, neurons can form even tighter couplings: the squid giant axon arises from the fusion of multiple axons.

Ramón y Cajal also postulated the Law of Dynamic Polarization, which states that a neuron receives signals at its dendrites and cell body and transmits them, as action potentials, along the axon in one direction: away from the cell body. The Law of Dynamic Polarization has important exceptions; dendrites can serve as synaptic output sites of neurons and axons can receive synaptic inputs.

Compartmental Model of Neurons

Although neurons are often described of as "fundamental units" of the brain, they perform internal computations. Neurons integrate input within dendrites, and this complexity is lost in models that assume neurons to be a fundamental unit. Dendritic branches can be modeled as spatial compartments, whose activity is related due to passive membrane properties, but may also be different depending on input from synapses. Compartmental modelling of dendrites is especially helpful for understanding the behavior of neurons that are too small to record with electrodes, as is the case for Drosophila melanogaster.

Neurons in the brain

The number of neurons in the brain varies dramatically from species to species. In a human, there are an estimated 10–20 billion neurons in the cerebral cortex and 55–70 billion neurons in the cerebellum. By contrast, the nematode worm Caenorhabditis elegans has just 302 neurons, making it an ideal model organism as scientists have been able to map all of its neurons. The fruit fly Drosophila melanogaster, a common subject in biological experiments, has around 100,000 neurons and exhibits many complex behaviors. Many properties of neurons, from the type of neurotransmitters used to ion channel composition, are maintained across species, allowing scientists to study processes occurring in more complex organisms in much simpler experimental systems. 

Neurological disorders

Charcot–Marie–Tooth disease (CMT) is a heterogeneous inherited disorder of nerves (neuropathy) that is characterized by loss of muscle tissue and touch sensation, predominantly in the feet and legs extending to the hands and arms in advanced stages. Presently incurable, this disease is one of the most common inherited neurological disorders, with 36 in 100,000 affected.

Alzheimer's disease (AD), also known simply as Alzheimer's, is a neurodegenerative disease characterized by progressive cognitive deterioration, together with declining activities of daily living and neuropsychiatric symptoms or behavioral changes. The most striking early symptom is loss of short-term memory (amnesia), which usually manifests as minor forgetfulness that becomes steadily more pronounced with illness progression, with relative preservation of older memories. As the disorder progresses, cognitive (intellectual) impairment extends to the domains of language (aphasia), skilled movements (apraxia), and recognition (agnosia), and functions such as decision-making and planning become impaired.

Parkinson's disease (PD), also known as Parkinson disease, is a degenerative disorder of the central nervous system that often impairs motor skills and speech. Parkinson's disease belongs to a group of conditions called movement disorders. It is characterized by muscle rigidity, tremor, a slowing of physical movement (bradykinesia), and in extreme cases, a loss of physical movement (akinesia). The primary symptoms are the results of decreased stimulation of the motor cortex by the basal ganglia, normally caused by the insufficient formation and action of dopamine, which is produced in the dopaminergic neurons of the brain. Secondary symptoms may include high level cognitive dysfunction and subtle language problems. PD is both chronic and progressive.

Myasthenia gravis is a neuromuscular disease leading to fluctuating muscle weakness and fatigability during simple activities. Weakness is typically caused by circulating antibodies that block acetylcholine receptors at the post-synaptic neuromuscular junction, inhibiting the stimulative effect of the neurotransmitter acetylcholine. Myasthenia is treated with immunosuppressants, cholinesterase inhibitors and, in selected cases, thymectomy. 

Demyelination

Guillain–Barré syndrome – demyelination

Demyelination is the act of demyelinating, or the loss of the myelin sheath insulating the nerves. When myelin degrades, conduction of signals along the nerve can be impaired or lost, and the nerve eventually withers. This leads to certain neurodegenerative disorders like multiple sclerosis and chronic inflammatory demyelinating polyneuropathy. 

Axonal degeneration

Although most injury responses include a calcium influx signaling to promote resealing of severed parts, axonal injuries initially lead to acute axonal degeneration, which is rapid separation of the proximal and distal ends within 30 minutes of injury. Degeneration follows with swelling of the axolemma, and eventually leads to bead like formation. Granular disintegration of the axonal cytoskeleton and inner organelles occurs after axolemma degradation. Early changes include accumulation of mitochondria in the paranodal regions at the site of injury. Endoplasmic reticulum degrades and mitochondria swell up and eventually disintegrate. The disintegration is dependent on ubiquitin and calpain proteases (caused by influx of calcium ion), suggesting that axonal degeneration is an active process that produces complete fragmentation. The process takes about roughly 24 hrs in the PNS and longer in the CNS. The signaling pathways leading to axolemma degeneration are unknown. 

Neurogenesis

Neurons are born through the process of neurogenesis, in which neural stem cells divide to produce differentiated neurons. Once fully differentiated neurons are formed, they are no longer capable of undergoing mitosis. Neurogenesis primarily occurs in the embryo of most organisms.

Neurogenesis can occur in the adult vertebrate brain, a finding that led to controversy in 1999. Later studies of the age of human neurons suggest that this process occurs only for a minority of cells, and a vast majority of neurons composing the neocortex forms before birth and persists without replacement. The extent to which adult neurogenesis exists in humans, and its contribution to cognition are controversial, with conflicting reports published in 2018.

The body contains a variety of stem cell types that have the capacity to differentiate into neurons. Researchers found a way to transform human skin cells into nerve cells using transdifferentiation, in which "cells are forced to adopt new identities".

During neurogenesis in the mammalian brain, progenitor and stem cells progress from proliferative divisions to differentiative divisions. This progression leads to the neurons and glia that populate cortical layers. Epigenetic modifications play a key role in regulating gene expression in differentiating neural stem cells, and are critical for cell fate determination in the developing and adult mammalian brain. Epigenetic modifications include DNA cytosine methylation to form 5-methylcytosine and 5-methylcytosine demethylation. These modifications are critical for cell fate determination in the developing and adult mammalian brain. DNA cytosine methylation is catalyzed by DNA methyltransferases (DNMTs). Methylcytosine demethylation is catalyzed in several stages by TET enzymes that carry out oxidative reactions (e.g. 5-methylcytosine to 5-hydroxymethylcytosine) and enzymes of the DNA base excision repair (BER) pathway.

At different stages of mammalian nervous system development two DNA repair processes are employed in the repair of DNA double-strand breaks. These pathways are homologous recombinational repair used in proliferating neural precursor cells, and non-homologous end joining used mainly at later developmental stages.

Nerve regeneration

Peripheral axons can regrow if they are severed, but one neuron cannot be functionally replaced by one of another type (Llinás' law)

Coding theory

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Coding_theory

 

A two-dimensional visualisation of the Hamming distance, a critical measure in coding theory.

Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data. 

There are four types of coding:

1. Data compression (or source coding)
2. Error control (or channel coding)
3. Cryptographic coding
4. Line coding

Data compression attempts to remove redundancy from the data from a source in order to transmit it more efficiently. For example, Zip data compression makes data files smaller, for purposes such as to reduce Internet traffic. Data compression and error correction may be studied in combination.

Error correction adds extra data bits to make the transmission of data more robust to disturbances present on the transmission channel. The ordinary user may not be aware of many applications using error correction. A typical music CD uses the Reed-Solomon code to correct for scratches and dust. In this application the transmission channel is the CD itself. Cell phones also use coding techniques to correct for the fading and noise of high frequency radio transmission. Data modems, telephone transmissions, and the NASA Deep Space Network all employ channel coding techniques to get the bits through, for example the turbo code and LDPC codes. 

History of coding theory

In 1948, Claude Shannon published "A Mathematical Theory of Communication", an article in two parts in the July and October issues of the Bell System Technical Journal. This work focuses on the problem of how best to encode the information a sender wants to transmit. In this fundamental work he used tools in probability theory, developed by Norbert Wiener, which were in their nascent stages of being applied to communication theory at that time. Shannon developed information entropy as a measure for the uncertainty in a message while essentially inventing the field of information theory.

The binary Golay code was developed in 1949. It is an error-correcting code capable of correcting up to three errors in each 24-bit word, and detecting a fourth.

Richard Hamming won the Turing Award in 1968 for his work at Bell Labs in numerical methods, automatic coding systems, and error-detecting and error-correcting codes. He invented the concepts known as Hamming codes, Hamming windows, Hamming numbers, and Hamming distance.

In 1972, Nasir Ahmed proposed the discrete cosine transform (DCT), which he developed with T. Natarajan and K. R. Rao in 1973. The DCT is the most widely used lossy compression algorithm, the basis for multimedia formats such as JPEG, MPEG and MP3. 

Source coding

The aim of source coding is to take the source data and make it smaller.

Definition

Data can be seen as a random variable ${\displaystyle X:\Omega \rightarrow {\mathcal {X}}}$, where ${\displaystyle x\in {\mathcal {X}}}$ appears with probability ${\displaystyle \mathbb {P} [X=x]}$.

Data are encoded by strings (words) over an alphabet ${\displaystyle \Sigma }$.

A code is a function

${\displaystyle C:{\mathcal {X}}\rightarrow \Sigma ^{*}}$ (or ${\displaystyle \Sigma ^{+}}$ if the empty string is not part of the alphabet). 

${\displaystyle C(x)}$ is the code word associated with ${\displaystyle x}$. 

Length of the code word is written as . 

Expected length of a code is .

The concatenation of code words ${\displaystyle C(x_{1},...,x_{k})=C(x_{1})C(x_{2})...C(x_{k})}$.

The code word of the empty string is the empty string itself:  .

Properties

1. ${\displaystyle C:{\mathcal {X}}\rightarrow \Sigma ^{*}}$ is non-singular if injective.
2. ${\displaystyle C:{\mathcal {X}}^{*}\rightarrow \Sigma ^{*}}$ is uniquely decodable if injective.
3. ${\displaystyle C:{\mathcal {X}}\rightarrow \Sigma ^{*}}$ is instantaneous if ${\displaystyle C(x_{1})}$ is not a prefix of ${\displaystyle C(x_{2})}$ (and vice versa).

Principle

Entropy of a source is the measure of information. Basically, source codes try to reduce the redundancy present in the source, and represent the source with fewer bits that carry more information. 

Data compression which explicitly tries to minimize the average length of messages according to a particular assumed probability model is called entropy encoding. 

Various techniques used by source coding schemes try to achieve the limit of Entropy of the source. C(x) ≥ H(x), where H(x) is entropy of source (bitrate), and C(x) is the bitrate after compression. In particular, no source coding scheme can be better than the entropy of the source. 

Example

Facsimile transmission uses a simple run length code. Source coding removes all data superfluous to the need of the transmitter, decreasing the bandwidth required for transmission. 

Channel coding

The purpose of channel coding theory is to find codes which transmit quickly, contain many valid code words and can correct or at least detect many errors. While not mutually exclusive, performance in these areas is a trade off. So, different codes are optimal for different applications. The needed properties of this code mainly depend on the probability of errors happening during transmission. In a typical CD, the impairment is mainly dust or scratches.

CDs use cross-interleaved Reed–Solomon coding to spread the data out over the disk.

Although not a very good code, a simple repeat code can serve as an understandable example. Suppose we take a block of data bits (representing sound) and send it three times. At the receiver we will examine the three repetitions bit by bit and take a majority vote. The twist on this is that we don't merely send the bits in order. We interleave them. The block of data bits is first divided into 4 smaller blocks. Then we cycle through the block and send one bit from the first, then the second, etc. This is done three times to spread the data out over the surface of the disk. In the context of the simple repeat code, this may not appear effective. However, there are more powerful codes known which are very effective at correcting the "burst" error of a scratch or a dust spot when this interleaving technique is used.

Other codes are more appropriate for different applications. Deep space communications are limited by the thermal noise of the receiver which is more of a continuous nature than a bursty nature. Likewise, narrowband modems are limited by the noise, present in the telephone network and also modeled better as a continuous disturbance. Cell phones are subject to rapid fading. The high frequencies used can cause rapid fading of the signal even if the receiver is moved a few inches. Again there are a class of channel codes that are designed to combat fading.

Linear codes

The term algebraic coding theory denotes the sub-field of coding theory where the properties of codes are expressed in algebraic terms and then further researched.

Algebraic coding theory is basically divided into two major types of codes:

1. Linear block codes
2. Convolutional codes

It analyzes the following three properties of a code – mainly:

• code word length
• total number of valid code words
• the minimum distance between two valid code words, using mainly the Hamming distance, sometimes also other distances like the Lee distance

Linear block codes

Linear block codes have the property of linearity, i.e. the sum of any two codewords is also a code word, and they are applied to the source bits in blocks, hence the name linear block codes. There are block codes that are not linear, but it is difficult to prove that a code is a good one without this property.

Linear block codes are summarized by their symbol alphabets (e.g., binary or ternary) and parameters (n,m,d_min) where

1. n is the length of the codeword, in symbols,
2. m is the number of source symbols that will be used for encoding at once,
3. d_min is the minimum hamming distance for the code.

There are many types of linear block codes, such as

1. Cyclic codes (e.g., Hamming codes)
2. Repetition codes
3. Parity codes
4. Polynomial codes (e.g., BCH codes)
5. Reed–Solomon codes
6. Algebraic geometric codes
7. Reed–Muller codes
8. Perfect codes

Block codes are tied to the sphere packing problem, which has received some attention over the years. In two dimensions, it is easy to visualize. Take a bunch of pennies flat on the table and push them together. The result is a hexagon pattern like a bee's nest. But block codes rely on more dimensions which cannot easily be visualized. The powerful (24,12) Golay code used in deep space communications uses 24 dimensions. If used as a binary code (which it usually is) the dimensions refer to the length of the codeword as defined above.

The theory of coding uses the N-dimensional sphere model. For example, how many pennies can be packed into a circle on a tabletop, or in 3 dimensions, how many marbles can be packed into a globe. Other considerations enter the choice of a code. For example, hexagon packing into the constraint of a rectangular box will leave empty space at the corners. As the dimensions get larger, the percentage of empty space grows smaller. But at certain dimensions, the packing uses all the space and these codes are the so-called "perfect" codes. The only nontrivial and useful perfect codes are the distance-3 Hamming codes with parameters satisfying (2^r – 1, 2^r – 1 – r, 3), and the [23,12,7] binary and [11,6,5] ternary Golay codes.

Another code property is the number of neighbors that a single codeword may have. Again, consider pennies as an example. First we pack the pennies in a rectangular grid. Each penny will have 4 near neighbors (and 4 at the corners which are farther away). In a hexagon, each penny will have 6 near neighbors. When we increase the dimensions, the number of near neighbors increases very rapidly. The result is the number of ways for noise to make the receiver choose a neighbor (hence an error) grows as well. This is a fundamental limitation of block codes, and indeed all codes. It may be harder to cause an error to a single neighbor, but the number of neighbors can be large enough so the total error probability actually suffers.

Properties of linear block codes are used in many applications. For example, the syndrome-coset uniqueness property of linear block codes is used in trellis shaping, one of the best known shaping codes. This same property is used in sensor networks for distributed source coding, and in lossy compression of noisy sparse sources.

Convolutional codes

The idea behind a convolutional code is to make every codeword symbol be the weighted sum of the various input message symbols. This is like convolution used in LTI systems to find the output of a system, when you know the input and impulse response. 

So we generally find the output of the system convolutional encoder, which is the convolution of the input bit, against the states of the convolution encoder, registers. 

Fundamentally, convolutional codes do not offer more protection against noise than an equivalent block code. In many cases, they generally offer greater simplicity of implementation over a block code of equal power. The encoder is usually a simple circuit which has state memory and some feedback logic, normally XOR gates. The decoder can be implemented in software or firmware.

The Viterbi algorithm is the optimum algorithm used to decode convolutional codes. There are simplifications to reduce the computational load. They rely on searching only the most likely paths. Although not optimum, they have generally been found to give good results in low noise environments.

Convolutional codes are used in voiceband modems (V.32, V.17, V.34) and in GSM mobile phones, as well as satellite and military communication devices.

Cryptographic coding

Cryptography or cryptographic coding is the practice and study of techniques for secure communication in the presence of third parties (called adversaries). More generally, it is about constructing and analyzing protocols that block adversaries; various aspects in information security such as data confidentiality, data integrity, authentication, and non-repudiation are central to modern cryptography. Modern cryptography exists at the intersection of the disciplines of mathematics, computer science, and electrical engineering. Applications of cryptography include ATM cards, computer passwords, and electronic commerce.

Cryptography prior to the modern age was effectively synonymous with encryption, the conversion of information from a readable state to apparent nonsense. The originator of an encrypted message shared the decoding technique needed to recover the original information only with intended recipients, thereby precluding unwanted persons from doing the same. Since World War I and the advent of the computer, the methods used to carry out cryptology have become increasingly complex and its application more widespread.

Modern cryptography is heavily based on mathematical theory and computer science practice; cryptographic algorithms are designed around computational hardness assumptions, making such algorithms hard to break in practice by any adversary. It is theoretically possible to break such a system, but it is infeasible to do so by any known practical means. These schemes are therefore termed computationally secure; theoretical advances, e.g., improvements in integer factorization algorithms, and faster computing technology require these solutions to be continually adapted. There exist information-theoretically secure schemes that provably cannot be broken even with unlimited computing power—an example is the one-time pad—but these schemes are more difficult to implement than the best theoretically breakable but computationally secure mechanisms.

Line coding

A line code (also called digital baseband modulation or digital baseband transmission method) is a code chosen for use within a communications system for baseband transmission purposes. Line coding is often used for digital data transport.

Line coding consists of representing the digital signal to be transported by an amplitude- and time-discrete signal that is optimally tuned for the specific properties of the physical channel (and of the receiving equipment). The waveform pattern of voltage or current used to represent the 1s and 0s of a digital data on a transmission link is called line encoding. The common types of line encoding are unipolar, polar, bipolar, and Manchester encoding.

Other applications of coding theory

Another concern of coding theory is designing codes that help synchronization. A code may be designed so that a phase shift can be easily detected and corrected and that multiple signals can be sent on the same channel.

Another application of codes, used in some mobile phone systems, is code-division multiple access (CDMA). Each phone is assigned a code sequence that is approximately uncorrelated with the codes of other phones. When transmitting, the code word is used to modulate the data bits representing the voice message. At the receiver, a demodulation process is performed to recover the data. The properties of this class of codes allow many users (with different codes) to use the same radio channel at the same time. To the receiver, the signals of other users will appear to the demodulator only as a low-level noise.

Another general class of codes are the automatic repeat-request (ARQ) codes. In these codes the sender adds redundancy to each message for error checking, usually by adding check bits. If the check bits are not consistent with the rest of the message when it arrives, the receiver will ask the sender to retransmit the message. All but the simplest wide area network protocols use ARQ. Common protocols include SDLC (IBM), TCP (Internet), X.25 (International) and many others. There is an extensive field of research on this topic because of the problem of matching a rejected packet against a new packet. Is it a new one or is it a retransmission? Typically numbering schemes are used, as in TCP."RFC793". RFCs. Internet Engineering Task Force (IETF). September 1981.

 

Group testing

Group testing uses codes in a different way. Consider a large group of items in which a very few are different in a particular way (e.g., defective products or infected test subjects). The idea of group testing is to determine which items are "different" by using as few tests as possible. The origin of the problem has its roots in the Second World War when the United States Army Air Forces needed to test its soldiers for syphilis.

Analog coding

Information is encoded analogously in the neural networks of brains, in analog signal processing, and analog electronics. Aspects of analog coding include analog error correction, analog data compression and analog encryption.

Neural coding

Neural coding is a neuroscience-related field concerned with how sensory and other information is represented in the brain by networks of neurons. The main goal of studying neural coding is to characterize the relationship between the stimulus and the individual or ensemble neuronal responses and the relationship among electrical activity of the neurons in the ensemble. It is thought that neurons can encode both digital and analog information, and that neurons follow the principles of information theory and compress information, and detect and correct errors in the signals that are sent throughout the brain and wider nervous system.