r-process

From Wikipedia, the free encyclopedia

Schematic illustrating the r-process as it occurs in supernovae or neutron star collisions. Neutrons are rapidly absorbed faster than the resulting nuclei can beta-decay; this allows the r-process to produce very neutron-rich nuclei follow the neutron drip line. There are waiting points located at magic numbers N = 50, 82, 126, where beta-decay is favored due to low neutron-capture cross sections resulting from the closed shells. The cycle then repeats until the next waiting point, creating yet heavier nuclei of elements up to the actinides; the natural abundance of these elements results entirely from the r-process. In the superheavy mass region (A ≥ 270), neutron-induced fission or spontaneous fission are expected to become dominant and end the r-process. Most nuclei along the hypothetical r-process path, however, are unknown.

 

The rapid neutron-capture process, or so-called r-process, is a set of nuclear reactions that in nuclear astrophysics is responsible for the creation (nucleosynthesis) of approximately half the abundances of the atomic nuclei heavier than iron, usually synthesizing the entire abundance of the two most neutron-rich stable isotopes of each heavy element. Chemical elements heavier than iron typically are enabled by the force between nucleons to be capable of six to ten stable isotopic forms having the same nuclear charge Z but differing in neutron number N, each of whose natural abundances contribute to the natural abundance of the chemical element. Each isotope is characterized by the number of neutrons that it contains. The r-process typically synthesizes new nuclei of the heaviest four isotopes of any heavy element, being totally responsible for the abundances of its two heaviest isotopes, which are referred to as r-only nuclei. The most abundant of these contribute to the r-process abundance peaks near atomic weights A = 82 (elements Se, Br and Kr), A = 130 (elements Te, I, and Xe) and A = 196 (elements Os, Ir and Pt).

The r-process entails a succession of rapid neutron captures (hence the name) by one or more heavy seed nuclei, typically beginning with nuclei in the abundance peak centered on ⁵⁶Fe. The captures must be rapid in the sense that the nuclei must not have time to undergo radioactive decay before another neutron arrives to be captured, a sequence that is halted only when the increasingly neutron-rich nuclei cannot physically retain another neutron. The r-process therefore must occur in locations where there exists a high density of free neutrons. Early studies reasoned that 10²⁴ free neutrons per cm³ would be required if the temperature were about one billion degrees in order that the waiting points, at which no more neutrons can be captured, be at the atomic numbers of the abundance peaks for r-process nuclei. This amounts to almost a gram of free neutrons in every cubic centimeter, an astonishing number requiring extreme locations. Traditionally this suggested the material ejected from the reexpanded core of a core-collapse supernova (as part of supernova nucleosynthesis) or decompression of neutron-star matter thrown off by a binary neutron star merger. The relative contributions of these sources to the astrophysical abundance of r-process elements is a matter of ongoing research.

A limited r-process-like series of neutron captures occurs to a minor extent in thermonuclear weapon explosions. These led to the discovery of the elements einsteinium (element 99) and fermium (element 100) in nuclear weapon fallout. 

The r-process contrasts with the s-process, the other predominant mechanism for the production of heavy elements, which is nucleosynthesis by means of slow captures of neutrons. The s-process primarily occurs within ordinary stars, particularly AGB stars, where the neutron flux is sufficient to cause neutron captures to recur every 10–100 years, much too slow for the r-process, which requires 100 captures per second. The s-process is secondary, meaning that it requires pre-existing heavy isotopes as seed nuclei to be converted into other heavy nuclei by a slow sequence of captures of free neutrons. The r-process scenarios create their own seed nuclei, so they might proceed in massive stars that contain no heavy seed nuclei. Taken together, the r- and s-processes account for almost the entire abundance of chemical elements heavier than iron. The historical challenge has been to locate physical settings appropriate for their time scales.

History

The need for a physical setting providing rapid capture of neutrons was seen from the relative abundances of isotopes of heavy chemical elements given in a table of abundances by Hans Suess and Harold Urey in 1956. Not only did their abundance table reveal larger than average abundances of natural isotopes containing magic numbers of neutrons but also abundance peaks about 10 amu lighter than those containing magic numbers of neutrons in their structure. They also realized that captures of free neutrons should be part of any explanation because of the lack of electric repulsion between nuclei and chargeless neutrons. This phenomenology suggested that these lighter subsidiary abundance peaks could result from radioactive nuclei having the magic neutron numbers but roughly ten fewer protons. To achieve this would require radioactive neutron-rich isotopes to capture another neutron faster than they can undergo beta decay in order to create abundance peaks that will decay subsequently to germanium, xenon, and platinum, elements prominent in the r-process abundance peaks. According to the nuclear shell model, radioactive nuclei that would decay into isotopes of these elements must have closed neutron shells near the neutron drip line, where more neutrons cannot be added. The neutron-capture flow must therefore wait for beta decay at those so-called waiting points, which therefore grow larger in abundance similar to water in a dammed up river. For those hitherto unexplained abundance peaks, which are approximately 10 u lighter than the s-process abundance peaks, to be created by rapid neutron capture implied that other neutron-rich nuclei would also be synthesized by the same process. That process, rapid neutron capture by neutron-rich isotopes, is called the r-process. A table apportioning the heavy isotopes phenomenologically between s-process and r-process isotopes was published in 1957 in the famous B²FH review paper which named the r-process and outlined the physics that guides it. Alastair G. W. Cameron also published a smaller study about the r-process in the same year.

The stationary r-process as described by the B²FH paper was first demonstrated in a time-dependent calculation at Caltech by Phillip A. Seeger, William A. Fowler and Donald D. Clayton, who found that no single temporal snapshot matched the solar r-process abundances, but, that when superposed, did achieve a successful characterization of the r-process abundance distribution. Shorter-time distributions emphasize abundances at atomic weights less than A = 140, whereas longer-time distributions emphasized those at atomic weights greater than A = 140. Subsequent treatments of the r-process reinforced those temporal features. Seeger et al. were also able to construct more quantitative apportionment between s-process and r-process of the abundance table of heavy isotopes, thereby establishing a more reliable abundance curve for the r-process isotopes than B²FH had been able to define. Today, the r-process abundances are determined using their technique of subtracting the more reliable s-process isotopic abundances from the total isotopic abundances and attributing the remainder to r-process nucleosynthesis. That r-process abundance curve (vs. atomic weight) has provided for many decades the target for theoretical computations of abundances synthesized by the physical r-process. 

The creation of free neutrons by electron capture during the rapid collapse to high density of a supernova core along with quick assembly of some neutron-rich seed nuclei makes the r process a primary nucleosynthesis process, meaning a process that can occur even in a star initially of pure H and He, in contrast to the B²FH designation as a secondary process building on preexisting iron. Primary stellar nucleosynthesis begins earlier in the galaxy than does secondary nucleosynthesis. Alternatively the high density of neutrons within neutron stars would be available for rapid assembly into r-process nuclei if a collision were to eject portions of a neutron star, which then rapidly expands freed from confinement. That sequence could also begin earlier in galactic time than would s-process nucleosynthesis; so each scenario fits the earlier growth of r-process abundances in the galaxy. Each of these scenarios is the subject of active theoretical research. Observational evidence of the early r-process enrichment of interstellar gas and of subsequent newly formed of stars, as applied to the abundance evolution of the galaxy of stars, was first laid out by James W. Truran in 1981. He and subsequent astronomers showed that the pattern of heavy-element abundances in the earliest metal-poor stars matched that of the shape of the solar r-process curve, as if the s-process component were missing. This was consistent with the hypothesis that the s-process had not yet begun to enrich interstellar gas when these young stars missing the s-process abundances were born from that gas, for it requires about 100 million years of galactic history for the s-process to get started whereas the r process can begin after two million years. These s-process-poor, r-process-rich stellar compositions must have been born earlier than any s-process, showing that the r-process emerges from quickly-evolving massive stars that become supernovae and leave neutron-star remnants that can merge with another neutron star. The primary nature of the early r-process thereby derives from observed abundance spectra in old stars that had been born early, when the galactic metallicity was still small, but that nonetheless contain their complement of r-process nuclei.

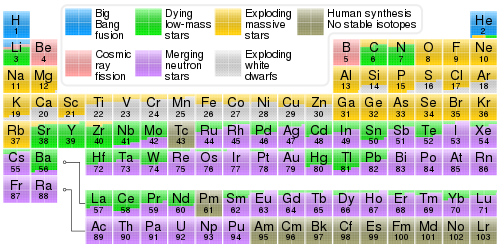
Periodic table showing the cosmogenic origin of each element. The elements heavier than iron with origins in supernovae are typically those produced by the r-process, which is powered by supernovae neutron bursts

 

Either interpretation, though generally supported by supernova experts, has yet to achieve a totally satisfactory calculation of r-process abundances because the overall problem is numerically formidable; but existing results are supportive. And in 2017 new data about the r-process was discovered when the LIGO and Virgo gravitational-wave observatories discovered a merger of two neutron stars ejecting r-process matter.

Noteworthy is that the r-process is responsible for our natural cohort of radioactive elements, such as uranium and thorium, as well as the most neutron-rich isotopes of each heavy element.

Nuclear physics

Immediately after the severe compression of electrons in a core-collapse supernova, beta-minus decay is blocked. This is because the high electron density fills all available free electron states up to a Fermi energy which is greater than the energy of nuclear beta decay. But nuclear capture of those free electrons still occurs, and causes increasing neutronization of matter. There results an extremely high density of free neutrons which cannot decay, and as a result a large neutron density (on the order of 10²⁴ neutrons per cm³) and high temperatures. As this re-expands and cools, neutron capture by still-existing heavy nuclei occurs much faster than beta-minus decay. As a consequence, the r-process runs up along the neutron drip line and highly-unstable neutron-rich nuclei are created. 

Three processes which affect the process of climbing the neutron drip line are; a notable decrease in the neutron-capture cross section at nuclei with closed neutron shells, the inhibiting process of photodisintegration, and the degree of nuclear stability in the heavy-isotope region. This last phenomenon terminates the r-process when its heaviest nuclei become unstable to spontaneous fission, which is currently believed to be in the neutron-rich region of the table of nuclides when the total number of nucleons approaches 270; even before this, the fission barrier may be low enough that neutron capture might induce fission instead of continuing up the neutron drip line. After the neutron flux decreases, these highly unstable radioactive nuclei undergo a rapid succession of beta decays until they reach more stable, neutron-rich nuclei. So, while the s-process creates an abundance of stable nuclei having closed neutron shells, the r-process in neutron-rich predecessor nuclei creates an abundance of radioactive nuclei about 10 amu below the s-process peaks after their decay back to stability.

The r-process also occurs in thermonuclear weapons, and was responsible for the initial discovery of neutron-rich almost stable isotopes of actinides like plutonium-244 and the new elements einsteinium and fermium (atomic numbers 99 and 100) in the 1950s. It has been suggested that multiple nuclear explosions would make it possible to reach the island of stability, as the affected nuclides (starting with uranium-238 as seed nuclei) would not have time to beta decay all the way to the quickly spontaneously fissioning nuclides at the line of beta stability before they absorbed more neutrons in the next explosion, thus providing a chance to reach neutron-rich superheavy nuclides like copernicium-291 and -293 which should have half-lives of centuries or millennia.

Astrophysical sites

The most probable candidate site for the r-process has long been suggested to be core-collapse supernovae (spectral types Ib, Ic and II), which may provide the necessary physical conditions for the r-process. However, the very low abundance of r-process nuclei in the interstellar gas limits the amount each can have ejected. It requires either that only a small fraction of supernovae eject r-process nuclei to the interstellar medium, or that each supernova ejects only a very small amount of r-process material. The ejected material must be relatively neutron-rich, a condition which has been difficult to achieve in models, so that astrophysicists remain uneasy about their adequacy for successful r-process yields. 

Entirely new astronomical data about the r process was discovered in 2017 when the LIGO and Virgo gravitational-wave observatories discovered a merger of two neutron stars. The localization on the sky of the source of the gravitational waves radiated by the collapse of the two neutron stars into a black hole, but with significant spun off mass of highly neutronized matter, enabled several teams to discover and study the optical counterpart of the merger, finding spectroscopic evidence of r-process material thrown off by the merging neutron stars. The bulk of this material seems to consist of two types: hot blue masses of highly radioactive r-process matter of lower-mass-range heavy nuclei (A < 140) and cooler red masses of higher mass-number r-process nuclei (A > 140) rich in actinides (such as uranium, thorium, californium etc). When released from the huge internal pressure of the neutron star, these ejecta expand and form seed heavy nuclei that rapidly capture free neutrons, and radiate detected optical light for about a week. Such duration of luminosity would not be possible without heating by internal radioactive decay, which is provided by r-process nuclei near their waiting points. Two distinct mass regions (A < 140 and A > 140) for the r-process yields have been known since the first time dependent calculations of the r-process. Because of these spectroscopic features it has been argued that such nucleosynthesis in the Milky Way has been primarily ejecta from neutron-star mergers rather than from supernovae.

These results offer a new possibility for clarifying six decades of uncertainty over the site of origin of r-process nuclei. Confirming relevance to the r-process is that it is radiogenic power from radioactive decay of r-process nuclei that maintains the visibility of these spun off r-process fragments. Otherwise they would dim quickly. Such alternative sites were first seriously proposed in 1974 as decompressing neutron star matter. It was proposed such matter is ejected from neutron stars merging with black holes in compact binaries. In 1989 (and 1999) this scenario was extended to binary neutron star mergers (a binary star system of two neutron stars that collide). After preliminary identification of these sites, the scenario was confirmed in GW170817.

Supernova nucleosynthesis

From Wikipedia, the free encyclopedia

Supernova nucleosynthesis is a theory of the nucleosynthesis of the natural abundances of the chemical elements in supernova explosions, advanced as the nucleosynthesis of elements from carbon to nickel in massive stars by Fred Hoyle in 1954. In massive stars, the nucleosynthesis by fusion of lighter elements into heavier ones occurs during sequential hydrostatic burning processes called helium burning, carbon burning, oxygen burning, and silicon burning, in which the ashes of one nuclear fuel become, after compressional heating, the fuel for the subsequent burning stage. During hydrostatic burning these fuels synthesize overwhelmingly the alpha-nucleus (A = 2Z) products. A rapid final explosive burning is caused by the sudden temperature spike owing to passage of the radially moving shock wave that was launched by the gravitational collapse of the core. W. D. Arnett and his Rice University colleagues demonstrated that the final shock burning would synthesize the non-alpha-nucleus isotopes more effectively than hydrostatic burning was able to do, suggesting that the expected shock-wave nucleosynthesis is an essential component of supernova nucleosynthesis. Together, shock-wave nucleosynthesis and hydrostatic-burning processes create most of the isotopes of the elements carbon (Z = 6), oxygen (Z = 8), and elements with Z = 10–28 (from neon to nickel). As a result of the ejection of the newly synthesized isotopes of the chemical elements by supernova explosions their abundances steadily increased within interstellar gas. That increase became evident to astronomers from the initial abundances in newly born stars exceeding those in earlier-born stars. To explain that temporal increase of the natural abundances of the elements was the main goal of stellar nucleosynthesis. Hoyle's paper was the founding paper of that theory; however, ideas about nuclear reactions in stars providing power for the stars is often confused with stellar nucleosynthesis. Realize that nuclear fusion in stars can occur with negligible impact on the abundances of the chemical elements. 

 

Elements heavier than nickel are comparatively rare owing to the decline with atomic weight of their nuclear binding energies per nucleon, but they too are created in part within supernovae. Of greatest interest historically has been their synthesis by rapid capture of neutrons during the r-process, reflecting the common belief that supernova cores are likely to provide the necessary conditions. But see the r-process below for a recently discovered alternative. The r-process isotopes are roughly a 100,000 times less abundant than the primary chemical elements fused in supernova shells above. Furthermore, other nucleosynthesis processes in supernovae are thought to also be responsible for some nucleosynthesis of other heavy elements, notably, the proton capture process known as the rp-process, the slow capture of neutrons (s-process) in the Helium-burning shells and in the carbon-burning shells of massive stars, and a photodisintegration process known as the γ-process (gamma-process). The latter synthesizes the lightest, most neutron-poor, isotopes of the elements heavier than iron from preexisting heavier isotopes.

History

The theory that nucleosynthesis of the chemical elements occurred primarily during advanced evolution of massive stars was first proposed by Hoyle in 1954, in which he predicted the existence of the excited state in the ¹²C nucleus that enables the triple-alpha process to burn resonantly, enabling it to heat the helium cores of stars while synthesizing massive quantities of carbon and oxygen; and he introduced the thermonuclear sequels of carbon-burning synthesizing Ne, Mg and Na and of oxygen-burning synthesizing Si, Al and S. Hoyle could not yet convincingly discern how silicon burning would happen, although he foresaw that it must be the final core fusion prior to operation of his thermal-equilibrium picture of iron formation. He also predicted that the collapse of the evolved cores of massive stars was "inevitable" owing to their increasing rate of energy loss by neutrinos. This work was so advanced relative to the state of astrophysics that it was hard to digest. Hoyle's 1954 theory fell into obscurity for decades after the more-famous B²FH paper was published in 1957 and, surprisingly, did not include Hoyle's original description of nucleosynthesis in massive stars. Donald D. Clayton has attributed the obscurity also to Hoyle's 1954 paper describing its key equation only in words, and a lack of careful review by Hoyle of the B²FH draft by coauthors who had themselves not adequately studied Hoyle's paper. During his 1955 discussions in Cambridge with his coauthors in preparation of the B2FH first draft in 1956 in Pasadena, Hoyle's modesty had inhibited him from emphasizing to them the great achievements of his 1954 theory. 

Thirteen years after the B2FH paper, W. D. Arnett and colleagues demonstrated that the final burning in the passing shock wave launched by collapse of the core could synthesize non-alpha-particle isotopes more effectively than hydrostatic burning could, suggesting that explosive nucleosynthesis is an essential component of supernova nucleosynthesis. A shock wave rebounded from matter collapsing onto the dense core, if strong enough to lead to mass ejection of the mantle of supernovae, would necessarily be strong enough to provide the sudden heating of the shells of massive stars needed for explosive thermonuclear burning within the mantle. Understanding how that shock wave can reach the mantle in the face of continuing infall onto the shock that became the theoretical difficulty. Supernova observations assured that it must occur.

Era of Computer Models

The papers of Hoyle (1946) and Hoyle (1954) and of B2FH (1957) were written by those scientists before the advent of the age of computers. They relied on hand calculations, deep thought, physical intuition, and familiarity with details of nuclear physics. Brilliant as these founding papers were, a cultural disconnect soon emerged with a younger generation of scientists who began to construct computer programs that would eventually yield numerical answers for the advanced evolution of stars and the nucleosynthesis within them. Most of this new generation never digested Hoyle (1954) carefully and in any case forgot what they had read in their focus on the immense task of computerizing massive stars. They usually did not cite Hoyle (1954), but they did cite B2FH as a needed default citation for stellar nucleosynthesis. This computer cultural revolution began in late 1960s. The upshot in regard to the puzzling confusion over Hoyle and B2FH that followed was made possible by the B2FH review's failure to describe Hoyle’s picture. Understandable was the feeling by the new generation of themselves discovering the correct picture that Hoyle had presented, albeit with huge numerical details that Hoyle could not provide. The computer models of massive stars demonstrated that core burning in massive stars occurred in smaller cores than the previous burning phase had. This shrinking of successive cores yielded an onion shell model of the sequence of burning phases, a shell model that was necessary for Hoyle's 1954 picture to work as simultaneous ejection of the abundances from each burning phase. Understanding this computer cultural revolution takes one far in understanding why Hoyle (1954) was forgotten and B2FH appeared to have been the work that founded stellar nucleosynthesis, as many even claimed. The field of working astronomers became devoted to B2FH owing to that paper's citation of about 100 research papers by astronomers showing evidence of abundance changes in stars owing to nuclear reactions. Such abundance alterations, which were visible at the telescopes, became confused with Hoyle's goal of understanding the origin of the huge interstellar abundances of the elements.

Cause

A supernova is a violent explosion of a star that occurs under two principal scenarios. The first is that a white dwarf star, which is the remnant of a low-mass star that has exhausted its nuclear fuel, undergoes a thermonuclear explosion after its mass is increased beyond its Chandrasekhar limit by accreting nuclear-fuel mass from a more diffuse companion star (usually a red giant) with which it is in binary orbit. The second, and about threefold more common, scenario occurs when a massive star (12–35 times more massive than the sun), usually a supergiant at the critical time, reaches nickel-56 in its core nuclear fusion (or burning) processes. Without exothermic energy from fusion, the core of the pre-supernova massive star loses heat needed for pressure support, and collapses owing to the strong gravitational pull. The energy transfer from the core collapse causes the supernova display. The nickel-56 isotope has one of the largest binding energies per nucleon of all isotopes, and is therefore the last isotope whose synthesis during core silicon burning releases energy by nuclear fusion, exothermically. The binding energy per nucleon declines for atomic weights heavier than A = 56, ending fusion's history of supplying thermal energy to the star. The thermal energy released when the infalling supernova mantle hits the semi-solid core is very large, about 10⁵³ ergs, about a hundred times the energy released by the supernova as the kinetic energy of its ejected mass. Dozens of research papers have been published in the attempt to describe the hydrodynamics of how that small one percent of the in falling energy is transmitted to the overlying mantle in the face of continuous infall onto the core. That uncertainty remains in the full description of core-collapse supernovae. 

Nuclear fusion reactions that produce elements heavier than iron absorb nuclear energy and are said to be endothermic reactions. When such reactions dominate, the internal temperature that supports the star's outer layers drops. Because the outer envelope is no longer sufficiently supported by the radiation pressure, the star's gravity pulls its mantle rapidly inward. As the star collapses, this mantle collides violently with the growing incompressible stellar core, which has a density almost as great as an atomic nucleus, producing a shockwave that rebounds outward through the unfused material of the outer shell. The increase of temperature by the passage of that shockwave is sufficient to induce fusion in that material, often called explosive nucleosynthesis. The energy deposited by the shockwave somehow leads to the star's explosion, dispersing fusing matter in the mantle above the core into interstellar space.

Silicon burning

After a star completes the oxygen burning process, its core is composed primarily of silicon and sulfur. If it has sufficiently high mass, it further contracts until its core reaches temperatures in the range of 2.7–3.5 billion Kelvin (230–300 keV). At these temperatures, silicon and other isotopes suffer photoejection of nucleons by energetic thermal photons (γ) ejecting especially alpha particles (⁴He). The nuclear process of silicon burning differs from earlier fusion stages of nucleosynthesis in that it entails a balance between alpha-particle captures and their inverse photo ejection which establishes abundances of all alpha-particle elements in the following sequence in which each alpha particle capture shown is opposed by its inverse reaction, namely, photo ejection of an alpha particle by the abundant thermal photons:

28Si	+		4He	⇌		32S	+	γ;
32S	+		4He	⇌		36Ar	+	γ;
36Ar	+		4He	⇌		40Ca	+	γ;
40Ca	+		4He	⇌		44Ti	+	γ;
44Ti	+		4He	⇌		48Cr	+	γ;
48Cr	+		4He	⇌		52Fe	+	γ;
52Fe	+		4He	⇌		56Ni	+	γ;
56Ni	+		4He	⇌		60Zn	+	γ.

The alpha-particle nuclei ⁴⁴Ti and those more massive in the final five reactions listed are all radioactive, but they decay after their ejection in supernova explosions into abundant isotopes of Ca, Ti, Cr, Fe and Ni. This post-supernova radioactivity became of great importance for the emergence of gamma-ray-line astronomy.

In these physical circumstances of rapid opposing reactions, namely alpha-particle capture and photo ejection of alpha particles, the abundances are not determined by alpha-particle-capture cross sections; rather they are determined by the values that the abundances must assume in order to balance the speeds of the rapid opposing-reaction currents. Each abundance takes on a stationary value that achieves that balance. This picture is called nuclear quasiequilibrium. Many computer calculations, for example, using the numerical rates of each reaction and of their reverse reactions have demonstrated that quasiequilibrium is not exact but does characterize well the computed abundances. Thus the quasiequilibrium picture presents a comprehensible picture of what actually happens. It also fills in an uncertainty in Hoyle's 1954 theory. The quasiequilibrium buildup shuts off after ⁵⁶Ni because the alpha-particle captures become slower whereas the photo ejections from heavier nuclei become faster. Non-alpha-particle nuclei also participate, using a host of reactions similar to ³⁶Ar + neutron ⇌ ³⁷Ar + photon and its inverse which set the stationary abundances of the non-alpha-particle isotopes, where the free densities of protons and neutrons are also established by the quasiequilibrium. However, the abundance of free neutrons is also proportional to the excess of neutrons over protons in the composition of the massive star; therefore the abundance of ³⁷Ar, using it as an example, is greater in ejecta from recent massive stars than it was from those in early stars of only H and He; therefore ³⁷Cl, to which ³⁷Ar decays after the nucleosynthesis, is called a "secondary isotope". The silicon burning in the star progresses through a temporal sequence of such nuclear quasiequilibria in which the abundance of ²⁸Si slowly declines and that of ⁵⁶Ni slowly increases. This amounts to a nuclear abundance change 2 ²⁸Si ≫ ⁵⁶Ni, which may be thought of as silicon burning into nickel in the nuclear sense. In interest of economy the photodisintegration rearrangement and the nuclear quasiequilibrium that it achieves is referred to as silicon burning. The entire silicon-burning sequence lasts about one day in the core of a contracting massive star and stops after ⁵⁶Ni has become the dominant abundance. The final explosive burning caused when the supernova shock passes through the silicon-burning shell lasts only seconds, but its roughly 50% increase in the temperature causes furious nuclear burning, which becomes the major contributor to nucleosynthesis in the mass range 28–60. The star can no longer release energy via nuclear fusion because a nucleus with 56 nucleons has the lowest mass per nucleon of all the elements in the sequence. The next step up in the alpha-particle chain would be ⁶⁰Zn, which has slightly more mass per nucleon and thus is less thermodynamically favorable. ⁵⁶Ni (which has 28 protons) has a half-life of 6.02 days and decays via β⁺ decay to ⁵⁶Co (27 protons), which in turn has a half-life of 77.3 days as it decays to ⁵⁶Fe (26 protons). However, only minutes are available for the ⁵⁶Ni to decay within the core of a massive star. This establishes ⁵⁶Ni as the most abundant of the radioactive nuclei created in this way. Its radioactivity energizes the late supernova light curve and creates the pathbreaking opportunity for gamma-ray-line astronomy. Clayton and Meyer have recently generalized this process still further by what they have named the secondary supernova machine, attributing the increasing radioactivity that energizes late supernova displays to the storage of increasing Coulomb energy within the quasiequilibrium nuclei called out above as the quasiequilibria shift from primarily ²⁸Si to primarily ⁵⁶Ni. The visible displays are powered by the decay of that excess Coulomb energy. 

During this phase of the core contraction, the potential energy of gravitational compression heats the interior to roughly three billion degrees K, which briefly maintains pressure support and opposes rapid core contraction. However, since no additional heat energy can be generated via new fusion reactions, the final unopposed contraction rapidly accelerates into a collapse lasting only a few seconds. The central portion of the star is now crushed into either a neutron star or, if the star is massive enough, a black hole. The outer layers of the star are blown off in an explosion triggered by the outward moving supernova shock, known as a Type II supernova whose displays last days to months. The escaping portion of the supernova core may initially contain a large density of free neutrons, which may synthesize, in about one second while inside the star, roughly half of the elements in the universe that are heavier than iron via a rapid neutron-capture mechanism known as the r-process. See below.

Nuclides synthesized

Composite image of Kepler's supernova from pictures by the Spitzer Space Telescope, Hubble Space Telescope, and Chandra X-ray Observatory.

 

Stars with initial masses less than about eight times the sun never develop a core large enough to collapse and they eventually lose their atmospheres to become white dwarfs, stable cooling spheres of carbon supported by the pressure of degenerate electrons. Nucleosynthesis within those lighter stars is therefore limited to nuclides that were fused in material located above the final white dwarf. This limits their modest yields returned to interstellar gas to carbon-13 and nitrogen-14, and to isotopes heavier than iron by slow capture of neutrons (the s-process). A significant minority of white dwarfs will nonetheless explode, however, because they formed in a binary orbit with a giant companion star that loses mass to the stronger gravitational field of the white dwarf, which then grows past its Chandrasekhar limit and explodes as a Type Ia supernova, synthesizing about a solar mass of radioactive ⁵⁶Ni isotopes. Its radioactive decay to iron keeps Type Ia optically very bright for weeks and creates more than half of all iron in the universe. Virtually all of the remainder of stellar nucleosynthesis occurs, however, in more frequent stars that are massive enough to end as Type II supernovae. In the presupernova massive star this includes helium burning, carbon burning, oxygen burning and silicon burning. Much of that yield may never leave the star but instead disappears into its collapsed core. The yield that is ejected is substantially fused in last-second explosive burning caused by the shock wave launched by core collapse. Prior to core collapse, fusion of elements between silicon and iron occurs only in the largest of stars, and then in limited amounts. Thus the nucleosynthesis of the abundant primary elements defined as those that could be synthesized in stars of initially only hydrogen and helium (left by the Big Bang), is substantially limited to core-collapse supernova nucleosynthesis.

The r-process

A version of the periodic table indicating the main origin of elements found on Earth. All elements past plutonium (element 94) are manmade.

 

During supernova nucleosynthesis, the r-process creates very neutron-rich heavy isotopes, which decay after the event to the first stable isotope, thereby creating the neutron-rich stable isotopes of all heavy elements. This neutron capture process occurs in high neutron density with high temperature conditions. In the r-process, any heavy nuclei are bombarded with a large neutron flux to form highly unstable neutron rich nuclei which very rapidly undergo beta decay to form more stable nuclei with higher atomic number and the same atomic mass. The neutron density is extremely high, about 10^22-24 neutrons per cubic centimeter. First calculation of an evolving r-process, showing the evolution of calculated results with time, also suggested that the r-process abundances are a superposition of differing neutron fluences. Small fluence produces the first r-process abundance peak near atomic weight A = 130 but no actinides, whereas large fluence produces the actinides uranium and thorium but no longer contains the A = 130 abundance peak. These processes occur in a fraction of a second to a few seconds, depending on details. Hundreds of subsequent papers published have utilized this time-dependent approach. The only modern nearby supernova, 1987A, has not revealed r-process enrichments. Modern thinking is that the r-process yield may be ejected from some supernovae but swallowed up in others as part of the residual neutron star or black hole. 

Entirely new astronomical data about the r-process was discovered in 2017 when the LIGO and Virgo gravitational-wave observatories discovered a merger of two neutron stars that had previously been orbiting one another That can happen when both massive stars in orbit with one another become core-collapse supernovae, leaving neutron-star remnants. Everyone could "hear" the replay of the increasing orbital frequency as the orbit became smaller and faster owing to energy loss by gravitational waves. The localization on the sky of the source of those gravitational waves radiated by that orbital collapse and merger of the two neutron stars, creating a black hole, but with significant spun off mass of highly neutronized matter, enabled several teams to discover and study the remaining optical counterpart of the merger, finding spectroscopic evidence of r-process material thrown off by the merging neutron stars. The bulk of this material seems to consist of two types: hot blue masses of highly radioactive r-process matter of lower-mass-range heavy nuclei (A < 140) and cooler red masses of higher mass-number r-process nuclei (A > 140) rich in lanthanides (such as uranium, thorium, californium etc.). When released from the huge internal pressure of the neutron star, these neutralized ejecta expand and radiate detected optical light for about a week. Such duration of luminosity would not be possible without heating by internal radioactive decay, which is provided by r-process nuclei near their waiting points. Two distinct mass regions (A < 140 and A > 140) for the r-process yields have been known since the first time dependent calculations of the r-process. Because of these spectroscopic features it has been argued that r-process nucleosynthesis in the Milky Way may have been primarily ejecta from neutron-star mergers rather than from supernovae. These results offer a new possibility for clarifying six decades of uncertainty over the site of origin of r-process nuclei. Confirming relevance of this discovery by gravitational-wave astronomy to the r-process is the radiogenic power from radioactive decay of r-process nuclei that maintains the visibility of these spun off r-process fragments. Otherwise they would dim quickly. Unquestionably this discovery raised support for such mergers being the main sources of the r-process nuclei rather than core-collapse supernovae; but that debate continues.

Type II supernova

From Wikipedia, the free encyclopedia

The expanding remnant of SN 1987A, a Type II-P supernova in the Large Magellanic Cloud. NASA image.

 

A Type II supernova (plural: supernovae or supernovas) results from the rapid collapse and violent explosion of a massive star. A star must have at least 8 times, but no more than 40 to 50 times, the mass of the Sun (M_☉) to undergo this type of explosion. Type II supernovae are distinguished from other types of supernovae by the presence of hydrogen in their spectra. They are usually observed in the spiral arms of galaxies and in H II regions, but not in elliptical galaxies. 

Stars generate energy by the nuclear fusion of elements. Unlike the Sun, massive stars possess the mass needed to fuse elements that have an atomic mass greater than hydrogen and helium, albeit at increasingly higher temperatures and pressures, causing increasingly shorter stellar life spans. The degeneracy pressure of electrons and the energy generated by these fusion reactions are sufficient to counter the force of gravity and prevent the star from collapsing, maintaining stellar equilibrium. The star fuses increasingly higher mass elements, starting with hydrogen and then helium, progressing up through the periodic table until a core of iron and nickel is produced. Fusion of iron or nickel produces no net energy output, so no further fusion can take place, leaving the nickel–iron core inert. Due to the lack of energy output creating outward thermal pressure, the core contracts due to gravity until the overlying weight of the star can be supported largely by electron degeneracy pressure. 

When the compacted mass of the inert core exceeds the Chandrasekhar limit of about 1.4 M_☉, electron degeneracy is no longer sufficient to counter the gravitational compression. A cataclysmic implosion of the core takes place within seconds. Without the support of the now-imploded inner core, the outer core collapses inwards under gravity and reaches a velocity of up to 23% of the speed of light and the sudden compression increases the temperature of the inner core to up to 100 billion kelvins. Neutrons and neutrinos are formed via reversed beta-decay, releasing about 10⁴⁶ joules (100 foe) in a ten-second burst. Also, the collapse of the inner core is halted by neutron degeneracy, causing the implosion to rebound and bounce outward. The energy of this expanding shock wave is sufficient to disrupt the overlying stellar material and accelerate it to escape velocity, forming a supernova explosion. The shock wave and extremely high temperature and pressure rapidly dissipate but are present for long enough to allow for a brief period during which the production of elements heavier than iron occurs. Depending on initial size of the star, the remnants of the core form a neutron star or a black hole. Because of the underlying mechanism, the resulting supernova is also described as a core-collapse supernova. 

There exist several categories of Type II supernova explosions, which are categorized based on the resulting light curve—a graph of luminosity versus time—following the explosion. Type II-L supernovae show a steady (linear) decline of the light curve following the explosion, whereas Type II-P display a period of slower decline (a plateau) in their light curve followed by a normal decay. Type Ib and Ic supernovae are a type of core-collapse supernova for a massive star that has shed its outer envelope of hydrogen and (for Type Ic) helium. As a result, they appear to be lacking in these elements.

Formation

The onion-like layers of a massive, evolved star just before core collapse. (Not to scale.)

 

Stars far more massive than the sun evolve in more complex ways. In the core of the star, hydrogen is fused into helium, releasing thermal energy that heats the sun's core and provides outward pressure that supports the sun's layers against collapse in a process known as stellar or hydrostatic equilibrium. The helium produced in the core accumulates there since temperatures in the core are not yet high enough to cause it to fuse. Eventually, as the hydrogen at the core is exhausted, fusion starts to slow down, and gravity causes the core to contract. This contraction raises the temperature high enough to initiate a shorter phase of helium fusion, which accounts for less than 10% of the star's total lifetime. In stars with fewer than eight solar masses, the carbon produced by helium fusion does not fuse, and the star gradually cools to become a white dwarf. White dwarf stars, if they have a near companion, may then become Type Ia supernovae. 

A much larger star, however, is massive enough to create temperatures and pressures needed to cause the carbon in the core to begin to fuse when the star contracts at the end of the helium-burning stage. The cores of these massive stars become layered like onions as progressively heavier atomic nuclei build up at the center, with an outermost layer of hydrogen gas, surrounding a layer of hydrogen fusing into helium, surrounding a layer of helium fusing into carbon via the triple-alpha process, surrounding layers that fuse to progressively heavier elements. As a star this massive evolves, it undergoes repeated stages where fusion in the core stops, and the core collapses until the pressure and temperature are sufficient to begin the next stage of fusion, reigniting to halt collapse.

Core-burning nuclear fusion stages for a 25-solar mass star

Process	Main fuel	Main products	25 M☉ star
			Temperature (K)	Density (g/cm3)	Duration
hydrogen burning	hydrogen	helium	7×107	10	107 years
triple-alpha process	helium	carbon, oxygen	2×108	2000	106 years
carbon burning process	carbon	Ne, Na, Mg, Al	8×108	106	1000 years
neon burning process	neon	O, Mg	1.6×109	107	3 years
oxygen burning process	oxygen	Si, S, Ar, Ca	1.8×109	107	0.3 years
silicon burning process	silicon	nickel (decays into iron)	2.5×109	108	5 days

Core collapse

The factor limiting this process is the amount of energy that is released through fusion, which is dependent on the binding energy that holds together these atomic nuclei. Each additional step produces progressively heavier nuclei, which release progressively less energy when fusing. In addition, from carbon-burning onwards, energy loss via neutrino production becomes significant, leading to a higher rate of reaction than would otherwise take place. This continues until nickel-56 is produced, which decays radioactively into cobalt-56 and then iron-56 over the course of a few months. As iron and nickel have the highest binding energy per nucleon of all the elements, energy cannot be produced at the core by fusion, and a nickel-iron core grows. This core is under huge gravitational pressure. As there is no fusion to further raise the star's temperature to support it against collapse, it is supported only by degeneracy pressure of electrons. In this state, matter is so dense that further compaction would require electrons to occupy the same energy states. However, this is forbidden for identical fermion particles, such as the electron – a phenomenon called the Pauli exclusion principle. 

When the core's mass exceeds the Chandrasekhar limit of about 1.4 M_☉, degeneracy pressure can no longer support it, and catastrophic collapse ensues. The outer part of the core reaches velocities of up to 70000 km/s (23% of the speed of light) as it collapses toward the center of the star. The rapidly shrinking core heats up, producing high-energy gamma rays that decompose iron nuclei into helium nuclei and free neutrons via photodisintegration. As the core's density increases, it becomes energetically favorable for electrons and protons to merge via inverse beta decay, producing neutrons and elementary particles called neutrinos. Because neutrinos rarely interact with normal matter, they can escape from the core, carrying away energy and further accelerating the collapse, which proceeds over a timescale of milliseconds. As the core detaches from the outer layers of the star, some of these neutrinos are absorbed by the star's outer layers, beginning the supernova explosion.

For Type II supernovae, the collapse is eventually halted by short-range repulsive neutron-neutron interactions, mediated by the strong force, as well as by degeneracy pressure of neutrons, at a density comparable to that of an atomic nucleus. When the collapse stops, the infalling matter rebounds, producing a shock wave that propagates outward. The energy from this shock dissociates heavy elements within the core. This reduces the energy of the shock, which can stall the explosion within the outer core.

The core collapse phase is so dense and energetic that only neutrinos are able to escape. As the protons and electrons combine to form neutrons by means of electron capture, an electron neutrino is produced. In a typical Type II supernova, the newly formed neutron core has an initial temperature of about 100 billion kelvins, 10⁴ times the temperature of the Sun's core. Much of this thermal energy must be shed for a stable neutron star to form, otherwise the neutrons would "boil away". This is accomplished by a further release of neutrinos. These 'thermal' neutrinos form as neutrino-antineutrino pairs of all flavors, and total several times the number of electron-capture neutrinos. The two neutrino production mechanisms convert the gravitational potential energy of the collapse into a ten-second neutrino burst, releasing about 10⁴⁶ joules (100 foe).

Through a process that is not clearly understood, about 1%, or 10⁴⁴ joules (1 foe), of the energy released (in the form of neutrinos) is reabsorbed by the stalled shock, producing the supernova explosion. Neutrinos generated by a supernova were observed in the case of Supernova 1987A, leading astrophysicists to conclude that the core collapse picture is basically correct. The water-based Kamiokande II and IMB instruments detected antineutrinos of thermal origin, while the gallium-71-based Baksan instrument detected neutrinos (lepton number = 1) of either thermal or electron-capture origin.

Within a massive, evolved star (a) the onion-layered shells of elements undergo fusion, forming a nickel-iron core (b) that reaches Chandrasekhar-mass and starts to collapse. The inner part of the core is compressed into neutrons (c), causing infalling material to bounce (d) and form an outward-propagating shock front (red). The shock starts to stall (e), but it is re-invigorated by neutrino interaction. The surrounding material is blasted away (f), leaving only a degenerate remnant.

 

When the progenitor star is below about 20 M_☉ – depending on the strength of the explosion and the amount of material that falls back – the degenerate remnant of a core collapse is a neutron star. Above this mass, the remnant collapses to form a black hole. The theoretical limiting mass for this type of core collapse scenario is about 40–50 M_☉. Above that mass, a star is believed to collapse directly into a black hole without forming a supernova explosion, although uncertainties in models of supernova collapse make calculation of these limits uncertain.

Theoretical models

The Standard Model of particle physics is a theory which describes three of the four known fundamental interactions between the elementary particles that make up all matter. This theory allows predictions to be made about how particles will interact under many conditions. The energy per particle in a supernova is typically 1–150 picojoules (tens to hundreds of MeV). The per-particle energy involved in a supernova is small enough that the predictions gained from the Standard Model of particle physics are likely to be basically correct. But the high densities may require corrections to the Standard Model. In particular, Earth-based particle accelerators can produce particle interactions which are of much higher energy than are found in supernovae, but these experiments involve individual particles interacting with individual particles, and it is likely that the high densities within the supernova will produce novel effects. The interactions between neutrinos and the other particles in the supernova take place with the weak nuclear force, which is believed to be well understood. However, the interactions between the protons and neutrons involve the strong nuclear force, which is much less well understood.

The major unsolved problem with Type II supernovae is that it is not understood how the burst of neutrinos transfers its energy to the rest of the star producing the shock wave which causes the star to explode. From the above discussion, only one percent of the energy needs to be transferred to produce an explosion, but explaining how that one percent of transfer occurs has proven very difficult, even though the particle interactions involved are believed to be well understood. In the 1990s, one model for doing this involved convective overturn, which suggests that convection, either from neutrinos from below, or infalling matter from above, completes the process of destroying the progenitor star. Heavier elements than iron are formed during this explosion by neutron capture, and from the pressure of the neutrinos pressing into the boundary of the "neutrinosphere", seeding the surrounding space with a cloud of gas and dust which is richer in heavy elements than the material from which the star originally formed.

Neutrino physics, which is modeled by the Standard Model, is crucial to the understanding of this process. The other crucial area of investigation is the hydrodynamics of the plasma that makes up the dying star; how it behaves during the core collapse determines when and how the shockwave forms and when and how it stalls and is reenergized.

In fact, some theoretical models incorporate a hydrodynamical instability in the stalled shock known as the "Standing Accretion Shock Instability" (SASI). This instability comes about as a consequence of non-spherical perturbations oscillating the stalled shock thereby deforming it. The SASI is often used in tandem with neutrino theories in computer simulations for re-energizing the stalled shock.

Computer models have been very successful at calculating the behavior of Type II supernovae when the shock has been formed. By ignoring the first second of the explosion, and assuming that an explosion is started, astrophysicists have been able to make detailed predictions about the elements produced by the supernova and of the expected light curve from the supernova.

Light curves for Type II-L and Type II-P supernovae

This graph of the luminosity as a function of time shows the characteristic shapes of the light curves for a Type II-L and II-P supernova.

 

When the spectrum of a Type II supernova is examined, it normally displays Balmer absorption lines – reduced flux at the characteristic frequencies where hydrogen atoms absorb energy. The presence of these lines is used to distinguish this category of supernova from a Type I supernova. 

When the luminosity of a Type II supernova is plotted over a period of time, it shows a characteristic rise to a peak brightness followed by a decline. These light curves have an average decay rate of 0.008 magnitudes per day; much lower than the decay rate for Type Ia supernovae. Type II is subdivided into two classes, depending on the shape of the light curve. The light curve for a Type II-L supernova shows a steady (linear) decline following the peak brightness. By contrast, the light curve of a Type II-P supernova has a distinctive flat stretch (called a plateau) during the decline; representing a period where the luminosity decays at a slower rate. The net luminosity decay rate is lower, at 0.0075 magnitudes per day for Type II-P, compared to 0.012 magnitudes per day for Type II-L.

The difference in the shape of the light curves is believed to be caused, in the case of Type II-L supernovae, by the expulsion of most of the hydrogen envelope of the progenitor star. The plateau phase in Type II-P supernovae is due to a change in the opacity of the exterior layer. The shock wave ionizes the hydrogen in the outer envelope – stripping the electron from the hydrogen atom – resulting in a significant increase in the opacity. This prevents photons from the inner parts of the explosion from escaping. When the hydrogen cools sufficiently to recombine, the outer layer becomes transparent.

Type IIn supernovae

The "n" denotes narrow, which indicates the presence of narrow or intermediate width hydrogen emission lines in the spectra. In the intermediate width case, the ejecta from the explosion may be interacting strongly with gas around the star – the circumstellar medium. The estimated circumstellar density required to explain the observational properties is much higher than that expected from the standard stellar evolution theory. It is generally assumed that the high circumstellar density is due to the high mass-loss rates of the Type IIn progenitors. The estimated mass-loss rates are typically higher than 10⁻³ M_☉ per year. There are indications that they originate as stars similar to Luminous blue variables with large mass losses before exploding. SN 1998S and SN 2005gl are examples of Type IIn supernovae; SN 2006gy, an extremely energetic supernova, may be another example.

Type IIb supernovae

A Type IIb supernova has a weak hydrogen line in its initial spectrum, which is why it is classified as a Type II. However, later on the H emission becomes undetectable, and there is also a second peak in the light curve that has a spectrum which more closely resembles a Type Ib supernova. The progenitor could have been a massive star that expelled most of its outer layers, or one which lost most of its hydrogen envelope due to interactions with a companion in a binary system, leaving behind the core that consisted almost entirely of helium. As the ejecta of a Type IIb expands, the hydrogen layer quickly becomes more transparent and reveals the deeper layers. The classic example of a Type IIb supernova is SN 1993J, while another example is Cassiopeia A. The IIb class was first introduced (as a theoretical concept) by Woosley et al. in 1987, and the class was soon applied to SN 1987K and SN 1993J.

Hypernovae

Hypernovae are a rare type of supernova substantially more luminous and energetic than standard supernovae. Examples are SN 1997ef (type Ic) and SN 1997cy (type IIn). Hypernovae are produced by more than one type of event: relativistic jets during formation of a black hole from fallback of material onto the neutron star core, the collapsar model; interaction with a dense envelope of circumstellar material, the CSM model; the highest mass pair instability supernovae; possibly others such as binary and quark star model. 

Stars with initial masses between about 25 and 90 times the sun develop cores large enough that after a supernova explosion, some material will fall back onto the neutron star core and create a black hole. In many cases this reduces the luminosity of the supernova, and above 90 M_☉ the star collapses directly into a black hole without a supernova explosion. However, if the progenitor is spinning quickly enough the infalling material generates relativistic jets that emit more energy than the original explosion. They may also be seen directly if beamed towards us, giving the impression of an even more luminous object. In some cases these can produce gamma-ray bursts, although not all gamma-ray bursts are from supernovae.

In some cases a type II supernova occurs when the star is surrounded by a very dense cloud of material, most likely expelled during luminous blue variable eruptions. This material is shocked by the explosion and becomes more luminous than a standard supernova. It is likely that there is a range of luminosities for these type IIn supernovae with only the brightest qualifying as a hypernova. 

Pair instability supernovae occur when an oxygen core in an extremely massive star becomes hot enough that gamma rays spontaneously produce electron-positron pairs. This causes the core to collapse, but where the collapse of an iron core causes endothermic fusion to heavier elements, the collapse of an oxygen core creates runaway exothermic fusion which completely unbinds the star. The total energy emitted depends on the initial mass, with much of the core being converted to nickel-56 and ejected which then powers the supernova for many months. At the lower end stars of about 140 M_☉ produce supernovae that are long-lived but otherwise typical, while the highest mass stars of around 250 M_☉ produce supernovae that are extremely luminous and also very long lived; hypernovae. More massive stars die by photodisintegration. Only population III stars, with very low metallicity, can reach this stage. Stars with more heavy elements are more opaque and blow away their outer layers until they are small enough to explode as a normal type Ibc supernova. It is thought that even in our own galaxy, mergers of old low metallicity stars may form massive stars capable of creating a pair instability supernova.