From Wikipedia, the free encyclopedia

As the temperature of a black body decreases, its intensity also decreases and its peak moves to longer wavelengths. Shown for comparison is the classical Rayleigh–Jeans law and its ultraviolet catastrophe.
A black body (also, blackbody) is an idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. A white body is one with a "rough surface [that] reflects all incident rays completely and uniformly in all directions."[1]
A black body in thermal equilibrium (that is, at a constant temperature) emits electromagnetic radiation called black-body radiation. The radiation is emitted according to Planck's law, meaning that it has a spectrum that is determined by the temperature alone (see figure at right), not by the body's shape or composition.
A black body in thermal equilibrium has two notable properties:[2]
- It is an ideal emitter: at every frequency, it emits as much energy as – or more energy than – any other body at the same temperature.
- It is a diffuse emitter: the energy is radiated isotropically, independent of direction.
Real materials emit energy at a fraction—called the emissivity—of black-body energy levels. By definition, a black body in thermal equilibrium has an emissivity of ε = 1.0. A source with lower emissivity independent of frequency often is referred to as a gray body.[5][6] Construction of black bodies with emissivity as close to one as possible remains a topic of current interest.[7]
In astronomy, the radiation from stars and planets is sometimes characterized in terms of an effective temperature, the temperature of a black body that would emit the same total flux of electromagnetic energy.
Definition
The idea of a black body originally was introduced by Gustav Kirchhoff in 1860 as follows:| ...the supposition that bodies can be imagined which, for infinitely small thicknesses, completely absorb all incident rays, and neither reflect nor transmit any. I shall call such bodies perfectly black, or, more briefly, black bodies.[8] |
A more modern definition drops the reference to "infinitely small thicknesses":[9]
An ideal body is now defined, called a blackbody. A blackbody allows all incident radiation to pass into it (no reflected energy) and internally absorbs all the incident radiation (no energy transmitted through the body). This is true for radiation of all wavelengths and for all angles of incidence. Hence the blackbody is a perfect absorber for all incident radiation. [10] |
Idealizations
This section describes some concepts developed in connection with black bodies.Cavity with a hole
A widely used model of a black surface is a small hole in a cavity with walls that are opaque to radiation.[10]Radiation incident on the hole will pass into the cavity, and is very unlikely to be re-emitted if the cavity is large. The hole is not quite a perfect black surface — in particular, if the wavelength of the incident radiation is longer than the diameter of the hole, part will be reflected. Similarly, even in perfect thermal equilibrium, the radiation inside a finite-sized cavity will not have an ideal Planck spectrum for wavelengths comparable to or larger than the size of the cavity.[11]
Suppose the cavity is held at a fixed temperature T and the radiation trapped inside the enclosure is at thermal equilibrium with the enclosure. The hole in the enclosure will allow some radiation to escape. If the hole is small, radiation passing in and out of the hole has negligible effect upon the equilibrium of the radiation inside the cavity. This escaping radiation will approximate black-body radiation that exhibits a distribution in energy characteristic of the temperature T and does not depend upon the properties of the cavity or the hole, at least for wavelengths smaller than the size of the hole.[11] See the figure in the Introduction for the spectrum as a function of the frequency of the radiation, which is related to the energy of the radiation by the equation E=hf, with E = energy, h = Planck's constant, f = frequency.
At any given time the radiation in the cavity may not be in thermal equilibrium, but the second law of thermodynamics states that if left undisturbed it will eventually reach equilibrium,[12] although the time it takes to do so may be very long.[13] Typically, equilibrium is reached by continual absorption and emission of radiation by material in the cavity or its walls.[3][4][14][15] Radiation entering the cavity will be "thermalized"; by this mechanism: the energy will be redistributed until the ensemble of photons achieves a Planck distribution. The time taken for thermalization is much faster with condensed matter present than with rarefied matter such as a dilute gas.
At temperatures below billions of Kelvin, direct photon–photon interactions[16] are usually negligible compared to interactions with matter.[17] Photons are an example of an interacting boson gas,[18] and as described by the H-theorem,[19] under very general conditions any interacting boson gas will approach thermal equilibrium.
Transmission, absorption, and reflection
A body's behavior with regard to thermal radiation is characterized by its transmission τ, absorption α, and reflection ρ.The boundary of a body forms an interface with its surroundings, and this interface may be rough or smooth. A nonreflecting interface separating regions with different refractive indices must be rough, because the laws of reflection and refraction governed by the Fresnel equations for a smooth interface require a reflected ray when the refractive indices of the material and its surroundings differ.[20] A few idealized types of behavior are given particular names:
An opaque body is one that transmits none of the radiation that reaches it, although some may be reflected.[21][22]
That is, τ=0 and α+ρ=1
A transparent body is one that transmits all the radiation that reaches it. That is, τ=1 and α=ρ=0.
A gray body is one where α, ρ and τ are uniform for all wavelengths. This term also is used to mean a body for which α is temperature and wavelength independent.
A white body is one for which all incident radiation is reflected uniformly in all directions: τ=0, α=0, and ρ=1.
For a black body, τ=0, α=1, and ρ=0. Planck offers a theoretical model for perfectly black bodies, which he noted do not exist in nature: besides their opaque interior, they have interfaces that are perfectly transmitting and non-reflective.[23]
Kirchhoff's perfect black bodies
Kirchhoff in 1860 introduced the theoretical concept of a perfect black body with a completely absorbing surface layer of infinitely small thickness, but Planck noted some severe restrictions upon this idea. Planck noted three requirements upon a black body: the body must (i) allow radiation to enter but not reflect; (ii) possess a minimum thickness adequate to absorb the incident radiation and prevent its re-emission; (iii) satisfy severe limitations upon scattering to prevent radiation from entering and bouncing back out. As a consequence, Kirchhoff's perfect black bodies that absorb all the radiation that falls on them cannot be realized in an infinitely thin surface layer, and impose conditions upon scattering of the light within the black body that are difficult to satisfy.[24][25]Realizations
A realization of a black body is a real world, physical embodiment. Here are a few.Cavity with a hole
In 1898, Otto Lummer and Ferdinand Kurlbaum published an account of their cavity radiation source.[26] Their design has been used largely unchanged for radiation measurements to the present day. It was a hole in the wall of a platinum box, divided by diaphragms, with its interior blackened with iron oxide. It was an important ingredient for the progressively improved measurements that led to the discovery of Planck's law.[27][28] A version described in 1901 had its interior blackened with a mixture of chromium, nickel, and cobalt oxides.[29]Near-black materials
There is interest in blackbody-like materials for camouflage and radar-absorbent materials for radar invisibility.[30][31] They also have application as solar energy collectors, and infrared thermal detectors. As a perfect emitter of radiation, a hot material with black body behavior would create an efficient infrared heater, particularly in space or in a vacuum where convective heating is unavailable.[32] They are also useful in telescopes and cameras as anti-reflection surfaces to reduce stray light, and to gather information about objects in high-contrast areas (for example, observation of planets in orbit around their stars), where blackbody-like materials absorb light that comes from the wrong sources.It has long been known that a lamp-black coating will make a body nearly black. An improvement on lamp-black is found in manufactured carbon nanotubes. Nano-porous materials can achieve refractive indices nearly that of vacuum, in one case obtaining average reflectance of 0.045%.[7][33] In 2009, a team of Japanese scientists created a material called nanoblack which is close to an ideal black body, based on vertically aligned single-walled carbon nanotubes. This absorbs between 98% and 99% of the incoming light in the spectral range from the ultra-violet to the far-infrared regions.[32]
Another example of a nearly perfect black material is super black, made by chemically etching a nickel–phosphorus alloy.[34]
Stars and planets
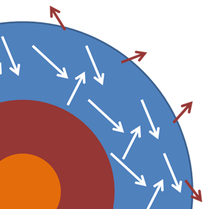
An idealized view of the cross-section of a star. The photosphere contains photons of light nearly in thermal equilibrium, and some escape into space as near-black-body radiation.
A star or planet often is modeled as a black body, and electromagnetic radiation emitted from these bodies as black-body radiation. The figure shows a highly schematic cross-section to illustrate the idea. The photosphere of the star, where the emitted light is generated, is idealized as a layer within which the photons of light interact with the material in the photosphere and achieve a common temperature T that is maintained over a long period of time.
Some photons escape and are emitted into space, but the energy they carry away is replaced by energy from within the star, so that the temperature of the photosphere is nearly steady. Changes in the core lead to changes in the supply of energy to the photosphere, but such changes are slow on the time scale of interest here. Assuming these circumstances can be realized, the outer layer of the star is somewhat analogous to the example of an enclosure with a small hole in it, with the hole replaced by the limited transmission into space at the outside of the photosphere.
With all these assumptions in place, the star emits black-body radiation at the temperature of the photosphere.[35]

Effective temperature of a black body compared with the B-V and U-B color index of main sequence and super giant stars in what is called a color-color diagram.[36]
Using this model the effective temperature of stars is estimated, defined as the temperature of a black body that yields the same surface flux of energy as the star. If a star were a black body, the same effective temperature would result from any region of the spectrum. For example, comparisons in the B (blue) or V (visible) range lead to the so-called B-V color index, which increases the redder the star,[37] with the Sun having an index of +0.648 ± 0.006.[38] Combining the U (ultraviolet) and the B indices leads to the U-B index, which becomes more negative the hotter the star and the more the UV radiation. Assuming the Sun is a type G2 V star, its U-B index is +0.12.[39] The two indices for two types of stars are compared in the figure with the effective surface temperature of the stars assuming they are black bodies. It can be seen that there is only a rough correlation. For example, for a given B-V index from the blue-visible region of the spectrum., the curves for both types of star lie below the corresponding black-body U-B index that includes the ultraviolet spectrum, showing that both types of star emit less ultraviolet light than a black body with the same B-V index. It is perhaps surprising that they fit a black body curve as well as they do, considering that stars have greatly different temperatures at different depths.[40] For example, the Sun has an effective temperature of 5780 K,[41] which can be compared to the temperature of the photosphere of the Sun (the region generating the light), which ranges from about 5000 K at its outer boundary with the chromosphere to about 9500 K at its inner boundary with the convection zone approximately 500 km (310 mi) deep.[42]
Black holes
A black hole is a region of spacetime from which nothing escapes. Around a black hole there is a mathematically defined surface called an event horizon that marks the point of no return. It is called "black" because it absorbs all the light that hits the horizon, reflecting nothing, making it almost an ideal black body[43] (radiation with a wavelength equal to or larger than the radius of the hole may not be absorbed, so black holes are not perfect black bodies).[44] Physicists believe that to an outside observer, black holes have a non-zero temperature and emit radiation with a nearly perfect black-body spectrum, ultimately evaporating.[45] The mechanism for this emission is related to vacuum fluctuations in which a virtual pair of particles is separated by the gravity of the hole, one member being sucked into the hole, and the other being emitted.[46] The energy distribution of emission is described by Planck's law with a temperature T:Cosmic microwave background radiation
The big bang theory is based upon the cosmological principle, which states that on large scales the Universe is homogeneous and isotropic. According to theory, the Universe approximately a second after its formation was a near-ideal black body in thermal equilibrium at a temperature above 1010 K. The temperature decreased as the Universe expanded and the matter and radiation in it cooled. The cosmic microwave background radiation observed today is "the most perfect black body ever measured in nature".[49] It has a nearly ideal Planck spectrum at a temperature of about 2.7K. It departs from the perfect isotropy of true black-body radiation by an observed anisotropy that varies with angle on the sky only to about one part in 100,000.Radiative cooling
The integration of Planck's law over all frequencies provides the total energy per unit of time per unit of surface area radiated by a black body maintained at a temperature T, and is known as the Stefan–Boltzmann law:The cooling of a body due to thermal radiation is often approximated using the Stefan–Boltzmann law supplemented with a "gray body" emissivity ε ≤ 1 (P/A = εσT4). The rate of decrease of the temperature of the emitting body can be estimated from the power radiated and the body's heat capacity.[51] This approach is a simplification that ignores details of the mechanisms behind heat redistribution (which may include changing composition, phase transitions or restructuring of the body) that occur within the body while it cools, and assumes that at each moment in time the body is characterized by a single temperature. It also ignores other possible complications, such as changes in the emissivity with temperature,[52][53] and the role of other accompanying forms of energy emission, for example, emission of particles like neutrinos.[54]
If a hot emitting body is assumed to follow the Stefan–Boltzmann law and its power emission P and temperature T is known, this law can be used to estimate the dimensions of the emitting object, because the total emitted power is proportional to the area of the emitting surface. In this way it was found that X-ray bursts observed by astronomers originated in neutron stars with a radius of about 10 km, rather than black holes as originally conjectured.[55] It should be noted that an accurate estimate of size requires some knowledge of the emissivity, particularly its spectral and angular dependence.[56]







 proportional to its thermodynamic temperature
proportional to its thermodynamic temperature 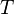 . In blue is a total energy according to the
. In blue is a total energy according to the 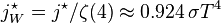
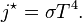
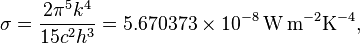
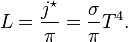
 :
:
 is the
is the 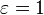 . In the still more general (and realistic) case, the emissivity depends on the wavelength,
. In the still more general (and realistic) case, the emissivity depends on the wavelength,  .
. :
:

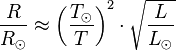
 , is the
, is the 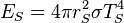

 . The amount of solar power absorbed by the Earth is thus given by:
. The amount of solar power absorbed by the Earth is thus given by:
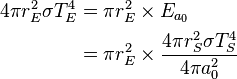

 can be derived using thermodynamics. It follows from the
can be derived using thermodynamics. It follows from the  is related to the internal energy density
is related to the internal energy density  :
: .
. ,
,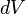 and fixing
and fixing  :
: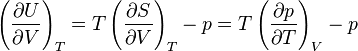 .
. .
.
 .
. ,
, and
and  .
. can be expressed as a relationship between only
can be expressed as a relationship between only 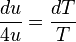 ,
, , with
, with  -dimensional space is given by
-dimensional space is given by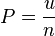 [
[
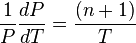
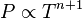

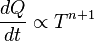
 [
[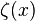 is Riemann's zeta function and
is Riemann's zeta function and 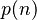 is a certain function of
is a certain function of  .
.
 is the amount of
is the amount of 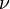 by a black body at temperature T.
by a black body at temperature T.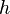 is
is  is the
is the  is
is  is the
is the 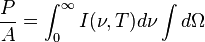
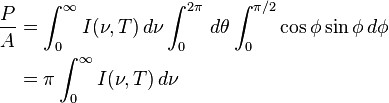

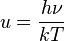


 , giving the result that, for a perfect blackbody surface:
, giving the result that, for a perfect blackbody surface:

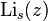 is the
is the  is the
is the 
 , we see that
, we see that  is minus 6 times the coefficient of
is minus 6 times the coefficient of  of the series expansion of
of the series expansion of  . So, if we can find a closed form for f(k), its
. So, if we can find a closed form for f(k), its 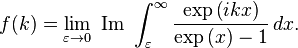

 is the contour from
is the contour from 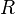 , then to
, then to  , then to
, then to  , then we go to the point
, then we go to the point 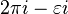 , avoiding the pole at
, avoiding the pole at  by taking a clockwise quarter circle with radius
by taking a clockwise quarter circle with radius  , and finally we return to
, and finally we return to 

 . In this limit the contribution from the segment from
. In this limit the contribution from the segment from 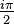 times the residues at the poles we find:
times the residues at the poles we find: . We can rewrite the integrand of the integral on the r.h.s. as follows:
. We can rewrite the integrand of the integral on the r.h.s. as follows:
 we find:
we find: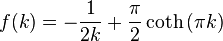

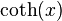 is given by:
is given by: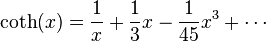
 . This then implies that
. This then implies that 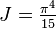 and the result
and the result
