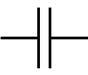Introduction to electromagnetism

From Wikipedia, the free encyclopedia

Electromagnetism is the study of forces between charged particles, electromagnetic fields, electric (scalar) potentials, magnetic vector potentials, the behavior of conductors and insulators in fields, circuits, magnetism, and electromagnetic waves. An understanding of electromagnetism is important for practical applications like electrical engineering and chemistry. In addition, concepts taught in courses on electromagnetism provide a basis for more advanced material in physics, such as quantum field theory and general relativity. This article focuses on a conceptual understanding of the topics rather than the details of the mathematics involved.

Electric charge

Electric charge is a quantity used to determine how a particle will behave in an electric field. There are three possible "types" of charge: positive, negative, and neutral. However, the distinction between positive and negative is by convention only. Electric charge is quantized in units of the elementary charge, ${\displaystyle e}$, where a proton has a charge of ${\displaystyle +e}$ and an electron has a charge of ${\displaystyle -e}$. The SI unit of charge is the coulomb.

Millikan's oil drop experiment.

 

The elementary charge ${\displaystyle e}$ was first measured by Robert Millikan in his oil drop experiment in which the electric force on the particle is set to exactly counter the gravitational force that pulls it down, and the terminal velocity of this particle can be used to calculate its charge. A neutron has no electric charge. 

Charge conservation states that the overall electric charge in a closed system cannot change. Research suggests that the overall charge in the universe is neutral.

Electric field

Electric force

Coulomb's law states that the force on a charged particle due to the field from another particle is dependent on the magnitudes of the two charges as well as the distance between them. The further away the particle is, the weaker the force on it is. Positive charges exert attractive forces on negative charges (and vice versa) while positive charges exert repulsive forces on other positive charges (and similarly for the force between negative charges). The SI units of force are newtons (N).

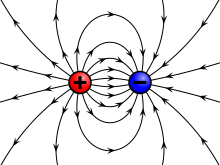
The force between two like charges (above), and between two opposite charges (below).

Field lines

Michael Faraday and James Clerk Maxwell, first introduced the concept of a field in his 1831 paper on electromagnetic induction, (called "lines of magnetic and electric force" in this publication):

"...by line of magnetic force, or magnetic line of force, or magnetic curve, I mean that exercise of magnetic force which is exerted in the lines usually called magnetic curves, and which equally exist as passing from or to magnetic poles, or forming concentric circles round an electric current. By line of electric force, I mean the force exerted in the lines joining two bodies, acting on each other according to the principles of static electric induction."

Certain conventions are followed when drawing and interpreting electric field lines:

1. Electric field lines start at positive charges and end at negative charges;
2. The density of the field lines corresponds to the strength of the field in that area and thus to the strength of the charge;
3. The lines never cross, since otherwise the field would be pointing in two directions in one location; and
4. The vector arrow represents the motion that a positive charge would undergo if placed in the field, while a negative charge would follow the direction opposite the arrow.

The SI unit of the electric field is volt per meter (V/m), or equivalently, newton per coulomb (N/C). In mathematical expressions it is often represented as a vector-valued function ${\displaystyle {\vec {E}}}$. The electric field can be calculated in many ways, including Gauss' law, Coulomb's law, or Maxwell's equations. The electric field can also be interpreted as the electric force per unit charge.

Electric flux

The flux line representation of the field between two oppositely-charged particles.

 

Flux is dependent on the angle between the field lines and the surface through which they pass.

 

Flux can be thought of as the flow of the electric or magnetic field through a surface. Fields can be represented by flux lines. Flux is analogous to the flow of a fluid through a surface since the angle of the surface to the direction of flow determines how much fluid can flow through the surface. Gauss' law states that the flux through a closed surface is proportional to the amount of charge enclosed. The SI units of flux are newton meters-squared per coulomb (${\displaystyle Nm^{2}C^{-1}}$), or equivalently, volt-meters (V m).

Electric potential

Potential energy

The electric potential energy of a system of charges is the work it takes to assemble that configuration of charges. The energies add pairwise; that is, the work to bring a third charge into a system of two charges is the energy associated with the first and third charge plus that associated with the second and third charge. The potential energy of the system is unique to the configuration itself. The SI unit of energy is the joule (J).

Equivalently, it may be thought of as the energy stored in the electric field. For instance, if one were to hold two like charges a certain distance away from one another and then release them, the charges would move away with kinetic energy equal to the energy stored in the configuration. As an analogy, if one were to lift up a mass to a certain height in a gravitational field, the work it took to do so is equal to the energy stored in that configuration, and the kinetic energy of the mass upon contact with the ground would be equal to the energy of the configuration beforehand.

Potential

The electric potential is the potential energy per unit charge. The SI unit of electric potential is the volt (V).^[2] The potential difference between two points determines the behavior of a particle. Positive charges move from high potentials to low potentials, whereas negative charges move from low to high potential. This may be thought of in terms of fluid flow. Take two identical containers filled with a fluid to unequal volumes. One container is at a higher level (potential) while the other container is at a lower level (potential). If connected by a pipe (a wire), the fluid (charge) would flow from the left container to the right container until the fluid heights (potentials) are equal. Mathematically, the potential is the line integral of the electric field. The electric field can be represented as the change in the potential with respect to distance.

Conductors and insulators

Conductors

A conductor is a material that allows electrons to flow easily. The most effective conductors are usually metals because their electrons can move around freely. This is described in the electron sea model of bonding in which electrons delocalize from the nuclei, leaving positive ions behind while the electrons are shared by all atoms in the lattice. Examples of good conductors include copper, aluminum, and silver. Wires in electronics are often made of copper. 

The main tenets of conductors are as follows:

1. The electric field is zero inside a conductor. This is because charges are free to move and thus when they are disturbed by a field due to some external (or internal charge), they rearrange themselves such that the field that their configuration produces exactly cancels that caused by the source charge.
2. The electric potential is the same everywhere inside the conductor and is constant across the surface of the conductor. This follows from the first statement because the field is zero everywhere inside the conductor and therefore the potential is not changing with distance inside the conductor.
3. The electric field is perpendicular to the surface of a conductor. If this were not the case, the field would have a nonzero component on the surface of the conductor, which would cause the charges in the conductor to move around until that component of the field is zero.
4. The net electric flux through a surface is proportional to the charge enclosed by the surface. This is a restatement of Gauss' law.

Semiconductors are materials that, depending on their temperature, become better or worse conductors. Germanium and silicon are examples of superconductors. Superconductors are materials that exhibit little to no resistance to the flow of electrons when cooled below a certain temperature.

The fields inside each of these conductors is zero because the external field due to the central charge induces charges on the conductors to move around such that their fields cancel the external field inside the conductors.

Insulators

An insulator is a material with electrons that are more tightly bound and thus not able to move as freely as those of conductors. Insulators are often used to cover conducting wires so that charge will stay on the wire and will not go elsewhere. 

Charge can be distributed inside an insulator thus the electric field inside an insulator is not necessarily zero. Examples of insulators are plastics and polymers.

Magnetic field and force

Magnetic field

The magnetic field is that which arises from moving charges, currents, and magnetic objects. The field is represented mathematically as a vector-valued function ${\displaystyle {\vec {B}}}$. The SI unit of the magnetic field is the tesla (T).

The magnetic field can be derived mathematically using Ampère's law, the Biot–Savart law, or Maxwell's equations.

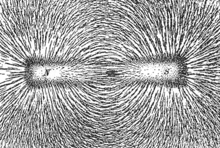
Magnetic field lines have a very similar representation to electric field lines. There is an analogous notion of magnetic flux. Magnetic field lines begin at north poles and end at south poles, and cannot cross. Magnetic fields arise due to the motion of charges, and also due to the alignment of the domains of magnetic materials where the magnetic moments of the atoms point in the same direction.

Magnetic field lines can be clearly visualized by sprinkling iron filings over a bar magnet.

 

The modern (post-Einstein) interpretation is that the magnetic field is equivalent to the electric field, but in a different reference frame. Since magnetic fields can be interpreted as electric fields in a different reference frame (and vice versa), special relativity connects the two fields. One postulate of special relativity is length contraction, and because of that, the charge density in the wire increases, so a current-carrying wire viewed in a moving reference frame experiences a length-contracted coulomb force as compared to the wire in a stationary frame. This force is called the magnetic force, and the associated field is the magnetic field. The direction of the magnetic force can be derived from the right-hand rule such that the force is perpendicular to both the direction of motion of the current (or charged particle) and the magnetic field.

Magnets

Permanent magnets make their own magnetic field. An example of a material from which a permanent magnet can be made is iron. It has a north and south pole, and cannot be split into a monopole — in other words, a north pole does not exist without a south pole.

Electrons moving around atoms can create a magnetic field if their effects sum up constructively. For magnetic materials like iron, the magnetic fields of the electrons moving around the nucleus add up, while for non-magnetic materials the effects average out to zero net magnetic field.

Inductance

Inductance is the ability of an object to resist a change in current. From Ampère's law one can conclude that the magnetic field within a coil of wire (also called a solenoid) is constant inside the coil and zero outside the coil. This property is useful in circuits to store energy within a magnetic field. 

Inductors resist change in currents, therefore it will produce a current opposing the change. This is also known as Lenz's law. Because of this property, inductors oppose alternating current.

Circuits

Circuits are connections of electrical components. Common components are as follows: 

Circuit components

Component	Main function	Schematic symbol
Resistor	Impedes the flow of current

Battery	Acts as a power source
Capacitor	Stores energy in electric fields, stores charge, passes low frequency alternating current
Inductor	Stores energy in magnetic fields, resists change in current

Current is defined as the change of charge per unit time, often represented as ${\displaystyle I}$and in units of amperes (A). Voltage is the difference in electric potential between two points in the circuit. In batteries, the potential difference is often called the emf (electromotive force) and is in units volt (V). 

Ohm's law states a relationship among the current, the voltage, and the resistance of a circuit: the current that flows is proportional to the voltage and inversely proportional to the resistance.

Direct current (DC) is constant current that flows in one direction. Alternating current (AC) is a current that switches direction according to a sinusoidal function, typically. Power grids use alternating current, and so residences and appliances are generally powered by AC.

Kirchhoff's junction rule

Kirchhoff's junction rule states that the current going into a junction (or node) must equal the current that leaves the node. This comes from charge conservation, as current is defined as the flow of charge over time. 

If a current splits as it exits a junction, the sum of the resultant split currents is equal to the incoming circuit.

Kirchhoff's loop rule

Kirchhoff's loop rule states that the sum of the voltage drops in a closed loop around a circuit equals zero. This comes from the conservation of energy, as voltage is defined as the energy per unit charge.

Parallel versus series

Components are said to be in parallel when the voltage drops across one branch is equal to that across another. Components are said to be in series when the current through one component is equal to that through another. Thus, the voltages across each path in a parallel circuit is the same, and the current through each component in a series circuit is the same.

Equivalent resistance in series is given by ${\displaystyle R_{equiv}=\sum _{k=1}^{N}R_{k}}$for ${\displaystyle N}$ resistors in series, while equivalent resistance in parallel is given by ${\displaystyle R_{equiv}={\frac {1}{\sum _{k=1}^{N}{\frac {1}{R_{k}}}}}}$ for ${\displaystyle N}$ resistors in parallel.

Equivalent capacitance in series is given by ${\displaystyle C_{equiv}={\frac {1}{\sum _{k=1}^{N}{\frac {1}{C_{k}}}}}}$, while equivalent capacitance in parallel is given by ${\displaystyle C_{equiv}=\sum _{k=1}^{N}C_{k}}$.

Electromagnetic waves

Electromagnetic spectrum

 

Electromagnetic waves are a result of Maxwell's equations which, in part, state that changing electric fields produce magnetic fields and vice versa. Due to this dependence, the fields form an electromagnetic wave, also called electromagnetic radiation (EMR). The electric and magnetic fields are transverse (or perpendicular) to each other, and transverse to the direction of propagation of the electromagnetic wave. From Maxwell's equations, one can show that electromagnetic waves propagate through a vacuum at speed

${\displaystyle c={\frac {1}{\sqrt {\epsilon _{0}\mu _{0}}}},}$

where ${\displaystyle \epsilon _{0}}$ is the permittivity of free space, and ${\displaystyle \mu _{0}}$ is the permeability of free space. Plugging in the values, one finds that ${\displaystyle c}$ is equal to the measured speed of light. Historically, this is what led Maxwell to suggest that visible light is an electromagnetic wave. Classified by wavelengths, electromagnetic waves include gamma rays, X-rays, ultraviolet, visible light, infrared, microwaves, and radio waves.

Fine-structure constant

From Wikipedia, the free encyclopedia

 

In physics, the fine-structure constant, also known as Sommerfeld's constant, commonly denoted by α (the Greek letter alpha), is a dimensionless physical constant characterizing the strength of the electromagnetic interaction between elementary charged particles. It is related to the elementary charge e, which characterizes the strength of the coupling of an elementary charged particle with the electromagnetic field, by the formula 4πε₀ħcα = e². As a dimensionless quantity, it has the same numerical value whatever system of units is being used, which is nearly 1/137.

While there are multiple physical interpretations for α, it received its name from Arnold Sommerfeld introducing it (1916) in extending the Bohr model of the atom: α quantifies the gap in the fine structure of the spectral lines of the hydrogen atom, which had been precisely measured by Michelson and Morley.

Definition

Some equivalent definitions of α in terms of other fundamental physical constants are:

${\displaystyle \alpha ={\frac {1}{4\pi \varepsilon _{0}}}{\frac {e^{2}}{\hbar c}}={\frac {\mu _{0}}{4\pi }}{\frac {e^{2}c}{\hbar }}={\frac {k_{\text{e}}e^{2}}{\hbar c}}={\frac {c\mu _{0}}{2R_{\text{K}}}}={\frac {e^{2}}{4\pi }}{\frac {Z_{0}}{\hbar }}}$

where:

• e is the elementary charge (:= 1.602176634×10⁻¹⁹ C);
• π is the mathematical constant pi;
• ħ = h/2π is the reduced Planck constant (:= 6.62607015×10⁻³⁴ J⋅s/2π);
• c is the speed of light in vacuum (:= 299792458 m/s);
• ε₀ is the electric constant or permittivity of free space;
• µ₀ is the magnetic constant or permeability of free space;
• k_e is the Coulomb constant;
• R_K is the von Klitzing constant;
• Z₀ is the vacuum impedance or impedance of free space.

The definition reflects the relationship between α and the permeability of free space µ₀, which equals µ₀ = 2hα/ce². In the 2019 redefinition of SI base units, 4π × 1.00000000082(20)×10⁻⁷ H⋅m⁻¹ is the value for µ₀ based upon more accurate measurements of the fine structure constant.

In non-SI units

In electrostatic cgs units, the unit of electric charge, the statcoulomb, is defined so that the Coulomb constant, k_e, or the permittivity factor, 4πε₀, is 1 and dimensionless. Then the expression of the fine-structure constant, as commonly found in older physics literature, becomes

${\displaystyle \alpha ={\frac {e^{2}}{\hbar c}}.}$

In natural units, commonly used in high energy physics, where ε₀ = c = ħ = 1, the value of the fine-structure constant is

${\displaystyle \alpha ={\frac {e^{2}}{4\pi }}.}$

As such, the fine-structure constant is just another, albeit dimensionless, quantity determining (or determined by) the elementary charge: e = √4πα ≈ 0.30282212 in terms of such a natural unit of charge.

In atomic units (e = m_e = ħ = 1 and ε₀ = 1/4π), the fine structure constant is

${\displaystyle \alpha ={\frac {1}{c}}.}$

Measurement

Two example eighth-order Feynman diagrams that contribute to the electron self-interaction. The horizontal line with an arrow represents the electron while the wavy lines are virtual photons, and the circles represent virtual electron–positron pairs.

 

The 2018 CODATA recommended value of α is

α = e²/4πε₀ħc = 0.0072973525693(11).

This has a relative standard uncertainty of 0.15 parts per billion.

For reasons of convenience, historically the value of the reciprocal of the fine-structure constant is often specified. The 2018 CODATA recommended value is given by

α⁻¹ = 137.035999084(21).

While the value of α can be estimated from the values of the constants appearing in any of its definitions, the theory of quantum electrodynamics (QED) provides a way to measure α directly using the quantum Hall effect or the anomalous magnetic moment of the electron. The theory of QED predicts a relationship between the dimensionless magnetic moment of the electron and the fine-structure constant α (the magnetic moment of the electron is also referred to as "Landé g-factor" and symbolized as g). The most precise value of α obtained experimentally (as of 2012) is based on a measurement of g using a one-electron so-called "quantum cyclotron" apparatus, together with a calculation via the theory of QED that involved 12672 tenth-order Feynman diagrams:

α⁻¹ = 137.035999174(35).

This measurement of α has a relative standard uncertainty of 2.5×10⁻¹⁰. This value and uncertainty are about the same as the latest experimental results.

Physical interpretations

The fine-structure constant, α, has several physical interpretations. α is:

• The square of the ratio of the elementary charge to the Planck charge

${\displaystyle \alpha =\left({\frac {e}{q_{\text{P}}}}\right)^{2}.}$

• The ratio of two energies: (i) the energy needed to overcome the electrostatic repulsion between two electrons a distance of d apart, and (ii) the energy of a single photon of wavelength λ = 2πd (or of angular wavelength d; see Planck relation):

${\displaystyle \alpha =\left.{\frac {e^{2}}{4\pi \varepsilon _{0}d}}\right/{\frac {hc}{\lambda }}={\frac {e^{2}}{4\pi \varepsilon _{0}d}}\times {\frac {2\pi d}{hc}}={\frac {e^{2}}{4\pi \varepsilon _{0}d}}\times {\frac {d}{\hbar c}}={\frac {e^{2}}{4\pi \varepsilon _{0}\hbar c}}.}$

• The ratio of the velocity of the electron in the first circular orbit of the Bohr model of the atom, which is 1/4πε₀ e²/ħ to the speed of light in vacuum, c. This is Sommerfeld's original physical interpretation. Then the square of α is the ratio between the Hartree energy (27.2 eV = twice the Rydberg energy = approximately twice its ionization energy) and the electron rest energy (511 keV).
• The two ratios of three characteristic lengths: the classical electron radius r_e, the Compton wavelength of the electron λ_e, and the Bohr radius a₀:

${\displaystyle r_{\text{e}}={\frac {\alpha \lambda _{\text{e}}}{2\pi }}=\alpha ^{2}a_{0}}$

• In quantum electrodynamics, α is directly related to the coupling constant determining the strength of the interaction between electrons and photons. The theory does not predict its value. Therefore, α must be determined experimentally. In fact, α is one of about 20 empirical parameters in the Standard Model of particle physics, whose value is not determined within the Standard Model.
• In the electroweak theory unifying the weak interaction with electromagnetism, α is absorbed into two other coupling constants associated with the electroweak gauge fields. In this theory, the electromagnetic interaction is treated as a mixture of interactions associated with the electroweak fields. The strength of the electromagnetic interaction varies with the strength of the energy field.
• Given two hypothetical point particles each of Planck mass and elementary charge, separated by any distance, α is the ratio of their electrostatic repulsive force to their gravitational attractive force.
• In the fields of electrical engineering and solid-state physics, the fine-structure constant is one fourth the product of the characteristic impedance of free space, Z₀ = μ₀c, and the conductance quantum, G₀ = 2e²/h:

${\displaystyle \alpha ={\tfrac {1}{4}}Z_{0}G_{0}}$.

The optical conductivity of graphene for visible frequencies is theoretically given by πG₀/4, and as a result its light absorption and transmission properties can be expressed in terms of the fine structure constant alone. The absorption value for normal-incident light on graphene in vacuum would then be given by πα/(1 + πα/2)² or 2.24%, and the transmission by 1/(1 + πα/2)² or 97.75% (experimentally observed to be between 97.6% and 97.8%).

• The fine-structure constant gives the maximum positive charge of an atomic nucleus that will allow a stable electron-orbit around it within the Bohr model (element feynmanium). For an electron orbiting an atomic nucleus with atomic number Z, mv²/r = 1/4πε₀ Ze²/r². The Heisenberg uncertainty principle momentum/position uncertainty relationship of such an electron is just mvr = ħ. The relativistic limiting value for v is c, and so the limiting value for Z is the reciprocal of the fine-structure constant, 137.
• The magnetic moment of the electron indicates that the charge is circulating at a radius r_Q with the velocity of light. It generates the radiation energy m_ec² and has an angular momentum L = 1 ħ = r_Qm_ec. The field energy of the stationary Coulomb field is m_ec² = e²/4πε₀r_e and defines the classical electron radius r_e. These values inserted into the definition of alpha yields α = r_e/r_Q. It compares the dynamic structure of the electron with the classical static assumption.
• Alpha is related to the probability that an electron will emit or absorb a photon.
• Some properties of subatomic particles exhibit a relation with α. A model for the observed relationship yields an approximation for α given by the two gamma functions Γ(1/3) |Γ(−1/3)| ≈ α⁻¹/4π.

When perturbation theory is applied to quantum electrodynamics, the resulting perturbative expansions for physical results are expressed as sets of power series in α. Because α is much less than one, higher powers of α are soon unimportant, making the perturbation theory practical in this case. On the other hand, the large value of the corresponding factors in quantum chromodynamics makes calculations involving the strong nuclear force extremely difficult.

Variation with energy scale

In quantum electrodynamics, the more thorough quantum field theory underlying the electromagnetic coupling, the renormalization group dictates how the strength of the electromagnetic interaction grows logarithmically as the relevant energy scale increases. The value of the fine-structure constant α is linked to the observed value of this coupling associated with the energy scale of the electron mass: the electron is a lower bound for this energy scale, because it (and the positron) is the lightest charged object whose quantum loops can contribute to the running. Therefore, 1/137.036 is the asymptotic value of the fine-structure constant at zero energy. At higher energies, such as the scale of the Z boson, about 90 GeV, one measures an effective α ≈ 1/127, instead. 

As the energy scale increases, the strength of the electromagnetic interaction in the Standard Model approaches that of the other two fundamental interactions, a feature important for grand unification theories. If quantum electrodynamics were an exact theory, the fine-structure constant would actually diverge at an energy known as the Landau pole—this fact undermines the consistency of quantum electrodynamics beyond perturbative expansions.

History

Sommerfeld memorial at University of Munich

 

Based on the precise measurement of the hydrogen atom spectrum by Michelson and Morley, Arnold Sommerfeld extended the Bohr model to include elliptical orbits and relativistic dependence of mass on velocity. He introduced a term for the fine-structure constant in 1916. The first physical interpretation of the fine-structure constant α was as the ratio of the velocity of the electron in the first circular orbit of the relativistic Bohr atom to the speed of light in the vacuum. Equivalently, it was the quotient between the minimum angular momentum allowed by relativity for a closed orbit, and the minimum angular momentum allowed for it by quantum mechanics. It appears naturally in Sommerfeld's analysis, and determines the size of the splitting or fine-structure of the hydrogenic spectral lines. 

With the development of quantum electrodynamics (QED) the significance of α has broadened from a spectroscopic phenomenon to a general coupling constant for the electromagnetic field, determining the strength of the interaction between electrons and photons. The term α/2π is engraved on the tombstone of one of the pioneers of QED, Julian Schwinger, referring to his calculation of the anomalous magnetic dipole moment.

Is the fine-structure constant actually constant?

Physicists have pondered whether the fine-structure constant is in fact constant, or whether its value differs by location and over time. A varying α has been proposed as a way of solving problems in cosmology and astrophysics. String theory and other proposals for going beyond the Standard Model of particle physics have led to theoretical interest in whether the accepted physical constants (not just α) actually vary. 

In the experiments below, Δα represents the change in α over time, which can be computed by α_prev − α_now. If the fine-structure constant really is a constant, then any experiment should show that

${\displaystyle {\frac {\Delta \alpha }{\alpha }}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\alpha _{\mathrm {prev} }-\alpha _{\mathrm {now} }}{\alpha _{\mathrm {now} }}}=0,}$

or as close to zero as experiment can measure. Any value far away from zero would indicate that α does change over time. So far, most experimental data is consistent with α being constant.

Past rate of change

The first experimenters to test whether the fine-structure constant might actually vary examined the spectral lines of distant astronomical objects and the products of radioactive decay in the Oklo natural nuclear fission reactor. Their findings were consistent with no variation in the fine-structure constant between these two vastly separated locations and times.

Improved technology at the dawn of the 21st century made it possible to probe the value of α at much larger distances and to a much greater accuracy. In 1999, a team led by John K. Webb of the University of New South Wales claimed the first detection of a variation in α. Using the Keck telescopes and a data set of 128 quasars at redshifts 0.5 < z < 3, Webb et al. found that their spectra were consistent with a slight increase in α over the last 10–12 billion years. Specifically, they found that

${\displaystyle {\frac {\Delta \alpha }{\alpha }}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\alpha _{\mathrm {prev} }-\alpha _{\mathrm {now} }}{\alpha _{\mathrm {now} }}}=\left(-5.7\pm 1.0\right)\times 10^{-6}.}$

In other words, they measured the value to be somewhere between −0.0000047 and −0.0000067. This is a very small value, nearly zero, but their error bars do not actually include zero. This result either indicates that α is not constant or that there is experimental error that the experimenters did not know how to measure. 

In 2004, a smaller study of 23 absorption systems by Chand et al., using the Very Large Telescope, found no measurable variation:

${\displaystyle {\frac {\Delta \alpha }{\alpha _{\mathrm {em} }}}=\left(-0.6\pm 0.6\right)\times 10^{-6}.}$

However, in 2007 simple flaws were identified in the analysis method of Chand et al., discrediting those results.

King et al. have used Markov chain Monte Carlo methods to investigate the algorithm used by the UNSW group to determine Δα/α from the quasar spectra, and have found that the algorithm appears to produce correct uncertainties and maximum likelihood estimates for Δα/α for particular models. This suggests that the statistical uncertainties and best estimate for Δα/α stated by Webb et al. and Murphy et al. are robust. 

Lamoreaux and Torgerson analyzed data from the Oklo natural nuclear fission reactor in 2004, and concluded that α has changed in the past 2 billion years by 45 parts per billion. They claimed that this finding was "probably accurate to within 20%". Accuracy is dependent on estimates of impurities and temperature in the natural reactor. These conclusions have to be verified.

In 2007, Khatri and Wandelt of the University of Illinois at Urbana-Champaign realized that the 21 cm hyperfine transition in neutral hydrogen of the early universe leaves a unique absorption line imprint in the cosmic microwave background radiation. They proposed using this effect to measure the value of α during the epoch before the formation of the first stars. In principle, this technique provides enough information to measure a variation of 1 part in 10⁹ (4 orders of magnitude better than the current quasar constraints). However, the constraint which can be placed on α is strongly dependent upon effective integration time, going as t^{−​1⁄₂}. The European LOFAR radio telescope would only be able to constrain Δα/α to about 0.3%. The collecting area required to constrain Δα/α to the current level of quasar constraints is on the order of 100 square kilometers, which is economically impracticable at the present time.

Present rate of change

In 2008, Rosenband et al. used the frequency ratio of
Al⁺ and
Hg⁺ in single-ion optical atomic clocks to place a very stringent constraint on the present-time temporal variation of α, namely α̇/α = (−1.6±2.3)×10⁻¹⁷ per year. Note that any present day null constraint on the time variation of alpha does not necessarily rule out time variation in the past. Indeed, some theories that predict a variable fine-structure constant also predict that the value of the fine-structure constant should become practically fixed in its value once the universe enters its current dark energy-dominated epoch.

Spatial variation – Australian dipole

In September 2010 researchers from Australia said they had identified a dipole-like structure in the variation of the fine-structure constant across the observable universe. They used data on quasars obtained by the Very Large Telescope, combined with the previous data obtained by Webb at the Keck telescopes. The fine-structure constant appears to have been larger by one part in 100,000 in the direction of the southern hemisphere constellation Ara, 10 billion years ago. Similarly, the constant appeared to have been smaller by a similar fraction in the northern direction, 10 billion years ago.

In September and October 2010, after Webb's released research, physicists Chad Orzel and Sean M. Carroll suggested various approaches of how Webb's observations may be wrong. Orzel argues that the study may contain wrong data due to subtle differences in the two telescopes, in which one of the telescopes the data set was slightly high and on the other slightly low, so that they cancel each other out when they overlapped. He finds it suspicious that the sources showing the greatest changes are all observed by one telescope, with the region observed by both telescopes aligning so well with the sources where no effect is observed. Carroll suggested a totally different approach; he looks at the fine-structure constant as a scalar field and claims that if the telescopes are correct and the fine-structure constant varies smoothly over the universe, then the scalar field must have a very small mass. However, previous research has shown that the mass is not likely to be extremely small. Both of these scientists' early criticisms point to the fact that different techniques are needed to confirm or contradict the results, as Webb, et al., also concluded in their study. 

In October 2011, Webb et al. reported a variation in α dependent on both redshift and spatial direction. They report "the combined data set fits a spatial dipole" with an increase in α with redshift in one direction and a decrease in the other. "Independent VLT and Keck samples give consistent dipole directions and amplitudes...."

Anthropic explanation

The anthropic principle is a controversial argument of why the fine-structure constant has the value it does: stable matter, and therefore life and intelligent beings, could not exist if its value were much different. For instance, were α to change by 4%, stellar fusion would not produce carbon, so that carbon-based life would be impossible. If α were greater than 0.1, stellar fusion would be impossible, and no place in the universe would be warm enough for life as we know it.

Numerological explanations and multiverse theory

As a dimensionless constant which does not seem to be directly related to any mathematical constant, the fine-structure constant has long fascinated physicists.

Arthur Eddington argued that the value could be "obtained by pure deduction" and he related it to the Eddington number, his estimate of the number of protons in the universe. This led him in 1929 to conjecture that the reciprocal of the fine-structure constant was not approximately the integer 137, but precisely the integer 137. Other physicists neither adopted this conjecture nor accepted his arguments but by the 1940s experimental values for 1/α deviated sufficiently from 137 to refute Eddington's argument.

The fine-structure constant so intrigued physicist Wolfgang Pauli that he collaborated with psychoanalyst Carl Jung in a quest to understand its significance. Similarly, Max Born believed that would the value of alpha differ, the universe would degenerate. Thus, he asserted that 1/137 is a law of nature.

Richard Feynman, one of the originators and early developers of the theory of quantum electrodynamics (QED), referred to the fine-structure constant in these terms:

There is a most profound and beautiful question associated with the observed coupling constant, e – the amplitude for a real electron to emit or absorb a real photon. It is a simple number that has been experimentally determined to be close to 0.08542455. (My physicist friends won't recognize this number, because they like to remember it as the inverse of its square: about 137.03597 with about an uncertainty of about 2 in the last decimal place. It has been a mystery ever since it was discovered more than fifty years ago, and all good theoretical physicists put this number up on their wall and worry about it.) Immediately you would like to know where this number for a coupling comes from: is it related to pi or perhaps to the base of natural logarithms? Nobody knows. It's one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man. You might say the "hand of God" wrote that number, and "we don't know how He pushed his pencil." We know what kind of a dance to do experimentally to measure this number very accurately, but we don't know what kind of dance to do on the computer to make this number come out, without putting it in secretly!

— Richard Feynman, Richard P. Feynman (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. p. 129. ISBN 978-0-691-08388-9.

Conversely, statistician I. J. Good argued that a numerological explanation would only be acceptable if it could be based on a good theory that is not yet known but "exists" in the sense of a Platonic Ideal.

Attempts to find a mathematical basis for this dimensionless constant have continued up to the present time. However, no numerological explanation has ever been accepted by the community.

In the early 21st century, multiple physicists, including Stephen Hawking in his book A Brief History of Time, began exploring the idea of a multiverse, and the fine-structure constant was one of several universal constants that suggested the idea of a fine-tuned universe.

Quotes

The mystery about α is actually a double mystery. The first mystery – the origin of its numerical value α ≈ 1/137 – has been recognized and discussed for decades. The second mystery – the range of its domain – is generally unrecognized.

— Malcolm H. Mac Gregor, M. H. MacGregor (2007). The Power of Alpha. World Scientific. p. 69. ISBN 978-981-256-961-5.