From Wikipedia, the free encyclopedia

Thomas Robert Malthus
|
|
| Born | 13 February 1766 Westcott, Surrey, Great Britain |
|---|---|
| Died | 29 December 1834 (aged 68) Bath, Somerset, United Kingdom |
| Field | demography, macroeconomics |
School or tradition
|
Classical economics |
| Influences | David Ricardo, Jean Charles Léonard de Sismondi |
| Influenced | Charles Darwin, Paul R. Ehrlich, Francis Place, Raynold Kaufgetz, Garrett Hardin, John Maynard Keynes, Pierre François Verhulst, Alfred Russel Wallace, William Thompson, Karl Marx, Mao Zedong |
| Contributions | Malthusian growth model |
The Reverend Thomas Robert Malthus FRS (13 February 1766 – 29 December 1834[1]) was an English cleric and scholar, influential in the fields of political economy and demography.[2] Malthus himself used only his middle name Robert.[3]
His An Essay on the Principle of Population observed that sooner or later population will be checked by famine and disease, leading to what is known as a Malthusian catastrophe. He wrote in opposition to the popular view in 18th-century Europe that saw society as improving and in principle as perfectible.[4] He thought that the dangers of population growth precluded progress towards a utopian society: "The power of population is indefinitely greater than the power in the earth to produce subsistence for man".[5] As a cleric, Malthus saw this situation as divinely imposed to teach virtuous behaviour.[6] Malthus wrote:
That the increase of population is necessarily limited by the means of subsistence,Malthus placed the longer-term stability of the economy above short-term expediency. He criticized the Poor Laws,[8] and (alone among important contemporary economists) supported the Corn Laws, which introduced a system of taxes on British imports of wheat.[9] His views became influential, and controversial, across economic, political, social and scientific thought. Pioneers of evolutionary biology read him, notably Charles Darwin and Alfred Russel Wallace.[10][11] He remains a much-debated writer.
That population does invariably increase when the means of subsistence increase, and,
That the superior power of population is repressed, and the actual population kept equal to the means of subsistence, by misery and vice.[7]
Early life and education
The seventh child of Henrietta Catherine (Graham) and Daniel Malthus,[12][13] Robert Malthus grew up in The Rookery, a country house in Westcott, near Dorking in Surrey. Petersen describes Daniel Malthus as "a gentleman of good family and independent means... [and] a friend of David Hume and Jean-Jacques Rousseau".[14] The young Malthus received his education at home in Bramcote, Nottinghamshire, and then at the Warrington Academy from 1782. Warrington was a dissenting academy, then at the end of its existence. and it closed in 1783. Malthus continued for a period to be tutored by Gilbert Wakefield who had taught him there.[15]Malthus entered Jesus College, Cambridge in 1784. There he took prizes in English declamation, Latin and Greek, and graduated with honours, Ninth Wrangler in mathematics. His tutor was William Frend.[15][16] He took the MA degree in 1791, and was elected a Fellow of Jesus College two years later.[3] In 1789, he took orders in the Church of England, and became a curate at Oakwood Chapel (also Okewood) in the parish of Wotton, Surrey.[17]
Population growth
Malthus came to prominence for his 1798 essay on population growth. In it he argued that population multiplies geometrically and food arithmetically; therefore, the population will eventually outstrip the food supply. Between 1798 and 1826 he published six editions of An Essay on the Principle of Population, updating each edition to incorporate new material, to address criticism, and to convey changes in his own perspectives on the subject. He wrote the original text in reaction to the optimism of his father and his father's associates (notably Rousseau) regarding the future improvement of society. Malthus also constructed his case as a specific response to writings of William Godwin (1756–1836) and of the Marquis de Condorcet (1743–1794).The Essay gave rise to the Malthusian controversy during the next decades. The content saw an emphasis on the birth rate and marriage rates. The neo-Malthusian controversy, or related debates of many years later, has seen a similar central role assigned to the numbers of children born.[18]
In 1799 Malthus made a European tour with William Otter, a close college friend, travelling part of the way with Edward Daniel Clarke and John Marten Cripps, visiting Germany, Scandinavia and Russia. Malthus used the trip to gather population data. Otter later wrote a Memoir of Malthus for the second (1836) edition of his Principles of Political Economy.[19][20] During the Peace of Amiens of 1802 he travelled to France and Switzerland, in a party that included his relation and future wife Harriet.[21] In 1803 he became rector of Walesby, Lincolnshire.[3]
Academic
In 1805 Malthus became Professor of History and Political Economy at the East India Company College in Hertfordshire.[22] His students affectionately referred to him as "Pop" or "Population" Malthus.At the end of 1816 the proposed appointment of Graves Champney Haughton to the College was made a pretext by Randle Jackson and Joseph Hume to launch an attempt to close it down. Malthus wrote a pamphlet defending the College, which was reprieved by the East India Company in 1817.[23] In 1818 Malthus became a Fellow of the Royal Society.
Malthus–Ricardo debate on political economy
During the 1820s there took place a set piece intellectual discussion within the proponents of political economy, often called the "Malthus–Ricardo debate", after the leading figures of Malthus and David Ricardo, a theorist of free trade, both of whom had written books with the title Principles of Political Economy. Under examination were the nature and methods of political economy itself, while it was simultaneously under attack from others.[24] The roots of the debate were in the previous decade. In The Nature of Rent (1815), Malthus had dealt with economic rent, a major concept in classical economics. Ricardo defined a theory of rent in his Principles of Political Economy and Taxation (1817): he regarded rent as value in excess of real production—something caused by ownership rather than by free trade. Rent therefore represented a kind of negative money that landlords could pull out of the production of the land, by means of its scarcity.[25] Contrary to this concept, Malthus proposed rent to be a kind of economic surplus.The debate developed over the economic concept of a general glut, and the possibility of failure of Say's Law.
Malthus laid importance on economic development and the persistence of disequilibrium.[26] The context was the post-war depression; Malthus had a supporter in William Blake, in denying that capital accumulation (saving) was always good in such circumstances, and John Stuart Mill attacked Blake on the fringes of the debate.[27]
Ricardo corresponded with Malthus from 1817 and his Principles. He was drawn into considering political economy in a less restricted sense, which might be adapted to legislation and its multiple objectives, by the thought of Malthus. In his own work Principles of Political Economy (1820), and elsewhere, Malthus addressed the tension, amounting to conflict, he saw between a narrow view of political economy, and the broader moral and political plane.[28] Leslie Stephen wrote:
If Malthus and Ricardo differed, it was a difference of men who accepted the same first principles. They both professed to interpret Adam Smith as the true prophet, and represented different shades of opinion rather than diverging sects.[29]It is now considered that the different purposes seen by Malthus and Ricardo for political economy affected their technical discussion, and contributed to the lack of compatible definitions.[26] For example, Jean-Baptiste Say used a definition of production based on goods and services and so queried the restriction of Malthus to "goods" alone.[30]
In terms of public policy, Malthus was a supporter of the protectionist Corn Laws from the end of the Napoleonic Wars. He emerged as the only economist of note to support duties on imported grain.[31] He changed his mind after 1814. By encouraging domestic production, Malthus argued, the Corn Laws would guarantee British self-sufficiency in food.[32] He also wished to abolish poor relief for paupers, a lifelong aim.[33]
Later life
Malthus was a founding member of the Political Economy Club in 1821; there John Cazenove tended to be his ally, against Ricardo and Mill.[34] He was elected in the beginning of 1824 as one of the ten royal associates of the Royal Society of Literature. He was also one of the first fellows of the Statistical Society, founded in March 1834. In 1827 he gave evidence to a committee of the House of Commons on emigration.[35]After Ricardo's death in 1823, Malthus became isolated among the younger British political economists, who tended to think he had lost the debate. In Definitions in Political Economy (1827) he attacked John Ramsay McCulloch. McCulloch replied cuttingly, implying that he wanted to dictate to others, and the reputation of Malthus as economist dropped away, for the rest of his life.[36]
Malthus died suddenly of heart disease on 23 December 1834, at his father-in-law's house. He was buried in Bath Abbey.[35] His portrait,[37] and descriptions by contemporaries, present him as tall and good-looking, but with a cleft lip and palate.[38] The cleft palate affected his speech: such birth defects had occurred before amongst his relatives.[39]
Family
On 13 March 1804, Malthus married Harriet, daughter of John Eckersall of Claverton House, St. Catherine's, near Bath, Somerset. They had a son and two daughters. His firstborn, son Henry, became vicar of Effingham, Surrey, in 1835, and of Donnington, West Sussex, in 1837; he married Sofia Otter (1807-1889), daughter of William Otter; Henry died in August 1882, aged 76. His middle child, Emily, died in 1885, outliving both of her parents and siblings and youngest, daughter, Lucille, died unmarried and childless in 1825, months before her 18th birthday.[35]An Essay on the Principle of Population
Malthus argued in his Essay (1798) that population growth generally expanded in times and in regions of plenty until the size of the population relative to the primary resources caused distress:"Yet in all societies, even those that are most vicious, the tendency to a virtuous attachment is so strong that there is a constant effort towards an increase of population. This constant effort as constantly tends to subject the lower classes of the society to distress and to prevent any great permanent amelioration of their condition".Malthus argued that two types of checks hold population within resource limits: positive checks, which raise the death rate; and preventive ones, which lower the birth rate. The positive checks include hunger, disease and war; the preventive checks, abortion, birth control, prostitution, postponement of marriage and celibacy.[40] In later editions of his essay, Malthus clarified his view that if society relied on human misery to limit population growth, then sources of misery (e.g., hunger, disease, and war) would inevitably afflict society, as would volatile economic cycles. On the other hand, "preventive checks" to population that limited birthrates, such as later marriages, could ensure a higher standard of living for all, while also increasing economic stability.[41] Regarding possibilities for freeing man from these limits, Malthus argued against a variety of imaginable solutions, such as the notion that agricultural improvements could expand without limit.
—Malthus T.R. 1798. An Essay on the Principle of Population. Chapter II, p 18 in Oxford World's Classics reprint.
Of the relationship between population and economics, Malthus wrote that when the population of laborers grows faster than the production of food, real wages fall because the growing population causes the cost of living (i.e., the cost of food) to go up. Difficulties of raising a family eventually reduce the rate of population growth, until the falling population again leads to higher real wages.
In the second and subsequent editions Malthus put more emphasis on moral restraint as the best means of easing the poverty of the lower classes."[42]
Editions and versions
- 1798: An Essay on the Principle of Population, as it affects the future improvement of society with remarks on the speculations of Mr. Godwin, M. Condorcet, and other writers.. Anonymously published.
- 1803: Second and much enlarged edition: An Essay on the Principle of Population; or, a view of its past and present effects on human happiness; with an enquiry into our prospects respecting the future removal or mitigation of the evils which it occasions. Authorship acknowledged.
- 1806, 1807, 1817 and 1826: editions 3–6, with relatively minor changes from the second edition.
- 1823: Malthus contributed the article on Population to the supplement of the Encyclopædia Britannica.
- 1830: Malthus had a long extract from the 1823 article reprinted as A summary view of the Principle of Population.[43]
Other works
1800: The present high price of provisions
In this work, his first published pamphlet, Malthus argues against the notion prevailing in his locale that the greed of intermediaries caused the high price of provisions. Instead, Malthus says that the high price stems from the Poor Laws which "increase the parish allowances in proportion to the price of corn". Thus, given a limited supply, the Poor Laws force up the price of daily necessities. But he concludes by saying that in time of scarcity such Poor Laws, by raising the price of corn more evenly, actually produce a beneficial effect.[44]1814: Observations on the effects of the Corn Laws
Although government in Britain had regulated the prices of grain, the Corn Laws originated in 1815. At the end of the Napoleonic Wars that year, Parliament passed legislation banning the importation of foreign corn into Britain until domestic corn cost 80 shillings per quarter. The high price caused the cost of food to increase and caused distress among the working classes in the towns. It led to serious rioting in London and to the "Peterloo Massacre" (1819) in Manchester.[45][46]In this pamphlet, printed during the parliamentary discussion, Malthus tentatively supported the free-traders. He argued that given the increasing expense of raising British corn, advantages accrued from supplementing it from cheaper foreign sources. This view he changed the following year.
1820: Principles of political economy
1836: Second edition, posthumously published.Malthus intended this work to rival Ricardo's Principles (1817).[47] It, and his 1827 Definitions in political economy, defended Sismondi's views on "general glut" rather than Say's Law, which in effect states "there can be no general glut".
Other publications
- 1807. A letter to Samuel Whitbread, Esq. M.P. on his proposed Bill for the Amendment of the Poor Laws. Johnson and Hatchard, London.
- 1808. Spence on Commerce. Edinburgh Review 11, January, 429–448.
- 1808. Newneham and others on the state of Ireland. Edinburgh Review 12, July, 336–355.
- 1809. Newneham on the state of Ireland, Edinburgh Review 14 April, 151–170.
- 1811. Depreciation of paper currency. Edinburgh Review 17, February, 340–372.
- 1812. Pamphlets on the bullion question. Edinburgh Review 18, August, 448–470.
- 1813. A letter to the Rt. Hon. Lord Grenville. Johnson, London.
- 1817. Statement respecting the East-India College. Murray, London.
- 1821. Godwin on Malthus. Edinburgh Review 35, July, 362–377.
- 1823. The Measure of Value, stated and illustrated
- 1823. Tooke – On high and low prices. Quarterly Review, 29 (57), April, 214–239.
- 1824. Political economy. Quarterly Review 30 (60), January, 297–334.
- 1829. On the measure of the conditions necessary to the supply of commodities. Transactions of the Royal Society of Literature of the United Kingdom. 1, 171–180. John Murray, London.
- 1829. On the meaning which is most usually and most correctly attached to the term Value of a Commodity. Transactions of the Royal Society of Literature of the United Kingdom. 2, 74–81. John Murray.
Reception and influence
Malthus developed the theory of demand-supply mismatches that he called gluts. Discounted at the time, this theory foreshadowed later works of an admirer, John Maynard Keynes.[48]The vast bulk of continuing commentary on Malthus, however, extends and expands on the "Malthusian controversy" of the early 19th century.
References in popular culture
- Ebenezer Scrooge from A Christmas Carol by Charles Dickens, represents the perceived ideas of Malthus,[49] famously illustrated by his explanation as to why he refuses to donate to the poor and destitute: "If they would rather die they had better do it, and decrease the surplus population". In general, Dickens had some Malthusian concerns (evident in Hard Times and other novels), and he concentrated his attacks on Utilitarianism and many of its proponents, like Smith, and Bentham, whom he thought of, along with Malthus, as unjust and inhumane people.[50]
- In Aldous Huxley's novel, Brave New World, people generally regard fertility as a nuisance, as in vitro breeding has enabled the society to maintain its population at precisely the level the controllers want. The women, therefore, carry contraceptives with them at all times in a "Malthusian belt".
- In the popular television show Wiseguy, Kevin Spacey played Mel Proffitt, a self-professed "Malthusian" who quotes Thomas Malthus and keeps a bust of his likeness on display.
- Officer Lockstock in the Broadway musical, Urinetown, a show in which the world's water resources have become sparse, cries, "Hail Malthus!", at the end of the show in reference to Malthus' theories regarding natural resource scarcity.
- The Professor on Sliders references Malthus in season 1 episode 10 "Luck of the Draw". The Sliders arrive in a Utopian world that has been implementing a lottery to keep the population low.
- Chapter 33 in Dan Brown's novel Inferno mentions 'The mathematics of Malthus'.
- The video game Hydrophobia tells about some eco-terrorists who name themselves "Malthusians" because their ideology is based on Malthus' theories.
- In the Green Lantern comic books published by DC Comics, the Guardians of the Universe began on a planet named "Maltus," which later became "an extremely overpopulated planet which serves as home to a poverty-stricken humanoid race of unknown origin. While advanced in technology, Maltus suffers from severe problems due to their overpopulation."
Epitaph
The epitaph of Malthus in Bath Abbey reads:
Sacred to the memory of the Rev Thomas Robert Malthus, long known to the lettered world by his admirable writings on the social branches of political economy, particularly by his essay on population.
One of the best men and truest philosophers of any age or country, raised by native dignity of mind above the misrepresentation of the ignorant and the neglect of the great, he lived a serene and happy life devoted to the pursuit and communication of truth.
Supported by a calm but firm conviction of the usefulness of his labours.
Content with the approbation of the wise and good.
His writings will be a lasting monument of the extent and correctness of his understanding.
The spotless integrity of his principles, the equity and candour of his nature, his sweetness of temper, urbanity of manners and tenderness of heart, his benevolence and his piety are still dearer recollections of his family and friends.
Born February 14, 1766 Died 29 December 1834.


 and only one undifferentiated quantity
and only one undifferentiated quantity  ; those involving
; those involving  and
and  ; and those involving more than two derivatives. As examples of the three cases, he solves the equations:
; and those involving more than two derivatives. As examples of the three cases, he solves the equations: ,
, , and
, and , respectively.
, respectively.
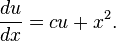



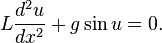

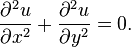
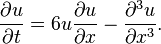
 in the xy-plane, define some rectangular region
in the xy-plane, define some rectangular region 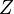 , such that
, such that ![Z = [l,m]\times[n,p]](http://upload.wikimedia.org/math/0/6/c/06c3b586eefc7610dc96c3d63cd5b0fe.png) and
and  and an initial condition
and an initial condition  , then there is a unique solution to this initial value problem if
, then there is a unique solution to this initial value problem if  and
and  are both continuous on
are both continuous on  .
.

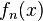 , if
, if  and
and  are continuous on some interval containing
are continuous on some interval containing  ,
, ![\frac{\part k(t)}{\part t} = s [k(t)]^\alpha - \delta k(t)](http://upload.wikimedia.org/math/5/6/8/56891c7fb05bf3c2568aa89fd1c33dd2.png)

