Gamma-ray burst

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Gamma-ray_burst

Artist's illustration showing the life of a massive star as nuclear fusion converts lighter elements into heavier ones. When fusion no longer generates enough pressure to counteract gravity, the star rapidly collapses to form a black hole. Theoretically, energy may be released during the collapse along the axis of rotation to form a GRB.

In gamma-ray astronomy, gamma-ray bursts (GRBs) are immensely energetic explosions that have been observed in distant galaxies. They are the most energetic and luminous electromagnetic events since the Big Bang. Bursts can last from ten milliseconds to several hours. After an initial flash of gamma rays, a longer-lived "afterglow" is usually emitted at longer wavelengths (X-ray, ultraviolet, optical, infrared, microwave and radio).

The intense radiation of most observed GRBs is thought to be released during a supernova or superluminous supernova as a high-mass star implodes to form a neutron star or a black hole. A subclass of GRBs appears to originate from the merger of binary neutron stars.

The sources of most GRBs are billions of light years away from Earth, implying that the explosions are both extremely energetic (a typical burst releases as much energy in a few seconds as the Sun will in its entire 10-billion-year lifetime) and extremely rare (a few per galaxy per million years). All observed GRBs have originated from outside the Milky Way galaxy, although a related class of phenomena, soft gamma repeaters, are associated with magnetars within the Milky Way. It has been hypothesized that a gamma-ray burst in the Milky Way, pointing directly towards the Earth, could cause a mass extinction event. The Late Ordovician mass extinction has been hypothesised by some researchers to have occurred as a result of such a gamma-ray burst.

GRBs were first detected in 1967 by the Vela satellites, which had been designed to detect covert nuclear weapons tests; after thorough analysis, this was published in 1973. Following their discovery, hundreds of theoretical models were proposed to explain these bursts, such as collisions between comets and neutron stars. Little information was available to verify these models until the 1997 detection of the first X-ray and optical afterglows and direct measurement of their redshifts using optical spectroscopy, and thus their distances and energy outputs. These discoveries, and subsequent studies of the galaxies and supernovae associated with the bursts, clarified the distance and luminosity of GRBs, definitively placing them in distant galaxies.

History

Main article: History of gamma-ray burst research

Positions on the sky of all gamma-ray bursts detected during the BATSE mission. The distribution is isotropic, with no concentration towards the plane of the Milky Way, which runs horizontally through the center of the image.

Gamma-ray bursts were first observed in the late 1960s by the U.S. Vela satellites, which were built to detect gamma radiation pulses emitted by nuclear weapons tested in space. The United States suspected that the Soviet Union might attempt to conduct secret nuclear tests after signing the Nuclear Test Ban Treaty in 1963. On July 2, 1967, at 14:19 UTC, the Vela 4 and Vela 3 satellites detected a flash of gamma radiation unlike any known nuclear weapons signature. Uncertain what had happened but not considering the matter particularly urgent, the team at the Los Alamos National Laboratory, led by Ray Klebesadel, filed the data away for investigation. As additional Vela satellites were launched with better instruments, the Los Alamos team continued to find inexplicable gamma-ray bursts in their data. By analyzing the different arrival times of the bursts as detected by different satellites, the team was able to determine rough estimates for the sky positions of 16 bursts and definitively rule out a terrestrial or solar origin. Contrary to popular belief, the data was never classified. After thorough analysis, the findings were published in 1973 as an Astrophysical Journal article entitled "Observations of Gamma-Ray Bursts of Cosmic Origin".

Most early theories of gamma-ray bursts posited nearby sources within the Milky Way Galaxy. From 1991, the Compton Gamma Ray Observatory (CGRO) and its Burst and Transient Source Explorer (BATSE) instrument, an extremely sensitive gamma-ray detector, provided data that showed the distribution of GRBs is isotropic – not biased towards any particular direction in space. If the sources were from within our own galaxy, they would be strongly concentrated in or near the galactic plane. The absence of any such pattern in the case of GRBs provided strong evidence that gamma-ray bursts must come from beyond the Milky Way. However, some Milky Way models are still consistent with an isotropic distribution.

Counterpart objects as candidate sources

For decades after the discovery of GRBs, astronomers searched for a counterpart at other wavelengths: i.e., any astronomical object in positional coincidence with a recently observed burst. Astronomers considered many distinct classes of objects, including white dwarfs, pulsars, supernovae, globular clusters, quasars, Seyfert galaxies, and BL Lac objects. All such searches were unsuccessful, and in a few cases particularly well-localized bursts (those whose positions were determined with what was then a high degree of accuracy) could be clearly shown to have no bright objects of any nature consistent with the position derived from the detecting satellites. This suggested an origin of either very faint stars or extremely distant galaxies. Even the most accurate positions contained numerous faint stars and galaxies, and it was widely agreed that final resolution of the origins of cosmic gamma-ray bursts would require both new satellites and faster communication.

Afterglow

The Italian–Dutch satellite BeppoSAX, launched in April 1996, provided the first accurate positions of gamma-ray bursts, allowing follow-up observations and identification of the sources.

Several models for the origin of gamma-ray bursts postulated that the initial burst of gamma rays should be followed by afterglow: slowly fading emission at longer wavelengths created by collisions between the burst ejecta and interstellar gas. Early searches for this afterglow were unsuccessful, largely because it is difficult to observe a burst's position at longer wavelengths immediately after the initial burst. The breakthrough came in February 1997 when the satellite BeppoSAX detected a gamma-ray burst (GRB 970228) and when the X-ray camera was pointed towards the direction from which the burst had originated, it detected fading X-ray emission. The William Herschel Telescope identified a fading optical counterpart 20 hours after the burst. Once the GRB faded, deep imaging was able to identify a faint, distant host galaxy at the location of the GRB as pinpointed by the optical afterglow.

Because of the very faint luminosity of this galaxy, its exact distance was not measured for several years. Well after then, another major breakthrough occurred with the next event registered by BeppoSAX, GRB 970508. This event was localized within four hours of its discovery, allowing research teams to begin making observations much sooner than any previous burst. The spectrum of the object revealed a redshift of z = 0.835, placing the burst at a distance of roughly 6 billion light years from Earth. This was the first accurate determination of the distance to a GRB, and together with the discovery of the host galaxy of 970228 proved that GRBs occur in extremely distant galaxies. Within a few months, the controversy about the distance scale ended: GRBs were extragalactic events originating within faint galaxies at enormous distances. The following year, GRB 980425 was followed within a day by a bright supernova (SN 1998bw), coincident in location, indicating a clear connection between GRBs and the deaths of very massive stars. This burst provided the first strong clue about the nature of the systems that produce GRBs.

More recent instruments

NASA's Swift Spacecraft launched in November 2004

BeppoSAX functioned until 2002 and CGRO (with BATSE) was deorbited in 2000. However, the revolution in the study of gamma-ray bursts motivated the development of a number of additional instruments designed specifically to explore the nature of GRBs, especially in the earliest moments following the explosion. The first such mission, HETE-2, was launched in 2000 and functioned until 2006, providing most of the major discoveries during this period. One of the most successful space missions to date, Swift, was launched in 2004 and as of January 2023 is still operational. Swift is equipped with a very sensitive gamma-ray detector as well as on-board X-ray and optical telescopes, which can be rapidly and automatically slewed to observe afterglow emission following a burst. More recently, the Fermi mission was launched carrying the Gamma-Ray Burst Monitor, which detects bursts at a rate of several hundred per year, some of which are bright enough to be observed at extremely high energies with Fermi's Large Area Telescope. Meanwhile, on the ground, numerous optical telescopes have been built or modified to incorporate robotic control software that responds immediately to signals sent through the Gamma-ray Burst Coordinates Network. This allows the telescopes to rapidly repoint towards a GRB, often within seconds of receiving the signal and while the gamma-ray emission itself is still ongoing.

New developments since the 2000s include the recognition of short gamma-ray bursts as a separate class (likely from merging neutron stars and not associated with supernovae), the discovery of extended, erratic flaring activity at X-ray wavelengths lasting for many minutes after most GRBs, and the discovery of the most luminous (GRB 080319B) and the former most distant (GRB 090423) objects in the universe. The most distant known GRB, GRB 090429B, is now the most distant known object in the universe.

In October 2018, astronomers reported that GRB 150101B (detected in 2015) and GW170817, a gravitational wave event detected in 2017 (which has been associated with GRB170817A, a burst detected 1.7 seconds later), may have been produced by the same mechanism – the merger of two neutron stars. The similarities between the two events, in terms of gamma ray, optical, and x-ray emissions, as well as to the nature of the associated host galaxies, are "striking", suggesting the two separate events may both be the result of the merger of neutron stars, and both may be a kilonova, which may be more common in the universe than previously understood, according to the researchers.

The highest energy light observed from a gamma-ray burst was one teraelectronvolt, from GRB 190114C in 2019. (Note, this is about a thousand times lower energy than the highest energy light observed from any source, which is 1.4 petaelectronvolts as of the year 2021.)

Classification

Gamma-ray burst light curves

The light curves of gamma-ray bursts are extremely diverse and complex. No two gamma-ray burst light curves are identical, with large variation observed in almost every property: the duration of observable emission can vary from milliseconds to tens of minutes, there can be a single peak or several individual subpulses, and individual peaks can be symmetric or with fast brightening and very slow fading. Some bursts are preceded by a "precursor" event, a weak burst that is then followed (after seconds to minutes of no emission at all) by the much more intense "true" bursting episode. The light curves of some events have extremely chaotic and complicated profiles with almost no discernible patterns.

Although some light curves can be roughly reproduced using certain simplified models, little progress has been made in understanding the full diversity observed. Many classification schemes have been proposed, but these are often based solely on differences in the appearance of light curves and may not always reflect a true physical difference in the progenitors of the explosions. However, plots of the distribution of the observed duration for a large number of gamma-ray bursts show a clear bimodality, suggesting the existence of two separate populations: a "short" population with an average duration of about 0.3 seconds and a "long" population with an average duration of about 30 seconds. Both distributions are very broad with a significant overlap region in which the identity of a given event is not clear from duration alone. Additional classes beyond this two-tiered system have been proposed on both observational and theoretical grounds.

Short gamma-ray bursts

Hubble Space Telescope captures infrared glow of a kilonova blast.

GRB 211106A , one of the most energetic short GRB registered, in the first-ever time-lapse movie of a short GRB in millimeter-wavelength light, as seen with the Atacama Large Millimeter/submillimeter Array (ALMA) and pinpointed to a distant host galaxy captured using the Hubble Space Telescope.

Events with a duration of less than about two seconds are classified as short gamma-ray bursts. These account for about 30% of gamma-ray bursts, but until 2005, no afterglow had been successfully detected from any short event and little was known about their origins. Since then, several dozen short gamma-ray burst afterglows have been detected and localized, several of which are associated with regions of little or no star formation, such as large elliptical galaxies. This rules out a link to massive stars, confirming that short events are physically distinct from long events. In addition, there has been no association with supernovae.

The true nature of these objects was initially unknown, and the leading hypothesis was that they originated from the mergers of binary neutron stars or a neutron star with a black hole. Such mergers were theorized to produce kilonovae, and evidence for a kilonova associated with GRB 130603B was seen. The mean duration of these events of 0.2 seconds suggests (because of causality) a source of very small physical diameter in stellar terms; less than 0.2 light-seconds (about 60,000 km or 37,000 miles – four times the Earth's diameter). The observation of minutes to hours of X-ray flashes after a short gamma-ray burst is consistent with small particles of a primary object like a neutron star initially swallowed by a black hole in less than two seconds, followed by some hours of lesser energy events, as remaining fragments of tidally disrupted neutron star material (no longer neutronium) remain in orbit to spiral into the black hole, over a longer period of time. A small fraction of short gamma-ray bursts are probably produced by giant flares from soft gamma repeaters in nearby galaxies.

The origin of short GRBs in kilonovae was confirmed when short GRB 170817A was detected only 1.7 s after the detection of gravitational wave GW170817, which was a signal from the merger of two neutron stars.

Long gamma-ray bursts

Swift captured the afterglow of GRB 221009A about an hour after it was first detected reaching Earth on October 9, 2022. The bright rings form as a result of X-rays scattered from otherwise unobservable dust layers within our galaxy that lie in the direction of the burst.

Most observed events (70%) have a duration of greater than two seconds and are classified as long gamma-ray bursts. Because these events constitute the majority of the population and because they tend to have the brightest afterglows, they have been observed in much greater detail than their short counterparts. Almost every well-studied long gamma-ray burst has been linked to a galaxy with rapid star formation, and in many cases to a core-collapse supernova as well, unambiguously associating long GRBs with the deaths of massive stars. Long GRB afterglow observations, at high redshift, are also consistent with the GRB having originated in star-forming regions. In December 2022, astronomers reported the first evidence of a long GRB produced by a neutron star merger.

Ultra-long gamma-ray bursts

These events are at the tail end of the long GRB duration distribution, lasting more than 10,000 seconds. They have been proposed to form a separate class, caused by the collapse of a blue supergiant star, a tidal disruption event or a new-born magnetar. Only a small number have been identified to date, their primary characteristic being their gamma ray emission duration. The most studied ultra-long events include GRB 101225A and GRB 111209A. The low detection rate may be a result of low sensitivity of current detectors to long-duration events, rather than a reflection of their true frequency. A 2013 study, on the other hand, shows that the existing evidence for a separate ultra-long GRB population with a new type of progenitor is inconclusive, and further multi-wavelength observations are needed to draw a firmer conclusion.

Energetics and beaming

Artist's illustration of a bright gamma-ray burst occurring in a star-forming region. Energy from the explosion is beamed into two narrow, oppositely directed jets.

Gamma-ray bursts are very bright as observed from Earth despite their typically immense distances. An average long GRB has a bolometric flux comparable to a bright star of our galaxy despite a distance of billions of light years (compared to a few tens of light years for most visible stars). Most of this energy is released in gamma rays, although some GRBs have extremely luminous optical counterparts as well. GRB 080319B, for example, was accompanied by an optical counterpart that peaked at a visible magnitude of 5.8, comparable to that of the dimmest naked-eye stars despite the burst's distance of 7.5 billion light years. This combination of brightness and distance implies an extremely energetic source. Assuming the gamma-ray explosion to be spherical, the energy output of GRB 080319B would be within a factor of two of the rest-mass energy of the Sun (the energy which would be released were the Sun to be converted entirely into radiation).

Gamma-ray bursts are thought to be highly focused explosions, with most of the explosion energy collimated into a narrow jet. The approximate angular width of the jet (that is, the degree of spread of the beam) can be estimated directly by observing the achromatic "jet breaks" in afterglow light curves: a time after which the slowly decaying afterglow begins to fade rapidly as the jet slows and can no longer beam its radiation as effectively. Observations suggest significant variation in the jet angle from between 2 and 20 degrees.

Because their energy is strongly focused, the gamma rays emitted by most bursts are expected to miss the Earth and never be detected. When a gamma-ray burst is pointed towards Earth, the focusing of its energy along a relatively narrow beam causes the burst to appear much brighter than it would have been were its energy emitted spherically. When this effect is taken into account, typical gamma-ray bursts are observed to have a true energy release of about 10⁴⁴ J, or about 1/2000 of a Solar mass (M_☉) energy equivalent – which is still many times the mass-energy equivalent of the Earth (about 5.5 × 10⁴¹ J). This is comparable to the energy released in a bright type Ib/c supernova and within the range of theoretical models. Very bright supernovae have been observed to accompany several of the nearest GRBs. Additional support for focusing of the output of GRBs has come from observations of strong asymmetries in the spectra of nearby type Ic supernovae and from radio observations taken long after bursts when their jets are no longer relativistic.

Short (time duration) GRBs appear to come from a lower-redshift (i.e. less distant) population and are less luminous than long GRBs. The degree of beaming in short bursts has not been accurately measured, but as a population they are likely less collimated than long GRBs or possibly not collimated at all in some cases.

Progenitors

Main article: Gamma-ray burst progenitors

Hubble Space Telescope image of Wolf–Rayet star WR 124 and its surrounding nebula. Wolf–Rayet stars are candidates for being progenitors of long-duration GRBs.

Because of the immense distances of most gamma-ray burst sources from Earth, identification of the progenitors, the systems that produce these explosions, is challenging. The association of some long GRBs with supernovae and the fact that their host galaxies are rapidly star-forming offer very strong evidence that long gamma-ray bursts are associated with massive stars. The most widely accepted mechanism for the origin of long-duration GRBs is the collapsar model, in which the core of an extremely massive, low-metallicity, rapidly rotating star collapses into a black hole in the final stages of its evolution. Matter near the star's core rains down towards the center and swirls into a high-density accretion disk. The infall of this material into a black hole drives a pair of relativistic jets out along the rotational axis, which pummel through the stellar envelope and eventually break through the stellar surface and radiate as gamma rays. Some alternative models replace the black hole with a newly formed magnetar, although most other aspects of the model (the collapse of the core of a massive star and the formation of relativistic jets) are the same.

The closest analogs within the Milky Way galaxy of the stars producing long gamma-ray bursts are likely the Wolf–Rayet stars, extremely hot and massive stars, which have shed most or all of their hydrogen envelope. Eta Carinae, Apep, and WR 104 have been cited as possible future gamma-ray burst progenitors. It is unclear if any star in the Milky Way has the appropriate characteristics to produce a gamma-ray burst.

The massive-star model probably does not explain all types of gamma-ray burst. There is strong evidence that some short-duration gamma-ray bursts occur in systems with no star formation and no massive stars, such as elliptical galaxies and galaxy halos. The favored theory for the origin of most short gamma-ray bursts is the merger of a binary system consisting of two neutron stars. According to this model, the two stars in a binary slowly spiral towards each other because gravitational radiation releases energy until tidal forces suddenly rip the neutron stars apart and they collapse into a single black hole. The infall of matter into the new black hole produces an accretion disk and releases a burst of energy, analogous to the collapsar model. Numerous other models have also been proposed to explain short gamma-ray bursts, including the merger of a neutron star and a black hole, the accretion-induced collapse of a neutron star, or the evaporation of primordial black holes.

An alternative explanation proposed by Friedwardt Winterberg is that in the course of a gravitational collapse and in reaching the event horizon of a black hole, all matter disintegrates into a burst of gamma radiation.

Tidal disruption events

Main article: Tidal disruption event

This new class of GRB-like events was first discovered through the detection of GRB 110328A by the Swift Gamma-Ray Burst Mission on 28 March 2011. This event had a gamma-ray duration of about 2 days, much longer than even ultra-long GRBs, and was detected in X-rays for many months. It occurred at the center of a small elliptical galaxy at redshift z = 0.3534. There is an ongoing debate as to whether the explosion was the result of stellar collapse or a tidal disruption event accompanied by a relativistic jet, although the latter explanation has become widely favoured.

A tidal disruption event of this sort is when a star interacts with a supermassive black hole, shredding the star, and in some cases creating a relativistic jet which produces bright emission of gamma ray radiation. The event GRB 110328A (also denoted Swift J1644+57) was initially argued to be produced by the disruption of a main sequence star by a black hole of several million times the mass of the Sun, although it has subsequently been argued that the disruption of a white dwarf by a black hole of mass about 10 thousand times the Sun may be more likely.

Emission mechanisms

Main article: Gamma-ray burst emission mechanisms

Gamma-ray burst mechanism

The means by which gamma-ray bursts convert energy into radiation remains poorly understood, and as of 2010 there was still no generally accepted model for how this process occurs. Any successful model of GRB emission must explain the physical process for generating gamma-ray emission that matches the observed diversity of light curves, spectra, and other characteristics. Particularly challenging is the need to explain the very high efficiencies that are inferred from some explosions: some gamma-ray bursts may convert as much as half (or more) of the explosion energy into gamma-rays. Early observations of the bright optical counterparts to GRB 990123 and to GRB 080319B, whose optical light curves were extrapolations of the gamma-ray light spectra, have suggested that inverse Compton scattering may be the dominant process in some events. In this model, pre-existing low-energy photons are scattered by relativistic electrons within the explosion, augmenting their energy by a large factor and transforming them into gamma-rays.

The nature of the longer-wavelength afterglow emission (ranging from X-ray through radio) that follows gamma-ray bursts is better understood. Any energy released by the explosion not radiated away in the burst itself takes the form of matter or energy moving outward at nearly the speed of light. As this matter collides with the surrounding interstellar gas, it creates a relativistic shock wave that then propagates forward into interstellar space. A second shock wave, the reverse shock, may propagate back into the ejected matter. Extremely energetic electrons within the shock wave are accelerated by strong local magnetic fields and radiate as synchrotron emission across most of the electromagnetic spectrum. This model has generally been successful in modeling the behavior of many observed afterglows at late times (generally, hours to days after the explosion), although there are difficulties explaining all features of the afterglow very shortly after the gamma-ray burst has occurred.

Rate of occurrence and potential effects on life

On 27 October 2015, at 22:40 GMT, the NASA/ASI/UKSA Swift satellite discovered its 1000th gamma-ray burst (GRB).

Gamma ray bursts can have harmful or destructive effects on life. Considering the universe as a whole, the safest environments for life similar to that on Earth are the lowest density regions in the outskirts of large galaxies. Our knowledge of galaxy types and their distribution suggests that life as we know it can only exist in about 10% of all galaxies. Furthermore, galaxies with a redshift, z, higher than 0.5 are unsuitable for life as we know it, because of their higher rate of GRBs and their stellar compactness.

All GRBs observed to date have occurred well outside the Milky Way galaxy and have been harmless to Earth. However, if a GRB were to occur within the Milky Way within 5,000 to 8,000 light-years and its emission were beamed straight towards Earth, the effects could be harmful and potentially devastating for its ecosystems. Currently, orbiting satellites detect on average approximately one GRB per day. The closest observed GRB as of March 2014 was GRB 980425, located 40 megaparsecs (130,000,000 ly) away (z=0.0085) in an SBc-type dwarf galaxy.^[118] GRB 980425 was far less energetic than the average GRB and was associated with the Type Ib supernova SN 1998bw.

Estimating the exact rate at which GRBs occur is difficult; for a galaxy of approximately the same size as the Milky Way, estimates of the expected rate (for long-duration GRBs) can range from one burst every 10,000 years, to one burst every 1,000,000 years. Only a small percentage of these would be beamed towards Earth. Estimates of rate of occurrence of short-duration GRBs are even more uncertain because of the unknown degree of collimation, but are probably comparable.

Since GRBs are thought to involve beamed emission along two jets in opposing directions, only planets in the path of these jets would be subjected to the high energy gamma radiation.

Although nearby GRBs hitting Earth with a destructive shower of gamma rays are only hypothetical events, high energy processes across the galaxy have been observed to affect the Earth's atmosphere.

Effects on Earth

Earth's atmosphere is very effective at absorbing high energy electromagnetic radiation such as x-rays and gamma rays, so these types of radiation would not reach any dangerous levels at the surface during the burst event itself. The immediate effect on life on Earth from a GRB within a few kiloparsecs would only be a short increase in ultraviolet radiation at ground level, lasting from less than a second to tens of seconds. This ultraviolet radiation could potentially reach dangerous levels depending on the exact nature and distance of the burst, but it seems unlikely to be able to cause a global catastrophe for life on Earth.

The long-term effects from a nearby burst are more dangerous. Gamma rays cause chemical reactions in the atmosphere involving oxygen and nitrogen molecules, creating first nitrogen oxide then nitrogen dioxide gas. The nitrogen oxides cause dangerous effects on three levels. First, they deplete ozone, with models showing a possible global reduction of 25–35%, with as much as 75% in certain locations, an effect that would last for years. This reduction is enough to cause a dangerously elevated UV index at the surface. Secondly, the nitrogen oxides cause photochemical smog, which darkens the sky and blocks out parts of the sunlight spectrum. This would affect photosynthesis, but models show only about a 1% reduction of the total sunlight spectrum, lasting a few years. However, the smog could potentially cause a cooling effect on Earth's climate, producing a "cosmic winter" (similar to an impact winter, but without an impact), but only if it occurs simultaneously with a global climate instability. Thirdly, the elevated nitrogen dioxide levels in the atmosphere would wash out and produce acid rain. Nitric acid is toxic to a variety of organisms, including amphibian life, but models predict that it would not reach levels that would cause a serious global effect. The nitrates might in fact be of benefit to some plants.

All in all, a GRB within a few kiloparsecs, with its energy directed towards Earth, will mostly damage life by raising the UV levels during the burst itself and for a few years thereafter. Models show that the destructive effects of this increase can cause up to 16 times the normal levels of DNA damage. It has proved difficult to assess a reliable evaluation of the consequences of this on the terrestrial ecosystem, because of the uncertainty in biological field and laboratory data.

Hypothetical effects on Earth in the past

There is a very good chance (but no certainty) that at least one lethal GRB took place during the past 5 billion years close enough to Earth as to significantly damage life. There is a 50% chance that such a lethal GRB took place within two kiloparsecs of Earth during the last 500 million years, causing one of the major mass extinction events.

The major Ordovician–Silurian extinction event 450 million years ago may have been caused by a GRB. Estimates suggest that approximately 20–60% of the total phytoplankton biomass in the Ordovician oceans would have perished in a GRB, because the oceans were mostly oligotrophic and clear. The late Ordovician species of trilobites that spent portions of their lives in the plankton layer near the ocean surface were much harder hit than deep-water dwellers, which tended to remain within quite restricted areas. This is in contrast to the usual pattern of extinction events, wherein species with more widely spread populations typically fare better. A possible explanation is that trilobites remaining in deep water would be more shielded from the increased UV radiation associated with a GRB. Also supportive of this hypothesis is the fact that during the late Ordovician, burrowing bivalve species were less likely to go extinct than bivalves that lived on the surface.

A case has been made that the 774–775 carbon-14 spike was the result of a short GRB, though a very strong solar flare is another possibility.

GRB candidates in the Milky Way

Illustration of a short gamma-ray burst caused by a collapsing star.

No gamma-ray bursts from within our own galaxy, the Milky Way, have been observed, and the question of whether one has ever occurred remains unresolved. In light of evolving understanding of gamma-ray bursts and their progenitors, the scientific literature records a growing number of local, past, and future GRB candidates. Long duration GRBs are related to superluminous supernovae, or hypernovae, and most luminous blue variables (LBVs) and rapidly spinning Wolf–Rayet stars are thought to end their life cycles in core-collapse supernovae with an associated long-duration GRB. Knowledge of GRBs, however, is from metal-poor galaxies of former epochs of the universe's evolution, and it is impossible to directly extrapolate to encompass more evolved galaxies and stellar environments with a higher metallicity, such as the Milky Way.

Complex number

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Complex_number 

A complex number can be visually represented as a pair of numbers (a, b) forming a vector on a diagram called an Argand diagram, representing the complex plane. Re is the real axis, Im is the imaginary axis, and i is the "imaginary unit", that satisfies i² = −1.

In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i, called the imaginary unit and satisfying the equation ${\displaystyle i^2=-1}$; every complex number can be expressed in the form ${\displaystyle a+bi}$, where a and b are real numbers. Because no real number satisfies the above equation, i was called an imaginary number by René Descartes. For the complex number ${\displaystyle a+bi}$, a is called the real part, and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols ${\displaystyle \mathbb{C}}$ or C. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world.

Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficients has a solution which is a complex number. For example, the equation ${\displaystyle (x+1{)}^2=-9}$ has no real solution, since the square of a real number cannot be negative, but has the two nonreal complex solutions ${\displaystyle -1+3i}$ and ${\displaystyle -1-3i}$.

Addition, subtraction and multiplication of complex numbers can be naturally defined by using the rule ${\displaystyle i^2=-1}$ combined with the associative, commutative, and distributive laws. Every nonzero complex number has a multiplicative inverse. This makes the complex numbers a field that has the real numbers as a subfield. The complex numbers also form a real vector space of dimension two, with {1, i} as a standard basis.

This standard basis makes the complex numbers a Cartesian plane, called the complex plane. This allows a geometric interpretation of the complex numbers and their operations, and conversely expressing in terms of complex numbers some geometric properties and constructions. For example, the real numbers form the real line which is identified to the horizontal axis of the complex plane. The complex numbers of absolute value one form the unit circle. The addition of a complex number is a translation in the complex plane, and the multiplication by a complex number is a similarity centered at the origin. The complex conjugation is the reflection symmetry with respect to the real axis. The complex absolute value is a Euclidean norm.

In summary, the complex numbers form a rich structure that is simultaneously an algebraically closed field, a commutative algebra over the reals, and a Euclidean vector space of dimension two.

Definition

An illustration of the complex number z = x + iy on the complex plane. The real part is x, and its imaginary part is y.

A complex number is a number of the form a + bi, where a and b are real numbers, and i is an indeterminate satisfying i² = −1. For example, 2 + 3i is a complex number.

This way, a complex number is defined as a polynomial with real coefficients in the single indeterminate i, for which the relation i² + 1 = 0 is imposed. Based on this definition, complex numbers can be added and multiplied, using the addition and multiplication for polynomials. The relation i² + 1 = 0 induces the equalities i^4k = 1, i^4k+1 = i, i^4k+2 = −1, and i^4k+3 = −i, which hold for all integers k; these allow the reduction of any polynomial that results from the addition and multiplication of complex numbers to a linear polynomial in i, again of the form a + bi with real coefficients a, b.

The real number a is called the real part of the complex number a + bi; the real number b is called its imaginary part. To emphasize, the imaginary part does not include a factor i; that is, the imaginary part is b, not bi.

Formally, the complex numbers are defined as the quotient ring of the polynomial ring in the indeterminate i, by the ideal generated by the polynomial i² + 1 (see below).

Notation

A real number a can be regarded as a complex number a + 0i, whose imaginary part is 0. A purely imaginary number bi is a complex number 0 + bi, whose real part is zero. As with polynomials, it is common to write a for a + 0i and bi for 0 + bi. Moreover, when the imaginary part is negative, that is, b = −|b| < 0, it is common to write a − |b|i instead of a + (−|b|)i; for example, for b = −4, 3 − 4i can be written instead of 3 + (−4)i.

Since the multiplication of the indeterminate i and a real is commutative in polynomials with real coefficients, the polynomial a + bi may be written as a + ib. This is often expedient for imaginary parts denoted by expressions, for example, when b is a radical.

The real part of a complex number z is denoted by Re(z), ${\displaystyle \mathcal{R}\mathcal{e}(z)}$, or ${\displaystyle \mathfrak{R}(z)}$; the imaginary part of a complex number z is denoted by Im(z), ${\displaystyle \mathcal{I}\mathcal{m}(z)}$, or ${\displaystyle \mathfrak{I}(z).}$ For example,

$${\displaystyle \mathrm{Re}(2+3i)=2\text{ and }\mathrm{Im}(2+3i)=3.}$$

The set of all complex numbers is denoted by ${\displaystyle \mathbb{C}}$ (blackboard bold) or C (upright bold).

In some disciplines, particularly in electromagnetism and electrical engineering, j is used instead of i as i is frequently used to represent electric current. In these cases, complex numbers are written as a + bj, or a + jb.

Visualization

Main article: Complex plane

A complex number z, as a point (black) and its position vector (blue)

A complex number z can thus be identified with an ordered pair ${\displaystyle (\mathrm{\Re }(z),\mathrm{\Im }(z))}$ of real numbers, which in turn may be interpreted as coordinates of a point in a two-dimensional space. The most immediate space is the Euclidean plane with suitable coordinates, which is then called complex plane or Argand diagram, named after Jean-Robert Argand. Another prominent space on which the coordinates may be projected is the two-dimensional surface of a sphere, which is then called Riemann sphere.

Cartesian complex plane

The definition of the complex numbers involving two arbitrary real values immediately suggests the use of Cartesian coordinates in the complex plane. The horizontal (real) axis is generally used to display the real part, with increasing values to the right, and the imaginary part marks the vertical (imaginary) axis, with increasing values upwards.

A charted number may be viewed either as the coordinatized point or as a position vector from the origin to this point. The coordinate values of a complex number z can hence be expressed in its Cartesian, rectangular, or algebraic form.

Notably, the operations of addition and multiplication take on a very natural geometric character, when complex numbers are viewed as position vectors: addition corresponds to vector addition, while multiplication (see below) corresponds to multiplying their magnitudes and adding the angles they make with the real axis. Viewed in this way, the multiplication of a complex number by i corresponds to rotating the position vector counterclockwise by a quarter turn (90°) about the origin—a fact which can be expressed algebraically as

$${\displaystyle (x+yi)i=-y+xi.}$$

Polar complex plane

Main article: Polar coordinate system

"Polar form" redirects here. For the higher-dimensional analogue, see Polar decomposition.

Argument φ and modulus r locate a point in the complex plane.

Modulus and argument

An alternative option for coordinates in the complex plane is the polar coordinate system that uses the distance of the point z from the origin (O), and the angle subtended between the positive real axis and the line segment Oz in a counterclockwise sense. This leads to the polar form

${\displaystyle z=r{e}^{i\phi }=r(\cos \phi +i\sin \phi )}$

of a complex number, where r is the absolute value of z, and ${\displaystyle \phi }$ is the argument of z.

The absolute value (or modulus or magnitude) of a complex number z = x + yi is

$${\displaystyle r=|z|=\sqrt{x^2+y^2}.}$$

If z is a real number (that is, if y = 0), then r = |x|. That is, the absolute value of a real number equals its absolute value as a complex number.

By Pythagoras' theorem, the absolute value of a complex number is the distance to the origin of the point representing the complex number in the complex plane.

The argument of z (in many applications referred to as the "phase" φ) is the angle of the radius Oz with the positive real axis, and is written as arg z. As with the modulus, the argument can be found from the rectangular form x + yi—by applying the inverse tangent to the quotient of imaginary-by-real parts. By using a half-angle identity, a single branch of the arctan suffices to cover the range (−π, π] of the arg-function, and avoids a more subtle case-by-case analysis

$${\displaystyle \phi =\arg (x+yi)=\{\begin{array}{ll}2\arctan \left({\displaystyle \frac{y}{x+\sqrt{x^2+y^2}}}\right)& \text{if }y\ne 0\text{ or }x>0,\\ \pi & \text{if }x<0\text{ and }y=0,\\ \text{undefined}& \text{if }x=0\text{ and }y=0.\end{array}}$$

Normally, as given above, the principal value in the interval (−π, π] is chosen. If the arg value is negative, values in the range (−π, π] or [0, 2π) can be obtained by adding 2π. The value of φ is expressed in radians in this article. It can increase by any integer multiple of 2π and still give the same angle, viewed as subtended by the rays of the positive real axis and from the origin through z. Hence, the arg function is sometimes considered as multivalued. The polar angle for the complex number 0 is indeterminate, but arbitrary choice of the polar angle 0 is common.

The value of φ equals the result of atan2:

$${\displaystyle \phi =\mathrm{atan2}\left(\mathrm{Im}(z),\mathrm{Re}(z)\right).}$$

Together, r and φ give another way of representing complex numbers, the polar form, as the combination of modulus and argument fully specify the position of a point on the plane. Recovering the original rectangular co-ordinates from the polar form is done by the formula called trigonometric form

$${\displaystyle z=r(\cos \phi +i\sin \phi ).}$$

Using Euler's formula this can be written as

$${\displaystyle z=r{e}^{i\phi }\text{ or }z=r\exp i\phi .}$$

Using the cis function, this is sometimes abbreviated to

$${\displaystyle z=r\mathrm{c}\mathrm{i}\mathrm{s}\phi .}$$

In angle notation, often used in electronics to represent a phasor with amplitude r and phase φ, it is written as

$${\displaystyle z=r\mathrm{\angle }\phi .}$$

Complex graphs

Main article: Domain coloring

A color wheel graph of the expression (z² − 1)(z − 2 − i)²/z² + 2 + 2i

When visualizing complex functions, both a complex input and output are needed. Because each complex number is represented in two dimensions, visually graphing a complex function would require the perception of a four dimensional space, which is possible only in projections. Because of this, other ways of visualizing complex functions have been designed.

In domain coloring the output dimensions are represented by color and brightness, respectively. Each point in the complex plane as domain is ornated, typically with color representing the argument of the complex number, and brightness representing the magnitude. Dark spots mark moduli near zero, brighter spots are farther away from the origin, the gradation may be discontinuous, but is assumed as monotonous. The colors often vary in steps of π/3 for 0 to 2π from red, yellow, green, cyan, blue, to magenta. These plots are called color wheel graphs. This provides a simple way to visualize the functions without losing information. The picture shows zeros for ±1, (2 + i) and poles at ${\displaystyle \pm \sqrt{-2-2i}.}$

History

See also: Negative number § History

The solution in radicals (without trigonometric functions) of a general cubic equation, when all three of its roots are real numbers, contains the square roots of negative numbers, a situation that cannot be rectified by factoring aided by the rational root test, if the cubic is irreducible; this is the so-called casus irreducibilis ("irreducible case"). This conundrum led Italian mathematician Gerolamo Cardano to conceive of complex numbers in around 1545 in his Ars Magna, though his understanding was rudimentary; moreover he later described complex numbers as "as subtle as they are useless". Cardano did use imaginary numbers, but described using them as "mental torture." This was prior to the use of the graphical complex plane. Cardano and other Italian mathematicians, notably Scipione del Ferro, in the 1500s created an algorithm for solving cubic equations which generally had one real solution and two solutions containing an imaginary number. Since they ignored the answers with the imaginary numbers, Cardano found them useless.

Work on the problem of general polynomials ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation of degree one or higher. Complex numbers thus form an algebraically closed field, where any polynomial equation has a root.

Many mathematicians contributed to the development of complex numbers. The rules for addition, subtraction, multiplication, and root extraction of complex numbers were developed by the Italian mathematician Rafael Bombelli. A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton, who extended this abstraction to the theory of quaternions.

The earliest fleeting reference to square roots of negative numbers can perhaps be said to occur in the work of the Greek mathematician Hero of Alexandria in the 1st century AD, where in his Stereometrica he considered, apparently in error, the volume of an impossible frustum of a pyramid to arrive at the term ${\displaystyle \sqrt{81-144}}$ in his calculations, which today would simplify to ${\displaystyle \sqrt{-63}=3i\sqrt{7}}$. Negative quantities were not conceived of in Hellenistic mathematics and Hero merely replaced it by its positive ${\displaystyle \sqrt{144-81}=3\sqrt{7}.}$

The impetus to study complex numbers as a topic in itself first arose in the 16th century when algebraic solutions for the roots of cubic and quartic polynomials were discovered by Italian mathematicians (Niccolò Fontana Tartaglia and Gerolamo Cardano). It was soon realized (but proved much later) that these formulas, even if one were interested only in real solutions, sometimes required the manipulation of square roots of negative numbers. In fact, it was proved later that the use of complex numbers is unavoidable when all three roots are real and distinct. However, the general formula can still be used in this case, with some care to deal with the ambiguity resulting from the existence of three cubic roots for nonzero complex numbers. Rafael Bombelli was the first to address explicitly these seemingly paradoxical solutions of cubic equations and developed the rules for complex arithmetic, trying to resolve these issues.

The term "imaginary" for these quantities was coined by René Descartes in 1637, who was at pains to stress their unreal nature:

... sometimes only imaginary, that is one can imagine as many as I said in each equation, but sometimes there exists no quantity that matches that which we imagine.
[... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine.]

A further source of confusion was that the equation ${\displaystyle {\sqrt{-1}}^2=\sqrt{-1}\sqrt{-1}=-1}$ seemed to be capriciously inconsistent with the algebraic identity ${\displaystyle \sqrt{a}\sqrt{b}=\sqrt{ab}}$, which is valid for non-negative real numbers a and b, and which was also used in complex number calculations with one of a, b positive and the other negative. The incorrect use of this identity in the case when both a and b are negative, and the related identity $\frac{1}{\sqrt{a}}=\sqrt{\frac{1}{a}}$, even bedeviled Leonhard Euler. This difficulty eventually led to the convention of using the special symbol i in place of ${\displaystyle \sqrt{-1}}$ to guard against this mistake. Even so, Euler considered it natural to introduce students to complex numbers much earlier than we do today. In his elementary algebra text book, Elements of Algebra, he introduces these numbers almost at once and then uses them in a natural way throughout.

In the 18th century complex numbers gained wider use, as it was noticed that formal manipulation of complex expressions could be used to simplify calculations involving trigonometric functions. For instance, in 1730 Abraham de Moivre noted that the identities relating trigonometric functions of an integer multiple of an angle to powers of trigonometric functions of that angle could be re-expressed by the following de Moivre's formula:

$${\displaystyle (\cos \theta +i\sin \theta {)}^n=\cos n\theta +i\sin n\theta .}$$

In 1748, Euler went further and obtained Euler's formula of complex analysis:

$${\displaystyle \cos \theta +i\sin \theta =e^{i\theta }}$$

by formally manipulating complex power series and observed that this formula could be used to reduce any trigonometric identity to much simpler exponential identities.

The idea of a complex number as a point in the complex plane (above) was first described by Danish–Norwegian mathematician Caspar Wessel in 1799, although it had been anticipated as early as 1685 in Wallis's A Treatise of Algebra.

Wessel's memoir appeared in the Proceedings of the Copenhagen Academy but went largely unnoticed. In 1806 Jean-Robert Argand independently issued a pamphlet on complex numbers and provided a rigorous proof of the fundamental theorem of algebra. Carl Friedrich Gauss had earlier published an essentially topological proof of the theorem in 1797 but expressed his doubts at the time about "the true metaphysics of the square root of −1". It was not until 1831 that he overcame these doubts and published his treatise on complex numbers as points in the plane, largely establishing modern notation and terminology:

If one formerly contemplated this subject from a false point of view and therefore found a mysterious darkness, this is in large part attributable to clumsy terminology. Had one not called +1, −1, ${\displaystyle \sqrt{-1}}$ positive, negative, or imaginary (or even impossible) units, but instead, say, direct, inverse, or lateral units, then there could scarcely have been talk of such darkness.

In the beginning of the 19th century, other mathematicians discovered independently the geometrical representation of the complex numbers: Buée, Mourey, Warren, Français and his brother, Bellavitis.

The English mathematician G.H. Hardy remarked that Gauss was the first mathematician to use complex numbers in "a really confident and scientific way" although mathematicians such as Norwegian Niels Henrik Abel and Carl Gustav Jacob Jacobi were necessarily using them routinely before Gauss published his 1831 treatise.

Augustin-Louis Cauchy and Bernhard Riemann together brought the fundamental ideas of complex analysis to a high state of completion, commencing around 1825 in Cauchy's case.

The common terms used in the theory are chiefly due to the founders. Argand called cos φ + i sin φ the direction factor, and ${\displaystyle r=\sqrt{a^2+b^2}}$ the modulus; Cauchy (1821) called cos φ + i sin φ the reduced form (l'expression réduite) and apparently introduced the term argument; Gauss used i for ${\displaystyle \sqrt{-1}}$, introduced the term complex number for a + bi, and called a² + b² the norm. The expression direction coefficient, often used for cos φ + i sin φ, is due to Hankel (1867), and absolute value, for modulus, is due to Weierstrass.

Later classical writers on the general theory include Richard Dedekind, Otto Hölder, Felix Klein, Henri Poincaré, Hermann Schwarz, Karl Weierstrass and many others. Important work (including a systematization) in complex multivariate calculus has been started at beginning of the 20th century. Important results have been achieved by Wilhelm Wirtinger in 1927.

Relations and operations

Equality

Complex numbers have a similar definition of equality to real numbers; two complex numbers a₁ + b₁i and a₂ + b₂i are equal if and only if both their real and imaginary parts are equal, that is, if a₁ = a₂ and b₁ = b₂. Nonzero complex numbers written in polar form are equal if and only if they have the same magnitude and their arguments differ by an integer multiple of 2π.

Ordering

Unlike the real numbers, there is no natural ordering of the complex numbers. In particular, there is no linear ordering on the complex numbers that is compatible with addition and multiplication. Hence, the complex numbers do not have the structure of an ordered field. One explanation for this is that every non-trivial sum of squares in an ordered field is nonzero, and i² + 1² = 0 is a non-trivial sum of squares. Thus, complex numbers are naturally thought of as existing on a two-dimensional plane.

Conjugate

See also: Complex conjugate

Geometric representation of z and its conjugate z in the complex plane

The complex conjugate of the complex number z = x + yi is given by x − yi. It is denoted by either z or z*.^[46] This unary operation on complex numbers cannot be expressed by applying only their basic operations addition, subtraction, multiplication and division.

Geometrically, z is the "reflection" of z about the real axis. Conjugating twice gives the original complex number

$${\displaystyle \overline{\overline{z}}=z,}$$

which makes this operation an involution. The reflection leaves both the real part and the magnitude of z unchanged, that is

$${\displaystyle \mathrm{Re}(\overline{z})=\mathrm{Re}(z)}$$

and ${\displaystyle |\overline{z}|=|z|.}$

The imaginary part and the argument of a complex number z change their sign under conjugation

$${\displaystyle \mathrm{Im}(\overline{z})=-\mathrm{Im}(z)\text{ and }\arg \overline{z}\equiv -\arg z(\mathrm{mod}2\pi ).}$$

For details on argument and magnitude, see the section on Polar form.

The product of a complex number z = x + yi and its conjugate is known as the absolute square. It is always a non-negative real number and equals the square of the magnitude of each:

$${\displaystyle z\cdot \overline{z}=x^2+y^2=|z{|}^2=|\overline{z}{|}^2.}$$

This property can be used to convert a fraction with a complex denominator to an equivalent fraction with a real denominator by expanding both numerator and denominator of the fraction by the conjugate of the given denominator. This process is sometimes called "rationalization" of the denominator (although the denominator in the final expression might be an irrational real number), because it resembles the method to remove roots from simple expressions in a denominator.

The real and imaginary parts of a complex number z can be extracted using the conjugation:

$${\displaystyle \mathrm{Re}(z)={\displaystyle \frac{z+\overline{z}}{2}},\text{ and }\mathrm{Im}(z)={\displaystyle \frac{z-\overline{z}}{2i}}.}$$

Moreover, a complex number is real if and only if it equals its own conjugate.

Conjugation distributes over the basic complex arithmetic operations:

$${\displaystyle \begin{array}{rl}\overline{z\pm w}& =\overline{z}\pm \overline{w},\\ \overline{z\cdot w}& =\overline{z}\cdot \overline{w},\\ \overline{z/w}& =\overline{z}/\overline{w}.\end{array}}$$

Conjugation is also employed in inversive geometry, a branch of geometry studying reflections more general than ones about a line. In the network analysis of electrical circuits, the complex conjugate is used in finding the equivalent impedance when the maximum power transfer theorem is looked for.

Addition and subtraction

Addition of two complex numbers can be done geometrically by constructing a parallelogram.

Two complex numbers ${\displaystyle a=x+yi}$ and ${\displaystyle b=u+vi}$ are most easily added by separately adding their real and imaginary parts. That is to say:

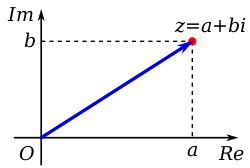
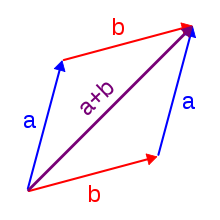
$${\displaystyle a+b=(x+yi)+(u+vi)=(x+u)+(y+v)i.}$$

Similarly, subtraction can be performed as

$${\displaystyle a-b=(x+yi)-(u+vi)=(x-u)+(y-v)i.}$$

Multiplication of a complex number ${\displaystyle a=x+yi}$ and a real number r can be done similarly by multiplying separately r and the real and imaginary parts of a:

$${\displaystyle ra=r(x+yi)=rx+ryi.}$$

In particular, subtraction can be done by negating the subtrahend (that is multiplying it with −1) and adding the result to the minuend:

$${\displaystyle a-b=a+(-1)b.}$$

Using the visualization of complex numbers in the complex plane, addition has the following geometric interpretation: the sum of two complex numbers a and b, interpreted as points in the complex plane, is the point obtained by building a parallelogram from the three vertices O, and the points of the arrows labeled a and b (provided that they are not on a line). Equivalently, calling these points A, B, respectively and the fourth point of the parallelogram X the triangles OAB and XBA are congruent.

Multiplication and square

The rules of the distributive property, the commutative properties (of addition and multiplication), and the defining property i² = −1 apply to complex numbers. It follows that

$${\displaystyle (x+yi)(u+vi)=(xu-yv)+(xv+yu)i.}$$

In particular,

$${\displaystyle (x+yi{)}^2=x^2-y^2+2xyi.}$$

Reciprocal and division

Using the conjugate, the reciprocal of a nonzero complex number ${\displaystyle z=x+yi}$ can be broken into real and imaginary components

$${\displaystyle \frac{1}{z}=\frac{\overline{z}}{z\overline{z}}=\frac{\overline{z}}{|z{|}^2}=\frac{x-yi}{x^2+y^2}=\frac{x}{x^2+y^2}-\frac{y}{x^2+y^2}i.}$$

This can be used to express a division of an arbitrary complex number ${\displaystyle w=u+vi}$ by a non-zero complex number ${\displaystyle z=x+yi}$ as

$${\displaystyle \frac{w}{z}=\frac{w\overline{z}}{|z{|}^2}=\frac{(u+vi)(x-iy)}{x^2+y^2}=\frac{ux+vy}{x^2+y^2}+\frac{vx-uy}{x^2+y^2}i.}$$

Multiplication and division in polar form

Multiplication of 2 + i (blue triangle) and 3 + i (red triangle). The red triangle is rotated to match the vertex of the blue one (the adding of both angles in the terms φ₁+φ₂ in the equation) and stretched by the length of the hypotenuse of the blue triangle (the multiplication of both radiuses, as per term r₁r₂ in the equation).

Formulas for multiplication, division and exponentiation are simpler in polar form than the corresponding formulas in Cartesian coordinates. Given two complex numbers z₁ = r₁(cos φ₁ + i sin φ₁) and z₂ = r₂(cos φ₂ + i sin φ₂), because of the trigonometric identities

$${\displaystyle \begin{array}{rlrl}\cos a\cos b& -\sin a\sin b& =& \cos (a+b)\\ \cos a\sin b& +\sin a\cos b& =& \sin (a+b).\end{array}}$$

we may derive

$${\displaystyle z_1{z}_2=r_1{r}_2(\cos ({\phi }_1+{\phi }_2)+i\sin ({\phi }_1+{\phi }_2)).}$$

In other words, the absolute values are multiplied and the arguments are added to yield the polar form of the product. For example, multiplying by i corresponds to a quarter-turn counter-clockwise, which gives back i² = −1. The picture at the right illustrates the multiplication of

$${\displaystyle (2+i)(3+i)=5+5i.}$$

Since the real and imaginary part of 5 + 5i are equal, the argument of that number is 45 degrees, or π/4 (in radian). On the other hand, it is also the sum of the angles at the origin of the red and blue triangles are arctan(1/3) and arctan(1/2), respectively. Thus, the formula

$${\displaystyle \frac{\pi }{4}=\arctan \left(\frac{1}{2}\right)+\arctan \left(\frac{1}{3}\right)}$$

holds. As the arctan function can be approximated highly efficiently, formulas like this – known as Machin-like formulas – are used for high-precision approximations of π.

Similarly, division is given by

$${\displaystyle \frac{z_1}{z_2}=\frac{r_1}{r_2}\left(\cos ({\phi }_1-{\phi }_2)+i\sin ({\phi }_1-{\phi }_2)\right).}$$

Square root

See also: Square roots of negative and complex numbers

The square roots of a + bi (with b ≠ 0) are ${\displaystyle \pm (\gamma +\delta i)}$, where

$${\displaystyle \gamma =\sqrt{\frac{a+\sqrt{a^2+b^2}}{2}}}$$

and

$${\displaystyle \delta =(\mathrm{sgn}b)\sqrt{\frac{-a+\sqrt{a^2+b^2}}{2}},}$$

where sgn is the signum function. This can be seen by squaring ${\displaystyle \pm (\gamma +\delta i)}$ to obtain a + bi. Here ${\displaystyle \sqrt{a^2+b^2}}$ is called the modulus of a + bi, and the square root sign indicates the square root with non-negative real part, called the principal square root; also ${\displaystyle \sqrt{a^2+b^2}=\sqrt{z\overline{z}},}$ where z = a + bi.

Exponential function

The exponential function ${\displaystyle \exp :\mathbb{C}\to \mathbb{C};z\mapsto \exp z}$ can be defined for every complex number z by the power series

$${\displaystyle \exp z=\sum _{n=0}^{\mathrm{\infty }}\frac{z^n}{n!},}$$

which has an infinite radius of convergence.

The value at 1 of the exponential function is Euler's number

$${\displaystyle e=\exp 1=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}\approx \mathrm{2.71828.}}$$

If z is real, one has ${\displaystyle \exp z=e^z.}$ Analytic continuation allows extending this equality for every complex value of z, and thus to define the complex exponentiation with base e as

$${\displaystyle e^z=\exp z.}$$

Functional equation

The exponential function satisfies the functional equation ${\displaystyle e^{z+t}=e^z{e}^t.}$ This can be proved either by comparing the power series expansion of both members or by applying analytic continuation from the restriction of the equation to real arguments.

Euler's formula

Euler's formula states that, for any real number y,

$${\displaystyle e^{iy}=\cos y+i\sin y.}$$

The functional equation implies thus that, if x and y are real, one has

$${\displaystyle e^{x+iy}=e^x(\cos y+i\sin y)=e^x\cos y+i{e}^x\sin y,}$$

which is the decomposition of the exponential function into its real and imaginary parts.

Complex logarithm

In the real case, the natural logarithm can be defined as the inverse ${\displaystyle \ln :{\mathbb{R}}^{+}\to \mathbb{R};x\mapsto \ln x}$ of the exponential function. For extending this to the complex domain, one can start from Euler's formula. It implies that, if a complex number ${\displaystyle z\in {\mathbb{C}}^{\times }}$ is written in polar form

$${\displaystyle z=r(\cos \phi +i\sin \phi )}$$

with ${\displaystyle r,\phi \in \mathbb{R},}$ then with

$${\displaystyle \ln z=\ln r+i\phi }$$

as complex logarithm one has a proper inverse:

$${\displaystyle \exp \ln z=\exp (\ln r+i\phi )=r\exp i\phi =r(\cos \phi +i\sin \phi )=z.}$$

However, because cosine and sine are periodic functions, the addition of an integer multiple of 2π to φ does not change z. For example, e^iπ = e^3iπ = −1 , so both iπ and 3iπ are possible values for the natural logarithm of −1.

Therefore, if the complex logarithm is not to be defined as a multivalued function

$${\displaystyle \ln z=\left\{\ln r+i(\phi +2\pi k)\mid k\in \mathbb{Z}\right\},}$$

one has to use a branch cut and to restrict the codomain, resulting in the bijective function

$${\displaystyle \ln :{\mathbb{C}}^{\times }\to {\mathbb{R}}^{+}+i\left(-\pi ,\pi \right].}$$

If ${\displaystyle z\in \mathbb{C}\setminus \left(-{\mathbb{R}}_{\ge 0}\right)}$ is not a non-positive real number (a positive or a non-real number), the resulting principal value of the complex logarithm is obtained with −π < φ < π. It is an analytic function outside the negative real numbers, but it cannot be prolongated to a function that is continuous at any negative real number ${\displaystyle z\in -{\mathbb{R}}^{+}}$, where the principal value is ln z = ln(−z) + iπ.

Exponentiation

If x > 0 is real and z complex, the exponentiation is defined as

$${\displaystyle x^z=e^{z\ln x},}$$

where ln denotes the natural logarithm.

It seems natural to extend this formula to complex values of x, but there are some difficulties resulting from the fact that the complex logarithm is not really a function, but a multivalued function.

It follows that if z is as above, and if t is another complex number, then the exponentiation is the multivalued function

$${\displaystyle z^t=\left\{e^{t\ln r}(\cos (\phi t+2\pi kt)+i\sin (\phi t+2\pi kt))\mid k\in \mathbb{Z}\right\}}$$

Integer and fractional exponents

Geometric representation of the 2nd to 6th roots of a complex number z, in polar form re^iφ  where r = |z | and φ = arg z. If z is real, φ = 0 or π. Principal roots are shown in black.

If, in the preceding formula, t is an integer, then the sine and the cosine are independent of k. Thus, if the exponent n is an integer, then zⁿ is well defined, and the exponentiation formula simplifies to de Moivre's formula:

$${\displaystyle z^n=(r(\cos \phi +i\sin \phi ){)}^n=r^n(\cos n\phi +i\sin n\phi ).}$$

The n nth roots of a complex number z are given by

$${\displaystyle z^{1/n}=\sqrt[n]{r}\left(\cos \left(\frac{\phi +2k\pi }{n}\right)+i\sin \left(\frac{\phi +2k\pi }{n}\right)\right)}$$

for 0 ≤ k ≤ n − 1. (Here ${\displaystyle \sqrt[n]{r}}$ is the usual (positive) nth root of the positive real number r.) Because sine and cosine are periodic, other integer values of k do not give other values.

While the nth root of a positive real number r is chosen to be the positive real number c satisfying cⁿ = r, there is no natural way of distinguishing one particular complex nth root of a complex number. Therefore, the nth root is a n-valued function of z. This implies that, contrary to the case of positive real numbers, one has

$${\displaystyle (z^n{)}^{1/n}\ne z,}$$

since the left-hand side consists of n values, and the right-hand side is a single value.

Properties

Field structure

The set ${\displaystyle \mathbb{C}}$ of complex numbers is a field. Briefly, this means that the following facts hold: first, any two complex numbers can be added and multiplied to yield another complex number. Second, for any complex number z, its additive inverse –z is also a complex number; and third, every nonzero complex number has a reciprocal complex number. Moreover, these operations satisfy a number of laws, for example the law of commutativity of addition and multiplication for any two complex numbers z₁ and z₂:

$${\displaystyle \begin{array}{rl}{z}_1+z_2& =z_2+z_1,\\ z_1{z}_2& =z_2{z}_1.\end{array}}$$

These two laws and the other requirements on a field can be proven by the formulas given above, using the fact that the real numbers themselves form a field.

Unlike the reals, ${\displaystyle \mathbb{C}}$ is not an ordered field, that is to say, it is not possible to define a relation z₁ < z₂ that is compatible with the addition and multiplication. In fact, in any ordered field, the square of any element is necessarily positive, so i² = −1 precludes the existence of an ordering on ${\displaystyle \mathbb{C}.}$

When the underlying field for a mathematical topic or construct is the field of complex numbers, the topic's name is usually modified to reflect that fact. For example: complex analysis, complex matrix, complex polynomial, and complex Lie algebra.

Solutions of polynomial equations

Given any complex numbers (called coefficients) a₀, ..., a_n, the equation

$${\displaystyle a_n{z}^n+\cdots +a_{1}z+a_0=0}$$

has at least one complex solution z, provided that at least one of the higher coefficients a₁, ..., a_n is nonzero. This is the statement of the fundamental theorem of algebra, of Carl Friedrich Gauss and Jean le Rond d'Alembert. Because of this fact, ${\displaystyle \mathbb{C}}$ is called an algebraically closed field. This property does not hold for the field of rational numbers ${\displaystyle \mathbb{Q}}$ (the polynomial x² − 2 does not have a rational root, since √2 is not a rational number) nor the real numbers ${\displaystyle \mathbb{R}}$ (the polynomial x² + a does not have a real root for a > 0, since the square of x is positive for any real number x).

There are various proofs of this theorem, by either analytic methods such as Liouville's theorem, or topological ones such as the winding number, or a proof combining Galois theory and the fact that any real polynomial of odd degree has at least one real root.

Because of this fact, theorems that hold for any algebraically closed field apply to ${\displaystyle \mathbb{C}.}$ For example, any non-empty complex square matrix has at least one (complex) eigenvalue.

Algebraic characterization

The field ${\displaystyle \mathbb{C}}$ has the following three properties:

• First, it has characteristic 0. This means that 1 + 1 + ⋯ + 1 ≠ 0 for any number of summands (all of which equal one).
• Second, its transcendence degree over ${\displaystyle \mathbb{Q}}$, the prime field of ${\displaystyle \mathbb{C},}$ is the cardinality of the continuum.
• Third, it is algebraically closed (see above).

It can be shown that any field having these properties is isomorphic (as a field) to ${\displaystyle \mathbb{C}.}$ For example, the algebraic closure of the field ${\displaystyle {\mathbb{Q}}_p}$ of the p-adic number also satisfies these three properties, so these two fields are isomorphic (as fields, but not as topological fields). Also, ${\displaystyle \mathbb{C}}$ is isomorphic to the field of complex Puiseux series. However, specifying an isomorphism requires the axiom of choice. Another consequence of this algebraic characterization is that ${\displaystyle \mathbb{C}}$ contains many proper subfields that are isomorphic to ${\displaystyle \mathbb{C}}$.

Characterization as a topological field

The preceding characterization of ${\displaystyle \mathbb{C}}$ describes only the algebraic aspects of ${\displaystyle \mathbb{C}.}$ That is to say, the properties of nearness and continuity, which matter in areas such as analysis and topology, are not dealt with. The following description of ${\displaystyle \mathbb{C}}$ as a topological field (that is, a field that is equipped with a topology, which allows the notion of convergence) does take into account the topological properties. ${\displaystyle \mathbb{C}}$ contains a subset P (namely the set of positive real numbers) of nonzero elements satisfying the following three conditions:

• P is closed under addition, multiplication and taking inverses.
• If x and y are distinct elements of P, then either x − y or y − x is in P.
• If S is any nonempty subset of P, then S + P = x + P for some x in ${\displaystyle \mathbb{C}.}$

Moreover, ${\displaystyle \mathbb{C}}$ has a nontrivial involutive automorphism x ↦ x* (namely the complex conjugation), such that x x* is in P for any nonzero x in ${\displaystyle \mathbb{C}.}$

Any field F with these properties can be endowed with a topology by taking the sets B(x, p) = { y | p − (y − x)(y − x)* ∈ P }  as a base, where x ranges over the field and p ranges over P. With this topology F is isomorphic as a topological field to ${\displaystyle \mathbb{C}.}$

The only connected locally compact topological fields are ${\displaystyle \mathbb{R}}$ and ${\displaystyle \mathbb{C}.}$ This gives another characterization of ${\displaystyle \mathbb{C}}$ as a topological field, since ${\displaystyle \mathbb{C}}$ can be distinguished from ${\displaystyle \mathbb{R}}$ because the nonzero complex numbers are connected, while the nonzero real numbers are not.

Formal construction

Construction as ordered pairs

William Rowan Hamilton introduced the approach to define the set ${\displaystyle \mathbb{C}}$ of complex numbers as the set ${\displaystyle {\mathbb{R}}^2}$ of ordered pairs (a, b) of real numbers, in which the following rules for addition and multiplication are imposed:

$${\displaystyle \begin{array}{rl}(a,b)+(c,d)& =(a+c,b+d)\\ (a,b)\cdot (c,d)& =(ac-bd,bc+ad).\end{array}}$$

It is then just a matter of notation to express (a, b) as a + bi.

Construction as a quotient field

Though this low-level construction does accurately describe the structure of the complex numbers, the following equivalent definition reveals the algebraic nature of ${\displaystyle \mathbb{C}}$ more immediately. This characterization relies on the notion of fields and polynomials. A field is a set endowed with addition, subtraction, multiplication and division operations that behave as is familiar from, say, rational numbers. For example, the distributive law

$${\displaystyle (x+y)z=xz+yz}$$

must hold for any three elements x, y and z of a field. The set ${\displaystyle \mathbb{R}}$ of real numbers does form a field. A polynomial p(X) with real coefficients is an expression of the form

$${\displaystyle a_n{X}^n+\cdots +a_{1}X+a_0,}$$

where the a₀, ..., a_n are real numbers. The usual addition and multiplication of polynomials endows the set ${\displaystyle \mathbb{R}[X]}$ of all such polynomials with a ring structure. This ring is called the polynomial ring over the real numbers.

The set of complex numbers is defined as the quotient ring ${\displaystyle \mathbb{R}[X]/(X^2+1).}$ This extension field contains two square roots of −1, namely (the cosets of) X and −X, respectively. (The cosets of) 1 and X form a basis of ${\displaystyle \mathbb{R}[X]/(X^2+1)}$ as a real vector space, which means that each element of the extension field can be uniquely written as a linear combination in these two elements. Equivalently, elements of the extension field can be written as ordered pairs (a, b) of real numbers. The quotient ring is a field, because X² + 1 is irreducible over ${\displaystyle \mathbb{R},}$ so the ideal it generates is maximal.

The formulas for addition and multiplication in the ring ${\displaystyle \mathbb{R}[X],}$ modulo the relation X² = −1, correspond to the formulas for addition and multiplication of complex numbers defined as ordered pairs. So the two definitions of the field ${\displaystyle \mathbb{C}}$ are isomorphic (as fields).

Accepting that ${\displaystyle \mathbb{C}}$ is algebraically closed, since it is an algebraic extension of ${\displaystyle \mathbb{R}}$ in this approach, ${\displaystyle \mathbb{C}}$ is therefore the algebraic closure of ${\displaystyle \mathbb{R}.}$

Matrix representation of complex numbers

Complex numbers a + bi can also be represented by 2 × 2 matrices that have the form:

$${\displaystyle \left(\begin{array}{cc}a& -b\\ b& a\end{array}\right)}$$

Here the entries a and b are real numbers. As the sum and product of two such matrices is again of this form, these matrices form a subring of the ring 2 × 2 matrices.

A simple computation shows that the map:

$${\displaystyle a+ib\mapsto \left(\begin{array}{cc}a& -b\\ b& a\end{array}\right)}$$

is a ring isomorphism from the field of complex numbers to the ring of these matrices. This isomorphism associates the square of the absolute value of a complex number with the determinant of the corresponding matrix, and the conjugate of a complex number with the transpose of the matrix.

The geometric description of the multiplication of complex numbers can also be expressed in terms of rotation matrices by using this correspondence between complex numbers and such matrices. The action of the matrix on a vector (x, y) corresponds to the multiplication of x + iy by a + ib. In particular, if the determinant is 1, there is a real number t such that the matrix has the form:

$${\displaystyle \left(\begin{array}{cc}\cos t& -\sin t\\ \sin t& \cos t\end{array}\right)}$$

In this case, the action of the matrix on vectors and the multiplication by the complex number ${\displaystyle \cos t+i\sin t}$ are both the rotation of the angle t.

Complex analysis

Color wheel graph of sin(1/z). White parts inside refer to numbers having large absolute values.

Main article: Complex analysis

The study of functions of a complex variable is known as complex analysis and has enormous practical use in applied mathematics as well as in other branches of mathematics. Often, the most natural proofs for statements in real analysis or even number theory employ techniques from complex analysis (see prime number theorem for an example). Unlike real functions, which are commonly represented as two-dimensional graphs, complex functions have four-dimensional graphs and may usefully be illustrated by color-coding a three-dimensional graph to suggest four dimensions, or by animating the complex function's dynamic transformation of the complex plane.

Complex exponential and related functions

The notions of convergent series and continuous functions in (real) analysis have natural analogs in complex analysis. A sequence of complex numbers is said to converge if and only if its real and imaginary parts do. This is equivalent to the (ε, δ)-definition of limits, where the absolute value of real numbers is replaced by the one of complex numbers. From a more abstract point of view, ${\displaystyle \mathbb{C}}$, endowed with the metric

$${\displaystyle \mathrm{d}(z_1,z_2)=|z_1-z_2|}$$

is a complete metric space, which notably includes the triangle inequality

$${\displaystyle |z_1+z_2|\le |z_1|+|z_2|}$$

for any two complex numbers z₁ and z₂.

Like in real analysis, this notion of convergence is used to construct a number of elementary functions: the exponential function exp z, also written e^z, is defined as the infinite series

$${\displaystyle \exp z:=1+z+\frac{z^2}{2\cdot 1}+\frac{z^3}{3\cdot 2\cdot 1}+\cdots =\sum _{n=0}^{\mathrm{\infty }}\frac{z^n}{n!}.}$$

The series defining the real trigonometric functions sine and cosine, as well as the hyperbolic functions sinh and cosh, also carry over to complex arguments without change. For the other trigonometric and hyperbolic functions, such as tangent, things are slightly more complicated, as the defining series do not converge for all complex values. Therefore, one must define them either in terms of sine, cosine and exponential, or, equivalently, by using the method of analytic continuation.

Euler's formula states:

$${\displaystyle \exp (i\phi )=\cos \phi +i\sin \phi }$$

for any real number φ, in particular

$${\displaystyle \exp (i\pi )=-1}$$

, which is Euler's identity. Unlike in the situation of real numbers, there is an infinitude of complex solutions z of the equation

$${\displaystyle \exp z=w}$$

for any complex number w ≠ 0. It can be shown that any such solution z – called complex logarithm of w – satisfies

$${\displaystyle \log w=\ln |w|+i\arg w,}$$

where arg is the argument defined above, and ln the (real) natural logarithm. As arg is a multivalued function, unique only up to a multiple of 2π, log is also multivalued. The principal value of log is often taken by restricting the imaginary part to the interval (−π, π].

Complex exponentiation z^ω is defined as

$${\displaystyle z^{\omega }=\exp (\omega \ln z),}$$

and is multi-valued, except when ω is an integer. For ω = 1 / n, for some natural number n, this recovers the non-uniqueness of nth roots mentioned above.

Complex numbers, unlike real numbers, do not in general satisfy the unmodified power and logarithm identities, particularly when naïvely treated as single-valued functions; see failure of power and logarithm identities. For example, they do not satisfy

$${\displaystyle a^{bc}={\left(a^b\right)}^c.}$$

Both sides of the equation are multivalued by the definition of complex exponentiation given here, and the values on the left are a subset of those on the right.

Holomorphic functions

A function f: ${\displaystyle \mathbb{C}}$ → ${\displaystyle \mathbb{C}}$ is called holomorphic if it satisfies the Cauchy–Riemann equations. For example, any ${\displaystyle \mathbb{R}}$-linear map ${\displaystyle \mathbb{C}}$ → ${\displaystyle \mathbb{C}}$ can be written in the form

$${\displaystyle f(z)=az+b\overline{z}}$$

with complex coefficients a and b. This map is holomorphic if and only if b = 0. The second summand ${\displaystyle b\overline{z}}$ is real-differentiable, but does not satisfy the Cauchy–Riemann equations.

Complex analysis shows some features not apparent in real analysis. For example, any two holomorphic functions f and g that agree on an arbitrarily small open subset of ${\displaystyle \mathbb{C}}$ necessarily agree everywhere. Meromorphic functions, functions that can locally be written as f(z)/(z − z₀)ⁿ with a holomorphic function f, still share some of the features of holomorphic functions. Other functions have essential singularities, such as sin(1/z) at z = 0.

Applications

Complex numbers have applications in many scientific areas, including signal processing, control theory, electromagnetism, fluid dynamics, quantum mechanics, cartography, and vibration analysis. Some of these applications are described below.

Geometry

Shapes

Three non-collinear points ${\displaystyle u,v,w}$ in the plane determine the shape of the triangle ${\displaystyle \{u,v,w\}}$. Locating the points in the complex plane, this shape of a triangle may be expressed by complex arithmetic as

$${\displaystyle S(u,v,w)=\frac{u-w}{u-v}.}$$

The shape ${\displaystyle S}$ of a triangle will remain the same, when the complex plane is transformed by translation or dilation (by an affine transformation), corresponding to the intuitive notion of shape, and describing similarity. Thus each triangle ${\displaystyle \{u,v,w\}}$ is in a similarity class of triangles with the same shape.

Fractal geometry

The Mandelbrot set with the real and imaginary axes labeled.

The Mandelbrot set is a popular example of a fractal formed on the complex plane. It is defined by plotting every location ${\displaystyle c}$ where iterating the sequence ${\displaystyle f_c(z)=z^2+c}$ does not diverge when iterated infinitely. Similarly, Julia sets have the same rules, except where ${\displaystyle c}$ remains constant.

Triangles

Every triangle has a unique Steiner inellipse – an ellipse inside the triangle and tangent to the midpoints of the three sides of the triangle. The foci of a triangle's Steiner inellipse can be found as follows, according to Marden's theorem: Denote the triangle's vertices in the complex plane as a = x_A + y_Ai, b = x_B + y_Bi, and c = x_C + y_Ci. Write the cubic equation ${\displaystyle (x-a)(x-b)(x-c)=0}$, take its derivative, and equate the (quadratic) derivative to zero. Marden's theorem says that the solutions of this equation are the complex numbers denoting the locations of the two foci of the Steiner inellipse.

Algebraic number theory

Construction of a regular pentagon using straightedge and compass.

As mentioned above, any nonconstant polynomial equation (in complex coefficients) has a solution in ${\displaystyle \mathbb{C}}$. A fortiori, the same is true if the equation has rational coefficients. The roots of such equations are called algebraic numbers – they are a principal object of study in algebraic number theory. Compared to ${\displaystyle \overline{\mathbb{Q}}}$, the algebraic closure of ${\displaystyle \mathbb{Q}}$, which also contains all algebraic numbers, ${\displaystyle \mathbb{C}}$ has the advantage of being easily understandable in geometric terms. In this way, algebraic methods can be used to study geometric questions and vice versa. With algebraic methods, more specifically applying the machinery of field theory to the number field containing roots of unity, it can be shown that it is not possible to construct a regular nonagon using only compass and straightedge – a purely geometric problem.

Another example is the Gaussian integers; that is, numbers of the form x + iy, where x and y are integers, which can be used to classify sums of squares.

Analytic number theory

Main article: Analytic number theory

Analytic number theory studies numbers, often integers or rationals, by taking advantage of the fact that they can be regarded as complex numbers, in which analytic methods can be used. This is done by encoding number-theoretic information in complex-valued functions. For example, the Riemann zeta function ζ(s) is related to the distribution of prime numbers.

Improper integrals

In applied fields, complex numbers are often used to compute certain real-valued improper integrals, by means of complex-valued functions. Several methods exist to do this; see methods of contour integration.

Dynamic equations

In differential equations, it is common to first find all complex roots r of the characteristic equation of a linear differential equation or equation system and then attempt to solve the system in terms of base functions of the form f(t) = e^rt. Likewise, in difference equations, the complex roots r of the characteristic equation of the difference equation system are used, to attempt to solve the system in terms of base functions of the form f(t) = r^t.

Linear algebra

Eigendecomposition is a useful tool for computing matrix powers and matrix exponentials. However, it often requires the use of complex numbers, even if the matrix is real (for example, a rotation matrix).

Complex numbers often generalize concepts originally conceived in the real numbers. For example, the conjugate transpose generalizes the transpose, hermitian matrices generalize symmetric matrices, and unitary matrices generalize orthogonal matrices.

In applied mathematics

Control theory

See also: Complex plane § Use in control theory

In control theory, systems are often transformed from the time domain to the complex frequency domain using the Laplace transform. The system's zeros and poles are then analyzed in the complex plane. The root locus, Nyquist plot, and Nichols plot techniques all make use of the complex plane.

In the root locus method, it is important whether zeros and poles are in the left or right half planes, that is, have real part greater than or less than zero. If a linear, time-invariant (LTI) system has poles that are

• in the right half plane, it will be unstable,
• all in the left half plane, it will be stable,
• on the imaginary axis, it will have marginal stability.

If a system has zeros in the right half plane, it is a nonminimum phase system.

Signal analysis

Complex numbers are used in signal analysis and other fields for a convenient description for periodically varying signals. For given real functions representing actual physical quantities, often in terms of sines and cosines, corresponding complex functions are considered of which the real parts are the original quantities. For a sine wave of a given frequency, the absolute value |z| of the corresponding z is the amplitude and the argument arg z is the phase.

If Fourier analysis is employed to write a given real-valued signal as a sum of periodic functions, these periodic functions are often written as complex-valued functions of the form

$${\displaystyle x(t)=\mathrm{Re}\{X(t)\}}$$

and

$${\displaystyle X(t)=A{e}^{i\omega t}=a{e}^{i\varphi }{e}^{i\omega t}=a{e}^{i(\omega t+\varphi )}}$$

where ω represents the angular frequency and the complex number A encodes the phase and amplitude as explained above.

This use is also extended into digital signal processing and digital image processing, which use digital versions of Fourier analysis (and wavelet analysis) to transmit, compress, restore, and otherwise process digital audio signals, still images, and video signals.

Another example, relevant to the two side bands of amplitude modulation of AM radio, is:

$${\displaystyle \begin{array}{rl}\cos ((\omega +\alpha )t)+\cos \left((\omega -\alpha )t\right)& =\mathrm{Re}\left(e^{i(\omega +\alpha )t}+e^{i(\omega -\alpha )t}\right)\\ & =\mathrm{Re}\left(\left(e^{i\alpha t}+e^{-i\alpha t}\right)\cdot e^{i\omega t}\right)\\ & =\mathrm{Re}\left(2\cos (\alpha t)\cdot e^{i\omega t}\right)\\ & =2\cos (\alpha t)\cdot \mathrm{Re}\left(e^{i\omega t}\right)\\ & =2\cos (\alpha t)\cdot \cos \left(\omega t\right).\end{array}}$$

In physics

Electromagnetism and electrical engineering

Main article: Alternating current

In electrical engineering, the Fourier transform is used to analyze varying voltages and currents. The treatment of resistors, capacitors, and inductors can then be unified by introducing imaginary, frequency-dependent resistances for the latter two and combining all three in a single complex number called the impedance. This approach is called phasor calculus.

In electrical engineering, the imaginary unit is denoted by j, to avoid confusion with I, which is generally in use to denote electric current, or, more particularly, i, which is generally in use to denote instantaneous electric current.

Since the voltage in an AC circuit is oscillating, it can be represented as

$${\displaystyle V(t)=V_0{e}^{j\omega t}=V_0\left(\cos \omega t+j\sin \omega t\right),}$$

To obtain the measurable quantity, the real part is taken:

$${\displaystyle v(t)=\mathrm{Re}(V)=\mathrm{Re}\left[V_0{e}^{j\omega t}\right]=V_0\cos \omega t.}$$

The complex-valued signal V(t) is called the analytic representation of the real-valued, measurable signal v(t). 

Fluid dynamics

In fluid dynamics, complex functions are used to describe potential flow in two dimensions.

Quantum mechanics

The complex number field is intrinsic to the mathematical formulations of quantum mechanics, where complex Hilbert spaces provide the context for one such formulation that is convenient and perhaps most standard. The original foundation formulas of quantum mechanics – the Schrödinger equation and Heisenberg's matrix mechanics – make use of complex numbers.

Relativity

In special and general relativity, some formulas for the metric on spacetime become simpler if one takes the time component of the spacetime continuum to be imaginary. (This approach is no longer standard in classical relativity, but is used in an essential way in quantum field theory.) Complex numbers are essential to spinors, which are a generalization of the tensors used in relativity.

Generalizations and related notions

Cayley Q8 quaternion graph showing cycles of multiplication by i, j and k

The process of extending the field ${\displaystyle \mathbb{R}}$ of reals to ${\displaystyle \mathbb{C}}$ is known as the Cayley–Dickson construction. It can be carried further to higher dimensions, yielding the quaternions ${\displaystyle \mathbb{H}}$ and octonions ${\displaystyle \mathbb{O}}$ which (as a real vector space) are of dimension 4 and 8, respectively. In this context the complex numbers have been called the binarions.

Just as by applying the construction to reals the property of ordering is lost, properties familiar from real and complex numbers vanish with each extension. The quaternions lose commutativity, that is, x·y ≠ y·x for some quaternions x, y, and the multiplication of octonions, additionally to not being commutative, fails to be associative: (x·y)·z ≠ x·(y·z) for some octonions x, y, z.

Reals, complex numbers, quaternions and octonions are all normed division algebras over ${\displaystyle \mathbb{R}}$. By Hurwitz's theorem they are the only ones; the sedenions, the next step in the Cayley–Dickson construction, fail to have this structure.

The Cayley–Dickson construction is closely related to the regular representation of ${\displaystyle \mathbb{C},}$ thought of as an ${\displaystyle \mathbb{R}}$-algebra (an ${\displaystyle \mathbb{R}}$-vector space with a multiplication), with respect to the basis (1, i). This means the following: the ${\displaystyle \mathbb{R}}$-linear map

$${\displaystyle \begin{array}{rl}\mathbb{C}& \to \mathbb{C}\\ z& \mapsto wz\end{array}}$$

for some fixed complex number w can be represented by a 2 × 2 matrix (once a basis has been chosen). With respect to the basis (1, i), this matrix is

$${\displaystyle \left(\begin{array}{cc}\mathrm{Re}(w)& -\mathrm{Im}(w)\\ \mathrm{Im}(w)& \mathrm{Re}(w)\end{array}\right),}$$

that is, the one mentioned in the section on matrix representation of complex numbers above. While this is a linear representation of ${\displaystyle \mathbb{C}}$ in the 2 × 2 real matrices, it is not the only one. Any matrix

$${\displaystyle J=\left(\begin{array}{cc}p& q\\ r& -p\end{array}\right),p^2+qr+1=0}$$

has the property that its square is the negative of the identity matrix: J² = −I. Then

$${\displaystyle \{z=aI+bJ:a,b\in \mathbb{R}\}}$$

is also isomorphic to the field ${\displaystyle \mathbb{C},}$ and gives an alternative complex structure on ${\displaystyle {\mathbb{R}}^2.}$ This is generalized by the notion of a linear complex structure.

Hypercomplex numbers also generalize ${\displaystyle \mathbb{R},}$ ${\displaystyle \mathbb{C},}$ ${\displaystyle \mathbb{H},}$ and ${\displaystyle \mathbb{O}.}$ For example, this notion contains the split-complex numbers, which are elements of the ring ${\displaystyle \mathbb{R}[x]/(x^2-1)}$ (as opposed to ${\displaystyle \mathbb{R}[x]/(x^2+1)}$ for complex numbers). In this ring, the equation a² = 1 has four solutions.

The field ${\displaystyle \mathbb{R}}$ is the completion of ${\displaystyle \mathbb{Q},}$ the field of rational numbers, with respect to the usual absolute value metric. Other choices of metrics on ${\displaystyle \mathbb{Q}}$ lead to the fields ${\displaystyle {\mathbb{Q}}_p}$ of p-adic numbers (for any prime number p), which are thereby analogous to ${\displaystyle \mathbb{R}}$. There are no other nontrivial ways of completing ${\displaystyle \mathbb{Q}}$ than ${\displaystyle \mathbb{R}}$ and ${\displaystyle {\mathbb{Q}}_p,}$ by Ostrowski's theorem. The algebraic closures ${\displaystyle \overline{{\mathbb{Q}}_p}}$ of ${\displaystyle {\mathbb{Q}}_p}$ still carry a norm, but (unlike ${\displaystyle \mathbb{C}}$) are not complete with respect to it. The completion ${\displaystyle {\mathbb{C}}_p}$ of ${\displaystyle \overline{{\mathbb{Q}}_p}}$ turns out to be algebraically closed. By analogy, the field is called p-adic complex numbers.

The fields ${\displaystyle \mathbb{R},}$ ${\displaystyle {\mathbb{Q}}_p,}$ and their finite field extensions, including ${\displaystyle \mathbb{C},}$ are called local fields.