From Wikipedia, the free encyclopedia
Statistical mechanics is a branch of theoretical physics and chemistry (and mathematical physics) that studies, using probability theory, the average behaviour of a mechanical system where the state of the system is uncertain.[1][2][3][note 1]
The classical view of the universe was that its fundamental laws are mechanical in nature, and that all physical systems are therefore governed by mechanical laws at a microscopic level. These laws are precise equations of motion that map any given initial state to a corresponding future state at a later time. There is however a disconnection between these laws and everyday life experiences, as we do not find it necessary (nor even theoretically possible) to know exactly at a microscopic level the simultaneous positions and velocities of each molecule while carrying out processes at the human scale (for example, when performing a chemical reaction).
Statistical mechanics is a collection of mathematical tools that are used to fill this disconnection between the laws of mechanics and the practical experience of incomplete knowledge.
A common use of statistical mechanics is in explaining the thermodynamic behaviour of large systems. Microscopic mechanical laws do not contain concepts such as temperature, heat, or entropy, however, statistical mechanics shows how these concepts arise from the natural uncertainty that arises about the state of a system when that system is prepared in practice. The benefit of using statistical mechanics is that it provides exact methods to connect thermodynamic quantities (such as heat capacity) to microscopic behaviour, whereas in classical thermodynamics the only available option would be to just measure and tabulate such quantities for various materials. Statistical mechanics also makes it possible to extend the laws of thermodynamics to cases which are not considered in classical thermodynamics, for example microscopic systems and other mechanical systems with few degrees of freedom.[1] This branch of statistical mechanics which treats and extends classical thermodynamics is known as statistical thermodynamics or equilibrium statistical mechanics.
Statistical mechanics also finds use outside equilibrium. An important subbranch known as non-equilibrium statistical mechanics deals with the issue of microscopically modelling the speed of irreversible processes that are driven by imbalances. Examples of such processes include chemical reactions, or flows of particles and heat. Unlike with equilibrium, there is no exact formalism that applies to non-equilibrium statistical mechanics in general and so this branch of statistical mechanics remains an active area of theoretical research.
Whereas ordinary mechanics only considers the behaviour of a single state, statistical mechanics introduces the statistical ensemble, which is a large collection of virtual, independent copies of the system in various states. The statistical ensemble is a probability distribution over all possible states of the system. In classical statistical mechanics, the ensemble is a probability distribution over phase points (as opposed to a single phase point in ordinary mechanics), usually represented as a distribution in a phase space with canonical coordinates. In quantum statistical mechanics, the ensemble is a probability distribution over pure states,[note 2] and can be compactly summarized as a density matrix.
As is usual for probabilities, the ensemble can be interpreted in different ways:[1]
However the probability is interpreted, each state in the ensemble evolves over time according to the equation of motion. Thus, the ensemble itself (the probability distribution over states) also evolves, as the virtual systems in the ensemble continually leave one state and enter another. The ensemble evolution is given by the Liouville equation (classical mechanics) or the von Neumann equation (quantum mechanics). These equations are simply derived by the application of the mechanical equation of motion separately to each virtual system contained in the ensemble, with the probability of the virtual system being conserved over time as it evolves from state to state.
One special class of ensemble is those ensembles that do not evolve over time. These ensembles are known as equilibrium ensembles and their condition is known as statistical equilibrium. Statistical equilibrium occurs if, for each state in the ensemble, the ensemble also contains all of its future and past states with probabilities equal to that state.[note 3] The study of equilibrium ensembles of isolated systems is the focus of statistical thermodynamics. Non-equilibrium statistical mechanics addresses the more general case of ensembles that change over time, and/or ensembles of non-isolated systems.
As an example, one might ask what is it about a thermodynamic system of NH3 molecules that determines the free energy characteristic of that compound? Classical thermodynamics does not provide the answer. If, for example, we were given spectroscopic data, of this body of gas molecules, such as bond length, bond angle, bond rotation, and flexibility of the bonds in NH3 we should see that the free energy could not be other than it is. To prove this true, we need to bridge the gap between the microscopic realm of atoms and molecules and the macroscopic realm of classical thermodynamics. Statistical mechanics demonstrates how the thermodynamic parameters of a system, such as temperature and pressure, are related to microscopic behaviours of such constituent atoms and molecules.[4]
Although we may understand a system generically, in general we lack information about the state of a specific instance of that system. For this reason the notion of statistical ensemble (a probability distribution over possible states) is necessary. Furthermore, in order to reflect that the material is in a thermodynamic equilibrium, it is necessary to introduce a corresponding statistical mechanical definition of equilibrium. The analogue of thermodynamic equilibrium in statistical thermodynamics is the ensemble property of statistical equilibrium, described in the previous section. An additional assumption in statistical thermodynamics is that the system is isolated (no varying external forces are acting on the system), so that its total energy does not vary over time. A sufficient (but not necessary) condition for statistical equilibrium with an isolated system is that the probability distribution is a function only of conserved properties (total energy, total particle numbers, etc.).[1]
A common approach found in many textbooks is to take the equal a priori probability postulate.[2] This postulate states that
In any case, the reason for establishing the microcanonical ensemble is mainly axiomatic.[6] The microcanonical ensemble itself is mathematically awkward to use for real calculations, and even very simple finite systems can only be solved approximately. However, it is possible to use the microcanonical ensemble to construct a hypothetical infinite thermodynamic reservoir that has an exactly defined notion of temperature and chemical potential. Once this reservoir has been established, it can be used to justify exactly the canonical ensemble or grand canonical ensemble (see below) for any other system by considering the contact of this system with the reservoir.[1] These other ensembles are those actually used in practical statistical mechanics calculations as they are mathematically simpler and also correspond to a much more realistic situation (energy not known exactly).[2]
The limit of large systems in statistical mechanics is known as the thermodynamic limit. In the thermodynamic limit the microcanonical, canonical, and grand canonical ensembles tend to give identical predictions about thermodynamic characteristics. This means that one can specify either total energy or temperature and arrive at the same result; likewise one can specify either total particle number or chemical potential. Given these considerations, the best ensemble to choose for the calculation of the properties of a macroscopic system is usually just the ensemble which allows the result to be derived most easily.[7]
Important cases where the thermodynamic ensembles do not give identical results include:
A simple way to prepare one litre sample of ammonia in a standard condition is to take a very large reservoir of ammonia at those standard conditions, and connect it to a previously evacuated one-litre container. After ammonia gas has entered the container and the container has been given time to reach thermodynamic equilibrium with the reservoir, the container is then sealed and isolated. In thermodynamics, this is a repeatable process resulting in a very well defined sample of gas with a precise description. We now consider the corresponding precise description in statistical thermodynamics.
Although this process is well defined and repeatable in a macroscopic sense, we have no information about the exact locations and velocities of each and every molecule in the container of gas. Moreover, we do not even know exactly how many molecules are in the container; even supposing we knew exactly the average density of the ammonia gas in general, we do not know how many molecules of the gas happened to be inside our container at the moment when we sealed it. The sample is in equilibrium and is in equilibrium with the reservoir: we could reconnect it to the reservoir for some time, and then re-seal it, and our knowledge about the state of the gas would not change. In this case, our knowledge about the state of the gas is precisely described by the grand canonical ensemble. Provided we have an accurate microscopic model of the ammonia gas, we could in principle compute all thermodynamic properties of this sample of gas by using the distribution provided by the grand canonical ensemble.
Hypothetically, we could use an extremely sensitive weight scale to measure exactly the mass of the container before and after introducing the ammonia gas, so that we can exactly know the number of ammonia molecules. After we make this measurement, then our knowledge about the gas would correspond to the canonical ensemble. Finally, suppose by some hypothetical apparatus we can measure exactly the number of molecules and also measure exactly the total energy of the system. Supposing furthermore that this apparatus gives us no further information about the molecules' positions and velocities, our knowledge about the system would correspond to the microcanonical ensemble.
Even after making such measurements, however, our expectations about the behaviour of the gas do not change appreciably. This is because the gas sample is macroscopic and approximates very well the thermodynamic limit, so the different ensembles behave similarly. This can be demonstrated by considering how small the actual fluctuations would be. Suppose that we knew the number density of ammonia gas was exactly 3.04×1022 molecules per liter inside the reservoir of ammonia gas used to fill the one-litre container. In describing the container with the grand canonical ensemble, then, the average number of molecules would be and the uncertainty (standard deviation) in the number of molecules would be
and the uncertainty (standard deviation) in the number of molecules would be  (assuming Poisson distribution), which is relatively very small compared to the total number of molecules. Upon measuring the particle number (thus arriving at a canonical ensemble) we should find very nearly 3.04×1022 molecules. For example the probability of finding more than 3.040001×1022 or less than 3.039999×1022 molecules would be about 1 in 103000000000.[note 5]
(assuming Poisson distribution), which is relatively very small compared to the total number of molecules. Upon measuring the particle number (thus arriving at a canonical ensemble) we should find very nearly 3.04×1022 molecules. For example the probability of finding more than 3.040001×1022 or less than 3.039999×1022 molecules would be about 1 in 103000000000.[note 5]
The field of non-equilibrium statistical mechanics is concerned with understanding these non-equilibrium processes at the microscopic level. (Statistical thermodynamics can only be used to calculate the final result, after the external imbalances have been removed and the ensemble has settled back down to equilibrium.)
In principle, non-equilibrium statistical mechanics could be mathematically exact: ensembles for an isolated system evolve over time according to deterministic equations such as Liouville's equation or its quantum equivalent, the von Neumann equation. These equations are the result of applying the mechanical equations of motion independently to each state in the ensemble. Unfortunately, these ensemble evolution equations inherit much of the complexity of the underlying mechanical motion, and so exact solutions are very difficult to obtain. Moreover, the ensemble evolution equations are fully reversible and do not destroy information (the ensemble's Gibbs entropy is preserved). In order to make headway in modelling irreversible processes, it is necessary to add additional ingredients besides probability and reversible mechanics.
Non-equilibrium mechanics is therefore an active area of theoretical research as the range of validity of these additional assumptions continues to be explored. A few approaches are described in the following subsections.
Essentially, a system that is slightly away from equilibrium—whether put there by external forces or by fluctuations—relaxes towards equilibrium in the same way, since the system cannot tell the difference or "know" how it came to be away from equilibrium.[3]:664
This provides an indirect avenue for obtaining numbers such as ohmic conductivity and thermal conductivity by extracting results from equilibrium statistical mechanics. Since equilibrium statistical mechanics is mathematically well defined and (in some cases) more amenable for calculations, the fluctuation-dissipation connection can be a convenient shortcut for calculations in near-equilibrium statistical mechanics.
A few of the theoretical tools used to make this connection include:
In 1859, after reading a paper on the diffusion of molecules by Rudolf Clausius, Scottish physicist James Clerk Maxwell formulated the Maxwell distribution of molecular velocities, which gave the proportion of molecules having a certain velocity in a specific range. This was the first-ever statistical law in physics.[11] Five years later, in 1864, Ludwig Boltzmann, a young student in Vienna, came across Maxwell’s paper and was so inspired by it that he spent much of his life developing the subject further.
Statistical mechanics proper was initiated in the 1870s with the work of Boltzmann, much of which was collectively published in his 1896 Lectures on Gas Theory.[12] Boltzmann's original papers on the statistical interpretation of thermodynamics, the H-theorem, transport theory, thermal equilibrium, the equation of state of gases, and similar subjects, occupy about 2,000 pages in the proceedings of the Vienna Academy and other societies. Boltzmann introduced the concept of an equilibrium statistical ensemble and also investigated for the first time non-equilibrium statistical mechanics, with his H-theorem.
The term "statistical mechanics" was coined by the American mathematical physicist J. Willard Gibbs in 1884.[13][note 6] "Probabilistic mechanics" might today seem a more appropriate term, but "statistical mechanics" is firmly entrenched.[14] Shortly before his death, Gibbs published in 1902 Elementary Principles in Statistical Mechanics, a book which formalized statistical mechanics as a fully general approach to address all mechanical systems—macroscopic or microscopic, gaseous or non-gaseous.[1] Gibbs' methods were initially derived in the framework classical mechanics, however they were of such generality that they were found to adapt easily to the later quantum mechanics, and still form the foundation of statistical mechanics to this day.[2]
The classical view of the universe was that its fundamental laws are mechanical in nature, and that all physical systems are therefore governed by mechanical laws at a microscopic level. These laws are precise equations of motion that map any given initial state to a corresponding future state at a later time. There is however a disconnection between these laws and everyday life experiences, as we do not find it necessary (nor even theoretically possible) to know exactly at a microscopic level the simultaneous positions and velocities of each molecule while carrying out processes at the human scale (for example, when performing a chemical reaction).
Statistical mechanics is a collection of mathematical tools that are used to fill this disconnection between the laws of mechanics and the practical experience of incomplete knowledge.
A common use of statistical mechanics is in explaining the thermodynamic behaviour of large systems. Microscopic mechanical laws do not contain concepts such as temperature, heat, or entropy, however, statistical mechanics shows how these concepts arise from the natural uncertainty that arises about the state of a system when that system is prepared in practice. The benefit of using statistical mechanics is that it provides exact methods to connect thermodynamic quantities (such as heat capacity) to microscopic behaviour, whereas in classical thermodynamics the only available option would be to just measure and tabulate such quantities for various materials. Statistical mechanics also makes it possible to extend the laws of thermodynamics to cases which are not considered in classical thermodynamics, for example microscopic systems and other mechanical systems with few degrees of freedom.[1] This branch of statistical mechanics which treats and extends classical thermodynamics is known as statistical thermodynamics or equilibrium statistical mechanics.
Statistical mechanics also finds use outside equilibrium. An important subbranch known as non-equilibrium statistical mechanics deals with the issue of microscopically modelling the speed of irreversible processes that are driven by imbalances. Examples of such processes include chemical reactions, or flows of particles and heat. Unlike with equilibrium, there is no exact formalism that applies to non-equilibrium statistical mechanics in general and so this branch of statistical mechanics remains an active area of theoretical research.
Principles: mechanics and ensembles
In physics there are two types of mechanics usually examined: classical mechanics and quantum mechanics. For both types of mechanics, the standard mathematical approach is to consider two ingredients:- The complete state of the mechanical system at a given time, mathematically encoded as a phase point (classical mechanics) or a pure quantum state vector (quantum mechanics).
- An equation of motion which carries the state forward in time: Hamilton's equations (classical mechanics) or the time-dependent Schrödinger equation (quantum mechanics)
Whereas ordinary mechanics only considers the behaviour of a single state, statistical mechanics introduces the statistical ensemble, which is a large collection of virtual, independent copies of the system in various states. The statistical ensemble is a probability distribution over all possible states of the system. In classical statistical mechanics, the ensemble is a probability distribution over phase points (as opposed to a single phase point in ordinary mechanics), usually represented as a distribution in a phase space with canonical coordinates. In quantum statistical mechanics, the ensemble is a probability distribution over pure states,[note 2] and can be compactly summarized as a density matrix.
As is usual for probabilities, the ensemble can be interpreted in different ways:[1]
- an ensemble can be taken to represent the various possible states that a single system could be in (epistemic probability, a form of knowledge), or
- the members of the ensemble can be understood as the states of the systems in experiments repeated on independent systems which have been prepared in a similar but imperfectly controlled manner (empirical probability), in the limit of an infinite number of trials.
However the probability is interpreted, each state in the ensemble evolves over time according to the equation of motion. Thus, the ensemble itself (the probability distribution over states) also evolves, as the virtual systems in the ensemble continually leave one state and enter another. The ensemble evolution is given by the Liouville equation (classical mechanics) or the von Neumann equation (quantum mechanics). These equations are simply derived by the application of the mechanical equation of motion separately to each virtual system contained in the ensemble, with the probability of the virtual system being conserved over time as it evolves from state to state.
One special class of ensemble is those ensembles that do not evolve over time. These ensembles are known as equilibrium ensembles and their condition is known as statistical equilibrium. Statistical equilibrium occurs if, for each state in the ensemble, the ensemble also contains all of its future and past states with probabilities equal to that state.[note 3] The study of equilibrium ensembles of isolated systems is the focus of statistical thermodynamics. Non-equilibrium statistical mechanics addresses the more general case of ensembles that change over time, and/or ensembles of non-isolated systems.
Statistical thermodynamics
The primary goal of statistical thermodynamics (also known as equilibrium statistical mechanics) is to explain the classical thermodynamics of materials in terms of the properties of their constituent particles and the interactions between them. In other words, statistical thermodynamics provides a connection between the macroscopic properties of materials in thermodynamic equilibrium, and the microscopic behaviours and motions occurring inside the material.As an example, one might ask what is it about a thermodynamic system of NH3 molecules that determines the free energy characteristic of that compound? Classical thermodynamics does not provide the answer. If, for example, we were given spectroscopic data, of this body of gas molecules, such as bond length, bond angle, bond rotation, and flexibility of the bonds in NH3 we should see that the free energy could not be other than it is. To prove this true, we need to bridge the gap between the microscopic realm of atoms and molecules and the macroscopic realm of classical thermodynamics. Statistical mechanics demonstrates how the thermodynamic parameters of a system, such as temperature and pressure, are related to microscopic behaviours of such constituent atoms and molecules.[4]
Although we may understand a system generically, in general we lack information about the state of a specific instance of that system. For this reason the notion of statistical ensemble (a probability distribution over possible states) is necessary. Furthermore, in order to reflect that the material is in a thermodynamic equilibrium, it is necessary to introduce a corresponding statistical mechanical definition of equilibrium. The analogue of thermodynamic equilibrium in statistical thermodynamics is the ensemble property of statistical equilibrium, described in the previous section. An additional assumption in statistical thermodynamics is that the system is isolated (no varying external forces are acting on the system), so that its total energy does not vary over time. A sufficient (but not necessary) condition for statistical equilibrium with an isolated system is that the probability distribution is a function only of conserved properties (total energy, total particle numbers, etc.).[1]
Fundamental postulate
There are many different equilibrium ensembles that can be considered, and only some of them correspond to thermodynamics.[1] An additional postulate is necessary to motivate why the ensemble for a given system should have one form or another.A common approach found in many textbooks is to take the equal a priori probability postulate.[2] This postulate states that
- For an isolated system with an exactly known energy and exactly known composition, the system can be found with equal probability in any microstate consistent with that knowledge.
- Ergodic hypothesis: An ergodic state is one that evolves over time to explore "all accessible" states: all those with the same energy and composition. In an ergodic system, the microcanonical ensemble is the only possible equilibrium ensemble with fixed energy. This approach has limited applicability, since most systems are not ergodic.
- Principle of indifference: In the absence of any further information, we can only assign equal probabilities to each compatible situation.
- Maximum information entropy: A more elaborate version of the principle of indifference states that the correct ensemble is the ensemble that is compatible with the known information and that has the largest Gibbs entropy (information entropy).[5]
In any case, the reason for establishing the microcanonical ensemble is mainly axiomatic.[6] The microcanonical ensemble itself is mathematically awkward to use for real calculations, and even very simple finite systems can only be solved approximately. However, it is possible to use the microcanonical ensemble to construct a hypothetical infinite thermodynamic reservoir that has an exactly defined notion of temperature and chemical potential. Once this reservoir has been established, it can be used to justify exactly the canonical ensemble or grand canonical ensemble (see below) for any other system by considering the contact of this system with the reservoir.[1] These other ensembles are those actually used in practical statistical mechanics calculations as they are mathematically simpler and also correspond to a much more realistic situation (energy not known exactly).[2]
Three thermodynamic ensembles
There are three equilibrium ensembles with a simple form that can be defined for any isolated system bounded inside a finite volume.[1] These are the most often discussed ensembles in statistical thermodynamics. In the macroscopic limit (defined below) they all correspond to classical thermodynamics.- The microcanonical ensemble describes a system with a precisely given energy and fixed composition (precise number of particles). The microcanonical ensemble contains with equal probability each possible state that is consistent with that energy and composition.
- The canonical ensemble describes a system of fixed composition that is in thermal equilibrium[note 4] with a heat bath of a precise temperature. The canonical ensemble contains states of varying energy but identical composition; the different states in the ensemble are accorded different probabilities depending on their total energy.
- The grand canonical ensemble describes a system with non-fixed composition (uncertain particle numbers) that is in thermal and chemical equilibrium with a thermodynamic reservoir. The reservoir has a precise temperature, and precise chemical potentials for various types of particle. The grand canonical ensemble contains states of varying energy and varying numbers of particles; the different states in the ensemble are accorded different probabilities depending on their total energy and total particle numbers.
Thermodynamic ensembles[1] Microcanonical Canonical Grand canonical Fixed variables N, E, V N, T, V μ, T, V Microscopic features -
Number of microstates -

Macroscopic function -
Statistical fluctuations and the macroscopic limit
The thermodynamic ensembles' most significant difference is that they either admit uncertainty in the variables of energy or particle number, or that those variables are fixed to particular values. While this difference can be observed in some cases, for macroscopic systems the thermodynamic ensembles are usually observationally equivalent.The limit of large systems in statistical mechanics is known as the thermodynamic limit. In the thermodynamic limit the microcanonical, canonical, and grand canonical ensembles tend to give identical predictions about thermodynamic characteristics. This means that one can specify either total energy or temperature and arrive at the same result; likewise one can specify either total particle number or chemical potential. Given these considerations, the best ensemble to choose for the calculation of the properties of a macroscopic system is usually just the ensemble which allows the result to be derived most easily.[7]
Important cases where the thermodynamic ensembles do not give identical results include:
- Systems at a phase transition.
- Systems with long-range interactions.
- Microscopic systems.
Illustrative example (a gas)
The above concepts can be illustrated for the specific case of one liter of ammonia gas at standard conditions. (Note that statistical thermodynamics is not restricted to the study of macroscopic gases, and the example of a gas is given here to illustrate concepts. Statistical mechanics and statistical thermodynamics apply to all mechanical systems (including microscopic systems) and to all phases of matter: liquids, solids, plasmas, gases, nuclear matter, quark matter.)A simple way to prepare one litre sample of ammonia in a standard condition is to take a very large reservoir of ammonia at those standard conditions, and connect it to a previously evacuated one-litre container. After ammonia gas has entered the container and the container has been given time to reach thermodynamic equilibrium with the reservoir, the container is then sealed and isolated. In thermodynamics, this is a repeatable process resulting in a very well defined sample of gas with a precise description. We now consider the corresponding precise description in statistical thermodynamics.
Although this process is well defined and repeatable in a macroscopic sense, we have no information about the exact locations and velocities of each and every molecule in the container of gas. Moreover, we do not even know exactly how many molecules are in the container; even supposing we knew exactly the average density of the ammonia gas in general, we do not know how many molecules of the gas happened to be inside our container at the moment when we sealed it. The sample is in equilibrium and is in equilibrium with the reservoir: we could reconnect it to the reservoir for some time, and then re-seal it, and our knowledge about the state of the gas would not change. In this case, our knowledge about the state of the gas is precisely described by the grand canonical ensemble. Provided we have an accurate microscopic model of the ammonia gas, we could in principle compute all thermodynamic properties of this sample of gas by using the distribution provided by the grand canonical ensemble.
Hypothetically, we could use an extremely sensitive weight scale to measure exactly the mass of the container before and after introducing the ammonia gas, so that we can exactly know the number of ammonia molecules. After we make this measurement, then our knowledge about the gas would correspond to the canonical ensemble. Finally, suppose by some hypothetical apparatus we can measure exactly the number of molecules and also measure exactly the total energy of the system. Supposing furthermore that this apparatus gives us no further information about the molecules' positions and velocities, our knowledge about the system would correspond to the microcanonical ensemble.
Even after making such measurements, however, our expectations about the behaviour of the gas do not change appreciably. This is because the gas sample is macroscopic and approximates very well the thermodynamic limit, so the different ensembles behave similarly. This can be demonstrated by considering how small the actual fluctuations would be. Suppose that we knew the number density of ammonia gas was exactly 3.04×1022 molecules per liter inside the reservoir of ammonia gas used to fill the one-litre container. In describing the container with the grand canonical ensemble, then, the average number of molecules would be
 and the uncertainty (standard deviation) in the number of molecules would be
and the uncertainty (standard deviation) in the number of molecules would be  (assuming Poisson distribution), which is relatively very small compared to the total number of molecules. Upon measuring the particle number (thus arriving at a canonical ensemble) we should find very nearly 3.04×1022 molecules. For example the probability of finding more than 3.040001×1022 or less than 3.039999×1022 molecules would be about 1 in 103000000000.[note 5]
(assuming Poisson distribution), which is relatively very small compared to the total number of molecules. Upon measuring the particle number (thus arriving at a canonical ensemble) we should find very nearly 3.04×1022 molecules. For example the probability of finding more than 3.040001×1022 or less than 3.039999×1022 molecules would be about 1 in 103000000000.[note 5]Calculation methods
Once the characteristic state function for an ensemble has been calculated for a given system, that system is 'solved' (macroscopic observables can be extracted from the characteristic state function). Calculating the characteristic state function of a thermodynamic ensemble is not necessarily a simple task, however, since it involves considering every possible state of the system. While some hypothetical systems have been exactly solved, the most general (and realistic) case is too complex for exact solution. Various approaches exist to approximate the true ensemble and allow calculation of average quantities.Exact
There are some cases which allow exact solutions.- For very small microscopic systems, the ensembles can be directly computed by simply enumerating over all possible states of the system (using exact diagonalization in quantum mechanics, or integral over all phase space in classical mechanics).
- Some large systems consist of many separable microscopic systems, and each of the subsystems can be analysed independently. Notably, idealized gases of non-interacting particles have this property, allowing exact derivations of Maxwell–Boltzmann statistics, Fermi–Dirac statistics, and Bose–Einstein statistics.[2]
- A few large systems with interaction have been solved. By the use of subtle mathematical techniques, exact solutions have been found for a few toy models.[8] Some examples include the Bethe ansatz, square-lattice Ising model in zero field, hard hexagon model.
Monte Carlo
One approximate approach that is particularly well suited to computers is the Monte Carlo method, which examines just a few of the possible states of the system, with the states chosen randomly (with a fair weight). As long as these states form a representative sample of the whole set of states of the system, the approximate characteristic function is obtained. As more and more random samples are included, the errors are reduced to an arbitrarily low level.- The Metropolis–Hastings algorithm is a classic Monte Carlo method which was initially used to sample the canonical ensemble.
- Path integral Monte Carlo, also used to sample the canonical ensemble.
Other
- For rarefied non-ideal gases, approaches such as the cluster expansion use perturbation theory to include the effect of weak interactions, leading to a virial expansion.[3]
- For dense fluids, another approximate approach is based on reduced distribution functions, in particular the radial distribution function.[3]
- Molecular dynamics computer simulations can be used to calculate microcanonical ensemble averages, in ergodic systems. With the inclusion of a connection to a stochastic heat bath, they can also model canonical and grand canonical conditions.
- Mixed methods involving non-equilibrium statistical mechanical results (see below) may be useful.
Non-equilibrium statistical mechanics
There are many physical phenomena of interest that involve quasi-thermodynamic processes out of equilibrium, for example:- heat transport by the internal motions in a material, driven by a temperature imbalance,
- electric currents carried by the motion of charges in a conductor, driven by a voltage imbalance,
- spontaneous chemical reactions driven by a decrease in free energy,
- friction, dissipation, quantum decoherence,
- systems being pumped by external forces (optical pumping, etc.),
- and irreversible processes in general.
The field of non-equilibrium statistical mechanics is concerned with understanding these non-equilibrium processes at the microscopic level. (Statistical thermodynamics can only be used to calculate the final result, after the external imbalances have been removed and the ensemble has settled back down to equilibrium.)
In principle, non-equilibrium statistical mechanics could be mathematically exact: ensembles for an isolated system evolve over time according to deterministic equations such as Liouville's equation or its quantum equivalent, the von Neumann equation. These equations are the result of applying the mechanical equations of motion independently to each state in the ensemble. Unfortunately, these ensemble evolution equations inherit much of the complexity of the underlying mechanical motion, and so exact solutions are very difficult to obtain. Moreover, the ensemble evolution equations are fully reversible and do not destroy information (the ensemble's Gibbs entropy is preserved). In order to make headway in modelling irreversible processes, it is necessary to add additional ingredients besides probability and reversible mechanics.
Non-equilibrium mechanics is therefore an active area of theoretical research as the range of validity of these additional assumptions continues to be explored. A few approaches are described in the following subsections.
Stochastic methods
One approach to non-equilibrium statistical mechanics is to incorporate stochastic (random) behaviour into the system. Stochastic behaviour destroys information contained in the ensemble. While this is technically inaccurate (aside from hypothetical situations involving black holes, a system cannot in itself cause loss of information), the randomness is added to reflect that information of interest becomes converted over time into subtle correlations within the system, or to correlations between the system and environment. These correlations appear as chaotic or pseudorandom influences on the variables of interest. By replacing these correlations with randomness proper, the calculations can be made much easier.- Boltzmann transport equation: An early form of stochastic mechanics appeared even before the term "statistical mechanics" had been coined, in studies of kinetic theory. James Clerk Maxwell had demonstrated that molecular collisions would lead to apparently chaotic motion inside a gas. Ludwig Boltzmann subsequently showed that, by taking this molecular chaos for granted as a complete randomization, the motions of particles in a gas would follow a simple Boltzmann transport equation that would rapidly restore a gas to an equilibrium state (see H-theorem).
The Boltzmann transport equation and related approaches are important tools in non-equilibrium statistical mechanics due to their extreme simplicity. These approximations work well in systems where the "interesting" information is immediately (after just one collision) scrambled up into subtle correlations, which essentially restricts them to rarefied gases. The Boltzmann transport equation has been found to be very useful in simulations of electron transport in lightly doped semiconductors (in transistors), where the electrons are indeed analogous to a rarefied gas.
A quantum technique related in theme is the random phase approximation.
- BBGKY hierarchy: In liquids and dense gases, it is not valid to immediately discard the correlations between particles after one collision. The BBGKY hierarchy (Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy) gives a method for deriving Boltzmann-type equations but also extending them beyond the dilute gas case, to include correlations after a few collisions.
- Keldysh formalism (a.k.a. NEGF—non-equilibrium Green functions): A quantum approach to including stochastic dynamics is found in the Keldysh formalism. This approach often used in electronic quantum transport calculations.
Near-equilibrium methods
Another important class of non-equilibrium statistical mechanical models deals with systems that are only very slightly perturbed from equilibrium. With very small perturbations, the response can be analysed in linear response theory. A remarkable result, as formalized by the fluctuation-dissipation theorem, is that the response of a system when near equilibrium is precisely related to the fluctuations that occur when the system is in total equilibrium.Essentially, a system that is slightly away from equilibrium—whether put there by external forces or by fluctuations—relaxes towards equilibrium in the same way, since the system cannot tell the difference or "know" how it came to be away from equilibrium.[3]:664
This provides an indirect avenue for obtaining numbers such as ohmic conductivity and thermal conductivity by extracting results from equilibrium statistical mechanics. Since equilibrium statistical mechanics is mathematically well defined and (in some cases) more amenable for calculations, the fluctuation-dissipation connection can be a convenient shortcut for calculations in near-equilibrium statistical mechanics.
A few of the theoretical tools used to make this connection include:
- Fluctuation–dissipation theorem
- Onsager reciprocal relations
- Green–Kubo relations
- Landauer–Büttiker formalism
- Mori–Zwanzig formalism
Hybrid methods
An advanced approach uses a combination of stochastic methods and linear response theory. As an example, one approach to compute quantum coherence effects (weak localization, conductance fluctuations) in the conductance of an electronic system is the use of the Green-Kubo relations, with the inclusion of stochastic dephasing by interactions between various electrons by use of the Keldysh method.[9][10]Applications outside thermodynamics
The ensemble formalism also can be used to analyze general mechanical systems with uncertainty in knowledge about the state of a system. Ensembles are also used in:- propagation of uncertainty over time,[1]
- regression analysis of gravitational orbits,
- ensemble forecasting of weather,
- dynamics of neural networks.
History
In 1738, Swiss physicist and mathematician Daniel Bernoulli published Hydrodynamica which laid the basis for the kinetic theory of gases. In this work, Bernoulli posited the argument, still used to this day, that gases consist of great numbers of molecules moving in all directions, that their impact on a surface causes the gas pressure that we feel, and that what we experience as heat is simply the kinetic energy of their motion.[6]In 1859, after reading a paper on the diffusion of molecules by Rudolf Clausius, Scottish physicist James Clerk Maxwell formulated the Maxwell distribution of molecular velocities, which gave the proportion of molecules having a certain velocity in a specific range. This was the first-ever statistical law in physics.[11] Five years later, in 1864, Ludwig Boltzmann, a young student in Vienna, came across Maxwell’s paper and was so inspired by it that he spent much of his life developing the subject further.
Statistical mechanics proper was initiated in the 1870s with the work of Boltzmann, much of which was collectively published in his 1896 Lectures on Gas Theory.[12] Boltzmann's original papers on the statistical interpretation of thermodynamics, the H-theorem, transport theory, thermal equilibrium, the equation of state of gases, and similar subjects, occupy about 2,000 pages in the proceedings of the Vienna Academy and other societies. Boltzmann introduced the concept of an equilibrium statistical ensemble and also investigated for the first time non-equilibrium statistical mechanics, with his H-theorem.
The term "statistical mechanics" was coined by the American mathematical physicist J. Willard Gibbs in 1884.[13][note 6] "Probabilistic mechanics" might today seem a more appropriate term, but "statistical mechanics" is firmly entrenched.[14] Shortly before his death, Gibbs published in 1902 Elementary Principles in Statistical Mechanics, a book which formalized statistical mechanics as a fully general approach to address all mechanical systems—macroscopic or microscopic, gaseous or non-gaseous.[1] Gibbs' methods were initially derived in the framework classical mechanics, however they were of such generality that they were found to adapt easily to the later quantum mechanics, and still form the foundation of statistical mechanics to this day.[2]






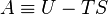
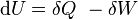 ,
, is the internal energy,
is the internal energy,  is the energy added by heating and
is the energy added by heating and 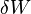 is the work done by the system. From the
is the work done by the system. From the  . Also, in case of a reversible change, the work done can be expressed as
. Also, in case of a reversible change, the work done can be expressed as 
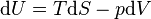
 ,
,





 (isothermal process)
(isothermal process)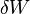 becomes dW) . dW includes all reversible work, mechanical (pressure-volume) work and non-mechanical work (e. g. electrical work).
becomes dW) . dW includes all reversible work, mechanical (pressure-volume) work and non-mechanical work (e. g. electrical work). . Therefore, to prevent a spontaneous change, we must also require that A be at a minimum.
. Therefore, to prevent a spontaneous change, we must also require that A be at a minimum. , the
, the  , and the total amount of work that can be extracted, performed by the system,
, and the total amount of work that can be extracted, performed by the system, 
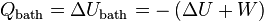





 , as keeping T and V constant seems to imply
, as keeping T and V constant seems to imply 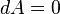 and hence
and hence  . In reality there is no contradiction. After the spontaneous change, the system, as described by thermodynamics, is a different system with a different free energy function than it was before the spontaneous change. Thus, we can say that
. In reality there is no contradiction. After the spontaneous change, the system, as described by thermodynamics, is a different system with a different free energy function than it was before the spontaneous change. Thus, we can say that  where the
where the  are different thermodynamic functions of state.
are different thermodynamic functions of state.
 are the numbers of particles of type j and the
are the numbers of particles of type j and the 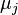 are the corresponding
are the corresponding 
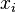 are the external variables and the
are the external variables and the  the corresponding
the corresponding 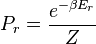






 . Then changing the system's temperature parameter by
. Then changing the system's temperature parameter by 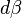 and the external variable by
and the external variable by 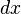 will lead to a change in
will lead to a change in  :
:
 as:
as:




 where
where 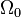 is the ground state degeneracy. The partition function in this limit is
is the ground state degeneracy. The partition function in this limit is  where
where  is the ground state energy. Thus, we see that
is the ground state energy. Thus, we see that  and that:
and that:
 of the model by a trial Hamiltonian
of the model by a trial Hamiltonian  , which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that
, which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that
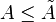
 is the free energy of the original Hamiltonian and
is the free energy of the original Hamiltonian and  is the free energy of the trial Hamiltonian. By including a large number of parameters in the trial Hamiltonian and minimizing the free energy we can expect to get a close approximation to the exact free energy.
is the free energy of the trial Hamiltonian. By including a large number of parameters in the trial Hamiltonian and minimizing the free energy we can expect to get a close approximation to the exact free energy.
 is exactly solvable, then we can apply the above inequality by defining
is exactly solvable, then we can apply the above inequality by defining
 to be the average of X over the canonical ensemble defined by
to be the average of X over the canonical ensemble defined by 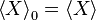

 . This means that
. This means that

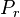 and
and 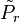 , respectively. The inequality:
, respectively. The inequality:

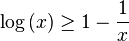


![P_{r}=\frac{\exp\left[-\beta H\left(r\right)\right]}{Z}\,](http://upload.wikimedia.org/math/5/d/2/5d21c9e5be02a1b14c0c32b6ea517d50.png)
![\tilde{P}_{r}=\frac{\exp\left[-\beta\tilde{H}\left(r\right)\right]}{\tilde{Z}}\,](http://upload.wikimedia.org/math/e/5/5/e55b932bbdfd68e905e27d0715f36a22.png)
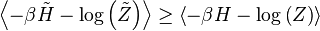

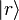 . We denote the diagonal components of the density matrices for the canonical distributions for
. We denote the diagonal components of the density matrices for the canonical distributions for ![P_{r}=\left\langle r\left|\frac{\exp\left[-\beta H\right]}{Z}\right|r\right\rangle\,](http://upload.wikimedia.org/math/c/1/3/c134d454990cfb0d8a3d392796f4e2ef.png)
![\tilde{P}_{r}=\left\langle r\left|\frac{\exp\left[-\beta\tilde{H}\right]}{\tilde{Z}}\right|r\right\rangle=\frac{\exp\left(-\beta\tilde{E}_{r}\right)}{\tilde{Z}}\,](http://upload.wikimedia.org/math/f/8/d/f8dc0d4f04021c2fb9b0b77a5a498adb.png)
 are the eigenvalues of
are the eigenvalues of 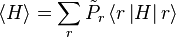
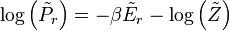

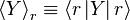
![\log\left[\left\langle\exp\left(X\right)\right\rangle_{r}\right]\geq\left\langle X\right\rangle_{r}\,](http://upload.wikimedia.org/math/3/1/3/313d7ba7a25528c08240d40cbc98ebf4.png)
![\log\left(P_{r}\right)=\log\left[\left\langle\exp\left(-\beta H - \log\left(Z\right)\right)\right\rangle_{r}\right]\geq\left\langle -\beta H - \log\left(Z\right)\right\rangle_{r}\,](http://upload.wikimedia.org/math/b/c/b/bcb635db154784912155f10a34df24d6.png)
 ) must be replaced by the product of volume,
) must be replaced by the product of volume, 
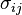 is the stress tensor, and
is the stress tensor, and  is the strain tensor. In the case of linear
is the strain tensor. In the case of linear 
 to obtain the Helmholtz energy:
to obtain the Helmholtz energy: