Bias

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Bias 

Interpretations of the random patterns of craters on the Moon. A common example of a perceptual bias caused by pareidolia.

 

Bias is a disproportionate weight in favor of or against an idea or thing, usually in a way that is closed-minded, prejudicial, or unfair. Biases can be innate or learned. People may develop biases for or against an individual, a group, or a belief. In science and engineering, a bias is a systematic error. Statistical bias results from an unfair sampling of a population, or from an estimation process that does not give accurate results on average.

Etymology

The word appears to derive from Old Provençal into Old French biais, "sideways, askance, against the grain". Whence comes French biais, "a slant, a slope, an oblique".

It seems to have entered English via the game of bowls, where it referred to balls made with a greater weight on one side. Which expanded to the figurative use, "a one-sided tendency of the mind", and, at first especially in law, "undue propensity or prejudice".

Types of bias

Cognitive biases

Main articles: Cognitive bias and List of cognitive biases

A cognitive bias is a repeating or basic misstep in thinking, assessing, recollecting, or other cognitive processes. That is, a pattern of deviation from standards in judgment, whereby inferences may be created unreasonably. People create their own "subjective social reality" from their own perceptions, their view of the world may dictate their behaviour. Thus, cognitive biases may sometimes lead to perceptual distortion, inaccurate judgment, illogical interpretation, or what is broadly called irrationality. However some cognitive biases are taken to be adaptive, and thus may lead to success in the appropriate situation. Furthermore, cognitive biases may allow speedier choices when speed is more valuable than precision. Other cognitive biases are a "by-product" of human processing limitations, coming about because of an absence of appropriate mental mechanisms, or just from human limitations in information processing.

Anchoring

Main article: Anchoring

Anchoring is a psychological heuristic that describes the propensity to rely on the first piece of information encountered when making decisions. According to this heuristic, individuals begin with an implicitly suggested reference point (the "anchor") and make adjustments to it to reach their estimate. For example, the initial price offered for a used car sets the standard for the rest of the negotiations, so that prices lower than the initial price seem more reasonable even if they are still higher than what the car is worth.

Apophenia

Main articles: Apophenia and Pareidolia

See also: Hindsight bias

Apophenia, also known as patternicity, or agenticity, is the human tendency to perceive meaningful patterns within random data. Apophenia is well documented as a rationalization for gambling. Gamblers may imagine that they see patterns in the numbers which appear in lotteries, card games, or roulette wheels. One manifestation of this is known as the "gambler's fallacy".

Pareidolia is the visual or auditory form of apophenia. It has been suggested that pareidolia combined with hierophany may have helped ancient societies organize chaos and make the world intelligible.

Attribution bias

Main article: Attribution bias

An attribution bias can happen when individuals assess or attempt to discover explanations behind their own and others' behaviors. People make attributions about the causes of their own and others' behaviors; but these attributions don't necessarily precisely reflect reality. Rather than operating as objective perceivers, individuals are inclined to perceptual slips that prompt biased understandings of their social world. When judging others we tend to assume their actions are the result of internal factors such as personality, whereas we tend to assume our own actions arise because of the necessity of external circumstances. There are a wide range of sorts of attribution biases, such as the ultimate attribution error, fundamental attribution error, actor-observer bias, and self-serving bias.

Examples of attribution bias:

Confirmation bias

Confirmation bias has been described as an internal "yes man", echoing back a person's beliefs like Charles Dickens' character Uriah Heep.

 

Main article: Confirmation bias

Confirmation bias is the tendency to search for, interpret, favor, and recall information in a way that confirms one's beliefs or hypotheses while giving disproportionately less attention to information that contradicts it. The effect is stronger for emotionally charged issues and for deeply entrenched beliefs. People also tend to interpret ambiguous evidence as supporting their existing position. Biased search, interpretation and memory have been invoked to explain attitude polarization (when a disagreement becomes more extreme even though the different parties are exposed to the same evidence), belief perseverance (when beliefs persist after the evidence for them is shown to be false), the irrational primacy effect (a greater reliance on information encountered early in a series) and illusory correlation (when people falsely perceive an association between two events or situations). Confirmation biases contribute to overconfidence in personal beliefs and can maintain or strengthen beliefs in the face of contrary evidence. Poor decisions due to these biases have been found in political and organizational contexts.

Framing

Main articles: Cultural bias and Framing (social sciences)

Framing involves the social construction of social phenomena by mass media sources, political or social movements, political leaders, and so on. It is an influence over how people organize, perceive, and communicate about reality. It can be positive or negative, depending on the audience and what kind of information is being presented. For political purposes, framing often presents facts in such a way that implicates a problem that is in need of a solution. Members of political parties attempt to frame issues in a way that makes a solution favoring their own political leaning appear as the most appropriate course of action for the situation at hand. As understood in social theory, framing is a schema of interpretation, a collection of anecdotes and stereotypes, that individuals rely on to understand and respond to events. People use filters to make sense of the world, the choices they then make are influenced by their creation of a frame.

Cultural bias is the related phenomenon of interpreting and judging phenomena by standards inherent to one's own culture. Numerous such biases exist, concerning cultural norms for color, location of body parts, mate selection, concepts of justice, linguistic and logical validity, acceptability of evidence, and taboos. Ordinary people may tend to imagine other people as basically the same, not significantly more or less valuable, probably attached emotionally to different groups and different land.

Halo effect and horn effect

Main articles: Halo effect and Horn effect

The halo effect and the horn effect are when an observer's overall impression of a person, organization, brand, or product influences their feelings about specifics of that entity's character or properties.

The name halo effect is based on the concept of the saint's halo, and is a specific type of confirmation bias, wherein positive sentiments in one area cause questionable or unknown characteristics to be seen positively. If the observer likes one aspect of something, they will have a positive predisposition toward everything about it. A person's appearance has been found to produce a halo effect. The halo effect is also present in the field of brand marketing, affecting perception of companies and non-governmental organizations (NGOs).

The opposite of the halo is the horn effect, when "individuals believe (that negative) traits are inter-connected." The term horn effect refers to Devil's horns. It works in a negative direction: if the observer dislikes one aspect of something, they will have a negative predisposition towards other aspects.

Both of these bias effects often clash with phrases such as "words mean something" and "Your words have a history."

Self-serving bias

Main article: Self-serving bias

Self-serving bias is the tendency for cognitive or perceptual processes to be distorted by the individual's need to maintain and enhance self-esteem. It is the propensity to credit accomplishment to our own capacities and endeavors, yet attribute failure to outside factors, to dismiss the legitimacy of negative criticism, concentrate on positive qualities and accomplishments yet disregard flaws and failures. Studies have demonstrated that this bias can affect behavior in the workplace, in interpersonal relationships, playing sports, and in consumer decisions.

Status quo bias

Main article: Status quo bias

Status quo bias is an emotional bias; a preference for the current state of affairs. The current baseline (or status quo) is taken as a reference point, and any change from that baseline is perceived as a loss. Status quo bias should be distinguished from a rational preference for the status quo ante, as when the current state of affairs is objectively superior to the available alternatives, or when imperfect information is a significant problem. A large body of evidence, however, shows that status quo bias frequently affects human decision-making.

Conflicts of interest

Main article: Conflict of interest

A conflict of interest is when a person or association has intersecting interests (financial, personal, etc.) which could potentially corrupt. The potential conflict is autonomous of actual improper actions, it can be found and intentionally defused before corruption, or the appearance of corruption, happens. "A conflict of interest is a set of circumstances that creates a risk that professional judgement or actions regarding a primary interest will be unduly influenced by a secondary interest." It exists if the circumstances are sensibly accepted to present a hazard that choices made may be unduly affected by auxiliary interests.

Bribery

Main article: Bribery

Bribery is giving of money, goods or other forms of recompense to in order to influence the recipient's behavior. Bribes can include money (including tips), goods, rights in action, property, privilege, emolument, gifts, perks, skimming, return favors, discounts, sweetheart deals, kickbacks, funding, donations, campaign contributions, sponsorships, stock options, secret commissions, or promotions. Expectations of when a monetary transaction is appropriate can differ from place to place. Political campaign contributions in the form of cash are considered criminal acts of bribery in some countries, while in the United States they are legal provided they adhere to election law. Tipping is considered bribery in some societies, but not others.

Favoritism

Main article: In-group favoritism

Favoritism, sometimes known as in-group favoritism, or in-group bias, refers to a pattern of favoring members of one's in-group over out-group members. This can be expressed in evaluation of others, in allocation of resources, and in many other ways. This has been researched by psychologists, especially social psychologists, and linked to group conflict and prejudice. Cronyism is favoritism of long-standing friends, especially by appointing them to positions of authority, regardless of their qualifications. Nepotism is favoritism granted to relatives.

Lobbying

Box offered by tobacco lobbyists to Dutch Member of the European Parliament Kartika Liotard in September 2013

 

Main article: Lobbying

Lobbying is the attempt to influence choices made by administrators, frequently lawmakers or individuals from administrative agencies. Lobbyists may be among a legislator's constituencies, or not; they may engage in lobbying as a business, or not. Lobbying is often spoken of with contempt, the implication is that people with inordinate socioeconomic power are corrupting the law in order to serve their own interests. When people who have a duty to act on behalf of others, such as elected officials with a duty to serve their constituents' interests or more broadly the common good, stand to benefit by shaping the law to serve the interests of some private parties, there is a conflict of interest. This can lead to all sides in a debate looking to sway the issue by means of lobbyists.

Regulatory issues

Main articles: Industry self-regulation and Regulatory capture

Self-regulation is the process whereby an organization monitors its own adherence to legal, ethical, or safety standards, rather than have an outside, independent agency such as a third party entity monitor and enforce those standards. Self-regulation of any group can create a conflict of interest. If any organization, such as a corporation or government bureaucracy, is asked to eliminate unethical behavior within their own group, it may be in their interest in the short run to eliminate the appearance of unethical behavior, rather than the behavior itself.

Regulatory capture is a form of political corruption that can occur when a regulatory agency, created to act in the public interest, instead advances the commercial or political concerns of special interest groups that dominate the industry or sector it is charged with regulating. Regulatory capture occurs because groups or individuals with a high-stakes interest in the outcome of policy or regulatory decisions can be expected to focus their resources and energies in attempting to gain the policy outcomes they prefer, while members of the public, each with only a tiny individual stake in the outcome, will ignore it altogether. Regulatory capture is a risk to which a regulatory agency is exposed by its very nature.

Shilling

Main article: Shill

Shilling is deliberately giving spectators the feeling that one is an energetic autonomous client of a vendor for whom one is working. The effectiveness of shilling relies on crowd psychology to encourage other onlookers or audience members to purchase the goods or services (or accept the ideas being marketed). Shilling is illegal in some places, but legal in others. An example of shilling is paid reviews that give the impression of being autonomous opinions.

Statistical biases

Main article: Bias (statistics)

Statistical bias is a systematic tendency in the process of data collection, which results in lopsided, misleading results. This can occur in any of a number of ways, in the way the sample is selected, or in the way data are collected. It is a property of a statistical technique or of its results whereby the expected value of the results differs from the true underlying quantitative parameter being estimated.

Forecast bias

Main article: Forecast bias

A forecast bias is when there are consistent differences between results and the forecasts of those quantities; that is: forecasts may have an overall tendency to be too high or too low.

Observer-expectancy effect

Main article: Observer-expectancy effect

The observer-expectancy effect is when a researcher's expectations cause them to subconsciously influence the people participating in an experiment. It is usually controlled using a double-blind system, and was an important reason for the development of double-blind experiments.

Reporting bias & social desirability bias

Main articles: Reporting bias and Social desirability bias

In epidemiology and empirical research, reporting bias is defined as "selective revealing or suppression of information" of undesirable behavior by subjects or researchers.  It refers to a tendency to under-report unexpected or undesirable experimental results, while being more trusting of expected or desirable results. This can propagate, as each instance reinforces the status quo, and later experimenters justify their own reporting bias by observing that previous experimenters reported different results.

Social desirability bias is a bias within social science research where survey respondents can tend to answer questions in a manner that will be viewed positively by others. It can take the form of over-reporting laudable behavior, or under-reporting undesirable behavior. This bias interferes with the interpretation of average tendencies as well as individual differences. The inclination represents a major issue with self-report questionnaires; of special concern are self-reports of abilities, personalities, sexual behavior, and drug use.

Selection bias

Main article: Selection bias

 

Sampling is supposed to collect of a representative sample of a population.

Selection bias is the conscious or unconscious bias introduced into a study by the way individuals, groups or data are selected for analysis, if such a way means that true randomization is not achieved, thereby ensuring that the sample obtained is not representative of the population intended to be analyzed. This results in a sample that may be significantly different from the overall population.

Prejudices

Main articles: Bigotry, Prejudice, and Cultural bias

Bias and prejudice are usually considered to be closely related. Prejudice is prejudgment, or forming an opinion before becoming aware of the relevant facts of a case. The word is often used to refer to preconceived, usually unfavorable, judgments toward people or a person because of gender, political opinion, social class, age, disability, religion, sexuality, race/ethnicity, language, nationality, or other personal characteristics. Prejudice can also refer to unfounded beliefs and may include "any unreasonable attitude that is unusually resistant to rational influence".

Ageism

Main article: Ageism

Ageism is the stereotyping and/or discrimination against individuals or groups on the basis of their age. It can be used in reference to prejudicial attitudes towards older people, or towards younger people.

Classism

Main article: Class discrimination

Classism is discrimination on the basis of social class. It includes attitudes that benefit the upper class at the expense of the lower class, or vice versa.

Lookism

Main article: Lookism

Lookism is stereotypes, prejudice, and discrimination on the basis of physical attractiveness, or more generally to people whose appearance matches cultural preferences. Many people make automatic judgments of others based on their physical appearance that influence how they respond to those people.

Racism

Main article: Racism

Racism consists of ideologies based on a desire to dominate or a belief in the inferiority of another race. It may also hold that members of different races should be treated differently.

Sexism

Main article: Sexism

Sexism is discrimination based on a person's sex or gender. Sexism can affect any gender, but it is particularly documented as affecting women and girls. It has been linked to stereotypes and gender roles, and may include the belief that one sex or gender is intrinsically superior to another.

Contextual biases

Biases in academia

See also: Statistical bias

Academic bias

Main article: Academic bias

Academic bias is the bias or perceived bias of scholars allowing their beliefs to shape their research and the scientific community. Claims of bias are often linked to claims by conservatives of pervasive bias against political conservatives and religious Christians. Some have argued that these claims are based upon anecdotal evidence which would not reliably indicate systematic bias, and have suggested that this divide is due to self-selection of conservatives choosing not to pursue academic careers. There is some evidence that perception of classroom bias may be rooted in issues of sexuality, race, class and sex as much or more than in religion.

Experimenter bias

Main article: Experimenter's bias

In science research, experimenter bias occurs when experimenter expectancies regarding study results bias the research outcome. Examples of experimenter bias include conscious or unconscious influences on subject behavior including creation of demand characteristics that influence subjects, and altered or selective recording of experimental results themselves.

Funding bias

Main article: Funding bias

Funding bias refers to the tendency of a scientific study to support the interests of the study's financial sponsor. This phenomenon is recognized sufficiently that researchers undertake studies to examine bias in past published studies. It can be caused by any or all of: a conscious or subconscious sense of obligation of researchers towards their employers, misconduct or malpractice, publication bias, or reporting bias.

Full text on net bias

Main article: FUTON bias

Full text on net (or FUTON) bias is a tendency of scholars to cite academic journals with open access—that is, journals that make their full text available on the internet without charge—in their own writing as compared with toll access publications. Scholars can more easily discover and access articles that have their full text on the internet, which increases authors' likelihood of reading, quoting, and citing these articles, this may increase the impact factor of open access journals relative to journals without open access.

The related bias, no abstract available bias (NAA bias) is scholars' tendency to cite journal articles that have an abstract available online more readily than articles that do not.

Publication bias

Main article: Publication bias

Publication bias is a type of bias with regard to what academic research is likely to be published because of a tendency of researchers, and journal editors, to prefer some outcomes rather than others e.g. results showing a significant finding, leads to a problematic bias in the published literature. This can propagate further as literature reviews of claims about support for a hypothesis will themselves be biased if the original literature is contaminated by publication bias. Studies with significant results often do not appear to be superior to studies with a null result with respect to quality of design. However, statistically significant results have been shown to be three times more likely to be published compared to papers with null results.

Biases in law enforcement

Driving while black

Main article: Driving while black

Driving while black refers to the racial profiling of African American drivers. The phrase implies that a motorist might be pulled over by a police officer, questioned, and searched, because of a racial bias.

Racial profiling

Main article: Racial profiling

Racial profiling, or ethnic profiling, is the act of suspecting or targeting a person of a certain race on the basis of racially observed characteristics or behavior, rather than on individual suspicion. Racial profiling is commonly referred to regarding its use by law enforcement, and its leading to discrimination against minorities.

Victim blaming

Main article: Victim blaming

Victim blaming occurs when the victim of a wrongful act is held at fault for the harm that befell them. The study of victimology seeks to mitigate the perception of victims as responsible.

Biases in media

Main articles: Media bias and Media manipulation

Media bias is the bias or perceived bias of journalists and news producers within the mass media in the selection of events, the stories that are reported, and how they are covered. The term generally implies a pervasive or widespread bias violating the standards of journalism, rather than the perspective of an individual journalist or article. The level of media bias in different nations is debated. There are also watchdog groups that report on media bias.

Practical limitations to media neutrality include the inability of journalists to report all available stories and facts, the requirement that selected facts be linked into a coherent narrative, government influence including overt and covert censorship, the influence of the owners of the news source, concentration of media ownership, the selection of staff, the preferences of an intended audience, and pressure from advertisers.

Bias has been a feature of the mass media since its birth with the invention of the printing press. The expense of early printing equipment restricted media production to a limited number of people. Historians have found that publishers often served the interests of powerful social groups.

Agenda setting

Main article: Agenda-setting theory

Agenda setting describes the capacity of the media to focus on particular stories, if a news item is covered frequently and prominently, the audience will regard the issue as more important. That is, its salience will increase.

Gatekeeping

Main article: Gatekeeping (communication)

Gatekeeping is the way in which information and news are filtered to the public, by each person or corporation along the way. It is the "process of culling and crafting countless bits of information into the limited number of messages that reach people every day, and it is the center of the media's role in modern public life. [...] This process determines not only which information is selected, but also what the content and nature of the messages, such as news, will be."

Sensationalism

Main article: Sensationalism

Sensationalism is when events and topics in news stories and pieces are overhyped to present skewed impressions of events, which may cause a misrepresentation of the truth of a story. Sensationalism may involve reporting about insignificant matters and events, or the presentation of newsworthy topics in a trivial or tabloid manner contrary to the standards of professional journalism.

Other contexts

Educational bias

Main article: Bias in education

Bias in education refers to real or perceived bias in the educational system. The content of school textbooks is often the issue of debate, as their target audience is young people, and the term "whitewashing" is used to refer to selective removal of critical or damaging evidence or comment. Religious bias in textbooks is observed in countries where religion plays a dominant role. There can be many forms of educational bias. Some overlooked aspects, occurring especially with the pedagogical circles of public and private schools—sources that are unrelated to fiduciary or mercantile impoverishment which may be unduly magnified—include teacher bias as well as a general bias against women who are going into STEM research.

Inductive bias

Main article: Inductive bias

Inductive bias occurs within the field of machine learning. In machine learning one seeks to develop algorithms that are able to learn to anticipate a particular output. To accomplish this, the learning algorithm is given training cases that show the expected connection. Then the learner is tested with new examples. Without further assumptions, this problem cannot be solved exactly as unknown situations may not be predictable. The inductive bias of the learning algorithm is the set of assumptions that the learner uses to predict outputs given inputs that it has not encountered. It may bias the learner towards the correct solution, the incorrect, or be correct some of the time. A classical example of an inductive bias is Occam's Razor, which assumes that the simplest consistent hypothesis is the best.

Insider trading

Main article: Insider trading

Insider trading is the trading of a public company's stock or other securities (such as bonds or stock options) by individuals with access to non-public information about the company. In various countries, trading based on insider information is illegal because it is seen as unfair to other investors who do not have access to the information as the investor with insider information could potentially make far larger profits that a typical investor could make.

Match fixing

Main articles: Match fixing and Spot-fixing

In organized sports, match fixing occurs when a match is played to a completely or partially pre-determined result, violating the rules of the game and often the law. There is a variety of reasons for this, but the most common is in exchange for a payoff from gamblers. Players might also intentionally perform poorly to get an advantage in the future (such as a better draft pick, or an easier opponent in a playoff), or to rig a handicap system. Match-fixing generally refers to fixing the final result of the game. Another form of match-fixing, known as spot-fixing, involves fixing small events within a match which can be gambled upon, but which are unlikely to prove decisive in determining the final result of the game.

Implicit bias

Main article: implicit stereotype

An implicit bias, or implicit stereotype, is the unconscious attribution of particular qualities to a member of a certain social group.

Implicit stereotypes are shaped by experience and based on learned associations between particular qualities and social categories, including race and/or gender. Individuals' perceptions and behaviors can be influenced by the implicit stereotypes they hold, even if they are unaware/unintentionally hold such stereotypes. Implicit bias is an aspect of implicit social cognition: the phenomenon that perceptions, attitudes, and stereotypes operate without conscious intention. The existence of implicit bias is supported by a variety of scientific articles in psychological literature. Implicit stereotype was first defined by psychologists Mahzarin Banaji and Anthony Greenwald in 1995.

Exponential distribution

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Exponential_distribution 

Exponential

Probability density function
Cumulative distribution function
Parameters	${\displaystyle \lambda >0,}$ rate, or inverse scale
Support	${\displaystyle x\in [0,\infty )}$
PDF	${\displaystyle \lambda e^{-\lambda x}}$
CDF	${\displaystyle 1-e^{-\lambda x}}$
Quantile	${\displaystyle -{\frac {\ln(1-p)}{\lambda }}}$
Mean	${\displaystyle {\frac {1}{\lambda }}}$
Median	${\displaystyle {\frac {\ln 2}{\lambda }}}$
Mode	${\displaystyle 0}$
Variance	${\displaystyle {\frac {1}{\lambda ^{2}}}}$
Skewness	${\displaystyle 2}$
Ex. kurtosis	${\displaystyle 6}$
Entropy	${\displaystyle 1-\ln \lambda }$
MGF	${\displaystyle {\frac {\lambda }{\lambda -t}},{\text{ for }}t<\lambda }$
CF	${\displaystyle {\frac {\lambda }{\lambda -it}}}$
Fisher information	${\displaystyle {\frac {1}{\lambda ^{2}}}}$
Kullback-Leibler divergence	${\displaystyle \ln {\frac {\lambda _{0}}{\lambda }}+{\frac {\lambda }{\lambda _{0}}}-1}$

In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.

The exponential distribution is not the same as the class of exponential families of distributions, which is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes the normal distribution, binomial distribution, gamma distribution, Poisson, and many others.

Definitions

Probability density function

The probability density function (pdf) of an exponential distribution is

${\displaystyle f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}}$

Here λ > 0 is the parameter of the distribution, often called the rate parameter. The distribution is supported on the interval [0, ∞). If a random variable X has this distribution, we write X ~ Exp(λ).

The exponential distribution exhibits infinite divisibility.

Cumulative distribution function

The cumulative distribution function is given by

${\displaystyle F(x;\lambda )={\begin{cases}1-e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}}$

Alternative parametrization

The exponential distribution is sometimes parametrized in terms of the scale parameter β = 1/λ, which is also the mean:

$${\displaystyle f(x;\beta )={\begin{cases}{\frac {1}{\beta }}e^{-x/\beta }&x\geq 0,\\0&x<0.\end{cases}}\qquad \qquad F(x;\beta )={\begin{cases}1-e^{-x/\beta }&x\geq 0,\\0&x<0.\end{cases}}}$$

Properties

Mean, variance, moments, and median

The mean is the probability mass centre, that is, the first moment.

 

The median is the preimage F⁻¹(1/2).

The mean or expected value of an exponentially distributed random variable X with rate parameter λ is given by

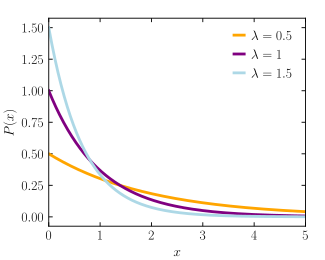
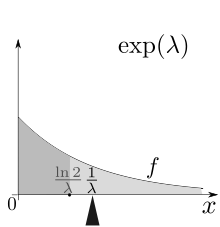
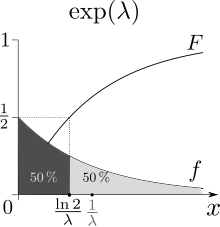
$${\displaystyle \operatorname {E} [X]={\frac {1}{\lambda }}.}$$

In light of the examples given below, this makes sense: if you receive phone calls at an average rate of 2 per hour, then you can expect to wait half an hour for every call.

The variance of X is given by

$${\displaystyle \operatorname {Var} [X]={\frac {1}{\lambda ^{2}}},}$$

so the standard deviation is equal to the mean.

The moments of X, for ${\displaystyle n\in \mathbb {N} }$ are given by

$${\displaystyle \operatorname {E} \left[X^{n}\right]={\frac {n!}{\lambda ^{n}}}.}$$

The central moments of X, for ${\displaystyle n\in \mathbb {N} }$ are given by

$${\displaystyle \mu _{n}={\frac {!n}{\lambda ^{n}}}={\frac {n!}{\lambda ^{n}}}\sum _{k=0}^{n}{\frac {(-1)^{k}}{k!}}.}$$

where !n is the subfactorial of n

The median of X is given by

$${\displaystyle \operatorname {m} [X]={\frac {\ln(2)}{\lambda }}<\operatorname {E} [X],}$$

where ln refers to the natural logarithm. Thus the absolute difference between the mean and median is

$${\displaystyle \left|\operatorname {E} \left[X\right]-\operatorname {m} \left[X\right]\right|={\frac {1-\ln(2)}{\lambda }}<{\frac {1}{\lambda }}=\operatorname {\sigma } [X],}$$

in accordance with the median-mean inequality.

Memorylessness

An exponentially distributed random variable T obeys the relation

$${\displaystyle \Pr \left(T>s+t\mid T>s\right)=\Pr(T>t),\qquad \forall s,t\geq 0.}$$

This can be seen by considering the complementary cumulative distribution function:

$${\displaystyle {\begin{aligned}\Pr \left(T>s+t\mid T>s\right)&={\frac {\Pr \left(T>s+t\cap T>s\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {\Pr \left(T>s+t\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {e^{-\lambda (s+t)}}{e^{-\lambda s}}}\\[4pt]&=e^{-\lambda t}\\[4pt]&=\Pr(T>t).\end{aligned}}}$$

When T is interpreted as the waiting time for an event to occur relative to some initial time, this relation implies that, if T is conditioned on a failure to observe the event over some initial period of time s, the distribution of the remaining waiting time is the same as the original unconditional distribution. For example, if an event has not occurred after 30 seconds, the conditional probability that occurrence will take at least 10 more seconds is equal to the unconditional probability of observing the event more than 10 seconds after the initial time.

The exponential distribution and the geometric distribution are the only memoryless probability distributions.

The exponential distribution is consequently also necessarily the only continuous probability distribution that has a constant failure rate.

Quantiles

Tukey criteria for anomalies.

The quantile function (inverse cumulative distribution function) for Exp(λ) is

$${\displaystyle F^{-1}(p;\lambda )={\frac {-\ln(1-p)}{\lambda }},\qquad 0\leq p<1}$$

The quartiles are therefore:

• first quartile: ln(4/3)/λ
• median: ln(2)/λ
• third quartile: ln(4)/λ

And as a consequence the interquartile range is ln(3)/λ.

Kullback–Leibler divergence

The directed Kullback–Leibler divergence in nats of ${\displaystyle e^{\lambda }}$ ("approximating" distribution) from ${\displaystyle e^{\lambda _{0}}}$ ('true' distribution) is given by

$${\displaystyle {\begin{aligned}\Delta (\lambda _{0}\parallel \lambda )&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {p_{\lambda _{0}}(x)}{p_{\lambda }(x)}}\right)\\&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {\lambda _{0}e^{\lambda _{0}x}}{\lambda e^{\lambda x}}}\right)\\&=\log(\lambda _{0})-\log(\lambda )-(\lambda _{0}-\lambda )E_{\lambda _{0}}(x)\\&=\log(\lambda _{0})-\log(\lambda )+{\frac {\lambda }{\lambda _{0}}}-1.\end{aligned}}}$$

Maximum entropy distribution

Among all continuous probability distributions with support [0, ∞) and mean μ, the exponential distribution with λ = 1/μ has the largest differential entropy. In other words, it is the maximum entropy probability distribution for a random variate X which is greater than or equal to zero and for which E[X] is fixed.

Distribution of the minimum of exponential random variables

Let X₁, …, X_n be independent exponentially distributed random variables with rate parameters λ₁, …, λ_n. Then

$${\displaystyle \min \left\{X_{1},\dotsc ,X_{n}\right\}}$$

is also exponentially distributed, with parameter

$${\displaystyle \lambda =\lambda _{1}+\dotsb +\lambda _{n}.}$$

This can be seen by considering the complementary cumulative distribution function:

$${\displaystyle {\begin{aligned}&\Pr \left(\min\{X_{1},\dotsc ,X_{n}\}>x\right)\\={}&\Pr \left(X_{1}>x,\dotsc ,X_{n}>x\right)\\={}&\prod _{i=1}^{n}\Pr \left(X_{i}>x\right)\\={}&\prod _{i=1}^{n}\exp \left(-x\lambda _{i}\right)=\exp \left(-x\sum _{i=1}^{n}\lambda _{i}\right).\end{aligned}}}$$

The index of the variable which achieves the minimum is distributed according to the categorical distribution

$${\displaystyle \Pr \left(X_{k}=\min\{X_{1},\dotsc ,X_{n}\}\right)={\frac {\lambda _{k}}{\lambda _{1}+\dotsb +\lambda _{n}}}.}$$

A proof can be seen by letting ${\displaystyle I=\operatorname {argmin} _{i\in \{1,\dotsb ,n\}}\{X_{1},\dotsc ,X_{n}\}}$. Then,

$${\displaystyle {\begin{aligned}\Pr(I=k)&=\int _{0}^{\infty }\Pr(X_{k}=x)\Pr(\forall _{i\neq k}X_{i}>x)\,dx\\&=\int _{0}^{\infty }\lambda _{k}e^{-\lambda _{k}x}\left(\prod _{i=1,i\neq k}^{n}e^{-\lambda _{i}x}\right)dx\\&=\lambda _{k}\int _{0}^{\infty }e^{-\left(\lambda _{1}+\dotsb +\lambda _{n}\right)x}dx\\&={\frac {\lambda _{k}}{\lambda _{1}+\dotsb +\lambda _{n}}}.\end{aligned}}}$$

Note that

$${\displaystyle \max\{X_{1},\dotsc ,X_{n}\}}$$

is not exponentially distributed, if X₁, …, X_n do not all have parameter 0.

Joint moments of i.i.d. exponential order statistics

Let ${\displaystyle X_{1},\dotsc ,X_{n}}$ be ${\displaystyle n}$ independent and identically distributed exponential random variables with rate parameter λ. Let ${\displaystyle X_{(1)},\dotsc ,X_{(n)}}$ denote the corresponding order statistics. For ${\displaystyle i<j}$ , the joint moment ${\displaystyle \operatorname {E} \left[X_{(i)}X_{(j)}\right]}$ of the order statistics ${\displaystyle X_{(i)}}$ and ${\displaystyle X_{(j)}}$ is given by

$${\displaystyle {\begin{aligned}\operatorname {E} \left[X_{(i)}X_{(j)}\right]&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\operatorname {E} \left[X_{(i)}\right]+\operatorname {E} \left[X_{(i)}^{2}\right]\\&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\sum _{k=0}^{i-1}{\frac {1}{(n-k)\lambda }}+\sum _{k=0}^{i-1}{\frac {1}{((n-k)\lambda )^{2}}}+\left(\sum _{k=0}^{i-1}{\frac {1}{(n-k)\lambda }}\right)^{2}.\end{aligned}}}$$

This can be seen by invoking the law of total expectation and the memoryless property:

$${\displaystyle {\begin{aligned}\operatorname {E} \left[X_{(i)}X_{(j)}\right]&=\int _{0}^{\infty }\operatorname {E} \left[X_{(i)}X_{(j)}\mid X_{(i)}=x\right]f_{X_{(i)}}(x)\,dx\\&=\int _{x=0}^{\infty }x\operatorname {E} \left[X_{(j)}\mid X_{(j)}\geq x\right]f_{X_{(i)}}(x)\,dx&&\left({\textrm {since}}~X_{(i)}=x\implies X_{(j)}\geq x\right)\\&=\int _{x=0}^{\infty }x\left[\operatorname {E} \left[X_{(j)}\right]+x\right]f_{X_{(i)}}(x)\,dx&&\left({\text{by the memoryless property}}\right)\\&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\operatorname {E} \left[X_{(i)}\right]+\operatorname {E} \left[X_{(i)}^{2}\right].\end{aligned}}}$$

The first equation follows from the law of total expectation. The second equation exploits the fact that once we condition on ${\displaystyle X_{(i)}=x}$, it must follow that ${\displaystyle X_{(j)}\geq x}$. The third equation relies on the memoryless property to replace ${\displaystyle \operatorname {E} \left[X_{(j)}\mid X_{(j)}\geq x\right]}$ with ${\displaystyle \operatorname {E} \left[X_{(j)}\right]+x}$.

Sum of two independent exponential random variables

The probability distribution function (PDF) of a sum of two independent random variables is the convolution of their individual PDFs. If ${\displaystyle X_{1}}$ and ${\displaystyle X_{2}}$ are independent exponential random variables with respective rate parameters ${\displaystyle \lambda _{1}}$ and ${\displaystyle \lambda _{2},}$ then the probability density of ${\displaystyle Z=X_{1}+X_{2}}$ is given by

$${\displaystyle {\begin{aligned}f_{Z}(z)&=\int _{-\infty }^{\infty }f_{X_{1}}(x_{1})f_{X_{2}}(z-x_{1})\,dx_{1}\\&=\int _{0}^{z}\lambda _{1}e^{-\lambda _{1}x_{1}}\lambda _{2}e^{-\lambda _{2}(z-x_{1})}\,dx_{1}\\&=\lambda _{1}\lambda _{2}e^{-\lambda _{2}z}\int _{0}^{z}e^{(\lambda _{2}-\lambda _{1})x_{1}}\,dx_{1}\\&={\begin{cases}{\dfrac {\lambda _{1}\lambda _{2}}{\lambda _{2}-\lambda _{1}}}\left(e^{-\lambda _{1}z}-e^{-\lambda _{2}z}\right)&{\text{ if }}\lambda _{1}\neq \lambda _{2}\\[4pt]\lambda ^{2}ze^{-\lambda z}&{\text{ if }}\lambda _{1}=\lambda _{2}=\lambda .\end{cases}}\end{aligned}}}$$

The entropy of this distribution is available in closed form: assuming ${\displaystyle \lambda _{1}>\lambda _{2}}$ (without loss of generality), then

$${\displaystyle {\begin{aligned}H(Z)&=1+\gamma +\ln \left({\frac {\lambda _{1}-\lambda _{2}}{\lambda _{1}\lambda _{2}}}\right)+\psi \left({\frac {\lambda _{1}}{\lambda _{1}-\lambda _{2}}}\right),\end{aligned}}}$$

where ${\displaystyle \gamma }$ is the Euler-Mascheroni constant, and ${\displaystyle \psi (\cdot )}$ is the digamma function.

In the case of equal rate parameters, the result is an Erlang distribution with shape 2 and parameter ${\displaystyle \lambda ,}$ which in turn is a special case of gamma distribution.

Related distributions

• If X ~ Laplace(μ, β^-1), then |X − μ| ~ Exp(β).
• If X ~ Pareto(1, λ), then log(X) ~ Exp(λ).
• If X ~ SkewLogistic(θ), then ${\displaystyle \log \left(1+e^{-X}\right)\sim \operatorname {Exp} (\theta )}$.
• If X_i ~ U(0, 1) then
  $${\displaystyle \lim _{n\to \infty }n\min \left(X_{1},\ldots ,X_{n}\right)\sim \operatorname {Exp} (1)}$$

  
• The exponential distribution is a limit of a scaled beta distribution:
  $${\displaystyle \lim _{n\to \infty }n\operatorname {Beta} (1,n)=\operatorname {Exp} (1).}$$

  
• Exponential distribution is a special case of type 3 Pearson distribution.
• If X ~ Exp(λ) and X_i ~ Exp(λ_i) then:
  • ${\displaystyle kX\sim \operatorname {Exp} \left({\frac {\lambda }{k}}\right)}$, closure under scaling by a positive factor.
  • 1 + X ~ BenktanderWeibull(λ, 1), which reduces to a truncated exponential distribution.
  • ke^X ~ Pareto(k, λ).
  • e^−X ~ Beta(λ, 1).
  • 1/ke^X ~ PowerLaw(k, λ)
  • ${\displaystyle {\sqrt {X}}\sim \operatorname {Rayleigh} \left({\frac {1}{\sqrt {2\lambda }}}\right)}$, the Rayleigh distribution
  • ${\displaystyle X\sim \operatorname {Weibull} \left({\frac {1}{\lambda }},1\right)}$, the Weibull distribution
  • ${\displaystyle X^{2}\sim \operatorname {Weibull} \left({\frac {1}{\lambda ^{2}}},{\frac {1}{2}}\right)}$
  • μ − β log(λX) ∼ Gumbel(μ, β).
  • ${\displaystyle \lfloor X\rfloor \sim \operatorname {Geometric} \left(1-e^{-\lambda }\right)}$, a geometric distribution on 0,1,2,3,...
  • ${\displaystyle \lceil X\rceil \sim \operatorname {Geometric} \left(1-e^{-\lambda }\right)}$, a geometric distribution on 1,2,3,4,...
  • If also Y ~ Erlang(n, λ) or${\displaystyle Y\sim \Gamma \left(n,{\frac {1}{\lambda }}\right)}$ then ${\displaystyle {\frac {X}{Y}}+1\sim \operatorname {Pareto} (1,n)}$
  • If also λ ~ Gamma(k, θ) (shape, scale parametrisation) then the marginal distribution of X is Lomax(k, 1/θ), the gamma mixture
  • λ₁X₁ − λ₂Y₂ ~ Laplace(0, 1).
  • min{X₁, ..., X_n} ~ Exp(λ₁ + ... + λ_n).
  • If also λ_i = λ then:
    • ${\displaystyle X_{1}+\cdots +X_{k}=\sum _{i}X_{i}\sim }$ Erlang(k, λ) = Gamma(k, λ⁻¹) = Gamma(k, λ) (in (k, θ) and (α, β) parametrization, respectively) with an integer shape parameter k.
    • X_i − X_j ~ Laplace(0, λ⁻¹).
  • If also X_i are independent, then:
    • ${\displaystyle {\frac {X_{i}}{X_{i}+X_{j}}}}$ ~ U(0, 1)
    • ${\displaystyle Z={\frac {\lambda _{i}X_{i}}{\lambda _{j}X_{j}}}}$ has probability density function ${\displaystyle f_{Z}(z)={\frac {1}{(z+1)^{2}}}}$. This can be used to obtain a confidence interval for ${\displaystyle {\frac {\lambda _{i}}{\lambda _{j}}}}$.
  • If also λ = 1:
    • ${\displaystyle \mu -\beta \log \left({\frac {e^{-X}}{1-e^{-X}}}\right)\sim \operatorname {Logistic} (\mu ,\beta )}$, the logistic distribution
    • ${\displaystyle \mu -\beta \log \left({\frac {X_{i}}{X_{j}}}\right)\sim \operatorname {Logistic} (\mu ,\beta )}$
    • μ − σ log(X) ~ GEV(μ, σ, 0).
    • Further if ${\displaystyle Y\sim \Gamma \left(\alpha ,{\frac {\beta }{\alpha }}\right)}$ then ${\displaystyle {\sqrt {XY}}\sim \operatorname {K} (\alpha ,\beta )}$ (K-distribution)
  • If also λ = 1/2 then X ∼ χ²
    ₂; i.e., X has a chi-squared distribution with 2 degrees of freedom. Hence:
    $${\displaystyle \operatorname {Exp} (\lambda )={\frac {1}{2\lambda }}\operatorname {Exp} \left({\frac {1}{2}}\right)\sim {\frac {1}{2\lambda }}\chi _{2}^{2}\Rightarrow \sum _{i=1}^{n}\operatorname {Exp} (\lambda )\sim {\frac {1}{2\lambda }}\chi _{2n}^{2}}$$

    
• If ${\displaystyle X\sim \operatorname {Exp} \left({\frac {1}{\lambda }}\right)}$ and ${\displaystyle Y\mid X}$ ~ Poisson(X) then ${\displaystyle Y\sim \operatorname {Geometric} \left({\frac {1}{1+\lambda }}\right)}$ (geometric distribution)
• The Hoyt distribution can be obtained from exponential distribution and arcsine distribution
• The exponential distribution is a limit of the κ-exponential distribution in the ${\displaystyle \kappa =0}$ case.
• Exponential distribution is a limit of the κ-Generalized Gamma distribution in the ${\displaystyle \alpha =1}$ and ${\displaystyle \nu =1}$ cases:

  ${\displaystyle \lim _{(\alpha ,\nu )\to (0,1)}p_{\kappa }(x)=(1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\Big )}}}{\frac {\alpha \lambda ^{\nu }}{\Gamma (\nu )}}x^{\alpha \nu -1}\exp _{\kappa }(-\lambda x^{\alpha })=\lambda e^{-\lambda x}}$

Other related distributions:

• Hyper-exponential distribution – the distribution whose density is a weighted sum of exponential densities.
• Hypoexponential distribution – the distribution of a general sum of exponential random variables.
• exGaussian distribution – the sum of an exponential distribution and a normal distribution.

Statistical inference

Below, suppose random variable X is exponentially distributed with rate parameter λ, and ${\displaystyle x_{1},\dotsc ,x_{n}}$ are n independent samples from X, with sample mean ${\displaystyle {\bar {x}}}$.

Parameter estimation

The maximum likelihood estimator for λ is constructed as follows.

The likelihood function for λ, given an independent and identically distributed sample x = (x₁, …, x_n) drawn from the variable, is:

$${\displaystyle L(\lambda )=\prod _{i=1}^{n}\lambda \exp(-\lambda x_{i})=\lambda ^{n}\exp \left(-\lambda \sum _{i=1}^{n}x_{i}\right)=\lambda ^{n}\exp \left(-\lambda n{\overline {x}}\right),}$$

where:

$${\displaystyle {\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$$

is the sample mean.

The derivative of the likelihood function's logarithm is:

$${\displaystyle {\frac {d}{d\lambda }}\ln L(\lambda )={\frac {d}{d\lambda }}\left(n\ln \lambda -\lambda n{\overline {x}}\right)={\frac {n}{\lambda }}-n{\overline {x}}\ {\begin{cases}>0,&0<\lambda <{\frac {1}{\overline {x}}},\\[8pt]=0,&\lambda ={\frac {1}{\overline {x}}},\\[8pt]<0,&\lambda >{\frac {1}{\overline {x}}}.\end{cases}}}$$

Consequently, the maximum likelihood estimate for the rate parameter is:

$${\displaystyle {\widehat {\lambda }}_{\text{mle}}={\frac {1}{\overline {x}}}={\frac {n}{\sum _{i}x_{i}}}}$$

This is not an unbiased estimator of ${\displaystyle \lambda ,}$ although ${\displaystyle {\overline {x}}}$ is an unbiased MLE estimator of ${\displaystyle 1/\lambda }$ and the distribution mean.

The bias of ${\displaystyle {\widehat {\lambda }}_{\text{mle}}}$ is equal to

$${\displaystyle B\equiv \operatorname {E} \left[\left({\widehat {\lambda }}_{\text{mle}}-\lambda \right)\right]={\frac {\lambda }{n-1}}}$$

which yields the bias-corrected maximum likelihood estimator

$${\displaystyle {\widehat {\lambda }}_{\text{mle}}^{*}={\widehat {\lambda }}_{\text{mle}}-B.}$$

An approximate minimizer of mean squared error (see also: bias–variance tradeoff) can be found, assuming a sample size greater than two, with a correction factor to the MLE:

$${\displaystyle {\widehat {\lambda }}=\left({\frac {n-2}{n}}\right)\left({\frac {1}{\bar {x}}}\right)={\frac {n-2}{\sum _{i}x_{i}}}}$$

This is derived from the mean and variance of the inverse-gamma distribution, ${\textstyle {\mbox{Inv-Gamma}}(n,\lambda )}$.

Fisher information

The Fisher information, denoted ${\displaystyle {\mathcal {I}}(\lambda )}$, for an estimator of the rate parameter ${\displaystyle \lambda }$ is given as:

$${\displaystyle {\mathcal {I}}(\lambda )=\operatorname {E} \left[\left.\left({\frac {\partial }{\partial \lambda }}\log f(x;\lambda )\right)^{2}\right|\lambda \right]=\int \left({\frac {\partial }{\partial \lambda }}\log f(x;\lambda )\right)^{2}f(x;\lambda )\,dx}$$

Plugging in the distribution and solving gives:

$${\displaystyle {\mathcal {I}}(\lambda )=\int _{0}^{\infty }\left({\frac {\partial }{\partial \lambda }}\log \lambda e^{-\lambda x}\right)^{2}\lambda e^{-\lambda x}\,dx=\int _{0}^{\infty }\left({\frac {1}{\lambda }}-x\right)^{2}\lambda e^{-\lambda x}\,dx=\lambda ^{-2}.}$$

This determines the amount of information each independent sample of an exponential distribution carries about the unknown rate parameter ${\displaystyle \lambda }$.

Confidence intervals

The 100(1 − α)% confidence interval for the rate parameter of an exponential distribution is given by:

$${\displaystyle {\frac {2n}{{\widehat {\lambda }}\chi _{1-{\frac {\alpha }{2}},2n}^{2}}}<{\frac {1}{\lambda }}<{\frac {2n}{{\widehat {\lambda }}\chi _{{\frac {\alpha }{2}},2n}^{2}}}}$$

which is also equal to:

$${\displaystyle {\frac {2n{\overline {x}}}{\chi _{1-{\frac {\alpha }{2}},2n}^{2}}}<{\frac {1}{\lambda }}<{\frac {2n{\overline {x}}}{\chi _{{\frac {\alpha }{2}},2n}^{2}}}}$$

where χ²
_p,v is the 100(p) percentile of the chi squared distribution with v degrees of freedom, n is the number of observations of inter-arrival times in the sample, and x-bar is the sample average. A simple approximation to the exact interval endpoints can be derived using a normal approximation to the χ²
_p,v distribution. This approximation gives the following values for a 95% confidence interval:

$${\displaystyle {\begin{aligned}\lambda _{\text{lower}}&={\widehat {\lambda }}\left(1-{\frac {1.96}{\sqrt {n}}}\right)\\\lambda _{\text{upper}}&={\widehat {\lambda }}\left(1+{\frac {1.96}{\sqrt {n}}}\right)\end{aligned}}}$$

This approximation may be acceptable for samples containing at least 15 to 20 elements.

Bayesian inference

The conjugate prior for the exponential distribution is the gamma distribution (of which the exponential distribution is a special case). The following parameterization of the gamma probability density function is useful:

$${\displaystyle \operatorname {Gamma} (\lambda ;\alpha ,\beta )={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\lambda ^{\alpha -1}\exp(-\lambda \beta ).}$$

The posterior distribution p can then be expressed in terms of the likelihood function defined above and a gamma prior:

$${\displaystyle {\begin{aligned}p(\lambda )&\propto L(\lambda )\Gamma (\lambda ;\alpha ,\beta )\\&=\lambda ^{n}\exp \left(-\lambda n{\overline {x}}\right){\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\lambda ^{\alpha -1}\exp(-\lambda \beta )\\&\propto \lambda ^{(\alpha +n)-1}\exp(-\lambda \left(\beta +n{\overline {x}}\right)).\end{aligned}}}$$

Now the posterior density p has been specified up to a missing normalizing constant. Since it has the form of a gamma pdf, this can easily be filled in, and one obtains:

$${\displaystyle p(\lambda )=\operatorname {Gamma} (\lambda ;\alpha +n,\beta +n{\overline {x}}).}$$

Here the hyperparameter α can be interpreted as the number of prior observations, and β as the sum of the prior observations. The posterior mean here is:

$${\displaystyle {\frac {\alpha +n}{\beta +n{\overline {x}}}}.}$$

Occurrence and applications

Occurrence of events

The exponential distribution occurs naturally when describing the lengths of the inter-arrival times in a homogeneous Poisson process.

The exponential distribution may be viewed as a continuous counterpart of the geometric distribution, which describes the number of Bernoulli trials necessary for a discrete process to change state. In contrast, the exponential distribution describes the time for a continuous process to change state.

In real-world scenarios, the assumption of a constant rate (or probability per unit time) is rarely satisfied. For example, the rate of incoming phone calls differs according to the time of day. But if we focus on a time interval during which the rate is roughly constant, such as from 2 to 4 p.m. during work days, the exponential distribution can be used as a good approximate model for the time until the next phone call arrives. Similar caveats apply to the following examples which yield approximately exponentially distributed variables:

• The time until a radioactive particle decays, or the time between clicks of a Geiger counter
• The time it takes before your next telephone call
• The time until default (on payment to company debt holders) in reduced-form credit risk modeling

Exponential variables can also be used to model situations where certain events occur with a constant probability per unit length, such as the distance between mutations on a DNA strand, or between roadkills on a given road.

In queuing theory, the service times of agents in a system (e.g. how long it takes for a bank teller etc. to serve a customer) are often modeled as exponentially distributed variables. (The arrival of customers for instance is also modeled by the Poisson distribution if the arrivals are independent and distributed identically.) The length of a process that can be thought of as a sequence of several independent tasks follows the Erlang distribution (which is the distribution of the sum of several independent exponentially distributed variables). Reliability theory and reliability engineering also make extensive use of the exponential distribution. Because of the memoryless property of this distribution, it is well-suited to model the constant hazard rate portion of the bathtub curve used in reliability theory. It is also very convenient because it is so easy to add failure rates in a reliability model. The exponential distribution is however not appropriate to model the overall lifetime of organisms or technical devices, because the "failure rates" here are not constant: more failures occur for very young and for very old systems.

Fitted cumulative exponential distribution to annually maximum 1-day rainfalls using CumFreq

In physics, if you observe a gas at a fixed temperature and pressure in a uniform gravitational field, the heights of the various molecules also follow an approximate exponential distribution, known as the Barometric formula. This is a consequence of the entropy property mentioned below.

In hydrology, the exponential distribution is used to analyze extreme values of such variables as monthly and annual maximum values of daily rainfall and river discharge volumes.

The blue picture illustrates an example of fitting the exponential distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysis.

In operating-rooms management, the distribution of surgery duration for a category of surgeries with no typical work-content (like in an emergency room, encompassing all types of surgeries).

Prediction

Having observed a sample of n data points from an unknown exponential distribution a common task is to use these samples to make predictions about future data from the same source. A common predictive distribution over future samples is the so-called plug-in distribution, formed by plugging a suitable estimate for the rate parameter λ into the exponential density function. A common choice of estimate is the one provided by the principle of maximum likelihood, and using this yields the predictive density over a future sample x_n+1, conditioned on the observed samples x = (x₁, ..., x_n) given by

$${\displaystyle p_{\rm {ML}}(x_{n+1}\mid x_{1},\ldots ,x_{n})=\left({\frac {1}{\overline {x}}}\right)\exp \left(-{\frac {x_{n+1}}{\overline {x}}}\right)}$$

The Bayesian approach provides a predictive distribution which takes into account the uncertainty of the estimated parameter, although this may depend crucially on the choice of prior.

A predictive distribution free of the issues of choosing priors that arise under the subjective Bayesian approach is

$${\displaystyle p_{\rm {CNML}}(x_{n+1}\mid x_{1},\ldots ,x_{n})={\frac {n^{n+1}\left({\overline {x}}\right)^{n}}{\left(n{\overline {x}}+x_{n+1}\right)^{n+1}}},}$$

which can be considered as

1. a frequentist confidence distribution, obtained from the distribution of the pivotal quantity ${\displaystyle {x_{n+1}}/{\overline {x}}}$;
2. a profile predictive likelihood, obtained by eliminating the parameter λ from the joint likelihood of x_n+1 and λ by maximization;
3. an objective Bayesian predictive posterior distribution, obtained using the non-informative Jeffreys prior 1/λ;
4. the Conditional Normalized Maximum Likelihood (CNML) predictive distribution, from information theoretic considerations.

The accuracy of a predictive distribution may be measured using the distance or divergence between the true exponential distribution with rate parameter, λ₀, and the predictive distribution based on the sample x. The Kullback–Leibler divergence is a commonly used, parameterisation free measure of the difference between two distributions. Letting Δ(λ₀||p) denote the Kullback–Leibler divergence between an exponential with rate parameter λ₀ and a predictive distribution p it can be shown that

$${\displaystyle {\begin{aligned}\operatorname {E} _{\lambda _{0}}\left[\Delta (\lambda _{0}\parallel p_{\rm {ML}})\right]&=\psi (n)+{\frac {1}{n-1}}-\log(n)\\\operatorname {E} _{\lambda _{0}}\left[\Delta (\lambda _{0}\parallel p_{\rm {CNML}})\right]&=\psi (n)+{\frac {1}{n}}-\log(n)\end{aligned}}}$$

where the expectation is taken with respect to the exponential distribution with rate parameter λ₀ ∈ (0, ∞), and ψ( · ) is the digamma function. It is clear that the CNML predictive distribution is strictly superior to the maximum likelihood plug-in distribution in terms of average Kullback–Leibler divergence for all sample sizes n > 0.

Random variate generation

Further information: Non-uniform random variate generation

A conceptually very simple method for generating exponential variates is based on inverse transform sampling: Given a random variate U drawn from the uniform distribution on the unit interval (0, 1), the variate

$${\displaystyle T=F^{-1}(U)}$$

has an exponential distribution, where F⁻¹ is the quantile function, defined by

$${\displaystyle F^{-1}(p)={\frac {-\ln(1-p)}{\lambda }}.}$$

Moreover, if U is uniform on (0, 1), then so is 1 − U. This means one can generate exponential variates as follows:

$${\displaystyle T={\frac {-\ln(U)}{\lambda }}.}$$

Other methods for generating exponential variates are discussed by Knuth and Devroye.

A fast method for generating a set of ready-ordered exponential variates without using a sorting routine is also available.