Sexual selection

From Wikipedia, the free encyclopedia

Sexual selection creates colourful differences between sexes (sexual dimorphism) in Goldie's bird-of-paradise. Male above; female below. Painting by John Gerrard Keulemans (d.1912)

 

Sexual selection is a form of natural selection where one sex prefers a specific characteristic in an individual of the other sex. Peafowls exhibit sexual selection, in that, peahens look for peacocks with more "eyes" on their tail feathers. This results in the peacocks with more eyes reproducing more, leading to peacocks with more eyes becoming more common in subsequent generations.

 

Sexual selection is a mode of natural selection where members of one biological sex choose mates of the other sex to mate with (intersexual selection), and compete with members of the same sex for access to members of the opposite sex (intrasexual selection). These two forms of selection mean that some individuals have better reproductive success than others within a population, either from being more attractive or preferring more attractive partners to produce offspring. For instance, in the breeding season, sexual selection in frogs occurs with the males first gathering at the water's edge and making their mating calls: croaking. The females then arrive and choose the males with the deepest croaks and best territories. In general, males benefit from frequent mating and monopolizing access to a group of fertile females. Females can have a limited number of offspring and maximize the return on the energy they invest in reproduction. 

The concept was first articulated by Charles Darwin and Alfred Russel Wallace who described it as driving species adaptations and that many organisms had evolved features whose function was deleterious to their individual survival, and then developed by Ronald Fisher in the early 20th century. Sexual selection can, typically, lead males to extreme efforts to demonstrate their fitness to be chosen by females, producing sexual dimorphism in secondary sexual characteristics, such as the ornate plumage of birds such as birds of paradise and peafowl, or the antlers of deer, or the manes of lions, caused by a positive feedback mechanism known as a Fisherian runaway, where the passing-on of the desire for a trait in one sex is as important as having the trait in the other sex in producing the runaway effect. Although the sexy son hypothesis indicates that females would prefer male offspring, Fisher's principle explains why the sex ratio is 1:1 almost without exception. Sexual selection is also found in plants and fungi.

The maintenance of sexual reproduction in a highly competitive world is one of the major puzzles in biology given that asexual reproduction can reproduce much more quickly as 50% of offspring are not males, unable to produce offspring themselves. Many non-exclusive hypotheses have been proposed, including the positive impact of an additional form of selection, sexual selection, on the probability of persistence of a species.

History

Darwin

Sexual selection was first proposed by Charles Darwin in The Origin of Species (1859) and developed in The Descent of Man and Selection in Relation to Sex (1871), as he felt that natural selection alone was unable to account for certain types of non-survival adaptations. He once wrote to a colleague that "The sight of a feather in a peacock's tail, whenever I gaze at it, makes me sick!" His work divided sexual selection into male-male competition and female choice.

... depends, not on a struggle for existence, but on a struggle between the males for possession of the females; the result is not death to the unsuccessful competitor, but few or no offspring.

... when the males and females of any animal have the same general habits ... but differ in structure, colour, or ornament, such differences have been mainly caused by sexual selection.

These views were to some extent opposed by Alfred Russel Wallace, mostly after Darwin's death. He accepted that sexual selection could occur, but argued that it was a relatively weak form of selection. He argued that male-male competitions were forms of natural selection, but that the "drab" peahen's coloration is itself adaptive as camouflage. In his opinion, ascribing mate choice to females was attributing the ability to judge standards of beauty to animals (such as beetles) far too cognitively undeveloped to be capable of aesthetic feeling.

Ronald Fisher

Ronald Fisher, the English statistician and evolutionary biologist developed a number of ideas about sexual selection in his 1930 book The Genetical Theory of Natural Selection including the sexy son hypothesis and Fisher's principle. The Fisherian runaway describes how sexual selection accelerates the preference for a specific ornament, causing the preferred trait and female preference for it to increase together in a positive feedback runaway cycle. In a remark that was not widely understood for another 50 years he said:

... plumage development in the male, and sexual preference for such developments in the female, must thus advance together, and so long as the process is unchecked by severe counterselection, will advance with ever-increasing speed. In the total absence of such checks, it is easy to see that the speed of development will be proportional to the development already attained, which will therefore increase with time exponentially, or in geometric progression. —Ronald Fisher, 1930

Male long-tailed widowbird

 

This causes a dramatic increase in both the male's conspicuous feature and in female preference for it, resulting in marked sexual dimorphism, until practical physical constraints halt further exaggeration. A positive feedback loop is created, producing extravagant physical structures in the non-limiting sex. A classic example of female choice and potential runaway selection is the long-tailed widowbird. While males have long tails that are selected for by female choice, female tastes in tail length are still more extreme with females being attracted to tails longer than those that naturally occur. Fisher understood that female preference for long tails may be passed on genetically, in conjunction with genes for the long tail itself. Long-tailed widowbird offspring of both sexes inherit both sets of genes, with females expressing their genetic preference for long tails, and males showing off the coveted long tail itself.

Richard Dawkins presents a non-mathematical explanation of the runaway sexual selection process in his book The Blind Watchmaker. Females that prefer long tailed males tend to have mothers that chose long-tailed fathers. As a result, they carry both sets of genes in their bodies. That is, genes for long tails and for preferring long tails become linked. The taste for long tails and tail length itself may therefore become correlated, tending to increase together. The more tails lengthen, the more long tails are desired. Any slight initial imbalance between taste and tails may set off an explosion in tail lengths. Fisher wrote that:

The exponential element, which is the kernel of the thing, arises from the rate of change in hen taste being proportional to the absolute average degree of taste. —Ronald Fisher, 1932

The peacock tail in flight, the classic example of a Fisherian runaway

 

The female widow bird chooses to mate with the most attractive long-tailed male so that her progeny, if male, will themselves be attractive to females of the next generation - thereby fathering many offspring that carry the female's genes. Since the rate of change in preference is proportional to the average taste amongst females, and as females desire to secure the services of the most sexually attractive males, an additive effect is created that, if unchecked, can yield exponential increases in a given taste and in the corresponding desired sexual attribute.

It is important to notice that the conditions of relative stability brought about by these or other means, will be far longer duration than the process in which the ornaments are evolved. In most existing species the runaway process must have been already checked, and we should expect that the more extraordinary developments of sexual plumage are not due like most characters to a long and even course of evolutionary progress, but to sudden spurts of change. —Ronald Fisher, 1930

Since Fisher's initial conceptual model of the 'runaway' process, Russell Lande and Peter O'Donald have provided detailed mathematical proofs that define the circumstances under which runaway sexual selection can take place.

Theory

Reproductive success

Extinct Irish elk (Megaloceros giganteus). These antlers span 2.7 metres (8.9 ft) and have a mass of 40 kg (88 lb).

 

The reproductive success of an organism is measured by the number of offspring left behind, and their quality or probable fitness. 

Sexual preference creates a tendency towards assortative mating or homogamy. The general conditions of sexual discrimination appear to be (1) the acceptance of one mate precludes the effective acceptance of alternative mates, and (2) the rejection of an offer is followed by other offers, either certainly or at such high chance that the risk of non-occurrence is smaller than the chance advantage to be gained by selecting a mate.

The conditions determining which sex becomes the more limited resource in intersexual selection have been hypothesized with Bateman's principle, which states that the sex which invests the most in producing offspring becomes a limiting resource for which the other sex competes, illustrated by the greater nutritional investment of an egg in a zygote, and the limited capacity of females to reproduce; for example, in humans, a woman can only give birth every ten months, whereas a male can become a father numerous times in the same period.

Modern interpretation

Male mountain gorilla, a tournament species

 

The sciences of evolutionary psychology, human behavioural ecology, and sociobiology study the influence of sexual selection in humans. 

Darwin's ideas on sexual selection were met with scepticism by his contemporaries and not considered of great importance in the early 20th century, until in the 1930s biologists decided to include sexual selection as a mode of natural selection. Only in the 21st century have they become more important in biology. The theory however is generally applicable and analogous to natural selection.

Flour beetle

 

Tungara frog

 

Research in 2015 indicates that sexual selection, including mate choice, "improves population health and protects against extinction, even in the face of genetic stress from high levels of inbreeding" and "ultimately dictates who gets to reproduce their genes into the next generation - so it's a widespread and very powerful evolutionary force." The study involved the flour beetle over a ten-year period where the only changes were in the intensity of sexual selection.

Another theory, the handicap principle of Amotz Zahavi, Russell Lande and W. D. Hamilton, holds that the fact that the male is able to survive until and through the age of reproduction with such a seemingly maladaptive trait is taken by the female to be a testament to his overall fitness. Such handicaps might prove he is either free of or resistant to disease, or that he possesses more speed or a greater physical strength that is used to combat the troubles brought on by the exaggerated trait. Zahavi's work spurred a re-examination of the field, which has produced an ever-accelerating number of theories. In 1984, Hamilton and Marlene Zuk introduced the "Bright Male" hypothesis, suggesting that male elaborations might serve as a marker of health, by exaggerating the effects of disease and deficiency. In 1990, Michael Ryan and A.S. Rand, working with the tungara frog, proposed the hypothesis of "Sensory Exploitation", where exaggerated male traits may provide a sensory stimulation that females find hard to resist. Subsequently, the theories of the "Gravity Hypothesis" by Jordi Moya-Larano et al. (2002), invoking a simple biomechanical model to account for the adaptive value for smaller male spiders of speed in clmbing vertical surfaces, and "Chase Away" by Brett Holland and William R. Rice have been added. In the late 1970s, Janzen and Mary Willson, noting that male flowers are often larger than female flowers, expanded the field of sexual selection into plants.

In the past few years, the field has exploded to include other areas of study, not all of which fit Darwin's definition of sexual selection. These include cuckoldry, nuptial gifts, sperm competition, infanticide (especially in primates), physical beauty, mating by subterfuge, species isolation mechanisms, male parental care, ambiparental care, mate location, polygamy, and homosexual rape in certain male animals. 

Focusing on the effect of sexual conflict, as hypothesized by William Rice, Locke Rowe et Göran Arnvist, Thierry Lodé argues that divergence of interest constitutes a key for evolutionary process. Sexual conflict leads to an antagonistic co-evolution in which one sex tends to control the other, resulting in a tug of war. Besides, the sexual propaganda theory only argued that mates were opportunistically led, on the basis of various factors determining the choice such as phenotypic characteristics, apparent vigour of individuals, strength of mate signals, trophic resources, territoriality, etc., but and could explain the maintenance of genetic diversity within populations.

Several workers have brought attention to the fact that elaborated characters that ought to be costly in one way or another for their bearers (e.g., the tails of some species of Xiphophorus fish) do not always appear to have a cost in terms of energetics, performance or even survival. One possible explanation for the apparent lack of costs is that "compensatory traits" have evolved in concert with the sexually selected traits.

Toolkit of natural selection

Protarchaeopteryx - skull based on Incisivosaurus and wings on Caudipteryx

 

Sexual selection may explain how certain characteristics (such as feathers) had distinct survival value at an early stage in their evolution. Geoffrey Miller proposes that sexual selection might have contributed by creating evolutionary modules such as Archaeopteryx feathers as sexual ornaments, at first. The earliest proto-birds such as China's Protarchaeopteryx, discovered in the early 1990s, had well-developed feathers but no sign of the top/bottom asymmetry that gives wings lift. Some have suggested that the feathers served as insulation, helping females incubate their eggs. But perhaps the feathers served as the kinds of sexual ornaments still common in most bird species, and especially in birds such as peacocks and birds-of-paradise today. If proto-bird courtship displays combined displays of forelimb feathers with energetic jumps, then the transition from display to aerodynamic functions could have been relatively smooth.

Sexual selection sometimes generates features that may help cause a species' extinction, as has been suggested for the giant antlers of the Irish elk (Megaloceros giganteus) that became extinct in Pleistocene Europe. However, sexual selection can also do the opposite, driving species divergence - sometimes through elaborate changes in genitalia - such that new species emerge.

Sexual dimorphism

Sex differences directly related to reproduction and serving no direct purpose in courtship are called primary sexual characteristics. Traits amenable to sexual selection, which give an organism an advantage over its rivals (such as in courtship) without being directly involved in reproduction, are called secondary sex characteristics. 

The rhinoceros beetle is a classic case of sexual dimorphism. Plate from Darwin's Descent of Man, male at top, female at bottom

 

In most sexual species the males and females have different equilibrium strategies, due to a difference in relative investment in producing offspring. As formulated in Bateman's principle, females have a greater initial investment in producing offspring (pregnancy in mammals or the production of the egg in birds and reptiles), and this difference in initial investment creates differences in variance in expected reproductive success and bootstraps the sexual selection processes. Classic examples of reversed sex-role species include the pipefish, and Wilson's phalarope. Also, unlike a female, a male (except in monogamous species) has some uncertainty about whether or not he is the true parent of a child, and so is less interested in spending his energy helping to raise offspring that may or may not be related to him. As a result of these factors, males are typically more willing to mate than females, and so females are typically the ones doing the choosing (except in cases of forced copulations, which can occur in certain species of primates, ducks, and others). The effects of sexual selection are thus held to typically be more pronounced in males than in females.

Differences in secondary sexual characteristics between males and females of a species are referred to as sexual dimorphisms. These can be as subtle as a size difference (sexual size dimorphism, often abbreviated as SSD) or as extreme as horns and colour patterns. Sexual dimorphisms abound in nature. Examples include the possession of antlers by only male deer, the brighter coloration of many male birds in comparison with females of the same species, or even more distinct differences in basic morphology, such as the drastically increased eye-span of the male stalk-eyed fly. The peacock, with its elaborate and colourful tail feathers, which the peahen lacks, is often referred to as perhaps the most extraordinary example of a dimorphism. Male and female black-throated blue warblers and Guianan cock-of-the-rocks also differ radically in their plumage. Early naturalists even believed the females to be a separate species. The largest sexual size dimorphism in vertebrates is the shell dwelling cichlid fish Neolamprologus callipterus in which males are up to 30 times the size of females. Many other fish such as guppies also exhibit sexual dimorphism. Extreme sexual size dimorphism, with females larger than males, is quite common in spiders and birds of prey.

The Role of Male-Male Competition in Sexual Selection

Male-male competition occurs when two males of the same species compete for the opportunity to mate with a female. Sexually dimorphic traits, size, sex ratio  and the social situation  may all play a role in the effects male-male competition has on the reproductive success of a male and the mate choice of a female.

Conditions that Influence Competition

Sex Ratio

Japanese medaka, Orzyas latipes.

 

There are multiple types of male-male competition that may occur in a population at different times depending on the conditions. Competition variation occurs based on the frequency of various mating behaviours present in the population. One factor that can influence the type of competition observed is the population density of males. When there is a high density of males present in the population, competition tends to be less aggressive and therefore sneak tactics and disruptions techniques are more often employed. These techniques often indicate a type of competition referred to as scramble competition. In Japanese medaka, Oryzias latipes, sneaking behaviours refer to when a male interrupts a mating pair during copulation by grasping on to either the male or the female and releasing their own sperm in the hopes of being the one to fertilize the female. Disruption is a technique which involves one male bumping the male that is copulating with the female away just before his sperm is released and the eggs are fertilized.

However, all techniques are not equally successful when in competition for reproductive success. Disruption results in a shorter copulation period and can therefore disrupt the fertilization of the eggs by the sperm, which frequently results in lower rates of fertilization and smaller clutch size.

Resource Value and Social Ranking

Another factor that can influence male-male competition is the value of the resource to competitors. Male-male competition can pose many risks to a male's fitness, such as high energy expenditure, physical injury, lower sperm quality and lost paternity. The risk of competition must therefore be worth the value of the resource. A male is more likely to engage in competition for a resource that improves their reproductive success if the resource value is higher. While male-male competition can occur in the presence or absence of a female, competition occurs more frequently in the presence of a female. The presence of a female directly increases the resource value of a territory or shelter and so the males are more likely to accept the risk of competition when a female is present. The smaller males of a species are also more likely to engage in competition with larger males in the presence of a female. Due to the higher level of risk for subordinate males, they tend to engage in competition less frequently than larger, more dominant males and therefore breed less frequently than dominant males. This is seen in many species, such as the Omei treefrog, Rhacophorus omeimontis, where larger males obtained more mating opportunities and successfully mated with larger mates. 

Winner-Loser Effects

A third factor that can impact the success of a male in competition is winner-loser effects. Burrowing crickets, velarifictorous aspersus, compete for burrows to attract females using their large mandibles for fighting.  Female burrowing crickets, are more likely to choose winner of a competition in the 2 hours after the fight. The presence winning male suppresses mating behaviours of the losing males because the winning male tends to produce more frequent and enhanced mating calls in this period of time.

Effect of Male-Male Competition on Female Fitness

Male-male competition can both positively and negatively affect female fitness. When there is a high density of males in a population and a large number of males attempting to mate with the female, she is more likely to resist mating attempts, resulting in lower fertilization rates. High levels of male-male competition can also result in a reduction in female investment in mating. Many forms of competition can also cause significant distress for the female negatively impacting her ability to reproduce. An increase in male-male competition can affect a females ability to select the best mates, and therefore decrease the likelihood of successful reproduction.

However, group mating in Japanese medaka has been shown to positively affect the fitness of females due to an increase in genetic variation, a higher likelihood of paternal care and a higher likelihood of successful fertilization.

Examples

A leaf-footed cactus bug, Narnia femorata.

 

In Japanese medaka, females mate daily during mating season. Males compete for the opportunity to mate with the female by displaying themselves aggressively and chasing each other. To obtain the selection of the females, they court the females prior to copulation by performing a courting behaviour referred to as "quick circles".

In leaf-footed cactus bugs, Narnia femorata, males compete for territories where females can lay their eggs. Males compete more intensely for cacti territories with fruit to attract females. In this species, the males possess sexually dimorphic traits, such as their larger size and hind legs, which are used to gain the most advantage over competitors when females are present, but are not used in the absence of females. 

Anuran (such as frogs) select habitats (pools) free of conspecifics in order to minimize male-male competition for both themselves and their offspring. Displays are used in attempt to keep competitors out of their territory and deter sneaking behaviours, while fighting is only used when necessary due to the high costs and risks associated with fighting.

In different taxa

SEM image of lateral view of a love dart of the land snail Monachoides vicinus. The scale bar is 500 μm (0.5 mm).

• Sexual selection in birds - mammals - humans -scaled reptiles - amphibians - insects - spiders - major histocompatibility complex

Human spermatozoa can reach 250 million in a single ejaculation

Sexual selection has been observed to occur in plants, animals and fungi. In certain hermaphroditic snail and slug species of molluscs the throwing of love darts is a form of sexual selection. Certain male insects of the lepidoptera order of insects cement the vaginal pores of their females.

A male bed bug (Cimex lectularius) traumatically inseminates a female bed bug (top). The female's ventral carapace is visibly cracked around the point of insemination.

 

Today, biologists say that certain evolutionary traits can be explained by intraspecific competition - competition between members of the same species - distinguishing between competition before or after sexual intercourse. 

Illustration from The Descent of Man showing the tufted coquette Lophornis ornatus: female on left, ornamented male on right

 

Before copulation, intrasexual selection - usually between males - may take the form of male-to-male combat. Also, intersexual selection, or mate choice, occurs when females choose between male mates. Traits selected by male combat are called secondary sexual characteristics (including horns, antlers, etc.), which Darwin described as "weapons", while traits selected by mate (usually female) choice are called "ornaments". Due to their sometimes greatly exaggerated nature, secondary sexual characteristics can prove to be a hindrance to an animal, thereby lowering its chances of survival. For example, the large antlers of a moose are bulky and heavy and slow the creature's flight from predators; they also can become entangled in low-hanging tree branches and shrubs, and undoubtedly have led to the demise of many individuals. Bright colourations and showy ornamenations, such as those seen in many male birds, in addition to capturing the eyes of females, also attract the attention of predators. Some of these traits also represent energetically costly investments for the animals that bear them. Because traits held to be due to sexual selection often conflict with the survival fitness of the individual, the question then arises as to why, in nature, in which survival of the fittest is considered the rule of thumb, such apparent liabilities are allowed to persist. However, one must also consider that intersexual selection can occur with an emphasis on resources that one sex possesses rather than morphological and physiological differences. For example, males of Euglossa imperialis, a non-social bee species, form aggregations of territories considered to be leks, to defend fragrant-rich primary territories. The purpose of these aggregations is only facultative, since the more suitable fragrant-rich sites there are, the more habitable territories there are to inhabit, giving females of this species a large selection of males with whom to potentially mate.

After copulation, male–male competition distinct from conventional aggression may take the form of sperm competition, as described by Parker in 1970. More recently, interest has arisen in cryptic female choice, a phenomenon of internally fertilised animals such as mammals and birds, where a female can get rid of a male's sperm without his knowledge.

Victorian cartoonists quickly picked up on Darwin's ideas about display in sexual selection. Here he is fascinated by the apparent steatopygia in the latest fashion.

 

Finally, sexual conflict is said to occur between breeding partners, sometimes leading to an evolutionary arms race between males and females. Sexual selection can also occur as a product of pheromone release, such as with the stingless bee, Trigona corvina.

Female mating preferences are widely recognized as being responsible for the rapid and divergent evolution of male secondary sexual traits. Females of many animal species prefer to mate with males with external ornaments - exaggerated features of morphology such as elaborate sex organs. These preferences may arise when an arbitrary female preference for some aspect of male morphology — initially, perhaps, a result of genetic drift — creates, in due course, selection for males with the appropriate ornament. One interpretation of this is known as the sexy son hypothesis. Alternatively, genes that enable males to develop impressive ornaments or fighting ability may simply show off greater disease resistance or a more efficient metabolism, features that also benefit females. This idea is known as the good genes hypothesis. 

Bright colors that develop in animals during mating season function to attract partners. It has been suggested that there is a causal link between strength of display of ornaments involved in sexual selection and free radical biology. To test this idea, experiments were performed on male painted dragon lizards. Male lizards are brightly conspicuous in their breeding coloration, but their color declines with aging. Experiments involving administration of antioxidants to these males led to the conclusion that breeding coloration is a reflection of innate anti-oxidation capacity that protects against oxidative damage, including oxidative DNA damage. Thus color could act as a “health certificate” that allows females to visualize the underlying oxidative stress induced damage in potential mates. 

Darwin conjectured that heritable traits such as beards and hairlessness in different human populations are results of sexual selection in humans. Geoffrey Miller has hypothesized that many human behaviours not clearly tied to survival benefits, such as humour, music, visual art, verbal creativity, and some forms of altruism, are courtship adaptations that have been favoured through sexual selection. In that view, many human artefacts could be considered subject to sexual selection as part of the extended phenotype, for instance clothing that enhances sexually selected traits. Some argue that the evolution of human intelligence is a sexually selected trait, as it would not confer enough fitness in itself relative to its high maintenance costs.

Fisherian runaway

From Wikipedia, the free encyclopedia

 

The peacock tail in flight, the classic example of an ornament assumed to be a Fisherian runaway

 

Fisherian runaway or runaway selection is a sexual selection mechanism proposed by the mathematical biologist Ronald Fisher in the early 20th century, to account for the evolution of exaggerated male ornamentation by persistent, directional female choice. An example is the colourful and elaborate peacock plumage compared to the relatively subdued peahen plumage; the costly ornaments, notably the bird's extremely long tail, appear to be incompatible with natural selection. Fisherian runaway can be postulated to include sexually dimorphic phenotypic traits such as behaviour expressed by either sex. 

Extreme and apparently maladaptive sexual dimorphism represented a paradox for evolutionary biologists from Charles Darwin's time up to the modern synthesis. Darwin attempted to resolve the paradox by assuming genetic bases for both the preference and the ornament, and supposed an "aesthetic sense" in higher animals, leading to powerful selection of both characteristics in subsequent generations. Fisher developed the theory further by assuming genetic correlation between the preference and the ornament, that initially the ornament signalled greater potential fitness (the likelihood of leaving more descendants), so preference for the ornament had a selective advantage. Subsequently, if strong enough, female preference for exaggerated ornamentation in mate selection could be enough to undermine natural selection even when the ornament has become non-adaptive. Over subsequent generations this could lead to runaway selection by positive feedback, and the speed with which the trait and the preference increase could (until counter-selection interferes) increase exponentially ("geometrically").

Fisherian runaway has been difficult to demonstrate empirically, because it has been difficult to detect both an underlying genetic mechanism and a process by which it is initiated.

History

Female (left) and male (right) pheasant, a sexually dimorphic species

 

Charles Darwin published a book on sexual selection in 1871 called The Descent of Man, and Selection in Relation to Sex, which garnered interest upon its release but by the 1880s the ideas had been deemed too controversial and were largely neglected. Alfred Russel Wallace disagreed with Darwin, particularly after Darwin's death, that sexual selection was a real phenomenon. R.A. Fisher was one of the few other biologists to engage with the question. When Wallace stated that animals show no sexual preference in his 1915 paper, The evolution of sexual preference, Fisher publicly disagreed:

The objection raised by Wallace ... that animals do not show any preference for their mates on account of their beauty, and in particular that female birds do not choose the males with the finest plumage, always seemed to the writer a weak one; partly from our necessary ignorance of the motives from which wild animals choose between a number of suitors; partly because there remains no satisfactory explanation either of the remarkable secondary sexual characters themselves, or of their careful display in love-dances, or of the evident interest aroused by these antics in the female; and partly also because this objection is apparently associated with the doctrine put forward by Sir Alfred Wallace in the same book, that the artistic faculties in man belong to his "spiritual nature," and therefore have come to him independently of his "animal nature" produced by natural selection.

Fisher, in the foundational 1930 book, The Genetical Theory of Natural Selection, first outlined a model by which runaway inter-sexual selection could lead to sexually dimorphic male ornamentation based upon female choice and a preference for "attractive" but otherwise non-adaptive traits in male mates. He suggested that selection for traits that increase fitness may be quite common:

[O]ccasions may not be infrequent when a sexual preference of a particular kind may confer a selective advantage, and therefore become established in the species. Whenever appreciable differences exist in a species, which are in fact correlated with selective advantage, there will be a tendency to select also those individuals of the opposite sex which most clearly discriminate the difference to be observed, and which most decidedly prefer the more advantageous type. Sexual preference originated in this way may or may not confer any direct advantage upon the individuals selected, and so hasten the effect of the Natural Selection in progress. It may therefore be far more widespread than the occurrence of striking secondary sexual characters.
Fisher, R.A. (1930) The Genetical Theory of Natural Selection. ISBN 0-19-850440-3

A strong female choice for the expression alone, as opposed to the function, of a male ornament can oppose and undermine the forces of natural selection and result in the runaway sexual selection that leads to the further exaggeration of the ornament (as well as the preference) until the costs (incurred by natural selection) of the expression become greater than the benefit (bestowed by sexual selection).

Peacocks and sexual dimorphism

The peacock, on the right, is courting the peahen, on the left.

 

The plumage dimorphism of the peacock and peahen of the species within the genus Pavo is a prime example of the ornamentation paradox that has long puzzled evolutionary biologists; Darwin wrote in 1860:

The sight of a feather in a peacock’s tail, whenever I gaze at it, makes me sick!

The peacock's colorful and elaborate tail requires a great deal of energy to grow and maintain. It also reduces the bird's agility, and may increase the animal's visibility to predators. The tail appears to lower the overall fitness of the individuals who possess it. Yet, it has evolved, indicating that peacocks with longer and more colorfully elaborate tails have some advantage over peacocks who don’t. Fisherian runaway posits that the evolution of the peacock tail is made possible if peahens have a preference to mate with peacocks that possess a longer and more colourful tail. Peahens that select males with these tails in turn have male offspring that are more likely to have long and colourful tails and thus are more likely to be sexually successful themselves. Equally importantly, the female offspring of these peahens are more likely to have a preference for peacocks with longer and more colourful tails. However, though the relative fitness of males with large tails is higher than those without, the absolute fitness levels of all the members of the population (both male and female) is less than it would be if none of the peahens (or only a small number) had a preference for a longer or more colorful tail.

Initiation

Fisher outlined two fundamental conditions that must be fulfilled in order for the Fisherian runaway mechanism to lead to the evolution of extreme ornamentation:

1. Sexual preference in at least one of the sexes
2. A corresponding reproductive advantage to the preference.

Fisher argued in his 1915 paper, "The evolution of sexual preference" that the type of female preference necessary for Fisherian runaway could be initiated without any understanding or appreciation for beauty. Fisher suggested that any visible features that indicate fitness, that are not themselves adaptive, that draw attention, and that vary in their appearance amongst the population of males so that the females can easily compare them, would be enough to initiate Fisherian runaway. This suggestion is compatible with his theory, and indicates that the choice of feature is essentially arbitrary, and could be different in different populations. Such arbitrariness is borne out by mathematical modelling, and by observation of isolated populations of sandgrouse, where the males can differ markedly from those in other populations.

Genetic basis

Fisherian runaway assumes that sexual preference in females and ornamentation in males are both genetically variable (heritable).

If instead of regarding the existence of sexual preference as a basic fact to be established only by direct observation, we consider that the tastes of organisms … be regarded as the products of evolutionary change, governed by the relative advantage which such tastes may confer. Whenever appreciable differences exist in a species … there will be a tendency to select also those individuals of the opposite sex which most clearly discriminate the difference to be observed, and which most decidedly prefer the more advantageous type.
Fisher, R.A. (1930) The Genetical Theory of Natural Selection. ISBN 0-19-850440-3

Female choice

Fisher argued that the selection for exaggerated male ornamentation is driven by the coupled exaggeration of female sexual preference for the ornament.

Certain remarkable consequences do, however, follow ... in a species in which the preferences of … the female, have a great influence on the number of offspring left by individual males. ... development will proceed, so long as the disadvantage is more than counterbalanced by the advantage in sexual selection … there will also be a net advantage in favour of giving to it a more decided preference.
Fisher, R.A. (1930) The Genetical Theory of Natural Selection. ISBN 0-19-850440-3

Positive feedback

Over time a positive feedback mechanism will see more exaggerated sons and choosier daughters being produced with each successive generation; resulting in the runaway selection for the further exaggeration of both the ornament and the preference (until the costs for producing the ornament outweigh the reproductive benefit of possessing it).

The two characteristics affected by such a process, namely [ornamental] development in the male, and sexual preference for such development in the female, must thus advance together, and … will advance with ever increasing speed. [I]t is easy to see that the speed of development will be proportional to the development already attained, which will therefore increase with time exponentially, or in a geometric progression.
Fisher, R.A. (1930) The Genetical Theory of Natural Selection. ISBN 0-19-850440-3

Such a process must soon run against some check. Two such are obvious. If carried far enough … counterselection in favour of less ornamented males will be encountered to balance the advantage of sexual preference; … elaboration and … female preference will be brought to a standstill, and a condition of relative stability will be attained. It will be more effective still if the disadvantage to the males of their sexual ornaments so diminishes their numbers surviving, relative to the females, as to cut at the root of the process, by demising the reproductive advantage to be conferred by female preference.
Fisher, R.A. (1930) The Genetical Theory of Natural Selection. ISBN 0-19-850440-3

Alternative hypotheses

Several alternative hypotheses use the same genetic runaway (or positive feedback) mechanism but differ in the mechanisms of the initiation. The sexy son hypothesis (also proposed by Fisher) suggests that females that choose desirably ornamented males will have desirably ornamented (or sexy) sons, and that the effect of that behaviour on spreading the female's genes through subsequent generations may outweigh other factors such as the level of parental investment by the father.

Indicator hypotheses suggest that females choose desirably ornamented males because the cost of producing the desirable ornaments is indicative of good genes by way of the individual's vigour. 

Other hypotheses for the evolution of male ornamentation include the sensory bias hypothesis, the compatibility hypothesis and the handicap principle.

Reliability engineering

From Wikipedia, the free encyclopedia

 
Reliability engineering is a sub-discipline of systems engineering that emphasizes dependability in the lifecycle management of a product. Dependability, or reliability, describes the ability of a system or component to function under stated conditions for a specified period of time. Reliability is closely related to availability, which is typically described as the ability of a component or system to function at a specified moment or interval of time.

Reliability is theoretically defined as the probability of success ${\displaystyle ({\text{Reliability}}=1-{\text{Probability of Failure}});}$ as the frequency of failures; or in terms of availability, as a probability derived from reliability, testability and maintainability. Testability, maintainability and maintenance are often defined as a part of "reliability engineering" in reliability programs. Reliability plays a key role in the cost-effectiveness of systems.

Reliability engineering deals with the estimation, prevention and management of high levels of "lifetime" engineering uncertainty and risks of failure. Although stochastic parameters define and affect reliability, reliability is not (solely) achieved by mathematics and statistics. One cannot really find a root cause (needed to effectively prevent failures) by only looking at statistics. "Nearly all teaching and literature on the subject emphasize these aspects, and ignore the reality that the ranges of uncertainty involved largely invalidate quantitative methods for prediction and measurement." For example, it is easy to represent "probability of failure" as a symbol or value in an equation, but it is almost impossible to predict its true magnitude in practice, which is massively multivariate, so having the equation for reliability does not begin to equal having an accurate predictive measurement of reliability.

Reliability engineering relates closely to safety engineering and to system safety, in that they use common methods for their analysis and may require input from each other. Reliability engineering focuses on costs of failure caused by system downtime, cost of spares, repair equipment, personnel, and cost of warranty claims. Safety engineering normally focuses more on preserving life and nature than on cost, and therefore deals only with particularly dangerous system-failure modes. High reliability (safety factor) levels also result from good engineering and from attention to detail, and almost never from only reactive failure management (using reliability accounting and statistics).

History

The word reliability can be traced back to 1816, and is first attested to the poet Samuel Taylor Coleridge. Before World War II the term was linked mostly to repeatability; a test (in any type of science) was considered "reliable" if the same results would be obtained repeatedly. In the 1920s, product improvement through the use of statistical process control was promoted by Dr. Walter A. Shewhart at Bell Labs, around the time that Waloddi Weibull was working on statistical models for fatigue. The development of reliability engineering was here on a parallel path with quality. The modern use of the word reliability was defined by the U.S. military in the 1940s, characterizing a product that would operate when expected and for a specified period of time.

In World War II, many reliability issues were due to the inherent unreliability of electronic equipment available at the time, and to fatigue issues. In 1945, M.A. Miner published the seminal paper titled "Cumulative Damage in Fatigue" in an ASME journal. A main application for reliability engineering in the military was for the vacuum tube as used in radar systems and other electronics, for which reliability proved to be very problematic and costly. The IEEE formed the Reliability Society in 1948. In 1950, the United States Department of Defense formed group called the "Advisory Group on the Reliability of Electronic Equipment" (AGREE) to investigate reliability methods for military equipment. This group recommended three main ways of working:

• Improve component reliability.
• Establish quality and reliability requirements for suppliers.
• Collect field data and find root causes of failures.

In the 1960s, more emphasis was given to reliability testing on component and system level. The famous military standard 781 was created at that time. Around this period also the much-used (and also much-debated) military handbook 217 was published by RCA and was used for the prediction of failure rates of components. The emphasis on component reliability and empirical research (e.g. Mil Std 217) alone slowly decreased. More pragmatic approaches, as used in the consumer industries, were being used. In the 1980s, televisions were increasingly made up of solid-state semiconductors. Automobiles rapidly increased their use of semiconductors with a variety of microcomputers under the hood and in the dash. Large air conditioning systems developed electronic controllers, as had microwave ovens and a variety of other appliances. Communications systems began to adopt electronics to replace older mechanical switching systems. Bellcore issued the first consumer prediction methodology for telecommunications, and SAE developed a similar document SAE870050 for automotive applications. The nature of predictions evolved during the decade, and it became apparent that die complexity wasn't the only factor that determined failure rates for integrated circuits (ICs). Kam Wong published a paper questioning the bathtub curve—see also reliability-centered maintenance. During this decade, the failure rate of many components dropped by a factor of 10. Software became important to the reliability of systems. By the 1990s, the pace of IC development was picking up. Wider use of stand-alone microcomputers was common, and the PC market helped keep IC densities following Moore's law and doubling about every 18 months. Reliability engineering was now changing as it moved towards understanding the physics of failure. Failure rates for components kept dropping, but system-level issues became more prominent. Systems thinking became more and more important. For software, the CMM model (Capability Maturity Model) was developed, which gave a more qualitative approach to reliability. ISO 9000 added reliability measures as part of the design and development portion of certification. The expansion of the World-Wide Web created new challenges of security and trust. The older problem of too little reliability information available had now been replaced by too much information of questionable value. Consumer reliability problems could now be discussed online in real time using data. New technologies such as micro-electromechanical systems (MEMS), handheld GPS, and hand-held devices that combined cell phones and computers all represent challenges to maintain reliability. Product development time continued to shorten through this decade and what had been done in three years was being done in 18 months. This meant that reliability tools and tasks had to be more closely tied to the development process itself. In many ways, reliability became part of everyday life and consumer expectations.

Overview

Objective

The objectives of reliability engineering, in decreasing order of priority, are:

1. To apply engineering knowledge and specialist techniques to prevent or to reduce the likelihood or frequency of failures.
2. To identify and correct the causes of failures that do occur despite the efforts to prevent them.
3. To determine ways of coping with failures that do occur, if their causes have not been corrected.
4. To apply methods for estimating the likely reliability of new designs, and for analysing reliability data.

The reason for the priority emphasis is that it is by far the most effective way of working, in terms of minimizing costs and generating reliable products. The primary skills that are required, therefore, are the ability to understand and anticipate the possible causes of failures, and knowledge of how to prevent them. It is also necessary to have knowledge of the methods that can be used for analysing designs and data.

Scope and techniques

Reliability engineering for "complex systems" requires a different, more elaborate systems approach than for non-complex systems. Reliability engineering may in that case involve:

• System availability and mission readiness analysis and related reliability and maintenance requirement allocation
• Functional system failure analysis and derived requirements specification
• Inherent (system) design reliability analysis and derived requirements specification for both hardware and software design
• System diagnostics design
• Fault tolerant systems (e.g. by redundancy)
• Predictive and preventive maintenance (e.g. reliability-centered maintenance)
• Human factors / human interaction / human errors
• Manufacturing- and assembly-induced failures (effect on the detected "0-hour quality" and reliability)
• Maintenance-induced failures
• Transport-induced failures
• Storage-induced failures
• Use (load) studies, component stress analysis, and derived requirements specification
• Software (systematic) failures
• Failure / reliability testing (and derived requirements)
• Field failure monitoring and corrective actions
• Spare parts stocking (availability control)
• Technical documentation, caution and warning analysis
• Data and information acquisition/organisation (creation of a general reliability development hazard log and FRACAS system)
• Chaos engineering

Effective reliability engineering requires understanding of the basics of failure mechanisms for which experience, broad engineering skills and good knowledge from many different special fields of engineering are required, for example:

• Tribology
• Stress (mechanics)
• Fracture mechanics / fatigue
• Thermal engineering
• Fluid mechanics / shock-loading engineering
• Electrical engineering
• Chemical engineering (e.g. corrosion)
• Material science

Definitions

Reliability may be defined in the following ways:

• The idea that an item is fit for a purpose with respect to time
• The capacity of a designed, produced, or maintained item to perform as required over time
• The capacity of a population of designed, produced or maintained items to perform as required over specified time
• The resistance to failure of an item over time
• The probability of an item to perform a required function under stated conditions for a specified period of time
• The durability of an object

Basics of a reliability assessment

Many engineering techniques are used in reliability risk assessments, such as reliability hazard analysis, failure mode and effects analysis (FMEA), fault tree analysis (FTA), Reliability Centered Maintenance, (probabilistic) load and material stress and wear calculations, (probabilistic) fatigue and creep analysis, human error analysis, manufacturing defect analysis, reliability testing, etc. It is crucial that these analyses are done properly and with much attention to detail to be effective. Because of the large number of reliability techniques, their expense, and the varying degrees of reliability required for different situations, most projects develop a reliability program plan to specify the reliability tasks (statement of work (SoW) requirements) that will be performed for that specific system.

Consistent with the creation of a safety cases, for example ARP4761, the goal of reliability assessments is to provide a robust set of qualitative and quantitative evidence that use of a component or system will not be associated with unacceptable risk. The basic steps to take are to:

• Thoroughly identify relevant unreliability "hazards", e.g. potential conditions, events, human errors, failure modes, interactions, failure mechanisms and root causes, by specific analysis or tests.
• Assess the associated system risk, by specific analysis or testing.
• Propose mitigation, e.g. requirements, design changes, detection logic, maintenance, training, by which the risks may be lowered and controlled for at an acceptable level.
• Determine the best mitigation and get agreement on final, acceptable risk levels, possibly based on cost/benefit analysis.

Risk here is the combination of probability and severity of the failure incident (scenario) occurring.

In a de minimis definition, severity of failures includes the cost of spare parts, man-hours, logistics, damage (secondary failures), and downtime of machines which may cause production loss. A more complete definition of failure also can mean injury, dismemberment, and death of people within the system (witness mine accidents, industrial accidents, space shuttle failures) and the same to innocent bystanders (witness the citizenry of cities like Bhopal, Love Canal, Chernobyl, or Sendai, and other victims of the 2011 Tōhoku earthquake and tsunami)—in this case, reliability engineering becomes system safety. What is acceptable is determined by the managing authority or customers or the affected communities. Residual risk is the risk that is left over after all reliability activities have finished, and includes the unidentified risk—and is therefore not completely quantifiable. 

Risk vs cost/complexity

 

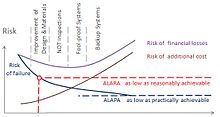
The complexity of the technical systems such as improvements of design and materials, planned inspections, fool-proof design, and backup redundancy decreases risk and increases the cost. The risk can be decreased to ALARA (as low as reasonably achievable) or ALAPA (as low as practically achievable) levels.

Reliability and availability program plan

Implementing a reliability program is not simply a software purchase; it is not just a checklist of items that must be completed that will ensure one has reliable products and processes. A reliability program is a complex learning and knowledge-based system unique to one's products and processes. It is supported by leadership, built on the skills that one develops within a team, integrated into business processes and executed by following proven standard work practices.

A reliability program plan is used to document exactly what "best practices" (tasks, methods, tools, analysis, and tests) are required for a particular (sub)system, as well as clarify customer requirements for reliability assessment. For large-scale complex systems, the reliability program plan should be a separate document. Resource determination for manpower and budgets for testing and other tasks is critical for a successful program. In general, the amount of work required for an effective program for complex systems is large.

A reliability program plan is essential for achieving high levels of reliability, testability, maintainability, and the resulting system availability, and is developed early during system development and refined over the system's life-cycle. It specifies not only what the reliability engineer does, but also the tasks performed by other stakeholders. A reliability program plan is approved by top program management, which is responsible for allocation of sufficient resources for its implementation. 

A reliability program plan may also be used to evaluate and improve the availability of a system by the strategy of focusing on increasing testability & maintainability and not on reliability. Improving maintainability is generally easier than improving reliability. Maintainability estimates (repair rates) are also generally more accurate. However, because the uncertainties in the reliability estimates are in most cases very large, they are likely to dominate the availability calculation (prediction uncertainty problem), even when maintainability levels are very high. When reliability is not under control, more complicated issues may arise, like manpower (maintainers / customer service capability) shortages, spare part availability, logistic delays, lack of repair facilities, extensive retro-fit and complex configuration management costs, and others. The problem of unreliability may be increased also due to the "domino effect" of maintenance-induced failures after repairs. Focusing only on maintainability is therefore not enough. If failures are prevented, none of the other issues are of any importance, and therefore reliability is generally regarded as the most important part of availability. Reliability needs to be evaluated and improved related to both availability and the total cost of ownership (TCO) due to cost of spare parts, maintenance man-hours, transport costs, storage cost, part obsolete risks, etc. But, as GM and Toyota have belatedly discovered, TCO also includes the downstream liability costs when reliability calculations have not sufficiently or accurately addressed customers' personal bodily risks. Often a trade-off is needed between the two. There might be a maximum ratio between availability and cost of ownership. Testability of a system should also be addressed in the plan, as this is the link between reliability and maintainability. The maintenance strategy can influence the reliability of a system (e.g., by preventive and/or predictive maintenance), although it can never bring it above the inherent reliability.

The reliability plan should clearly provide a strategy for availability control. Whether only availability or also cost of ownership is more important depends on the use of the system. For example, a system that is a critical link in a production system—e.g., a big oil platform—is normally allowed to have a very high cost of ownership if that cost translates to even a minor increase in availability, as the unavailability of the platform results in a massive loss of revenue which can easily exceed the high cost of ownership. A proper reliability plan should always address RAMT analysis in its total context. RAMT stands for reliability, availability, maintainability/maintenance, and testability in the context of the customer's needs.

Reliability requirements

For any system, one of the first tasks of reliability engineering is to adequately specify the reliability and maintainability requirements allocated from the overall availability needs and, more importantly, derived from proper design failure analysis or preliminary prototype test results. Clear requirements (able to designed to) should constrain the designers from designing particular unreliable items / constructions / interfaces / systems. Setting only availability, reliability, testability, or maintainability targets (e.g., max. failure rates) is not appropriate. This is a broad misunderstanding about Reliability Requirements Engineering. Reliability requirements address the system itself, including test and assessment requirements, and associated tasks and documentation. Reliability requirements are included in the appropriate system or subsystem requirements specifications, test plans, and contract statements. Creation of proper lower-level requirements is critical. Provision of only quantitative minimum targets (e.g., MTBF values or failure rates) is not sufficient for different reasons. One reason is that a full validation (related to correctness and verifiability in time) of a quantitative reliability allocation (requirement spec) on lower levels for complex systems can (often) not be made as a consequence of (1) the fact that the requirements are probabilistic, (2) the extremely high level of uncertainties involved for showing compliance with all these probabilistic requirements, and because (3) reliability is a function of time, and accurate estimates of a (probabilistic) reliability number per item are available only very late in the project, sometimes even after many years of in-service use. Compare this problem with the continuous (re-)balancing of, for example, lower-level-system mass requirements in the development of an aircraft, which is already often a big undertaking. Notice that in this case, masses do only differ in terms of only some %, are not a function of time, the data is non-probabilistic and available already in CAD models. In case of reliability, the levels of unreliability (failure rates) may change with factors of decades (multiples of 10) as result of very minor deviations in design, process, or anything else. The information is often not available without huge uncertainties within the development phase. This makes this allocation problem almost impossible to do in a useful, practical, valid manner that does not result in massive over- or under-specification. A pragmatic approach is therefore needed—for example: the use of general levels / classes of quantitative requirements depending only on severity of failure effects. Also, the validation of results is a far more subjective task than for any other type of requirement. (Quantitative) reliability parameters—in terms of MTBF—are by far the most uncertain design parameters in any design. 

Furthermore, reliability design requirements should drive a (system or part) design to incorporate features that prevent failures from occurring, or limit consequences from failure in the first place. Not only would it aid in some predictions, this effort would keep from distracting the engineering effort into a kind of accounting work. A design requirement should be precise enough so that a designer can "design to" it and can also prove—through analysis or testing—that the requirement has been achieved, and, if possible, within some a stated confidence. Any type of reliability requirement should be detailed and could be derived from failure analysis (Finite-Element Stress and Fatigue analysis, Reliability Hazard Analysis, FTA, FMEA, Human Factor Analysis, Functional Hazard Analysis, etc.) or any type of reliability testing. Also, requirements are needed for verification tests (e.g., required overload stresses) and test time needed. To derive these requirements in an effective manner, a systems engineering-based risk assessment and mitigation logic should be used. Robust hazard log systems must be created that contain detailed information on why and how systems could or have failed. Requirements are to be derived and tracked in this way. These practical design requirements shall drive the design and not be used only for verification purposes. These requirements (often design constraints) are in this way derived from failure analysis or preliminary tests. Understanding of this difference compared to only purely quantitative (logistic) requirement specification (e.g., Failure Rate / MTBF target) is paramount in the development of successful (complex) systems.

The maintainability requirements address the costs of repairs as well as repair time. Testability (not to be confused with test requirements) requirements provide the link between reliability and maintainability and should address detectability of failure modes (on a particular system level), isolation levels, and the creation of diagnostics (procedures). As indicated above, reliability engineers should also address requirements for various reliability tasks and documentation during system development, testing, production, and operation. These requirements are generally specified in the contract statement of work and depend on how much leeway the customer wishes to provide to the contractor. Reliability tasks include various analyses, planning, and failure reporting. Task selection depends on the criticality of the system as well as cost. A safety-critical system may require a formal failure reporting and review process throughout development, whereas a non-critical system may rely on final test reports. The most common reliability program tasks are documented in reliability program standards, such as MIL-STD-785 and IEEE 1332. Failure reporting analysis and corrective action systems are a common approach for product/process reliability monitoring.

Reliability culture / human errors / human factors

In practice, most failures can be traced back to some type of human error, for example in:

• Management decisions (e.g. in budgeting, timing, and required tasks)
• Systems Engineering: Use studies (load cases)
• Systems Engineering: Requirement analysis / setting
• Systems Engineering: Configuration control
• Assumptions
• Calculations / simulations / FEM analysis
• Design
• Design drawings
• Testing (e.g. incorrect load settings or failure measurement)
• Statistical analysis
• Manufacturing
• Quality control
• Maintenance
• Maintenance manuals
• Training
• Classifying and ordering of information
• Feedback of field information (e.g. incorrect or too vague)
• etc.

However, humans are also very good at detecting such failures, correcting for them, and improvising when abnormal situations occur. Therefore, policies that completely rule out human actions in design and production processes to improve reliability may not be effective. Some tasks are better performed by humans and some are better performed by machines.

Furthermore, human errors in management; the organization of data and information; or the misuse or abuse of items, may also contribute to unreliability. This is the core reason why high levels of reliability for complex systems can only be achieved by following a robust systems engineering process with proper planning and execution of the validation and verification tasks. This also includes careful organization of data and information sharing and creating a "reliability culture", in the same way that having a "safety culture" is paramount in the development of safety critical systems.

Reliability prediction and improvement

Reliability prediction combines:

• creation of a proper reliability model (see further on this page)
• estimation (and justification) of input parameters for this model (e.g. failure rates for a particular failure mode or event and the mean time to repair the system for a particular failure)
• estimation of output reliability parameters at system or part level (i.e. system availability or frequency of a particular functional failure) The emphasis on quantification and target setting (e.g. MTBF) might imply there is a limit to achievable reliability, however, there is no inherent limit and development of higher reliability does not need to be more costly. In addition, they argue that prediction of reliability from historic data can be very misleading, with comparisons only valid for identical designs, products, manufacturing processes, and maintenance with identical operating loads and usage environments. Even minor changes in any of these could have major effects on reliability. Furthermore, the most unreliable and important items (i.e. the most interesting candidates for a reliability investigation) are most likely to be modified and re-engineered since historical data was gathered, making the standard (re-active or pro-active) statistical methods and processes used in e.g. medical or insurance industries less effective. Another surprising — but logical — argument is that to be able to accurately predict reliability by testing, the exact mechanisms of failure must be known and therefore — in most cases — could be prevented! Following the incorrect route of trying to quantify and solve a complex reliability engineering problem in terms of MTBF or probability using an-incorrect – for example, the re-active – approach is referred to by Barnard as "Playing the Numbers Game" and is regarded as bad practice.

For existing systems, it is arguable that any attempt by a responsible program to correct the root cause of discovered failures may render the initial MTBF estimate invalid, as new assumptions (themselves subject to high error levels) of the effect of this correction must be made. Another practical issue is the general unavailability of detailed failure data, with those available often featuring inconsistent filtering of failure (feedback) data, and ignoring statistical errors (which are very high for rare events like reliability related failures). Very clear guidelines must be present to count and compare failures related to different type of root-causes (e.g. manufacturing-, maintenance-, transport-, system-induced or inherent design failures). Comparing different types of causes may lead to incorrect estimations and incorrect business decisions about the focus of improvement.

To perform a proper quantitative reliability prediction for systems may be difficult and very expensive if done by testing. At the individual part-level, reliability results can often be obtained with comparatively high confidence, as testing of many sample parts might be possible using the available testing budget. However, unfortunately these tests may lack validity at a system-level due to assumptions made at part-level testing. These authors emphasized the importance of initial part- or system-level testing until failure, and to learn from such failures to improve the system or part. The general conclusion is drawn that an accurate and absolute prediction — by either field-data comparison or testing — of reliability is in most cases not possible. An exception might be failures due to wear-out problems such as fatigue failures. In the introduction of MIL-STD-785 it is written that reliability prediction should be used with great caution, if not used solely for comparison in trade-off studies.

Design for reliability

Design for Reliability (DfR) is a process that encompasses tools and procedures to ensure that a product meets its reliability requirements, under its use environment, for the duration of its lifetime. DfR is implemented in the design stage of a product to proactively improve product reliability. DfR is often used as part of an overall Design for Excellence (DfX) strategy.

Statistics-based approach (i.e. MTBF)

Reliability design begins with the development of a (system) model. Reliability and availability models use block diagrams and Fault Tree Analysis to provide a graphical means of evaluating the relationships between different parts of the system. These models may incorporate predictions based on failure rates taken from historical data. While the (input data) predictions are often not accurate in an absolute sense, they are valuable to assess relative differences in design alternatives. Maintainability parameters, for example Mean time to repair (MTTR), can also be used as inputs for such models. 

The most important fundamental initiating causes and failure mechanisms are to be identified and analyzed with engineering tools. A diverse set of practical guidance as to performance and reliability should be provided to designers so that they can generate low-stressed designs and products that protect, or are protected against, damage and excessive wear. Proper validation of input loads (requirements) may be needed, in addition to verification for reliability "performance" by testing. 

A fault tree diagram

 

One of the most important design techniques is redundancy. This means that if one part of the system fails, there is an alternate success path, such as a backup system. The reason why this is the ultimate design choice is related to the fact that high-confidence reliability evidence for new parts or systems is often not available, or is extremely expensive to obtain. By combining redundancy, together with a high level of failure monitoring, and the avoidance of common cause failures; even a system with relatively poor single-channel (part) reliability, can be made highly reliable at a system level (up to mission critical reliability). No testing of reliability has to be required for this. In conjunction with redundancy, the use of dissimilar designs or manufacturing processes (e.g. via different suppliers of similar parts) for single independent channels, can provide less sensitivity to quality issues (e.g. early childhood failures at a single supplier), allowing very-high levels of reliability to be achieved at all moments of the development cycle (from early life to long-term). Redundancy can also be applied in systems engineering by double checking requirements, data, designs, calculations, software, and tests to overcome systematic failures.

Another effective way to deal with reliability issues is to perform analysis that predicts degradation, enabling the prevention of unscheduled downtime events / failures. RCM (Reliability Centered Maintenance) programs can be used for this.

Physics-of-failure-based approach

For electronic assemblies, there has been an increasing shift towards a different approach called physics of failure. This technique relies on understanding the physical static and dynamic failure mechanisms. It accounts for variation in load, strength, and stress that lead to failure with a high level of detail, made possible with the use of modern finite element method (FEM) software programs that can handle complex geometries and mechanisms such as creep, stress relaxation, fatigue, and probabilistic design (Monte Carlo Methods/DOE). The material or component can be re-designed to reduce the probability of failure and to make it more robust against such variations. Another common design technique is component derating: i.e. selecting components whose specifications significantly exceed the expected stress levels, such as using heavier gauge electrical wire than might normally be specified for the expected electric current.

Common tools and techniques

Many of the tasks, techniques, and analyses used in Reliability Engineering are specific to particular industries and applications, but can commonly include:

• Physics of failure (PoF)
• Built-in self-test (BIT) (testability analysis)
• Failure mode and effects analysis (FMEA)
• Reliability hazard analysis
• Reliability block-diagram analysis
• Dynamic reliability block-diagram analysis
• Fault tree analysis
• Root cause analysis
• Statistical engineering, design of experiments – e.g. on simulations / FEM models or with testing
• Sneak circuit analysis
• Accelerated testing
• Reliability growth analysis (re-active reliability)
• Weibull analysis (for testing or mainly "re-active" reliability)
• Thermal analysis by finite element analysis (FEA) and / or measurement
• Thermal induced, shock and vibration fatigue analysis by FEA and / or measurement
• Electromagnetic analysis
• Avoidance of single point of failure (SPOF)
• Functional analysis and functional failure analysis (e.g., function FMEA, FHA or FFA)
• Predictive and preventive maintenance: reliability centered maintenance (RCM) analysis
• Testability analysis
• Failure diagnostics analysis (normally also incorporated in FMEA)
• Human error analysis
• Operational hazard analysis
• Preventative/Planned Maintenance Optimization (PMO)
• Manual screening
• Integrated logistics support

Results from these methods are presented during reviews of part or system design, and logistics. Reliability is just one requirement among many for a complex part or system. Engineering trade-off studies are used to determine the optimum balance between reliability requirements and other constraints.

The importance of language

Reliability engineers, whether using quantitative or qualitative methods to describe a failure or hazard, rely on language to pinpoint the risks and enable issues to be solved. The language used must help create an orderly description of the function/item/system and its complex surrounding as it relates to the failure of these functions/items/systems. Systems engineering is very much about finding the correct words to describe the problem (and related risks), so that they can be readily solved via engineering solutions. Jack Ring said that a systems engineer's job is to "language the project." (Ring et al. 2000) For part/system failures, reliability engineers should concentrate more on the "why and how", rather that predicting "when". Understanding "why" a failure has occurred (e.g. due to over-stressed components or manufacturing issues) is far more likely to lead to improvement in the designs and processes used  than quantifying "when" a failure is likely to occur (e.g. via determining MTBF). To do this, first the reliability hazards relating to the part/system need to be classified and ordered (based on some form of qualitative and quantitative logic if possible) to allow for more efficient assessment and eventual improvement. This is partly done in pure language and proposition logic, but also based on experience with similar items. This can for example be seen in descriptions of events in fault tree analysis, FMEA analysis, and hazard (tracking) logs. In this sense language and proper grammar (part of qualitative analysis) plays an important role in reliability engineering, just like it does in safety engineering or in-general within systems engineering.

Correct use of language can also be key to identifying or reducing the risks of human error, which are often the root cause of many failures. This can include proper instructions in maintenance manuals, operation manuals, emergency procedures, and others to prevent systematic human errors that may result in system failures. These should be written by trained or experienced technical authors using so-called simplified English or Simplified Technical English, where words and structure are specifically chosen and created so as to reduce ambiguity or risk of confusion (e.g. an "replace the old part" could ambiguously refer to a swapping a worn-out part with a non worn-out part, or replacing a part with one using a more recent and hopefully improved design).

Reliability modeling

Reliability modeling is the process of predicting or understanding the reliability of a component or system prior to its implementation. Two types of analysis that are often used to model a complete system's availability behavior (including effects from logistics issues like spare part provisioning, transport and manpower) are Fault Tree Analysis and reliability block diagrams. At a component level, the same types of analyses can be used together with others. The input for the models can come from many sources including testing; prior operational experience; field data; as well as data handbooks from similar or related industries. Regardless of source, all model input data must be used with great caution, as predictions are only valid in cases where the same product was used in the same context. As such, predictions are often only used to help compare alternatives. 

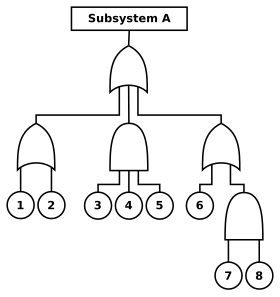
A reliability block diagram showing a "1oo3" (1 out of 3) redundant designed subsystem

For part level predictions, two separate fields of investigation are common:

• The physics of failure approach uses an understanding of physical failure mechanisms involved, such as mechanical crack propagation or chemical corrosion degradation or failure;
• The parts stress modeling approach is an empirical method for prediction based on counting the number and type of components of the system, and the stress they undergo during operation.

Software reliability is a more challenging area that must be considered when computer code provides a considerable component of a system's functionality.

Reliability theory

Reliability is defined as the probability that a device will perform its intended function during a specified period of time under stated conditions. Mathematically, this may be expressed as,

${\displaystyle R(t)=Pr\{T>t\}=\int _{t}^{\infty }f(x)\,dx\ \!}$,

where ${\displaystyle f(x)\!}$ is the failure probability density function and ${\displaystyle t}$ is the length of the period of time (which is assumed to start from time zero). 

There are a few key elements of this definition:

1. Reliability is predicated on "intended function:" Generally, this is taken to mean operation without failure. However, even if no individual part of the system fails, but the system as a whole does not do what was intended, then it is still charged against the system reliability. The system requirements specification is the criterion against which reliability is measured.
2. Reliability applies to a specified period of time. In practical terms, this means that a system has a specified chance that it will operate without failure before time ${\displaystyle t\!}$. Reliability engineering ensures that components and materials will meet the requirements during the specified time. Note that units other than time may sometimes be used (e.g. "a mission", "operation cycles").
3. Reliability is restricted to operation under stated (or explicitly defined) conditions. This constraint is necessary because it is impossible to design a system for unlimited conditions. A Mars Rover will have different specified conditions than a family car. The operating environment must be addressed during design and testing. That same rover may be required to operate in varying conditions requiring additional scrutiny.
4. Two notable references on reliability theory and its mathematical and statistical foundations are Barlow, R. E. and Proschan, F. (1982) and Samaniego, F. J. (2007).

Quantitative system reliability parameters—theory

Quantitative requirements are specified using reliability parameters. The most common reliability parameter is the mean time to failure (MTTF), which can also be specified as the failure rate (this is expressed as a frequency or conditional probability density function (PDF)) or the number of failures during a given period. These parameters may be useful for higher system levels and systems that are operated frequently (i.e. vehicles, machinery, and electronic equipment). Reliability increases as the MTTF increases. The MTTF is usually specified in hours, but can also be used with other units of measurement, such as miles or cycles. Using MTTF values on lower system levels can be very misleading, especially if they do not specify the associated Failures Modes and Mechanisms (The F in MTTF).

In other cases, reliability is specified as the probability of mission success. For example, reliability of a scheduled aircraft flight can be specified as a dimensionless probability or a percentage, as often used in system safety engineering.

A special case of mission success is the single-shot device or system. These are devices or systems that remain relatively dormant and only operate once. Examples include automobile airbags, thermal batteries and missiles. Single-shot reliability is specified as a probability of one-time success or is subsumed into a related parameter. Single-shot missile reliability may be specified as a requirement for the probability of a hit. For such systems, the probability of failure on demand (PFD) is the reliability measure — this is actually an "unavailability" number. The PFD is derived from failure rate (a frequency of occurrence) and mission time for non-repairable systems.

For repairable systems, it is obtained from failure rate, mean-time-to-repair (MTTR), and test interval. This measure may not be unique for a given system as this measure depends on the kind of demand. In addition to system level requirements, reliability requirements may be specified for critical subsystems. In most cases, reliability parameters are specified with appropriate statistical confidence intervals.

Reliability testing

The purpose of reliability testing is to discover potential problems with the design as early as possible and, ultimately, provide confidence that the system meets its reliability requirements. 

Reliability testing may be performed at several levels and there are different types of testing. Complex systems may be tested at component, circuit board, unit, assembly, subsystem and system levels. (The test level nomenclature varies among applications.) For example, performing environmental stress screening tests at lower levels, such as piece parts or small assemblies, catches problems before they cause failures at higher levels. Testing proceeds during each level of integration through full-up system testing, developmental testing, and operational testing, thereby reducing program risk. However, testing does not mitigate unreliability risk. 

With each test both a statistical type 1 and type 2 error could be made and depends on sample size, test time, assumptions and the needed discrimination ratio. There is risk of incorrectly accepting a bad design (type 1 error) and the risk of incorrectly rejecting a good design (type 2 error).

It is not always feasible to test all system requirements. Some systems are prohibitively expensive to test; some failure modes may take years to observe; some complex interactions result in a huge number of possible test cases; and some tests require the use of limited test ranges or other resources. In such cases, different approaches to testing can be used, such as (highly) accelerated life testing, design of experiments, and simulations. 

The desired level of statistical confidence also plays a role in reliability testing. Statistical confidence is increased by increasing either the test time or the number of items tested. Reliability test plans are designed to achieve the specified reliability at the specified confidence level with the minimum number of test units and test time. Different test plans result in different levels of risk to the producer and consumer. The desired reliability, statistical confidence, and risk levels for each side influence the ultimate test plan. The customer and developer should agree in advance on how reliability requirements will be tested.

A key aspect of reliability testing is to define "failure". Although this may seem obvious, there are many situations where it is not clear whether a failure is really the fault of the system. Variations in test conditions, operator differences, weather and unexpected situations create differences between the customer and the system developer. One strategy to address this issue is to use a scoring conference process. A scoring conference includes representatives from the customer, the developer, the test organization, the reliability organization, and sometimes independent observers. The scoring conference process is defined in the statement of work. Each test case is considered by the group and "scored" as a success or failure. This scoring is the official result used by the reliability engineer.

As part of the requirements phase, the reliability engineer develops a test strategy with the customer. The test strategy makes trade-offs between the needs of the reliability organization, which wants as much data as possible, and constraints such as cost, schedule and available resources. Test plans and procedures are developed for each reliability test, and results are documented.

Reliability testing is common in the Photonics industry. Examples of reliability tests of lasers are life test and burn-in. These tests consist of the highly accelerated aging, under controlled conditions, of a group of lasers. The data collected from these life tests are used to predict laser life expectancy under the intended operating characteristics.

Reliability test requirements

Reliability test requirements can follow from any analysis for which the first estimate of failure probability, failure mode or effect needs to be justified. Evidence can be generated with some level of confidence by testing. With software-based systems, the probability is a mix of software and hardware-based failures. Testing reliability requirements is problematic for several reasons. A single test is in most cases insufficient to generate enough statistical data. Multiple tests or long-duration tests are usually very expensive. Some tests are simply impractical, and environmental conditions can be hard to predict over a systems life-cycle. 

Reliability engineering is used to design a realistic and affordable test program that provides empirical evidence that the system meets its reliability requirements. Statistical confidence levels are used to address some of these concerns. A certain parameter is expressed along with a corresponding confidence level: for example, an MTBF of 1000 hours at 90% confidence level. From this specification, the reliability engineer can, for example, design a test with explicit criteria for the number of hours and number of failures until the requirement is met or failed. Different sorts of tests are possible. 

The combination of required reliability level and required confidence level greatly affects the development cost and the risk to both the customer and producer. Care is needed to select the best combination of requirements—e.g. cost-effectiveness. Reliability testing may be performed at various levels, such as component, subsystem and system. Also, many factors must be addressed during testing and operation, such as extreme temperature and humidity, shock, vibration, or other environmental factors (like loss of signal, cooling or power; or other catastrophes such as fire, floods, excessive heat, physical or security violations or other myriad forms of damage or degradation). For systems that must last many years, accelerated life tests may be needed.

Accelerated testing

The purpose of accelerated life testing (ALT test) is to induce field failure in the laboratory at a much faster rate by providing a harsher, but nonetheless representative, environment. In such a test, the product is expected to fail in the lab just as it would have failed in the field—but in much less time. The main objective of an accelerated test is either of the following:

• To discover failure modes
• To predict the normal field life from the high stress lab life

An Accelerated testing program can be broken down into the following steps:

• Define objective and scope of the test
• Collect required information about the product
• Identify the stress(es)
• Determine level of stress(es)
• Conduct the accelerated test and analyze the collected data.

Common ways to determine a life stress relationship are:

• Arrhenius model
• Eyring model
• Inverse power law model
• Temperature–humidity model
• Temperature non-thermal model

Software reliability

Software reliability is a special aspect of reliability engineering. System reliability, by definition, includes all parts of the system, including hardware, software, supporting infrastructure (including critical external interfaces), operators and procedures. Traditionally, reliability engineering focuses on critical hardware parts of the system. Since the widespread use of digital integrated circuit technology, software has become an increasingly critical part of most electronics and, hence, nearly all present day systems.

There are significant differences, however, in how software and hardware behave. Most hardware unreliability is the result of a component or material failure that results in the system not performing its intended function. Repairing or replacing the hardware component restores the system to its original operating state. However, software does not fail in the same sense that hardware fails. Instead, software unreliability is the result of unanticipated results of software operations. Even relatively small software programs can have astronomically large combinations of inputs and states that are infeasible to exhaustively test. Restoring software to its original state only works until the same combination of inputs and states results in the same unintended result. Software reliability engineering must take this into account.

Despite this difference in the source of failure between software and hardware, several software reliability models based on statistics have been proposed to quantify what we experience with software: the longer software is run, the higher the probability that it will eventually be used in an untested manner and exhibit a latent defect that results in a failure (Shooman 1987), (Musa 2005), (Denney 2005).

As with hardware, software reliability depends on good requirements, design and implementation. Software reliability engineering relies heavily on a disciplined software engineering process to anticipate and design against unintended consequences. There is more overlap between software quality engineering and software reliability engineering than between hardware quality and reliability. A good software development plan is a key aspect of the software reliability program. The software development plan describes the design and coding standards, peer reviews, unit tests, configuration management, software metrics and software models to be used during software development. 

A common reliability metric is the number of software faults, usually expressed as faults per thousand lines of code. This metric, along with software execution time, is key to most software reliability models and estimates. The theory is that the software reliability increases as the number of faults (or fault density) decreases or goes down. Establishing a direct connection between fault density and mean-time-between-failure is difficult, however, because of the way software faults are distributed in the code, their severity, and the probability of the combination of inputs necessary to encounter the fault. Nevertheless, fault density serves as a useful indicator for the reliability engineer. Other software metrics, such as complexity, are also used. This metric remains controversial, since changes in software development and verification practices can have dramatic impact on overall defect rates.

Testing is even more important for software than hardware. Even the best software development process results in some software faults that are nearly undetectable until tested. As with hardware, software is tested at several levels, starting with individual units, through integration and full-up system testing. Unlike hardware, it is inadvisable to skip levels of software testing. During all phases of testing, software faults are discovered, corrected, and re-tested. Reliability estimates are updated based on the fault density and other metrics. At a system level, mean-time-between-failure data can be collected and used to estimate reliability. Unlike hardware, performing exactly the same test on exactly the same software configuration does not provide increased statistical confidence. Instead, software reliability uses different metrics, such as code coverage.

Eventually, the software is integrated with the hardware in the top-level system, and software reliability is subsumed by system reliability. The Software Engineering Institute's capability maturity model is a common means of assessing the overall software development process for reliability and quality purposes.

Structural reliability

Structural reliability or the reliability of structures is the application of reliability theory to the behavior of structures. It is used in both the design and maintenance of different types of structures including concrete and steel structures. In structural reliability studies both loads and resistances are modeled as probabilistic variables. Using this approach the probability of failure of a structure is calculated.

Comparison to safety engineering

Reliability engineering is concerned with overall minimisation of failures that could lead to financial losses for the responsible entity, whereas safety engineering focuses on minimising a specific set of failure types that in general could lead to large scale, widespread issues beyond the responsible entity.

Reliability hazards could transform into incidents leading to a loss of revenue for the company or the customer, for example due to direct and indirect costs associated with: loss of production due to system unavailability; unexpected high or low demands for spares; repair costs; man-hours; (multiple) re-designs; interruptions to normal production etc.

Safety engineering is often highly specific, relating only to certain tightly regulated industries, applications, or areas. It primarily focuses on system safety hazards that could lead to severe accidents including: loss of life; destruction of equipment; or environmental damage. As such, the related system functional reliability requirements are often extremely high. Although it deals with unwanted failures in the same sense as reliability engineering, it, however, has less of a focus on direct costs, and is not concerned with post-failure repair actions. Another difference is the level of impact of failures on society, leading to a tendency for strict control by governments or regulatory bodies (e.g. nuclear, aerospace, defense, rail and oil industries).

This can occasionally lead to safety engineering and reliability engineering having contradictory requirements or conflicting choices at a system architecture level. For example, in train signal control systems it is common practice to use a "fail-safe" system design concept. In this example, a wrong-side failure needs an extremely low failure rate as such failures can lead to such severe effects, like frontal collisions of two trains where a signalling failure leads to two oncoming trains on the same track being given GREEN lights. Such systems should be (and thankfully are) designed in a way that the vast majority of failures (e.g. temporary or total loss of signals or open contacts of relays) will generate RED lights for all trains. This is the safe state. This means in the event of a failure, all trains are stopped immediately. This fail-safe logic might, unfortunately, lower the reliability of the system. The reason for this is the higher risk of false tripping, as any failure whether temporary or not may be trigger such a safe – but costly – shut-down state. Different solutions can be applied for similar issues. See the section on fault tolerance below.

Fault tolerance

Reliability can be increased by using "1oo2" (1 out of 2) redundancy at a part or system level. However, if both redundant elements disagree it can be difficult to know which is to be relied upon. In the previous train signalling example this could lead to lower safety levels as there are more possibilities for allowing "wrong side" or other undetected dangerous failures. Fault-tolerant systems often rely on additional redundancy (e.g. 2003 voting logic) where multiple redundant elements must agree on a potentially unsage action before it is performed. This increases both reliability and safety at a system level and is often used for so-called "operational" or "mission" systems. This is common practice in Aerospace systems that need continued availability and do not have a fail-safe mode. For example, aircraft may use triple modular redundancy for flight computers and control surfaces (including occasionally different modes of operation e.g. electrical/mechanical/hydraulic) as these need to always be operational, due to the fact that there are no "safe" default positions for control surfaces such as rudders or ailerons when the aircraft is flying.

Basic reliability and mission (operational) reliability

The above example of a 2oo3 fault tolerant system increases both mission reliability as well as safety. However, the "basic" reliability of the system will in this case still be lower than a non-redundant (1oo1) or 2oo2 system. Basic reliability engineering covers all failures, including those that might not result in system failure, but do result in additional cost due to: maintenance repair actions; logistics; spare parts etc. For example, replacement or repair of 1 faulty channel in a 2oo3 voting system, (the system is still operating, although with one failed channel it has actually become a 2oo2 system) is contributing to basic unreliability but not mission unreliability. As an example, the failure of the tail-light of an aircraft will not prevent the plane from flying (and so is not considered a mission failure), but it does need to be remedied (with a related cost, and so does contribute to the basic unreliability levels).

Detectability and common cause failures

When using fault tolerant (redundant architectures) systems or systems that are equipped with protection functions, detectability of failures and avoidance of common cause failures becomes paramount for safe functioning and/or mission reliability.

Reliability versus quality (Six Sigma)

Six Sigma has its roots in manufacturing. Reliability engineering is a specialty engineering part of systems engineering. The systems engineering process is a discovery process that is quite unlike a manufacturing process. A manufacturing process is focused on repetitive activities that achieve high quality outputs with minimum cost and time. The systems engineering process must begin by discovering a real (potential) problem that needs to be solved; the biggest failure that can be made in systems engineering is finding an elegant solution to the wrong problem (or in terms of reliability: "providing elegant solutions to the wrong root causes of system failures"). 

The everyday usage term "quality of a product" is loosely taken to mean its inherent degree of excellence. In industry, a more precise definition of quality as "conformance to requirements or specifications at the start of use" is used. Assuming the final product specification adequately captures the original requirements and customer/system needs, the quality level can be measured as the fraction of product units shipped that meet specifications.

Variation of this static output may affect quality and reliability, but this is not the total picture. More inherent aspects may play a role, and in some cases, these may not be readily measured or controlled by any means. At a part level microscopic material variations such as unavoidable micro-cracks and chemical impurities may over time (due to physical or chemical "loading") become macroscopic defects. At a system level, systematic failures may play a dominant role (e.g. requirement errors or software or software compiler or design flaws).

Furthermore, for more complex systems it should be questioned if derived or lower-level requirements and related product specifications are truly valid and correct? Will these result in premature failure due to excessive wear, fatigue, corrosion, and debris accumulation, or other issues such as maintenance induced failures? Are there any interactions at a system level (as investigated by for example Fault Tree Analysis)? How many of these systems still meet function and fulfill the needs after a week of operation? What performance losses occurred? Did full system failure occur? What happens after the end of a one-year warranty period? And what happens after 50 years (a common lifetime for aircraft, trains, nuclear systems, etc.)? That is where "reliability" comes in. These issues are far more complex and can not be controlled only by a standard "quality" (six sigma) way of working. They need a systems engineering approach.

Quality is a snapshot at the start of life and mainly related to control of lower-level product specifications. This includes time-zero defects i.e. where manufacturing mistakes escaped final Quality Control. In theory the quality level might be described by a single fraction of defective products. Reliability (as a part of systems engineering) acts as more of an ongoing account of operational capabilities, often over many years. Theoretically, all items will fail over an infinite period of time. Defects that appear over time are referred to as reliability fallout. To describe reliability fallout a probability model that describes the fraction fallout over time is needed. This is known as the life distribution model. Some of these reliability issues may be due to inherent design issues, which may exist even though the product conforms to specifications. Even items that are produced perfectly may fail over time due to one or more failure mechanisms (e.g. due to human error or mechanical, electrical, and chemical factors). These reliability issues can also be influenced by acceptable levels of variation during initial production. 

Quality is therefore related to manufacturing, and reliability is more related to the validation of sub-system or lower item requirements, (system or part) inherent design and life cycle solutions. Items that do not conform to (any) product specification will generally do worse in terms of reliability (having a lower MTTF), but this does not always have to be the case. The full mathematical quantification (in statistical models) of this combined relation is in general very difficult or even practically impossible. In cases where manufacturing variances can be effectively reduced, six sigma tools may be useful to find optimal process solutions which can increase reliability. Six Sigma may also help to design products that are more robust to manufacturing induced failures. 

In contrast with Six Sigma, reliability engineering solutions are generally found by focusing on a (system) design and not on the manufacturing process. Solutions are found in different ways, such as by simplifying a system to allow more of the mechanisms of failure involved to be understood; performing detailed calculations of material stress levels allowing suitable safety factors to be determined; finding possible abnormal system load conditions and using this to increase robustness of a design to manufacturing variance related failure mechanisms. Furthermore, reliability engineering uses system-level solutions, like designing redundant and fault-tolerant systems for situations with high availability needs.

Six-Sigma is also more quantified (measurement-based). The core of Six-Sigma is built on empirical research and statistical analysis (e.g. to find transfer functions) of directly measurable parameters. This can not be translated practically to most reliability issues, as reliability is not (easily) measurable due to being very much a function of time (large times may be involved), especially during the requirements-specification and design phases, where reliability engineering is the most efficient. Full quantification of reliability is in this phase extremely difficult or costly (due to the amount of testing required). It also may foster re-active management (waiting for system failures to be measured before a decision can be taken). Furthermore, as explained on this page, Reliability problems are likely to come from many different causes (e.g. inherent failures, human error, systematic failures) besides manufacturing induced defects. 

Note: A "defect" in six-sigma/quality literature is not the same as a "failure" (Field failure | e.g. fractured item) in reliability. A six-sigma/quality defect refers generally to non-conformance with a requirement (e.g. basic functionality or a key dimension). Items can, however, fail over time, even if these requirements are all fulfilled. Quality is generally not concerned with asking the crucial question "are the requirements actually correct?", whereas reliability is. 

Within an entity, departments related to Quality (i.e. concerning manufacturing), Six Sigma (i.e. concerning process control), and Reliability (product design) should provide input to each other to cover the complete risks more efficiently.

Reliability operational assessment

Once systems or parts are being produced, reliability engineering attempts to monitor, assess, and correct deficiencies. Monitoring includes electronic and visual surveillance of critical parameters identified during the fault tree analysis design stage. Data collection is highly dependent on the nature of the system. Most large organizations have quality control groups that collect failure data on vehicles, equipment and machinery. Consumer product failures are often tracked by the number of returns. For systems in dormant storage or on standby, it is necessary to establish a formal surveillance program to inspect and test random samples. Any changes to the system, such as field upgrades or recall repairs, require additional reliability testing to ensure the reliability of the modification. Since it is not possible to anticipate all the failure modes of a given system, especially ones with a human element, failures will occur. The reliability program also includes a systematic root cause analysis that identifies the causal relationships involved in the failure such that effective corrective actions may be implemented. When possible, system failures and corrective actions are reported to the reliability engineering organization.

Some of the most common methods to apply to a reliability operational assessment are failure reporting, analysis, and corrective action systems (FRACAS). This systematic approach develops a reliability, safety, and logistics assessment based on failure/incident reporting, management, analysis, and corrective/preventive actions. Organizations today are adopting this method and utilizing commercial systems (such as Web-based FRACAS applications) that enable them to create a failure/incident data repository from which statistics can be derived to view accurate and genuine reliability, safety, and quality metrics. 

It is extremely important for an organization to adopt a common FRACAS system for all end items. Also, it should allow test results to be captured in a practical way. Failure to adopt one easy-to-use (in terms of ease of data-entry for field engineers and repair shop engineers) and easy-to-maintain integrated system is likely to result in a failure of the FRACAS program itself.

Some of the common outputs from a FRACAS system include Field MTBF, MTTR, spares consumption, reliability growth, failure/incidents distribution by type, location, part no., serial no., and symptom. 

The use of past data to predict the reliability of new comparable systems/items can be misleading as reliability is a function of the context of use and can be affected by small changes in design/manufacturing.

Reliability organizations

Systems of any significant complexity are developed by organizations of people, such as a commercial company or a government agency. The reliability engineering organization must be consistent with the company's organizational structure. For small, non-critical systems, reliability engineering may be informal. As complexity grows, the need arises for a formal reliability function. Because reliability is important to the customer, the customer may even specify certain aspects of the reliability organization. 

There are several common types of reliability organizations. The project manager or chief engineer may employ one or more reliability engineers directly. In larger organizations, there is usually a product assurance or specialty engineering organization, which may include reliability, maintainability, quality, safety, human factors, logistics, etc. In such case, the reliability engineer reports to the product assurance manager or specialty engineering manager. 

In some cases, a company may wish to establish an independent reliability organization. This is desirable to ensure that the system reliability, which is often expensive and time-consuming, is not unduly slighted due to budget and schedule pressures. In such cases, the reliability engineer works for the project day-to-day, but is actually employed and paid by a separate organization within the company. 

Because reliability engineering is critical to early system design, it has become common for reliability engineers, however, the organization is structured, to work as part of an integrated product team.

Education

Some universities offer graduate degrees in reliability engineering. Other reliability engineers typically have an engineering degree, which can be in any field of engineering, from an accredited university or college program. Many engineering programs offer reliability courses, and some universities have entire reliability engineering programs. A reliability engineer may be registered as a professional engineer by the state, but this is not required by most employers. There are many professional conferences and industry training programs available for reliability engineers. Several professional organizations exist for reliability engineers, including the American Society for Quality Reliability Division (ASQ-RD), the IEEE Reliability Society, the American Society for Quality (ASQ), and the Society of Reliability Engineers (SRE).

A group of engineers have provided a list of useful tools for reliability engineering. These include: RelCalc software, Military Handbook 217 (Mil-HDBK-217), and the NAVMAT P-4855-1A manual. Analyzing failures and successes coupled with a quality standards process also provides systemized information to making informed engineering designs.