Shape of the universe

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Shape_of_the_universe 

The shape of the universe, in physical cosmology, is the local and global geometry of the universe. The local features of the geometry of the universe are primarily described by its curvature, whereas the topology of the universe describes general global properties of its shape as of a continuous object. The spatial curvature is related to general relativity, which describes how spacetime is curved and bent by mass and energy. The spatial topology cannot be determined from its curvature, due to the fact that there exist (mathematically) locally indistinguishable spaces with different topologies.

Cosmologists distinguish between the observable universe and the entire universe, the former being a ball-shaped portion of the latter that can, in principle, be accessible by astronomical observations. Assuming the cosmological principle, the observable universe is similar from all contemporary vantage points, which allows cosmologists to discuss properties of the entire universe with only information from studying their observable universe.

Several potential topological or geometric attributes of the universe interest may be discussed. Some of these are:

1. Boundedness (whether the universe is finite or infinite)
2. Flat (zero curvature), hyperbolic (negative curvature), or spherical (positive curvature)
3. Connectivity: how the universe is put together, i.e., simply connected space or multiply connected space.

There are certain logical connections among these properties. For example, a universe with positive curvature is necessarily finite. Although it is usually assumed in the literature that a flat or negatively curved universe is infinite, this need not be the case if the topology is not the trivial one: for example, a three-torus is flat but finite.

The exact shape is still a matter of debate in physical cosmology, but experimental data from various independent sources (WMAP, BOOMERanG, and Planck for example) confirm that the universe is flat with only a 0.4% margin of error. On the other hand, any non-zero curvature is possible for a sufficiently large curved universe (analogously to how a small portion of a sphere can look flat). Theorists have been trying to construct a formal mathematical model of the shape of the universe. In formal terms, this is a 3-manifold model corresponding to the spatial section (in comoving coordinates) of the four-dimensional spacetime of the universe. The model most theorists currently use is the Friedmann–Lemaître–Robertson–Walker (FLRW) model. Arguments have been put forward that the observational data best fit with the conclusion that the shape of the global universe is infinite and flat, but the data are also consistent with other possible shapes, such as the so-called Poincaré dodecahedral space and the Sokolov–Starobinskii space (quotient of the upper half-space model of hyperbolic space by a 2-dimensional lattice).

Shape of the observable universe

As stated in the introduction, there are two aspects to consider:

1. its local geometry, which predominantly concerns the curvature of the universe, particularly the observable universe, and
2. its global geometry, which concerns the topology of the universe as a whole.

The observable universe can be thought of as a sphere that extends outwards from any observation point for 46.5 billion light-years, going farther back in time and more redshifted the more distant away one looks. Ideally, one can continue to look back all the way to the Big Bang; in practice, however, the farthest away one can look using light and other electromagnetic radiation is the cosmic microwave background (CMB), as anything past that was opaque. Experimental investigations show that the observable universe is very close to isotropic and homogeneous.

If the observable universe encompasses the entire universe, we may be able to determine the structure of the entire universe by observation. However, if the observable universe is smaller than the entire universe, our observations will be limited to only a part of the whole, and we may not be able to determine its global geometry through measurement. From experiments, it is possible to construct different mathematical models of the global geometry of the entire universe, all of which are consistent with current observational data; thus it is currently unknown whether the observable universe is identical to the global universe, or is instead many orders of magnitude smaller. The universe may be small in some dimensions and not in others (analogous to the way a cuboid is longer in the dimension of length than it is in the dimensions of width and depth). To test whether a given mathematical model describes the universe accurately, scientists look for the model's novel implications—what are some phenomena in the universe that we have not yet observed, but that must exist if the model is correct—and they devise experiments to test whether those phenomena occur or not. For example, if the universe is a small closed loop, one would expect to see multiple images of an object in the sky, although not necessarily images of the same age.

Cosmologists normally work with a given space-like slice of spacetime called the comoving coordinates, the existence of a preferred set of which is possible and widely accepted in present-day physical cosmology. The section of spacetime that can be observed is the backward light cone (all points within the cosmic light horizon, given time to reach a given observer), while the related term Hubble volume can be used to describe either the past light cone or comoving space up to the surface of last scattering. To speak of "the shape of the universe (at a point in time)" is ontologically naive from the point of view of special relativity alone: due to the relativity of simultaneity we cannot speak of different points in space as being "at the same point in time" nor, therefore, of "the shape of the universe at a point in time". However, the comoving coordinates (if well-defined) provide a strict sense to those by using the time since the Big Bang (measured in the reference of CMB) as a distinguished universal time.

Curvature of the universe

The curvature is a quantity describing how the geometry of a space differs locally from the one of the flat space. The curvature of any locally isotropic space (and hence of a locally isotropic universe) falls into one of the three following cases:

1. Zero curvature (flat); a drawn triangle's angles add up to 180° and the Pythagorean theorem holds; such 3-dimensional space is locally modeled by Euclidean space E³.
2. Positive curvature; a drawn triangle's angles add up to more than 180°; such 3-dimensional space is locally modeled by a region of a 3-sphere S³.
3. Negative curvature; a drawn triangle's angles add up to less than 180°; such 3-dimensional space is locally modeled by a region of a hyperbolic space H³.

Curved geometries are in the domain of Non-Euclidean geometry. An example of a positively curved space would be the surface of a sphere such as the Earth. A triangle drawn from the equator to a pole will have at least two angles equal 90°, which makes the sum of the 3 angles greater than 180°. An example of a negatively curved surface would be the shape of a saddle or mountain pass. A triangle drawn on a saddle surface will have the sum of the angles adding up to less than 180°.

The local geometry of the universe is determined by whether the density parameter Ω is greater than, less than, or equal to 1.
From top to bottom: a spherical universe with Ω > 1, a hyperbolic universe with Ω < 1, and a flat universe with Ω = 1. These depictions of two-dimensional surfaces are merely easily visualizable analogs to the 3-dimensional structure of (local) space.

General relativity explains that mass and energy bend the curvature of spacetime and is used to determine what curvature the universe has by using a value called the density parameter, represented with Omega (Ω). The density parameter is the average density of the universe divided by the critical energy density, that is, the mass energy needed for a universe to be flat. Put another way,

• If Ω = 1, the universe is flat.
• If Ω > 1, there is positive curvature.
• If Ω < 1 there is negative curvature.

One can experimentally calculate this Ω to determine the curvature two ways. One is to count up all the mass-energy in the universe and take its average density then divide that average by the critical energy density. Data from Wilkinson Microwave Anisotropy Probe (WMAP) as well as the Planck spacecraft give values for the three constituents of all the mass-energy in the universe – normal mass (baryonic matter and dark matter), relativistic particles (photons and neutrinos), and dark energy or the cosmological constant:

Ω_mass ≈ 0.315±0.018

Ω_relativistic ≈ 9.24×10⁻⁵

Ω_Λ ≈ 0.6817±0.0018

Ω_total = Ω_mass + Ω_relativistic + Ω_Λ = 1.00±0.02

The actual value for critical density value is measured as ρ_critical = 9.47×10⁻²⁷ kg m⁻³. From these values, within experimental error, the universe seems to be flat.

Another way to measure Ω is to do so geometrically by measuring an angle across the observable universe. We can do this by using the CMB and measuring the power spectrum and temperature anisotropy. For instance, one can imagine finding a gas cloud that is not in thermal equilibrium due to being so large that light speed cannot propagate the thermal information. Knowing this propagation speed, we then know the size of the gas cloud as well as the distance to the gas cloud, we then have two sides of a triangle and can then determine the angles. Using a method similar to this, the BOOMERanG experiment has determined that the sum of the angles to 180° within experimental error, corresponding to an Ω_total ≈ 1.00±0.12.

These and other astronomical measurements constrain the spatial curvature to be very close to zero, although they do not constrain its sign. This means that although the local geometries of spacetime are generated by the theory of relativity based on spacetime intervals, we can approximate 3-space by the familiar Euclidean geometry.

The Friedmann–Lemaître–Robertson–Walker (FLRW) model using Friedmann equations is commonly used to model the universe. The FLRW model provides a curvature of the universe based on the mathematics of fluid dynamics, that is, modeling the matter within the universe as a perfect fluid. Although stars and structures of mass can be introduced into an "almost FLRW" model, a strictly FLRW model is used to approximate the local geometry of the observable universe. Another way of saying this is that if all forms of dark energy are ignored, then the curvature of the universe can be determined by measuring the average density of matter within it, assuming that all matter is evenly distributed (rather than the distortions caused by 'dense' objects such as galaxies). This assumption is justified by the observations that, while the universe is "weakly" inhomogeneous and anisotropic, it is on average homogeneous and isotropic.

Global universe structure

Global structure covers the geometry and the topology of the whole universe—both the observable universe and beyond. While the local geometry does not determine the global geometry completely, it does limit the possibilities, particularly a geometry of a constant curvature. The universe is often taken to be a geodesic manifold, free of topological defects; relaxing either of these complicates the analysis considerably. A global geometry is a local geometry plus a topology. It follows that a topology alone does not give a global geometry: for instance, Euclidean 3-space and hyperbolic 3-space have the same topology but different global geometries.

As stated in the introduction, investigations within the study of the global structure of the universe include:

• whether the universe is infinite or finite in extent,
• whether the geometry of the global universe is flat, positively curved, or negatively curved, and,
• whether the topology is simply connected like a sphere or multiply connected, like a torus.

Infinite or finite

One of the presently unanswered questions about the universe is whether it is infinite or finite in extent. For intuition, it can be understood that a finite universe has a finite volume that, for example, could be in theory filled up with a finite amount of material, while an infinite universe is unbounded and no numerical volume could possibly fill it. Mathematically, the question of whether the universe is infinite or finite is referred to as boundedness. An infinite universe (unbounded metric space) means that there are points arbitrarily far apart: for any distance d, there are points that are of a distance at least d apart. A finite universe is a bounded metric space, where there is some distance d such that all points are within distance d of each other. The smallest such d is called the diameter of the universe, in which case the universe has a well-defined "volume" or "scale."

With or without boundary

Assuming a finite universe, the universe can either have an edge or no edge. Many finite mathematical spaces, e.g., a disc, have an edge or boundary. Spaces that have an edge are difficult to treat, both conceptually and mathematically. Namely, it is very difficult to state what would happen at the edge of such a universe. For this reason, spaces that have an edge are typically excluded from consideration.

However, there exist many finite spaces, such as the 3-sphere and 3-torus, which have no edges. Mathematically, these spaces are referred to as being compact without boundary. The term compact means that it is finite in extent ("bounded") and complete. The term "without boundary" means that the space has no edges. Moreover, so that calculus can be applied, the universe is typically assumed to be a differentiable manifold. A mathematical object that possesses all these properties, compact without boundary and differentiable, is termed a closed manifold. The 3-sphere and 3-torus are both closed manifolds.

Curvature

The curvature of the universe places constraints on the topology. If the spatial geometry is spherical, i.e., possess positive curvature, the topology is compact. For a flat (zero curvature) or a hyperbolic (negative curvature) spatial geometry, the topology can be either compact or infinite. Many textbooks erroneously state that a flat universe implies an infinite universe; however, the correct statement is that a flat universe that is also simply connected implies an infinite universe. For example, Euclidean space is flat, simply connected, and infinite, but the torus is flat, multiply connected, finite, and compact.

In general, local to global theorems in Riemannian geometry relate the local geometry to the global geometry. If the local geometry has constant curvature, the global geometry is very constrained, as described in Thurston geometries.

The latest research shows that even the most powerful future experiments (like the SKA) will not be able to distinguish between flat, open and closed universe if the true value of cosmological curvature parameter is smaller than 10⁻⁴. If the true value of the cosmological curvature parameter is larger than 10⁻³ we will be able to distinguish between these three models even now.

Results of the Planck mission released in 2015 show the cosmological curvature parameter, Ω_K, to be 0.000±0.005, consistent with a flat universe.

Universe with zero curvature

In a universe with zero curvature, the local geometry is flat. The most obvious global structure is that of Euclidean space, which is infinite in extent. Flat universes that are finite in extent include the torus and Klein bottle. Moreover, in three dimensions, there are 10 finite closed flat 3-manifolds, of which 6 are orientable and 4 are non-orientable. These are the Bieberbach manifolds. The most familiar is the aforementioned 3-torus universe.

In the absence of dark energy, a flat universe expands forever but at a continually decelerating rate, with expansion asymptotically approaching zero. With dark energy, the expansion rate of the universe initially slows down, due to the effect of gravity, but eventually increases. The ultimate fate of the universe is the same as that of an open universe.

A flat universe can have zero total energy.

Universe with positive curvature

A positively curved universe is described by elliptic geometry, and can be thought of as a three-dimensional hypersphere, or some other spherical 3-manifold (such as the Poincaré dodecahedral space), all of which are quotients of the 3-sphere.

Poincaré dodecahedral space is a positively curved space, colloquially described as "soccerball-shaped", as it is the quotient of the 3-sphere by the binary icosahedral group, which is very close to icosahedral symmetry, the symmetry of a soccer ball. This was proposed by Jean-Pierre Luminet and colleagues in 2003 and an optimal orientation on the sky for the model was estimated in 2008.

Universe with negative curvature

A hyperbolic universe, one of a negative spatial curvature, is described by hyperbolic geometry, and can be thought of locally as a three-dimensional analog of an infinitely extended saddle shape. There are a great variety of hyperbolic 3-manifolds, and their classification is not completely understood. Those of finite volume can be understood via the Mostow rigidity theorem. For hyperbolic local geometry, many of the possible three-dimensional spaces are informally called "horn topologies", so called because of the shape of the pseudosphere, a canonical model of hyperbolic geometry. An example is the Picard horn, a negatively curved space, colloquially described as "funnel-shaped".

Curvature: open or closed

When cosmologists speak of the universe as being "open" or "closed", they most commonly are referring to whether the curvature is negative or positive. These meanings of open and closed are different from the mathematical meaning of open and closed used for sets in topological spaces and for the mathematical meaning of open and closed manifolds, which gives rise to ambiguity and confusion. In mathematics, there are definitions for a closed manifold (i.e., compact without boundary) and open manifold (i.e., one that is not compact and without boundary). A "closed universe" is necessarily a closed manifold. An "open universe" can be either a closed or open manifold. For example, in the Friedmann–Lemaître–Robertson–Walker (FLRW) model the universe is considered to be without boundaries, in which case "compact universe" could describe a universe that is a closed manifold.

Milne model (hyperbolic expanding)

If one applies Minkowski space-based special relativity to expansion of the universe, without resorting to the concept of a curved spacetime, then one obtains the Milne model. Any spatial section of the universe of a constant age (the proper time elapsed from the Big Bang) will have a negative curvature; this is merely a pseudo-Euclidean geometric fact analogous to one that concentric spheres in the flat Euclidean space are nevertheless curved. Spatial geometry of this model is an unbounded hyperbolic space. The entire universe in this model can be modelled by embedding it in Minkowski spacetime, in which case the universe is included inside a future light cone of a Minkowski spacetime. The Milne model in this case is the future interior of the light cone and the light cone itself is the Big Bang.

For any given moment t > 0 of coordinate time within the Milne model (assuming the Big Bang has t = 0), any cross-section of the universe at constant t' in the Minkowski spacetime is bounded by a sphere of radius c t = c t'. The apparent paradox of an infinite universe "contained" within a sphere is an effect of the mismatch between coordinate systems of the Milne model and the Minkowski spacetime in which it is embedded.

This model is essentially a degenerate FLRW for Ω = 0. It is incompatible with observations that definitely rule out such a large negative spatial curvature. However, as a background in which gravitational fields (or gravitons) can operate, due to diffeomorphism invariance, the space on the macroscopic scale, is equivalent to any other (open) solution of Einstein's field equations

Spontaneous symmetry breaking

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Spontaneous_symmetry_breaking 

Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or the Lagrangian obey symmetries, but the lowest-energy vacuum solutions do not exhibit that same symmetry. When the system goes to one of those vacuum solutions, the symmetry is broken for perturbations around that vacuum even though the entire Lagrangian retains that symmetry.

Overview

In explicit symmetry breaking, if two outcomes are considered, the probability of a pair of outcomes can be different. By definition, spontaneous symmetry breaking requires the existence of a symmetric probability distribution—any pair of outcomes has the same probability. In other words, the underlying laws are invariant under a symmetry transformation.

The system, as a whole, changes under such transformations.

Phases of matter, such as crystals, magnets, and conventional superconductors, as well as simple phase transitions can be described by spontaneous symmetry breaking. Notable exceptions include topological phases of matter like the fractional quantum Hall effect.

Examples

Sombrero potential

Consider a symmetric upward dome with a trough circling the bottom. If a ball is put at the very peak of the dome, the system is symmetric with respect to a rotation around the center axis. But the ball may spontaneously break this symmetry by rolling down the dome into the trough, a point of lowest energy. Afterward, the ball has come to a rest at some fixed point on the perimeter. The dome and the ball retain their individual symmetry, but the system does not.

Graph of Goldstone's "sombrero" potential function ${\displaystyle V(\phi )}$.

In the simplest idealized relativistic model, the spontaneously broken symmetry is summarized through an illustrative scalar field theory. The relevant Lagrangian of a scalar field ${\displaystyle \phi }$, which essentially dictates how a system behaves, can be split up into kinetic and potential terms,

${\displaystyle {\mathcal {L}}=\partial ^{\mu }\phi \partial _{\mu }\phi -V(\phi ).}$

(1)

It is in this potential term ${\displaystyle V(\phi )}$ that the symmetry breaking is triggered. An example of a potential, due to Jeffrey Goldstone is illustrated in the graph at the left.

${\displaystyle V(\phi )=-5|\phi |^{2}+|\phi |^{4}\,}$.

(2)

This potential has an infinite number of possible minima (vacuum states) given by

${\displaystyle \phi ={\sqrt {5}}e^{i\theta }}$.

(3)

for any real θ between 0 and 2π. The system also has an unstable vacuum state corresponding to Φ = 0. This state has a U(1) symmetry. However, once the system falls into a specific stable vacuum state (amounting to a choice of θ), this symmetry will appear to be lost, or "spontaneously broken".

In fact, any other choice of θ would have exactly the same energy, implying the existence of a massless Nambu–Goldstone boson, the mode running around the circle at the minimum of this potential, and indicating there is some memory of the original symmetry in the Lagrangian.

Other examples

• For ferromagnetic materials, the underlying laws are invariant under spatial rotations. Here, the order parameter is the magnetization, which measures the magnetic dipole density. Above the Curie temperature, the order parameter is zero, which is spatially invariant, and there is no symmetry breaking. Below the Curie temperature, however, the magnetization acquires a constant nonvanishing value, which points in a certain direction (in the idealized situation where we have full equilibrium; otherwise, translational symmetry gets broken as well). The residual rotational symmetries which leave the orientation of this vector invariant remain unbroken, unlike the other rotations which do not and are thus spontaneously broken.
• The laws describing a solid are invariant under the full Euclidean group, but the solid itself spontaneously breaks this group down to a space group. The displacement and the orientation are the order parameters.
• General relativity has a Lorentz symmetry, but in FRW cosmological models, the mean 4-velocity field defined by averaging over the velocities of the galaxies (the galaxies act like gas particles at cosmological scales) acts as an order parameter breaking this symmetry. Similar comments can be made about the cosmic microwave background.
• For the electroweak model, as explained earlier, a component of the Higgs field provides the order parameter breaking the electroweak gauge symmetry to the electromagnetic gauge symmetry. Like the ferromagnetic example, there is a phase transition at the electroweak temperature. The same comment about us not tending to notice broken symmetries suggests why it took so long for us to discover electroweak unification.
• In superconductors, there is a condensed-matter collective field ψ, which acts as the order parameter breaking the electromagnetic gauge symmetry.
• Take a thin cylindrical plastic rod and push both ends together. Before buckling, the system is symmetric under rotation, and so visibly cylindrically symmetric. But after buckling, it looks different, and asymmetric. Nevertheless, features of the cylindrical symmetry are still there: ignoring friction, it would take no force to freely spin the rod around, displacing the ground state in time, and amounting to an oscillation of vanishing frequency, unlike the radial oscillations in the direction of the buckle. This spinning mode is effectively the requisite Nambu–Goldstone boson.
• Consider a uniform layer of fluid over an infinite horizontal plane. This system has all the symmetries of the Euclidean plane. But now heat the bottom surface uniformly so that it becomes much hotter than the upper surface. When the temperature gradient becomes large enough, convection cells will form, breaking the Euclidean symmetry.
• Consider a bead on a circular hoop that is rotated about a vertical diameter. As the rotational velocity is increased gradually from rest, the bead will initially stay at its initial equilibrium point at the bottom of the hoop (intuitively stable, lowest gravitational potential). At a certain critical rotational velocity, this point will become unstable and the bead will jump to one of two other newly created equilibria, equidistant from the center. Initially, the system is symmetric with respect to the diameter, yet after passing the critical velocity, the bead ends up in one of the two new equilibrium points, thus breaking the symmetry.

Spontaneous symmetry breaking in physics

Spontaneous symmetry breaking illustrated: At high energy levels (left), the ball settles in the center, and the result is symmetric. At lower energy levels (right), the overall "rules" remain symmetric, but the symmetric "Sombrero" enforces an asymmetric outcome, since eventually the ball must rest at some random spot on the bottom, "spontaneously", and not all others.

Particle physics

In particle physics, the force carrier particles are normally specified by field equations with gauge symmetry; their equations predict that certain measurements will be the same at any point in the field. For instance, field equations might predict that the mass of two quarks is constant. Solving the equations to find the mass of each quark might give two solutions. In one solution, quark A is heavier than quark B. In the second solution, quark B is heavier than quark A by the same amount. The symmetry of the equations is not reflected by the individual solutions, but it is reflected by the range of solutions.

An actual measurement reflects only one solution, representing a breakdown in the symmetry of the underlying theory. "Hidden" is a better term than "broken", because the symmetry is always there in these equations. This phenomenon is called spontaneous symmetry breaking (SSB) because nothing (that we know of) breaks the symmetry in the equations.

Chiral symmetry

Chiral symmetry breaking is an example of spontaneous symmetry breaking affecting the chiral symmetry of the strong interactions in particle physics. It is a property of quantum chromodynamics, the quantum field theory describing these interactions, and is responsible for the bulk of the mass (over 99%) of the nucleons, and thus of all common matter, as it converts very light bound quarks into 100 times heavier constituents of baryons. The approximate Nambu–Goldstone bosons in this spontaneous symmetry breaking process are the pions, whose mass is an order of magnitude lighter than the mass of the nucleons. It served as the prototype and significant ingredient of the Higgs mechanism underlying the electroweak symmetry breaking.

Higgs mechanism

The strong, weak, and electromagnetic forces can all be understood as arising from gauge symmetries. The Higgs mechanism, the spontaneous symmetry breaking of gauge symmetries, is an important component in understanding the superconductivity of metals and the origin of particle masses in the standard model of particle physics. One important consequence of the distinction between true symmetries and gauge symmetries, is that the spontaneous breaking of a gauge symmetry does not give rise to characteristic massless Nambu–Goldstone physical modes, but only massive modes, like the plasma mode in a superconductor, or the Higgs mode observed in particle physics.

In the standard model of particle physics, spontaneous symmetry breaking of the SU(2) × U(1) gauge symmetry associated with the electro-weak force generates masses for several particles, and separates the electromagnetic and weak forces. The W and Z bosons are the elementary particles that mediate the weak interaction, while the photon mediates the electromagnetic interaction. At energies much greater than 100 GeV, all these particles behave in a similar manner. The Weinberg–Salam theory predicts that, at lower energies, this symmetry is broken so that the photon and the massive W and Z bosons emerge. In addition, fermions develop mass consistently.

Without spontaneous symmetry breaking, the Standard Model of elementary particle interactions requires the existence of a number of particles. However, some particles (the W and Z bosons) would then be predicted to be massless, when, in reality, they are observed to have mass. To overcome this, spontaneous symmetry breaking is augmented by the Higgs mechanism to give these particles mass. It also suggests the presence of a new particle, the Higgs boson, detected in 2012.

Superconductivity of metals is a condensed-matter analog of the Higgs phenomena, in which a condensate of Cooper pairs of electrons spontaneously breaks the U(1) gauge symmetry associated with light and electromagnetism.

Condensed matter physics

Most phases of matter can be understood through the lens of spontaneous symmetry breaking. For example, crystals are periodic arrays of atoms that are not invariant under all translations (only under a small subset of translations by a lattice vector). Magnets have north and south poles that are oriented in a specific direction, breaking rotational symmetry. In addition to these examples, there are a whole host of other symmetry-breaking phases of matter — including nematic phases of liquid crystals, charge- and spin-density waves, superfluids, and many others.

There are several known examples of matter that cannot be described by spontaneous symmetry breaking, including: topologically ordered phases of matter, such as fractional quantum Hall liquids, and spin-liquids. These states do not break any symmetry, but are distinct phases of matter. Unlike the case of spontaneous symmetry breaking, there is not a general framework for describing such states.

Continuous symmetry

The ferromagnet is the canonical system that spontaneously breaks the continuous symmetry of the spins below the Curie temperature and at h = 0, where h is the external magnetic field. Below the Curie temperature, the energy of the system is invariant under inversion of the magnetization m(x) such that m(x) = −m(−x). The symmetry is spontaneously broken as h → 0 when the Hamiltonian becomes invariant under the inversion transformation, but the expectation value is not invariant.

Spontaneously-symmetry-broken phases of matter are characterized by an order parameter that describes the quantity which breaks the symmetry under consideration. For example, in a magnet, the order parameter is the local magnetization.

Spontaneous breaking of a continuous symmetry is inevitably accompanied by gapless (meaning that these modes do not cost any energy to excite) Nambu–Goldstone modes associated with slow, long-wavelength fluctuations of the order parameter. For example, vibrational modes in a crystal, known as phonons, are associated with slow density fluctuations of the crystal's atoms. The associated Goldstone mode for magnets are oscillating waves of spin known as spin-waves. For symmetry-breaking states, whose order parameter is not a conserved quantity, Nambu–Goldstone modes are typically massless and propagate at a constant velocity.

An important theorem, due to Mermin and Wagner, states that, at finite temperature, thermally activated fluctuations of Nambu–Goldstone modes destroy the long-range order, and prevent spontaneous symmetry breaking in one- and two-dimensional systems. Similarly, quantum fluctuations of the order parameter prevent most types of continuous symmetry breaking in one-dimensional systems even at zero temperature. (An important exception is ferromagnets, whose order parameter, magnetization, is an exactly conserved quantity and does not have any quantum fluctuations.)

Other long-range interacting systems, such as cylindrical curved surfaces interacting via the Coulomb potential or Yukawa potential, have been shown to break translational and rotational symmetries. It was shown, in the presence of a symmetric Hamiltonian, and in the limit of infinite volume, the system spontaneously adopts a chiral configuration — i.e., breaks mirror plane symmetry.

Dynamical symmetry breaking

Dynamical symmetry breaking (DSB) is a special form of spontaneous symmetry breaking in which the ground state of the system has reduced symmetry properties compared to its theoretical description (i.e., Lagrangian).

Dynamical breaking of a global symmetry is a spontaneous symmetry breaking, which happens not at the (classical) tree level (i.e., at the level of the bare action), but due to quantum corrections (i.e., at the level of the effective action).

Dynamical breaking of a gauge symmetry is subtler. In the conventional spontaneous gauge symmetry breaking, there exists an unstable Higgs particle in the theory, which drives the vacuum to a symmetry-broken phase. (See, for example, electroweak interaction.) In dynamical gauge symmetry breaking, however, no unstable Higgs particle operates in the theory, but the bound states of the system itself provide the unstable fields that render the phase transition. For example, Bardeen, Hill, and Lindner published a paper that attempts to replace the conventional Higgs mechanism in the standard model by a DSB that is driven by a bound state of top-antitop quarks. (Such models, in which a composite particle plays the role of the Higgs boson, are often referred to as "Composite Higgs models".) Dynamical breaking of gauge symmetries is often due to creation of a fermionic condensate — e.g., the quark condensate, which is connected to the dynamical breaking of chiral symmetry in quantum chromodynamics. Conventional superconductivity is the paradigmatic example from the condensed matter side, where phonon-mediated attractions lead electrons to become bound in pairs and then condense, thereby breaking the electromagnetic gauge symmetry.

Generalisation and technical usage

For spontaneous symmetry breaking to occur, there must be a system in which there are several equally likely outcomes. The system as a whole is therefore symmetric with respect to these outcomes. However, if the system is sampled (i.e. if the system is actually used or interacted with in any way), a specific outcome must occur. Though the system as a whole is symmetric, it is never encountered with this symmetry, but only in one specific asymmetric state. Hence, the symmetry is said to be spontaneously broken in that theory. Nevertheless, the fact that each outcome is equally likely is a reflection of the underlying symmetry, which is thus often dubbed "hidden symmetry", and has crucial formal consequences.

When a theory is symmetric with respect to a symmetry group, but requires that one element of the group be distinct, then spontaneous symmetry breaking has occurred. The theory must not dictate which member is distinct, only that one is. From this point on, the theory can be treated as if this element actually is distinct, with the proviso that any results found in this way must be resymmetrized, by taking the average of each of the elements of the group being the distinct one.

The crucial concept in physics theories is the order parameter. If there is a field (often a background field) which acquires an expectation value (not necessarily a vacuum expectation value) which is not invariant under the symmetry in question, we say that the system is in the ordered phase, and the symmetry is spontaneously broken. This is because other subsystems interact with the order parameter, which specifies a "frame of reference" to be measured against. In that case, the vacuum state does not obey the initial symmetry (which would keep it invariant, in the linearly realized Wigner mode in which it would be a singlet), and, instead changes under the (hidden) symmetry, now implemented in the (nonlinear) Nambu–Goldstone mode. Normally, in the absence of the Higgs mechanism, massless Goldstone bosons arise.

The symmetry group can be discrete, such as the space group of a crystal, or continuous (e.g., a Lie group), such as the rotational symmetry of space. However, if the system contains only a single spatial dimension, then only discrete symmetries may be broken in a vacuum state of the full quantum theory, although a classical solution may break a continuous symmetry.

Nobel Prize

On October 7, 2008, the Royal Swedish Academy of Sciences awarded the 2008 Nobel Prize in Physics to three scientists for their work in subatomic physics symmetry breaking. Yoichiro Nambu, of the University of Chicago, won half of the prize for the discovery of the mechanism of spontaneous broken symmetry in the context of the strong interactions, specifically chiral symmetry breaking. Physicists Makoto Kobayashi and Toshihide Maskawa, of Kyoto University, shared the other half of the prize for discovering the origin of the explicit breaking of CP symmetry in the weak interactions. This origin is ultimately reliant on the Higgs mechanism, but, so far understood as a "just so" feature of Higgs couplings, not a spontaneously broken symmetry phenomenon.

Inflation (cosmology)

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Inflation_(cosmology)

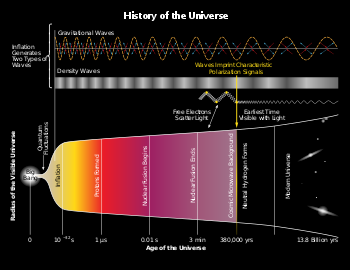
In physical cosmology, cosmic inflation, cosmological inflation, or just inflation, is a theory of exponential expansion of space in the early universe. The inflationary epoch lasted from 10⁻³⁶ seconds after the conjectured Big Bang singularity to some time between 10⁻³³ and 10⁻³² seconds after the singularity. Following the inflationary period, the universe continued to expand, but at a slower rate. The acceleration of this expansion due to dark energy began after the universe was already over 7.7 billion years old (5.4 billion years ago).

Inflation theory was developed in the late 1970s and early 80s, with notable contributions by several theoretical physicists, including Alexei Starobinsky at Landau Institute for Theoretical Physics, Alan Guth at Cornell University, and Andrei Linde at Lebedev Physical Institute. Alexei Starobinsky, Alan Guth, and Andrei Linde won the 2014 Kavli Prize "for pioneering the theory of cosmic inflation." It was developed further in the early 1980s. It explains the origin of the large-scale structure of the cosmos. Quantum fluctuations in the microscopic inflationary region, magnified to cosmic size, become the seeds for the growth of structure in the Universe (see galaxy formation and evolution and structure formation). Many physicists also believe that inflation explains why the universe appears to be the same in all directions (isotropic), why the cosmic microwave background radiation is distributed evenly, why the universe is flat, and why no magnetic monopoles have been observed.

The detailed particle physics mechanism responsible for inflation is unknown. The basic inflationary paradigm is accepted by most physicists, as a number of inflation model predictions have been confirmed by observation; however, a substantial minority of scientists dissent from this position. The hypothetical field thought to be responsible for inflation is called the inflaton.

In 2002 three of the original architects of the theory were recognized for their major contributions; physicists Alan Guth of M.I.T., Andrei Linde of Stanford, and Paul Steinhardt of Princeton shared the prestigious Dirac Prize "for development of the concept of inflation in cosmology". In 2012 Guth and Linde were awarded the Breakthrough Prize in Fundamental Physics for their invention and development of inflationary cosmology.

Overview

Around 1930, Edwin Hubble discovered that light from remote galaxies was redshifted; the more remote, the more shifted. This was quickly interpreted as meaning galaxies were receding from Earth. If Earth is not in some special, privileged, central position in the universe, then it would mean all galaxies are moving apart, and the further away, the faster they are moving away. It is now understood that the universe is expanding, carrying the galaxies with it, and causing this observation. Many other observations agree, and also lead to the same conclusion. However, for many years it was not clear why or how the universe might be expanding, or what it might signify.

Based on a huge amount of experimental observation and theoretical work, it is now believed that the reason for the observation is that space itself is expanding, and that it expanded very rapidly within the first fraction of a second after the Big Bang. This kind of expansion is known as a "metric" expansion. In the terminology of mathematics and physics, a "metric" is a measure of distance that satisfies a specific list of properties, and the term implies that the sense of distance within the universe is itself changing. Today, metric variation is far too small an effect to see on less than an intergalactic scale.

The modern explanation for the metric expansion of space was proposed by physicist Alan Guth in 1979, while investigating the problem of why no magnetic monopoles are seen today. He found that if the universe contained a field in a positive-energy false vacuum state, then according to general relativity it would generate an exponential expansion of space. It was very quickly realized that such an expansion would resolve many other long-standing problems. These problems arise from the observation that to look like it does today, the Universe would have to have started from very finely tuned, or "special" initial conditions at the Big Bang. Inflation theory largely resolves these problems as well, thus making a universe like ours much more likely in the context of Big Bang theory.

No physical field has yet been discovered that is responsible for this inflation. However such a field would be scalar and the first relativistic scalar field proven to exist, the Higgs field, was only discovered in 2012–2013 and is still being researched. So it is not seen as problematic that a field responsible for cosmic inflation and the metric expansion of space has not yet been discovered. The proposed field and its quanta (the subatomic particles related to it) have been named the inflaton. If this field did not exist, scientists would have to propose a different explanation for all the observations that strongly suggest a metric expansion of space has occurred, and is still occurring (much more slowly) today.

Theory

An expanding universe generally has a cosmological horizon, which, by analogy with the more familiar horizon caused by the curvature of Earth's surface, marks the boundary of the part of the Universe that an observer can see. Light (or other radiation) emitted by objects beyond the cosmological horizon in an accelerating universe never reaches the observer, because the space in between the observer and the object is expanding too rapidly.

History of the Universe – gravitational waves are hypothesized to arise from cosmic inflation, a faster-than-light expansion just after the Big Bang (17 March 2014).

The observable universe is one causal patch of a much larger unobservable universe; other parts of the Universe cannot communicate with Earth yet. These parts of the Universe are outside our current cosmological horizon. In the standard hot big bang model, without inflation, the cosmological horizon moves out, bringing new regions into view. Yet as a local observer sees such a region for the first time, it looks no different from any other region of space the local observer has already seen: its background radiation is at nearly the same temperature as the background radiation of other regions, and its space-time curvature is evolving lock-step with the others. This presents a mystery: how did these new regions know what temperature and curvature they were supposed to have? They couldn't have learned it by getting signals, because they were not previously in communication with our past light cone.

Inflation answers this question by postulating that all the regions come from an earlier era with a big vacuum energy, or cosmological constant. A space with a cosmological constant is qualitatively different: instead of moving outward, the cosmological horizon stays put. For any one observer, the distance to the cosmological horizon is constant. With exponentially expanding space, two nearby observers are separated very quickly; so much so, that the distance between them quickly exceeds the limits of communications. The spatial slices are expanding very fast to cover huge volumes. Things are constantly moving beyond the cosmological horizon, which is a fixed distance away, and everything becomes homogeneous.

As the inflationary field slowly relaxes to the vacuum, the cosmological constant goes to zero and space begins to expand normally. The new regions that come into view during the normal expansion phase are exactly the same regions that were pushed out of the horizon during inflation, and so they are at nearly the same temperature and curvature, because they come from the same originally small patch of space.

The theory of inflation thus explains why the temperatures and curvatures of different regions are so nearly equal. It also predicts that the total curvature of a space-slice at constant global time is zero. This prediction implies that the total ordinary matter, dark matter and residual vacuum energy in the Universe have to add up to the critical density, and the evidence supports this. More strikingly, inflation allows physicists to calculate the minute differences in temperature of different regions from quantum fluctuations during the inflationary era, and many of these quantitative predictions have been confirmed.

Space expands

In a space that expands exponentially (or nearly exponentially) with time, any pair of free-floating objects that are initially at rest will move apart from each other at an accelerating rate, at least as long as they are not bound together by any force. From the point of view of one such object, the spacetime is something like an inside-out Schwarzschild black hole—each object is surrounded by a spherical event horizon. Once the other object has fallen through this horizon it can never return, and even light signals it sends will never reach the first object (at least so long as the space continues to expand exponentially).

In the approximation that the expansion is exactly exponential, the horizon is static and remains a fixed physical distance away. This patch of an inflating universe can be described by the following metric:

${\displaystyle ds^{2}=-(1-\Lambda r^{2})\,dt^{2}+{1 \over 1-\Lambda r^{2}}\,dr^{2}+r^{2}\,d\Omega ^{2}.}$

This exponentially expanding spacetime is called a de Sitter space, and to sustain it there must be a cosmological constant, a vacuum energy density that is constant in space and time and proportional to Λ in the above metric. For the case of exactly exponential expansion, the vacuum energy has a negative pressure p equal in magnitude to its energy density ρ; the equation of state is p=−ρ.

Inflation is typically not an exactly exponential expansion, but rather quasi- or near-exponential. In such a universe the horizon will slowly grow with time as the vacuum energy density gradually decreases.

Few inhomogeneities remain

Because the accelerating expansion of space stretches out any initial variations in density or temperature to very large length scales, an essential feature of inflation is that it smooths out inhomogeneities and anisotropies, and reduces the curvature of space. This pushes the Universe into a very simple state in which it is completely dominated by the inflaton field and the only significant inhomogeneities are tiny quantum fluctuations. Inflation also dilutes exotic heavy particles, such as the magnetic monopoles predicted by many extensions to the Standard Model of particle physics. If the Universe was only hot enough to form such particles before a period of inflation, they would not be observed in nature, as they would be so rare that it is quite likely that there are none in the observable universe. Together, these effects are called the inflationary "no-hair theorem" by analogy with the no hair theorem for black holes.

The "no-hair" theorem works essentially because the cosmological horizon is no different from a black-hole horizon, except for philosophical disagreements about what is on the other side. The interpretation of the no-hair theorem is that the Universe (observable and unobservable) expands by an enormous factor during inflation. In an expanding universe, energy densities generally fall, or get diluted, as the volume of the Universe increases. For example, the density of ordinary "cold" matter (dust) goes down as the inverse of the volume: when linear dimensions double, the energy density goes down by a factor of eight; the radiation energy density goes down even more rapidly as the Universe expands since the wavelength of each photon is stretched (redshifted), in addition to the photons being dispersed by the expansion. When linear dimensions are doubled, the energy density in radiation falls by a factor of sixteen (see the solution of the energy density continuity equation for an ultra-relativistic fluid). During inflation, the energy density in the inflaton field is roughly constant. However, the energy density in everything else, including inhomogeneities, curvature, anisotropies, exotic particles, and standard-model particles is falling, and through sufficient inflation these all become negligible. This leaves the Universe flat and symmetric, and (apart from the homogeneous inflaton field) mostly empty, at the moment inflation ends and reheating begins.

Duration

A key requirement is that inflation must continue long enough to produce the present observable universe from a single, small inflationary Hubble volume. This is necessary to ensure that the Universe appears flat, homogeneous and isotropic at the largest observable scales. This requirement is generally thought to be satisfied if the Universe expanded by a factor of at least 10²⁶ during inflation.

Reheating

Inflation is a period of supercooled expansion, when the temperature drops by a factor of 100,000 or so. (The exact drop is model-dependent, but in the first models it was typically from 10²⁷ K down to 10²² K.) This relatively low temperature is maintained during the inflationary phase. When inflation ends the temperature returns to the pre-inflationary temperature; this is called reheating or thermalization because the large potential energy of the inflaton field decays into particles and fills the Universe with Standard Model particles, including electromagnetic radiation, starting the radiation dominated phase of the Universe. Because the nature of the inflation is not known, this process is still poorly understood, although it is believed to take place through a parametric resonance.

Motivations

Inflation resolves several problems in Big Bang cosmology that were discovered in the 1970s. Inflation was first proposed by Alan Guth in 1979 while investigating the problem of why no magnetic monopoles are seen today; he found that a positive-energy false vacuum would, according to general relativity, generate an exponential expansion of space. It was very quickly realised that such an expansion would resolve many other long-standing problems. These problems arise from the observation that to look like it does today, the Universe would have to have started from very finely tuned, or "special" initial conditions at the Big Bang. Inflation attempts to resolve these problems by providing a dynamical mechanism that drives the Universe to this special state, thus making a universe like ours much more likely in the context of the Big Bang theory.

Horizon problem

The horizon problem is the problem of determining why the Universe appears statistically homogeneous and isotropic in accordance with the cosmological principle. For example, molecules in a canister of gas are distributed homogeneously and isotropically because they are in thermal equilibrium: gas throughout the canister has had enough time to interact to dissipate inhomogeneities and anisotropies. The situation is quite different in the big bang model without inflation, because gravitational expansion does not give the early universe enough time to equilibrate. In a big bang with only the matter and radiation known in the Standard Model, two widely separated regions of the observable universe cannot have equilibrated because they move apart from each other faster than the speed of light and thus have never come into causal contact. In the early Universe, it was not possible to send a light signal between the two regions. Because they have had no interaction, it is difficult to explain why they have the same temperature (are thermally equilibrated). Historically, proposed solutions included the Phoenix universe of Georges Lemaître, the related oscillatory universe of Richard Chase Tolman, and the Mixmaster universe of Charles Misner. Lemaître and Tolman proposed that a universe undergoing a number of cycles of contraction and expansion could come into thermal equilibrium. Their models failed, however, because of the buildup of entropy over several cycles. Misner made the (ultimately incorrect) conjecture that the Mixmaster mechanism, which made the Universe more chaotic, could lead to statistical homogeneity and isotropy.

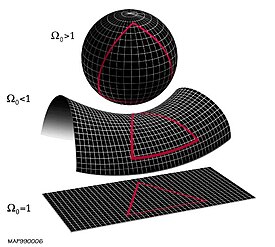
Flatness problem

The flatness problem is sometimes called one of the Dicke coincidences (along with the cosmological constant problem). It became known in the 1960s that the density of matter in the Universe was comparable to the critical density necessary for a flat universe (that is, a universe whose large scale geometry is the usual Euclidean geometry, rather than a non-Euclidean hyperbolic or spherical geometry).

Therefore, regardless of the shape of the universe the contribution of spatial curvature to the expansion of the Universe could not be much greater than the contribution of matter. But as the Universe expands, the curvature redshifts away more slowly than matter and radiation. Extrapolated into the past, this presents a fine-tuning problem because the contribution of curvature to the Universe must be exponentially small (sixteen orders of magnitude less than the density of radiation at Big Bang nucleosynthesis, for example). This problem is exacerbated by recent observations of the cosmic microwave background that have demonstrated that the Universe is flat to within a few percent.

Magnetic-monopole problem

The magnetic monopole problem, sometimes called the exotic-relics problem, says that if the early universe were very hot, a large number of very heavy, stable magnetic monopoles would have been produced. This is a problem with Grand Unified Theories, which propose that at high temperatures (such as in the early universe) the electromagnetic force, strong, and weak nuclear forces are not actually fundamental forces but arise due to spontaneous symmetry breaking from a single gauge theory. These theories predict a number of heavy, stable particles that have not been observed in nature. The most notorious is the magnetic monopole, a kind of stable, heavy "charge" of magnetic field.Monopoles are predicted to be copiously produced following Grand Unified Theories at high temperature, and they should have persisted to the present day, to such an extent that they would become the primary constituent of the Universe. Not only is that not the case, but all searches for them have failed, placing stringent limits on the density of relic magnetic monopoles in the Universe. A period of inflation that occurs below the temperature where magnetic monopoles can be produced would offer a possible resolution of this problem: monopoles would be separated from each other as the Universe around them expands, potentially lowering their observed density by many orders of magnitude. Though, as cosmologist Martin Rees has written, "Skeptics about exotic physics might not be hugely impressed by a theoretical argument to explain the absence of particles that are themselves only hypothetical. Preventive medicine can readily seem 100 percent effective against a disease that doesn't exist!"

History

Precursors

In the early days of General Relativity, Albert Einstein introduced the cosmological constant to allow a static solution, which was a three-dimensional sphere with a uniform density of matter. Later, Willem de Sitter found a highly symmetric inflating universe, which described a universe with a cosmological constant that is otherwise empty. It was discovered that Einstein's universe is unstable, and that small fluctuations cause it to collapse or turn into a de Sitter universe.

In the early 1970s Zeldovich noticed the flatness and horizon problems of Big Bang cosmology; before his work, cosmology was presumed to be symmetrical on purely philosophical grounds. In the Soviet Union, this and other considerations led Belinski and Khalatnikov to analyze the chaotic BKL singularity in General Relativity. Misner's Mixmaster universe attempted to use this chaotic behavior to solve the cosmological problems, with limited success.

False vacuum

In the late 1970s, Sidney Coleman applied the instanton techniques developed by Alexander Polyakov and collaborators to study the fate of the false vacuum in quantum field theory. Like a metastable phase in statistical mechanics—water below the freezing temperature or above the boiling point—a quantum field would need to nucleate a large enough bubble of the new vacuum, the new phase, in order to make a transition. Coleman found the most likely decay pathway for vacuum decay and calculated the inverse lifetime per unit volume. He eventually noted that gravitational effects would be significant, but he did not calculate these effects and did not apply the results to cosmology.

The universe could have been spontaneously created from nothing (no space, time, nor matter) by quantum fluctuations of metastable false vacuum causing an expanding bubble of true vacuum.

Starobinsky inflation

In the Soviet Union, Alexei Starobinsky noted that quantum corrections to general relativity should be important for the early universe. These generically lead to curvature-squared corrections to the Einstein–Hilbert action and a form of f(R) modified gravity. The solution to Einstein's equations in the presence of curvature squared terms, when the curvatures are large, leads to an effective cosmological constant. Therefore, he proposed that the early universe went through an inflationary de Sitter era. This resolved the cosmology problems and led to specific predictions for the corrections to the microwave background radiation, corrections that were then calculated in detail. Starobinsky used the action

${\displaystyle S={\frac {1}{2}}\int d^{4}x\left(R+{\frac {R^{2}}{6M^{2}}}\right)}$

which corresponds to the potential

${\displaystyle \quad V(\phi )=\Lambda ^{4}\left(1-e^{-{\sqrt {2/3}}\phi /M_{p}^{2}}\right)^{2}}$

in the Einstein frame. This results in the observables: ${\displaystyle n_{s}=1-{\frac {2}{N}},\quad \quad r={\frac {12}{N^{2}}}.}$

Monopole problem

In 1978, Zeldovich noted the monopole problem, which was an unambiguous quantitative version of the horizon problem, this time in a subfield of particle physics, which led to several speculative attempts to resolve it. In 1980 Alan Guth realized that false vacuum decay in the early universe would solve the problem, leading him to propose a scalar-driven inflation. Starobinsky's and Guth's scenarios both predicted an initial de Sitter phase, differing only in mechanistic details.

Early inflationary models

Guth proposed inflation in January 1981 to explain the nonexistence of magnetic monopoles; it was Guth who coined the term "inflation". At the same time, Starobinsky argued that quantum corrections to gravity would replace the initial singularity of the Universe with an exponentially expanding de Sitter phase. In October 1980, Demosthenes Kazanas suggested that exponential expansion could eliminate the particle horizon and perhaps solve the horizon problem, while Sato suggested that an exponential expansion could eliminate domain walls (another kind of exotic relic). In 1981 Einhorn and Sato published a model similar to Guth's and showed that it would resolve the puzzle of the magnetic monopole abundance in Grand Unified Theories. Like Guth, they concluded that such a model not only required fine tuning of the cosmological constant, but also would likely lead to a much too granular universe, i.e., to large density variations resulting from bubble wall collisions.

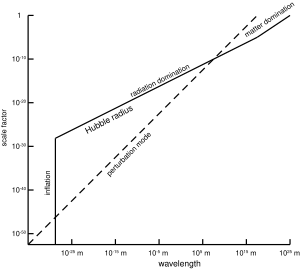
The physical size of the Hubble radius (solid line) as a function of the linear expansion (scale factor) of the universe. During cosmological inflation, the Hubble radius is constant. The physical wavelength of a perturbation mode (dashed line) is also shown. The plot illustrates how the perturbation mode grows larger than the horizon during cosmological inflation before coming back inside the horizon, which grows rapidly during radiation domination. If cosmological inflation had never happened, and radiation domination continued back until a gravitational singularity, then the mode would never have been inside the horizon in the very early universe, and no causal mechanism could have ensured that the universe was homogeneous on the scale of the perturbation mode.

Guth proposed that as the early universe cooled, it was trapped in a false vacuum with a high energy density, which is much like a cosmological constant. As the very early universe cooled it was trapped in a metastable state (it was supercooled), which it could only decay out of through the process of bubble nucleation via quantum tunneling. Bubbles of true vacuum spontaneously form in the sea of false vacuum and rapidly begin expanding at the speed of light. Guth recognized that this model was problematic because the model did not reheat properly: when the bubbles nucleated, they did not generate any radiation. Radiation could only be generated in collisions between bubble walls. But if inflation lasted long enough to solve the initial conditions problems, collisions between bubbles became exceedingly rare. In any one causal patch it is likely that only one bubble would nucleate.

... Kazanas (1980) called this phase of the early Universe "de Sitter's phase." The name "inflation" was given by Guth (1981). ... Guth himself did not refer to work of Kazanas until he published a book on the subject under the title "The inflationary universe: the quest for a new theory of cosmic origin" (1997), where he apologizes for not having referenced the work of Kazanas and of others, related to inflation.

Slow-roll inflation

The bubble collision problem was solved by Linde and independently by Andreas Albrecht and Paul Steinhardt in a model named new inflation or slow-roll inflation (Guth's model then became known as old inflation). In this model, instead of tunneling out of a false vacuum state, inflation occurred by a scalar field rolling down a potential energy hill. When the field rolls very slowly compared to the expansion of the Universe, inflation occurs. However, when the hill becomes steeper, inflation ends and reheating can occur.

Effects of asymmetries

Eventually, it was shown that new inflation does not produce a perfectly symmetric universe, but that quantum fluctuations in the inflaton are created. These fluctuations form the primordial seeds for all structure created in the later universe. These fluctuations were first calculated by Viatcheslav Mukhanov and G. V. Chibisov in analyzing Starobinsky's similar model.

 In the context of inflation, they were worked out independently of the work of Mukhanov and Chibisov at the three-week 1982 Nuffield Workshop on the Very Early Universe at Cambridge University. The fluctuations were calculated by four groups working separately over the course of the workshop: Stephen Hawking; Starobinsky; Guth and So-Young Pi; and Bardeen, Steinhardt and Turner.

Observational status

Inflation is a mechanism for realizing the cosmological principle, which is the basis of the standard model of physical cosmology: it accounts for the homogeneity and isotropy of the observable universe. In addition, it accounts for the observed flatness and absence of magnetic monopoles. Since Guth's early work, each of these observations has received further confirmation, most impressively by the detailed observations of the cosmic microwave background made by the Planck spacecraft. This analysis shows that the Universe is flat to within 0.5 percent, and that it is homogeneous and isotropic to one part in 100,000.

Inflation predicts that the structures visible in the Universe today formed through the gravitational collapse of perturbations that were formed as quantum mechanical fluctuations in the inflationary epoch. The detailed form of the spectrum of perturbations, called a nearly-scale-invariant Gaussian random field is very specific and has only two free parameters. One is the amplitude of the spectrum and the spectral index, which measures the slight deviation from scale invariance predicted by inflation (perfect scale invariance corresponds to the idealized de Sitter universe). The other free parameter is the tensor to scalar ratio. The simplest inflation models, those without fine-tuning, predict a tensor to scalar ratio near 0.1.

Inflation predicts that the observed perturbations should be in thermal equilibrium with each other (these are called adiabatic or isentropic perturbations). This structure for the perturbations has been confirmed by the Planck spacecraft, WMAP spacecraft and other cosmic microwave background (CMB) experiments, and galaxy surveys, especially the ongoing Sloan Digital Sky Survey. These experiments have shown that the one part in 100,000 inhomogeneities observed have exactly the form predicted by theory. There is evidence for a slight deviation from scale invariance. The spectral index, n_s is one for a scale-invariant Harrison–Zel'dovich spectrum. The simplest inflation models predict that n_s is between 0.92 and 0.98. This is the range that is possible without fine-tuning of the parameters related to energy. From Planck data it can be inferred that n_s=0.968 ± 0.006, and a tensor to scalar ratio that is less than 0.11. These are considered an important confirmation of the theory of inflation.

Various inflation theories have been proposed that make radically different predictions, but they generally have much more fine tuning than should be necessary. As a physical model, however, inflation is most valuable in that it robustly predicts the initial conditions of the Universe based on only two adjustable parameters: the spectral index (that can only change in a small range) and the amplitude of the perturbations. Except in contrived models, this is true regardless of how inflation is realized in particle physics.

Occasionally, effects are observed that appear to contradict the simplest models of inflation. The first-year WMAP data suggested that the spectrum might not be nearly scale-invariant, but might instead have a slight curvature. However, the third-year data revealed that the effect was a statistical anomaly. Another effect remarked upon since the first cosmic microwave background satellite, the Cosmic Background Explorer is that the amplitude of the quadrupole moment of the CMB is unexpectedly low and the other low multipoles appear to be preferentially aligned with the ecliptic plane. Some have claimed that this is a signature of non-Gaussianity and thus contradicts the simplest models of inflation. Others have suggested that the effect may be due to other new physics, foreground contamination, or even publication bias.

An experimental program is underway to further test inflation with more precise CMB measurements. In particular, high precision measurements of the so-called "B-modes" of the polarization of the background radiation could provide evidence of the gravitational radiation produced by inflation, and could also show whether the energy scale of inflation predicted by the simplest models (10¹⁵–10¹⁶ GeV) is correct. In March 2014, the BICEP2 team announced B-mode CMB polarization confirming inflation had been demonstrated. The team announced the tensor-to-scalar power ratio ${\displaystyle r}$ was between 0.15 and 0.27 (rejecting the null hypothesis; ${\displaystyle r}$ is expected to be 0 in the absence of inflation). However, on 19 June 2014, lowered confidence in confirming the findings was reported; on 19 September 2014, a further reduction in confidence was reported and, on 30 January 2015, even less confidence yet was reported. By 2018, additional data suggested, with 95% confidence, that ${\displaystyle r}$ is 0.06 or lower: consistent with the null hypothesis, but still also consistent with many remaining models of inflation.

Other potentially corroborating measurements are expected from the Planck spacecraft, although it is unclear if the signal will be visible, or if contamination from foreground sources will interfere. Other forthcoming measurements, such as those of 21 centimeter radiation (radiation emitted and absorbed from neutral hydrogen before the first stars formed), may measure the power spectrum with even greater resolution than the CMB and galaxy surveys, although it is not known if these measurements will be possible or if interference with radio sources on Earth and in the galaxy will be too great.

Theoretical status

Unsolved problem in physics:

Is the theory of cosmological inflation correct, and if so, what are the details of this epoch? What is the hypothetical inflaton field giving rise to inflation?

In Guth's early proposal, it was thought that the inflaton was the Higgs field, the field that explains the mass of the elementary particles. It is now believed by some that the inflaton cannot be the Higgs field although the recent discovery of the Higgs boson has increased the number of works considering the Higgs field as inflaton. One problem of this identification is the current tension with experimental data at the electroweak scale, which is currently under study at the Large Hadron Collider (LHC). Other models of inflation relied on the properties of Grand Unified Theories. Since the simplest models of grand unification have failed, it is now thought by many physicists that inflation will be included in a supersymmetric theory such as string theory or a supersymmetric grand unified theory. At present, while inflation is understood principally by its detailed predictions of the initial conditions for the hot early universe, the particle physics is largely ad hoc modelling. As such, although predictions of inflation have been consistent with the results of observational tests, many open questions remain.

Fine-tuning problem

One of the most severe challenges for inflation arises from the need for fine tuning. In new inflation, the slow-roll conditions must be satisfied for inflation to occur. The slow-roll conditions say that the inflaton potential must be flat (compared to the large vacuum energy) and that the inflaton particles must have a small mass. New inflation requires the Universe to have a scalar field with an especially flat potential and special initial conditions. However, explanations for these fine-tunings have been proposed. For example, classically scale invariant field theories, where scale invariance is broken by quantum effects, provide an explanation of the flatness of inflationary potentials, as long as the theory can be studied through perturbation theory.

Linde proposed a theory known as chaotic inflation in which he suggested that the conditions for inflation were actually satisfied quite generically. Inflation will occur in virtually any universe that begins in a chaotic, high energy state that has a scalar field with unbounded potential energy. However, in his model the inflaton field necessarily takes values larger than one Planck unit: for this reason, these are often called large field models and the competing new inflation models are called small field models. In this situation, the predictions of effective field theory are thought to be invalid, as renormalization should cause large corrections that could prevent inflation. This problem has not yet been resolved and some cosmologists argue that the small field models, in which inflation can occur at a much lower energy scale, are better models. While inflation depends on quantum field theory (and the semiclassical approximation to quantum gravity) in an important way, it has not been completely reconciled with these theories.

Brandenberger commented on fine-tuning in another situation. The amplitude of the primordial inhomogeneities produced in inflation is directly tied to the energy scale of inflation. This scale is suggested to be around 10¹⁶ GeV or 10⁻³ times the Planck energy. The natural scale is naïvely the Planck scale so this small value could be seen as another form of fine-tuning (called a hierarchy problem): the energy density given by the scalar potential is down by 10⁻¹² compared to the Planck density. This is not usually considered to be a critical problem, however, because the scale of inflation corresponds naturally to the scale of gauge unification.

Eternal inflation

In many models, the inflationary phase of the Universe's expansion lasts forever in at least some regions of the Universe. This occurs because inflating regions expand very rapidly, reproducing themselves. Unless the rate of decay to the non-inflating phase is sufficiently fast, new inflating regions are produced more rapidly than non-inflating regions. In such models, most of the volume of the Universe is continuously inflating at any given time.

All models of eternal inflation produce an infinite, hypothetical multiverse, typically a fractal. The multiverse theory has created significant dissension in the scientific community about the viability of the inflationary model.

Paul Steinhardt, one of the original architects of the inflationary model, introduced the first example of eternal inflation in 1983. He showed that the inflation could proceed forever by producing bubbles of non-inflating space filled with hot matter and radiation surrounded by empty space that continues to inflate. The bubbles could not grow fast enough to keep up with the inflation. Later that same year, Alexander Vilenkin showed that eternal inflation is generic.

Although new inflation is classically rolling down the potential, quantum fluctuations can sometimes lift it to previous levels. These regions in which the inflaton fluctuates upwards expand much faster than regions in which the inflaton has a lower potential energy, and tend to dominate in terms of physical volume. It has been shown that any inflationary theory with an unbounded potential is eternal. There are well-known theorems that this steady state cannot continue forever into the past. Inflationary spacetime, which is similar to de Sitter space, is incomplete without a contracting region. However, unlike de Sitter space, fluctuations in a contracting inflationary space collapse to form a gravitational singularity, a point where densities become infinite. Therefore, it is necessary to have a theory for the Universe's initial conditions.

In eternal inflation, regions with inflation have an exponentially growing volume, while regions that are not inflating don't. This suggests that the volume of the inflating part of the Universe in the global picture is always unimaginably larger than the part that has stopped inflating, even though inflation eventually ends as seen by any single pre-inflationary observer. Scientists disagree about how to assign a probability distribution to this hypothetical anthropic landscape. If the probability of different regions is counted by volume, one should expect that inflation will never end or applying boundary conditions that a local observer exists to observe it, that inflation will end as late as possible.

Some physicists believe this paradox can be resolved by weighting observers by their pre-inflationary volume. Others believe that there is no resolution to the paradox and that the multiverse is a critical flaw in the inflationary paradigm. Paul Steinhardt, who first introduced the eternal inflationary model, later became one of its most vocal critics for this reason.

Initial conditions

Some physicists have tried to avoid the initial conditions problem by proposing models for an eternally inflating universe with no origin. These models propose that while the Universe, on the largest scales, expands exponentially it was, is and always will be, spatially infinite and has existed, and will exist, forever.

Other proposals attempt to describe the ex nihilo creation of the Universe based on quantum cosmology and the following inflation. Vilenkin put forth one such scenario. Hartle and Hawking offered the no-boundary proposal for the initial creation of the Universe in which inflation comes about naturally.

Guth described the inflationary universe as the "ultimate free lunch": new universes, similar to our own, are continually produced in a vast inflating background. Gravitational interactions, in this case, circumvent (but do not violate) the first law of thermodynamics (energy conservation) and the second law of thermodynamics (entropy and the arrow of time problem). However, while there is consensus that this solves the initial conditions problem, some have disputed this, as it is much more likely that the Universe came about by a quantum fluctuation. Don Page was an outspoken critic of inflation because of this anomaly. He stressed that the thermodynamic arrow of time necessitates low entropy initial conditions, which would be highly unlikely. According to them, rather than solving this problem, the inflation theory aggravates it – the reheating at the end of the inflation era increases entropy, making it necessary for the initial state of the Universe to be even more orderly than in other Big Bang theories with no inflation phase.

Hawking and Page later found ambiguous results when they attempted to compute the probability of inflation in the Hartle-Hawking initial state. Other authors have argued that, since inflation is eternal, the probability doesn't matter as long as it is not precisely zero: once it starts, inflation perpetuates itself and quickly dominates the Universe. However, Albrecht and Lorenzo Sorbo argued that the probability of an inflationary cosmos, consistent with today's observations, emerging by a random fluctuation from some pre-existent state is much higher than that of a non-inflationary cosmos. This is because the "seed" amount of non-gravitational energy required for the inflationary cosmos is so much less than that for a non-inflationary alternative, which outweighs any entropic considerations.

Another problem that has occasionally been mentioned is the trans-Planckian problem or trans-Planckian effects. Since the energy scale of inflation and the Planck scale are relatively close, some of the quantum fluctuations that have made up the structure in our universe were smaller than the Planck length before inflation. Therefore, there ought to be corrections from Planck-scale physics, in particular the unknown quantum theory of gravity. Some disagreement remains about the magnitude of this effect: about whether it is just on the threshold of detectability or completely undetectable.

Hybrid inflation

Another kind of inflation, called hybrid inflation, is an extension of new inflation. It introduces additional scalar fields, so that while one of the scalar fields is responsible for normal slow roll inflation, another triggers the end of inflation: when inflation has continued for sufficiently long, it becomes favorable to the second field to decay into a much lower energy state.

In hybrid inflation, one scalar field is responsible for most of the energy density (thus determining the rate of expansion), while another is responsible for the slow roll (thus determining the period of inflation and its termination). Thus fluctuations in the former inflaton would not affect inflation termination, while fluctuations in the latter would not affect the rate of expansion. Therefore, hybrid inflation is not eternal. When the second (slow-rolling) inflaton reaches the bottom of its potential, it changes the location of the minimum of the first inflaton's potential, which leads to a fast roll of the inflaton down its potential, leading to termination of inflation.

Relation to dark energy

Dark energy is broadly similar to inflation and is thought to be causing the expansion of the present-day universe to accelerate. However, the energy scale of dark energy is much lower, 10⁻¹² GeV, roughly 27 orders of magnitude less than the scale of inflation.

Inflation and string cosmology

The discovery of flux compactifications opened the way for reconciling inflation and string theory. Brane inflation suggests that inflation arises from the motion of D-branes in the compactified geometry, usually towards a stack of anti-D-branes. This theory, governed by the Dirac-Born-Infeld action, is different from ordinary inflation. The dynamics are not completely understood. It appears that special conditions are necessary since inflation occurs in tunneling between two vacua in the string landscape. The process of tunneling between two vacua is a form of old inflation, but new inflation must then occur by some other mechanism.

Inflation and loop quantum gravity

When investigating the effects the theory of loop quantum gravity would have on cosmology, a loop quantum cosmology model has evolved that provides a possible mechanism for cosmological inflation. Loop quantum gravity assumes a quantized spacetime. If the energy density is larger than can be held by the quantized spacetime, it is thought to bounce back.

Alternatives and adjuncts

Other models have been advanced that are claimed to explain some or all of the observations addressed by inflation.

Big bounce

The big bounce hypothesis attempts to replace the cosmic singularity with a cosmic contraction and bounce, thereby explaining the initial conditions that led to the big bang. The flatness and horizon problems are naturally solved in the Einstein-Cartan-Sciama-Kibble theory of gravity, without needing an exotic form of matter or free parameters. This theory extends general relativity by removing a constraint of the symmetry of the affine connection and regarding its antisymmetric part, the torsion tensor, as a dynamical variable. The minimal coupling between torsion and Dirac spinors generates a spin-spin interaction that is significant in fermionic matter at extremely high densities. Such an interaction averts the unphysical Big Bang singularity, replacing it with a cusp-like bounce at a finite minimum scale factor, before which the Universe was contracting. The rapid expansion immediately after the Big Bounce explains why the present Universe at largest scales appears spatially flat, homogeneous and isotropic. As the density of the Universe decreases, the effects of torsion weaken and the Universe smoothly enters the radiation-dominated era.

Ekpyrotic and cyclic models

The ekpyrotic and cyclic models are also considered adjuncts to inflation. These models solve the horizon problem through an expanding epoch well before the Big Bang, and then generate the required spectrum of primordial density perturbations during a contracting phase leading to a Big Crunch. The Universe passes through the Big Crunch and emerges in a hot Big Bang phase. In this sense they are reminiscent of Richard Chace Tolman's oscillatory universe; in Tolman's model, however, the total age of the Universe is necessarily finite, while in these models this is not necessarily so. Whether the correct spectrum of density fluctuations can be produced, and whether the Universe can successfully navigate the Big Bang/Big Crunch transition, remains a topic of controversy and current research. Ekpyrotic models avoid the magnetic monopole problem as long as the temperature at the Big Crunch/Big Bang transition remains below the Grand Unified Scale, as this is the temperature required to produce magnetic monopoles in the first place. As things stand, there is no evidence of any 'slowing down' of the expansion, but this is not surprising as each cycle is expected to last on the order of a trillion years.

String gas cosmology

String theory requires that, in addition to the three observable spatial dimensions, additional dimensions exist that are curled up or compactified (see also Kaluza–Klein theory). Extra dimensions appear as a frequent component of supergravity models and other approaches to quantum gravity. This raised the contingent question of why four space-time dimensions became large and the rest became unobservably small. An attempt to address this question, called string gas cosmology, was proposed by Robert Brandenberger and Cumrun Vafa. This model focuses on the dynamics of the early universe considered as a hot gas of strings. Brandenberger and Vafa show that a dimension of spacetime can only expand if the strings that wind around it can efficiently annihilate each other. Each string is a one-dimensional object, and the largest number of dimensions in which two strings will generically intersect (and, presumably, annihilate) is three. Therefore, the most likely number of non-compact (large) spatial dimensions is three. Current work on this model centers on whether it can succeed in stabilizing the size of the compactified dimensions and produce the correct spectrum of primordial density perturbations. The original model did not "solve the entropy and flatness problems of standard cosmology", although Brandenburger and coauthors later argued that these problems can be eliminated by implementing string gas cosmology in the context of a bouncing-universe scenario.

Varying c

Cosmological models employing a variable speed of light have been proposed to resolve the horizon problem of and provide an alternative to cosmic inflation. In the VSL models, the fundamental constant c, denoting the speed of light in vacuum, is greater in the early universe than its present value, effectively increasing the particle horizon at the time of decoupling sufficiently to account for the observed isotropy of the CMB.

Criticisms

Since its introduction by Alan Guth in 1980, the inflationary paradigm has become widely accepted. Nevertheless, many physicists, mathematicians, and philosophers of science have voiced criticisms, claiming untestable predictions and a lack of serious empirical support. In 1999, John Earman and Jesús Mosterín published a thorough critical review of inflationary cosmology, concluding, "we do not think that there are, as yet, good grounds for admitting any of the models of inflation into the standard core of cosmology."

In order to work, and as pointed out by Roger Penrose from 1986 on, inflation requires extremely specific initial conditions of its own, so that the problem (or pseudo-problem) of initial conditions is not solved: "There is something fundamentally misconceived about trying to explain the uniformity of the early universe as resulting from a thermalization process. [...] For, if the thermalization is actually doing anything [...] then it represents a definite increasing of the entropy. Thus, the universe would have been even more special before the thermalization than after." The problem of specific or "fine-tuned" initial conditions would not have been solved; it would have gotten worse. At a conference in 2015, Penrose said that "inflation isn't falsifiable, it's falsified. [...] BICEP did a wonderful service by bringing all the Inflation-ists out of their shell, and giving them a black eye."

A recurrent criticism of inflation is that the invoked inflaton field does not correspond to any known physical field, and that its potential energy curve seems to be an ad hoc contrivance to accommodate almost any data obtainable. Paul Steinhardt, one of the founding fathers of inflationary cosmology, has recently become one of its sharpest critics. He calls 'bad inflation' a period of accelerated expansion whose outcome conflicts with observations, and 'good inflation' one compatible with them: "Not only is bad inflation more likely than good inflation, but no inflation is more likely than either [...] Roger Penrose considered all the possible configurations of the inflaton and gravitational fields. Some of these configurations lead to inflation [...] Other configurations lead to a uniform, flat universe directly – without inflation. Obtaining a flat universe is unlikely overall. Penrose's shocking conclusion, though, was that obtaining a flat universe without inflation is much more likely than with inflation – by a factor of 10 to the googol (10 to the 100) power!" Together with Anna Ijjas and Abraham Loeb, he wrote articles claiming that the inflationary paradigm is in trouble in view of the data from the Planck satellite. Counter-arguments were presented by Alan Guth, David Kaiser, and Yasunori Nomura and by Andrei Linde, saying that "cosmic inflation is on a stronger footing than ever before".