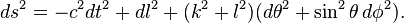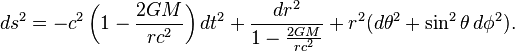For a simplified notion of a wormhole,
space can be visualized as a two-dimensional (2D) surface. In this case, a wormhole would appear as a hole in that surface, lead into a
3D tube (the inside surface of a cylinder), then re-emerge at another location on the 2D surface with a hole similar to the entrance. An actual wormhole would be analogous to this, but with the spatial dimensions raised by one. For example, instead of circular holes on a 2D plane, the entry and exit points could be visualized as spheres in 3D space.
Overview
Researchers have no observational evidence for wormholes, but the equations of the theory of
general relativity have valid solutions that contain wormholes. The first type of wormhole solution discovered was the Schwarzschild wormhole, which would be present in the
Schwarzschild metric describing an eternal
black hole, but it was found that it would collapse too quickly for anything to cross from one end to the other. Wormholes that could be crossed in both directions, known as
traversable wormholes, would only be possible if
exotic matter with negative
energy density could be used to stabilize them. Wormholes are also a very powerful mathematical metaphor for teaching general relativity.
The
Casimir effect shows that quantum field theory allows the energy density in certain regions of space to be negative relative to the ordinary vacuum energy, and it has been shown theoretically that quantum field theory allows states where energy can be
arbitrarily negative at a given point.
[1] Many physicists, such as
Stephen Hawking,
[2] Kip Thorne[3] and others,
[4][5][6] therefore argue that such effects might make it possible to stabilize a traversable wormhole. Physicists have not found any natural process that would be predicted to form a wormhole naturally in the context of general relativity, although the
quantum foam hypothesis is sometimes used to suggest that tiny wormholes might appear and disappear spontaneously at the
Planck scale,
[7][8] and stable versions of such wormholes have been suggested as
dark matter candidates.
[9][10] It has also been proposed that, if a tiny wormhole held open by a
negative mass cosmic string had appeared around the time of the
Big Bang, it could have been inflated to
macroscopic size by
cosmic inflation.
[11]
The American
theoretical physicist John Archibald Wheeler coined the term
wormhole in 1957; the German mathematician
Hermann Weyl, however, had proposed the wormhole theory in 1921, in connection with mass analysis of
electromagnetic field energy.
[12]
This analysis forces one to consider situations... where there is a net flux of lines of force, through what topologists would call "a handle" of the multiply-connected space, and what physicists might perhaps be excused for more vividly terming a "wormhole".
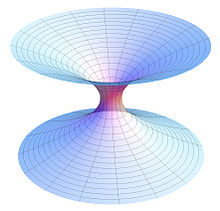
"Embedding diagram" of a Schwarzschild wormhole (see below)
Definition
The basic notion of an intra-universe wormhole is that it is a
compact region of spacetime whose boundary is topologically trivial, but whose interior is not
simply connected. Formalizing this idea leads to definitions such as the following, taken from Matt Visser's
Lorentzian Wormholes.
If a Minkowski spacetime contains a compact region Ω, and if the topology of Ω is of the form Ω ~ R x Σ, where Σ is a three-manifold of the nontrivial topology, whose boundary has topology of the form ∂Σ ~ S2, and if, furthermore, the hypersurfaces Σ are all spacelike, then the region Ω contains a quasipermanent intra-universe wormhole.
Wormholes have been defined
geometrically, as opposed to topologically,
[clarification needed] as regions of spacetime that constrain the incremental deformation of closed surfaces. For example, in Enrico Rodrigo’s
The Physics of Stargates, a wormhole is defined informally as:
a region of spacetime containing a "world tube" (the time evolution of a closed surface) that cannot be continuously deformed (shrunk) to a world line (the time evolution of a point).
Schwarzschild wormholes

An artist's impression of a wormhole from an observer's perspective, crossing the
event horizon of a Schwarzschild wormhole that bridges two different universes. The observer originates from the right, and another universe becomes visible in the center of the wormhole’s shadow once the horizon is crossed, the observer seeing light that has fallen into the
black hole interior region from the other universe; however, this other universe is unreachable in the case of a Schwarzschild wormhole, as the bridge always collapses before the observer has time to cross it, and everything that has fallen through the event horizon of either universe is inevitably crushed in the
singularity.
Lorentzian wormholes known as
Schwarzschild wormholes or
Einstein–Rosen bridges are connections between areas of space that can be modeled as
vacuum solutions to the
Einstein field equations, and that are now understood to be intrinsic parts of the
maximally extended version of the
Schwarzschild metric describing an eternal
black hole with no charge and no rotation. Here, "maximally extended" refers to the idea that the spacetime should not have any "edges": for any possible trajectory of a free-falling particle (following a
Geodesic in the spacetime, it should be possible to continue this path arbitrarily far into the particle's future or past, unless the trajectory hits a
gravitational singularity like the one at the center of the black hole's interior. In order to satisfy this requirement, it turns out that in addition to the black hole interior region that particles enter when they fall through the
event horizon from the outside, there must be a separate
white hole interior region that allows us to extrapolate the trajectories of particles that an outside observer sees rising up
away from the event horizon. And just as there are two separate interior regions of the maximally extended spacetime, there are also two separate exterior regions, sometimes called two different "universes", with the second universe allowing us to extrapolate some possible particle trajectories in the two interior regions. This means that the interior black hole region can contain a mix of particles that fell in from either universe (and thus an observer who fell in from one universe might be able to see light that fell in from the other one), and likewise particles from the interior white hole region can escape into either universe. All four regions can be seen in a spacetime diagram that uses
Kruskal–Szekeres coordinates.
In this spacetime, it is possible to come up with coordinate systems such that if you pick a hypersurface of constant time (a set of points that all have the same time coordinate, such that every point on the surface has a
space-like separation, giving what is called a 'space-like surface') and draw an "embedding diagram" depicting the curvature of space at that time, the embedding diagram will look like a tube connecting the two exterior regions, known as an "Einstein–Rosen bridge". Note that the Schwarzschild metric describes an idealized black hole that exists eternally from the perspective of external observers; a more realistic black hole that forms at some particular time from a collapsing star would require a different metric. When the infalling stellar matter is added to a diagram of a black hole's history, it removes the part of the diagram corresponding to the white hole interior region, along with the part of the diagram corresponding to the other universe.
[13]
The Einstein–Rosen bridge was discovered by
Ludwig Flamm[14] in 1916, a few months after Schwarzschild published his solution, and was rediscovered (although it is hard to imagine that Einstein had not seen Flamm's paper when it came out) by
Albert Einstein and his colleague
Nathan Rosen, who published their result in 1935. However, in 1962,
John A. Wheeler and
Robert W. Fuller published a paper showing that this type of wormhole is unstable if it connects two parts of the same universe, and that it will pinch off too quickly for light (or any particle moving slower than light) that falls in from one exterior region to make it to the other exterior region.
According to general relativity, the gravitational collapse of a sufficiently compact mass forms a singular Schwarzschild black hole. In the
Einstein–Cartan–Sciama–Kibble theory of gravity, however, it forms a regular Einstein–Rosen bridge. This theory extends general relativity by removing a constraint of the symmetry of the affine connection and regarding its antisymmetric part, the
torsion tensor, as a dynamical variable. Torsion naturally accounts for the quantum-mechanical, intrinsic angular momentum (
spin) of matter. The minimal coupling between torsion and
Dirac spinors generates a repulsive spin–spin interaction that is significant in fermionic matter at extremely high densities. Such an interaction prevents the formation of a gravitational singularity.
[clarification needed] Instead, the collapsing matter reaches an enormous but finite density and rebounds, forming the other side of the bridge.
[15]
Before the stability problems of Schwarzschild wormholes were apparent, it was proposed that
quasars were white holes forming the ends of wormholes of this type.
[citation needed]
Although Schwarzschild wormholes are not traversable in both directions, their existence inspired
Kip Thorne to imagine traversable wormholes created by holding the "throat" of a Schwarzschild wormhole open with
exotic matter (material that has negative mass/energy).
Traversable wormholes

Image of a simulated traversable wormhole that connects the square in front of the physical institutes of
University of Tübingen with the sand dunes near Boulogne sur Mer in the north of France. The image is calculated with 4D
raytracing in a Morris–Thorne wormhole metric, but the gravitational effects on the wavelength of light have not been simulated.
[16]
Lorentzian traversable wormholes would allow travel in both directions from one part of the universe to another part of that same universe very quickly or would allow travel from one universe to another. The possibility of traversable wormholes in general relativity was first demonstrated by
Kip Thorne and his graduate student
Mike Morris in a 1988 paper. For this reason, the type of traversable wormhole they proposed, held open by a spherical shell of
exotic matter, is referred to as a
Morris–Thorne wormhole. Later, other types of traversable wormholes were discovered as allowable solutions to the equations of general relativity, including a variety analyzed in a 1989 paper by
Matt Visser, in which a path through the wormhole can be made where the traversing path does not pass through a region of exotic matter. However, in the pure
Gauss–Bonnet gravity (a modification to general relativity involving extra spatial dimensions which is sometimes studied in the context of
brane cosmology) exotic matter is not needed in order for wormholes to exist—they can exist even with no matter.
[17] A type held open by negative mass
cosmic strings was put forth by Visser in collaboration with
Cramer et al.,
[11] in which it was proposed that such wormholes could have been naturally created in the early universe.
Wormholes connect two points in spacetime, which means that they would in principle allow
travel in time, as well as in space. In 1988, Morris, Thorne and Yurtsever worked out explicitly how to convert a wormhole traversing space into one traversing time.
[3] However, according to general relativity, it would not be possible to use a wormhole to travel back to a time earlier than when the wormhole was first converted into a time machine by accelerating one of its two mouths.
[18]
Raychaudhuri's theorem and exotic matter
To see why exotic matter is required, consider an incoming light front traveling along geodesics, which then crosses the wormhole and re-expands on the other side. The
expansion goes from negative to positive. As the wormhole neck is of finite size, we would not expect caustics to develop, at least within the vicinity of the neck. According to the optical
Raychaudhuri's theorem, this requires a violation of the
averaged null energy condition. Quantum effects such as the
Casimir effect cannot violate the averaged null energy condition in any neighborhood of space with zero curvature,
[19] but calculations in
semiclassical gravity suggest that quantum effects may be able to violate this condition in curved spacetime.
[20] Although it was hoped recently that quantum effects could not violate an achronal version of the averaged null energy condition,
[21] violations have nevertheless been found,
[22] so it remains an open possibility that quantum effects might be used to support a wormhole.
Faster-than-light travel
The impossibility of faster-than-light relative speed only applies locally. Wormholes might allow superluminal (
faster-than-light) travel by ensuring that the speed of light is not exceeded locally at any time. While traveling through a wormhole, subluminal (slower-than-light) speeds are used. If two points are connected by a wormhole whose length is shorter than the distance between them
outside the wormhole, the time taken to traverse it could be less than the time it would take a light beam to make the journey if it took a path through the space
outside the wormhole. However, a light beam traveling through the wormhole would of course beat the traveler.
Time travel
The theory of general relativity predicts that if traversable wormholes exist, they could allow
time travel.
[3] This would be accomplished by accelerating one end of the wormhole to a high velocity relative to the other, and then sometime later bringing it back;
relativistic time dilation would result in the accelerated wormhole mouth aging less than the stationary one as seen by an external observer, similar to what is seen in the
twin paradox. However, time connects differently through the wormhole than outside it, so that
synchronized clocks at each mouth will remain synchronized to someone traveling through the wormhole itself, no matter how the mouths move around.
[23] This means that anything which entered the accelerated wormhole mouth would exit the stationary one at a point in time prior to its entry.
For example, consider two clocks at both mouths both showing the date as 2000. After being taken on a trip at relativistic velocities, the accelerated mouth is brought back to the same region as the stationary mouth with the accelerated mouth's clock reading 2004 while the stationary mouth's clock read 2012. A traveler who entered the accelerated mouth at this moment would exit the stationary mouth when its clock also read 2004, in the same region but now eight years in the past. Such a configuration of wormholes would allow for a particle's
world line to form a closed loop in spacetime, known as a
closed timelike curve. An object traveling through a wormhole could carry energy or charge from one time to another, but this would not violate conservation of energy or charge in each time, because the energy/charge of the wormhole mouth itself would change to compensate for the object that fell into it or emerged from it.
[24][25]
It is thought that it may not be possible to convert a wormhole into a time machine in this manner; the predictions are made in the context of general relativity, but general relativity does not include quantum effects. Analyses using the
semiclassical approach to incorporating quantum effects into general relativity have sometimes indicated that a feedback loop of
virtual particles would circulate through the wormhole and pile up on themselves, driving the energy density in the region very high and possibly destroying it before any information could be passed through it, in keeping with the
chronology protection conjecture. The debate on this matter is described by
Kip S. Thorne in the book
Black Holes and Time Warps, and a more technical discussion can be found in
The quantum physics of chronology protection by
Matt Visser.
[26] There is also the
Roman ring, which is a configuration of more than one wormhole. This ring seems to allow a closed time loop with stable wormholes when analyzed using semiclassical gravity, although without a full theory of
quantum gravity it is uncertain whether the semiclassical approach is reliable in this case.
Interuniversal travel
A possible resolution to the paradoxes resulting from wormhole-enabled time travel rests on the
many-worlds interpretation of
quantum mechanics. In 1991 David Deutsch showed that quantum theory is fully consistent (in the sense that the so-called density matrix can be made free of discontinuities) in spacetimes with closed timelike curves.
[27] However, later it was shown that such model of closed timelike curve can have internal inconsistencies as it will lead to strange phenomena like distinguishing non orthogonal quantum states and distinguishing proper and improper mixture.
[28][29] Accordingly, the destructive positive feedback loop of virtual particles circulating through a wormhole time machine, a result indicated by semi-classical calculations, is averted. A particle returning from the future does not return to its universe of origination but to a parallel universe. This suggests that a wormhole time machine with an exceedingly short time jump is a theoretical bridge between contemporaneous parallel universes.
[30] Because a wormhole time-machine introduces a type of nonlinearity into quantum theory, this sort of communication between parallel universes is consistent with Joseph Polchinski’s discovery of an "Everett phone" in Steven Weinberg’s formulation of nonlinear quantum mechanics.
[31] Such a possibility is depicted in the science-fiction 2014 movie
Interstellar.
Metrics
Theories of
wormhole metrics describe the spacetime geometry of a wormhole and serve as theoretical models for time travel. An example of a (traversable) wormhole
metric is the following:
[clarification needed (equations that are not discussed, not part of general discussion)]
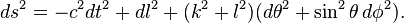
One type of non-traversable wormhole
metric is the
Schwarzschild solution (see the first diagram):
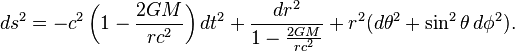
In fiction
Wormholes are a common element in
science fiction as they allow interstellar, intergalactic, and sometimes interuniversal travel within human timescales. They have also served as a method for time travel.