
Percentage of diffusely reflected sunlight in relation to various surface conditions
Albedo (
), or
reflection coefficient, derived from
Latin albedo "whiteness" (or reflected sunlight) in turn from
albus "white", is the
diffuse reflectivity or reflecting power of a surface.
It is the ratio of reflected radiation from the surface to incident radiation upon it. Its
dimensionless nature lets it be expressed as a percentage and is measured on a scale from zero for no reflection of a perfectly black surface to 1 for perfect reflection of a white surface. NOTE: Since it is the ratio of all reflected radiation to incident radiation it will include the diffuse AND the specular radiation reflected. It is, however, common to assume a surface reflects in either a totally specular manner or a totally diffuse manner, as this can simplify calculations.
Albedo depends on the
frequency of the radiation. When quoted unqualified, it usually refers to some appropriate average across the spectrum of
visible light. In general, the albedo depends on the directional distribution of incident radiation, except for
Lambertian surfaces, which scatter radiation in all directions according to a cosine function and therefore have an albedo that is independent of the incident distribution. In practice, a
bidirectional reflectance distribution function (BRDF) may be required to accurately characterize the scattering properties of a surface, but albedo is very useful as a first approximation.
The albedo is an important concept in
climatology,
astronomy, and calculating
reflectivity of surfaces in
LEED sustainable-rating systems for buildings. The average overall albedo of Earth, its
planetary albedo, is 30 to 35% because of cloud cover, but widely varies locally across the surface because of different geological and environmental features.
[1]
The term was introduced into optics by
Johann Heinrich Lambert in his 1760 work
Photometria.
Terrestrial albedo
Sample albedos
| Surface |
Typical
albedo |
| Fresh asphalt |
0.04[2] |
| Worn asphalt |
0.12[2] |
Conifer forest
(Summer) |
0.08,[3] 0.09 to 0.15[4] |
| Deciduous trees |
0.15 to 0.18[4] |
| Bare soil |
0.17[5] |
| Green grass |
0.25[5] |
| Desert sand |
0.40[6] |
| New concrete |
0.55[5] |
| Ocean ice |
0.5–0.7[5] |
| Fresh snow |
0.80–0.90[5] |
Albedos of typical materials in visible light range from up to 0.9 for fresh snow to about 0.04 for charcoal, one of the darkest substances. Deeply shadowed cavities can achieve an effective albedo approaching the zero of a
black body. When seen from a distance, the ocean surface has a low albedo, as do most forests, whereas desert areas have some of the highest albedos among landforms. Most land areas are in an albedo range of 0.1 to 0.4.
[7] The average albedo of
Earth is about 0.3.
[8] This is far higher than for the ocean primarily because of the contribution of clouds.
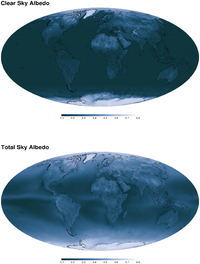
2003–2004 mean annual clear-sky and total-sky albedo
Earth's surface albedo is regularly estimated via
Earth observation satellite sensors such as
NASA's
MODIS instruments on board the
Terra and
Aqua satellites. As the total amount of reflected radiation cannot be directly measured by satellite, a
mathematical model of the BRDF is used to translate a sample set of satellite reflectance measurements into estimates of
directional-hemispherical reflectance and bi-hemispherical reflectance (e.g.
[9]).
Earth's average surface temperature due to its albedo and the
greenhouse effect is currently about 15 °C. If Earth were frozen entirely (and hence be more reflective) the average temperature of the planet would drop below −40 °C.
[10] If only the continental land masses became covered by glaciers, the mean temperature of the planet would drop to about 0 °C.
[11] In contrast, if the entire Earth is covered by water—a so-called aquaplanet—the average temperature on the planet would rise to just under 27 °C.
[12]
White-sky and black-sky albedo
It has been shown that for many applications involving terrestrial albedo, the albedo at a particular
solar zenith angle θi can reasonably be approximated by the proportionate sum of two terms: the directional-hemispherical reflectance at that solar zenith angle,
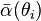
, and the bi-hemispherical reflectance,

the proportion concerned being defined as the proportion of diffuse illumination
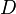
.
Albedo
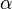
can then be given as:

Directional-hemispherical reflectance is sometimes referred to as black-sky albedo and
bi-hemispherical reflectance as white-sky albedo. These terms are important because they allow the albedo to be calculated for any given illumination conditions from a knowledge of the intrinsic properties of the surface.
[13]
Astronomical albedo
The albedos of
planets,
satellites and
asteroids can be used to infer much about their properties. The study of albedos, their dependence on wavelength, lighting angle ("phase angle"), and variation in time comprises a major part of the astronomical field of
photometry. For small and far objects that cannot be resolved by telescopes, much of what we know comes from the study of their albedos. For example, the absolute albedo can indicate the surface ice content of outer
Solar System objects, the variation of albedo with phase angle gives information about
regolith properties, whereas unusually high radar albedo is indicative of high metal content in
asteroids.
Enceladus, a moon of Saturn, has one of the highest known albedos of any body in the Solar System, with 99% of EM radiation reflected. Another notable high-albedo body is
Eris, with an albedo of 0.96.
[14] Many small objects in the outer Solar System
[15] and
asteroid belt have low albedos down to about 0.05.
[16] A typical
comet nucleus has an albedo of 0.04.
[17] Such a dark surface is thought to be indicative of a primitive and heavily
space weathered surface containing some
organic compounds.
The overall albedo of the
Moon is around 0.12, but it is strongly directional and non-Lambertian, displaying also a strong
opposition effect.
[18] Although such reflectance properties are different from those of any terrestrial terrains, they are typical of the
regolith surfaces of airless Solar System bodies.
Two common albedos that are used in astronomy are the (V-band)
geometric albedo (measuring brightness when illumination comes from directly behind the observer) and the
Bond albedo (measuring total proportion of electromagnetic energy reflected). Their values can differ significantly, which is a common source of confusion.
In detailed studies, the directional reflectance properties of astronomical bodies are often expressed in terms of the five
Hapke parameters which semi-empirically describe the variation of albedo with
phase angle, including a characterization of the opposition effect of
regolith surfaces.
The correlation between astronomical (geometric) albedo,
absolute magnitude and diameter is:
[19] 
,
where

is the astronomical albedo,

is the diameter in kilometers, and

is the absolute magnitude.
Examples of terrestrial albedo effects
Illumination
Although the albedo–temperature effect is best known in colder, whiter regions on Earth, the maximum albedo is actually found in the tropics where year-round illumination is greater. The maximum is additionally in the northern hemisphere, varying between three and twelve degrees north.
[20] The minima are found in the subtropical regions of the northern and southern hemispheres, beyond which albedo increases without respect to illumination.
[20]
Insolation effects
The intensity of albedo temperature effects depend on the amount of albedo and the level of local
insolation (solar irradiance); high albedo areas in the
arctic and
antarctic regions are cold due to low insolation, where areas such as the
Sahara Desert, which also have a relatively high albedo, will be hotter due to high insolation.
Tropical and
sub-tropical rain forest areas have low albedo, and are much hotter than their
temperate forest counterparts, which have lower insolation. Because insolation plays such a big role in the heating and cooling effects of albedo, high insolation areas like the tropics will tend to show a more pronounced fluctuation in local temperature when local albedo changes.
[citation needed]
Climate and weather
Albedo affects
climate and drives
weather. All weather is a result of the uneven heating of Earth caused by different areas of the planet having different albedos. Essentially, for the driving of weather, there are two types of albedo regions on Earth: Land and ocean. Land and ocean regions produce the four basic different types of
air masses, depending on latitude and therefore
insolation: Warm and dry, which form over tropical and sub-tropical land masses; warm and wet, which form over tropical and sub-tropical oceans; cold and dry which form over temperate, polar and sub-polar land masses; and cold and wet, which form over temperate, polar and sub-polar oceans. Different temperatures between the air masses result in different air pressures, and the masses develop into
pressure systems. High pressure systems flow toward lower pressure, driving weather from north to south in the northern hemisphere, and south to north in the lower; however due to the spinning of Earth, the
Coriolis effect further complicates flow and creates several weather/climate bands and the
jet streams.
Albedo–temperature feedback
When an area's albedo changes due to snowfall, a snow–temperature
feedback results. A layer of snowfall increases local albedo, reflecting away sunlight, leading to local cooling. In principle, if no outside temperature change affects this area (e.g. a warm
air mass), the raised albedo and lower temperature would maintain the current snow and invite further snowfall, deepening the snow–temperature feedback. However, because local
weather is dynamic due to the change of
seasons, eventually warm air masses and a more direct angle of sunlight (higher
insolation) cause melting. When the melted area reveals surfaces with lower albedo, such as grass or soil, the effect is reversed: the darkening surface lowers albedo, increasing local temperatures, which induces more melting and thus reducing the albedo further, resulting in still more heating.
Snow
Snow albedo is highly variable, ranging from as high as 0.9 for freshly fallen snow, to about 0.4 for melting snow, and as low as 0.2 for dirty snow.
[21] Over
Antarctica they average a little more than 0.8. If a marginally snow-covered area warms, snow tends to melt, lowering the albedo, and hence leading to more snowmelt because more radiation is being absorbed by the snowpack (the ice–albedo
positive feedback).
Cryoconite, powdery windblown
dust containing soot, sometimes reduces albedo on glaciers and ice sheets.
[22] Hence, small errors in albedo can lead to large errors in energy estimates, which is why it is important to measure the albedo of snow-covered areas through remote sensing techniques rather than applying a single value over broad regions.
Small-scale effects
Albedo works on a smaller scale, too. In sunlight, dark clothes absorb more heat and light-coloured clothes reflect it better, thus allowing some control over body temperature by exploiting the albedo effect of the colour of external clothing.
[23]
Solar photovoltaic effects
Albedo can affect the
electrical energy output of solar
photovoltaic devices. For example, the effects of a spectrally responsive albedo are illustrated by the differences between the spectrally weighted albedo of solar photovoltaic technology based on hydrogenated amorphous silicon (a-Si:H) and crystalline silicon (c-Si)-based compared to traditional spectral-integrated albedo predictions. Research showed impacts of over 10%.
[24] More recently, the analysis was extended to the effects of spectral bias due to the specular reflectivity of 22 commonly occurring surface materials (both human-made and natural) and analyzes the albedo effects on the performance of seven photovoltaic materials covering three common photovoltaic system topologies: industrial (solar farms), commercial flat rooftops and residential pitched-roof applications.
[25]
Trees
Because forests generally have a low albedo, (the majority of the ultraviolet and
visible spectrum is absorbed through
photosynthesis), some scientists have suggested that greater heat absorption by trees could offset some of the carbon benefits of afforestation (or offset the negative climate impacts of
deforestation). In the case of evergreen forests with seasonal snow cover albedo reduction may be great enough for deforestation to cause a net cooling effect.
[26] Trees also impact climate in extremely complicated ways through
evapotranspiration. The water vapor causes cooling on the land surface, causes heating where it condenses, acts a strong greenhouse gas, and can increase albedo when it condenses into clouds
[27] Scientists generally treat evapotranspiration as a net cooling impact, and the net climate impact of albedo and evapotranspiration changes from deforestation depends greatly on local climate
[28]
In seasonally snow-covered zones, winter albedos of treeless areas are 10% to 50% higher than nearby forested areas because snow does not cover the trees as readily.
Deciduous trees have an albedo value of about 0.15 to 0.18 whereas
coniferous trees have a value of about 0.09 to 0.15.
[4]
Studies by the
Hadley Centre have investigated the relative (generally warming) effect of albedo change and (cooling) effect of
carbon sequestration on planting forests. They found that new forests in tropical and midlatitude areas tended to cool; new forests in high latitudes (e.g. Siberia) were neutral or perhaps warming.
[29]
Water
Water reflects light very differently from typical terrestrial materials. The reflectivity of a water surface is calculated using the
Fresnel equations (see graph).

Reflectivity of smooth water at 20 °C (refractive index=1.333)
At the scale of the wavelength of light even wavy water is always smooth so the light is reflected in a locally
specular manner (not
diffusely). The glint of light off water is a commonplace effect of this. At small
angles of incident light,
waviness results in reduced reflectivity because of the steepness of the reflectivity-vs.-incident-angle curve and a locally increased average incident angle.
[30]
Although the reflectivity of water is very low at low and medium angles of incident light, it becomes very high at high angles of incident light such as those that occur on the illuminated side of Earth near the
terminator (early morning, late afternoon, and near the poles). However, as mentioned above, waviness causes an appreciable reduction. Because light specularly reflected from water does not usually reach the viewer, water is usually considered to have a very low albedo in spite of its high reflectivity at high angles of incident light.
Note that white caps on waves look white (and have high albedo) because the water is foamed up, so there are many superimposed bubble surfaces which reflect, adding up their reflectivities. Fresh 'black' ice exhibits Fresnel reflection.
Clouds
Cloud albedo has substantial influence over atmospheric temperatures. Different types of clouds exhibit different reflectivity, theoretically ranging in albedo from a minimum of near 0 to a maximum approaching 0.8. "On any given day, about half of Earth is covered by clouds, which reflect more sunlight than land and water. Clouds keep Earth cool by reflecting sunlight, but they can also serve as blankets to trap warmth."
[31]
Albedo and climate in some areas are affected by artificial clouds, such as those created by the
contrails of heavy commercial airliner traffic.
[32] A study following the burning of the Kuwaiti oil fields during Iraqi occupation showed that temperatures under the burning oil fires were as much as 10 °C colder than temperatures several miles away under clear skies.
[33]
Aerosol effects
Aerosols (very fine particles/droplets in the atmosphere) have both direct and indirect effects on Earth's radiative balance. The direct (albedo) effect is generally to cool the planet; the indirect effect (the particles act as
cloud condensation nuclei and thereby change cloud properties) is less certain.
[34] As per
[35] the effects are:
- Aerosol direct effect. Aerosols directly scatter and absorb radiation. The scattering of radiation causes atmospheric cooling, whereas absorption can cause atmospheric warming.
- Aerosol indirect effect. Aerosols modify the properties of clouds through a subset of the aerosol population called cloud condensation nuclei. Increased nuclei concentrations lead to increased cloud droplet number concentrations, which in turn leads to increased cloud albedo, increased light scattering and radiative cooling (first indirect effect), but also leads to reduced precipitation efficiency and increased lifetime of the cloud (second indirect effect).
Black carbon
Another albedo-related effect on the climate is from
black carbon particles. The size of this effect is difficult to quantify: the
Intergovernmental Panel on Climate Change estimates that the global mean radiative forcing for black carbon aerosols from fossil fuels is +0.2 W m
−2, with a range +0.1 to +0.4 W m
−2.
[36] Black carbon is a bigger cause of the melting of the polar ice cap in the Arctic than carbon dioxide due to its effect on the albedo.
[37]
Human activities
Human activities (e.g. deforestation, farming, and urbanization) change the albedo of various areas around the globe. However, quantification of this effect on the global scale is difficult.
[citation needed]
Other types of albedo
Single-scattering albedo is used to define scattering of electromagnetic waves on small particles. It depends on properties of the material (
refractive index); the size of the particle or particles; and the wavelength of the incoming radiation.
 , or
, or , or
, or
 , or
, or , or
, or
 , or
, or , or
, or ,
, , or
, or , or
, or
 , or
, or , or
, or
 , or
, or , or
, or



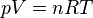

 ,
,
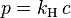


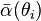 , and the bi-hemispherical reflectance,
, and the bi-hemispherical reflectance,  the proportion concerned being defined as the proportion of diffuse illumination
the proportion concerned being defined as the proportion of diffuse illumination 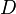 .
.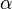 can then be given as:
can then be given as:
 ,
, is the astronomical albedo,
is the astronomical albedo,  is the diameter in kilometers, and
is the diameter in kilometers, and  is the absolute magnitude.
is the absolute magnitude.
