Efficient energy use

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Efficient_energy_use 

 

Simplified electrical grid with energy storage.

Efficient energy use, sometimes simply called energy efficiency, is the goal to reduce the amount of energy required to provide products and services. For example, insulating a building allows it to use less heating and cooling energy to achieve and maintain a thermal comfort. Installing light-emitting diode bulbs, fluorescent lighting, or natural skylight windows reduces the amount of energy required to attain the same level of illumination compared to using traditional incandescent light bulbs. Improvements in energy efficiency are generally achieved by adopting a more efficient technology or production process or by application of commonly accepted methods to reduce energy losses.

There are many motivations to improve energy efficiency. Decreasing energy use reduces energy costs and may result in a financial cost saving to consumers if the energy savings offset any additional costs of implementing an energy-efficient technology. Reducing energy use is also seen as a solution to the problem of minimizing greenhouse gas emissions. According to the International Energy Agency, improved energy efficiency in buildings, industrial processes and transportation could reduce the world's energy needs in 2050 by one third, and help control global emissions of greenhouse gases. Another important solution is to remove government-led energy subsidies that promote high energy consumption and inefficient energy use in more than half of the countries in the world.

Energy efficiency and renewable energy are said to be the twin pillars of sustainable energy policy and are high priorities in the sustainable energy hierarchy. In many countries energy efficiency is also seen to have a national security benefit because it can be used to reduce the level of energy imports from foreign countries and may slow down the rate of energy at which domestic energy resources are depleted.

Overview

Energy efficiency has proved to be a cost-effective strategy for building economies without necessarily increasing energy consumption. For example, the state of California began implementing energy-efficiency measures in the mid-1970s, including building code and appliance standards with strict efficiency requirements. During the following years, California's energy consumption has remained approximately flat on a per capita basis while national US consumption doubled. As part of its strategy, California implemented a "loading order" for new energy resources that puts energy efficiency first, renewable electricity supplies second, and new fossil-fired power plants last. States such as Connecticut and New York have created quasi-public Green Banks to help residential and commercial building-owners finance energy efficiency upgrades that reduce emissions and cut consumers' energy costs.

Lovin's Rocky Mountain Institute points out that in industrial settings, "there are abundant opportunities to save 70% to 90% of the energy and cost for lighting, fan, and pump systems; 50% for electric motors; and 60% in areas such as heating, cooling, office equipment, and appliances." In general, up to 75% of the electricity used in the US today could be saved with efficiency measures that cost less than the electricity itself, the same holds true for home settings. The US Department of Energy has stated that there is potential for energy saving in the magnitude of 90 Billion kWh by increasing home energy efficiency.

Other studies have emphasized this. A report published in 2006 by the McKinsey Global Institute, asserted that "there are sufficient economically viable opportunities for energy-productivity improvements that could keep global energy-demand growth at less than 1 percent per annum"—less than half of the 2.2 percent average growth anticipated through 2020 in a business-as-usual scenario. Energy productivity, which measures the output and quality of goods and services per unit of energy input, can come from either reducing the amount of energy required to produce something, or from increasing the quantity or quality of goods and services from the same amount of energy.

The Vienna Climate Change Talks 2007 Report, under the auspices of the United Nations Framework Convention on Climate Change, clearly shows "that energy efficiency can achieve real emission reductions at low cost."

International standards ISO 17743 and ISO 17742 provide a documented methodology for calculating and reporting on energy savings and energy efficiency for countries and cities.

The energy intensity of a country or region, the ratio of energy use to Gross Domestic Product or some other measure of economic output", differs from its energy efficiency. Energy intensity is affected by climate, economic structure (e.g. services vs manufacturing), trade, as well as the energy efficiency of buildings, vehicles, and industry. 

Benefits

From the point of view of an energy consumer, the main motivation of energy efficiency is often simply saving money by lowering the cost of purchasing energy. Additionally, from an energy policy point of view, there has been a long trend in a wider recognition of energy efficiency as the "first fuel", meaning the ability to replace or avoid the consumption of actual fuels. In fact, International Energy Agency has calculated that the application of energy efficiency measures in the years 1974-2010 has succeeded in avoiding more energy consumption in its member states than is the consumption of any particular fuel, including oil, coal and natural gas.

Moreover, it has long been recognized that energy efficiency brings other benefits additional to the reduction of energy consumption. Some estimates of the value of these other benefits, often called multiple benefits, co-benefits, ancillary benefits or non-energy benefits, have put their summed value even higher than that of the direct energy benefits. These multiple benefits of energy efficiency include things such as reduced climate change impact, reduced air pollution and improved health, improved indoor conditions, improved energy security and reduction of the price risk for energy consumers. Methods for calculating the monetary value of these multiple benefits have been developed, including e.g. the choice experiment method for improvements that have a subjective component (such as aesthetics or comfort) and Tuominen-Seppänen method for price risk reduction. When included in the analysis, the economic benefit of energy efficiency investments can be shown to be significantly higher than simply the value of the saved energy.

Appliances

Modern appliances, such as, freezers, ovens, stoves, dishwashers, and clothes washers and dryers, use significantly less energy than older appliances. Installing a clothesline will significantly reduce one's energy consumption as their dryer will be used less. Current energy-efficient refrigerators, for example, use 40 percent less energy than conventional models did in 2001. Following this, if all households in Europe changed their more than ten-year-old appliances into new ones, 20 billion kWh of electricity would be saved annually, hence reducing CO₂ emissions by almost 18 billion kg. In the US, the corresponding figures would be 17 billion kWh of electricity and 27,000,000,000 lb (1.2×10¹⁰ kg) CO₂. According to a 2009 study from McKinsey & Company the replacement of old appliances is one of the most efficient global measures to reduce emissions of greenhouse gases. Modern power management systems also reduce energy usage by idle appliances by turning them off or putting them into a low-energy mode after a certain time. Many countries identify energy-efficient appliances using energy input labeling.

The impact of energy efficiency on peak demand depends on when the appliance is used. For example, an air conditioner uses more energy during the afternoon when it is hot. Therefore, an energy-efficient air conditioner will have a larger impact on peak demand than off-peak demand. An energy-efficient dishwasher, on the other hand, uses more energy during the late evening when people do their dishes. This appliance may have little to no impact on peak demand.

Building design

Receiving a Gold rating for energy and environmental design in September 2011, the Empire State Building is the tallest and largest LEED certified building in the United States and Western Hemisphere., though it will likely be overtaken by New York's own One World Trade Center.

Buildings are an important field for energy efficiency improvements around the world because of their role as a major energy consumer. However, the question of energy use in buildings is not straightforward as the indoor conditions that can be achieved with energy use vary a lot. The measures that keep buildings comfortable, lighting, heating, cooling and ventilation, all consume energy. Typically the level of energy efficiency in a building is measured by dividing energy consumed with the floor area of the building which is referred to as specific energy consumption or energy use intensity:

${\displaystyle {\frac {\text{Energy consumed}}{\text{Built area}}}}$

However, the issue is more complex as building materials have embodied energy in them. On the other hand, energy can be recovered from the materials when the building is dismantled by reusing materials or burning them for energy. Moreover, when the building is used, the indoor conditions can vary resulting in higher and lower quality indoor environments. Finally, overall efficiency is affected by the use of the building: is the building occupied most of the time and are spaces efficiently used — or is the building largely empty? It has even been suggested that for a more complete accounting of energy efficiency, specific energy consumption should be amended to include these factors:

${\displaystyle {\frac {{\text{Embodied energy}}+{\text{Energy consumed}}-{\text{Energy recovered}}}{{\text{Built area}}\times {\text{Utilization rate}}\times {\text{Quality factor}}}}}$

Thus a balanced approach to energy efficiency in buildings should be more comprehensive than simply trying to minimize energy consumed. Issues such as quality of indoor environment and efficiency of space use should be factored in. Thus the measures used to improve energy efficiency can take many different forms. Often they include passive measures that inherently reduce the need to use energy, such as better insulation. Many serve various functions improving the indoor conditions as well as reducing energy use, such as increased use of natural light.

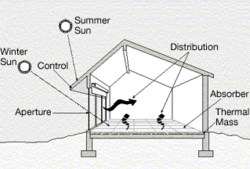
A building's location and surroundings play a key role in regulating its temperature and illumination. For example, trees, landscaping, and hills can provide shade and block wind. In cooler climates, designing northern hemisphere buildings with south facing windows and southern hemisphere buildings with north facing windows increases the amount of sun (ultimately heat energy) entering the building, minimizing energy use, by maximizing passive solar heating. Tight building design, including energy-efficient windows, well-sealed doors, and additional thermal insulation of walls, basement slabs, and foundations can reduce heat loss by 25 to 50 percent.

Dark roofs may become up to 39 °C (70 °F) hotter than the most reflective white surfaces. They transmit some of this additional heat inside the building. US Studies have shown that lightly colored roofs use 40 percent less energy for cooling than buildings with darker roofs. White roof systems save more energy in sunnier climates. Advanced electronic heating and cooling systems can moderate energy consumption and improve the comfort of people in the building.

Proper placement of windows and skylights as well as the use of architectural features that reflect light into a building can reduce the need for artificial lighting. Increased use of natural and task lighting has been shown by one study to increase productivity in schools and offices. Compact fluorescent lamps use two-thirds less energy and may last 6 to 10 times longer than incandescent light bulbs. Newer fluorescent lights produce a natural light, and in most applications they are cost effective, despite their higher initial cost, with payback periods as low as a few months. LED lamps use only about 10% of the energy an incandescent lamp requires.

Effective energy-efficient building design can include the use of low cost passive infra reds to switch-off lighting when areas are unoccupied such as toilets, corridors or even office areas out-of-hours. In addition, lux levels can be monitored using daylight sensors linked to the building's lighting scheme to switch on/off or dim the lighting to pre-defined levels to take into account the natural light and thus reduce consumption. Building management systems link all of this together in one centralised computer to control the whole building's lighting and power requirements.

In an analysis that integrates a residential bottom-up simulation with an economic multi-sector model, it has been shown that variable heat gains caused by insulation and air-conditioning efficiency can have load-shifting effects that are not uniform on the electricity load. The study also highlighted the impact of higher household efficiency on the power generation capacity choices that are made by the power sector.

The choice of which space heating or cooling technology to use in buildings can have a significant impact on energy use and efficiency. For example, replacing an older 50% efficient natural gas furnace with a new 95% efficient one will dramatically reduce energy use, carbon emissions, and winter natural gas bills. Ground source heat pumps can be even more energy-efficient and cost-effective. These systems use pumps and compressors to move refrigerant fluid around a thermodynamic cycle in order to "pump" heat against its natural flow from hot to cold, for the purpose of transferring heat into a building from the large thermal reservoir contained within the nearby ground. The end result is that heat pumps typically use four times less electrical energy to deliver an equivalent amount of heat than a direct electrical heater does. Another advantage of a ground source heat pump is that it can be reversed in summertime and operate to cool the air by transferring heat from the building to the ground. The disadvantage of ground source heat pumps is their high initial capital cost, but this is typically recouped within five to ten years as a result of lower energy use.

Smart meters are slowly being adopted by the commercial sector to highlight to staff and for internal monitoring purposes the building's energy usage in a dynamic presentable format. The use of power quality analysers can be introduced into an existing building to assess usage, harmonic distortion, peaks, swells and interruptions amongst others to ultimately make the building more energy-efficient. Often such meters communicate by using wireless sensor networks.

Green Building XML is an emerging scheme, a subset of the Building Information Modeling efforts, focused on green building design and operation. It is used as input in several energy simulation engines. But with the development of modern computer technology, a large number of building performance simulation tools are available on the market. When choosing which simulation tool to use in a project, the user must consider the tool's accuracy and reliability, considering the building information they have at hand, which will serve as input for the tool. Yezioro, Dong and Leite developed an artificial intelligence approach towards assessing building performance simulation results and found that more detailed simulation tools have the best simulation performance in terms of heating and cooling electricity consumption within 3% of mean absolute error.

Leadership in Energy and Environmental Design (LEED) is a rating system organized by the US Green Building Council (USGBC) to promote environmental responsibility in building design. They currently offer four levels of certification for existing buildings (LEED-EBOM) and new construction (LEED-NC) based on a building's compliance with the following criteria: Sustainable sites, water efficiency, energy and atmosphere, materials and resources, indoor environmental quality, and innovation in design. In 2013, USGBC developed the LEED Dynamic Plaque, a tool to track building performance against LEED metrics and a potential path to recertification. The following year, the council collaborated with Honeywell to pull data on energy and water use, as well as indoor air quality from a BAS to automatically update the plaque, providing a near-real-time view of performance. The USGBC office in Washington, D.C. is one of the first buildings to feature the live-updating LEED Dynamic Plaque.

A deep energy retrofit is a whole-building analysis and construction process that uses to achieve much larger energy savings than conventional energy retrofits. Deep energy retrofits can be applied to both residential and non-residential (“commercial”) buildings. A deep energy retrofit typically results in energy savings of 30 percent or more, perhaps spread over several years, and may significantly improve the building value. The Empire State Building has undergone a deep energy retrofit process that was completed in 2013. The project team, consisting of representatives from Johnson Controls, Rocky Mountain Institute, Clinton Climate Initiative, and Jones Lang LaSalle will have achieved an annual energy use reduction of 38% and $4.4 million. For example, the 6,500 windows were remanufactured onsite into superwindows which block heat but pass light. Air conditioning operating costs on hot days were reduced and this saved $17 million of the project's capital cost immediately, partly funding other retrofitting. Receiving a gold Leadership in Energy and Environmental Design (LEED) rating in September 2011, the Empire State Building is the tallest LEED certified building in the United States. The Indianapolis City-County Building recently underwent a deep energy retrofit process, which has achieved an annual energy reduction of 46% and $750,000 annual energy saving.

Energy retrofits, including deep, and other types undertaken in residential, commercial or industrial locations are generally supported through various forms of financing or incentives. Incentives include pre-packaged rebates where the buyer/user may not even be aware that the item being used has been rebated or "bought down". "Upstream" or "Midstream" buy downs are common for efficient lighting products. Other rebates are more explicit and transparent to the end user through the use of formal applications. In addition to rebates, which may be offered through government or utility programs, governments sometimes offer tax incentives for energy efficiency projects. Some entities offer rebate and payment guidance and facilitation services that enable energy end use customers tap into rebate and incentive programs.

To evaluate the economic soundness of energy efficiency investments in buildings, cost-effectiveness analysis or CEA can be used. A CEA calculation will produce the value of energy saved, sometimes called negawatts, in $/kWh. The energy in such a calculation is virtual in the sense that it was never consumed but rather saved due to some energy efficiency investment being made. Thus CEA allows comparing the price of negawatts with price of energy such as electricity from the grid or the cheapest renewable alternative. The benefit of the CEA approach in energy systems is that it avoids the need to guess future energy prices for the purposes of the calculation, thus removing the major source of uncertainty in the appraisal of energy efficiency investments.

Energy efficiency by country

Europe

Energy efficiency targets for 2020 and 2030.

The first EU-wide energy efficiency target was set in 1998. Member states agreed to improve energy efficiency by 1 percent a year over twelve years. In addition, legislation about products, industry, transport and buildings has contributed to a general energy efficiency framework. More effort is needed to address heating and cooling: there is more heat wasted during electricity production in Europe than is required to heat all buildings in the continent. All in all, EU energy efficiency legislation is estimated to deliver savings worth the equivalent of up to 326 million tons of oil per year by 2020.

The EU set itself a 20% energy savings target by 2020 compared to 1990 levels, but member states decide individually how energy savings will be achieved. At an EU summit in October 2014, EU countries agreed on a new energy efficiency target of 27% or greater by 2030. One mechanism used to achieve the target of 27% is the 'Suppliers Obligations & White Certificates'. The ongoing debate around the 2016 Clean Energy Package also puts an emphasis on energy efficiency, but the goal will probably remain around 30% greater efficiency compared to 1990 levels. Some have argued that this will not be enough for the EU to meet its Paris Agreement goals of reducing greenhouse gas emissions by 40% compared to 1990 levels.

Australia

The Australian national government is actively leading the country in efforts to increase their energy efficiency, mainly through the government's Department of Industry and Science. In July 2009, the Council of Australian Governments, which represents the individual states and territories of Australia, agreed to a National Strategy on Energy Efficiency (NSEE).

This is a ten-year plan accelerating the implementation of a nationwide adoption of energy-efficient practices and a preparation for the country's transformation into a low carbon future. There are several different areas of energy use addressed within the NSEE. But, the chapter devoted to the approach on energy efficiency that is to be adopted on a national level stresses four points in achieving stated levels of energy efficiency. They are:

• To help households and businesses transition to a low carbon future
• To streamline the adoption of efficient energy
• To make buildings more energy-efficient
• For governments to work in partnership and lead the way to energy efficiency

The overriding agreement that governs this strategy is the National Partnership Agreement on Energy Efficiency.

This document also explains the role of both the commonwealth and the individual states and territories in the NSEE, as well provides for the creation of benchmarks and measurement devices which will transparently show the nation's progress in relation to the stated goals, and addresses the need for funding of the strategy in order to enable it to move forward.

Canada

In August 2017, the Government of Canada released Build Smart - Canada's Buildings Strategy, as a key driver of the Pan-Canadian Framework on Clean Growth and Climate Change, Canada's national climate strategy.

The Build Smart strategy seeks to dramatically increase the energy-efficiency performance of existing and new Canadian buildings, and establishes five goals to that end:

• Federal, provincial, and territorial governments will work to develop and adopt increasingly stringent model building codes, starting in 2020, with the goal that provinces and territories adopt a “net-zero energy ready” model building code by 2030.
• Federal, provincial, and territorial governments will work to develop a model code for existing buildings by 2022, with the goal that provinces and territories adopt the code.
• Federal, provincial, and territorial governments will work together with the aim of requiring labelling of building energy use by as early as 2019.
• The federal government will set new standards for heating equipment and other key technologies to the highest level of efficiency that is economically and technically achievable.
• Provincial and territorial governments will work to sustain and expand efforts to retrofit existing buildings by supporting energy efficiency improvements and by accelerating the adoption of high-efficiency equipment while tailoring their programs to regional circumstances.

The strategy details a range of activities the Government of Canada will pursue, and investments it will make, in support of the goals. As of early 2018, only one of Canada's 10 provinces and three territories, British Columbia, has developed a policy in support of federal government's goal to reach net zero energy ready ambitions: the BC Energy Step Code.

Local British Columbia governments may use the BC Energy Step Code, if they wish, to incentivize or require a level of energy efficiency in new construction that goes above and beyond the requirements of the base building code. The regulation and standard is designed as a technical roadmap to help the province reach its target that all new buildings will attain a net zero energy ready level of performance by 2032.

Germany

Energy efficiency is central to energy policy in Germany. As of late 2015, national policy includes the following efficiency and consumption targets (with actual values for 2014):

Efficiency and consumption target	2014	2020	2050
Primary energy consumption (base year 2008)	−8.7%	−20%	−50%
Final energy productivity (2008–2050)	1.6%/year (2008–2014)	2.1%/year (2008–2050)
Gross electricity consumption (base year 2008)	−4.6%	−10%	−25%
Primary energy consumption in buildings (base year 2008)	−14.8%		−80%
Heat consumption in buildings (base year 2008)	−12.4%	−20%
Final energy consumption in transport (base year 2005)	1.7%	−10%	−40%

Recent progress toward improved efficiency has been steady aside from the financial crisis of 2007–08. Some however believe energy efficiency is still under-recognised in terms of its contribution to Germany's energy transformation (or Energiewende).

Efforts to reduce final energy consumption in transport sector have not been successful, with a growth of 1.7% between 2005–2014. This growth is due to both road passenger and road freight transport. Both sectors increased their overall distance travelled to record the highest figures ever for Germany. Rebound effects played a significant role, both between improved vehicle efficiency and the distance travelled, and between improved vehicle efficiency and an increase in vehicle weights and engine power.

On 3 December 2014, the German federal government released its National Action Plan on Energy Efficiency (NAPE). The areas covered are the energy efficiency of buildings, energy conservation for companies, consumer energy efficiency, and transport energy efficiency. The policy contains both immediate and forward-looking measures. The central short-term measures of NAPE include the introduction of competitive tendering for energy efficiency, the raising of funding for building renovation, the introduction of tax incentives for efficiency measures in the building sector, and the setting up energy efficiency networks together with business and industry. German industry is expected to make a sizeable contribution.

On 12 August 2016, the German government released a green paper on energy efficiency for public consultation (in German). It outlines the potential challenges and actions needed to reduce energy consumption in Germany over the coming decades. At the document's launch, economics and energy minister Sigmar Gabriel said "we do not need to produce, store, transmit and pay for the energy that we save". The green paper prioritizes the efficient use of energy as the "first" response and also outlines opportunities for sector coupling, including using renewable power for heating and transport. Other proposals include a flexible energy tax which rises as petrol prices fall, thereby incentivizing fuel conservation despite low oil prices.

Poland

In May 2016 Poland adopted a new Act on Energy Efficiency, to enter into force on 1 October 2016.

United States

A 2011 Energy Modeling Forum study covering the United States examines how energy efficiency opportunities will shape future fuel and electricity demand over the next several decades. The US economy is already set to lower its energy and carbon intensity, but explicit policies will be necessary to meet climate goals. These policies include: a carbon tax, mandated standards for more efficient appliances, buildings and vehicles, and subsidies or reductions in the upfront costs of new more energy-efficient equipment.

Industry

Industries use a large amount of energy to power a diverse range of manufacturing and resource extraction processes. Many industrial processes require large amounts of heat and mechanical power, most of which is delivered as natural gas, petroleum fuels, and electricity. In addition some industries generate fuel from waste products that can be used to provide additional energy.

Because industrial processes are so diverse it is impossible to describe the multitude of possible opportunities for energy efficiency in industry. Many depend on the specific technologies and processes in use at each industrial facility. There are, however, a number of processes and energy services that are widely used in many industries.

Various industries generate steam and electricity for subsequent use within their facilities. When electricity is generated, the heat that is produced as a by-product can be captured and used for process steam, heating or other industrial purposes. Conventional electricity generation is about 30% efficient, whereas combined heat and power (also called co-generation) converts up to 90 percent of the fuel into usable energy.

Advanced boilers and furnaces can operate at higher temperatures while burning less fuel. These technologies are more efficient and produce fewer pollutants.

Over 45 percent of the fuel used by US manufacturers is burnt to make steam. The typical industrial facility can reduce this energy usage 20 percent (according to the US Department of Energy) by insulating steam and condensate return lines, stopping steam leakage, and maintaining steam traps.

Electric motors usually run at a constant speed, but a variable speed drive allows the motor's energy output to match the required load. This achieves energy savings ranging from 3 to 60 percent, depending on how the motor is used. Motor coils made of superconducting materials can also reduce energy losses. Motors may also benefit from voltage optimisation.

Industry uses a large number of pumps and compressors of all shapes and sizes and in a wide variety of applications. The efficiency of pumps and compressors depends on many factors but often improvements can be made by implementing better process control and better maintenance practices. Compressors are commonly used to provide compressed air which is used for sand blasting, painting, and other power tools. According to the US Department of Energy, optimizing compressed air systems by installing variable speed drives, along with preventive maintenance to detect and fix air leaks, can improve energy efficiency 20 to 50 percent.

Transportation

Energy Efficiency of different Transport Modes

Automobiles

Toyota Prius used by NYPD Traffic Enforcement

The estimated energy efficiency for an automobile is 280 Passenger-Mile/10⁶ Btu. There are several ways to enhance a vehicle's energy efficiency. Using improved aerodynamics to minimize drag can increase vehicle fuel efficiency. Reducing vehicle weight can also improve fuel economy, which is why composite materials are widely used in car bodies.

More advanced tires, with decreased tire to road friction and rolling resistance, can save gasoline. Fuel economy can be improved by up to 3.3% by keeping tires inflated to the correct pressure. Replacing a clogged air filter can improve a cars fuel consumption by as much as 10 percent on older vehicles. On newer vehicles (1980s and up) with fuel-injected, computer-controlled engines, a clogged air filter has no effect on mpg but replacing it may improve acceleration by 6-11 percent. Aerodynamics also aid in efficiency of a vehicle. The design of a car impacts the amount of gas needed to move it through air. Aerodynamics involves the air around the car, which can affect the efficiency of the energy expended.

Turbochargers can increase fuel efficiency by allowing a smaller displacement engine. The 'Engine of the year 2011' is a Fiat 500 engine equipped with an MHI turbocharger. "Compared with a 1.2-liter 8v engine, the new 85 HP turbo has 23% more power and a 30% better performance index. The performance of the two-cylinder is not only equivalent to a 1.4-liter 16v engine, but fuel consumption is 30% lower."

Energy-efficient vehicles may reach twice the fuel efficiency of the average automobile. Cutting-edge designs, such as the diesel Mercedes-Benz Bionic concept vehicle have achieved a fuel efficiency as high as 84 miles per US gallon (2.8 L/100 km; 101 mpg_‑imp), four times the current conventional automotive average.

The mainstream trend in automotive efficiency is the rise of electric vehicles (all-electric or hybrid electric). Electric engines have more than double the efficiency of internal combustion engines. Hybrids, like the Toyota Prius, use regenerative braking to recapture energy that would dissipate in normal cars; the effect is especially pronounced in city driving. Plug-in hybrids also have increased battery capacity, which makes it possible to drive for limited distances without burning any gasoline; in this case, energy efficiency is dictated by whatever process (such as coal-burning, hydroelectric, or renewable source) created the power. Plug-ins can typically drive for around 40 miles (64 km) purely on electricity without recharging; if the battery runs low, a gas engine kicks in allowing for extended range. Finally, all-electric cars are also growing in popularity; the Tesla Model S sedan is the only high-performance all-electric car currently on the market.

Street lighting

Cities around the globe light up millions of streets with 300 million lights. Some cities are seeking to reduce street light power consumption by dimming lights during off-peak hours or switching to LED lamps. LED lamps are known to reduce the energy consumption by 50% to 80%.

Aircraft

There are several ways to reduce energy usage in air transportation, from modifications to the planes themselves, to how air traffic is managed. As in cars, turbochargers are an effective way to reduce energy consumption; however, instead of allowing for the use of a smaller-displacement engine, turbochargers in jet turbines operate by compressing the thinner air at higher altitudes. This allows the engine to operate as if it were at sea-level pressures while taking advantage of the reduced drag on the aircraft at higher altitudes.

Air traffic management systems are another way to increase the efficiency of not just the aircraft but the airline industry as a whole. New technology allows for superior automation of takeoff, landing, and collision avoidance, as well as within airports, from simple things like HVAC and lighting to more complex tasks such as security and scanning.

Alternative fuels

Typical Brazilian filling station with four alternative fuels for sale: biodiesel (B3), gasohol (E25), neat ethanol (E100), and compressed natural gas (CNG). Piracicaba, Brazil.

Alternative fuels, known as non-conventional or advanced fuels, are any materials or substances that can be used as fuels, other than conventional fuels. Some well known alternative fuels include biodiesel, bioalcohol (methanol, ethanol, butanol), chemically stored electricity (batteries and fuel cells), hydrogen, non-fossil methane, non-fossil natural gas, vegetable oil, and other biomass sources. The production efficiency of these fuels greatly differs.

Energy conservation

Elements of passive solar energy design, shown in a direct gain application

Energy conservation is broader than energy efficiency in including active efforts to decrease energy consumption, for example through behaviour change, in addition to using energy more efficiently. Examples of conservation without efficiency improvements are heating a room less in winter, using the car less, air-drying your clothes instead of using the dryer, or enabling energy saving modes on a computer. As with other definitions, the boundary between efficient energy use and energy conservation can be fuzzy, but both are important in environmental and economic terms. This is especially the case when actions are directed at the saving of fossil fuels. Energy conservation is a challenge requiring policy programmes, technological development and behavior change to go hand in hand. Many energy intermediary organisations, for example governmental or non-governmental organisations on local, regional, or national level, are working on often publicly funded programmes or projects to meet this challenge. Psychologists have also engaged with the issue of energy conservation and have provided guidelines for realizing behavior change to reduce energy consumption while taking technological and policy considerations into account.

The National Renewable Energy Laboratory maintains a comprehensive list of apps useful for energy efficiency.

Commercial property managers that plan and manage energy efficiency projects generally use a software platform to perform energy audits and to collaborate with contractors to understand their full range of options. The Department of Energy (DOE) Software Directory describes EnergyActio software, a cloud based platform designed for this purpose.

Sustainable energy

Energy efficiency and renewable energy are considered as main elements in sustainable energy policy. Both strategies must be developed concurrently in order to stabilize and reduce carbon dioxide emissions. Efficient energy use is essential to slowing the energy demand growth so that rising clean energy supplies can make deep cuts in fossil fuel use. If energy use grows too rapidly, renewable energy development will chase a receding target. Likewise, unless clean energy supplies come online rapidly, slowing demand growth will only begin to reduce total carbon emissions; a reduction in the carbon content of energy sources is also needed. A sustainable energy economy thus requires major commitments to both efficiency and renewables.

Rebound effect

If the demand for energy services remains constant, improving energy efficiency will reduce energy consumption and carbon emissions. However, many efficiency improvements do not reduce energy consumption by the amount predicted by simple engineering models. This is because they make energy services cheaper, and so consumption of those services increases. For example, since fuel efficient vehicles make travel cheaper, consumers may choose to drive farther, thereby offsetting some of the potential energy savings. Similarly, an extensive historical analysis of technological efficiency improvements has conclusively shown that energy efficiency improvements were almost always outpaced by economic growth, resulting in a net increase in resource use and associated pollution. These are examples of the direct rebound effect.

Estimates of the size of the rebound effect range from roughly 5% to 40%. The rebound effect is likely to be less than 30% at the household level and may be closer to 10% for transport. A rebound effect of 30% implies that improvements in energy efficiency should achieve 70% of the reduction in energy consumption projected using engineering models. Saunders et al. showed in 2010 that lighting has accounted for about 0.7% of GDP across many societies and hundreds of years, implying a rebound effect of 100%. However, some of the authors argue in a followup paper that increased lighting generally increases economic welfare and has substantial benefits. A 2014 study has shown the rebound effect to be rather low for household lighting, in particular for high use bulbs.

Energy density

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Energy_density 

Energy density is the amount of energy stored in a given system or region of space per unit volume. It may also be used for energy per unit mass, though the accurate term for this is specific energy. Often only the useful or extractable energy is measured, which is to say that inaccessible energy (such as rest mass energy) is ignored. In cosmological and other general relativistic contexts, however, the energy densities considered are those that correspond to the elements of the stress–energy tensor and therefore do include mass energy as well as energy densities associated with the pressures described in the next paragraph.

Energy per unit volume has the same physical units as pressure, and in many circumstances is a synonym: for example, the energy density of a magnetic field may be expressed as (and behaves as) a physical pressure, and the energy required to compress a compressed gas a little more may be determined by multiplying the difference between the gas pressure and the external pressure by the change in volume. In short, pressure is a measure of the enthalpy per unit volume of a system. A pressure gradient has the potential to perform work on the surroundings by converting enthalpy to work until equilibrium is reached.

Introduction to energy density

There are different types of energy stored in materials, and it takes a particular type of reaction to release each type of energy. In order of the typical magnitude of the energy released, these types of reactions are: nuclear, chemical, electrochemical, and electrical.

Nuclear reactions take place in stars and nuclear power plants, both of which derive energy from the binding energy of nuclei. Chemical reactions are used by animals to derive energy from food, and by automobiles to derive energy from gasoline. Liquid hydrocarbons (fuels such as gasoline, diesel and kerosene) are today the most dense way known to economically store and transport chemical energy at a very large scale (1 kg of diesel fuel burns with the oxygen contained in ~15 kg of air). Electrochemical reactions are used by most mobile devices such as laptop computers and mobile phones to release the energy from batteries.

Types of energy content

There are several different types of energy content. One is the theoretical total amount of thermodynamic work that can be derived from a system, with a given temperature and pressure for the surroundings. This is called exergy. Another is the theoretical amount of work that can be derived from reactants that are initially at room temperature and atmospheric pressure. This is given by the change in standard Gibbs free energy. But as a source of heat or for use in a heat engine, the relevant quantity is the change in standard enthalpy or the heat of combustion.

There are two kinds of heat of combustion:

• The higher value (HHV), or gross heat of combustion, includes all the heat released as the products cool to room temperature and whatever water vapor is present condenses.
• The lower value (LHV), or net heat of combustion, does not include the heat which could be released by condensing water vapor, and may not include the heat released on cooling all the way down to room temperature.

A convenient table of HHV and LHV of some fuels can be found in the references.

Energy density in energy storage and in fuel

Selected energy densities plot

In energy storage applications the energy density relates the energy in an energy store to the volume of the storage facility, e.g. the fuel tank. The higher the energy density of the fuel, the more energy may be stored or transported for the same amount of volume. The energy density of a fuel per unit mass is called the specific energy of that fuel. In general an engine using that fuel will generate less kinetic energy due to inefficiencies and thermodynamic considerations—hence the specific fuel consumption of an engine will always be greater than its rate of production of the kinetic energy of motion.

Broad implications

Energy density differs from energy conversion efficiency (net output per input) or embodied energy (the energy output costs to provide, as harvesting, refining, distributing, and dealing with pollution all use energy). Large scale, intensive energy use impacts and is impacted by climate, waste storage, and environmental consequences.

No single energy storage method boasts the best in specific power, specific energy, and energy density. Peukert's law describes how the amount of useful energy that can be obtained (for a lead-acid cell) depends on how quickly it is pulled out. To maximize both specific energy and energy density, one can compute the specific energy density of a substance by multiplying the two values together, where the higher the number, the better the substance is at storing energy efficiently.

Alternative options are discussed for energy storage to increase energy density and decrease charging time.

Gravimetric and volumetric energy density of some fuels and storage technologies (modified from the Gasoline article):

Nuclear energy sources

The greatest energy source by far is mass itself. This energy, E = mc², where m = ρV, ρ is the mass per unit volume, V is the volume of the mass itself and c is the speed of light. This energy, however, can be released only by the processes of nuclear fission (0.1%), nuclear fusion (1%), or the annihilation of some or all of the matter in the volume V by matter-antimatter collisions (100%). Nuclear reactions cannot be realized by chemical reactions such as combustion. Although greater matter densities can be achieved, the density of a neutron star would approximate the most dense system capable of matter-antimatter annihilation possible. A black hole, although denser than a neutron star, does not have an equivalent anti-particle form, but would offer the same 100% conversion rate of mass to energy in the form of Hawking radiation. In the case of relatively small black holes (smaller than astronomical objects) the power output would be tremendous.

The highest density sources of energy aside from antimatter are fusion and fission. Fusion includes energy from the sun which will be available for billions of years (in the form of sunlight) but so far (2018), sustained fusion power production continues to be elusive.

Power from fission of uranium and thorium in nuclear power plants will be available for many decades or even centuries because of the plentiful supply of the elements on earth, though the full potential of this source can only be realised through breeder reactors, which are, apart from the BN-600 reactor, not yet used commercially. Coal, gas, and petroleum are the current primary energy sources in the U.S. but have a much lower energy density. Burning local biomass fuels supplies household energy needs (cooking fires, oil lamps, etc.) worldwide.

Thermal power of nuclear fission reactors

The density of thermal energy contained in the core of a light water reactor (PWR or BWR) of typically 1 GWe (1 000 MW electrical corresponding to ~3 000 MW thermal) is in the range of 10 to 100 MW of thermal energy per cubic meter of cooling water depending on the location considered in the system (the core itself (~30 m³), the reactor pressure vessel (~50 m³), or the whole primary circuit (~300 m³)). This represents a considerable density of energy which requires under all circumstances a continuous water flow at high velocity in order to be able to remove the heat from the core, even after an emergency shutdown of the reactor. The incapacity to cool the cores of three boiling water reactors (BWR) at Fukushima in 2011 after the tsunami and the resulting loss of the external electrical power and of the cold source was the cause of the meltdown of the three cores in only a few hours, even though the three reactors were correctly shut down just after the Tōhoku earthquake. This extremely high power density distinguishes nuclear power plants (NPP's) from any thermal power plants (burning coal, fuel or gas) or any chemical plants and explains the large redundancy required to permanently control the neutron reactivity and to remove the residual heat from the core of NPP's.

Energy density of electric and magnetic fields

Electric and magnetic fields store energy. In a vacuum, the (volumetric) energy density is given by

${\displaystyle u={\frac {\varepsilon _{0}}{2}}\mathbf {E} ^{2}+{\frac {1}{2\mu _{0}}}\mathbf {B} ^{2}}$

where E is the electric field and B is the magnetic field. The solution will be (in SI units) in Joules per cubic metre. In the context of magnetohydrodynamics, the physics of conductive fluids, the magnetic energy density behaves like an additional pressure that adds to the gas pressure of a plasma.

In normal (linear and nondispersive) substances, the energy density (in SI units) is

${\displaystyle u={\frac {1}{2}}(\mathbf {E} \cdot \mathbf {D} +\mathbf {H} \cdot \mathbf {B} )}$

where D is the electric displacement field and H is the magnetizing field.

In the case of absence of magnetic fields, by exploiting Fröhlich's relationships it is also possible to extend these equations to anisotropic and nonlinear dielectrics, as well as to calculate the correlated Helmholtz free energy and entropy densities.

When a pulsed laser impacts a surface, the radiant exposure, i.e. the energy deposited per unit of surface, may be called energy density or fluence.

 

Mass–energy equivalence

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Mass%E2%80%93energy_equivalence 

 

E = mc² explained

In physics, mass–energy equivalence is the principle that anything having mass has an equivalent amount of energy and vice versa. These fundamental quantities are directly related to one another according to Albert Einstein's famous formula:

$${\displaystyle E=m\,c^{2}}$$

This formula states that mass has an equivalent energy (E) which can be calculated as mass (m) multiplied by the speed of light squared (c²). Similarly, energy has an equivalent mass (m) which can be calculated as energy (E) divided by the speed of light squared (c²). Because the speed of light is a large number in everyday units (approximately 3×10⁸ m/s), the formula implies that even an everyday object at rest with a modest amount of mass has a very large amount of intrinsic energy. Chemical reactions, nuclear reactions, and other energy transformations may cause a system to lose some of its energy content to the environment (and thus some corresponding mass), for example, by releasing it as thermal energy or as radiant energy, such as light.

Mass–energy equivalence arose originally from special relativity as a paradox described by Henri Poincaré. Einstein proposed it on 21 November 1905, in the paper Does the inertia of a body depend upon its energy-content?, one of his Annus Mirabilis (Miraculous Year) papers. Einstein was the first to propose that the equivalence of mass and energy is a general principle and a consequence of the symmetries of space and time.

A consequence of the mass–energy equivalence is that if a body or system is at rest—or more precisely, within its center-of-momentum frame—it still has internal or intrinsic energy called rest energy; rest energy is directly proportional to rest mass, and is independent of the composition of matter. Rest mass is mass measured while having zero momentum; it is also called invariant mass, as it is a physical property that remains independent of momentum, even at extreme speeds approaching the speed of light. Massless particles such as photons have zero invariant mass, but massless free particles have both momentum and energy.

When a body or system has momentum, its total energy (which is also called relativistic energy) is greater than its rest energy, and is equal to the sum of its rest energy and kinetic energy (that is, energy due to motion). The energy–momentum relation is the relation between total energy, invariant mass, and momentum. So for a body or system with momentum, its total energy is a function of both its invariant mass and momentum. The relativistic mass of a body or system can be derived from its total energy divided by the speed of light squared; and for a body or system with momentum its relativistic mass will be greater than its invariant mass, as it will have more energy than at rest.

Nomenclature

The formula was initially written in many different notations, and its interpretation and justification was further developed in several steps. In "Does the inertia of a body depend upon its energy content?" (1905), Einstein used V to mean the speed of light in a vacuum and L to mean the energy lost by a body in the form of radiation. Consequently, the equation E = mc² was not originally written as a formula but as a sentence in German saying that "if a body gives off the energy L in the form of radiation, its mass diminishes by L/V²." A remark placed above it informed that the equation was approximated by neglecting "magnitudes of fourth and higher orders" of a series expansion.

In May 1907, Einstein explained that the expression for energy ε of a moving mass point assumes the simplest form, when its expression for the state of rest is chosen to be ε₀ = μV² (where μ is the mass), which is in agreement with the "principle of the equivalence of mass and energy". In addition, Einstein used the formula μ = E₀/V², with E₀ being the energy of a system of mass points, to describe the energy and mass increase of that system when the velocity of the differently moving mass points is increased.

In June 1907, Max Planck rewrote Einstein's mass–energy relationship as M = E₀ + pV₀/c², where p is the pressure and V₀ the volume to express the relation between mass, its latent energy, and thermodynamic energy within the body. Subsequently, in October 1907, this was rewritten as M₀ = E₀/c² and given a quantum interpretation by Johannes Stark, who assumed its validity and correctness (Gültigkeit).

In December 1907, Einstein expressed the equivalence in the form M = μ + E₀/c² and concluded: "A mass μ is equivalent, as regards inertia, to a quantity of energy μc². [...] It appears far more natural to consider every inertial mass as a store of energy."

In 1909, Gilbert N. Lewis and Richard C. Tolman used two variations of the formula: m = E/c² and m₀ = E₀/c², with E being the relativistic energy (the energy of an object when the object is moving), E₀ is the rest energy (the energy when not moving), m is the relativistic mass (the rest mass and the extra mass gained when moving), and m₀ is the rest mass (the mass when not moving). The same relations in different notation were used by Hendrik Lorentz in 1913 (published 1914), though he placed the energy on the left-hand side: ε = Mc² and ε₀ = mc², with ε being the total energy (rest energy plus kinetic energy) of a moving material point, ε₀ its rest energy, M the relativistic mass, and m the invariant (or rest) mass.

In 1911, Max von Laue gave a more comprehensive proof of M₀ = E₀/c² from the stress–energy tensor, which was later (1918) generalized by Felix Klein.

Einstein returned to the topic once again after World War II and this time he wrote E = mc² in the title of his article intended as an explanation for a general reader by analogy.

Conservation of mass and energy

According to Einstein, mass and energy can be seen as two names for the same underlying, conserved physical quantity. Hence, the laws of conservation of energy and conservation of mass are "one and the same". Einstein elaborated in a 1946 essay that "the principle of the conservation of mass [...] proved inadequate in the face of the special theory of relativity. It was therefore merged with the energy conservation principle—just as, about 60 years before, the principle of the conservation of mechanical energy had been combined with the principle of the conservation of heat [thermal energy]. We might say that the principle of the conservation of energy, having previously swallowed up that of the conservation of heat, now proceeded to swallow that of the conservation of mass—and holds the field alone."

From the point of view of an inertial reference frame, when an object is pushed in the direction of motion, it gains momentum and energy, but when the object is already traveling near the speed of light, it cannot move much faster, no matter how much energy it absorbs. Its momentum and energy continue to increase without bounds, whereas its speed approaches (but never reaches) a constant value—the speed of light. This implies that in relativity the momentum of an object cannot be a constant times the velocity, nor can the kinetic energy be a constant times the square of the velocity.

Mass in Special Relativity

A property called the relativistic mass is defined as the ratio of the momentum of an object to its velocity. Relativistic mass depends on the motion of the object, so that different observers in relative motion see different values for it. If the object is moving slowly, the relativistic mass is nearly equal to the rest mass and both are nearly equal to the classical inertial mass (as it appears in Newton's laws of motion). If the object is moving quickly, the relativistic mass is greater than the rest mass by an amount equal to the mass associated with the kinetic energy of the object. As the object approaches the speed of light, the relativistic mass grows infinitely, because the kinetic energy grows infinitely and this energy is associated with mass. The relativistic mass of a moving object is larger than the relativistic mass of an object that is not moving, because a moving object has extra kinetic energy. The rest mass of an object is defined as the mass of an object when it is at rest, so that the rest mass is always the same, independent of the motion of the observer: it is the same in all inertial frames.

Just as the relativistic mass of an isolated system is conserved through time, so also is its invariant mass. This property allows the conservation of all types of mass in systems, and also conservation of all types of mass in reactions where matter is destroyed (annihilated), leaving behind the energy that was associated with it (which is now in non-material form, rather than material form). Matter may appear and disappear in various reactions, but mass and energy are both unchanged in this process. Note, this only holds true in isolated systems and is a consequence of an isolated system's inability to expel energy to its environment. In general, invariant mass is not conserved in relativistic collisions. 

The relativistic mass is always equal to the total energy (rest energy plus kinetic energy) divided by c². Because the relativistic mass is exactly proportional to the energy, relativistic mass and relativistic energy are nearly synonyms; the only difference between them is the units. If length and time are measured in natural units, the speed of light is equal to 1, and even this difference disappears. Then mass and energy have the same units and are always equal, so it is redundant to speak about relativistic mass, because it is just another name for the energy. This is why physicists usually reserve the useful short word "mass" to mean rest mass, or invariant mass, and not relativistic mass. Thus, the conservation of mass law does not hold true in special relativity, but the conservation of momentum and conservation of energy laws do. The mass (equivalently, rest energy) of a particle can be converted, not "to energy" (it already is energy), but rather to other forms of energy that require motion, such as kinetic energy, thermal energy, or radiant energy. Similarly, kinetic or radiant energy can be converted to other kinds of particles that have mass. This view requires that if either kinetic energy or mass disappears from a system, it is always found to have simply changed forms.

Composite systems

For closed systems made up of many parts, like an atomic nucleus, planet, or star, the relativistic energy is given by the sum of the relativistic energies of each of the parts, because energies are additive in these systems. This is not true in open systems, however, if energy is allowed to escape. For example, if a system is bound by attractive forces, and the energy gained due to the forces of attraction in excess of the work done is removed from the system, then mass is lost with this removed energy. For example, the mass of an atomic nucleus is less than the total mass of the protons and neutrons that make it up, but this is only true after this energy from binding has been removed in the form of a gamma ray (which in this system, carries away the mass of the energy of binding). This mass decrease is also equivalent to the energy required to break up the nucleus into individual protons and neutrons (in this case, work and mass would need to be supplied). Similarly, the mass of the solar system is slightly less than the sum of the individual masses of the sun and planets.

For an isolated system of particles moving in different directions, the invariant mass of the system is the analog of the rest mass, and is the same for all observers, even those in relative motion. It is defined as the total energy (divided by c²) in the center of momentum frame (where by definition, the system's total momentum is zero). A simple example of an object with moving parts but zero total momentum is a container of gas. In this case, the mass of the container is given by its total energy (including the kinetic energy of the gas molecules), since the system's total energy and invariant mass are the same in any reference frame where the momentum is zero, and such a reference frame is also the only frame in which the object can be weighed. In a similar way, the theory of special relativity posits that the thermal energy in all objects (including solids) contributes to their total masses and weights, even though this energy is present as the kinetic and potential energies of the atoms in the object, and it (in a similar way to the gas) is not seen in the rest masses of the atoms that make up the object.

In a similar manner, even photons (light quanta), if trapped in an isolated container (as a photon gas or thermal radiation), would contribute a mass associated with their energy to the container. Such an extra mass, in theory, could be weighed in the same way as any other type of rest mass. This is true in special relativity theory, even though individually photons have no rest mass. The property that trapped energy in any form adds weighable mass to systems that have no net momentum is one of the characteristic and notable consequences of relativity. It has no counterpart in classical Newtonian physics, in which radiation, light, heat, and kinetic energy never exhibit weighable mass under any circumstances.

Applicability of the strict formula

As is noted above, two different definitions of mass have been used in special relativity, and also two different definitions of energy. The simple equation ${\displaystyle E=mc^{2}}$ is not generally applicable to all these types of mass and energy, except in the special case that the total additive momentum is zero for the system under consideration. In such a case, which is always guaranteed when observing the system from either its center of momentum frame, ${\displaystyle E=mc^{2}}$ is always true for any type of mass and energy that are chosen. Thus, for example, in the center of momentum frame, the total energy of an object or system is equal to its rest mass times ${\displaystyle c^{2}}$, a useful equality. This is the relationship used for the container of gas in the previous example. It is not true in other reference frames where the object is in motion. In these systems or for such an object, its total energy depends on both its rest (or invariant) mass, and its (total) momentum.

In inertial reference frames other than the center of momentum frame, the equation ${\displaystyle E=mc^{2}}$ remains true only for the relativistic mass. However, connection of the total or relativistic energy (${\displaystyle E_{r}}$) with the rest or invariant mass (${\displaystyle m_{0}}$) requires consideration of the system's total momentum, in systems and reference frames where the total momentum (of magnitude p) has a non-zero value. The formula then required to connect the two different kinds of mass and energy, is the extended version of Einstein's equation, called the relativistic energy–momentum relation:

${\displaystyle {\begin{aligned}E_{r}^{2}-|{\vec {p}}\,|^{2}c^{2}&=m_{0}^{2}c^{4}\\E_{r}^{2}-(pc)^{2}&=(m_{0}c^{2})^{2}\end{aligned}}}$

or

${\displaystyle E_{r}={\sqrt {(m_{0}c^{2})^{2}+(pc)^{2}}}\,\!}$

Here the ${\displaystyle (pc)^{2}}$ term represents the square of the Euclidean norm (total vector length) of the various momentum vectors in the system, which reduces to the square of the simple momentum magnitude, if only a single particle is considered. This equation reduces to ${\displaystyle E=mc^{2}}$ when the momentum term is zero. For photons where ${\displaystyle m_{0}=0}$, the equation reduces to ${\displaystyle E_{r}=pc}$.

Meanings of the strict formula

The mass–energy equivalence formula was displayed on Taipei 101 during the event of the World Year of Physics 2005.

Mass–energy equivalence states that any object has a certain energy, even when it is stationary. In Newtonian mechanics, a motionless body has no kinetic energy, and it may or may not have other amounts of internal stored energy, like chemical energy or thermal energy, in addition to any potential energy it may have from its position in a field of force. In Newtonian mechanics, all of these energies are much smaller than the mass of the object times the speed of light squared.

In relativity, all the energy that moves with an object (that is, all the energy present in the object's rest frame) contributes to the total mass of the body, which measures how much it resists acceleration. Each bit of potential and kinetic energy makes a proportional contribution to the mass. As noted above, even if an isolated box of ideal mirrors "contains" light, then the individually massless photons still contribute to the total mass of the box, by the amount of their energy divided by c².

For an observer in the center of momentum frame, therefore, removing energy is the same as removing mass and the formula m = E/c² indicates how much mass is lost when energy is removed. In a nuclear reaction, the mass of the atoms that come out is less than the mass of the atoms that go in, and the difference in mass shows up as heat and light with the same relativistic mass as the difference. In this case, the E in the formula is the energy released and removed, and the mass m is how much the mass decreases. In the same way, when any sort of energy is added to an isolated system, the increase in the mass is equal to the added energy divided by c². For example, when water is heated it gains about 1.11×10⁻¹⁷ kg of mass for every joule of heat added to the water.

An object moves with different speeds in different frames of reference, depending on the motion of the observer. This implies the kinetic energy, in both Newtonian mechanics and relativity, is frame dependent, which means that the amount of relativistic energy, and therefore the amount of relativistic mass, that an object is measured to have depends on the observer. The rest mass or invariant mass (typically denoted as just mass) is defined as the relativistic mass that an object has when it is not moving (as observed from an inertial frame of reference). The invariant mass is the smallest possible value of the relativistic mass of the object or system. It is also a conserved quantity, so long as the system is isolated. Because of the way it is calculated, the effects of moving observers are subtracted, so the mass does not depend on the motion of the observer, hence it is invariant.

The rest mass is almost never additive: the mass of an object is not the sum of the masses of its parts. The rest mass of an object is the total energy of all the parts, including kinetic energy, as observed from the center of momentum frame. The masses adds up only if the constituents are at rest (as observed from the center of momentum frame) and do not attract or repel, so that they do not have any extra kinetic or potential energy. The other possibility is that they have a positive kinetic energy and a negative potential energy that exactly cancels.

Binding energy and the "mass defect"

The difference between the rest mass of a bound system and of its unbound parts is called the mass defect of the system, and is associated with the binding energy of the system, which is the minimum energy required to disassemble the system. The mass defect is calculated from the binding energy of the system as Δm = ΔE/c². For example, a water molecule weighs a little less than two free hydrogen atoms and an oxygen atom. The minuscule mass difference is the energy needed to split the molecule into three individual atoms (divided by c²), which was given off as heat when the molecule formed (this heat had mass). Likewise, a stick of dynamite in theory weighs a little bit more than the fragments after the explosion, but this is true only so long as the fragments are cooled and the heat removed. In this case the mass difference is the energy/heat that is released when the dynamite explodes.

Such a change in mass may only happen when the system is open, and the energy and mass are allowed to escape. Thus, if a stick of dynamite is blown up in a hermetically sealed chamber, the mass of the chamber and fragments, the heat, sound, and light would still be equal to the original mass of the chamber and dynamite. If sitting on a scale, the weight and mass would not change. This would in theory also happen even with a nuclear bomb, if it could be kept in an ideal box of infinite strength, which did not rupture or pass radiation. Thus, a 21.5 kiloton (9×10¹³ joule) nuclear bomb produces about one gram of heat and electromagnetic radiation, but the mass of this energy would not be detectable in an exploded bomb in an ideal box sitting on a scale; instead, the contents of the box would be heated to millions of degrees without changing total mass and weight. If then, however, a transparent window (passing only electromagnetic radiation) were opened in such an ideal box after the explosion, and a beam of X-rays and other lower-energy light allowed to escape the box, it would eventually be found to weigh one gram less than it had before the explosion. This weight loss and mass loss would happen as the box was cooled by this process, to room temperature. However, any surrounding mass that absorbed the X-rays (and other "heat") would gain this gram of mass from the resulting heating, thus, in this case, the mass "loss" would represent merely its relocation.

Massless particles

Massless particles have zero rest mass. Their relativistic mass is simply their relativistic energy, divided by c², or m_rel = E/c². The energy for photons is E = hf, where h is Planck's constant and f is the photon frequency. This frequency and thus the relativistic energy are frame-dependent.

If an observer runs away from a photon in the direction the photon travels from a source, and it catches up with the observer—when the photon catches up, the observer sees it as having less energy than it had at the source. The faster the observer is traveling with regard to the source when the photon catches up, the less energy the photon has. As an observer approaches the speed of light with regard to the source, the photon looks redder and redder, by relativistic Doppler effect (the Doppler shift is the relativistic formula), and the energy of a very long-wavelength photon approaches zero. This is because the photon is massless—the rest mass of a photon is zero.

Massless particles contribute rest mass and invariant mass to systems

Two photons moving in different directions cannot both be made to have arbitrarily small total energy by changing frames, or by moving toward or away from them. The reason is that in a two-photon system, the energy of one photon is decreased by chasing after it, but the energy of the other increases with the same shift in observer motion. (see relativistic Doppler effect) Two photons not moving in the same direction comprise an inertial frame where the combined energy is smallest, but not zero. This is called the center of momentum frame. The term center of mass frame is also sometimes used, where the center of mass frame is a special case of the center of momentum frame where the center of mass is put at the origin. The most that chasing a pair of photons can accomplish to decrease their energy is to put the observer in a frame where the photons have equal energy and are moving directly away from each other. In this frame, the observer is now moving in the same direction and speed as the center of momentum of the two photons. The total momentum of the photons is now zero, since their momenta are equal and opposite. In this frame the two photons, as an isolated system, have a mass equal to their total energy divided by c². This is called the invariant mass of the isolated system. It is, by definition, the smallest mass and energy the system may be seen to have, by any observer. It is only the invariant mass of a two-photon system that can be used to make a single particle with the same rest mass.

If the photons are formed by the collision of a particle and an antiparticle, the invariant mass of the system of particles is equivalent to the total energy of the particle and antiparticle (their rest energy plus the kinetic energy), in the center of momentum frame, where they automatically move in equal and opposite directions (since they have equal momentum in this frame). If the photons are formed by the disintegration of a single particle with a well-defined rest mass, like the neutral pion, the invariant mass of the system is equal to the rest mass of the pion. In this case, the center of momentum frame for the pion is just the frame where the pion is at rest, and the center of momentum does not change after it disintegrates into two photons. After the two photons are formed, their center of momentum is still moving the same way the pion did, and their total energy in this frame adds up to the mass energy of the pion.

A similar calculation illustrates that the invariant mass of isolated systems is conserved, even when massive particles (particles with rest mass) within the system are converted to massless particles (such as photons). In such cases, the photons contribute to the invariant mass of the system, even though they individually have no mass. Thus, an electron and positron (each of which has rest mass) may undergo annihilation with each other to produce two photons, each of which is massless. However, in such circumstances, the overall mass of the isolated system remains unchanged. Instead, the system of photons moving away from each other has an invariant mass, which acts like a rest mass for any system in which the photons are trapped (isolated) and that can be weighed.

Relation to gravity

In physics, there are two distinct concepts of mass: the gravitational mass and the inertial mass. The gravitational mass is the quantity that determines the strength of the gravitational field generated by an object, as well as the gravitational force acting on the object when it is immersed in a gravitational field produced by other bodies. The inertial mass, on the other hand, quantifies how much an object accelerates if a given force is applied to it. The mass–energy equivalence in special relativity refers to the inertial mass. However, already in the context of Newton gravity, the Weak Equivalence Principle is postulated: the gravitational and the inertial mass of every object are the same. Thus, the mass–energy equivalence, combined with the Weak Equivalence Principle, results in the prediction that all forms of energy contribute to the gravitational field generated by an object. This observation is one of the pillars of the general theory of relativity.

The above prediction, that all forms of energy interact gravitationally, has been subject to experimental tests. The first observation testing this prediction was made in 1919. During a solar eclipse, Arthur Eddington observed that the light from stars passing close to the Sun was bent. The effect is due to the gravitational attraction of light by the Sun. The observation confirmed that the energy carried by light indeed is equivalent to a gravitational mass. Another seminal experiment, the Pound–Rebka experiment, was performed in 1960. In this test a beam of light was emitted from the top of a tower and detected at the bottom. The frequency of the light detected was higher than the light emitted. This result confirms that the energy of photons increases when they fall in the gravitational field of the Earth. The energy, and therefore the gravitational mass, of photons is proportional to their frequency as stated by the Planck's relation.

Application to nuclear physics

Task Force One, the world's first nuclear-powered task force. Enterprise, Long Beach and Bainbridge in formation in the Mediterranean, 18 June 1964. Enterprise crew members are spelling out Einstein's mass–energy equivalence formula E = mc² on the flight deck.

Max Planck pointed out that the mass–energy equivalence formula implied that bound systems would have a mass less than the sum of their constituents, once the binding energy had been allowed to escape. However, Planck was thinking about chemical reactions, where the binding energy is too small to measure. Einstein suggested that radioactive materials such as radium would provide a test of the theory, but even though a large amount of energy is released per atom in radium, due to the half-life of the substance (1602 years), only a small fraction of radium atoms decay over an experimentally measurable period of time.

Once the nucleus was discovered, experimenters realized that the very high binding energies of the atomic nuclei should allow calculation of their binding energies, simply from mass differences. But it was not until the discovery of the neutron in 1932, and the measurement of the neutron mass, that this calculation could actually be performed (see nuclear binding energy for example calculation). A little while later, the Cockcroft–Walton accelerator produced the first transmutation reaction (⁷
₃Li + ¹
₁p → 2 ⁴
₂He), verifying Einstein's formula to an accuracy of ±0.5%. In 2005, Rainville et al. published a direct test of the energy-equivalence of mass lost in the binding energy of a neutron to atoms of particular isotopes of silicon and sulfur, by comparing the mass lost to the energy of the emitted gamma ray associated with the neutron capture. The binding mass-loss agreed with the gamma ray energy to a precision of ±0.00004%, the most accurate test of E = mc² to date.

The mass–energy equivalence formula was used in the understanding of nuclear fission reactions, and implies the great amount of energy that can be released by a nuclear fission chain reaction, used in both nuclear weapons and nuclear power. By measuring the mass of different atomic nuclei and subtracting from that number the total mass of the protons and neutrons as they would weigh separately, one gets the exact binding energy available in an atomic nucleus. This is used to calculate the energy released in any nuclear reaction, as the difference in the total mass of the nuclei that enter and exit the reaction.

Practical examples

Einstein used the CGS system of units (centimeters, grams, seconds, dynes, and ergs), but the formula is independent of the system of units. In natural units, the numerical value of the speed of light is set to equal 1, and the formula expresses an equality of numerical values: E = m. In the SI system (expressing the ratio E/m in joules per kilogram using the value of c in meters per second):

E/m = c² = (299792458 m/s)² = 89875517873681764 J/kg (≈ 9.0 × 10¹⁶ joules per kilogram).

So the energy equivalent of one kilogram of mass is

• 89.9 petajoules
• 25.0 billion kilowatt-hours (≈ 25,000 GW·h)
• 21.5 trillion kilocalories (≈ 21 Pcal)
• 85.2 trillion BTUs
• 0.0852 quads

or the energy released by combustion of the following:

• 21 500 kilotons of TNT-equivalent energy (≈ 21 Mt)
• 2630000000 litres or 695000000 US gallons of automotive gasoline

Any time energy is released, the process can be evaluated from an E = mc² perspective. For instance, the "Gadget"-style bomb used in the Trinity test and the bombing of Nagasaki had an explosive yield equivalent to 21 kt of TNT. About 1 kg of the approximately 6.15 kg of plutonium in each of these bombs fissioned into lighter elements totaling almost exactly one gram less, after cooling. The electromagnetic radiation and kinetic energy (thermal and blast energy) released in this explosion carried the missing one gram of mass. This occurs because nuclear binding energy is released whenever elements with more than 62 nucleons fission.

Whenever energy is added to a system, the system gains mass, as shown when the equation is rearranged:

• A spring's mass increases whenever it is put into compression or tension. Its added mass arises from the added potential energy stored within it, which is bound in the stretched chemical (electron) bonds linking the atoms within the spring.
• Raising the temperature of an object (increasing its heat energy) increases its mass. For example, consider the world's primary mass standard for the kilogram, made of platinum/iridium. If its temperature is allowed to change by 1 °C, its mass changes by 1.5 picograms (1 pg = 1×10⁻¹² g).
• A spinning ball weighs more than a ball that is not spinning. Its increase of mass is exactly the equivalent of the mass of energy of rotation, which is itself the sum of the kinetic energies of all the moving parts of the ball. For example, the Earth itself is more massive due to its rotation, than it would be with no rotation. This rotational energy (2.14×10²⁹ J) represents 2.38 billion metric tons of added mass.

Efficiency

Although mass is conserved in isolated systems in some reactions matter particles (which contain a form of rest energy) can be destroyed and the energy released can be converted to other types of energy that are more usable and obvious as forms of energy—such as light and energy of motion (heat, etc.). However, the total amount of energy and mass does not change in such a transformation. Even when particles are not destroyed, a certain fraction of the ill-defined "matter" in ordinary objects can be destroyed, and its associated energy liberated and made available as the more dramatic energies of light and heat, even though no identifiable real particles are destroyed, and even though (again) the total energy is unchanged. Such conversions between types of energy (resting to active energy) happen in nuclear weapons, in which the protons and neutrons in atomic nuclei lose a small fraction of their average mass, but this mass loss is not due to the destruction of any protons or neutrons (or even, in general, lighter particles like electrons).

In nuclear reactions, typically only a small fraction of the total mass–energy of the bomb converts into the mass–energy of heat, light, radiation, and motion—which are "active" forms that can be used. When an atom fissions, it loses only about 0.1% of its mass (which escapes from the system and does not disappear), and additionally, in a bomb or reactor not all the atoms can fission. In a modern fission-based atomic bomb, the efficiency is only about 40%, so only 40% of the fissionable atoms actually fission, and only about 0.03% of the fissile core mass appears as energy in the end. In nuclear fusion, more of the mass is released as usable energy, roughly 0.3%. But in a fusion bomb, the bomb mass is partly casing and non-reacting components, so that in practicality, again (coincidentally) no more than about 0.03% of the total mass of the entire weapon is released as usable energy. See nuclear weapon yield for practical details of this ratio in modern nuclear weapons.

In theory, it should be possible to destroy matter and convert all of the rest-energy associated with matter into heat and light (which would of course have the same mass, if observed as an isolated system), but none of the theoretically known methods are practical. One way to convert all the energy within matter into usable energy is to annihilate matter with antimatter. But antimatter is rare in our universe, and must be made first. Due to inefficient mechanisms of production, making antimatter always requires far more usable energy than would be released when it was annihilated.

Since most of the mass of ordinary objects resides in protons and neutrons, converting all the energy of ordinary matter into more useful energy requires that the protons and neutrons be converted to lighter particles, or particles with no mass at all. In the Standard Model of particle physics, the number of protons plus neutrons is nearly exactly conserved. Still, Gerard 't Hooft showed that there is a process that converts protons and neutrons to antielectrons and neutrinos. This is the weak SU(2) instanton proposed by Belavin Polyakov Schwarz and Tyupkin. This process, can in principle destroy matter and convert all the energy of matter into neutrinos and usable energy, but it is normally extraordinarily slow. Later it became clear that this process happens at a fast rate at very high temperatures, since then, instanton-like configurations are copiously produced from thermal fluctuations. The temperature required is so high that it would only have been reached shortly after the Big Bang.

Many extensions of the standard model contain magnetic monopoles, and in some models of grand unification, these monopoles catalyze proton decay, a process known as the Callan-Rubakov effect. This process would be an efficient mass–energy conversion at ordinary temperatures, but it requires making monopoles and anti-monopoles first. The energy required to produce monopoles is believed to be enormous, but magnetic charge is conserved, so that the lightest monopole is stable. All these properties are deduced in theoretical models—magnetic monopoles have never been observed, nor have they been produced in any experiment so far.

A third known method of total matter–energy "conversion" (which again in practice only means conversion of one form of energy into a different form of energy), is using gravity, specifically black holes. Stephen Hawking theorized that black holes radiate thermally with no regard to how they are formed. So, it is theoretically possible to throw matter into a black hole and use the emitted heat to generate power. According to the theory of Hawking radiation, however, the black hole used radiates at a higher rate the smaller it is, producing usable powers at only small black hole masses, where usable may for example be something greater than the local background radiation. It is also worth noting that the ambient irradiated power would change with the mass of the black hole, increasing as the mass of the black hole decreases, or decreasing as the mass increases, at a rate where power is proportional to the inverse square of the mass. In a "practical" scenario, mass and energy could be dumped into the black hole to regulate this growth, or keep its size, and thus power output, near constant. This could result from the fact that mass and energy are lost from the hole with its thermal radiation.

Background

Mass–velocity relationship

In developing special relativity, Einstein found that the kinetic energy of a moving body is

${\displaystyle E_{k}=m_{0}c^{2}(\gamma -1)=m_{0}c^{2}\left({\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}-1\right),}$

with v the velocity, m₀ the rest mass, and γ the Lorentz factor.

He included the second term on the right to make sure that for small velocities the energy would be the same as in classical mechanics, thus satisfying the correspondence principle:

${\displaystyle E_{k}={\frac {1}{2}}m_{0}v^{2}+\cdots }$

Without this second term, there would be an additional contribution in the energy when the particle is not moving.

Einstein found that the total momentum of a moving particle is:

${\displaystyle P={\frac {m_{0}v}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}.}$

It is this quantity that is conserved in collisions. The ratio of the momentum to the velocity is the relativistic mass, m.

${\displaystyle m={\frac {m_{0}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

And the relativistic mass and the relativistic kinetic energy are related by the formula:

${\displaystyle E_{k}=mc^{2}-m_{0}c^{2}.\,}$

Einstein wanted to omit the unnatural second term on the right-hand side, whose only purpose is to make the energy at rest zero, and to declare that the particle has a total energy, which obeys:

${\displaystyle E=mc^{2}\,}$

which is a sum of the rest energy m₀c² and the kinetic energy. This total energy is mathematically more elegant, and fits better with the momentum in relativity. But to come to this conclusion, Einstein needed to think carefully about collisions. This expression for the energy implied that matter at rest has a huge amount of energy, and it is not clear whether this energy is physically real, or just a mathematical artifact with no physical meaning.

In a collision process where all the rest-masses are the same at the beginning as at the end, either expression for the energy is conserved. The two expressions only differ by a constant that is the same at the beginning and at the end of the collision. Still, by analyzing the situation where particles are thrown off a heavy central particle, it is easy to see that the inertia of the central particle is reduced by the total energy emitted. This allowed Einstein to conclude that the inertia of a heavy particle is increased or diminished according to the energy it absorbs or emits.

Relativistic mass

After Einstein first made his proposal, it became clear that the word mass can have two different meanings. Some denote the relativistic mass with an explicit index:

${\displaystyle m_{\mathrm {rel} }={\frac {m_{0}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}.}$

This mass is the ratio of momentum to velocity, and it is also the relativistic energy divided by c² (it is not Lorentz-invariant, in contrast to ${\displaystyle m_{0}}$). The equation E = m_relc² holds for moving objects. When the velocity is small, the relativistic mass and the rest mass are almost exactly the same.

• E = mc² either means E = m₀c² for an object at rest, or E = m_relc² when the object is moving.

Also Einstein (following Hendrik Lorentz and Max Abraham) used velocity- and direction-dependent mass concepts (longitudinal and transverse mass) in his 1905 electrodynamics paper and in another paper in 1906. However, in his first paper on E = mc² (1905), he treated m as what would now be called the rest mass. Some claim that (in later years) he did not like the idea of "relativistic mass".  When modern physicists say "mass", they are usually talking about rest mass, since if they meant "relativistic mass", they would just say "energy".

Considerable debate has ensued over the use of the concept "relativistic mass" and the connection of "mass" in relativity to "mass" in Newtonian dynamics. For example, one view is that only rest mass is a viable concept and is a property of the particle; while relativistic mass is a conglomeration of particle properties and properties of spacetime. A perspective that avoids this debate, due to Kjell Vøyenli, is that the Newtonian concept of mass as a particle property and the relativistic concept of mass have to be viewed as embedded in their own theories and as having no precise connection.

Low speed expansion

We can rewrite the expression E = γm₀c² as a Taylor series:

${\displaystyle E=m_{0}c^{2}\left[1+{\frac {1}{2}}\left({\frac {v}{c}}\right)^{2}+{\frac {3}{8}}\left({\frac {v}{c}}\right)^{4}+{\frac {5}{16}}\left({\frac {v}{c}}\right)^{6}+\ldots \right].}$

For speeds much smaller than the speed of light, higher-order terms in this expression get smaller and smaller because v/c is small. For low speeds we can ignore all but the first two terms:

${\displaystyle E\approx m_{0}c^{2}+{\frac {1}{2}}m_{0}v^{2}.}$

The total energy is a sum of the rest energy and the Newtonian kinetic energy.

The classical energy equation ignores both the m₀c² part, and the high-speed corrections. This is appropriate, as all the higher-order corrections are small. Since only changes in energy affect the behavior of objects, whether we include the m₀c² part makes no difference, since it is constant. For the same reason, it is possible to subtract the rest energy from the total energy in relativity. By considering the emission of energy in different frames, Einstein could show that the rest energy has a real physical meaning.

The higher-order terms are extra corrections to Newtonian mechanics, and become important at higher speeds. The Newtonian equation is only a low-speed approximation, but an extraordinarily good one. Adding in the third term yields:

${\displaystyle E\approx m_{0}c^{2}+{\frac {1}{2}}m_{0}v^{2}\left(1+{\frac {3v^{2}}{4c^{2}}}\right)}$

The difference between the two approximations is then given by ${\displaystyle {\frac {3v^{2}}{4c^{2}}}}$. As an example of how small this is for everyday objects, in 2018 NASA announced the Parker Solar Probe was the fastest ever, with a speed of 153,454 miles per hour.  For this system, ${\displaystyle {\frac {3v^{2}}{4c^{2}}}\approx 3.9*10^{-8}}$ and accounts for an energy correction of four parts per hundred million. To put these numbers in perspective, the gravitational constant has a standard relative uncertainty of about ${\displaystyle 2.2*10^{-5}}$.

History

While Einstein was the first to have correctly deduced the mass–energy equivalence formula, he was not the first to have related energy with mass. But nearly all previous authors thought that the energy that contributes to mass comes only from electromagnetic fields.

Newton: matter and light

In 1717 Isaac Newton speculated that light particles and matter particles were interconvertible in "Query 30" of the Opticks, where he asks:

Are not the gross bodies and light convertible into one another, and may not bodies receive much of their activity from the particles of light which enter their composition?

Swedenborg: matter composed of "pure and total motion"

In 1734 the Swedish scientist and theologian Emanuel Swedenborg in his Principia theorized that all matter is ultimately composed of dimensionless points of "pure and total motion". He described this motion as being without force, direction or speed, but having the potential for force, direction and speed everywhere within it.

Electromagnetic mass

There were many attempts in the 19th and the beginning of the 20th century—like those of J. J. Thomson (1881), Oliver Heaviside (1888), and George Frederick Charles Searle (1897), Wilhelm Wien (1900), Max Abraham (1902), Hendrik Antoon Lorentz (1904) — to understand how the mass of a charged object depends on the electrostatic field. This concept was called electromagnetic mass, and was considered as being dependent on velocity and direction as well. Lorentz (1904) gave the following expressions for longitudinal and transverse electromagnetic mass:

${\displaystyle m_{L}={\frac {m_{0}}{\left({\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\right)^{3}}},\quad m_{T}={\frac {m_{0}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$,

where

${\displaystyle m_{0}={\frac {4}{3}}{\frac {E_{em}}{c^{2}}}}$

Radiation pressure and inertia

Another way of deriving some sort of electromagnetic mass was based on the concept of radiation pressure. In 1900, Henri Poincaré associated electromagnetic radiation energy with a "fictitious fluid" having momentum and mass

${\displaystyle m_{em}={\frac {E_{em}}{c^{2}}}\,.}$

By that, Poincaré tried to save the center of mass theorem in Lorentz's theory, though his treatment led to radiation paradoxes.

Friedrich Hasenöhrl showed in 1904, that electromagnetic cavity radiation contributes the "apparent mass"

${\displaystyle m_{0}={\frac {4}{3}}{\frac {E_{em}}{c^{2}}}}$

to the cavity's mass. He argued that this implies mass dependence on temperature as well.

Einstein: mass–energy equivalence

Albert Einstein did not formulate exactly the formula E = mc² in his 1905 Annus Mirabilis paper "Does the Inertia of an object Depend Upon Its Energy Content?"; rather, the paper states that if a body gives off the energy L in the form of radiation, its mass diminishes by L/c². (Here, "radiation" means electromagnetic radiation, or light, and mass means the ordinary Newtonian mass of a slow-moving object.) This formulation relates only a change Δm in mass to a change L in energy without requiring the absolute relationship.

Objects with zero mass presumably have zero energy, so the extension that all mass is proportional to energy is obvious from this result. In 1905, even the hypothesis that changes in energy are accompanied by changes in mass was untested. Not until the discovery of the first type of antimatter (the positron in 1932) was it found that all of the mass of pairs of resting particles could be converted to radiation.

The first derivation by Einstein (1905)

Already in his relativity paper "On the electrodynamics of moving bodies", Einstein derived the correct expression for the kinetic energy of particles:

${\displaystyle E_{k}=mc^{2}\left({\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}-1\right)}$.

Now the question remained open as to which formulation applies to bodies at rest. This was tackled by Einstein in his paper "Does the inertia of a body depend upon its energy content?", where he used a body emitting two light pulses in opposite directions, having energies of E₀ before and E₁ after the emission as seen in its rest frame. As seen from a moving frame, this becomes H₀ and H₁. Einstein obtained:

${\displaystyle \left(H_{0}-E_{0}\right)-\left(H_{1}-E_{1}\right)=E\left({\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}-1\right)}$

then he argued that H − E can only differ from the kinetic energy K by an additive constant, which gives

${\displaystyle K_{0}-K_{1}=E\left({\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}-1\right)}$

Neglecting effects higher than third order in v/c after a Taylor series expansion of the right side of this gives:

${\displaystyle K_{0}-K_{1}={\frac {E}{c^{2}}}{\frac {v^{2}}{2}}.}$

Einstein concluded that the emission reduces the body's mass by E/c², and that the mass of a body is a measure of its energy content.

The correctness of Einstein's 1905 derivation of E = mc² was criticized by Max Planck (1907), who argued that it is only valid to first approximation. Another criticism was formulated by Herbert Ives (1952) and Max Jammer (1961), asserting that Einstein's derivation is based on begging the question. On the other hand, John Stachel and Roberto Torretti (1982) argued that Ives' criticism was wrong, and that Einstein's derivation was correct. Hans Ohanian (2008) agreed with Stachel/Torretti's criticism of Ives, though he argued that Einstein's derivation was wrong for other reasons. For a recent review, see Hecht (2011).

Alternative version

An alternative version of Einstein's thought experiment was proposed by Fritz Rohrlich (1990), who based his reasoning on the Doppler effect. Like Einstein, he considered a body at rest with mass M. If the body is examined in a frame moving with nonrelativistic velocity v, it is no longer at rest and in the moving frame it has momentum P = Mv. Then he supposed the body emits two pulses of light to the left and to the right, each carrying an equal amount of energy E/2. In its rest frame, the object remains at rest after the emission since the two beams are equal in strength and carry opposite momentum.

However, if the same process is considered in a frame that moves with velocity v to the left, the pulse moving to the left is redshifted, while the pulse moving to the right is blue shifted. The blue light carries more momentum than the red light, so that the momentum of the light in the moving frame is not balanced: the light is carrying some net momentum to the right.

The object has not changed its velocity before or after the emission. Yet in this frame it has lost some right-momentum to the light. The only way it could have lost momentum is by losing mass. This also solves Poincaré's radiation paradox, discussed above.

The velocity is small, so the right-moving light is blueshifted by an amount equal to the nonrelativistic Doppler shift factor 1 − v/c. The momentum of the light is its energy divided by c, and it is increased by a factor of v/c. So the right-moving light is carrying an extra momentum ΔP given by:

${\displaystyle \Delta P={v \over c}{E \over 2c}.}$

The left-moving light carries a little less momentum, by the same amount ΔP. So the total right-momentum in both light pulses is twice ΔP. This is the right-momentum that the object lost.

${\displaystyle 2\Delta P=v{E \over c^{2}}.}$

The momentum of the object in the moving frame after the emission is reduced to this amount:

${\displaystyle P'=Mv-2\Delta P=\left(M-{E \over c^{2}}\right)v.}$

So the change in the object's mass is equal to the total energy lost divided by c². Since any emission of energy can be carried out by a two step process, where first the energy is emitted as light and then the light is converted to some other form of energy, any emission of energy is accompanied by a loss of mass. Similarly, by considering absorption, a gain in energy is accompanied by a gain in mass.

Relativistic center-of-mass theorem (1906)

Like Poincaré, Einstein concluded in 1906 that the inertia of electromagnetic energy is a necessary condition for the center-of-mass theorem to hold. On this occasion, Einstein referred to Poincaré's 1900 paper and wrote:

Although the merely formal considerations, which we will need for the proof, are already mostly contained in a work by H. Poincaré², for the sake of clarity I will not rely on that work.

In Einstein's more physical, as opposed to formal or mathematical, point of view, there was no need for fictitious masses. He could avoid the perpetuum mobile problem because, on the basis of the mass–energy equivalence, he could show that the transport of inertia that accompanies the emission and absorption of radiation solves the problem. Poincaré's rejection of the principle of action–reaction can be avoided through Einstein's E = mc², because mass conservation appears as a special case of the energy conservation law.

Others

During the nineteenth century there were several speculative attempts to show that mass and energy were proportional in various ether theories.  In 1873 Nikolay Umov pointed out a relation between mass and energy for ether in the form of Е = kmc², where 0.5 ≤ k ≤ 1. The writings of Samuel Tolver Preston, and a 1903 paper by Olinto De Pretto, presented a mass–energy relation. Bartocci (1999) observed that there were only three degrees of separation linking De Pretto to Einstein, concluding that Einstein was probably aware of De Pretto's work.

Preston and De Pretto, following Le Sage, imagined that the universe was filled with an ether of tiny particles that always move at speed c. Each of these particles has a kinetic energy of mc² up to a small numerical factor. The nonrelativistic kinetic energy formula did not always include the traditional factor of 1/2, since Leibniz introduced kinetic energy without it, and the 1/2 is largely conventional in prerelativistic physics. By assuming that every particle has a mass that is the sum of the masses of the ether particles, the authors concluded that all matter contains an amount of kinetic energy either given by E = mc² or 2E = mc² depending on the convention. A particle ether was usually considered unacceptably speculative science at the time, and since these authors did not formulate relativity, their reasoning is completely different from that of Einstein, who used relativity to change frames.

Independently, Gustave Le Bon in 1905 speculated that atoms could release large amounts of latent energy, reasoning from an all-encompassing qualitative philosophy of physics.

Radioactivity and nuclear energy

It was quickly noted after the discovery of radioactivity in 1897, that the total energy due to radioactive processes is about one million times greater than that involved in any known molecular change. However, it raised the question where this energy is coming from. After eliminating the idea of absorption and emission of some sort of Lesagian ether particles, the existence of a huge amount of latent energy, stored within matter, was proposed by Ernest Rutherford and Frederick Soddy in 1903. Rutherford also suggested that this internal energy is stored within normal matter as well. He went on to speculate in 1904:

If it were ever found possible to control at will the rate of disintegration of the radio-elements, an enormous amount of energy could be obtained from a small quantity of matter.

Einstein's equation is in no way an explanation of the large energies released in radioactive decay (this comes from the powerful nuclear forces involved; forces that were still unknown in 1905). In any case, the enormous energy released from radioactive decay (which had been measured by Rutherford) was much more easily measured than the (still small) change in the gross mass of materials as a result. Einstein's equation, by theory, can give these energies by measuring mass differences before and after reactions, but in practice, these mass differences in 1905 were still too small to be measured in bulk. Prior to this, the ease of measuring radioactive decay energies with a calorimeter was thought possibly likely to allow measurement of changes in mass difference, as a check on Einstein's equation itself. Einstein mentions in his 1905 paper that mass–energy equivalence might perhaps be tested with radioactive decay, which releases enough energy (the quantitative amount known roughly by 1905) to possibly be "weighed," when missing from the system (having been given off as heat). However, radioactivity seemed to proceed at its own unalterable (and quite slow, for radioactives known then) pace, and even when simple nuclear reactions became possible using proton bombardment, the idea that these great amounts of usable energy could be liberated at will with any practicality, proved difficult to substantiate. Rutherford was reported in 1933 to have declared that this energy could not be exploited efficiently: "Anyone who expects a source of power from the transformation of the atom is talking moonshine."

The popular connection between Einstein, E = mc², and the atomic bomb was prominently indicated on the cover of Time magazine in July 1946 by the writing of the equation on the mushroom cloud.

This situation changed dramatically in 1932 with the discovery of the neutron and its mass, allowing mass differences for single nuclides and their reactions to be calculated directly, and compared with the sum of masses for the particles that made up their composition. In 1933, the energy released from the reaction of lithium-7 plus protons giving rise to 2 alpha particles (as noted above by Rutherford), allowed Einstein's equation to be tested to an error of ±0.5%. However, scientists still did not see such reactions as a practical source of power, due to the energy cost of accelerating reaction particles.

After the very public demonstration of huge energies released from nuclear fission after the atomic bombings of Hiroshima and Nagasaki in 1945, the equation E = mc² became directly linked in the public eye with the power and peril of nuclear weapons. The equation was featured as early as page 2 of the Smyth Report, the official 1945 release by the US government on the development of the atomic bomb, and by 1946 the equation was linked closely enough with Einstein's work that the cover of Time magazine prominently featured a picture of Einstein next to an image of a mushroom cloud emblazoned with the equation. Einstein himself had only a minor role in the Manhattan Project: he had cosigned a letter to the U.S. President in 1939 urging funding for research into atomic energy, warning that an atomic bomb was theoretically possible. The letter persuaded Roosevelt to devote a significant portion of the wartime budget to atomic research. Without a security clearance, Einstein's only scientific contribution was an analysis of an isotope separation method in theoretical terms. It was inconsequential, on account of Einstein not being given sufficient information (for security reasons) to fully work on the problem.

While E = mc² is useful for understanding the amount of energy potentially released in a fission reaction, it was not strictly necessary to develop the weapon, once the fission process was known, and its energy measured at 200 MeV (which was directly possible, using a quantitative Geiger counter, at that time). As the physicist and Manhattan Project participant Robert Serber put it: "Somehow the popular notion took hold long ago that Einstein's theory of relativity, in particular his famous equation E = mc², plays some essential role in the theory of fission. Albert Einstein had a part in alerting the United States government to the possibility of building an atomic bomb, but his theory of relativity is not required in discussing fission. The theory of fission is what physicists call a non-relativistic theory, meaning that relativistic effects are too small to affect the dynamics of the fission process significantly." However the association between E = mc² and nuclear energy has since stuck, and because of this association, and its simple expression of the ideas of Albert Einstein himself, it has become "the world's most famous equation".

While Serber's view of the strict lack of need to use mass–energy equivalence in designing the atomic bomb is correct, it does not take into account the pivotal role this relationship played in making the fundamental leap to the initial hypothesis that large atoms were energetically allowed to split into approximately equal parts (before this energy was in fact measured). In late 1938, Lise Meitner and Otto Robert Frisch—while on a winter walk during which they solved the meaning of Hahn's experimental results and introduced the idea that would be called atomic fission—directly used Einstein's equation to help them understand the quantitative energetics of the reaction that overcame the "surface tension-like" forces that hold the nucleus together, and allowed the fission fragments to separate to a configuration from which their charges could force them into an energetic fission. To do this, they used packing fraction, or nuclear binding energy values for elements, which Meitner had memorized. These, together with use of E = mc² allowed them to realize on the spot that the basic fission process was energetically possible:

...We walked up and down in the snow, I on skis and she on foot. ...and gradually the idea took shape... explained by Bohr's idea that the nucleus is like a liquid drop; such a drop might elongate and divide itself... We knew there were strong forces that would resist, ..just as surface tension. But nuclei differed from ordinary drops. At this point we both sat down on a tree trunk and started to calculate on scraps of paper. ...the Uranium nucleus might indeed be a very wobbly, unstable drop, ready to divide itself... But, ...when the two drops separated they would be driven apart by electrical repulsion, about 200 MeV in all. Fortunately Lise Meitner remembered how to compute the masses of nuclei... and worked out that the two nuclei formed... would be lighter by about one-fifth the mass of a proton. Now whenever mass disappears energy is created, according to Einstein's formula E = mc², and... the mass was just equivalent to 200 MeV; it all fitted!