Blood pressure

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Blood_pressure

 

Blood pressure
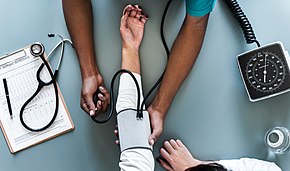
A healthcare worker measuring blood pressure using a sphygmomanometer.
MeSH	D001795
MedlinePlus	007490
LOINC	35094-2

Blood pressure (BP) is the pressure of circulating blood against the walls of blood vessels. Most of this pressure results from the heart pumping blood through the circulatory system. When used without qualification, the term "blood pressure" refers to the pressure in a brachial artery, where it is most commonly measured. Blood pressure is usually expressed in terms of the systolic pressure (maximum pressure during one heartbeat) over diastolic pressure (minimum pressure between two heartbeats) in the cardiac cycle. It is measured in millimeters of mercury (mmHg) above the surrounding atmospheric pressure, or in kilopascals (kPa).

Blood pressure is one of the vital signs—together with respiratory rate, heart rate, oxygen saturation, and body temperature—that healthcare professionals use in evaluating a patient's health. Normal resting blood pressure, in an adult is approximately 120 millimetres of mercury (16 kPa) systolic over 80 millimetres of mercury (11 kPa) diastolic, denoted as "120/80 mmHg". Globally, the average blood pressure, age standardized, has remained about the same since 1975 to the present, at approx. 127/79 mmHg in men and 122/77 mmHg in women, although these average data mask significantly diverging regional trends.

Traditionally, a health-care worker measured blood pressure non-invasively by auscultation (listening) through a stethoscope for sounds in one arm's artery as the artery is squeezed, closer to the heart, by an aneroid gauge or a mercury-tube sphygmomanometer. Auscultation is still generally considered to be the gold standard of accuracy for non-invasive blood pressure readings in clinic. However, semi-automated methods have become common, largely due to concerns about potential mercury toxicity, although cost, ease of use and applicability to ambulatory blood pressure or home blood pressure measurements have also influenced this trend. Early automated alternatives to mercury-tube sphygmomanometers were often seriously inaccurate, but modern devices validated to international standards achieve an average difference between two standardized reading methods of 5 mm Hg or less, and a standard deviation of less than 8 mm Hg. Most of these semi-automated methods measure blood pressure using oscillometry (measurement by a pressure transducer in the cuff of the device of small oscillations of intra-cuff pressure accompanying heartbeat-induced changes in the volume of each pulse).

Blood pressure is influenced by cardiac output, systemic vascular resistance, blood volume and arterial stiffness, and varies depending on patient's situation, emotional state, activity and relative health or disease state. In the short term, blood pressure is regulated by baroreceptors, which act via the brain to influence the nervous and the endocrine systems.

Blood pressure that is too low is called hypotension, pressure that is consistently too high is called hypertension, and normal pressure is called normotension. Both hypertension and hypotension have many causes and may be of sudden onset or of long duration. Long-term hypertension is a risk factor for many diseases, including stroke, heart disease, and kidney failure. Long-term hypertension is more common than long-term hypotension.

Classification, normal and abnormal values

Systemic arterial pressure

The Task Force for the management of arterial hypertension of the European Society of Cardiology (ESC) and the European Society of Hypertension (ESH) classification of office blood pressure (BP)^a and definitions of hypertension grade^b.

Category	Systolic BP, mmHg	Diastolic BP, mmHg
Optimal	< 120	< 80
Normal	120–129	80–84
High normal	130–139	85–89
Grade 1 hypertension	140–159	90–99
Grade 2 hypertension	160–179	100–109
Grade 3 hypertension	≥ 180	≥ 110
Isolated systolic hypertensionb	≥ 140	< 90
The same classification is used for all ages from 16 years. a BP category is defined according to seated clinic BP and by the highest level of BP, whether systolic or diastolic. b Isolated systolic hypertension is graded 1, 2, or 3 according to systolic BP values in the ranges indicated.

Diastolic vs systolic blood pressure chart comparing European Society of Cardiology and European Society of Hypertension classification with reference ranges in children

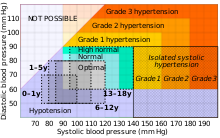
The risk of cardiovascular disease increases progressively above 115/75 mmHg, below this level there is limited evidence.

Observational studies demonstrate that people who maintain arterial pressures at the low end of these pressure ranges have much better long-term cardiovascular health. There is an ongoing medical debate over what is the optimal level of blood pressure to target when using drugs to lower blood pressure with hypertension, particularly in older people.

The table shows the 2018 classification of office (or clinic) blood pressure by The Task Force for the management of arterial hypertension of the European Society of Cardiology (ESC) and the European Society of Hypertension (ESH). Similar thresholds had been adopted by the American Heart Association for adults who are 18 years and older, but in November 2017 the American Heart Association announced revised definitions for blood pressure categories that increased the number of people considered to have high blood pressure.

Blood pressure fluctuates from minute to minute and normally shows a circadian rhythm over a 24-hour period, with highest readings in the early morning and evenings and lowest readings at night. Loss of the normal fall in blood pressure at night is associated with a greater future risk of cardiovascular disease and there is evidence that night-time blood pressure is a stronger predictor of cardiovascular events than day-time blood pressure. Blood pressure varies over longer time periods (months to years) and this variability predicts adverse outcomes. Blood pressure also changes in response to temperature, noise, emotional stress, consumption of food or liquid, dietary factors, physical activity, changes in posture (such as standing-up), drugs, and disease. The variability in blood pressure and the better predictive value of ambulatory blood pressure measurements has led some authorities, such as the National Institute for Health and Care Excellence (NICE) in the UK, to advocate for the use of ambulatory blood pressure as the preferred method for diagnosis of hypertension.

A digital sphygmomanometer used for measuring blood pressure

Various other factors, such as age and sex, also influence a person's blood pressure. Differences between left-arm and right-arm blood pressure measurements tend to be small. However, occasionally there is a consistent difference greater than 10 mmHg which may need further investigation, e.g. for peripheral arterial disease, obstructive arterial disease or aortic dissection.

There is no accepted diagnostic standard for hypotension, although pressures less than 90/60 are commonly regarded as hypotensive. In practice blood pressure is considered too low only if symptoms are present.

Systemic arterial pressure and age

Fetal blood pressure

Further information: Fetal circulation § Blood pressure

In pregnancy, it is the fetal heart and not the mother's heart that builds up the fetal blood pressure to drive blood through the fetal circulation. The blood pressure in the fetal aorta is approximately 30 mmHg at 20 weeks of gestation, and increases to approximately 45 mmHg at 40 weeks of gestation.

The average blood pressure for full-term infants:

• Systolic 65–95 mmHg
• Diastolic 30–60 mmHg

Childhood

Reference ranges for blood pressure (BP) in children

Stage	Approximate age	Systolic BP, mmHg	Diastolic BP, mmHg
Infants	0–12 months	75–100	50–70
Toddlers and preschoolers	1–5 years	80–110	50–80
School age	6–12 years	85–120	50–80
Adolescents	13–18 years	95–140	60–90

In children the normal ranges for blood pressure are lower than for adults and depend on height. Reference blood pressure values have been developed for children in different countries, based on the distribution of blood pressure in children of these countries.

Aging adults

In adults in most societies, systolic blood pressure tends to rise from early adulthood onward, up to at least age 70; diastolic pressure tends to begin to rise at the same time but to start to fall earlier in mid-life, approximately age 55. Mean blood pressure rises from early adulthood, plateauing in mid-life, while pulse pressure rises quite markedly after the age of 40. Consequently, in many older people, systolic blood pressure often exceeds the normal adult range, if the diastolic pressure is in the normal range this is termed isolated systolic hypertension. The rise in pulse pressure with age is attributed to increased stiffness of the arteries. An age-related rise in blood pressure is not considered healthy and is not observed in some isolated unacculturated communities.

Systemic venous pressure

Site		Normal pressure range (in mmHg)
Central venous pressure		3–8
Right ventricular pressure	systolic	15–30
	diastolic	3–8
Pulmonary artery pressure	systolic	15–30
	diastolic	4–12
Pulmonary vein/ Pulmonary capillary wedge pressure		2–15
Left ventricular pressure	systolic	100–140
	diastolic	3–12

Blood pressure generally refers to the arterial pressure in the systemic circulation. However, measurement of pressures in the venous system and the pulmonary vessels plays an important role in intensive care medicine but requires invasive measurement of pressure using a catheter.

Venous pressure is the vascular pressure in a vein or in the atria of the heart. It is much lower than arterial pressure, with common values of 5 mmHg in the right atrium and 8 mmHg in the left atrium.

Variants of venous pressure include:

• Central venous pressure, which is a good approximation of right atrial pressure, which is a major determinant of right ventricular end diastolic volume. (However, there can be exceptions in some cases.)
• The jugular venous pressure (JVP) is the indirectly observed pressure over the venous system. It can be useful in the differentiation of different forms of heart and lung disease.
• The portal venous pressure is the blood pressure in the portal vein. It is normally 5–10 mmHg

Pulmonary pressure

Main article: Pulmonary artery pressure

Normally, the pressure in the pulmonary artery is about 15 mmHg at rest.

Increased blood pressure in the capillaries of the lung causes pulmonary hypertension, leading to interstitial edema if the pressure increases to above 20 mmHg, and to pulmonary edema at pressures above 25 mmHg.

Mean systemic pressure

Main article: Mean systemic pressure

If the heart is stopped, blood pressure falls, but it does not fall to zero. The remaining pressure measured after cessation of the heart beat and redistribution of blood throughout the circulation is termed the mean systemic pressure or mean circulatory filling pressure; typically this is proximally ~7mm Hg.

Disorders of blood pressure

Disorders of blood pressure control include high blood pressure, low blood pressure, and blood pressure that shows excessive or maladaptive fluctuation.

High blood pressure

Main article: Hypertension

Overview of main complications of persistent high blood pressure.

Arterial hypertension can be an indicator of other problems and may have long-term adverse effects. Sometimes it can be an acute problem, such as in a hypertensive emergency when blood pressure is more than 180/120 mmHg.

Levels of arterial pressure put mechanical stress on the arterial walls. Higher pressures increase heart workload and progression of unhealthy tissue growth (atheroma) that develops within the walls of arteries. The higher the pressure, the more stress that is present and the more atheroma tend to progress and the heart muscle tends to thicken, enlarge and become weaker over time.

Persistent hypertension is one of the risk factors for strokes, heart attacks, heart failure, and arterial aneurysms, and is the leading cause of chronic kidney failure. Even moderate elevation of arterial pressure leads to shortened life expectancy. At severely high pressures, mean arterial pressures 50% or more above average, a person can expect to live no more than a few years unless appropriately treated.

Both high systolic pressure and high pulse pressure (the numerical difference between systolic and diastolic pressures) are risk factors. In some cases, it appears that a decrease in excessive diastolic pressure can actually increase risk, probably due to the increased difference between systolic and diastolic pressures. If systolic blood pressure is elevated (>140 mmHg) with a normal diastolic blood pressure (<90 mmHg), it is called isolated systolic hypertension and may present a health concern. According to the 2017  American Heart Association blood pressure guidelines state that a systolic blood pressure of 130-139 mmHg with a diastolic pressure of 80-89 mmHg is "stage one hypertension".

For those with heart valve regurgitation, a change in its severity may be associated with a change in diastolic pressure. In a study of people with heart valve regurgitation that compared measurements two weeks apart for each person, there was an increased severity of aortic and mitral regurgitation when diastolic blood pressure increased, whereas when diastolic blood pressure decreased, there was a decreased severity.

Low blood pressure

Main article: Hypotension

Blood pressure that is too low is known as hypotension. This is a medical concern if it causes signs or symptoms, such as dizziness, fainting, or in extreme cases, circulatory shock.

Causes of low arterial pressure include:

• Sepsis
• Hemorrhage – blood loss
• Cardiogenic shock
• Neurally mediated hypotension (or reflex syncope)
• Toxins including toxic doses of blood pressure medicine
• Hormonal abnormalities, such as Addison's disease
• Eating disorders, particularly anorexia nervosa and bulimia

Orthostatic hypotension

Main article: Orthostatic hypotension

A large fall in blood pressure upon standing (persistent systolic/diastolic blood pressure decrease of >20/10 mm Hg) is termed orthostatic hypotension (postural hypotension) and represents a failure of the body to compensate for the effect of gravity on the circulation. Standing results in an increased hydrostatic pressure in the blood vessels of the lower limbs. The consequent distension of the veins below the diaphragm (venous pooling) causes ~500 ml of blood to be relocated from the chest and upper body. This results in a rapid decrease in central blood volume and a reduction of ventricular preload which in turn reduces stroke volume, and mean arterial pressure. Normally this is compensated for by multiple mechanisms, including activation of the autonomic nervous system which increases heart rate, myocardial contractility and systemic arterial vasoconstriction to preserve blood pressure and elicits venous vasoconstriction to decrease venous compliance. Decreased venous compliance also results from an intrinsic myogenic increase in venous smooth muscle tone in response to the elevated pressure in the veins of the lower body.

Other compensatory mechanisms include the veno-arteriolar axon reflex, the 'skeletal muscle pump' and 'respiratory pump'. Together these mechanisms normally stabilize blood pressure within a minute or less. If these compensatory mechanisms fail and arterial pressure and blood flow decrease beyond a certain point, the perfusion of the brain becomes critically compromised (i.e., the blood supply is not sufficient), causing lightheadedness, dizziness, weakness or fainting. Usually this failure of compensation is due to disease, or drugs that affect the sympathetic nervous system. A similar effect is observed following the experience of excessive gravitational forces (G-loading), such as routinely experienced by aerobatic or combat pilots 'pulling Gs' where the extreme hydrostatic pressures exceed the ability of the body's compensatory mechanisms.

Variable or fluctuating blood pressure

Some fluctuation or variation in blood pressure is normal. Variations in pressure that are significantly greater than the norm are associated with increased risk of cardiovascular disease brain small vessel disease, and dementia independent of the average blood pressure level. Recent evidence from clinical trials has also linked variation in blood pressure to mortality, stroke, heart failure, and cardiac changes that may give rise to heart failure. These data have prompted discussion of whether excessive variation in blood pressure should be treated, even among normotensive older adults.

Older individuals and those who had received blood pressure medications are more likely to exhibit larger fluctuations in pressure, and there is some evidence that different antihypertensive agents have different effects on blood pressure variability; whether these differences translate to benefits in outcome is uncertain.

Physiology

Cardiac systole and diastole

Blood flow velocity waveforms in the central retinal artery (red) and vein (blue), measured by laser Doppler imaging in the eye fundus of a healthy volunteer.

During each heartbeat, blood pressure varies between a maximum (systolic) and a minimum (diastolic) pressure. The blood pressure in the circulation is principally due to the pumping action of the heart. However, blood pressure is also regulated by neural regulation from the brain (see Hypertension and the brain), as well as osmotic regulation from the kidney. Differences in mean blood pressure drive the flow of blood around the circulation. The rate of mean blood flow depends on both blood pressure and the resistance to flow presented by the blood vessels. In the absence of hydrostatic effects (e.g. standing), mean blood pressure decreases as the circulating blood moves away from the heart through arteries and capillaries due to viscous losses of energy. Mean blood pressure drops over the whole circulation, although most of the fall occurs along the small arteries and arterioles. Pulsatility also diminishes in the smaller elements of the arterial circulation, although some transmitted pulsatility is observed in capillaries.

Schematic of pressures in the circulation

Gravity affects blood pressure via hydrostatic forces (e.g., during standing), and valves in veins, breathing, and pumping from contraction of skeletal muscles also influence blood pressure, particularly in veins.

Hemodynamics

Main article: Hemodynamics

A simple view of the hemodynamics of systemic arterial pressure is based around mean arterial pressure (MAP) and pulse pressure. Most influences on blood pressure can be understood in terms of their effect on cardiac output, systemic vascular resistance, or arterial stiffness (the inverse of arterial compliance). Cardiac output is the product of stroke volume and heart rate. Stroke volume is influenced by 1) the end diastolic volume or filling pressure of the ventricle acting via the Frank Starling mechanism—this is influenced by blood volume; 2) cardiac contractility; and 3) afterload, the impedance to blood flow presented by the circulation. In the short-term, the greater the blood volume, the higher the cardiac output. This has been proposed as an explanation of the relationship between high dietary salt intake and increased blood pressure; however, responses to increased dietary sodium intake vary between individuals and are highly dependent on autonomic nervous system responses and the renin–angiotensin system, changes in plasma osmolarity may also be important. In the longer-term the relationship between volume and blood pressure is more complex. In simple terms, systemic vascular resistance is mainly determined by the caliber of small arteries and arterioles. The resistance attributable to a blood vessel depends on its radius as described by the Hagen-Poiseuille's equation (resistance∝1/radius⁴). Hence, the smaller the radius, the higher the resistance. Other physical factors that affect resistance include: vessel length (the longer the vessel, the higher the resistance), blood viscosity (the higher the viscosity, the higher the resistance) and the number of vessels, particularly the smaller numerous, arterioles and capillaries. The presence of a severe arterial stenosis increases resistance to flow, however this increase in resistance rarely increases systemic blood pressure because its contribution to total systemic resistance is small, although it may profoundly decrease downstream flow. Substances called vasoconstrictors reduce the caliber of blood vessels, thereby increasing blood pressure. Vasodilators (such as nitroglycerin) increase the caliber of blood vessels, thereby decreasing arterial pressure. In the longer term a process termed remodeling also contributes to changing the caliber of small blood vessels and influencing resistance and reactivity to vasoactive agents. Reductions in capillary density, termed capillary rarefaction, may also contribute to increased resistance in some circumstances.

In practice, each individual's autonomic nervous system and other systems regulating blood pressure, notably the kidney, respond to and regulate all these factors so that, although the above issues are important, they rarely act in isolation and the actual arterial pressure response of a given individual can vary widely in the short and long term.

Mean arterial pressure

Main article: Mean arterial pressure

Mean Arterial Pressure (MAP) is the average of blood pressure over a cardiac cycle and is determined by the cardiac output (CO), systemic vascular resistance (SVR), and central venous pressure (CVP):

${\displaystyle \text{MAP}=(\text{CO}\cdot \text{SVR})+\text{CVP}}$

In practice, the contribution of CVP (which is small) is generally ignored and so

${\displaystyle \text{MAP}=\text{CO}\cdot \text{SVR}}$

MAP is often estimated from measurements of the systolic pressure, ${\displaystyle P_{\text{sys}}}$ and the diastolic pressure, ${\displaystyle P_{\text{dias}}}$  using the equation:

${\displaystyle \text{MAP}\approxeq P_{\text{dias}}+k(P_{\text{sys}}-P_{\text{dias}})}$

where k = 0.333 although other values for k have been advocated.

Pulse pressure

Main article: Pulse pressure

A schematic representation of the arterial pressure waveform over one cardiac cycle. The notch in the curve is associated with closing of the aortic valve.

The pulse pressure is the difference between the measured systolic and diastolic pressures,

${\displaystyle P_{\text{pulse}}=P_{\text{sys}}-P_{\text{dias}}.}$

The pulse pressure is a consequence of the pulsatile nature of the cardiac output, i.e. the heartbeat. The magnitude of the pulse pressure is usually attributed to the interaction of the stroke volume of the heart, the compliance (ability to expand) of the arterial system—largely attributable to the aorta and large elastic arteries—and the resistance to flow in the arterial tree.

Regulation of blood pressure

Main articles: Blood pressure regulation and Renin–angiotensin system

The endogenous, homeostatic regulation of arterial pressure is not completely understood, but the following mechanisms of regulating arterial pressure have been well-characterized:

• Baroreceptor reflex: Baroreceptors in the high pressure receptor zones detect changes in arterial pressure. These baroreceptors send signals ultimately to the medulla of the brain stem, specifically to the rostral ventrolateral medulla (RVLM). The medulla, by way of the autonomic nervous system, adjusts the mean arterial pressure by altering both the force and speed of the heart's contractions, as well as the systemic vascular resistance. The most important arterial baroreceptors are located in the left and right carotid sinuses and in the aortic arch.
• Renin–angiotensin system (RAS): This system is generally known for its long-term adjustment of arterial pressure. This system allows the kidney to compensate for loss in blood volume or drops in arterial pressure by activating an endogenous vasoconstrictor known as angiotensin II.
• Aldosterone release: This steroid hormone is released from the adrenal cortex in response to activation of the renin-angiotensin system, high serum potassium levels, or elevated adrenocorticotropic hormone (ACTH). Renin converts angiotensinogen to angiotensin I, which is converted by angiotensin converting enzyme to angiotensin II. Angiotensin II then signals to the adrenal cortex to release aldosterone. Aldosterone stimulates sodium retention and potassium excretion by the kidneys and the consequent salt and water retention increases plasma volume, and indirectly, arterial pressure. Aldosterone may also exert direct pressor effects on vascular smooth muscle and central effects on sympathetic nervous system activity.
• Baroreceptors in low pressure receptor zones (mainly in the venae cavae and the pulmonary veins, and in the atria) result in feedback by regulating the secretion of antidiuretic hormone (ADH/Vasopressin), renin and aldosterone. The resultant increase in blood volume results in an increased cardiac output by the Frank–Starling law of the heart, in turn increasing arterial blood pressure.

These different mechanisms are not necessarily independent of each other, as indicated by the link between the RAS and aldosterone release. When blood pressure falls many physiological cascades commence in order to return the blood pressure to a more appropriate level.

1. The blood pressure fall is detected by a decrease in blood flow and thus a decrease in glomerular filtration rate (GFR).
2. Decrease in GFR is sensed as a decrease in Na⁺ levels by the macula densa.
3. The macula densa causes an increase in Na⁺ reabsorption, which causes water to follow in via osmosis and leads to an ultimate increase in plasma volume. Further, the macula densa releases adenosine which causes constriction of the afferent arterioles.
4. At the same time, the juxtaglomerular cells sense the decrease in blood pressure and release renin.
5. Renin converts angiotensinogen (inactive form) to angiotensin I (active form).
6. Angiotensin I flows in the bloodstream until it reaches the capillaries of the lungs where angiotensin-converting enzyme (ACE) acts on it to convert it into angiotensin II.
7. Angiotensin II is a vasoconstrictor that will increase blood flow to the heart and subsequently the preload, ultimately increasing the cardiac output.
8. Angiotensin II also causes an increase in the release of aldosterone from the adrenal glands.
9. Aldosterone further increases the Na⁺ and H₂O reabsorption in the distal convoluted tubule of the nephron.

Currently, the RAS is targeted pharmacologically by ACE inhibitors and angiotensin II receptor antagonists, also known as angiotensin receptor blockers (ARBs). The aldosterone system is directly targeted by spironolactone, an aldosterone antagonist. The fluid retention may be targeted by diuretics; the antihypertensive effect of diuretics is due to its effect on blood volume. Generally, the baroreceptor reflex is not targeted in hypertension because if blocked, individuals may experience orthostatic hypotension and fainting.

Taking blood pressure with a sphygmomanometer

Measurement

Main article: Blood pressure measurement

Measuring systolic and diastolic blood pressure using a mercury sphygmomanometer

Arterial pressure is most commonly measured via a sphygmomanometer, which uses the height of a column of mercury, or an aneroid gauge, to reflect the blood pressure by auscultation. The most common automated blood pressure measurement technique is based on the oscillometric method. Fully automated oscillometric measurement has been available since 1981. This principle has recently been used to measure blood pressure with a smartphone. Measuring pressure invasively, by penetrating the arterial wall to take the measurement, is much less common and usually restricted to a hospital setting. Novel methods to measure blood pressure without penetrating the arterial wall, and without applying any pressure on patient's body are currently being explored. So-called cuffless measurements, these methods open the door to more comfortable and acceptable blood pressure monitors. An example is a cuffless blood pressure monitor at the wrist that uses only optical sensors.

One common problem in office blood pressure measurement in the United States is terminal digit preference. According to one study, approximately 40% of recorded measurements ended with the digit zero, whereas "without bias, 10%–20% of measurements are expected to end in zero" Therefore, addressing digit preference is a key issue for improving blood pressure measurement accuracy.

In animals

Blood pressure levels in non-human mammals may vary depending on the species. Heart rate differs markedly, largely depending on the size of the animal (larger animals have slower heart rates). The giraffe has a distinctly high arterial pressure of about 190 mm Hg, enabling blood perfusion through the 2 metres (6 ft 7 in)-long neck to the head. In other species subjected to orthostatic blood pressure, such as arboreal snakes, blood pressure is higher than in non-arboreal snakes. A heart near to the head (short heart-to-head distance) and a long tail with tight integument favor blood perfusion to the head.

As in humans, blood pressure in animals differs by age, sex, time of day, and environmental circumstances: measurements made in laboratories or under anesthesia may not be representative of values under free-living conditions. Rats, mice, dogs and rabbits have been used extensively to study the regulation of blood pressure.

Blood pressure and heart rate of various mammals

Species	Blood pressure mm Hg		Heart rate beats per minute
	Systolic	Diastolic
Calves	140	70	75–146
Cats	155	68	100–259
Dogs	161	51	62–170
Goats	140	90	80–120
Guinea-pigs	140	90	240–300
Mice	120	75	580–680
Pigs	169	55	74–116
Rabbits	118	67	205–306
Rats	153	51	305–500
Rhesus monkeys	160	125	180–210
Sheep	140	80	63–210

Hypertension in cats and dogs

Hypertension in cats and dogs is generally diagnosed if the blood pressure is greater than 150 mm Hg (systolic), although sight hounds have higher blood pressures than most other dog breeds; a systolic pressure greater than 180 mmHg is considered abnormal in these dogs.

Quadratic equation

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Quadratic_equation

In algebra, a quadratic equation (from Latin quadratus 'square') is any equation that can be rearranged in standard form as

$${\displaystyle a{x}^2+bx+c=0,}$$

where x represents an unknown value, and a, b, and c represent known numbers, where a ≠ 0. (If a = 0 and b ≠ 0 then the equation is linear, not quadratic.) The numbers a, b, and c are the coefficients of the equation and may be distinguished by respectively calling them, the quadratic coefficient, the linear coefficient and the constant coefficient or free term.

The values of x that satisfy the equation are called solutions of the equation, and roots or zeros of the expression on its left-hand side. A quadratic equation has at most two solutions. If there is only one solution, one says that it is a double root. If all the coefficients are real numbers, there are either two real solutions, or a single real double root, or two complex solutions that are complex conjugates of each other. A quadratic equation always has two roots, if complex roots are included; and a double root is counted for two. A quadratic equation can be factored into an equivalent equation

$${\displaystyle a{x}^2+bx+c=a(x-r)(x-s)=0}$$

where r and s are the solutions for x.

The quadratic formula

$${\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}}$$

expresses the solutions in terms of a, b, and c. Completing the square is one of several ways for deriving the formula.

Solutions to problems that can be expressed in terms of quadratic equations were known as early as 2000 BC.

Because the quadratic equation involves only one unknown, it is called "univariate". The quadratic equation contains only powers of x that are non-negative integers, and therefore it is a polynomial equation. In particular, it is a second-degree polynomial equation, since the greatest power is two.

Solving the quadratic equation

Figure 1. Plots of quadratic function y = ax² + bx + c, varying each coefficient separately while the other coefficients are fixed (at values a = 1, b = 0, c = 0)

A quadratic equation with real or complex coefficients has two solutions, called roots. These two solutions may or may not be distinct, and they may or may not be real.

Factoring by inspection

It may be possible to express a quadratic equation ax² + bx + c = 0 as a product (px + q)(rx + s) = 0. In some cases, it is possible, by simple inspection, to determine values of p, q, r, and s that make the two forms equivalent to one another. If the quadratic equation is written in the second form, then the "Zero Factor Property" states that the quadratic equation is satisfied if px + q = 0 or rx + s = 0. Solving these two linear equations provides the roots of the quadratic.

For most students, factoring by inspection is the first method of solving quadratic equations to which they are exposed. If one is given a quadratic equation in the form x² + bx + c = 0, the sought factorization has the form (x + q)(x + s), and one has to find two numbers q and s that add up to b and whose product is c (this is sometimes called "Vieta's rule" and is related to Vieta's formulas). As an example, x² + 5x + 6 factors as (x + 3)(x + 2). The more general case where a does not equal 1 can require a considerable effort in trial and error guess-and-check, assuming that it can be factored at all by inspection.

Except for special cases such as where b = 0 or c = 0, factoring by inspection only works for quadratic equations that have rational roots. This means that the great majority of quadratic equations that arise in practical applications cannot be solved by factoring by inspection.

Completing the square

Main article: Completing the square

Figure 2. For the quadratic function y = x² − x − 2, the points where the graph crosses the x-axis, x = −1 and x = 2, are the solutions of the quadratic equation x² − x − 2 = 0.

The process of completing the square makes use of the algebraic identity

${\displaystyle x^2+2hx+h^2=(x+h{)}^2,}$

which represents a well-defined algorithm that can be used to solve any quadratic equation. Starting with a quadratic equation in standard form, ax² + bx + c = 0

1. Divide each side by a, the coefficient of the squared term.
2. Subtract the constant term c/a from both sides.
3. Add the square of one-half of b/a, the coefficient of x, to both sides. This "completes the square", converting the left side into a perfect square.
4. Write the left side as a square and simplify the right side if necessary.
5. Produce two linear equations by equating the square root of the left side with the positive and negative square roots of the right side.
6. Solve each of the two linear equations.

We illustrate use of this algorithm by solving 2x² + 4x − 4 = 0

${\displaystyle 2x^2+4x-4=0}$

${\displaystyle x^2+2x-2=0}$

${\displaystyle x^2+2x=2}$

${\displaystyle x^2+2x+1=2+1}$

${\displaystyle {\left(x+1\right)}^2=3}$

${\displaystyle x+1=\pm \sqrt{3}}$

${\displaystyle x=-1\pm \sqrt{3}}$

The plus–minus symbol "±" indicates that both x = −1 + √3 and x = −1 − √3 are solutions of the quadratic equation.

Quadratic formula and its derivation

Main article: Quadratic formula

Completing the square can be used to derive a general formula for solving quadratic equations, called the quadratic formula. The mathematical proof will now be briefly summarized. It can easily be seen, by polynomial expansion, that the following equation is equivalent to the quadratic equation:

${\displaystyle {\left(x+\frac{b}{2a}\right)}^2=\frac{b^2-4ac}{4a^2}.}$

Taking the square root of both sides, and isolating x, gives:

${\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.}$

Some sources, particularly older ones, use alternative parameterizations of the quadratic equation such as ax² + 2bx + c = 0 or ax² − 2bx + c = 0 , where b has a magnitude one half of the more common one, possibly with opposite sign. These result in slightly different forms for the solution, but are otherwise equivalent.

A number of alternative derivations can be found in the literature. These proofs are simpler than the standard completing the square method, represent interesting applications of other frequently used techniques in algebra, or offer insight into other areas of mathematics.

A lesser known quadratic formula, as used in Muller's method, provides the same roots via the equation

${\displaystyle x=\frac{2c}{-b\pm \sqrt{b^2-4ac}}.}$

This can be deduced from the standard quadratic formula by Vieta's formulas, which assert that the product of the roots is c/a. It also follows from dividing the quadratic equation by ${\displaystyle x^2}$ giving ${\displaystyle c{x}^{-2}+b{x}^{-1}+a=0,}$ solving this for ${\displaystyle x^{-1},}$ and then inverting.

One property of this form is that it yields one valid root when a = 0, while the other root contains division by zero, because when a = 0, the quadratic equation becomes a linear equation, which has one root. By contrast, in this case, the more common formula has a division by zero for one root and an indeterminate form 0/0 for the other root. On the other hand, when c = 0, the more common formula yields two correct roots whereas this form yields the zero root and an indeterminate form 0/0.

When neither a nor c is zero, the equality between the standard quadratic formula and Muller's method,

${\displaystyle \frac{2c}{-b-\sqrt{b^2-4ac}}=\frac{-b+\sqrt{b^2-4ac}}{2a},}$

can be verified by cross multiplication, and similarly for the other choice of signs.

Reduced quadratic equation

It is sometimes convenient to reduce a quadratic equation so that its leading coefficient is one. This is done by dividing both sides by a, which is always possible since a is non-zero. This produces the reduced quadratic equation:

${\displaystyle x^2+px+q=0,}$

where p = b/a and q = c/a. This monic polynomial equation has the same solutions as the original.

The quadratic formula for the solutions of the reduced quadratic equation, written in terms of its coefficients, is:

${\displaystyle x=\frac{1}{2}\left(-p\pm \sqrt{p^2-4q}\right),}$

or equivalently:

${\displaystyle x=-\frac{p}{2}\pm \sqrt{{\left(\frac{p}{2}\right)}^2-q}.}$

Discriminant

Figure 3. Discriminant signs

In the quadratic formula, the expression underneath the square root sign is called the discriminant of the quadratic equation, and is often represented using an upper case D or an upper case Greek delta:

${\displaystyle \mathrm{\Delta }=b^2-4ac.}$

A quadratic equation with real coefficients can have either one or two distinct real roots, or two distinct complex roots. In this case the discriminant determines the number and nature of the roots. There are three cases:

• If the discriminant is positive, then there are two distinct roots

${\displaystyle \frac{-b+\sqrt{\mathrm{\Delta }}}{2a}\text{and}\frac{-b-\sqrt{\mathrm{\Delta }}}{2a},}$

both of which are real numbers. For quadratic equations with rational coefficients, if the discriminant is a square number, then the roots are rational—in other cases they may be quadratic irrationals.

• If the discriminant is zero, then there is exactly one real root ${\displaystyle -\frac{b}{2a},}$ sometimes called a repeated or double root or two equal roots.

• If the discriminant is negative, then there are no real roots. Rather, there are two distinct (non-real) complex roots${\displaystyle -\frac{b}{2a}+i\frac{\sqrt{-\mathrm{\Delta }}}{2a}\text{and}-\frac{b}{2a}-i\frac{\sqrt{-\mathrm{\Delta }}}{2a},}$

which are complex conjugates of each other. In these expressions i is the imaginary unit.

Thus the roots are distinct if and only if the discriminant is non-zero, and the roots are real if and only if the discriminant is non-negative.

Geometric interpretation

Graph of y = ax² + bx + c, where a and the discriminant b² − 4ac are positive, with

• Roots and y-intercept in red
• Vertex and axis of symmetry in blue
• Focus and directrix in pink

Visualisation of the complex roots of y = ax² + bx + c: the parabola is rotated 180° about its vertex (orange). Its x-intercepts are rotated 90° around their mid-point, and the Cartesian plane is interpreted as the complex plane (green).

The function f(x) = ax² + bx + c is a quadratic function. The graph of any quadratic function has the same general shape, which is called a parabola. The location and size of the parabola, and how it opens, depend on the values of a, b, and c. As shown in Figure 1, if a > 0, the parabola has a minimum point and opens upward. If a < 0, the parabola has a maximum point and opens downward. The extreme point of the parabola, whether minimum or maximum, corresponds to its vertex. The x-coordinate of the vertex will be located at ${\displaystyle x=\frac{-b}{2a}}$, and the y-coordinate of the vertex may be found by substituting this x-value into the function. The y-intercept is located at the point (0, c).

The solutions of the quadratic equation ax² + bx + c = 0 correspond to the roots of the function f(x) = ax² + bx + c, since they are the values of x for which f(x) = 0. As shown in Figure 2, if a, b, and c are real numbers and the domain of f is the set of real numbers, then the roots of f are exactly the x-coordinates of the points where the graph touches the x-axis. As shown in Figure 3, if the discriminant is positive, the graph touches the x-axis at two points; if zero, the graph touches at one point; and if negative, the graph does not touch the x-axis.

Quadratic factorization

The term

${\displaystyle x-r}$

is a factor of the polynomial

${\displaystyle a{x}^2+bx+c}$

if and only if r is a root of the quadratic equation

${\displaystyle a{x}^2+bx+c=0.}$

It follows from the quadratic formula that

${\displaystyle a{x}^2+bx+c=a\left(x-\frac{-b+\sqrt{b^2-4ac}}{2a}\right)\left(x-\frac{-b-\sqrt{b^2-4ac}}{2a}\right).}$

In the special case b² = 4ac where the quadratic has only one distinct root (i.e. the discriminant is zero), the quadratic polynomial can be factored as

${\displaystyle a{x}^2+bx+c=a{\left(x+\frac{b}{2a}\right)}^2.}$

Graphical solution

Figure 4. Graphing calculator computation of one of the two roots of the quadratic equation 2x² + 4x − 4 = 0. Although the display shows only five significant figures of accuracy, the retrieved value of xc is 0.732050807569, accurate to twelve significant figures.

A quadratic function without real root: y = (x − 5)² + 9. The "3" is the imaginary part of the x-intercept. The real part is the x-coordinate of the vertex. Thus the roots are 5 ± 3i.

The solutions of the quadratic equation

${\displaystyle a{x}^2+bx+c=0}$

may be deduced from the graph of the quadratic function

${\displaystyle f(x)=a{x}^2+bx+c,}$

which is a parabola.

If the parabola intersects the x-axis in two points, there are two real roots, which are the x-coordinates of these two points (also called x-intercept).

If the parabola is tangent to the x-axis, there is a double root, which is the x-coordinate of the contact point between the graph and parabola.

If the parabola does not intersect the x-axis, there are two complex conjugate roots. Although these roots cannot be visualized on the graph, their real and imaginary parts can be.

Let h and k be respectively the x-coordinate and the y-coordinate of the vertex of the parabola (that is the point with maximal or minimal y-coordinate. The quadratic function may be rewritten

${\displaystyle y=a(x-h{)}^2+k.}$

Let d be the distance between the point of y-coordinate 2k on the axis of the parabola, and a point on the parabola with the same y-coordinate (see the figure; there are two such points, which give the same distance, because of the symmetry of the parabola). Then the real part of the roots is h, and their imaginary part are ±d. That is, the roots are

${\displaystyle h+id\text{and}h-id,}$

or in the case of the example of the figure

${\displaystyle 5+3i\text{and}5-3i.}$

Avoiding loss of significance

Although the quadratic formula provides an exact solution, the result is not exact if real numbers are approximated during the computation, as usual in numerical analysis, where real numbers are approximated by floating point numbers (called "reals" in many programming languages). In this context, the quadratic formula is not completely stable.

This occurs when the roots have different order of magnitude, or, equivalently, when b² and b² − 4ac are close in magnitude. In this case, the subtraction of two nearly equal numbers will cause loss of significance or catastrophic cancellation in the smaller root. To avoid this, the root that is smaller in magnitude, r, can be computed as ${\displaystyle (c/a)/R}$ where R is the root that is bigger in magnitude. This is equivalent to using the formula

${\displaystyle x=\frac{-2c}{b\pm \sqrt{b^2-4ac}}}$

using the plus sign if ${\displaystyle b>0}$ and the minus sign if ${\displaystyle b<0.}$

A second form of cancellation can occur between the terms b² and 4ac of the discriminant, that is when the two roots are very close. This can lead to loss of up to half of correct significant figures in the roots.

Examples and applications

The trajectory of the cliff jumper is parabolic because horizontal displacement is a linear function of time ${\displaystyle x=v_{x}t}$, while vertical displacement is a quadratic function of time ${\displaystyle y=\frac{1}{2}a{t}^2+v_{y}t+h}$. As a result, the path follows quadratic equation ${\displaystyle y=\frac{a}{2v_x^2}{x}^2+\frac{v_y}{v_x}x+h}$, where ${\displaystyle v_x}$ and ${\displaystyle v_y}$ are horizontal and vertical components of the original velocity, a is gravitational acceleration and h is original height. The a value should be considered negative here, as its direction (downwards) is opposite to the height measurement (upwards).

The golden ratio is found as the positive solution of the quadratic equation ${\displaystyle x^2-x-1=0.}$

The equations of the circle and the other conic sections—ellipses, parabolas, and hyperbolas—are quadratic equations in two variables.

Given the cosine or sine of an angle, finding the cosine or sine of the angle that is half as large involves solving a quadratic equation.

The process of simplifying expressions involving the square root of an expression involving the square root of another expression involves finding the two solutions of a quadratic equation.

Descartes' theorem states that for every four kissing (mutually tangent) circles, their radii satisfy a particular quadratic equation.

The equation given by Fuss' theorem, giving the relation among the radius of a bicentric quadrilateral's inscribed circle, the radius of its circumscribed circle, and the distance between the centers of those circles, can be expressed as a quadratic equation for which the distance between the two circles' centers in terms of their radii is one of the solutions. The other solution of the same equation in terms of the relevant radii gives the distance between the circumscribed circle's center and the center of the excircle of an ex-tangential quadrilateral.

Critical points of a cubic function and inflection points of a quartic function are found by solving a quadratic equation.

History

Babylonian mathematicians, as early as 2000 BC (displayed on Old Babylonian clay tablets) could solve problems relating the areas and sides of rectangles. There is evidence dating this algorithm as far back as the Third Dynasty of Ur. In modern notation, the problems typically involved solving a pair of simultaneous equations of the form:

${\displaystyle x+y=p,xy=q,}$

which is equivalent to the statement that x and y are the roots of the equation:

${\displaystyle z^2+q=pz.}$

The steps given by Babylonian scribes for solving the above rectangle problem, in terms of x and y, were as follows:

1. Compute half of p.
2. Square the result.
3. Subtract q.
4. Find the (positive) square root using a table of squares.
5. Add together the results of steps (1) and (4) to give x.

In modern notation this means calculating ${\displaystyle x=\left(\frac{p}{2}\right)+\sqrt{{\left(\frac{p}{2}\right)}^2-q}}$, which is equivalent to the modern day quadratic formula for the larger real root (if any) ${\displaystyle x=\frac{-b+\sqrt{b^2-4ac}}{2a}}$ with a = 1, b = −p, and c = q.

Geometric methods were used to solve quadratic equations in Babylonia, Egypt, Greece, China, and India. The Egyptian Berlin Papyrus, dating back to the Middle Kingdom (2050 BC to 1650 BC), contains the solution to a two-term quadratic equation. Babylonian mathematicians from circa 400 BC and Chinese mathematicians from circa 200 BC used geometric methods of dissection to solve quadratic equations with positive roots. Rules for quadratic equations were given in The Nine Chapters on the Mathematical Art, a Chinese treatise on mathematics. These early geometric methods do not appear to have had a general formula. Euclid, the Greek mathematician, produced a more abstract geometrical method around 300 BC. With a purely geometric approach Pythagoras and Euclid created a general procedure to find solutions of the quadratic equation. In his work Arithmetica, the Greek mathematician Diophantus solved the quadratic equation, but giving only one root, even when both roots were positive.

In 628 AD, Brahmagupta, an Indian mathematician, gave the first explicit (although still not completely general) solution of the quadratic equation ax² + bx = c as follows: "To the absolute number multiplied by four times the [coefficient of the] square, add the square of the [coefficient of the] middle term; the square root of the same, less the [coefficient of the] middle term, being divided by twice the [coefficient of the] square is the value." (Brahmasphutasiddhanta, Colebrook translation, 1817, page 346) This is equivalent to

${\displaystyle x=\frac{\sqrt{4ac+b^2}-b}{2a}.}$

The Bakhshali Manuscript written in India in the 7th century AD contained an algebraic formula for solving quadratic equations, as well as quadratic indeterminate equations (originally of type ax/c = y). Muhammad ibn Musa al-Khwarizmi (9th century), possibly inspired by Brahmagupta, developed a set of formulas that worked for positive solutions. Al-Khwarizmi goes further in providing a full solution to the general quadratic equation, accepting one or two numerical answers for every quadratic equation, while providing geometric proofs in the process. He also described the method of completing the square and recognized that the discriminant must be positive, which was proven by his contemporary 'Abd al-Hamīd ibn Turk (Central Asia, 9th century) who gave geometric figures to prove that if the discriminant is negative, a quadratic equation has no solution. While al-Khwarizmi himself did not accept negative solutions, later Islamic mathematicians that succeeded him accepted negative solutions, as well as irrational numbers as solutions. Abū Kāmil Shujā ibn Aslam (Egypt, 10th century) in particular was the first to accept irrational numbers (often in the form of a square root, cube root or fourth root) as solutions to quadratic equations or as coefficients in an equation. The 9th century Indian mathematician Sridhara wrote down rules for solving quadratic equations.

The Jewish mathematician Abraham bar Hiyya Ha-Nasi (12th century, Spain) authored the first European book to include the full solution to the general quadratic equation. His solution was largely based on Al-Khwarizmi's work. The writing of the Chinese mathematician Yang Hui (1238–1298 AD) is the first known one in which quadratic equations with negative coefficients of 'x' appear, although he attributes this to the earlier Liu Yi. By 1545 Gerolamo Cardano compiled the works related to the quadratic equations. The quadratic formula covering all cases was first obtained by Simon Stevin in 1594. In 1637 René Descartes published La Géométrie containing the quadratic formula in the form we know today.

Advanced topics

Alternative methods of root calculation

Vieta's formulas

Main article: Vieta's formulas

Graph of the difference between Vieta's approximation for the smallest root of the quadratic equation x² + bx + c = 0 compared with the value calculated using the quadratic formula

Vieta's formulas (named after François Viète) are the relations

${\displaystyle x_1+x_2=-\frac{b}{a},x_1{x}_2=\frac{c}{a}}$

between the roots of a quadratic polynomial and its coefficients. They result from comparing term by term the relation

${\displaystyle \left(x-x_1\right)\left(x-x_2\right)=x^2-\left(x_1+x_2\right)x+x_1{x}_2=0}$

with the equation

${\displaystyle x^2+\frac{b}{a}x+\frac{c}{a}=0.}$

The first Vieta's formula is useful for graphing a quadratic function. Since the graph is symmetric with respect to a vertical line through the vertex, the vertex's x-coordinate is located at the average of the roots (or intercepts). Thus the x-coordinate of the vertex is

${\displaystyle x_V=\frac{x_1+x_2}{2}=-\frac{b}{2a}.}$

The y-coordinate can be obtained by substituting the above result into the given quadratic equation, giving

${\displaystyle y_V=-\frac{b^2}{4a}+c=-\frac{b^2-4ac}{4a}.}$

These formulas for the vertex can also deduced directly from the formula (see Completing the square)

${\displaystyle a{x}^2+bx+c=a\left({\left(x-\frac{b}{2a}\right)}^2-\frac{b^2-4ac}{4a}\right).}$

For numerical computation, Vieta's formulas provide a useful method for finding the roots of a quadratic equation in the case where one root is much smaller than the other. If |x₂| << |x₁|, then x₁ + x₂ ≈ x₁, and we have the estimate:

${\displaystyle x_1\approx -\frac{b}{a}.}$

The second Vieta's formula then provides:

${\displaystyle x_2=\frac{c}{a{x}_1}\approx -\frac{c}{b}.}$

These formulas are much easier to evaluate than the quadratic formula under the condition of one large and one small root, because the quadratic formula evaluates the small root as the difference of two very nearly equal numbers (the case of large b), which causes round-off error in a numerical evaluation. The figure shows the difference between (i) a direct evaluation using the quadratic formula (accurate when the roots are near each other in value) and (ii) an evaluation based upon the above approximation of Vieta's formulas (accurate when the roots are widely spaced). As the linear coefficient b increases, initially the quadratic formula is accurate, and the approximate formula improves in accuracy, leading to a smaller difference between the methods as b increases. However, at some point the quadratic formula begins to lose accuracy because of round off error, while the approximate method continues to improve. Consequently, the difference between the methods begins to increase as the quadratic formula becomes worse and worse.

This situation arises commonly in amplifier design, where widely separated roots are desired to ensure a stable operation (see Step response).

Trigonometric solution

In the days before calculators, people would use mathematical tables—lists of numbers showing the results of calculation with varying arguments—to simplify and speed up computation. Tables of logarithms and trigonometric functions were common in math and science textbooks. Specialized tables were published for applications such as astronomy, celestial navigation and statistics. Methods of numerical approximation existed, called prosthaphaeresis, that offered shortcuts around time-consuming operations such as multiplication and taking powers and roots. Astronomers, especially, were concerned with methods that could speed up the long series of computations involved in celestial mechanics calculations.

It is within this context that we may understand the development of means of solving quadratic equations by the aid of trigonometric substitution. Consider the following alternate form of the quadratic equation,

[1]   ${\displaystyle a{x}^2+bx\pm c=0,}$

where the sign of the ± symbol is chosen so that a and c may both be positive. By substituting

[2]   ${\displaystyle x=\sqrt{c/a}\tan \theta }$

and then multiplying through by cos²(θ) / c, we obtain

[3]   ${\displaystyle {\sin }^2\theta +\frac{b}{\sqrt{ac}}\sin \theta \cos \theta \pm {\cos }^2\theta =0.}$

Introducing functions of 2θ and rearranging, we obtain

[4]   ${\displaystyle \tan 2{\theta }_n=+2\frac{\sqrt{ac}}{b},}$

[5]   ${\displaystyle \sin 2{\theta }_p=-2\frac{\sqrt{ac}}{b},}$

where the subscripts n and p correspond, respectively, to the use of a negative or positive sign in equation [1]. Substituting the two values of θ_n or θ_p found from equations [4] or [5] into [2] gives the required roots of [1]. Complex roots occur in the solution based on equation [5] if the absolute value of sin 2θ_p exceeds unity. The amount of effort involved in solving quadratic equations using this mixed trigonometric and logarithmic table look-up strategy was two-thirds the effort using logarithmic tables alone. Calculating complex roots would require using a different trigonometric form.

To illustrate, let us assume we had available seven-place logarithm and trigonometric tables, and wished to solve the following to six-significant-figure accuracy:

${\displaystyle 4.16130x^2+9.15933x-11.4207=0}$

1. A seven-place lookup table might have only 100,000 entries, and computing intermediate results to seven places would generally require interpolation between adjacent entries.
2. ${\displaystyle \log a=0.6192290,\log b=0.9618637,\log c=1.0576927}$
3. ${\displaystyle 2\sqrt{ac}/b=2\times {10}^{(0.6192290+1.0576927)/2-0.9618637}=1.505314}$
4. ${\displaystyle \theta =({\tan }^{-1}1.505314)/2={28.20169}^{\circ }\text{ or }-{61.79831}^{\circ }}$
5. ${\displaystyle \log |\tan \theta |=-0.2706462\text{ or }0.2706462}$
6. ${\displaystyle \log \sqrt{c/a}=(1.0576927-0.6192290)/2=0.2192318}$
7. ${\displaystyle x_1={10}^{0.2192318-0.2706462}=0.888353}$ (rounded to six significant figures)

${\displaystyle x_2=-{10}^{0.2192318+0.2706462}=-3.08943}$

Solution for complex roots in polar coordinates

If the quadratic equation ${\displaystyle a{x}^2+bx+c=0}$ with real coefficients has two complex roots—the case where ${\displaystyle b^2-4ac<0,}$ requiring a and c to have the same sign as each other—then the solutions for the roots can be expressed in polar form as

${\displaystyle x_1,x_2=r(\cos \theta \pm i\sin \theta ),}$

where ${\displaystyle r=\sqrt{\frac{c}{a}}}$ and ${\displaystyle \theta ={\cos }^{-1}\left(\frac{-b}{2\sqrt{ac}}\right).}$

Geometric solution

Figure 6. Geometric solution of ax² + bx + c = 0 using Lill's method. Solutions are −AX1/SA, −AX2/SA

The quadratic equation may be solved geometrically in a number of ways. One way is via Lill's method. The three coefficients a, b, c are drawn with right angles between them as in SA, AB, and BC in Figure 6. A circle is drawn with the start and end point SC as a diameter. If this cuts the middle line AB of the three then the equation has a solution, and the solutions are given by negative of the distance along this line from A divided by the first coefficient a or SA. If a is 1 the coefficients may be read off directly. Thus the solutions in the diagram are −AX1/SA and −AX2/SA.

Carlyle circle of the quadratic equation x² − sx + p = 0.

The Carlyle circle, named after Thomas Carlyle, has the property that the solutions of the quadratic equation are the horizontal coordinates of the intersections of the circle with the horizontal axis. Carlyle circles have been used to develop ruler-and-compass constructions of regular polygons.

Generalization of quadratic equation

The formula and its derivation remain correct if the coefficients a, b and c are complex numbers, or more generally members of any field whose characteristic is not 2. (In a field of characteristic 2, the element 2a is zero and it is impossible to divide by it.)

The symbol

${\displaystyle \pm \sqrt{b^2-4ac}}$

in the formula should be understood as "either of the two elements whose square is b² − 4ac, if such elements exist". In some fields, some elements have no square roots and some have two; only zero has just one square root, except in fields of characteristic 2. Even if a field does not contain a square root of some number, there is always a quadratic extension field which does, so the quadratic formula will always make sense as a formula in that extension field.

Characteristic 2

In a field of characteristic 2, the quadratic formula, which relies on 2 being a unit, does not hold. Consider the monic quadratic polynomial

${\displaystyle x^2+bx+c}$

over a field of characteristic 2. If b = 0, then the solution reduces to extracting a square root, so the solution is

${\displaystyle x=\sqrt{c}}$

and there is only one root since

${\displaystyle -\sqrt{c}=-\sqrt{c}+2\sqrt{c}=\sqrt{c}.}$

In summary,

${\displaystyle {\displaystyle x^2+c=(x+\sqrt{c}{)}^2.}}$

See quadratic residue for more information about extracting square roots in finite fields.

In the case that b ≠ 0, there are two distinct roots, but if the polynomial is irreducible, they cannot be expressed in terms of square roots of numbers in the coefficient field. Instead, define the 2-root R(c) of c to be a root of the polynomial x² + x + c, an element of the splitting field of that polynomial. One verifies that R(c) + 1 is also a root. In terms of the 2-root operation, the two roots of the (non-monic) quadratic ax² + bx + c are

${\displaystyle \frac{b}{a}R\left(\frac{ac}{b^2}\right)}$

and

${\displaystyle \frac{b}{a}\left(R\left(\frac{ac}{b^2}\right)+1\right).}$

For example, let a denote a multiplicative generator of the group of units of F₄, the Galois field of order four (thus a and a + 1 are roots of x² + x + 1 over F₄. Because (a + 1)² = a, a + 1 is the unique solution of the quadratic equation x² + a = 0. On the other hand, the polynomial x² + ax + 1 is irreducible over F₄, but it splits over F₁₆, where it has the two roots ab and ab + a, where b is a root of x² + x + a in F₁₆.

This is a special case of Artin–Schreier theory.