Octonion

From Wikipedia, the free encyclopedia

 

In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold ${\displaystyle \mathbb {O} }$. Octonions have eight dimensions; twice the number of dimensions of the quaternions, of which they are an extension. Along with the real numbers R, complex numbers C, and quaternions H, octonions complete the set of numbers capable of being added, subtracted, multiplied or divided; as such, they are believed by some researchers to have fundamental importance in physical theory^. They are noncommutative and nonassociative, but satisfy a weaker form of associativity; namely, they are alternative.

Octonions are not as well known as the quaternions and complex numbers, which are much more widely studied and used. Despite this, they have some interesting properties and are related to a number of exceptional structures in mathematics, among them the exceptional Lie groups. Additionally, octonions have applications in fields such as string theory, special relativity, and quantum logic. Applying the Cayley-Dickson construction to the octonions produces the sedenions.

The octonions were discovered in 1843 by John T. Graves, inspired by his friend W. R. Hamilton's discovery of quaternions. Graves called his discovery octaves, and mentioned them in a letter to Hamilton dated 16 December 1843, but his first publication of his result in (Graves 1845) was slightly later than Arthur Cayley's article on them. The octonions were discovered independently by Cayley^[2] and are sometimes referred to as Cayley numbers or the Cayley algebra. Hamilton described the early history of Graves' discovery.^[3]

Definition

The octonions can be thought of as octets (or 8-tuples) of real numbers. Every octonion is a real linear combination of the unit octonions:

${\displaystyle \{e_{0},e_{1},e_{2},e_{3},e_{4},e_{5},e_{6},e_{7}\},}$

where e₀ is the scalar or real element; it may be identified with the real number 1. That is, every octonion x can be written in the form

${\displaystyle x=x_{0}e_{0}+x_{1}e_{1}+x_{2}e_{2}+x_{3}e_{3}+x_{4}e_{4}+x_{5}e_{5}+x_{6}e_{6}+x_{7}e_{7},\,}$

with real coefficients {x_i}.

Addition and subtraction of octonions is done by adding and subtracting corresponding terms and hence their coefficients, like quaternions. Multiplication is more complex. Multiplication is distributive over addition, so the product of two octonions can be calculated by summing the products of all the terms, again like quaternions. The product of each pair of terms can be given by multiplication of the coefficients and a multiplication table of the unit octonions.

Most off-diagonal elements of the table are antisymmetric, making it almost a skew-symmetric matrix except for the elements on the main diagonal, as well as the row and column for which e₀ is an operand.

The table can be summarized as follows:^[5]
${\displaystyle e_{i}e_{j}={\begin{cases}e_{j},&{\text{if }}i=0\\e_{i},&{\text{if }}j=0\\-\delta _{ij}e_{0}+\varepsilon _{ijk}e_{k},&{\text{otherwise}}\end{cases}}}$

where ${\displaystyle \delta _{ij}}$ is the Kronecker delta and ${\displaystyle \varepsilon _{ijk}}$ is a completely antisymmetric tensor with value +1 when ijk = 123, 145, 176, 246, 257, 347, 365.

The above definition though is not unique, but is only one of 480 possible definitions for octonion multiplication with e₀ = 1. The others can be obtained by permuting and changing the signs of the non-scalar basis elements. The 480 different algebras are isomorphic, and there is rarely a need to consider which particular multiplication rule is used. Each of these 480 definitions is invariant up to signs under some 7-cycle of the points (1234567), and for each 7-cycle there are four definitions, differing by signs and reversal of order. A common choice is to use the definition invariant under the 7-cycle (1234567) with e₁e₂ = e₄ as it is particularly easy to remember the multiplication.

A variation of this sometimes used is to label the elements of the basis by the elements ∞, 0, 1, 2, ..., 6, of the projective line over the finite field of order 7. The multiplication is then given by e_∞ = 1 and e₁e₂ = e₄, and all expressions obtained from this by adding a constant (mod 7) to all subscripts: in other words using the 7 triples (124) (235) (346) (450) (561) (602) (013). These are the nonzero codewords of the quadratic residue code of length 7 over the Galois field of two elements, GF(2). There is a symmetry of order 7 given by adding a constant mod 7 to all subscripts, and also a symmetry of order 3 given by multiplying all subscripts by one of the quadratic residues 1, 2, 4 mod 7.^[6][7]

The multiplication table for a geometric algebra of signature (−−−−) can be given in terms of the following 7 quaternionic triples (omitting the identity element): (I,j,k), (i,J,k), (i,j,K), (I,J,K), (∗I,i,m), (∗J,j,m), (∗K,k,m) in which the lowercase items are vectors (mathematics and physics) and the uppercase ones are bivectors and ∗ = mijk (which is in fact the Hodge star operator). If the ∗ is forced to be equal to the identity then the multiplication ceases to be associative, but the ∗ may be removed from the multiplication table resulting in an octonion multiplication table.

Note that in keeping ∗ = mijk associative and thus not reducing the 4-dimensional geometric algebra to an octonion one, the whole multiplication table can be derived from the equation for ∗. Consider the gamma matrices. The formula defining the fifth gamma matrix shows that it is the ∗ of a four-dimensional geometric algebra of the gamma matrices.

Cayley–Dickson construction

A more systematic way of defining the octonions is via the Cayley–Dickson construction. Just as quaternions can be defined as pairs of complex numbers, the octonions can be defined as pairs of quaternions. Addition is defined pairwise. The product of two pairs of quaternions (a, b) and (c, d) is defined by

${\displaystyle (a,b)(c,d)=(ac-d^{*}b,da+bc^{*}),}$

where ${\displaystyle z^{*}}$ denotes the conjugate of the quaternion z. This definition is equivalent to the one given above when the eight unit octonions are identified with the pairs

(1,0), (i,0), (j,0), (k,0), (0,1), (0,i), (0,j), (0,k)

Fano plane mnemonic

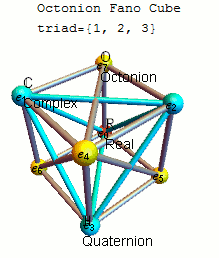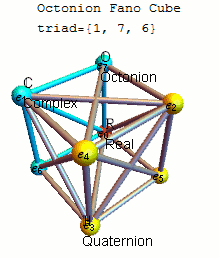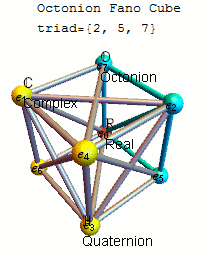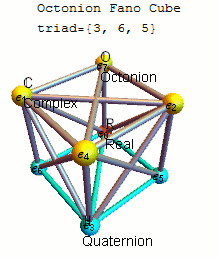
A mnemonic for the products of the unit octonions.^[8]

 

A 3D mnemonic visualization showing the 7 triads as hyperplanes through the Real (${\displaystyle e_{0}}$) vertex of the octonion example given above.^[8]

A convenient mnemonic for remembering the products of unit octonions is given by the diagram at the right, which represents the multiplication table of Cayley and Graves.^[4][9] This diagram with seven points and seven lines (the circle through 1, 2, and 3 is considered a line) is called the Fano plane. The lines are oriented. The seven points correspond to the seven standard basis elements of Im(O) (see definition below). Each pair of distinct points lies on a unique line and each line runs through exactly three points.

Let (a, b, c) be an ordered triple of points lying on a given line with the order specified by the direction of the arrow. Then multiplication is given by

ab = c and ba = −c

together with cyclic permutations. These rules together with

• 1 is the multiplicative identity,
• e_i² = −1 for each point in the diagram

completely defines the multiplicative structure of the octonions. Each of the seven lines generates a subalgebra of O isomorphic to the quaternions H.

Conjugate, norm, and inverse

The conjugate of an octonion

${\displaystyle x=x_{0}\,e_{0}+x_{1}\,e_{1}+x_{2}\,e_{2}+x_{3}\,e_{3}+x_{4}\,e_{4}+x_{5}\,e_{5}+x_{6}\,e_{6}+x_{7}\,e_{7}}$

is given by

${\displaystyle x^{*}=x_{0}\,e_{0}-x_{1}\,e_{1}-x_{2}\,e_{2}-x_{3}\,e_{3}-x_{4}\,e_{4}-x_{5}\,e_{5}-x_{6}\,e_{6}-x_{7}\,e_{7}.}$

Conjugation is an involution of O and satisfies (xy)^∗ = y^∗ x^∗ (note the change in order).

The real part of x is given by

${\displaystyle {\frac {x+x^{*}}{2}}=x_{0}\,e_{0}}$

and the imaginary part by

${\displaystyle {\frac {x-x^{*}}{2}}=x_{1}\,e_{1}+x_{2}\,e_{2}+x_{3}\,e_{3}+x_{4}\,e_{4}+x_{5}\,e_{5}+x_{6}\,e_{6}+x_{7}\,e_{7}.}$

The set of all purely imaginary octonions span a 7 dimension subspace of O, denoted Im(O).
Conjugation of octonions satisfies the equation

${\displaystyle x^{*}=-{\frac {1}{6}}(x+(e_{1}x)e_{1}+(e_{2}x)e_{2}+(e_{3}x)e_{3}+(e_{4}x)e_{4}+(e_{5}x)e_{5}+(e_{6}x)e_{6}+(e_{7}x)e_{7}).}$

The product of an octonion with its conjugate, x^∗ x = x x^∗, is always a nonnegative real number:

${\displaystyle x^{*}x=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}+x_{5}^{2}+x_{6}^{2}+x_{7}^{2}.}$

Using this the norm of an octonion can be defined, as

${\displaystyle \|x\|={\sqrt {x^{*}x}}.}$

This norm agrees with the standard Euclidean norm on R⁸.

The existence of a norm on O implies the existence of inverses for every nonzero element of O. The inverse of x ≠ 0 is given by

${\displaystyle x^{-1}={\frac {x^{*}}{\|x\|^{2}}}.}$

It satisfies x x⁻¹ = x⁻¹ x = 1.

Properties

Octonionic multiplication is neither commutative:

${\displaystyle e_{i}e_{j}=-e_{j}e_{i}\neq e_{j}e_{i}\,}$ if ${\displaystyle i,j}$ are distinct and non-zero,

nor associative:

${\displaystyle (e_{i}e_{j})e_{k}=-e_{i}(e_{j}e_{k})\neq e_{i}(e_{j}e_{k})\,}$ if ${\displaystyle i,j,k}$ are distinct, non-zero or if ${\displaystyle e_{i}e_{j}\neq \pm e_{k}}$.

The octonions do satisfy a weaker form of associativity: they are alternative. This means that the subalgebra generated by any two elements is associative. Actually, one can show that the subalgebra generated by any two elements of O is isomorphic to R, C, or H, all of which are associative. Because of their non-associativity, octonions do not have matrix representations, unlike quaternions.

The octonions do retain one important property shared by R, C, and H: the norm on O satisfies

${\displaystyle \|xy\|=\|x\|\|y\|}$

This equation means that the octonions form a composition algebra. The higher-dimensional algebras defined by the Cayley–Dickson construction (e.g., the sedenions) all fail to satisfy this property. They all have zero divisors.

Wider number systems exist which have a multiplicative modulus (e.g. 16-dimensional conic sedenions). Their modulus is defined differently from their norm, and they also contain zero divisors.

As shown by Hurwitz, the only normed division algebras over the reals are R, C, H, and O. These four algebras also form the only alternative, finite-dimensional division algebras over the reals (up to isomorphism).

Not being associative, the nonzero elements of O do not form a group. They do, however, form a loop, indeed a Moufang loop.

Commutator and cross product

The commutator of two octonions x and y is given by

${\displaystyle [x,y]=xy-yx.}$

This is antisymmetric and imaginary. If it is considered only as a product on the imaginary subspace Im(O) it defines a product on that space, the seven-dimensional cross product, given by

${\displaystyle x\times y={\frac {1}{2}}(xy-yx).}$

Like the cross product in three dimensions this is a vector orthogonal to x and y with magnitude

${\displaystyle \|x\times y\|=\|x\|\|y\|\sin \theta .}$

But like the octonion product it is not uniquely defined. Instead there are many different cross products, each one dependent on the choice of octonion product.^[10]

Automorphisms

An automorphism, A, of the octonions is an invertible linear transformation of O which satisfies

${\displaystyle A(xy)=A(x)A(y).}$

The set of all automorphisms of O forms a group called G₂.^[11] The group G₂ is a simply connected, compact, real Lie group of dimension 14. This group is the smallest of the exceptional Lie groups and is isomorphic to the subgroup of Spin(7) that preserves any chosen particular vector in its 8-dimensional real spinor representation. The group Spin(7) is in turn a subgroup of the group of isotopies described below.

See also: PSL(2,7) – the automorphism group of the Fano plane.

Isotopies

An isotopy of an algebra is a triple of bijective linear maps a, b, c such that if xy = z then a(x)b(y) = c(z). For a = b = c this is the same as an automorphism. The isotopy group of an algebra is the group of all isotopies, which contains the group of automorphisms as a subgroup.

The isotopy group of the octonions is the group Spin₈(R), with a, b, and c acting as the three 8-dimensional representations.^[12] The subgroup of elements where c fixes the identity is the subgroup Spin₇(R), and the subgroup where a, b, and c all fix the identity is the automorphism group G₂.

Integral octonions

There are several natural ways to choose an integral form of the octonions. The simplest is just to take the octonions whose coordinates are integers. This gives a nonassociative algebra over the integers called the Gravesian octonions. However it is not a maximal order (in the sense of ring theory); there are exactly 7 maximal orders containing it. These 7 maximal orders are all equivalent under automorphisms. The phrase "integral octonions" usually refers to a fixed choice of one of these seven orders.

These maximal orders were constructed by Kirmse (1925), Dickson and Bruck as follows. Label the 8 basis vectors by the points of the projective plane over the field with 7 elements. First form the "Kirmse integers" : these consist of octonions whose coordinates are integers or half integers, and that are half integers (that is, halves of odd integers) on one of the 16 sets

∅ (∞124) (∞235) (∞346) (∞450) (∞561) (∞602) (∞013) (∞0123456) (0356) (1460) (2501) (3612) (4023) (5134) (6245)

of the extended quadratic residue code of length 8 over the field of 2 elements, given by ∅, (∞124) and its images under adding a constant mod 7, and the complements of these 8 sets. Then switch infinity and any one other coordinate; this operation creates a bijection of the Kirmse integers onto a different set, which is a maximal order. There are 7 ways to do this, giving 7 maximal orders, which are all equivalent under cyclic permutations of the 7 coordinates 0123456. (Kirmse incorrectly claimed that the Kirmse integers also form a maximal order, so he thought there were 8 maximal orders rather than 7, but as Coxeter (1946) pointed out they are not closed under multiplication; this mistake occurs in several published papers.)

The Kirmse integers and the 7 maximal orders are all isometric to the E₈ lattice rescaled by a factor of 1/√2. In particular there are 240 elements of minimum nonzero norm 1 in each of these orders, forming a Moufang loop of order 240.

The integral octonions have a "division with remainder" property: given integral octonions a and b ≠ 0, we can find q and r with a = qb + r, where the remainder r has norm less than that of b.

In the integral octonions, all left ideals and right ideals are 2-sided ideals, and the only 2-sided ideals are the principal ideals nO where n is a non-negative integer.

The integral octonions have a version of factorization into primes, though it is not straightforward to state because the octonions are not associative so the product of octonions depends on the order in which one does the products. The irreducible integral octonions are exactly those of prime norm, and every integral octonion can be written as a product of irreducible octonions. More precisely an integral octonion of norm mn can be written as a product of integral octonions of norms m and n.

The automorphism group of the integral octonions is the group G₂(F₂) of order 12096, which has a simple subgroup of index 2 isomorphic to the unitary group ²A₂(3²). The isotopy group of the integral octonions is the perfect double cover of the group of rotations of the E₈ lattice.

Milloy & Dunn testimony to EPA on science transparency

This afternoon, I delivered the following remarks on EPA’s proposed science transparency rule at the public hearing. I commented on behalf of myself and Dr. John Dunn. We are trying to open the black box.

Open Black Box

My name is Steve Milloy. I publish JunkScience.com.

I am speaking on behalf of myself and Dr. John Dunn, an emergency physician in Texas.

We are commenting in support the proposed transparency initiative.

Science transparency in EPA regulatory action is long past overdue.

When I first started working on EPA issues in 1990, the main controversy with EPA science was the use of science policy and default assumptions – like the linear no-threshold model of carcinogenesis.

The problem wasn’t necessarily the use of science policy and default assumptions. The problem was, rather, EPA’s failure to disclose the nature of those default assumptions.

In other words: what part was science; what part was guesswork and; what part was politics.

When I first reported on this problem for the Department of Energy in 1994, the Clinton administration tried to censor my report. But they couldn’t and so here we are so many years later finally making progress on this important issue.

More recently, the major problem with EPA science has been what has become known as “secret science.”

Since 1990s, EPA grantees like Harvard’s Doug Dockery and Brigham Young University’s Arden Pope have refused to make available to the public the raw data used in their epidemiologic studies.

And this is true despite the fact that these studies were cited by EPA as the principal scientific bases for major air quality rules like those that were the Obama administration’s war-on-coal.

Worse, prior EPA administrations have actually aided and abetted Dockery and Pope hiding their data from public review. Prior EPA administrations have ignored the requests of the EPA’s own independent science advisors and Congress to release the data.

I can only conclude this is because independent review of the Harvard Six City and American Cancer Society line of studies would prove them to be highly problematic, embarrassing or even fraudulent.

Desperate to defend the indefensible, supporters of Dockery and Pope have wrongly maintained that making the data in question public would violate medial and personal privacy rights.

Nothing could be further from the truth.

For the most part, the data is electronic. Scrubbed files with the key data needed for independent review can easily be made available. No one is interested in any personal and medical data. It has no value.

The state of California has made such data files available for use for years. I know. I have obtained this data (over 2 million death certificates to be precise) and with it enabled research to be published that completely debunks the secret science of Dockery and Pope.

Fear of exposure of their research as faulty, if not fake, is why Dockery and Pope are so scared of producing their data for independent review.

To make these comments current, efforts have been made this month to obtain the Dockery and Pope data. But they continue to keep their data secret.

Given that the Dockery and Pope research and the related PM2.5 research has been funded by taxpayers – to the tune of more than $600 million dollars, and then this research is used to regulate the public, costing untold billions more dollars without providing any public health benefit — the conspiratorial hiding of this secret data is more akin to crime than science.

If EPA wants to regulate, that is fine. But the basis of and reasons for that regulation must be clearly laid out so their can be full and fair debate.

Harvard’s Doug Dockery and Brigham Young’s Arden Pope don’t want independent scientists to check their work for some reason. Dockery and Pope’s supporters may offer whatever excuses they like. But we all know what the reality is – fear of exposure.

Commutative property

From Wikipedia, the free encyclopedia

An operation ${\displaystyle \circ }$ is commutative iff ${\displaystyle x\circ y=y\circ x}$ for each ${\displaystyle x}$ and ${\displaystyle y}$. This image illustrates this property with the concept of an operation as a "calculation machine". It doesn't matter for the output ${\displaystyle x\circ y}$ or ${\displaystyle y\circ x}$ respectively which order the arguments ${\displaystyle x}$ and ${\displaystyle y}$ have – the final outcome is the same.

In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of the property that says "3 + 4 = 4 + 3" or "2 × 5 = 5 × 2", the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it (for example, "3 − 5 ≠ 5 − 3"); such operations are not commutative, and so are referred to as noncommutative operations. The idea that simple operations such as the multiplication and addition of numbers are commutative, was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized. A corresponding property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is symmetric as two equal mathematical objects are equal regardless of their order.

Common uses

The commutative property (or commutative law) is a property generally associated with binary operations and functions. If the commutative property holds for a pair of elements under a certain binary operation then the two elements are said to commute under that operation.

Mathematical definitions

The term "commutative" is used in several related senses.^[4][5]

1. A binary operation ${\displaystyle *}$ on a set S is called commutative if:

   ${\displaystyle x*y=y*x\qquad {\mbox{for all }}x,y\in S}$

   An operation that does not satisfy the above property is called non-commutative.
2. One says that x commutes with y under ${\displaystyle *}$ if:

   ${\displaystyle x*y=y*x}$

3. A binary function ${\displaystyle f\colon A\times A\to B}$ is called commutative if:
   ${\displaystyle f(x,y)=f(y,x)\qquad {\mbox{for all }}x,y\in A}$

Examples

Commutative operations in everyday life

The cumulation of apples, which can be seen as an addition of natural numbers, is commutative.

• Putting on socks resembles a commutative operation since which sock is put on first is unimportant. Either way, the result (having both socks on), is the same. In contrast, putting on underwear and trousers is not commutative.
• The commutativity of addition is observed when paying for an item with cash. Regardless of the order the bills are handed over in, they always give the same total.

Commutative operations in mathematics

The addition of vectors is commutative, because ${\displaystyle {\vec {a}}+{\vec {b}}={\vec {b}}+{\vec {a}}}$.

Two well-known examples of commutative binary operations:^[4]

• The addition of real numbers is commutative, since

${\displaystyle y+z=z+y\qquad {\mbox{for all }}y,z\in \mathbb {R} }$

For example 4 + 5 = 5 + 4, since both expressions equal 9.

• The multiplication of real numbers is commutative, since

${\displaystyle yz=zy\qquad {\mbox{for all }}y,z\in \mathbb {R} }$

For example, 3 × 5 = 5 × 3, since both expressions equal 15.

• Some binary truth functions are also commutative, since the truth tables for the functions are the same when one changes the order of the operands.

For example, the logical biconditional function p ↔ q is equivalent to q ↔ p. This function is also written as p IFF q, or as p ≡ q, or as Epq.

The last form is an example of the most concise notation in the article on truth functions, which lists the sixteen possible binary truth functions of which eight are commutative: Vpq = Vqp; Apq (OR) = Aqp; Dpq (NAND) = Dqp; Epq (IFF) = Eqp; Jpq = Jqp; Kpq (AND) = Kqp; Xpq (NOR) = Xqp; Opq = Oqp.

• Further examples of commutative binary operations include addition and multiplication of complex numbers, addition and scalar multiplication of vectors, and intersection and union of sets.

Noncommutative operations in daily life

• Concatenation, the act of joining character strings together, is a noncommutative operation. For example,

EA + T = EAT ≠ TEA = T + EA

• Washing and drying clothes resembles a noncommutative operation; washing and then drying produces a markedly different result to drying and then washing.
• Rotating a book 90° around a vertical axis then 90° around a horizontal axis produces a different orientation than when the rotations are performed in the opposite order.
• The twists of the Rubik's Cube are noncommutative. This can be studied using group theory.
• Thought processes are noncommutative: A person asked a question (A) and then a question (B) may give different answers to each question than a person asked first (B) and then (A), because asking a question may change the person's state of mind.
• The act of dressing is either commutative or non-commutative, depending on the items. Putting on underwear and normal clothing is noncommutative. Putting on left and right socks is commutative.

Noncommutative operations in mathematics

Some noncommutative binary operations:^[6]

Subtraction and division

Subtraction is noncommutative, since ${\displaystyle 0-1\neq 1-0}$.
Division is noncommutative, since ${\displaystyle 1\div 2\neq 2\div 1}$.

Truth functions

Some truth functions are noncommutative, since the truth tables for the functions are different when one changes the order of the operands. For example, the truth tables for f (A, B) = A Λ ¬B (A AND NOT B) and f (B, A) = B Λ ¬A are

A	B	f (A, B)	f (B, A)
F	F	F	F
F	T	F	T
T	F	T	F
T	T	F	F

For the eight noncommutative functions, Bqp = Cpq; Mqp = Lpq; Cqp = Bpq; Lqp = Mpq; Fqp = Gpq; Iqp = Hpq; Gqp = Fpq; Hqp = Ipq.^[7]

Matrix multiplication

Matrix multiplication is almost always noncommutative, for example:

${\displaystyle {\begin{bmatrix}0&2\\0&1\end{bmatrix}}={\begin{bmatrix}1&1\\0&1\end{bmatrix}}\cdot {\begin{bmatrix}0&1\\0&1\end{bmatrix}}\neq {\begin{bmatrix}0&1\\0&1\end{bmatrix}}\cdot {\begin{bmatrix}1&1\\0&1\end{bmatrix}}={\begin{bmatrix}0&1\\0&1\end{bmatrix}}}$

Vector product

The vector product (or cross product) of two vectors in three dimensions is anti-commutative; i.e., b × a = −(a × b).

History and etymology

The first known use of the term was in a French Journal published in 1814

Records of the implicit use of the commutative property go back to ancient times. The Egyptians used the commutative property of multiplication to simplify computing products.^[8][9] Euclid is known to have assumed the commutative property of multiplication in his book Elements.^[10] Formal uses of the commutative property arose in the late 18th and early 19th centuries, when mathematicians began to work on a theory of functions. Today the commutative property is a well-known and basic property used in most branches of mathematics.

The first recorded use of the term commutative was in a memoir by François Servois in 1814,^[1][11] which used the word commutatives when describing functions that have what is now called the commutative property. The word is a combination of the French word commuter meaning "to substitute or switch" and the suffix -ative meaning "tending to" so the word literally means "tending to substitute or switch." The term then appeared in English in 1838^[2] in Duncan Farquharson Gregory's article entitled "On the real nature of symbolical algebra" published in 1840 in the Transactions of the Royal Society of Edinburgh.^[12]

Propositional logic

Rule of replacement

In truth-functional propositional logic, commutation,^[13][14] or commutativity^[15] refer to two valid rules of replacement. The rules allow one to transpose propositional variables within logical expressions in logical proofs. The rules are:

${\displaystyle (P\lor Q)\Leftrightarrow (Q\lor P)}$

and

${\displaystyle (P\land Q)\Leftrightarrow (Q\land P)}$

where "${\displaystyle \Leftrightarrow }$" is a metalogical symbol representing "can be replaced in a proof with."

Truth functional connectives

Commutativity is a property of some logical connectives of truth functional propositional logic. The following logical equivalences demonstrate that commutativity is a property of particular connectives. The following are truth-functional tautologies.

Commutativity of conjunction

${\displaystyle (P\land Q)\leftrightarrow (Q\land P)}$

 

Commutativity of disjunction

${\displaystyle (P\lor Q)\leftrightarrow (Q\lor P)}$

 

Commutativity of implication (also called the law of permutation)

${\displaystyle (P\to (Q\to R))\leftrightarrow (Q\to (P\to R))}$

 

Commutativity of equivalence (also called the complete commutative law of equivalence)

${\displaystyle (P\leftrightarrow Q)\leftrightarrow (Q\leftrightarrow P)}$

Set theory

In group and set theory, many algebraic structures are called commutative when certain operands satisfy the commutative property. In higher branches of mathematics, such as analysis and linear algebra the commutativity of well-known operations (such as addition and multiplication on real and complex numbers) is often used (or implicitly assumed) in proofs.^[16][17][18]

Mathematical structures and commutativity

• A commutative semigroup is a set endowed with a total, associative and commutative operation.
• If the operation additionally has an identity element, we have a commutative monoid
• An abelian group, or commutative group is a group whose group operation is commutative.^[17]
• A commutative ring is a ring whose multiplication is commutative. (Addition in a ring is always commutative.)^[19]
• In a field both addition and multiplication are commutative.^[20]

Related properties

Associativity

The associative property is closely related to the commutative property. The associative property of an expression containing two or more occurrences of the same operator states that the order operations are performed in does not affect the final result, as long as the order of terms doesn't change. In contrast, the commutative property states that the order of the terms does not affect the final result.
Most commutative operations encountered in practice are also associative. However, commutativity does not imply associativity. A counterexample is the function

${\displaystyle f(x,y)={\frac {x+y}{2}},}$

which is clearly commutative (interchanging x and y does not affect the result), but it is not associative (since, for example, ${\displaystyle f(-4,f(0,+4))=-1}$ but ${\displaystyle f(f(-4,0),+4)=+1}$). More such examples may be found in commutative non-associative magmas.

Symmetry

Graph showing the symmetry of the addition function

Some forms of symmetry can be directly linked to commutativity. When a commutative operator is written as a binary function then the resulting function is symmetric across the line y = x. As an example, if we let a function f represent addition (a commutative operation) so that f(x,y) = x + y then f is a symmetric function, which can be seen in the image on the right.

For relations, a symmetric relation is analogous to a commutative operation, in that if a relation R is symmetric, then ${\displaystyle aRb\Leftrightarrow bRa}$.

Non-commuting operators in quantum mechanics

In quantum mechanics as formulated by Schrödinger, physical variables are represented by linear operators such as x (meaning multiply by x), and ${\displaystyle {\frac {d}{dx}}}$. These two operators do not commute as may be seen by considering the effect of their compositions ${\displaystyle x{\frac {d}{dx}}}$ and ${\displaystyle {\frac {d}{dx}}x}$ (also called products of operators) on a one-dimensional wave function ${\displaystyle \psi (x)}$:

${\displaystyle x\cdot {\mathrm {d} \over \mathrm {d} x}\psi =x\cdot \psi '\ \neq \ \psi +x\cdot \psi '={\mathrm {d} \over \mathrm {d} x}\left(x\cdot \psi \right)}$

According to the uncertainty principle of Heisenberg, if the two operators representing a pair of variables do not commute, then that pair of variables are mutually complementary, which means they cannot be simultaneously measured or known precisely. For example, the position and the linear momentum in the x-direction of a particle are represented by the operators ${\displaystyle x}$ and ${\displaystyle -i\hbar {\frac {\partial }{\partial x}}}$, respectively (where ${\displaystyle \hbar }$ is the reduced Planck constant). This is the same example except for the constant ${\displaystyle -i\hbar }$, so again the operators do not commute and the physical meaning is that the position and linear momentum in a given direction are complementary.