Hybrid solar cell

From Wikipedia, the free encyclopedia

 

Hybrid solar cells combine advantages of both organic and inorganic semiconductors. Hybrid photovoltaics have organic materials that consist of conjugated polymers that absorb light as the donor and transport holes. Inorganic materials in hybrid cells are used as the acceptor and electron transporter in the structure. The hybrid photovoltaic devices have a potential for not only low-cost by roll-to-roll processing but also for scalable solar power conversion.

Theory

Solar cells are devices that convert sunlight into electricity by the photovoltaic effect. Electrons in a solar cell absorb photon energy in sunlight which excites them to the conduction band from the valence band. This generates a hole-electron pair, which is separated by a potential barrier (such as a p-n junction), and induces a current. Organic solar cells use organic materials in their active layers. Molecular, polymer, and hybrid organic photovoltaics are the main kinds of organic photovoltaic devices currently studied.

Hybrid solar cell

Figure 1. Energy diagram of the donor and acceptor. The conduction band of the acceptor is lower than the LUMO of the polymer, allowing for transfer of the electron.

 

In hybrid solar cells, an organic material is mixed with a high electron transport material to form the photoactive layer. The two materials are assembled together in a heterojunction-type photoactive layer, which can have a greater power conversion efficiency than a single material. One of the materials acts as the photon absorber and exciton donor. The other material facilitates exciton dissociation at the junction. Charge is transferred and then separated after an exciton created in the donor is delocalized on a donor-acceptor complex.

The acceptor material needs a suitable energy offset to the binding energy of the exciton to the absorber. Charge transfer is favorable if the following condition is satisfied:

${\displaystyle E_{A}^{A}-E_{A}^{D}>U_{D}}$

where superscripts A and D refer to the acceptor and donor respectively, E_A is the electron affinity, and U the coulombic binding energy of the exciton on the donor. An energy diagram of the interface is shown in figure 1. In commonly used photovoltaic polymers such as MEH-PPV, the exciton binding energy ranges from 0.3 eV to 1.4 eV.

The energy required to separate the exciton is provided by the energy offset between the LUMOs or conduction bands of the donor and acceptor. After dissociation, the carriers are transported to the respective electrodes through a percolation network.

The average distance an exciton can diffuse through a material before annihilation by recombination is the exciton diffusion length. This is short in polymers, on the order of 5–10 nanometers. The time scale for radiative and non-radiative decay is from 1 picosecond to 1 nanosecond. Excitons generated within this length close to an acceptor would contribute to the photocurrent. 

Figure 2. Two different structures of heterojunctions, a) phase separated bi-layer and b) bulk heterojunction. The bulk heterojunction allows for more interfacial contact between the two phases, which is beneficial for the nanoparticle-polymer compound as it provides more surface area for charge transfer.

 

To deal with the problem of the short exciton diffusion length, a bulk heterojunction structure is used rather than a phase-separated bilayer. Dispersing the particles throughout the polymer matrix creates a larger interfacial area for charge transfer to occur. Figure 2 displays the difference between a bilayer and a bulk heterojunction.

Types of interfaces and structures

Controlling the interface of inorganic-organic hybrid solar cells can increase the efficiency of the cells. This increased efficiency can be achieved by increasing the interfacial surface area between the organic and the inorganic to facilitate charge separation and by controlling the nanoscale lengths and periodicity of each structure so that charges are allowed to separate and move toward the appropriate electrode without recombining. The three main nanoscale structures used are mesoporous inorganic films infused with electron-donating organic, alternatining inorganic-organic lamellar structures, and nanowire structures.

Mesoporous films

Mesoporous films have been used for a relatively high-efficiency hybrid solar cell. The structure of mesoporous thin film solar cells usually includes a porous inorganic that is saturated with organic surfactant. The organic absorbs light, and transfers electrons to the inorganic semiconductor (usually a transparent conducting oxide), which then transfers the electron to the electrode. Problems with these cells include their random ordering and the difficulty of controlling their nanoscale structure to promote charge conduction.

Ordered lamellar films

Recently, the use of alternating layers of organic and inorganic compounds has been controlled through electrodeposition-based self-assembly. This is of particular interest because it has been shown that the lamellar structure and periodicity of the alternating organic-inorganic layers can be controlled through solution chemistry. To produce this type of cell with practical efficiencies, larger organic surfactants that absorb more of the visible spectrum must be deposited between the layers of electron-accepting inorganic.

Films of ordered nanostructures

Researchers have been able to grow nanostructure-based solar cells that use ordered nanostructures like nanowires or nanotubes of inorganic surrounding by electron-donating organics utilizing self-organization processes. Ordered nanostructures offer the advantage of directed charge transport and controlled phase separation between donor and acceptor materials. The nanowire-based morphology offers reduced internal reflection, facile strain relaxation and increased defect tolerance. The ability to make single-crystalline nanowires on low-cost substrates such as aluminum foil and to relax strain in subsequent layers removes two more major cost hurdles associated with high-efficiency cells. There have been rapid increases in efficiencies of nanowire-based solar cells and they seem to be one of the most promising nanoscale solar hybrid technologies.

Fundamental challenge factors

Hybrid cell efficiency must be increased to start large-scale manufacturing. Three factors affect efficiency. First, the bandgap should be reduced to absorb red photons, which contain a significant fraction of the energy in the solar spectrum. Current organic photovoltaics have shown 70% of quantum efficiency for blue photons. Second, contact resistance between each layer in the device should be minimized to offer higher fill factor and power conversion efficiency. Third, charge-carrier mobility should be increased to allow the photovoltaics to have thicker active layers while minimizing carrier recombination and keeping the series resistance of the device low.

Types of hybrid solar cells

Polymer–nanoparticle composite

Nanoparticles are a class of semiconductor materials whose size in at least one dimension ranges from 1 to 100 nanometers, on the order of exciton wavelengths. This size control creates quantum confinement and allows for the tuning of optoelectronic properties, such as band gap and electron affinity. Nanoparticles also have a large surface area to volume ratio, which presents more area for charge transfer to occur.

The photoactive layer can be created by mixing nanoparticles into a polymer matrix. Solar devices based on polymer-nanoparticle composites most resemble polymer solar cells. In this case, the nanoparticles take the place of the fullerene based acceptors used in fully organic polymer solar cells. Hybrid solar cells based upon nanoparticles are an area of research interest because nanoparticles have several properties that could make them preferable to fullerenes, such as:

• Fullerenes are synthesized by a combination of a high temperature arc method and continuous gas-phase synthesis, which makes their production difficult and energy intensive. The colloidal synthesis of nanoparticles by contrast is a low temperature process.
• PCBM (a common fullerene acceptor) diffuses during long timespans or when exposed to heat, which can alter the morphology and lower the efficiency of a polymer solar cell. Limited testing of nanoparticle solar cells indicates they may be more stable over time.
• Nanoparticles are more absorbent than fullerenes, meaning more light can be theoretically absorbed in a thinner device.
• Nanoparticle size can affect absorption. This combined with the fact that there are many possible semiconducting nanoparticles allows for highly customizable bandgaps that can be easily tuned to certain frequencies, which would be advantageous in tandem solar cells.
• Nanoparticles with size near their Bohr radius can generate two excitons when struck by a sufficiently energetic photon.

Structure and processing

Figure 3. Four different structures of nanoparticles, which have at least 1 dimension in the 1–100 nm range, retaining quantum confinement. Left is a nanocrystal, next to it is nanorod, third is tetrapod, and right is hyperbranched.

 

For polymers used in this device, hole mobilities are greater than electron mobilities, so the polymer phase is used to transport holes. The nanoparticles transport electrons to the electrode.

The interfacial area between the polymer phase and the nanoparticles needs to be large. This is achieved by dispersing the particles throughout the polymer matrix. However, the nanoparticles need to be interconnected to form percolation networks for electron transport, which occurs by hopping events.

Efficiency is affected by aspect ratio, geometry, and volume fraction of the nanoparticles. Nanoparticle structures include nanocrystals, nanorods, and hyperbranched structures. Figure 3 contains a picture of each structure. Different structures change the conversion efficiency by effecting nanoparticle dispersion in the polymer and providing pathways for electron transport.

The nanoparticle phase is required to provide a pathway for the electrons to reach the electrode. By using nanorods instead of nanocrystals, the hopping event from one crystal to another can be avoided.

Fabrication methods include mixing the two materials in a solution and spin-coating it onto a substrate, and solvent evaporation (sol-gel). Most of these methods do not involve high-temperature processing. Annealing increases order in the polymer phase, increasing conductivity. However, annealing for too long causes the polymer domain size to increase, eventually making it larger than the exciton diffusion length, and possibly allowing some of the metal from the contact to diffuse into the photoactive layer, reducing the efficiency of the device.

Materials

Inorganic semiconductor nanoparticles used in hybrid cells include CdSe (size ranges from 6–20 nm), ZnO, TiO, and PbS. Common polymers used as photo materials have extensive conjugation and are also hydrophobic. Their efficiency as a photo-material is affected by the HOMO level position and the ionization potential, which directly affects the open circuit voltage and the stability in air. The most common polymers used are P3HT (poly (3-hexylthiophene)), and M3H-PPV (poly[2-methoxy, 5-(2′-ethyl-hexyloxy)-p-phenylenevinylene)]). P3HT has a bandgap of 2.1 eV and M3H-PPV has a bandgap of ~2.4 eV. These values correspond with the bandgap of CdSe, 2.10 eV. The electron affinity of CdSe ranges from 4.4 to 4.7 eV. When the polymer used is MEH-PPV, which has an electron affinity of 3.0 eV, the difference between the electron affinities is large enough to drive electron transfer from the CdSe to the polymer. CdSe also has a high electron mobility (600 cm²·V⁻¹·s⁻¹).

Performance values

The highest demonstrated efficiency is 3.2%, based upon a PCPDTBT polymer donor and CdSe nanoparticle acceptor. The device exhibited a short circuit current of 10.1 mA·cm⁻², an open circuit voltage of .68 V, and a fill factor of .51.

Challenges

Hybrid solar cells need increased efficiencies and stability over time before commercialization is feasible. In comparison to the 2.4% of the CdSe-PPV system, silicon photodevices have power conversion efficiencies greater than 20%. 

Problems include controlling the amount of nanoparticle aggregation as the photolayer forms. The particles need to be dispersed in order to maximize interface area, but need to aggregate to form networks for electron transport. The network formation is sensitive to the fabrication conditions. Dead end pathways can impede flow. A possible solution is implementing ordered heterojunctions, where the structure is well controlled.

The structures can undergo morphological changes over time, namely phase separation. Eventually, the polymer domain size will be greater than the carrier diffusion length, which lowers performance.

Even though the nanoparticle bandgap can be tuned, it needs to be matched with the corresponding polymer. The 2.0 eV bandgap of CdSe is larger than an ideal bandgap of 1.4 for absorbance of light.

The nanoparticles involved are typically colloids, which are stabilized in solution by ligands. The ligands decrease device efficiency because they serve as insulators which impede interaction between the donor and nanoparticle acceptor as well as decreasing the electron mobility. Some, but not complete success has been had by exchanging the initial ligands for pyridine or another short chain ligand.

Hybrid solar cells exhibit material properties inferior to those of bulk silicon semiconductors. The carrier mobilities are much smaller than that of silicon. Electron mobility in silicon is 1000 cm²·V⁻¹·s⁻¹, compared to 600 cm²·V⁻¹·s⁻¹ in CdSe, and less than 10 cm²·V⁻¹·s⁻¹ in other quantum dot materials. Hole mobility in MEH-PPV is 0.1 cm²·V⁻¹·s⁻¹, while in silicon it is 450 cm²·V⁻¹·s⁻¹.

Carbon nanotubes

Carbon nanotubes (CNTs) have high electron conductivity, high thermal conductivity, robustness, and flexibility. Field emission displays (FED), strain sensors, and field effect transistors (FET) using CNTs have been demonstrated. Each application shows the potential of CNTs for nanoscale devices and for flexible electronics applications. Photovoltaic applications have also been explored for this material.

Mainly, CNTs have been used as either the photo-induced exciton carrier transport medium impurity within a polymer-based photovoltaic layer or as the photoactive (photon-electron conversion) layer. Metallic CNT is preferred for the former application, while semiconducting CNT is preferred for the later.

Efficient carrier transport medium

Device diagram for CNT as efficient carrier transport medium.

 

To increase the photovoltaic efficiency, electron-accepting impurities must be added to the photoactive region. By incorporating CNTs into the polymer, dissociation of the exciton pair can be accomplished by the CNT matrix. The high surface area (~1600 m²/g)  of CNTs offers a good opportunity for exciton dissociation. The separated carriers within the polymer-CNT matrix are transported by the percolation pathways of adjacent CNTs, providing the means for high carrier mobility and efficient charge transfer. The factors of performance of CNT-polymer hybrid photovoltaics are low compared to those of inorganic photovoltaics. SWNT in P3OT semiconductor polymer demonstrated open circuit voltage (V_oc) of below 0.94 V, with short circuit current (I_sc) of 0.12 mA/cm².

Metal nanoparticles may be applied to the exterior of CNTs to increase the exciton separation efficiency. The metal provides a higher electric field at the CNT-polymer interface, accelerating the exciton carriers to transfer them more effectively to the CNT matrix. In this case, V_oc = 0.3396 V and I_sc = 5.88 mA/cm². The fill factor is 0.3876%, and the white light conversion factor 0.775%.

Photoactive matrix layer

CNT may be used as a photovoltaic device not only as an add-in material to increase carrier transport, but also as the photoactive layer itself. The semiconducting single walled CNT (SWCNT) is a potentially attractive material for photovoltaic applications for the unique structural and electrical properties. SWCNT has high electric conductivity (100 times that of copper) and shows ballistic carrier transport, greatly decreasing carrier recombination. The bandgap of the SWCNT is inversely proportional to the tube diameter, which means that SWCNT may show multiple direct bandgaps matching the solar spectrum.

A strong built-in electric field in SWCNT for efficient photogenerated electron-hole pair separation has been demonstrated by using two asymmetrical metal electrodes with high and low work functions. The open circuit voltage (V_oc) is 0.28 V, with short circuit current (I_sc) 1.12 nA·cm⁻² with an incident light source of 8.8 W·cm⁻². The resulting white light conversion factor is 0.8%.

Challenges

Several challenges must be addressed for CNT to be used in photovoltaic applications. CNT degrades over time in an oxygen-rich environment. The passivation layer required to prevent CNT oxidation may reduce the optical transparency of the electrode region and lower the photovoltaic efficiency.

Challenges as efficient carrier transport medium

Additional challenges involve the dispersion of CNT within the polymer photoactive layer. The CNT is required to be well dispersed within the polymer matrix to form charge-transfer-efficient pathways between the excitons and the electrode

Challenges as photoactive matrix layer

Challenges of CNT for the photoactive layer include its lack of capability to form a p-n junction, due to the difficulty of doping certain segments of a CNT. (A p-n junction creates an internal built-in potential, providing a pathway for efficient carrier separation within the photovoltaic.) To overcome this difficulty, energy band bending has been done by the use of two electrodes of different work functions. A strong built-in electric field covering the whole SWCNT channel is formed for high-efficiency carrier separation. The oxidation issue with CNT is more critical for this application. Oxidized CNTs have a tendency to become more metallic, and so less useful as a photovoltaic material.

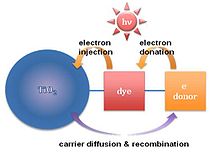
Dye-sensitized

Dye-sensitized solar cells consists of a photo-sensitized anode, an electrolyte, and a photo-electrochemical system. Hybrid solar cells based on dye-sensitized solar cells are formed with inorganic materials (TiO₂) and organic materials.

Materials

Hybrid solar cells based on dye-sensitized solar cells are fabricated by dye-absorbed inorganic materials and organic materials. TiO₂ is the preferred inorganic material since this material is easy to synthesize and acts as a n-type semiconductor due to the donor-like oxygen vacancies. However, titania only absorbs a small fraction of the UV spectrum. Molecular sensitizers (dye molecules) attached to the semiconductor surface are used to collect a greater portion of the spectrum. In the case of titania dye-sensitized solar cells, a photon absorbed by a dye-sensitizer molecule layer induces electron injection into the conduction band of titania, resulting in current flow. However, short diffusion length (diffusivity, D_n≤10⁻⁴cm²/s) in titania dye-sensitized solar cells decrease the solar-to-energy conversion efficiency. To enhance diffusion length (or carrier lifetime), a variety of organic materials are attached to the titania.

Fabrication scheme

Dye-sensitized photoelectrochemical cell (Grätzel cell)

Fig. 5. Schematic representation of electron-hole generation and recombination

 

TiO₂ nanoparticles are synthesized in several tens of nanometer scales (~100 nm). In order to make a photovoltaic cell, molecular sensitizers (dye molecules) are attached to the titania surface. The dye-absorbed titania is finally enclosed by a liquid electrolyte. This type of dye-sensitized solar cell is also known as a Grätzel cell. Dye-sensitized solar cell has a disadvantage of a short diffusion length. Recently, supermolecular or multifunctional sensitizers have been investigated so as to enhance carrier diffusion length. For example, a dye chromophore has been modified by the addition of secondary electron donors. Minority carriers (holes in this case) diffuse to the attached electron donors to recombine. Therefore, electron-hole recombination is retarded by the physical separation between the dye–cation moiety and the TiO₂ surface, as shown in Fig. 5. Finally, this process raises the carrier diffusion length, resulting in the increase of carrier lifetime.

Solid-state dye sensitized solar cell

Mesoporous materials contain pores with diameters between 2 and 50 nm. A dye-sensitized mesoporous film of TiO₂ can be used for making photovoltaic cells and this solar cell is called a ‘solid-state dye sensitized solar cell’. The pores in mesoporous TiO₂ thin film are filled with a solid hole-conducting material such as p-type semiconductors or organic hole conducting material. Replacing the liquid electrolyte in Grätzel’s cells with a solid charge-transport material can be beneficial. The process of electron-hole generation and recombination is the same as Grätzel cells. Electrons are injected from photoexcited dye into the conduction band of titania and holes are transported by a solid charge transport electrolyte to an electrode. Many organic materials have been tested to obtain a high solar-to-energy conversion efficiency in dye synthesized solar cells based on mesoporous titania thin film.

Efficiency factors

Efficiency factors demonstrated for dye-sensitized solar cells are:

Parameters	Types of dye sensitized solar cells
	Grätzel cell	Solid-state
Efficiency (%)	~ 10–11	~ 4
Voc (V)	~ 0.7	~ 0.40
Jsc (mA/cm2)	~ 20	~ 9.10
Fill factor	~ 0.67	~ 0.6

Challenges

Liquid organic electrolytes contain highly corrosive iodine, leading to problems of leakage, sealing, handling, dye desorption, and maintenance. Much attention is now focused on the electrolyte to address these problems. 

For solid-state dye sensitized solar cells, the first challenge originates from disordered titania mesoporous structures. Mesoporous titania structures should be fabricated with well-ordered titania structures of uniform size (~ 10 nm). The second challenge comes from developing the solid electrolyte, which is required to have these properties:

1. The electrolyte should be transparent to the visible spectrum (wide band gap).
2. Fabrication should be possible for depositing the solid electrolyte without degrading the dye molecule layer on titania.
3. The LUMO of the dye molecule should be higher than the conduction band of titania.
4. Several p-type semiconductors tend to crystallize inside the mesoporous titania films, destroying the dye molecule-titania contact. Therefore, the solid electrolyte needs to be stable during operation.

Nanostructured inorganic — small molecules

In 2008, scientists were able to create a nanostructured lamellar structure that provides an ideal design for bulk heterojunction solar cells. The observed structure is composed of ZnO and small, conducting organic molecules, which co-assemble into alternating layers of organic and inorganic components. This highly organized structure, which is stabilized by π-π stacking between the organic molecules, allows for conducting pathways in both the organic and inorganic layers. The thicknesses of the layers (about 1–3 nm) are well within the exciton diffusion length, which ideally minimizes recombination among charge carriers. This structure also maximizes the interface between the inorganic ZnO and the organic molecules, which enables a high chromophore loading density within the structure. Due to the choice of materials, this system is non-toxic and environmentally friendly, unlike many other systems which use lead or cadmium.

Although this system has not yet been incorporated into a photovoltaic device, preliminary photoconductivity measurements have shown that this system exhibits among the highest values measured for organic, hybrid, and amorphous silicon photoconductors, and so, offers promise in creating efficient hybrid photovoltaic devices.

Multi-junction solar cell

From Wikipedia, the free encyclopedia

,

Black light test of Dawn's triple-junction gallium arsenide solar cells

 

Multi-junction (MJ) solar cells are solar cells with multiple p–n junctions made of different semiconductor materials. Each material's p-n junction will produce electric current in response to different wavelengths of light. The use of multiple semiconducting materials allows the absorbance of a broader range of wavelengths, improving the cell's sunlight to electrical energy conversion efficiency. 

Traditional single-junction cells have a maximum theoretical efficiency of 33.16%. Theoretically, an infinite number of junctions would have a limiting efficiency of 86.8% under highly concentrated sunlight.

Currently, the best lab examples of traditional crystalline silicon (c-Si) solar cells have efficiencies between 20% and 25%, while lab examples of multi-junction cells have demonstrated performance over 46% under concentrated sunlight. Commercial examples of tandem cells are widely available at 30% under one-sun illumination, and improve to around 40% under concentrated sunlight. However, this efficiency is gained at the cost of increased complexity and manufacturing price. To date, their higher price and higher price-to-performance ratio have limited their use to special roles, notably in aerospace where their high power-to-weight ratio is desirable. In terrestrial applications, these solar cells are emerging in concentrator photovoltaics (CPV), with a growing number of installations around the world.

Tandem fabrication techniques have been used to improve the performance of existing designs. In particular, the technique can be applied to lower cost thin-film solar cells using amorphous silicon, as opposed to conventional crystalline silicon, to produce a cell with about 10% efficiency that is lightweight and flexible. This approach has been used by several commercial vendors, but these products are currently limited to certain niche roles, like roofing materials.

Description

Basics of solar cells

Figure A. Band diagram illustration of the photovoltaic effect. Photons give their energy to electrons in the depletion or quasi-neutral regions. These move from the valence band to the conduction band. Depending on the location, electrons and holes are accelerated by E_drift, which gives generation photocurrent, or by E_scatt, which gives scattering photocurrent.

 

Traditional photovoltaic cells are commonly composed of doped silicon with metallic contacts deposited on the top and bottom. The doping is normally applied to a thin layer on the top of the cell, producing a pn-junction with a particular bandgap energy, E_g. 

Photons that hit the top of the solar cell are either reflected or transmitted into the cell. Transmitted photons have the potential to give their energy, hν, to an electron if hν ≥ E_g, generating an electron-hole pair. In the depletion region, the drift electric field E_drift accelerates both electrons and holes towards their respective n-doped and p-doped regions (up and down, respectively). The resulting current I_g is called the generated photocurrent. In the quasi-neutral region, the scattering electric field E_scatt accelerates holes (electrons) towards the p-doped (n-doped) region, which gives a scattering photocurrent I_pscatt (I_nscatt). Consequently, due to the accumulation of charges, a potential V and a photocurrent I_ph appear. The expression for this photocurrent is obtained by adding generation and scattering photocurrents: I_ph = I_g + I_nscatt + I_pscatt. 

The J-V characteristics (J is current density, i.e. current per unit area) of a solar cell under illumination are obtained by shifting the J-V characteristics of a diode in the dark downward by I_ph. Since solar cells are designed to supply power and not absorb it, the power P = V·I_ph must be negative. Hence, the operating point (V_m, J_m) is located in the region where V>0 and I_ph<0 a="" and="" chosen="" href="https://en.wikipedia.org/wiki/Absolute_value" maximize="" the="" title="Absolute value" to="">absolute value

of the power |P|.

Loss mechanisms

The Shockley-Queisser limit for the efficiency of a single-junction solar cell. It is essentially impossible for a single-junction solar cell, under unconcentrated sunlight, to have more than ~34% efficiency. A multi-junction cell, however, can exceed that limit.

 

The theoretical performance of a solar cell was first studied in depth in the 1960s, and is today known as the Shockley–Queisser limit. The limit describes several loss mechanisms that are inherent to any solar cell design. 

The first are the losses due to blackbody radiation, a loss mechanism that affects any material object above absolute zero. In the case of solar cells at standard temperature and pressure, this loss accounts for about 7% of the power. The second is an effect known as "recombination", where the electrons created by the photoelectric effect meet the electron holes left behind by previous excitations. In silicon, this accounts for another 10% of the power. 

However, the dominant loss mechanism is the inability of a solar cell to extract all of the power in the light, and the associated problem that it cannot extract any power at all from certain photons. This is due to the fact that the photons must have enough energy to overcome the bandgap of the material. 

If the photon has less energy than the bandgap, it is not collected at all. This is a major consideration for conventional solar cells, which are not sensitive to most of the infrared spectrum, although that represents almost half of the power coming from the sun. Conversely, photons with more energy than the bandgap, say blue light, initially eject an electron to a state high above the bandgap, but this extra energy is lost through collisions in a process known as "relaxation". This lost energy turns into heat in the cell, which has the side-effect of further increasing blackbody losses.

Combining all of these factors, the maximum efficiency for a single-bandgap material, like conventional silicon cells, is about 34%. That is, 66% of the energy in the sunlight hitting the cell will be lost. Practical concerns further reduce this, notably reflection off the front surface or the metal terminals, with modern high-quality cells at about 22%.

Lower, also called narrower, bandgap materials will convert longer wavelength, lower energy photons. Higher, or wider bandgap materials will convert shorter wavelength, higher energy light. An analysis of the AM1.5 spectrum, shows the best balance is reached at about 1.1 eV (about 1100 nm, in the near infrared), which happens to be very close to the natural bandgap in silicon and a number of other useful semiconductors.

Multi-junction cells

Cells made from multiple materials layers can have multiple bandgaps and will therefore respond to multiple light wavelengths, capturing and converting some of the energy that would otherwise be lost to relaxation as described above.

For instance, if one had a cell with two bandgaps in it, one tuned to red light and the other to green, then the extra energy in green, cyan and blue light would be lost only to the bandgap of the green-sensitive material, while the energy of the red, yellow and orange would be lost only to the bandgap of the red-sensitive material. Following analysis similar to those performed for single-bandgap devices, it can be demonstrated that the perfect bandgaps for a two-gap device are at 1.1 eV and 1.8 eV.

Conveniently, light of a particular wavelength does not interact strongly with materials that are of bigger bandgap. This means that you can make a multi-junction cell by layering the different materials on top of each other, shortest wavelengths (biggest bandgap) on the "top" and increasing through the body of the cell. As the photons have to pass through the cell to reach the proper layer to be absorbed, transparent conductors need to be used to collect the electrons being generated at each layer. 

Figure C. (a) The structure of an MJ solar cell. There are six important types of layers: pn junctions, back surface field (BSF) layers, window layers, tunnel junctions, anti-reflective coating and metallic contacts. (b) Graph of spectral irradiance E vs. wavelength λ over the AM1.5 solar spectrum, together with the maximum electricity conversion efficiency for every junction as a function of the wavelength.

 

Producing a tandem cell is not an easy task, largely due to the thinness of the materials and the difficulties extracting the current between the layers. The easy solution is to use two mechanically separate thin film solar cells and then wire them together separately outside the cell. This technique is widely used by amorphous silicon solar cells, Uni-Solar's products use three such layers to reach efficiencies around 9%. Lab examples using more exotic thin-film materials have demonstrated efficiencies over 30%.

The more difficult solution is the "monolithically integrated" cell, where the cell consists of a number of layers that are mechanically and electrically connected. These cells are much more difficult to produce because the electrical characteristics of each layer have to be carefully matched. In particular, the photocurrent generated in each layer needs to be matched, otherwise electrons will be absorbed between layers. This limits their construction to certain materials, best met by the III-V semiconductors.

Material choice

The choice of materials for each sub-cell is determined by the requirements for lattice-matching, current-matching, and high performance opto-electronic properties. 

For optimal growth and resulting crystal quality, the crystal lattice constant a of each material must be closely matched, resulting in lattice-matched devices. This constraint has been relaxed somewhat in recently developed metamorphic solar cells which contain a small degree of lattice mismatch. However, a greater degree of mismatch or other growth imperfections can lead to crystal defects causing a degradation in electronic properties.

Since each sub-cell is connected electrically in series, the same current flows through each junction. The materials are ordered with decreasing bandgaps, E_g, allowing sub-bandgap light (hc/λ < e·E_g) to transmit to the lower sub-cells. Therefore, suitable bandgaps must be chosen such that the design spectrum will balance the current generation in each of the sub-cells, achieving current matching. Figure C(b) plots spectral irradiance E(λ), which is the source power density at a given wavelength λ. It is plotted together with the maximum conversion efficiency for every junction as a function of the wavelength, which is directly related to the number of photons available for conversion into photocurrent. 

Finally, the layers must be electrically optimal for high performance. This necessitates usage of materials with strong absorption coefficients α(λ), high minority carrier lifetimes τ_minority, and high mobilities µ.

The favorable values in the table below justify the choice of materials typically used for multi-junction solar cells: InGaP for the top sub-cell (E_g = 1.8 − 1.9 eV), InGaAs for the middle sub-cell (E_g = 1.4 eV), and Germanium for the bottom sub-cell (E_g = 0.67 eV). The use of Ge is mainly due to its lattice constant, robustness, low cost, abundance, and ease of production.

Because the different layers are closely lattice-matched, the fabrication of the device typically employs metal-organic chemical vapor deposition (MOCVD). This technique is preferable to the molecular beam epitaxy (MBE) because it ensures high crystal quality and large scale production.

Material	Eg, eV	a, nm	absorption (λ = 0.8 μm), 1/µm	µn, cm2/(V·s)	τp, µs	Hardness (Mohs)	α, µm/K	S, m/s
c-Si	1.12	0.5431	0.102	1400	1	7	2.6	0.1–60
InGaP	1.86	0.5451	2	500	–	5	5.3	50
GaAs	1.4	0.5653	0.9	8500	3	4–5	6	50
Ge	0.65	0.5657	3	3900	1000	6	7	1000
InGaAs	1.2	0.5868	30	1200	–	–	5.66	100–1000

Structural elements

Metallic contacts

The metallic contacts are low-resistivity electrodes that make contact with the semiconductor layers. They are often aluminum. This provides an electrical connection to a load or other parts of a solar cell array. They are usually on two sides of the cell. And are important to be on the back face so that shadowing on the lighting surface is reduced.

Anti-reflective coating

Anti-reflective (AR) coating is generally composed of several layers in the case of MJ solar cells. The top AR layer has usually a NaOH surface texturation with several pyramids in order to increase the transmission coefficient T, the trapping of the light in the material (because photons cannot easily get out the MJ structure due to pyramids) and therefore, the path length of photons in the material. On the one hand, the thickness of each AR layer is chosen to get destructive interferences. Therefore, the reflection coefficient R decreases to 1%. In the case of two AR layers L₁ (the top layer, usually SiO
₂) and L₂ (usually TiO
₂), there must be ${\displaystyle n_{L2}=n_{AlInP}^{1/2}\cdot n_{L1}}$ to have the same amplitudes for reflected fields and n_L1d_L1 = 4λ_min,n_L2d_L2 = λ_min/4 to have opposite phase for reflected fields. On the other hand, the thickness of each AR layer is also chosen to minimize the reflectance at wavelengths for which the photocurrent is the lowest. Consequently, this maximizes J_SC by matching currents of the three subcells. As example, because the current generated by the bottom cell is greater than the currents generated by the other cells, the thickness of AR layers is adjusted so that the infrared (IR) transmission (which corresponds to the bottom cell) is degraded while the ultraviolet transmission (which corresponds to the top cell) is upgraded. Particularly, an AR coating is very important at low wavelengths because, without it, T would be strongly reduced to 70%.

Tunnel junctions

Figure D: Layers and band diagram of the tunnel junction. Because the length of the depletion region is narrow and the band gap is high, electrons can tunnel.

 

The main goal of tunnel junctions is to provide a low electrical resistance and optically low-loss connection between two subcells. Without it, the p-doped region of the top cell would be directly connected with the n-doped region of the middle cell. Hence, a pn junction with opposite direction to the others would appear between the top cell and the middle cell. Consequently, the photovoltage would be lower than if there would be no parasitic diode. In order to decrease this effect, a tunnel junction is used. It is simply a wide band gap, highly doped diode. The high doping reduces the length of the depletion region because

${\displaystyle l_{depl}={\sqrt {{\frac {2\epsilon (\phi _{0}-V)}{q}}{\frac {N_{A}+N_{D}}{N_{A}N_{D}}}}}}$

Hence, electrons can easily tunnel through the depletion region. The J-V characteristic of the tunnel junction is very important because it explains why tunnel junctions can be used to have a low electrical resistance connection between two pn junctions. Figure D shows three different regions: the tunneling region, the negative differential resistance region and the thermal diffusion region. The region where electrons can tunnel through the barrier is called the tunneling region. There, the voltage must be low enough so that energy of some electrons who are tunneling is equal to energy states available on the other side of the barrier. Consequently, current density through the tunnel junction is high (with maximum value of ${\displaystyle J_{P}}$, the peak current density) and the slope near the origin is therefore steep. Then, the resistance is extremely low and consequently, the voltage too. This is why tunnel junctions are ideal for connecting two pn junctions without having a voltage drop. When voltage is higher, electrons cannot cross the barrier because energy states are no longer available for electrons. Therefore, the current density decreases and the differential resistance is negative. The last region, called thermal diffusion region, corresponds to the J-V characteristic of the usual diode:

${\displaystyle J=J_{S}\left(\exp \left({\frac {qV}{kT}}\right)-1\right)}$

In order to avoid the reduction of the MJ solar cell performances, tunnel junctions must be transparent to wavelengths absorbed by the next photovoltaic cell, the middle cell, i.e. E_gTunnel > E_gMiddleCell.

Window layer and back-surface field

Figure E: (a) Layers and band diagram of a window layer. The surface recombination is reduced. (b) Layers and band diagram of a BSF layer. The scattering of carriers is reduced.

A window layer is used in order to reduce the surface recombination velocity S. Similarly, a back-surface field (BSF) layer reduces the scattering of carriers towards the tunnel junction. The structure of these two layers is the same: it is a heterojunction which catches electrons (holes). Indeed, despite the electric field E_d, these cannot jump above the barrier formed by the heterojunction because they don't have enough energy, as illustrated in figure E. Hence, electrons (holes) cannot recombine with holes (electrons) and cannot diffuse through the barrier. By the way, window and BSF layers must be transparent to wavelengths absorbed by the next pn junction i.e. E_gWindow > E_gEmitter and E_gBSF > E_gEmitter. Furthermore, the lattice constant must be close to the one of InGaP and the layer must be highly doped (n ≥ 10¹⁸ cm⁻³).

J-V characteristic

For maximum efficiency, each subcell should be operated at its optimal J-V parameters, which are not necessarily equal for each subcell. If they are different, the total current through the solar cell is the lowest of the three. By approximation, it results in the same relationship for the short-circuit current of the MJ solar cell: J_SC = min (J_SC1, J_SC2, J_SC3) where J_SCi(λ) is the short-circuit current density at a given wavelength λ for the subcell i. 

Because of the impossibility to obtain J_SC1, J_SC2, J_SC3 directly from the total J-V characteristic, the quantum efficiency QE(λ) is utilized. It measures the ratio between the amount of electron-hole pairs created and the incident photons at a given wavelength λ. Let φ_i(λ) be the photon flux of corresponding incident light in subcell iandQE_i(λ) be the quantum efficiency of the subcell i. By definition, this equates to:

${\displaystyle QE_{i}(\lambda )={\frac {J_{SCi}(\lambda )}{q\phi _{i}(\lambda )}}\Rightarrow J_{SCi}=\int _{0}^{\lambda 2}q\phi _{i}(\lambda )QE_{i}(\lambda )\,d\lambda }$

The value of ${\displaystyle QE_{i}(\lambda )}$ is obtained by linking it with the absorption coefficient ${\displaystyle \alpha (\lambda )}$, i.e. the number of photons absorbed per unit of length by a material. If it is assumed that each photon absorbed by a subcell creates an electron/hole pair (which is a good approximation), this leads to where d_i is the thickness of the subcell i and ${\displaystyle e^{-\alpha (\lambda )d_{i}}}$ is the percentage of incident light which is not absorbed by the subcell i.

Similarly, because

${\displaystyle V=\sum _{i=1}^{3}V_{i}}$, the following approximation can be used: ${\displaystyle V_{OC}=\sum _{i=1}^{3}V_{OCi}}$.

The values of ${\displaystyle V_{OCi}}$ are then given by the J-V diode equation:

${\displaystyle J_{i}=J_{0i}\left(e^{\frac {qV_{i}}{kT}}-1\right)-J_{SCi}\Rightarrow V_{OCi}\approx {\frac {kT}{q}}\ln({\frac {J_{SCi}}{J_{0i}}})}$

Theoretical limiting efficiency

We can estimate the limiting efficiency of ideal infinite multi-junction solar cells using the graphical quantum-efficiency (QE) analysis invented by C. H. Henry. To fully take advantage of Henry's method, the unit of the AM1.5 spectral irradiance should be converted to that of photon flux (i.e., number of photons/m²/s). To do that, it is necessary to carry out an intermediate unit conversion from the power of electromagnetic radiation incident per unit area per photon energy to the photon flux per photon energy (i.e., from [W/m²/eV] to [number of photons/m2/s/eV]). For this intermediate unit conversion, the following points have to be considered: A photon has a distinct energy which is defined as follows:

(1): E_ph = h∙f = h∙(c/λ)

where E_ph is photon energy, h is Planck's constant (h = 6.626*10⁻³⁴ [J∙s]), c is speed of light (c = 2.998*10⁸ [m/s]), f is frequency [1/s], and λ is wavelength [nm]. 

Then the photon flux per photon energy, dn_ph/dhν, with respect to certain irradiance E [W/m²/eV] can be calculated as follows:

(2): ${\displaystyle {\frac {dn_{ph}}{dhv}}\,={\frac {E}{E_{ph}}}\,}$ = E/{h∙(c/λ)} = E[W/(m²∙eV)]∙λ∙(10⁻⁹ [m])/(1.998∙10⁻²⁵ [J∙s∙m/s]) = E∙λ∙5.03∙10¹⁵ [(# of photons)/(m²∙s∙eV)]

As a result of this intermediate unit conversion, the AM1.5 spectral irradiance is given in unit of the photon flux per photon energy, [number of photons/m²/s/eV], as shown in Figure 1.

Figure 1. Photon flux per photon energy from standard solar energy spectrum (AM of 1.5). 

Based on the above result from the intermediate unit conversion, we can derive the photon flux by numerically integrating the photon flux per photon energy with respect to photon energy. The numerically integrated photon flux is calculated using the Trapezoidal rule, as follows:

(3): ${\displaystyle n_{ph}(E_{g})=\int _{E_{g}}^{\infty }{\frac {dn_{ph}}{dhv}}\,dhv=\sum _{i=E_{g}}^{\infty }(hv_{i+1}-hv_{i}){\frac {1}{2}}({\frac {dn_{ph}}{dhv}}(hv_{i+1})+{\frac {dn_{ph}}{dhv}}(hv_{i}))\,}$

As a result of this numerical integration, the AM1.5 spectral irradiance is given in unit of the photon flux, [number of photons/m2/s], as shown in Figure 2.

Figure 2. Photon flux from standard solar energy spectrum (AM of 1.5).

It is should be noted that there are no photon flux data in the small photon energy range from 0 eV to 0.3096 eV because the standard (AM1.5) solar energy spectrum for hν < 0.31 eV are not available. Regardless of this data unavailability, however, the graphical QE analysis can be done using the only available data with a reasonable assumption that semiconductors are opaque for photon energies greater than their bandgap energy, but transparent for photon energies less than their bandgap energy. This assumption accounts for the first intrinsic loss in the efficiency of solar cells, which is caused by the inability of single-junction solar cells to properly match the broad solar energy spectrum. However, the current graphical QE analysis still cannot reflect the second intrinsic loss in the efficiency of solar cells, radiative recombination. To take the radiative recombination into account, we need to evaluate the radiative current density, J_rad, first. According to Shockley and Queisser method, J_rad can be approximated as follows:

(4): ${\displaystyle J_{rad}=Aexp({\frac {eV-E_{g}}{kT}})\,}$

(5): ${\displaystyle A={\frac {2\pi \,exp(n^{2}+1)E_{g}^{2}kT}{h^{3}c^{2}}}\,}$

where E_g is in electron volts and n is evaluated to be 3.6, the value for GaAs. The incident absorbed thermal radiation J_th is given by J_rad with V = 0.

(6): ${\displaystyle J_{th}=Aexp({\frac {-E_{g}}{kT}})\,}$

The current density delivered to the load is the difference of the current densities due to absorbed solar and thermal radiation and the current density of radiation emitted from the top surface or absorbed in the substrate. Defining J_ph = en_ph, we have:

(7): J = J_ph + J_th − J_rad

The second term, J_th, is negligible compared to J_ph for all semiconductors with E_g. ≥ 0.3 eV, as can be shown by evaluation of the above J_th equation. Thus, we will neglect this term to simplify the following discussion. Then we can express J as follows:

(8): ${\displaystyle J=en_{ph}-Aexp({\frac {eV-E_{g}}{kT}})\,}$

The open-circuit voltage is found by setting J = 0.

(9): ${\displaystyle eV_{OC}=E_{g}-kTln({\frac {A}{en_{ph}}})\,}$

The maximum power point (J_m, V_m) is found by stetting the derivative ${\displaystyle {\frac {dJV}{dV}}\,=0}$. The familiar result of this calculation is:

(10): ${\displaystyle eV_{m}=eV_{OC}-kTln(1+{\frac {eV_{m}}{kT}})\,}$

(11): ${\displaystyle J_{m}={\frac {en_{ph}}{1+kT/eV_{m}}}\,}$

Finally, the maximum work (W_m) done per absorbed photon, Wm is given by:

(12): ${\displaystyle W_{m}={\frac {J_{m}V_{m}}{n_{ph}}}\,={\frac {eV_{m}}{1+kT/eV_{m}}}\,=eV_{m}-kT}$

Combining the last three equations, we have:

(13): ${\displaystyle W_{m}=E_{g}-kT[ln({\frac {A}{en_{ph}}})+ln(1+{\frac {eV_{m}}{kT}})+1]\,}$

Using the above equation, W_m (red line) is plotted in Figure 3 for different values of E_g (or n_ph):

Figure 3. Maximum work by ideal infinite multi-junction solar cells under standard AM1.5 spectral irradiance.

Now, we can fully use Henry's graphical QE analysis, taking into account the two major intrinsic losses in the efficiency of solar cells. The two main intrinsic losses are radiative recombination, and the inability of single junction solar cells to properly match the broad solar energy spectrum. The shaded area under the red line represents the maximum work done by ideal infinite multi-junction solar cells. Hence, the limiting efficiency of ideal infinite multi-junction solar cells is evaluated to be 68.8% by comparing the shaded area defined by the red line with the total photon-flux area determined by the black line. (This is why this method is called "graphical" QE analysis.) Although this limiting efficiency value is consistent with the values published by Parrott and Vos in 1979: 64% and 68.2% respectively, there is a small gap between the estimated value in this report and literature values. This minor difference is most likely due to the different ways how to approximate the photon flux from 0 eV to 0.3096 eV. Here, we approximated the photon flux from 0 eV to 0.3096 eV as the same as the photon flux at 0.31 eV.

Materials

The majority of multi-junction cells that have been produced to date use three layers (although many tandem a-Si:H/mc-Si modules have been produced and are widely available). However, the triple junction cells require the use of semiconductors that can be tuned to specific frequencies, which has led to most of them being made of gallium arsenide (GaAs) compounds, often germanium for the bottom-, GaAs for the middle-, and GaInP₂ for the top-cell.

Gallium arsenide substrate

Dual junction cells can be made on Gallium arsenide wafers. Alloys of Indium gallium phosphide in the range In_.5Ga_.5P through In_.53Ga_.47P serve as the high band gap alloy. This alloy range provides for the ability to have band gaps in the range of 1.92eV to 1.87eV. The lower GaAs junction has a band gap of 1.42eV.

Germanium substrate

Triple junction cells consisting of indium gallium phosphide (InGaP), gallium arsenide (GaAs) or indium gallium arsenide (InGaAs) and germanium (Ge) can be fabricated on germanium wafers. Early cells used straight gallium arsenide in the middle junction. Later cells have utilized In_0.015Ga_0.985As, due to the better lattice match to Ge, resulting in a lower defect density.

Due to the huge band gap difference between GaAs (1.42eV), and Ge (0.66eV), the current match is very poor, with the Ge junction operated significantly current limited.

Current efficiencies for commercial InGaP/GaAs/Ge cells approach 40% under concentrated sunlight. Lab cells (partly using additional junctions between the GaAs and Ge junction) have demonstrated efficiencies above 40%.

Indium phosphide substrate

Indium phosphide may be used as a substrate to fabricate cells with band gaps between 1.35eV and 0.74eV. Indium Phosphide has a band gap of 1.35eV. Indium gallium arsenide (In_0.53Ga_0.47As) is lattice matched to Indium Phosphide with a band gap of 0.74eV. A quaternary alloy of Indium gallium arsenide phosphide can be lattice matched for any band gap in between the two.

Indium phosphide-based cells have the potential to work in tandem with gallium arsenide cells. The two cells can be optically connected in series (with the InP cell below the GaAs cell), or in parallel through the use of spectra splitting using a Dichroic filter.

Indium gallium nitride substrate

Indium gallium nitride (InGaN) is a semiconductor material made of a mix of gallium nitride (GaN) and indium nitride (InN). It is a ternary group III/V direct bandgap semiconductor. Its bandgap can be tuned by varying the amount of indium in the alloy from 0.7 eV to 3.4 eV, thus making it an ideal material for solar cells. However, its conversion efficiencies because of technological factors unrelated to bandgap are still not high enough to be competitive in the market.

Performance improvements

Structure

Many MJ photovoltaic cells use III-V semiconductor materials. GaAsSb-based heterojunction tunnel diodes, instead of conventional InGaP highly doped tunnel diodes described above, have a lower tunneling distance. Indeed, in the heterostructure formed by GaAsSb and InGaAs, the valence band of GaAsSb is higher than the valence band of the adjoining p-doped layer. Consequently, the tunneling distance d_tunnel is reduced and so the tunneling current, which exponentially depends of d_tunnel, is increased. Hence, the voltage is lower than that of the InGaP tunnel junction. GaAsSb heterojunction tunnel diodes offer other advantages. The same current can be achieved by using a lower doping. Secondly, because the lattice constant is larger for GaAsSb than Ge, one can use a wider range of materials for the bottom cell because more materials are lattice-matched to GaAsSb than to Ge.

Chemical components can be added to some layers. Adding about one percent of indium in each layer better matches lattice constants of the different layers. Without it, there is about 0.08 percent of mismatching between layers, which inhibits performance. Adding aluminium to the top cell increases its band gap to 1.96 eV, covering a larger part of the solar spectrum and obtain a higher open-circuit voltage V_OC. 

The theoretical efficiency of MJ solar cells is 86.8% for an infinite number of pn junctions, implying that more junctions increase efficiency. The maximum theoretical efficiency is 37, 50, 56, 72% for 1, 2, 3, 36 pn junctions, respectively, with the number of junctions increasing exponentially to achieve equal efficiency increments. The exponential relationship implies that as the cell approaches the limit of efficiency, the increase cost and complexity grow rapidly. Decreasing the thickness of the top cell increases the transmission coefficient T.

Finally, an InGaP hetero-layer between the p-Ge layer and the InGaAs layer can be added in order to create automatically the n-Ge layer by scattering during MOCVD growth and increase significantly the quantum efficiency QE(λ) of the bottom cell. InGaP is advantageous because of its high scattering coefficient and low solubility in Ge.

Spectral variations

Solar spectrum at the Earth surface changes constantly depending on the weather and sun position. This results in the variation of φ(λ), QE(λ), α(λ) and thus the short-circuit currents J_SCi. As a result, the current densities J_i are not necessarily matched and the total current becomes lower. These variations can be quantified using the average photon energy (APE) which is the ratio between the spectral irradiance G(λ) (the power density of the light source in a specific wavelength λ) and the total photon flux density. It can be shown that a high (low) value for APE means low (high) wavelengths spectral conditions and higher (lower) efficiencies. Thus APE is a good indicator for quantifying the effects of the solar spectrum variations on performances and has the added advantage of being independent of the device structure and the absorption profile of the device.

Use of light concentrators

Light concentrators increase efficiencies and reduce the cost/efficiency ratio. The three types of light concentrators in use are refractive lenses like Fresnel lenses, reflective dishes (parabolic or cassegraine), and light guide optics. Thanks to these devices, light arriving on a large surface can be concentrated on a smaller cell. The intensity concentration ratio (or “suns”) is the average intensity of the focused light divided by 1 kW/m² (reasonable value related to solar constant). If its value is X then the MJ current becomes X higher under concentrated illumination.

Using concentrations on the order of 500 to 1000, meaning that a 1 cm² cell can use the light collected from 0.1 m² (as 1 m² equal 10000 cm²), produces the highest efficiencies seen to date. Three-layer cells are fundamentally limited to 63%, but existing commercial prototypes have already demonstrated over 40%. These cells capture about 2/3 of their theoretical maximum performance, so assuming the same is true for a non-concentrated version of the same design, one might expect a three-layer cell of 30% efficiency. This is not enough of an advantage over traditional silicon designs to make up for their extra production costs. For this reason, almost all multi-junction cell research for terrestrial use is dedicated to concentrator systems, normally using mirrors or fresnel lenses.

Using a concentrator also has the added benefit that the number of cells needed to cover a given amount of ground area is greatly reduced. A conventional system covering 1 m² would require 625 16 cm² cells, but for a concentrator system only a single cell is needed, along with a concentrator. The argument for concentrated Multi-junction cells has been that the high cost of the cells themselves would be more than offset by the reduction in total number of cells. However, the downside of the concentrator approach is that efficiency drops off very quickly under lower lighting conditions. In order to maximize its advantage over traditional cells and thus be cost competitive, the concentrator system has to track the sun as it moves to keep the light focused on the cell and maintain maximum efficiency as long as possible. This requires a solar tracker system, which increases yield, but also cost.

Fabrication

As of 2014 multi-junction cells were expensive to produce, using techniques similar to semiconductor device fabrication, usually metalorganic vapour phase epitaxy but on "chip" sizes on the order of centimeters. 

A new technique was announced that year that allowed such cells to use a substrate of glass or steel, lower-cost vapors in reduced quantities that was claimed to offer costs competitive with conventional silicon cells.

Comparison with other technologies

There are four main categories of photovoltaic cells: conventional mono and multi crystalline silicon (c-Si) cells, thin film solar cells (a-Si, CIGS and CdTe), and multi-junction (MJ) solar cells. The fourth category, emerging photovoltaics, contains technologies that are still in the research or development phase and are not listed in the table below.

Categories	Technology	η (%)	VOC (V)	ISC (A)	W/m2	t (µm)	Refs
Crystalline silicon cells	Monocrystalline	24.7	0.5	0.8	63	100
	Polysilicon	20.3	0.615	8.35	211	200
Thin film solar cells	Amorphous silicon	11.1	0.63	0.089	33	1
	CdTe	16.5	0.86	0.029	–	5
	CIGS	19.5	–	–	–	1
Multi-junction cells	MJ	40.7	2.6	1.81	476	140

MJ solar cells and other photovoltaic devices have significant differences (see the table above). Physically, the main property of a MJ solar cell is having more than one pn junction in order to catch a larger photon energy spectrum while the main property of the thin film solar cell is to use thin films instead of thick layers in order to decrease the cost efficiency ratio. As of 2010, MJ solar panels are more expensive than others. These differences imply different applications: MJ solar cells are preferred in space and c-Si solar cells for terrestrial applications.

National Renewable Energy Laboratory graph of solar cell efficiency over time.

 

The efficiencies of solar cells and Si solar technology are relatively stable, while the efficiency of solar modules and multi-junction technology are progressing.

Measurements on MJ solar cells are usually made in laboratory, using light concentrators (this is often not the case for the other cells) and under standard test conditions (STCs). STCs prescribe, for terrestrial applications, the AM1.5 spectrum as the reference. This air mass (AM) corresponds to a fixed position of the sun in the sky of 48° and a fixed power of 833 W/m². Therefore, spectral variations of incident light and environmental parameters are not taken into account under STC.

Consequently, performance of MJ solar cells in terrestrial environment is inferior to that achieved in laboratory. Moreover, MJ solar cells are designed such that currents are matched under STC, but not necessarily under field conditions. One can use QE(λ) to compare performances of different technologies, but QE(λ) contains no information on the matching of currents of subcells. An important comparison point is rather the output power per unit area generated with the same incident light.

Applications

As of 2010, the cost of MJ solar cells was too high to allow use outside of specialized applications. The high cost is mainly due to the complex structure and the high price of materials. Nevertheless, with light concentrators under illumination of at least 400 suns, MJ solar panels become practical.

As less expensive multi-junction materials become available other applications involve bandgap engineering for microclimates with varied atmospheric conditions.

MJ cells are currently being utilized in the Mars rover missions.

The environment in space is quite different. Because there is no atmosphere, the solar spectrum is different (AM0). The cells have a poor current match due to a greater photon flux of photons above 1.87eV vs. those between 1.87eV and 1.42eV. This results in too little current in the GaAs junction, and hampers the overall efficiency since the InGaP junction operates below MPP current and the GaAs junction operates above MPP current. To improve current match, the InGaP layer is intentionally thinned to allow additional photons to penetrate to the lower GaAs layer.

In terrestrial concentrating applications, the scatter of blue light by the atmosphere reduces the photon flux above 1.87eV, better balancing the junction currents. Radiation particles that are no longer filtered can damage the cell. There are two kinds of damage: ionization and atomic displacement. Still, MJ cells offer higher radiation resistance, higher efficiency and a lower temperature coefficient.