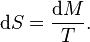Moore's Law Keeps Going, Defying Expectations

It’s a mystery why Gordon Moore’s “law,” which forecasts processor power will double every two years, still holds true a half century later

 

By Annie Sneed | May 19, 2015

 

Original link:  http://www.scientificamerican.com/article/moore-s-law-keeps-going-defying-expectations/?WT.mc_id=SA_Facebook

Credit: Jon Sullivan/Wikimedia Commons

SAN FRANCISCO—Personal computers, cellphones, self-driving cars—Gordon Moore predicted the invention of all these technologies half a century ago in a 1965 article for Electronics magazine. The enabling force behind those inventions would be computing power, and Moore laid out how he thought computing power would evolve over the coming decade. Last week the tech world celebrated his prediction here because it has held true with uncanny accuracy—for the past 50 years.

It is now called Moore’s law, although Moore (who co-founded the chip maker Intel) doesn’t much like the name. “For the first 20 years I couldn’t utter the term Moore’s law. It was embarrassing,” the 86-year-old visionary said in an interview with New York Times columnist Thomas Friedman at the gala event, held at Exploratorium science museum. “Finally, I got accustomed to it where now I could say it with a straight face.” He and Friedman chatted in front of a rapt audience, with Moore cracking jokes the whole time and doling out advice, like how once you’ve made one successful prediction, you should avoid making another. In the background Intel’s latest gadgets whirred quietly: collision-avoidance drones, dancing spider robots, a braille printer—technologies all made possible via advances in processing power anticipated by Moore’s law.

Of course, Moore’s law is not really a law like those describing gravity or the conservation of energy. It is a prediction that the number of transistors (a computer’s electrical switches used to represent 0s and 1s) that can fit on a silicon chip will double every two years as technology advances. This leads to incredibly fast growth in computing power without a concomitant expense and has led to laptops and pocket-size gadgets with enormous processing ability at fairly low prices. Advances under Moore’s law have also enabled smartphone verbal search technologies such as Siri—it takes enormous computing power to analyze spoken words, turn them into digital representations of sound and then interpret them to give a spoken answer in a matter of seconds.

Another way to think about Moore’s law is to apply it to a car. Intel CEO Brian Krzanich explained that if a 1971 Volkswagen Beetle had advanced at the pace of Moore’s law over the past 34 years, today “you would be able to go with that car 300,000 miles per hour. You would get two million miles per gallon of gas, and all that for the mere cost of four cents.”

Moore anticipated the two-year doubling trend based on what he had seen happen in the early years of computer-chip manufacture. In his 1965 paper he plotted the number of transistors that fit on a chip since 1959 and saw a pattern of yearly doubling that he then extrapolated for the next 10 years. (He later revised the trend to a doubling about every two years.) “Moore was just making an observation,” says Peter Denning, a computer scientist at the Naval Postgraduate School in California. “He was the head of research at Fairchild Semiconductor and wanted to look down the road at how much computing power they’d have in a decade. And in 1975 his prediction came pretty darn close.”

But Moore never thought his prediction would last 50 years. “The original prediction was to look at 10 years, which I thought was a stretch,” he told Friedman last week, “This was going from about 60 elements on an integrated circuit to 60,000—a 1,000-fold extrapolation over 10 years. I thought that was pretty wild. The fact that something similar is going on for 50 years is truly amazing.”

Just why Moore’s law has endured so long is hard to say. His doubling prediction turned into an industry objective for competing companies. “It might be a self-fulfilling law,” Denning explains. But it is not clear why it is a constant doubling every couple of years, as opposed to a different rate or fluctuating spikes in progress. “Science has mysteries, and in some ways this is one of those mysteries,” Denning adds. Certainly, if the rate could have gone faster, someone would have done it, notes computer scientist Calvin Lin of the University of Texas at Austin.

Many technologists have forecast the demise of Moore’s doubling over the years, and Moore himself states that this exponential growth can’t last forever. Still, his law persists today, and hence the computational growth it predicts will continue to profoundly change our world. As he put it: “We’ve just seen the beginning of what computers are going to do for us.”

Holographic principle

From Wikipedia, the free encyclopedia

The holographic principle is a property of string theories and a supposed property of quantum gravity that states that the description of a volume of space can be thought of as encoded on a boundary to the region—preferably a light-like boundary like a gravitational horizon. First proposed by Gerard 't Hooft, it was given a precise string-theory interpretation by Leonard Susskind^[1] who combined his ideas with previous ones of 't Hooft and Charles Thorn.^[1][2] As pointed out by Raphael Bousso,^[3] Thorn observed in 1978 that string theory admits a lower-dimensional description in which gravity emerges from it in what would now be called a holographic way.

In a larger sense, the theory suggests that the entire universe can be seen as a two-dimensional information structure "painted" on the cosmological horizon^{[clarification needed]}, such that the three dimensions we observe are an effective description only at macroscopic scales and at low energies. Cosmological holography has not been made mathematically precise, partly because the particle horizon has a non-zero area and grows with time.^[4][5]

The holographic principle was inspired by black hole thermodynamics, which conjectures that the maximal entropy in any region scales with the radius squared, and not cubed as might be expected. In the case of a black hole, the insight was that the informational content of all the objects that have fallen into the hole might be entirely contained in surface fluctuations of the event horizon. The holographic principle resolves the black hole information paradox within the framework of string theory.^[6] However, there exist classical solutions to the Einstein equations that allow values of the entropy larger than those allowed by an area law, hence in principle larger than those of a black hole.
These are the so-called "Wheeler's bags of gold". The existence of such solutions conflicts with the holographic interpretation, and their effects in a quantum theory of gravity including the holographic principle are not yet fully understood.^[7]

Black hole entropy

An object with entropy is microscopically random, like a hot gas. A known configuration of classical fields has zero entropy: there is nothing random about electric and magnetic fields, or gravitational waves. Since black holes are exact solutions of Einstein's equations, they were thought not to have any entropy either.

But Jacob Bekenstein noted that this leads to a violation of the second law of thermodynamics. If one throws a hot gas with entropy into a black hole, once it crosses the event horizon, the entropy would disappear. The random properties of the gas would no longer be seen once the black hole had absorbed the gas and settled down. One way of salvaging the second law is if black holes are in fact random objects, with an enormous entropy whose increase is greater than the entropy carried by the gas.

Bekenstein assumed that black holes are maximum entropy objects—that they have more entropy than anything else in the same volume. In a sphere of radius R, the entropy in a relativistic gas increases as the energy increases. The only known limit is gravitational; when there is too much energy the gas collapses into a black hole. Bekenstein used this to put an upper bound on the entropy in a region of space, and the bound was proportional to the area of the region. He concluded that the black hole entropy is directly proportional to the area of the event horizon.^[8]

Stephen Hawking had shown earlier that the total horizon area of a collection of black holes always increases with time. The horizon is a boundary defined by light-like geodesics; it is those light rays that are just barely unable to escape. If neighboring geodesics start moving toward each other they eventually collide, at which point their extension is inside the black hole. So the geodesics are always moving apart, and the number of geodesics which generate the boundary, the area of the horizon, always increases. Hawking's result was called the second law of black hole thermodynamics, by analogy with the law of entropy increase, but at first, he did not take the analogy too seriously.

Hawking knew that if the horizon area were an actual entropy, black holes would have to radiate. When heat is added to a thermal system, the change in entropy is the increase in mass-energy divided by temperature:

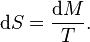
If black holes have a finite entropy, they should also have a finite temperature. In particular, they would come to equilibrium with a thermal gas of photons. This means that black holes would not only absorb photons, but they would also have to emit them in the right amount to maintain detailed balance.

Time independent solutions to field equations do not emit radiation, because a time independent background conserves energy. Based on this principle, Hawking set out to show that black holes do not radiate. But, to his surprise, a careful analysis convinced him that they do, and in just the right way to come to equilibrium with a gas at a finite temperature. Hawking's calculation fixed the constant of proportionality at 1/4; the entropy of a black hole is one quarter its horizon area in Planck units.^[9]

The entropy is proportional to the logarithm of the number of microstates, the ways a system can be configured microscopically while leaving the macroscopic description unchanged. Black hole entropy is deeply puzzling — it says that the logarithm of the number of states of a black hole is proportional to the area of the horizon, not the volume in the interior.^[10]

Later, Raphael Bousso came up with a covariant version of the bound based upon null sheets.

Black hole information paradox

Hawking's calculation suggested that the radiation which black holes emit is not related in any way to the matter that they absorb. The outgoing light rays start exactly at the edge of the black hole and spend a long time near the horizon, while the infalling matter only reaches the horizon much later. The infalling and outgoing mass/energy only interact when they cross. It is implausible that the outgoing state would be completely determined by some tiny residual scattering.
Hawking interpreted this to mean that when black holes absorb some photons in a pure state described by a wave function, they re-emit new photons in a thermal mixed state described by a density matrix. This would mean that quantum mechanics would have to be modified, because in quantum mechanics, states which are superpositions with probability amplitudes never become states which are probabilistic mixtures of different possibilities.^{[note 1]}

Troubled by this paradox, Gerard 't Hooft analyzed the emission of Hawking radiation in more detail. He noted that when Hawking radiation escapes, there is a way in which incoming particles can modify the outgoing particles. Their gravitational field would deform the horizon of the black hole, and the deformed horizon could produce different outgoing particles than the undeformed horizon. When a particle falls into a black hole, it is boosted relative to an outside observer, and its gravitational field assumes a universal form. 't Hooft showed that this field makes a logarithmic tent-pole shaped bump on the horizon of a black hole, and like a shadow, the bump is an alternate description of the particle's location and mass. For a four-dimensional spherical uncharged black hole, the deformation of the horizon is similar to the type of deformation which describes the emission and absorption of particles on a string-theory world sheet. Since the deformations on the surface are the only imprint of the incoming particle, and since these deformations would have to completely determine the outgoing particles, 't Hooft believed that the correct description of the black hole would be by some form of string theory.

This idea was made more precise by Leonard Susskind, who had also been developing holography, largely independently. Susskind argued that the oscillation of the horizon of a black hole is a complete description^{[note 2]} of both the infalling and outgoing matter, because the world-sheet theory of string theory was just such a holographic description. While short strings have zero entropy, he could identify long highly excited string states with ordinary black holes. This was a deep advance because it revealed that strings have a classical interpretation in terms of black holes.

This work showed that the black hole information paradox is resolved when quantum gravity is described in an unusual string-theoretic way assuming the string-theoretical description is complete, unambiguous and non-redundant.^[12] The space-time in quantum gravity would emerge as an effective description of the theory of oscillations of a lower-dimensional black-hole horizon, and suggest that any black hole with appropriate properties, not just strings, would serve as a basis for a description of string theory.

In 1995, Susskind, along with collaborators Tom Banks, Willy Fischler, and Stephen Shenker, presented a formulation of the new M-theory using a holographic description in terms of charged point black holes, the D0 branes of type IIA string theory. The Matrix theory they proposed was first suggested as a description of two branes in 11-dimensional supergravity by Bernard de Wit, Jens Hoppe, and Hermann Nicolai. The later authors reinterpreted the same matrix models as a description of the dynamics of point black holes in particular limits.
Holography allowed them to conclude that the dynamics of these black holes give a complete non-perturbative formulation of M-theory. In 1997, Juan Maldacena gave the first holographic descriptions of a higher-dimensional object, the 3+1-dimensional type IIB membrane, which resolved a long-standing problem of finding a string description which describes a gauge theory. These developments simultaneously explained how string theory is related to some forms of supersymmetric quantum field theories.

Limit on information density

Entropy, if considered as information (see information entropy), is measured in bits. The total quantity of bits is related to the total degrees of freedom of matter/energy.

For a given energy in a given volume, there is an upper limit to the density of information (the Bekenstein bound) about the whereabouts of all the particles which compose matter in that volume, suggesting that matter itself cannot be subdivided infinitely many times and there must be an ultimate level of fundamental particles. As the degrees of freedom of a particle are the product of all the degrees of freedom of its sub-particles, were a particle to have infinite subdivisions into lower-level particles, then the degrees of freedom of the original particle must be infinite, violating the maximal limit of entropy density. The holographic principle thus implies that the subdivisions must stop at some level, and that the fundamental particle is a bit (1 or 0) of information.

The most rigorous realization of the holographic principle is the AdS/CFT correspondence by Juan Maldacena. However, J.D. Brown and Marc Henneaux had rigorously proved already in 1986, that the asymptotic symmetry of 2+1 dimensional gravity gives rise to a Virasoro algebra, whose corresponding quantum theory is a 2-dimensional conformal field theory.^[13]

High-level summary

The physical universe is widely seen to be composed of "matter" and "energy". In his 2003 article published in Scientific American magazine, Jacob Bekenstein summarized a current trend started by John Archibald Wheeler, which suggests scientists may "regard the physical world as made of information, with energy and matter as incidentals." Bekenstein asks "Could we, as William Blake memorably penned, 'see a world in a grain of sand,' or is that idea no more than 'poetic license,'"^[14] referring to the holographic principle.

Unexpected connection

Bekenstein's topical overview "A Tale of Two Entropies"^[15] describes potentially profound implications of Wheeler's trend, in part by noting a previously unexpected connection between the world of information theory and classical physics. This connection was first described shortly after the seminal 1948 papers of American applied mathematician Claude E. Shannon introduced today's most widely used measure of information content, now known as Shannon entropy. As an objective measure of the quantity of information, Shannon entropy has been enormously useful, as the design of all modern communications and data storage devices, from cellular phones to modems to hard disk drives and DVDs, rely on Shannon entropy.

In thermodynamics (the branch of physics dealing with heat), entropy is popularly described as a measure of the "disorder" in a physical system of matter and energy. In 1877 Austrian physicist Ludwig Boltzmann described it more precisely in terms of the number of distinct microscopic states that the particles composing a macroscopic "chunk" of matter could be in while still looking like the same macroscopic "chunk". As an example, for the air in a room, its thermodynamic entropy would equal the logarithm of the count of all the ways that the individual gas molecules could be distributed in the room, and all the ways they could be moving.

Energy, matter, and information equivalence

Shannon's efforts to find a way to quantify the information contained in, for example, an e-mail message, led him unexpectedly to a formula with the same form as Boltzmann's. In an article in the August 2003 issue of Scientific American titled "Information in the Holographic Universe", Bekenstein summarizes that "Thermodynamic entropy and Shannon entropy are conceptually equivalent: the number of arrangements that are counted by Boltzmann entropy reflects the amount of Shannon information one would need to implement any particular arrangement..." of matter and energy. The only salient difference between the thermodynamic entropy of physics and Shannon's entropy of information is in the units of measure; the former is expressed in units of energy divided by temperature, the latter in essentially dimensionless "bits" of information, and so the difference is merely a matter of convention.

The holographic principle states that the entropy of ordinary mass (not just black holes) is also proportional to surface area and not volume; that volume itself is illusory and the universe is really a hologram which is isomorphic to the information "inscribed" on the surface of its boundary.^[10]

Experimental tests

The Fermilab physicist Craig Hogan claims that the holographic principle would imply quantum fluctuations in spatial position^[16] that would lead to apparent background noise or "holographic noise" measurable at gravitational wave detectors, in particular GEO 600.^[17] However these claims have not been widely accepted, or cited, among quantum gravity researchers and appear to be in direct conflict with string theory calculations.^[18]

Analyses in 2011 of measurements of gamma ray burst GRB 041219A in 2004 by the INTEGRAL space observatory launched in 2002 by the European Space Agency shows that Craig Hogan's noise is absent down to a scale of 10⁻⁴⁸ meters, as opposed to scale of 10⁻³⁵ meters predicted by Hogan, and the scale of 10⁻¹⁶ meters found in measurements of the GEO 600 instrument.^[19] Research continues at Fermilab under Hogan as of 2013.^[20]

Jacob Bekenstein also claims to have found a way to test the holographic principle with a tabletop photon experiment.^[21]

Tests of Maldacena's conjecture

Hyakutake et al. in 2013/4 published two papers^[22] that bring computational evidence that Maldacena’s conjecture is true. One paper computes the internal energy of a black hole, the position of its event horizon, its entropy and other properties based on the predictions of string theory and the effects of virtual particles. The other paper calculates the internal energy of the corresponding lower-dimensional cosmos with no gravity. The two simulations match. The papers are not an actual proof of Maldacena's conjecture for all cases but a demonstration that the conjecture works for a particular theoretical case and a verification of the AdS/CFT correspondence for a particular situation.^[23]

Multiverse

From Wikipedia, the free encyclopedia

The multiverse (or meta-universe) is the hypothetical set of infinite or finite possible universes (including the Universe we consistently experience) that together comprise everything that exists: the entirety of space, time, matter, and energy as well as the physical laws and constants that describe them. The various universes within the multiverse are sometimes called "parallel universes" or "alternate universes".

The structure of the multiverse, the nature of each universe within it and the relationships among the various constituent universes, depend on the specific multiverse hypothesis considered. Multiple universes have been hypothesized in cosmology, physics, astronomy, religion, philosophy, transpersonal psychology, and fiction, particularly in science fiction and fantasy. In these contexts, parallel universes are also called "alternate universes", "quantum universes", "interpenetrating dimensions", "parallel dimensions", "parallel worlds", "alternate realities", "alternate timelines", and "dimensional planes", among others. The term 'multiverse' was coined in 1895 by the American philosopher and psychologist William James in a different context.^[1]

The multiverse hypothesis is a source of debate within the physics community. Physicists disagree about whether the multiverse exists, and whether the multiverse is a proper subject of scientific inquiry.^[2] Supporters of one of the multiverse hypotheses include Stephen Hawking,^[3] Brian Greene,^[4][5] Max Tegmark,^[6] Alan Guth,^[7] Andrei Linde,^[8] Michio Kaku,^[9] David Deutsch,^[10] Leonard Susskind,^[11] Raj Pathria,^[12] Alexander Vilenkin,^[13] Laura Mersini-Houghton,^[14][15] Neil deGrasse Tyson^[16] and Sean Carroll.^[17] In contrast, those who are not proponents of the multiverse include: Nobel laureate Steven Weinberg,^[18] Nobel laureate David Gross,^[19] Paul Steinhardt,^[20] Neil Turok,^[21] Viatcheslav Mukhanov,^[22] George Ellis,^[23][24] Jim Baggott,^[25] and Paul Davies. Some argue that the multiverse question is philosophical rather than scientific, that the multiverse cannot be a scientific question because it lacks falsifiability, or even that the multiverse hypothesis is harmful or pseudoscientific.

Multiverse hypotheses in physics

Categories

Max Tegmark and Brian Greene have devised classification schemes that categorize the various theoretical types of multiverse, or types of universe that might theoretically comprise a multiverse ensemble.

Max Tegmark's four levels

Cosmologist Max Tegmark has provided a taxonomy of universes beyond the familiar observable universe. The levels according to Tegmark's classification are arranged such that subsequent levels can be understood to encompass and expand upon previous levels, and they are briefly described below.^[26][27]

Level I: Beyond our cosmological horizon

A generic prediction of chaotic inflation is an infinite ergodic universe, which, being infinite, must contain Hubble volumes realizing all initial conditions.

Accordingly, an infinite universe will contain an infinite number of Hubble volumes, all having the same physical laws and physical constants. In regard to configurations such as the distribution of matter, almost all will differ from our Hubble volume. However, because there are infinitely many, far beyond the cosmological horizon, there will eventually be Hubble volumes with similar, and even identical, configurations. Tegmark estimates that an identical volume to ours should be about 10¹⁰¹¹⁵ meters away from us.^[6] Given infinite space, there would, in fact, be an infinite number of Hubble volumes identical to ours in the Universe.^[28] This follows directly from the cosmological principle, wherein it is assumed our Hubble volume is not special or unique.

Level II: Universes with different physical constants

"Bubble universes": every disk is a bubble universe (Universe 1 to Universe 6 are different bubbles; they have physical constants that are different from our universe); our universe is just one of the bubbles.

In the chaotic inflation theory, a variant of the cosmic inflation theory, the multiverse as a whole is stretching and will continue doing so forever,^[29] but some regions of space stop stretching and form distinct bubbles, like gas pockets in a loaf of rising bread. Such bubbles are embryonic level I multiverses. Linde and Vanchurin calculated the number of these universes to be on the scale of 10^1010,000,000.^[30]

Different bubbles may experience different spontaneous symmetry breaking resulting in different properties such as different physical constants.^[28]

This level also includes John Archibald Wheeler's oscillatory universe theory and Lee Smolin's fecund universes theory.

Level III: Many-worlds interpretation of quantum mechanics

Hugh Everett's many-worlds interpretation (MWI) is one of several mainstream interpretations of quantum mechanics. In brief, one aspect of quantum mechanics is that certain observations cannot be predicted absolutely.
Instead, there is a range of possible observations, each with a different probability. According to the MWI, each of these possible observations corresponds to a different universe. Suppose a six-sided die is thrown and that the result of the throw corresponds to a quantum mechanics observable. All six possible ways the die can fall correspond to six different universes.

Tegmark argues that a level III multiverse does not contain more possibilities in the Hubble volume than a level I-II multiverse. In effect, all the different "worlds" created by "splits" in a level III multiverse with the same physical constants can be found in some Hubble volume in a level I multiverse. Tegmark writes that "The only difference between Level I and Level III is where your doppelgängers reside. In Level I they live elsewhere in good old three-dimensional space. In Level III they live on another quantum branch in infinite-dimensional Hilbert space." Similarly, all level II bubble universes with different physical constants can in effect be found as "worlds" created by "splits" at the moment of spontaneous symmetry breaking in a level III multiverse.^[28] According to Nomura^[31] and Bousso and Susskind,^[11] this is because global spacetime appearing in the (eternally) inflating multiverse is a redundant concept. This implies that the multiverses of Level I, II, and III are, in fact, the same thing. This hypothesis is referred to as "Multiverse = Quantum Many Worlds".

Related to the many-worlds idea are Richard Feynman's multiple histories interpretation and H. Dieter Zeh's many-minds interpretation.

Level IV: Ultimate ensemble

The ultimate ensemble or mathematical universe hypothesis is the hypothesis of Tegmark himself.^[32] This level considers equally real all universes that can be described by different mathematical structures. Tegmark writes that "abstract mathematics is so general that any Theory Of Everything (TOE) that is definable in purely formal terms (independent of vague human terminology) is also a mathematical structure. For instance, a TOE involving a set of different types of entities (denoted by words, say) and relations between them (denoted by additional words) is nothing but what mathematicians call a set-theoretical model, and one can generally find a formal system that it is a model of." He argues this "implies that any conceivable parallel universe theory can be described at Level IV" and "subsumes all other ensembles, therefore brings closure to the hierarchy of multiverses, and there cannot be say a Level V."^[6]

Jürgen Schmidhuber, however, says the "set of mathematical structures" is not even well-defined, and admits only universe representations describable by constructive mathematics, that is, computer programs. He explicitly includes universe representations describable by non-halting programs whose output bits converge after finite time, although the convergence time itself may not be predictable by a halting program, due to Kurt Gödel's limitations.^[33][34][35] He also explicitly discusses the more restricted ensemble of quickly computable universes.^[36]

Brian Greene's nine types

American theoretical physicist and string theorist Brian Greene discussed nine types of parallel universes:^[37]

Quilted

The quilted multiverse works only in an infinite universe. With an infinite amount of space, every possible event will occur an infinite number of times. However, the speed of light prevents us from being aware of these other identical areas.

Inflationary

The inflationary multiverse is composed of various pockets where inflation fields collapse and form new universes.

Brane

The brane multiverse follows from M-theory and states that our universe is a 3-dimensional brane that exists with many others on a higher-dimensional brane or "bulk". Particles are bound to their respective branes except for gravity.

Cyclic

The cyclic multiverse (via the ekpyrotic scenario) has multiple branes (each a universe) that collided, causing Big Bangs. The universes bounce back and pass through time, until they are pulled back together and again collide, destroying the old contents and creating them anew.

Landscape

The landscape multiverse relies on string theory's Calabi–Yau shapes. Quantum fluctuations drop the shapes to a lower energy level, creating a pocket with a different set of laws from the surrounding space.

Quantum

The quantum multiverse creates a new universe when a diversion in events occurs, as in the many-worlds interpretation of quantum mechanics.

Holographic

The holographic multiverse is derived from the theory that the surface area of a space can simulate the volume of the region.

Simulated

The simulated multiverse exists on complex computer systems that simulate entire universes.

Ultimate

The ultimate multiverse contains every mathematically possible universe under different laws of physics.

Cyclic theories

In several theories there is a series of infinite, self-sustaining cycles (for example: an eternity of Big Bang-Big crunches).

M-theory

A multiverse of a somewhat different kind has been envisaged within string theory and its higher-dimensional extension, M-theory.^[38] These theories require the presence of 10 or 11 spacetime dimensions respectively. The extra 6 or 7 dimensions may either be compactified on a very small scale, or our universe may simply be localized on a dynamical (3+1)-dimensional object, a D-brane. This opens up the possibility that there are other branes which could support "other universes".^[39][40] This is unlike the universes in the "quantum multiverse", but both concepts can operate at the same time.^{[citation needed]}
Some scenarios postulate that our big bang was created, along with our universe, by the collision of two branes.^[39][40]

Black-hole cosmology

A black-hole cosmology is a cosmological model in which the observable universe is the interior of a black hole existing as one of possibly many inside a larger universe. This includes the theory of white holes of which are on the opposite side of space time. While a black hole sucks everything in including light, a white hole releases matter and light, hence the name "white hole".

Anthropic principle

The concept of other universes has been proposed to explain how our own universe appears to be fine-tuned for conscious life as we experience it. If there were a large (possibly infinite) number of universes, each with possibly different physical laws (or different fundamental physical constants), some of these universes, even if very few, would have the combination of laws and fundamental parameters that are suitable for the development of matter, astronomical structures, elemental diversity, stars, and planets that can exist long enough for life to emerge and evolve. The weak anthropic principle could then be applied to conclude that we (as conscious beings) would only exist in one of those few universes that happened to be finely tuned, permitting the existence of life with developed consciousness. Thus, while the probability might be extremely small that any particular universe would have the requisite conditions for life (as we understand life) to emerge and evolve, this does not require intelligent design as an explanation for the conditions in the Universe that promote our existence in it.

Search for evidence

Around 2010, scientists such as Stephen M. Feeney analyzed Wilkinson Microwave Anisotropy Probe (WMAP) data and claimed to find preliminary evidence suggesting that our universe collided with other (parallel) universes in the distant past.^{[41][unreliable source?][42][43][44]} However, a more thorough analysis of data from the WMAP and from the Planck satellite, which has a resolution 3 times higher than WMAP, failed to find any statistically significant evidence of such a bubble universe collision.^[45][46] In addition, there is no evidence of any gravitational pull of other universes on ours.^[47][48]

Criticism

Non-scientific claims

In his 2003 NY Times opinion piece, A Brief History of the Multiverse, author and cosmologist, Paul Davies, offers a variety of arguments that multiverse theories are non-scientific :^[49]

For a start, how is the existence of the other universes to be tested? To be sure, all cosmologists accept that there are some regions of the universe that lie beyond the reach of our telescopes, but somewhere on the slippery slope between that and the idea that there are an infinite number of universes, credibility reaches a limit. As one slips down that slope, more and more must be accepted on faith, and less and less is open to scientific verification. Extreme multiverse explanations are therefore reminiscent of theological discussions. Indeed, invoking an infinity of unseen universes to explain the unusual features of the one we do see is just as ad hoc as invoking an unseen Creator. The multiverse theory may be dressed up in scientific language, but in essence it requires the same leap of faith.

— Paul Davies, A Brief History of the Multiverse

Taking cosmic inflation as a popular case in point, George Ellis, writing in August 2011, provides a balanced criticism of not only the science, but as he suggests, the scientific philosophy, by which multiverse theories are generally substantiated. He, like most cosmologists, accepts Tegmark's level I "domains", even though they lie far beyond the cosmological horizon. Likewise, the multiverse of cosmic inflation is said to exist very far away. It would be so far away, however, that it's very unlikely any evidence of an early interaction will be found. He argues that for many theorists, the lack of empirical testability or falsifiability is not a major concern. "Many physicists who talk about the multiverse, especially advocates of the string landscape, do not care much about parallel universes per se. For them, objections to the multiverse as a concept are unimportant. Their theories live or die based on internal consistency and, one hopes, eventual laboratory testing." Although he believes there's little hope that will ever be possible, he grants that the theories on which the speculation is based, are not without scientific merit. He concludes that multiverse theory is a "productive research program":^[50]

As skeptical as I am, I think the contemplation of the multiverse is an excellent opportunity to reflect on the nature of science and on the ultimate nature of existence: why we are here… In looking at this concept, we need an open mind, though not too open. It is a delicate path to tread. Parallel universes may or may not exist; the case is unproved. We are going to have to live with that uncertainty. Nothing is wrong with scientifically based philosophical speculation, which is what multiverse proposals are. But we should name it for what it is.

— George Ellis, Scientific American, Does the Multiverse Really Exist?

Occam's razor

Proponents and critics disagree about how to apply Occam's razor. Critics argue that to postulate a practically infinite number of unobservable universes just to explain our own seems contrary to Occam's razor.^[51] In contrast, proponents argue that, in terms of Kolmogorov complexity, the proposed multiverse is simpler than a single idiosyncratic universe.^[28]

For example, multiverse proponent Max Tegmark argues:

[A]n entire ensemble is often much simpler than one of its members. This principle can be stated more formally using the notion of algorithmic information content. The algorithmic information content in a number is, roughly speaking, the length of the shortest computer program that will produce that number as output. For example, consider the set of all integers. Which is simpler, the whole set or just one number? Naively, you might think that a single number is simpler, but the entire set can be generated by quite a trivial computer program, whereas a single number can be hugely long. Therefore, the whole set is actually simpler... (Similarly), the higher-level multiverses are simpler. Going from our universe to the Level I multiverse eliminates the need to specify initial conditions, upgrading to Level II eliminates the need to specify physical constants, and the Level IV multiverse eliminates the need to specify anything at all.... A common feature of all four multiverse levels is that the simplest and arguably most elegant theory involves parallel universes by default. To deny the existence of those universes, one needs to complicate the theory by adding experimentally unsupported processes and ad hoc postulates: finite space, wave function collapse and ontological asymmetry. Our judgment therefore comes down to which we find more wasteful and inelegant: many worlds or many words. Perhaps we will gradually get used to the weird ways of our cosmos and find its strangeness to be part of its charm.^[28]

— Max Tegmark, "Parallel universes. Not just a staple of science fiction, other universes are a direct implication of cosmological observations." Scientific American 2003 May;288(5):40–51

Princeton cosmologist Paul Steinhardt used the 2014 Annual Edge Question to voice his opposition to multiverse theorizing:

A pervasive idea in fundamental physics and cosmology that should be retired: the notion that we live in a multiverse in which the laws of physics and the properties of the cosmos vary randomly from one patch of space to another. According to this view, the laws and properties within our observable universe cannot be explained or predicted because they are set by chance. Different regions of space too distant to ever be observed have different laws and properties, according to this picture. Over the entire multiverse, there are infinitely many distinct patches. Among these patches, in the words of Alan Guth, "anything that can happen will happen—and it will happen infinitely many times". Hence, I refer to this concept as a Theory of Anything. Any observation or combination of observations is consistent with a Theory of Anything. No observation or combination of observations can disprove it. Proponents seem to revel in the fact that the Theory cannot be falsified. The rest of the scientific community should be up in arms since an unfalsifiable idea lies beyond the bounds of normal science. Yet, except for a few voices, there has been surprising complacency and, in some cases, grudging acceptance of a Theory of Anything as a logical possibility. The scientific journals are full of papers treating the Theory of Anything seriously. What is going on?^[20]

— Paul Steinhardt, "Theories of Anything" edge.com'

Steinhardt claims that multiverse theories have gained currency mostly because too much has been invested in theories that have failed, e.g. inflation or string theory. He tends to see in them an attempt to redefine the values of science to which he objects even more strongly:

A Theory of Anything is useless because it does not rule out any possibility and worthless because it submits to no do-or-die tests. (Many papers discuss potential observable consequences, but these are only possibilities, not certainties, so the Theory is never really put at risk.)^[20]

— Paul Steinhardt, "Theories of Anything" edge.com'

Multiverse hypotheses in philosophy and logic

Modal realism

Possible worlds are a way of explaining probability, hypothetical statements and the like, and some philosophers such as David Lewis believe that all possible worlds exist, and are just as real as the actual world (a position known as modal realism).^[52]

Trans-world identity

A metaphysical issue that crops up in multiverse schema that posit infinite identical copies of any given universe is that of the notion that there can be identical objects in different possible worlds. According to the counterpart theory of David Lewis, the objects should be regarded as similar rather than identical.^[53][54]

Fictional realism

The view that because fictions exist, fictional characters exist as well. There are fictional entities, in the same sense in which, setting aside philosophical disputes, there are people, Mondays, numbers and planets.^[55][56]

Telescope

From Wikipedia, the free encyclopedia

The 100 inch (2.54 m) Hooker reflecting telescope at Mount Wilson Observatory near Los Angeles, USA.

A telescope is an instrument that aids in the observation of remote objects by collecting electromagnetic radiation (such as visible light). The first known practical telescopes were invented in the Netherlands at the beginning of the 17th century, using glass lenses. They found use in terrestrial applications and astronomy.

Within a few decades, the reflecting telescope was invented, which used mirrors. In the 20th century many new types of telescopes were invented, including radio telescopes in the 1930s and infrared telescopes in the 1960s. The word telescope now refers to a wide range of instruments detecting different regions of the electromagnetic spectrum, and in some cases other types of detectors.

The word "telescope" (from the Greek τῆλε, tele "far" and σκοπεῖν, skopein "to look or see"; τηλεσκόπος, teleskopos "far-seeing") was coined in 1611 by the Greek mathematician Giovanni Demisiani for one of Galileo Galilei's instruments presented at a banquet at the Accademia dei Lincei.^[1][2][3] In the Starry Messenger, Galileo had used the term "perspicillum".

History

Modern telescopes typically use CCDs instead of film for recording images. This is the sensor array in the Kepler spacecraft.

28-inch telescope and 40-foot telescope in Greenwich in 2015.

The earliest recorded working telescopes were the refracting telescopes that appeared in the Netherlands in 1608. Their development is credited to three individuals: Hans Lippershey and Zacharias Janssen, who were spectacle makers in Middelburg, and Jacob Metius of Alkmaar.^[4] Galileo heard about the Dutch telescope in June 1609, built his own within a month,^[5] and improved upon the design in the following year.

The idea that the objective, or light-gathering element, could be a mirror instead of a lens was being investigated soon after the invention of the refracting telescope.^[6] The potential advantages of using parabolic mirrors—reduction of spherical aberration and no chromatic aberration—led to many proposed designs and several attempts to build reflecting telescopes.^[7] In 1668, Isaac Newton built the first practical reflecting telescope, of a design which now bears his name, the Newtonian reflector.

The invention of the achromatic lens in 1733 partially corrected color aberrations present in the simple lens and enabled the construction of shorter, more functional refracting telescopes. Reflecting telescopes, though not limited by the color problems seen in refractors, were hampered by the use of fast tarnishing speculum metal mirrors employed during the 18th and early 19th century—a problem alleviated by the introduction of silver coated glass mirrors in 1857,^[8] and aluminized mirrors in 1932.^[9] The maximum physical size limit for refracting telescopes is about 1 meter (40 inches), dictating that the vast majority of large optical researching telescopes built since the turn of the 20th century have been reflectors. The largest reflecting telescopes currently have objectives larger than 10 m (33 feet), and work is underway on several 30-40m designs.

The 20th century also saw the development of telescopes that worked in a wide range of wavelengths from radio to gamma-rays. The first purpose built radio telescope went into operation in 1937. Since then, a tremendous variety of complex astronomical instruments have been developed.

Types

The name "telescope" covers a wide range of instruments. Most detect electromagnetic radiation, but there are major differences in how astronomers must go about collecting light (electromagnetic radiation) in different frequency bands.

Telescopes may be classified by the wavelengths of light they detect:

• X-ray telescopes, using shorter wavelengths than ultraviolet light
• Ultraviolet telescopes, using shorter wavelengths than visible light
• Optical telescopes, using visible light
• Infrared telescopes, using longer wavelengths than visible light
• Submillimetre telescopes, using longer wavelengths than infrared light

Light Comparison
Name	Wavelength	Frequency (Hz)	Photon Energy (eV)
Gamma ray	less than 0.01 nm	more than 10 EHZ	100 keV – 300+ GeV	X
X-Ray	0.01 to 10 nm	30 PHz – 30 EHZ	120 eV to 120 keV	X
Ultraviolet	10 nm – 400 nm	30 EHZ – 790 THz	3 eV to 124 eV
Visible	390 nm – 750 nm	790 THz – 405 THz	1.7 eV – 3.3 eV	X
Infrared	750 nm – 1 mm	405 THz – 300 GHz	1.24 meV – 1.7 eV	X
Microwave	1 mm – 1 meter	300 GHz – 300 MHz	1.24 meV – 1.24 µeV
Radio	1 mm – km	300 GHz – 3 Hz	1.24 meV – 12.4 feV	X

As wavelengths become longer, it becomes easier to use antenna technology to interact with electromagnetic radiation (although it is possible to make very tiny antenna). The near-infrared can be handled much like visible light, however in the far-infrared and submillimetre range, telescopes can operate more like a radio telescope. For example the James Clerk Maxwell Telescope observes from wavelengths from 3 μm (0.003 mm) to 2000 μm (2 mm), but uses a parabolic aluminum antenna.^[10]

On the other hand, the Spitzer Space Telescope, observing from about 3 μm (0.003 mm) to 180 μm (0.18 mm) uses a mirror (reflecting optics). Also using reflecting optics, the Hubble Space Telescope with Wide Field Camera 3 can observe from about 0.2 μm (0.0002 mm) to 1.7 μm (0.0017 mm) (from ultra-violet to infrared light).^[11]

• Fresnel Imager, an optical lens technology
• X-ray optics, optics for certain X-ray wavelengths

Another threshold in telescope design, as photon energy increases (shorter wavelengths and higher frequency) is the use of fully reflecting optics rather than glancing-incident optics. Telescopes such as TRACE and SOHO use special mirrors to reflect Extreme ultraviolet, producing higher resolution and brighter images than otherwise possible. A larger aperture does not just mean that more light is collected, it also enables a finer angular resolution.

Telescopes may also be classified by location: ground telescope, space telescope, or flying telescope. They may also be classified by whether they are operated by professional astronomers or amateur astronomers. A vehicle or permanent campus containing one or more telescopes or other instruments is called an observatory.

Optical telescopes

50 cm refracting telescope at Nice Observatory.

An optical telescope gathers and focuses light mainly from the visible part of the electromagnetic spectrum (although some work in the infrared and ultraviolet).^[12] Optical telescopes increase the apparent angular size of distant objects as well as their apparent brightness. In order for the image to be observed, photographed, studied, and sent to a computer, telescopes work by employing one or more curved optical elements, usually made from glass lenses and/or mirrors, to gather light and other electromagnetic radiation to bring that light or radiation to a focal point. Optical telescopes are used for astronomy and in many non-astronomical instruments, including: theodolites (including transits), spotting scopes, monoculars, binoculars, camera lenses, and spyglasses. There are three main optical types:

• The refracting telescope which uses lenses to form an image.
• The reflecting telescope which uses an arrangement of mirrors to form an image.
• The catadioptric telescope which uses mirrors combined with lenses to form an image.

Beyond these basic optical types there are many sub-types of varying optical design classified by the task they perform such as astrographs, comet seekers, solar telescope, etc.

Radio telescopes

The Very Large Array at Socorro, New Mexico, United States.

Radio telescopes are directional radio antennas used for radio astronomy. The dishes are sometimes constructed of a conductive wire mesh whose openings are smaller than the wavelength being observed. Multi-element Radio telescopes are constructed from pairs or larger groups of these dishes to synthesize large 'virtual' apertures that are similar in size to the separation between the telescopes; this process is known as aperture synthesis. As of 2005, the current record array size is many times the width of the Earth—utilizing space-based Very Long Baseline Interferometry (VLBI) telescopes such as the Japanese HALCA (Highly Advanced Laboratory for Communications and Astronomy) VSOP (VLBI Space Observatory Program) satellite. Aperture synthesis is now also being applied to optical telescopes using optical interferometers (arrays of optical telescopes) and aperture masking interferometry at single reflecting telescopes. Radio telescopes are also used to collect microwave radiation, which is used to collect radiation when any visible light is obstructed or faint, such as from quasars. Some radio telescopes are used by programs such as SETI and the Arecibo Observatory to search for extraterrestrial life.

X-ray telescopes

Einstein Observatory was a space-based focusing optical X-ray telescope from 1978.^[13]

X-ray telescopes can use X-ray optics, such as a Wolter telescopes composed of ring-shaped 'glancing' mirrors made of heavy metals that are able to reflect the rays just a few degrees. The mirrors are usually a section of a rotated parabola and a hyperbola, or ellipse. In 1952, Hans Wolter outlined 3 ways a telescope could be built using only this kind of mirror.^[14][15] Examples of an observatory using this type of telescope are the Einstein Observatory, ROSAT, and the Chandra X-Ray Observatory. By 2010, Wolter focusing X-ray telescopes are possible up to 79 keV.^[13]

Gamma-ray telescopes

Higher energy X-ray and Gamma-ray telescopes refrain from focusing completely and use coded aperture masks: the patterns of the shadow the mask creates can be reconstructed to form an image.

X-ray and Gamma-ray telescopes are usually on Earth-orbiting satellites or high-flying balloons since the Earth's atmosphere is opaque to this part of the electromagnetic spectrum. However, high energy X-rays and gamma-rays do not form an image in the same way as telescopes at visible wavelengths. An example of this type of telescope is the Fermi Gamma-ray Space Telescope.

The detection of very high energy gamma rays, with shorter wavelength and higher frequency than regular gamma rays, requires further specialization. An example of this type of observatory is VERITAS. Very high energy gamma-rays are still photons, like visible light, whereas cosmic rays includes particles like electrons, protons, and heavier nuclei.

A discovery in 2012 may allow focusing gamma-ray telescopes.^[16] At photon energies greater than 700 keV, the index of refraction starts to increase again.^[16]

High-energy particle telescopes

High-energy astronomy requires specialized telescopes to make observations since most of these particles go through most metals and glasses.

In other types of high energy particle telescopes there is no image-forming optical system. Cosmic-ray telescopes usually consist of an array of different detector types spread out over a large area. A Neutrino telescope consists of a large mass of water or ice, surrounded by an array of sensitive light detectors known as photomultiplier tubes. Energetic neutral atom observatories like Interstellar Boundary Explorer detect particles traveling at certain energies.

Other types of telescopes

Equatorial-mounted Keplerian telescope

Astronomy is not limited to using electromagnetic radiation. Additional information can be obtained using other media. The detectors used to observe the Universe are analogous to telescopes, these are:

• Gravitational-wave detector, the equivalent of a gravitational wave telescope, used for gravitational-wave astronomy.
• Neutrino detector, the equivalent of a neutrino telescope, used for neutrino astronomy.

Types of mount

A telescope mount is a mechanical structure which supports a telescope. Telescope mounts are designed to support the mass of the telescope and allow for accurate pointing of the instrument. Many sorts of mounts have been developed over the years, with the majority of effort being put into systems that can track the motion of the stars as the Earth rotates. The two main types of tracking mount are:

• Altazimuth mount
• Equatorial mount

Atmospheric electromagnetic opacity

Since the atmosphere is opaque for most of the electromagnetic spectrum, only a few bands can be observed from the Earth's surface. These bands are visible – near-infrared and a portion of the radio-wave part of the spectrum. For this reason there are no X-ray or far-infrared ground-based telescopes as these have to be flown in space to observe. 

Even if a wavelength is observable from the ground, it might still be advantageous to fly it on a satellite due to astronomical seeing.

A diagram of the electromagnetic spectrum with the Earth's atmospheric transmittance (or opacity) and the types of telescopes used to image parts of the spectrum.

Telescopic image from different telescope types

Different types of telescope, operating in different wavelength bands, provide different information about the same object. Together they provide a more comprehensive understanding.

A 6′ wide view of the Crab nebula supernova remnant, viewed at different wavelengths of light by various telescopes

By spectrum

Telescopes that operate in the electromagnetic spectrum:

Name	Telescope	Astronomy	Wavelength
Radio	Radio telescope	Radio astronomy (Radar astronomy)	more than 1 mm
Submillimetre	Submillimetre telescopes*	Submillimetre astronomy	0.1 mm – 1 mm
Far Infrared	–	Far-infrared astronomy	30 µm – 450 µm
Infrared	Infrared telescope	Infrared astronomy	700 nm – 1 mm
Visible	Visible spectrum telescopes	Visible-light astronomy	400 nm – 700 nm
Ultraviolet	Ultraviolet telescopes*	Ultraviolet astronomy	10 nm – 400 nm
X-ray	X-ray telescope	X-ray astronomy	0.01 nm – 10 nm
Gamma-ray	–	Gamma-ray astronomy	less than 0.01 nm

*Links to categories.

Lists of telescopes

• List of optical telescopes
• List of largest optical reflecting telescopes
• List of largest optical refracting telescopes
• List of largest optical telescopes historically
• List of radio telescopes
• List of solar telescopes
• List of space observatories
• List of telescope parts and construction
• List of telescope types
• Category:Telescopes
• Category:Cosmic-ray telescopes
• Category:Gamma-ray telescopes
• Category:Gravitational wave telescopes
• Category:High energy particle telescopes
• Category:Infrared telescopes
• Category:Submillimetre telescopes
• Category:Ultraviolet telescopes
• Category:X-ray telescopes