Noble metal

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Noble_metal 

 

---

Periodic table extract showing approximately how often each element tends to recognized as a noble metal:

---

 7  most often (Ru, Rh, Pd, Os, Ir, Pt, Au)  1  often (Ag)  2  sometimes (Cu, Hg)  6  in a limited sense (Tc, Re, As, Sb, Bi, Po)

---

The thick black line encloses the seven to eight metals most often to often so recognized. Silver is sometimes not recognized as a noble metal on account of its greater reactivity.

---

* may be tarnished in moist air or corrode in an acidic solution containing oxygen and an oxidant † attacked by sulfur or hydrogen sulfide
§ self-attacked by radiation-generated ozone

A noble metal is ordinarily regarded as a metallic chemical element that is generally resistant to corrosion and is usually found in nature in its raw form. Gold, platinum, and the other platinum group metals (ruthenium, rhodium, palladium, osmium, iridium) are most often so classified. Silver, copper and mercury are less often to sometimes included as noble metals although each of these usually occurs in nature combined with sulfur.

In more specialized fields of study and applications the number of elements counted as noble metals can be smaller or larger. In physics, there are only three noble metals: copper, silver and gold. In dentistry, silver is not always counted as a noble metal since it is subject to corrosion when present in the mouth. In chemistry, the term noble metal is sometimes applied more broadly to any metallic or semimetallic element that does not react with a weak acid and give off hydrogen gas in the process. This broader set includes copper, mercury, technetium, rhenium, arsenic, antimony, bismuth and polonium, as well as gold, the six platinum group metals, and silver.

Meaning and history

While noble metal lists can differ, they tend to cluster around the six platinum group metals (ruthenium, rhodium, palladium, osmium, iridium, platinum) plus gold.

In addition to this term's function as a compound noun, there are circumstances where noble is used as an adjective for the noun metal. A galvanic series is a hierarchy of metals (or other electrically conductive materials, including composites and semimetals) that runs from noble to active, and allows one to predict how materials will interact in the environment used to generate the series. In this sense of the word, graphite is more noble than silver and the relative nobility of many materials is highly dependent upon context, as for aluminium and stainless steel in conditions of varying pH.

The term noble metal can be traced back to at least the late 14th century and has slightly different meanings in different fields of study and application.

Prior to Mendeleev's publication in 1869 of the first (eventually) widely accepted periodic table, Odling published a table in 1864, in which the "noble metals" rhodium, ruthenium, palladium; and platinum, iridium, and osmium were grouped together, and adjacent to silver and gold.

• 

  Chalcopyrite, which is copper iron sulfide (CuFeS₂), is the most abundant copper ore mineral
• 

  One half of a ruthenium bar. Size ~ 40 × 15 × 10 mm. Weight ~44 g

• 

  Rhodium: 1 g powder, 1g pressed cylinder, 1 g pellet.
• 

  Palladium
• 

  Acanthite, or silver sulfide (Ag₂S), is the most important silver ore
• 

  Osmium crystals, 2.2 g
• 

  Pieces of pure iridium, 1 g, size: 1–3 mm each
• 

  Crystals of pure platinum
• 

  Gold nugget from Australia, nearly 9,000 g or 64 oz
• 

  Cinnabar or mercury sulfide (HgS) is the most common source ore for refining elemental mercury

Properties

Abundance of the chemical elements in the Earth's crust as a function of atomic number. The rarest elements (shown in yellow, including the noble metals) are not the heaviest, but are rather the siderophile (iron-loving) elements in the Goldschmidt classification of elements. These have been depleted by being relocated deeper into the Earth's core. Their abundance in meteoroid materials is relatively higher. Tellurium and selenium have been depleted from the crust due to formation of volatile hydrides.

Geochemical

The noble metals are siderophiles (iron-lovers). They tend to sink into the Earth's core because they dissolve readily in iron either as solid solutions or in the molten state. Most siderophile elements have practically no affinity whatsoever for oxygen: indeed, oxides of gold are thermodynamically unstable with respect to the elements.

Copper, silver, gold, and the six platinum group metals are the only native metals that occur naturally in relatively large amounts.^{[citation needed]}

Corrosion resistance

Copper is dissolved by nitric acid and aqueous potassium cyanide.

Ruthenium can be dissolved in aqua regia, a highly concentrated mixture of hydrochloric acid and nitric acid, only when in the presence of oxygen, while rhodium must be in a fine pulverized form. Palladium and silver are soluble in nitric acid, with the solubility of silver being limited by the formation of silver chloride precipitate.

Rhenium reacts with oxidizing acids, and hydrogen peroxide, and is said to be tarnished by moist air. Osmium and iridium are chemically inert in ambient conditions. Platinum and gold can be dissolved in aqua regia. Mercury reacts with oxidising acids.

In 2010, US researchers discovered that an organic "aqua regia" in the form of a mixture of thionyl chloride SOCl₂ and the organic solvent pyridine C₅H₅N achieved "high dissolution rates of noble metals under mild conditions, with the added benefit of being tunable to a specific metal" for example, gold but not palladium or platinum.

Electronic

In physics, the expression "noble metal" is sometimes confined to copper, silver, and gold, since their full d-subshells contribute to what noble character they have. In contrast, the other noble metals, especially the platinum group metals, have notable catalytic applications, arising from their partially filled d-subshells. This is the case with palladium which has a full d-subshell in the atomic state but in condensed form has a partially filled sp band at the expense of d-band occupancy.

The difference in reactivity can be seen during the preparation of clean metal surfaces in an ultra-high vacuum: surfaces of "physically defined" noble metals (e.g., gold) are easy to clean and keep clean for a long time, while those of platinum or palladium, for example, are covered by carbon monoxide very quickly.

Electrochemical

Standard reduction potentials in aqueous solution are also a useful way of predicting the non-aqueous chemistry of the metals involved. Thus, metals with high negative potentials, such as sodium, or potassium, will ignite in air, forming the respective oxides. These fires cannot be extinguished with water, which also react with the metals involved to give hydrogen, which is itself explosive. Noble metals, in contrast, are disinclined to react with oxygen and, for that reason (as well as their scarcity) have been valued for millennia, and used in jewellery and coins.

Electrochemical properties of some metals and metalloids

Element	Z	G	P	Reaction	SRP(V)	EN	EA
Gold ✣	79	11	6	Au3+ + 3 e− → Au	1.5	2.54	223
Platinum ✣	78	10	6	Pt2+ + 2 e− → Pt	1.2	2.28	205
Iridium ✣	77	9	6	Ir3+ + 3 e− → Ir	1.16	2.2	151
Palladium ✣	46	10	5	Pd2+ + 2 e− → Pd	0.915	2.2	54
Osmium ✣	76	8	6	OsO 2 + 4 H+ + 4 e− → Os + 2 H 2O	0.85	2.2	104
Mercury	80	12	6	Hg2+ + 2 e− → Hg	0.85	2.0	−50
Rhodium ✣	45	9	5	Rh3+ + 3 e− → Rh	0.8	2.28	110
Silver ✣	47	11	5	Ag+ + e− → Ag	0.7993	1.93	126
Ruthenium ✣	44	8	5	Ru3+ + 3 e− → Ru	0.6	2.2	101
Polonium ☢	84	16	6	Po2+ + 2 e− → Po	0.6	2.0	136
Water				2 H 2O + 4 e− +O 2 → 4 OH−	0.4
Copper	29	11	4	Cu2+ + 2 e− → Cu	0.339	2.0	119
Bismuth	83	15	6	Bi3+ + 3 e− → Bi	0.308	2.02	91
Technetium ☢	43	7	6	TcO 2 + 4 H+ + 4 e− → Tc + 2 H 2O	0.28	1.9	53
Rhenium	75	7	6	ReO 2 + 4 H+ + 4 e− → Re + 2 H 2O	0.251	1.9	6
ArsenicMD	33	15	4	As 4O 6 + 12 H+ + 12 e− → 4 As + 6 H 2O	0.24	2.18	78
AntimonyMD	51	15	5	Sb 2O 3 + 6 H+ + 6 e− → 2 Sb + 3 H 2O	0.147	2.05	101
Z atomic number; G group; P period; SRP standard reduction potential; EN electronegativity; EA electron affinity
✣ traditionally recognized as a noble metal; MD metalloid; ☢ radioactive

The adjacent table lists standard reduction potential in volts; electronegativity (revised Pauling); and electron affinity values (kJ/mol), for some metals and metalloids.

The simplified entries in the reaction column can be read in detail from the Pourbaix diagrams of the considered element in water. Noble metals have large positive potentials; elements not in this table have a negative standard potential or are not metals.

Electronegativity is included since it is reckoned to be, "a major driver of metal nobleness and reactivity".

On account of their high electron affinity values, the incorporation of a noble metal in the electrochemical photolysis process, such as platinum and gold, among others, can increase photoactivity.

Arsenic and antimony are usually considered to be metalloids rather than noble metals. However, physically speaking their most stable allotropes are metallic. Semiconductors, such as selenium and tellurium, have been excluded.

The black tarnish commonly seen on silver arises from its sensitivity to hydrogen sulfide: 2Ag + H₂S + 1/2O₂ → Ag₂S + H₂O. Rayner-Canham contends that, "silver is so much more chemically-reactive and has such a different chemistry, that it should not be considered as a 'noble metal'." In dentistry, silver is not regarded as a noble metal due to its tendency to corrode in the oral environment.

The relevance of the entry for water is addressed by Li et al. in the context of galvanic corrosion. Such a process will only occur when:

"(1) two metals which have different electrochemical potentials are...connected, (2) an aqueous phase with electrolyte exists, and (3) one of the two metals has...potential lower than the potential of the reaction (H
₂O + 4e +O
₂ = 4 OH^•) which is 0.4 V...The...metal with...a potential less than 0.4 V acts as an anode...loses electrons...and dissolves in the aqueous medium. The noble metal (with higher electrochemical potential) acts as a cathode and, under many conditions, the reaction on this electrode is generally H
₂O − 4 e^• − O
₂ = 4 OH^•)."

The superheavy elements from hassium (element 108) to livermorium (116) inclusive are expected to be "partially very noble metals"; chemical investigations of hassium has established that it behaves like its lighter congener osmium, and preliminary investigations of nihonium and flerovium have suggested but not definitively established noble behavior. Copernicium's behaviour seems to partly resemble both its lighter congener mercury and the noble gas radon.

Oxides

Oxide melting points, °C

Element	I	II	III	IV	VI	VII
Copper		1326
Ruthenium				d1300 d75+
Rhodium			d1100 ?
Palladium		d750
Silver	d200
Rhenium						327
Osmium				d500
Iridium				d1100 ?
Platinum				450 d100
Gold			d150
Mercury		d500
Strontium‡		2430
Molybdenum‡					801 d70
AntimonyMD			655
Lanthanum‡			2320
Bismuth‡			817
d = decomposes; if there are two figures, the 2nd is for the hydrated form; ‡ = not a noble metal; MD = metalloid

As long ago as 1890, Hiorns observed as follows:

"Noble Metals. Gold, Platinum, Silver, and a few rare metals. The members of this class have little or no tendency to unite with oxygen in the free state, and when placed in water at a red heat do not alter its composition. The oxides are readily decomposed by heat in consequence of the feeble affinity between the metal and oxygen."

Smith, writing in 1946, continued the theme:

"There is no sharp dividing line [between 'noble metals' and 'base metals'] but perhaps the best definition of a noble metal is a metal whose oxide is easily decomposed at a temperature below a red heat."

"It follows from this that noble metals...have little attraction for oxygen and are consequently not oxidised or discoloured at moderate temperatures."

Such nobility is mainly associated with the relatively high electronegativity values of the noble metals, resulting in only weakly polar covalent bonding with oxygen. The table lists the melting points of the oxides of the noble metals, and for some of those of the non-noble metals, for the elements in their most stable oxidation states.

Catalytic properties

Many of the noble metals can act as catalysts. For example, platinum is used in catalytic converters, devices which convert toxic gases produced in car engines, such as the oxides of nitrogen, into non-polluting substances.

Gold has many industrial applications; it is used as a catalyst in hydrogenation and the water gas shift reaction.

Bus (computing)

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Bus_(computing) 

Four PCI Express bus card slots (from top to 2nd bottom: ×4, ×16, ×1 and ×16), compared to a 32-bit conventional PCI bus card slot (very bottom)

In computer architecture, a bus (shortened form of the Latin omnibus, and historically also called data highway or databus) is a communication system that transfers data between components inside a computer, or between computers. This expression covers all related hardware components (wire, optical fiber, etc.) and software, including communication protocols.

Early computer buses were parallel electrical wires with multiple hardware connections, but the term is now used for any physical arrangement that provides the same logical function as a parallel electrical busbar. Modern computer buses can use both parallel and bit serial connections, and can be wired in either a multidrop (electrical parallel) or daisy chain topology, or connected by switched hubs, as in the case of Universal Serial Bus (USB).

Background and nomenclature

Computer systems generally consist of three main parts:

• The central processing unit (CPU) that processes data,
• The memory that holds the programs and data to be processed, and
• I/O (input/output) devices as peripherals that communicate with the outside world.

An early computer might contain a hand-wired CPU of vacuum tubes, a magnetic drum for main memory, and a punch tape and printer for reading and writing data respectively. A modern system might have a multi-core CPU, DDR4 SDRAM for memory, a solid-state drive for secondary storage, a graphics card and LCD as a display system, a mouse and keyboard for interaction, and a Wi-Fi connection for networking. In both examples, computer buses of one form or another move data between all of these devices.

In most traditional computer architectures, the CPU and main memory tend to be tightly coupled. A microprocessor conventionally is a single chip which has a number of electrical connections on its pins that can be used to select an "address" in the main memory and another set of pins to read and write the data stored at that location. In most cases, the CPU and memory share signalling characteristics and operate in synchrony. The bus connecting the CPU and memory is one of the defining characteristics of the system, and often referred to simply as the system bus.

It is possible to allow peripherals to communicate with memory in the same fashion, attaching adaptors in the form of expansion cards directly to the system bus. This is commonly accomplished through some sort of standardized electrical connector, several of these forming the expansion bus or local bus. However, as the performance differences between the CPU and peripherals varies widely, some solution is generally needed to ensure that peripherals do not slow overall system performance. Many CPUs feature a second set of pins similar to those for communicating with memory, but able to operate at very different speeds and using different protocols. Others use smart controllers to place the data directly in memory, a concept known as direct memory access. Most modern systems combine both solutions, where appropriate.

As the number of potential peripherals grew, using an expansion card for every peripheral became increasingly untenable. This has led to the introduction of bus systems designed specifically to support multiple peripherals. Common examples are the SATA ports in modern computers, which allow a number of hard drives to be connected without the need for a card. However, these high-performance systems are generally too expensive to implement in low-end devices, like a mouse. This has led to the parallel development of a number of low-performance bus systems for these solutions, the most common example being the standardized Universal Serial Bus (USB). All such examples may be referred to as peripheral buses, although this terminology is not universal.

In modern systems the performance difference between the CPU and main memory has grown so great that increasing amounts of high-speed memory is built directly into the CPU, known as a cache. In such systems, CPUs communicate using high-performance buses that operate at speeds much greater than memory, and communicate with memory using protocols similar to those used solely for peripherals in the past. These system buses are also used to communicate with most (or all) other peripherals, through adaptors, which in turn talk to other peripherals and controllers. Such systems are architecturally more similar to multicomputers, communicating over a bus rather than a network. In these cases, expansion buses are entirely separate and no longer share any architecture with their host CPU (and may in fact support many different CPUs, as is the case with PCI). What would have formerly been a system bus is now often known as a front-side bus.

Given these changes, the classical terms "system", "expansion" and "peripheral" no longer have the same connotations. Other common categorization systems are based on the bus's primary role, connecting devices internally or externally, PCI vs. SCSI for instance. However, many common modern bus systems can be used for both; SATA and the associated eSATA are one example of a system that would formerly be described as internal, while certain automotive applications use the primarily external IEEE 1394 in a fashion more similar to a system bus. Other examples, like InfiniBand and I²C were designed from the start to be used both internally and externally.

Internal buses

The internal bus, also known as internal data bus, memory bus, system bus or front-side bus, connects all the internal components of a computer, such as CPU and memory, to the motherboard. Internal data buses are also referred to as local buses, because they are intended to connect to local devices. This bus is typically rather quick and is independent of the rest of the computer operations.

External buses

The external bus, or expansion bus, is made up of the electronic pathways that connect the different external devices, such as printer etc., to the computer.

Address bus

An address bus is a bus that is used to specify a physical address. When a processor or DMA-enabled device needs to read or write to a memory location, it specifies that memory location on the address bus (the value to be read or written is sent on the data bus). The width of the address bus determines the amount of memory a system can address. For example, a system with a 32-bit address bus can address 2³² (4,294,967,296) memory locations. If each memory location holds one byte, the addressable memory space is 4 GiB.

Address multiplexing

Early processors used a wire for each bit of the address width. For example, a 16-bit address bus had 16 physical wires making up the bus. As the buses became wider and lengthier, this approach became expensive in terms of the number of chip pins and board traces. Beginning with the Mostek 4096 DRAM, address multiplexing implemented with multiplexers became common. In a multiplexed address scheme, the address is sent in two equal parts on alternate bus cycles. This halves the number of address bus signals required to connect to the memory. For example, a 32-bit address bus can be implemented by using 16 lines and sending the first half of the memory address, immediately followed by the second half memory address.

Typically two additional pins in the control bus -- a row-address strobe (RAS) and the column-address strobe (CAS) -- are used to tell the DRAM whether the address bus is currently sending the first half of the memory address or the second half.

Implementation

Accessing an individual byte frequently requires reading or writing the full bus width (a word) at once. In these instances the least significant bits of the address bus may not even be implemented - it is instead the responsibility of the controlling device to isolate the individual byte required from the complete word transmitted. This is the case, for instance, with the VESA Local Bus which lacks the two least significant bits, limiting this bus to aligned 32-bit transfers.

Historically, there were also some examples of computers which were only able to address words -- word machines.

Memory bus

The memory bus is the bus which connects the main memory to the memory controller in computer systems. Originally, general-purpose buses like VMEbus and the S-100 bus were used, but to reduce latency, modern memory buses are designed to connect directly to DRAM chips, and thus are designed by chip standards bodies such as JEDEC. Examples are the various generations of SDRAM, and serial point-to-point buses like SLDRAM and RDRAM. An exception is the Fully Buffered DIMM which, despite being carefully designed to minimize the effect, has been criticized for its higher latency.

Implementation details

Buses can be parallel buses, which carry data words in parallel on multiple wires, or serial buses, which carry data in bit-serial form. The addition of extra power and control connections, differential drivers, and data connections in each direction usually means that most serial buses have more conductors than the minimum of one used in 1-Wire and UNI/O. As data rates increase, the problems of timing skew, power consumption, electromagnetic interference and crosstalk across parallel buses become more and more difficult to circumvent. One partial solution to this problem has been to double pump the bus. Often, a serial bus can be operated at higher overall data rates than a parallel bus, despite having fewer electrical connections, because a serial bus inherently has no timing skew or crosstalk. USB, FireWire, and Serial ATA are examples of this. Multidrop connections do not work well for fast serial buses, so most modern serial buses use daisy-chain or hub designs.

Network connections such as Ethernet are not generally regarded as buses, although the difference is largely conceptual rather than practical. An attribute generally used to characterize a bus is that power is provided by the bus for the connected hardware. This emphasizes the busbar origins of bus architecture as supplying switched or distributed power. This excludes, as buses, schemes such as serial RS-232, parallel Centronics, IEEE 1284 interfaces and Ethernet, since these devices also needed separate power supplies. Universal Serial Bus devices may use the bus supplied power, but often use a separate power source. This distinction is exemplified by a telephone system with a connected modem, where the RJ11 connection and associated modulated signalling scheme is not considered a bus, and is analogous to an Ethernet connection. A phone line connection scheme is not considered to be a bus with respect to signals, but the Central Office uses buses with cross-bar switches for connections between phones.

However, this distinction‍—‌that power is provided by the bus‍—‌is not the case in many avionic systems, where data connections such as ARINC 429, ARINC 629, MIL-STD-1553B (STANAG 3838), and EFABus (STANAG 3910) are commonly referred to as “data buses” or, sometimes, "databuses". Such avionic data buses are usually characterized by having several equipments or Line Replaceable Items/Units (LRI/LRUs) connected to a common, shared media. They may, as with ARINC 429, be simplex, i.e. have a single source LRI/LRU or, as with ARINC 629, MIL-STD-1553B, and STANAG 3910, be duplex, allow all the connected LRI/LRUs to act, at different times (half duplex), as transmitters and receivers of data.

Bus multiplexing

Main article: Bus encoding § Other examples of bus encoding

The simplest system bus has completely separate input data lines, output data lines, and address lines. To reduce cost, most microcomputers have a bidirectional data bus, re-using the same wires for input and output at different times.

Some processors use a dedicated wire for each bit of the address bus, data bus, and the control bus. For example, the 64-pin STEbus is composed of 8 physical wires dedicated to the 8-bit data bus, 20 physical wires dedicated to the 20-bit address bus, 21 physical wires dedicated to the control bus, and 15 physical wires dedicated to various power buses.

Bus multiplexing requires fewer wires, which reduces costs in many early microprocessors and DRAM chips. One common multiplexing scheme, address multiplexing, has already been mentioned. Another multiplexing scheme re-uses the address bus pins as the data bus pins, an approach used by conventional PCI and the 8086. The various "serial buses" can be seen as the ultimate limit of multiplexing, sending each of the address bits and each of the data bits, one at a time, through a single pin (or a single differential pair).

History

Over time, several groups of people worked on various computer bus standards, including the IEEE Bus Architecture Standards Committee (BASC), the IEEE "Superbus" study group, the open microprocessor initiative (OMI), the open microsystems initiative (OMI), the "Gang of Nine" that developed EISA, etc.

First generation

Early computer buses were bundles of wire that attached computer memory and peripherals. Anecdotally termed the "digit trunk", they were named after electrical power buses, or busbars. Almost always, there was one bus for memory, and one or more separate buses for peripherals. These were accessed by separate instructions, with completely different timings and protocols.

One of the first complications was the use of interrupts. Early computer programs performed I/O by waiting in a loop for the peripheral to become ready. This was a waste of time for programs that had other tasks to do. Also, if the program attempted to perform those other tasks, it might take too long for the program to check again, resulting in loss of data. Engineers thus arranged for the peripherals to interrupt the CPU. The interrupts had to be prioritized, because the CPU can only execute code for one peripheral at a time, and some devices are more time-critical than others.

High-end systems introduced the idea of channel controllers, which were essentially small computers dedicated to handling the input and output of a given bus. IBM introduced these on the IBM 709 in 1958, and they became a common feature of their platforms. Other high-performance vendors like Control Data Corporation implemented similar designs. Generally, the channel controllers would do their best to run all of the bus operations internally, moving data when the CPU was known to be busy elsewhere if possible, and only using interrupts when necessary. This greatly reduced CPU load, and provided better overall system performance.

Single system bus

To provide modularity, memory and I/O buses can be combined into a unified system bus. In this case, a single mechanical and electrical system can be used to connect together many of the system components, or in some cases, all of them.

Later computer programs began to share memory common to several CPUs. Access to this memory bus had to be prioritized, as well. The simple way to prioritize interrupts or bus access was with a daisy chain. In this case signals will naturally flow through the bus in physical or logical order, eliminating the need for complex scheduling.

Minis and micros

Digital Equipment Corporation (DEC) further reduced cost for mass-produced minicomputers, and mapped peripherals into the memory bus, so that the input and output devices appeared to be memory locations. This was implemented in the Unibus of the PDP-11 around 1969.

Early microcomputer bus systems were essentially a passive backplane connected directly or through buffer amplifiers to the pins of the CPU. Memory and other devices would be added to the bus using the same address and data pins as the CPU itself used, connected in parallel. Communication was controlled by the CPU, which read and wrote data from the devices as if they are blocks of memory, using the same instructions, all timed by a central clock controlling the speed of the CPU. Still, devices interrupted the CPU by signaling on separate CPU pins.

For instance, a disk drive controller would signal the CPU that new data was ready to be read, at which point the CPU would move the data by reading the "memory location" that corresponded to the disk drive. Almost all early microcomputers were built in this fashion, starting with the S-100 bus in the Altair 8800 computer system.

In some instances, most notably in the IBM PC, although similar physical architecture can be employed, instructions to access peripherals (in and out) and memory (mov and others) have not been made uniform at all, and still generate distinct CPU signals, that could be used to implement a separate I/O bus.

These simple bus systems had a serious drawback when used for general-purpose computers. All the equipment on the bus had to talk at the same speed, as it shared a single clock.

Increasing the speed of the CPU becomes harder, because the speed of all the devices must increase as well. When it is not practical or economical to have all devices as fast as the CPU, the CPU must either enter a wait state, or work at a slower clock frequency temporarily, to talk to other devices in the computer. While acceptable in embedded systems, this problem was not tolerated for long in general-purpose, user-expandable computers.

Such bus systems are also difficult to configure when constructed from common off-the-shelf equipment. Typically each added expansion card requires many jumpers in order to set memory addresses, I/O addresses, interrupt priorities, and interrupt numbers.

Second generation

"Second generation" bus systems like NuBus addressed some of these problems. They typically separated the computer into two "worlds", the CPU and memory on one side, and the various devices on the other. A bus controller accepted data from the CPU side to be moved to the peripherals side, thus shifting the communications protocol burden from the CPU itself. This allowed the CPU and memory side to evolve separately from the device bus, or just "bus". Devices on the bus could talk to each other with no CPU intervention. This led to much better "real world" performance, but also required the cards to be much more complex. These buses also often addressed speed issues by being "bigger" in terms of the size of the data path, moving from 8-bit parallel buses in the first generation, to 16 or 32-bit in the second, as well as adding software setup (now standardised as Plug-n-play) to supplant or replace the jumpers.

However, these newer systems shared one quality with their earlier cousins, in that everyone on the bus had to talk at the same speed. While the CPU was now isolated and could increase speed, CPUs and memory continued to increase in speed much faster than the buses they talked to. The result was that the bus speeds were now very much slower than what a modern system needed, and the machines were left starved for data. A particularly common example of this problem was that video cards quickly outran even the newer bus systems like PCI, and computers began to include AGP just to drive the video card. By 2004 AGP was outgrown again by high-end video cards and other peripherals and has been replaced by the new PCI Express bus.

An increasing number of external devices started employing their own bus systems as well. When disk drives were first introduced, they would be added to the machine with a card plugged into the bus, which is why computers have so many slots on the bus. But through the 1980s and 1990s, new systems like SCSI and IDE were introduced to serve this need, leaving most slots in modern systems empty. Today there are likely to be about five different buses in the typical machine, supporting various devices.

Third generation

See also: Bus network

"Third generation" buses have been emerging into the market since about 2001, including HyperTransport and InfiniBand. They also tend to be very flexible in terms of their physical connections, allowing them to be used both as internal buses, as well as connecting different machines together. This can lead to complex problems when trying to service different requests, so much of the work on these systems concerns software design, as opposed to the hardware itself. In general, these third generation buses tend to look more like a network than the original concept of a bus, with a higher protocol overhead needed than early systems, while also allowing multiple devices to use the bus at once.

Buses such as Wishbone have been developed by the open source hardware movement in an attempt to further remove legal and patent constraints from computer design.

The Compute Express Link (CXL) is an open standard interconnect for high-speed CPU-to-device and CPU-to-memory, designed to accelerate next-generation data center performance.

Examples of internal computer buses

Parallel

• Asus Media Bus proprietary, used on some Asus Socket 7 motherboards
• Computer Automated Measurement and Control (CAMAC) for instrumentation systems
• Extended ISA or EISA
• Industry Standard Architecture or ISA
• Low Pin Count or LPC
• MBus
• MicroChannel or MCA
• Multibus for industrial systems
• NuBus or IEEE 1196
• OPTi local bus used on early Intel 80486 motherboards.
• Conventional PCI
• Parallel ATA (also known as Advanced Technology Attachment, ATA, PATA, IDE, EIDE, ATAPI, etc.), Hard disk drive, optical disk drive, tape drive peripheral attachment bus
• S-100 bus or IEEE 696, used in the Altair 8800 and similar microcomputers
• SBus or IEEE 1496
• SS-50 Bus
• Runway bus, a proprietary front side CPU bus developed by Hewlett-Packard for use by its PA-RISC microprocessor family
• GSC/HSC, a proprietary peripheral bus developed by Hewlett-Packard for use by its PA-RISC microprocessor family
• Precision Bus, a proprietary bus developed by Hewlett-Packard for use by its HP3000 computer family
• STEbus
• STD Bus (for STD-80 [8-bit] and STD32 [16-/32-bit]), FAQ Archived 2012-02-27 at the Wayback Machine
• Unibus, a proprietary bus developed by Digital Equipment Corporation for their PDP-11 and early VAX computers.
• Q-Bus, a proprietary bus developed by Digital Equipment Corporation for their PDP and later VAX computers.
• VESA Local Bus or VLB or VL-bus
• VMEbus, the VERSAmodule Eurocard bus
• PC/104
• PC/104-Plus
• PCI-104
• PCI/104-Express
• PCI/104
• Zorro II and Zorro III, used in Amiga computer systems

Serial

• 1-Wire
• HyperTransport
• I²C
• I3C (bus)
• SLIMbus
• PCI Express or PCIe
• Serial ATA (SATA), Hard disk drive, solid state drive, optical disc drive, tape drive peripheral attachment bus
• Serial Peripheral Interface (SPI) bus
• UNI/O
• SMBus

Examples of external computer buses

Parallel

• HIPPI High Performance Parallel Interface
• IEEE-488 (also known as GPIB, General-Purpose Interface Bus, and HPIB, Hewlett-Packard Instrumentation Bus)
• PC Card, previously known as PCMCIA, much used in laptop computers and other portables, but fading with the introduction of USB and built-in network and modem connections

Serial

• Camera Link
• CAN bus ("Controller Area Network")
• eSATA
• ExpressCard
• Fieldbus
• IEEE 1394 interface (FireWire)
• RS-232
• RS-485
• Thunderbolt
• USB

Examples of internal/external computer buses

• Futurebus
• InfiniBand
• PCI Express External Cabling
• QuickRing
• Scalable Coherent Interface (SCI)
• Small Computer System Interface (SCSI), Hard disk drive and tape drive peripheral attachment bus
• Serial Attached SCSI (SAS) and other serial SCSI buses
• Thunderbolt
• Yapbus, a proprietary bus developed for the Pixar Image Computer

Metamaterial cloaking

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Metamaterial_cloaking 

Metamaterial cloaking is the usage of metamaterials in an invisibility cloak. This is accomplished by manipulating the paths traversed by light through a novel optical material. Metamaterials direct and control the propagation and transmission of specified parts of the light spectrum and demonstrate the potential to render an object seemingly invisible. Metamaterial cloaking, based on transformation optics, describes the process of shielding something from view by controlling electromagnetic radiation. Objects in the defined location are still present, but incident waves are guided around them without being affected by the object itself.

Electromagnetic metamaterials

Main articles: Metamaterials and Split-ring resonator

Electromagnetic metamaterials respond to chosen parts of radiated light, also known as the electromagnetic spectrum, in a manner that is difficult or impossible to achieve with natural materials. In other words, these metamaterials can be further defined as artificially structured composite materials, which exhibit interaction with light usually not available in nature (electromagnetic interactions). At the same time, metamaterials have the potential to be engineered and constructed with desirable properties that fit a specific need. That need will be determined by the particular application.

The artificial structure for cloaking applications is a lattice design – a sequentially repeating network – of identical elements. Additionally, for microwave frequencies, these materials are analogous to crystals for optics. Also, a metamaterial is composed of a sequence of elements and spacings, which are much smaller than the selected wavelength of light. The selected wavelength could be radio frequency, microwave, or other radiations, now just beginning to reach into the visible frequencies. Macroscopic properties can be directly controlled by adjusting characteristics of the rudimentary elements, and their arrangement on, or throughout the material. Moreover, these metamaterials are a basis for building very small cloaking devices in anticipation of larger devices, adaptable to a broad spectrum of radiated light.

Hence, although light consists of an electric field and a magnetic field, ordinary optical materials, such as optical microscope lenses, have a strong reaction only to the electric field. The corresponding magnetic interaction is essentially nil. This results in only the most common optical effects, such as ordinary refraction with common diffraction limitations in lenses and imaging.

Since the beginning of optical sciences, centuries ago, the ability to control the light with materials has been limited to these common optical effects. Metamaterials, on the other hand, are capable of a very strong interaction, or coupling, with the magnetic component of light. Therefore, the range of response to radiated light is expanded beyond the ordinary optical limitations that are described by the sciences of physical optics and optical physics. In addition, as artificially constructed materials, both the magnetic and electric components of the radiated light can be controlled at will, in any desired fashion as it travels, or more accurately propagates, through the material. This is because a metamaterial's behavior is typically formed from individual components, and each component responds independently to a radiated spectrum of light. At this time, however, metamaterials are limited. Cloaking across a broad spectrum of frequencies has not been achieved, including the visible spectrum. Dissipation, absorption, and dispersion are also current drawbacks, but this field is still in its optimistic infancy.

Metamaterials and transformation optics

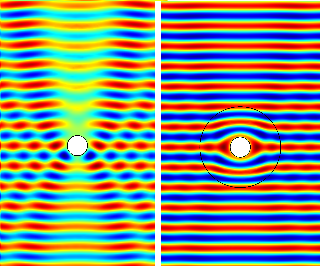
Left:The cross section of a PEC cylinder subject to a plane wave (only the electric field component of the wave is shown). The field is scattered. Right: a circular cloak, designed using transformation optics methods, is used to cloak the cylinder. In this case the field remains unchanged outside the cloak and the cylinder is invisible electromagnetically. Note the special distortion pattern of the field inside the cloak.

Main article: transformation optics

The field of transformation optics is founded on the effects produced by metamaterials.

Transformation optics has its beginnings in the conclusions of two research endeavors. They were published on May 25, 2006, in the same issue of Science, a peer reviewed journal. The two papers are tenable theories on bending or distorting light to electromagnetically conceal an object. Both papers notably map the initial configuration of the electromagnetic fields on to a Cartesian mesh. Twisting the Cartesian mesh, in essence, transforms the coordinates of the electromagnetic fields, which in turn conceal a given object. Hence, with these two papers, transformation optics is born.

Transformation optics subscribes to the capability of bending light, or electromagnetic waves and energy, in any preferred or desired fashion, for a desired application. Maxwell's equations do not vary even though coordinates transform. Instead it is the values of the chosen parameters of the materials which "transform", or alter, during a certain time period. So, transformation optics developed from the capability to choose the parameters for a given material. Hence, since Maxwell's equations retain the same form, it is the successive values of the parameters, permittivity and permeability, which change over time. Furthermore, permittivity and permeability are in a sense responses to the electric and magnetic fields of a radiated light source respectively, among other descriptions. The precise degree of electric and magnetic response can be controlled in a metamaterial, point by point. Since so much control can be maintained over the responses of the material, this leads to an enhanced and highly flexible gradient-index material. Conventionally predetermined refractive index of ordinary materials instead become independent spatial gradients in a metamaterial, which can be controlled at will. Therefore, transformation optics is a new method for creating novel and unique optical devices.

Science of cloaking devices

The purpose of a cloaking device is to hide something, so that a defined region of space is invisibly isolated from passing electromagnetic fields (or sound waves), as with Metamaterial cloaking.

Cloaking objects, or making them appear invisible with metamaterials, is roughly analogous to a magician's sleight of hand, or his tricks with mirrors. The object or subject doesn't really disappear; the vanishing is an illusion. With the same goal, researchers employ metamaterials to create directed blind spots by deflecting certain parts of the light spectrum (electromagnetic spectrum). It is the light spectrum, as the transmission medium, that determines what the human eye can see.

In other words, light is refracted or reflected determining the view, color, or illusion that is seen. The visible extent of light is seen in a chromatic spectrum such as the rainbow. However, visible light is only part of a broad spectrum, which extends beyond the sense of sight. For example, there are other parts of the light spectrum which are in common use today. The microwave spectrum is employed by radar, cell phones, and wireless Internet. The infrared spectrum is used for thermal imaging technologies, which can detect a warm body amidst a cooler night time environment, and infrared illumination is combined with specialized digital cameras for night vision. Astronomers employ the terahertz band for submillimeter observations to answer deep cosmological questions.

Furthermore, electromagnetic energy is light energy, but only a small part of it is visible light. This energy travels in waves. Shorter wavelengths, such as visible light and infrared, carry more energy per photon than longer waves, such as microwaves and radio waves. For the sciences, the light spectrum is known as the electromagnetic spectrum.

The properties of optics and light

Prisms, mirrors, and lenses have a long history of altering the diffracted visible light that surrounds all. However, the control exhibited by these ordinary materials is limited. Moreover, the one material which is common among these three types of directors of light is conventional glass. Hence, these familiar technologies are constrained by the fundamental, physical laws of optics. With metamaterials in general, and the cloaking technology in particular, it appears these barriers disintegrate with advancements in materials and technologies never before realized in the natural physical sciences. These unique materials became notable because electromagnetic radiation can be bent, reflected, or skewed in new ways. The radiated light could even be slowed or captured before transmission. In other words, new ways to focus and project light and other radiation are being developed. Furthermore, the expanded optical powers presented in the science of cloaking objects appear to be technologically beneficial across a wide spectrum of devices already in use. This means that every device with basic functions that rely on interaction with the radiated electromagnetic spectrum could technologically advance. With these beginning steps a whole new class of optics has been established.

Interest in the properties of optics and light

Interest in the properties of optics, and light, date back to almost 2000 years to Ptolemy (AD 85 – 165). In his work entitled Optics, he writes about the properties of light, including reflection, refraction, and color. He developed a simplified equation for refraction without trigonometric functions. About 800 years later, in AD 984, Ibn Sahl discovered a law of refraction mathematically equivalent to Snell's law. He was followed by the most notable Islamic scientist, Ibn Al-Haytham (c.965–1039), who is considered to be "one of the few most outstanding figures in optics in all times." He made significant advances in the science of physics in general, and optics in particular. He anticipated the universal laws of light articulated by seventeenth century scientists by hundreds of years.

In the seventeenth century both Willebrord Snellius and Descartes were credited with discovering the law of refraction. It was Snellius who noted that Ptolemy's equation for refraction was inexact. Consequently, these laws have been passed along, unchanged for about 400 years, like the laws of gravity.

Perfect cloak and theory

Electromagnetic radiation and matter have a symbiotic relationship. Radiation does not simply act on a material, nor is it simply acted upon by a given material. Radiation interacts with matter. Cloaking applications which employ metamaterials alter how objects interact with the electromagnetic spectrum. The guiding vision for the metamaterial cloak is a device that directs the flow of light smoothly around an object, like water flowing past a rock in a stream, without reflection, rendering the object invisible. In reality, the simple cloaking devices of the present are imperfect, and have limitations. One challenge up to the present date has been the inability of metamaterials, and cloaking devices, to interact at frequencies, or wavelengths, within the visible light spectrum.

Challenges presented by the first cloaking device

The principle of cloaking, with a cloaking device, was first proved (demonstrated) at frequencies in the microwave radiation band on October 19, 2006. This demonstration used a small cloaking device. Its height was less than one half inch (< 13 mm) and its diameter five inches (125 mm), and it successfully diverted microwaves around itself. The object to be hidden from view, a small cylinder, was placed in the center of the device. The invisibility cloak deflected microwave beams so they flowed around the cylinder inside with only minor distortion, making it appear almost as if nothing were there at all.

Such a device typically involves surrounding the object to be cloaked with a shell which affects the passage of light near it. There was reduced reflection of electromagnetic waves (microwaves), from the object. Unlike a homogeneous natural material with its material properties the same everywhere, the cloak's material properties vary from point to point, with each point designed for specific electromagnetic interactions (inhomogeneity), and are different in different directions (anisotropy). This accomplishes a gradient in the material properties. The associated report was published in the journal Science.

Although a successful demonstration, three notable limitations can be shown. First, since its effectiveness was only in the microwave spectrum the small object is somewhat invisible only at microwave frequencies. This means invisibility had not been achieved for the human eye, which sees only within the visible spectrum. This is because the wavelengths of the visible spectrum are tangibly shorter than microwaves. However, this was considered the first step toward a cloaking device for visible light, although more advanced nanotechnology-related techniques would be needed due to light's short wavelengths. Second, only small objects can be made to appear as the surrounding air. In the case of the 2006 proof of cloaking demonstration, the hidden from view object, a copper cylinder, would have to be less than five inches in diameter, and less than one half inch tall. Third, cloaking can only occur over a narrow frequency band, for any given demonstration. This means that a broad band cloak, which works across the electromagnetic spectrum, from radio frequencies to microwave to the visible spectrum, and to x-ray, is not available at this time. This is due to the dispersive nature of present-day metamaterials. The coordinate transformation (transformation optics) requires extraordinary material parameters that are only approachable through the use of resonant elements, which are inherently narrow band, and dispersive at resonance.

Usage of metamaterials

At the very beginning of the new millennium, metamaterials were established as an extraordinary new medium, which expanded control capabilities over matter. Hence, metamaterials are applied to cloaking applications for a few reasons. First, the parameter known as material response has broader range. Second, the material response can be controlled at will.

Third, optical components, such as lenses, respond within a certain defined range to light. As stated earlier – the range of response has been known, and studied, going back to Ptolemy – eighteen hundred years ago. The range of response could not be effectively exceeded, because natural materials proved incapable of doing so. In scientific studies and research, one way to communicate the range of response is the refractive index of a given optical material. Every natural material so far only allows for a positive refractive index. Metamaterials, on the other hand, are an innovation that are able to achieve negative refractive index, zero refractive index, and fractional values in between zero and one. Hence, metamaterials extend the material response, among other capabilities. However, negative refraction is not the effect that creates invisibility-cloaking. It is more accurate to say that gradations of refractive index, when combined, create invisibility-cloaking. Fourth, and finally, metamaterials demonstrate the capability to deliver chosen responses at will.

Device

Before actually building the device, theoretical studies were conducted. The following is one of two studies accepted simultaneously by a scientific journal, as well being distinguished as one of the first published theoretical works for an invisibility cloak.

Controlling electromagnetic fields

Orthogonal coordinates — Cartesian plane as it transforms from rectangular to curvilinear coordinates

The exploitation of "light", the electromagnetic spectrum, is accomplished with common objects and materials which control and direct the electromagnetic fields. For example, a glass lens in a camera is used to produce an image, a metal cage may be used to screen sensitive equipment, and radio antennas are designed to transmit and receive daily FM broadcasts. Homogeneous materials, which manipulate or modulate electromagnetic radiation, such as glass lenses, are limited in the upper limit of refinements to correct for aberrations. Combinations of inhomogeneous lens materials are able to employ gradient refractive indices, but the ranges tend to be limited.

Metamaterials were introduced about a decade ago, and these expand control of parts of the electromagnetic spectrum; from microwave, to terahertz, to infrared. Theoretically, metamaterials, as a transmission medium, will eventually expand control and direction of electromagnetic fields into the visible spectrum. Hence, a design strategy was introduced in 2006, to show that a metamaterial can be engineered with arbitrarily assigned positive or negative values of permittivity and permeability, which can also be independently varied at will. Then direct control of electromagnetic fields becomes possible, which is relevant to novel and unusual lens design, as well as a component of the scientific theory for cloaking of objects from electromagnetic detection.

Each component responds independently to a radiated electromagnetic wave as it travels through the material, resulting in electromagnetic inhomogeneity for each component. Each component has its own response to the external electric and magnetic fields of the radiated source. Since these components are smaller than the radiated wavelength it is understood that a macroscopic view includes an effective value for both permittivity and permeability. These materials obey the laws of physics, but behave differently from normal materials. Metamaterials are artificial materials engineered to provide properties which "may not be readily available in nature". These materials usually gain their properties from structure rather than composition, using the inclusion of small inhomogeneities to enact effective macroscopic behavior.

The structural units of metamaterials can be tailored in shape and size. Their composition, and their form or structure, can be finely adjusted. Inclusions can be designed, and then placed at desired locations in order to vary the function of a given material. As the lattice is constant, the cells are smaller than the radiated light.

The design strategy has at its core inhomogeneous composite metamaterials which direct, at will, conserved quantities of electromagnetism. These quantities are specifically, the electric displacement field D, the magnetic field intensity B, and the Poynting vector S. Theoretically, when regarding the conserved quantities, or fields, the metamaterial exhibits a twofold capability. First, the fields can be concentrated in a given direction. Second, they can be made to avoid or surround objects, returning without perturbation to their original path. These results are consistent with Maxwell's equations and are more than only ray approximation found in geometrical optics. Accordingly, in principle, these effects can encompass all forms of electromagnetic radiation phenomena on all length scales.

The hypothesized design strategy begins with intentionally choosing a configuration of an arbitrary number of embedded sources. These sources become localized responses of permittivity, ε, and magnetic permeability, μ. The sources are embedded in an arbitrarily selected transmission medium with dielectric and magnetic characteristics. As an electromagnetic system the medium can then be schematically represented as a grid.

The first requirement might be to move a uniform electric field through space, but in a definite direction, which avoids an object or obstacle. Next remove and embed the system in an elastic medium that can be warped, twisted, pulled or stretched as desired. The initial condition of the fields is recorded on a Cartesian mesh. As the elastic medium is distorted in one, or combination, of the described possibilities, the same pulling and stretching process is recorded by the Cartesian mesh. The same set of contortions can now be recorded, occurring as coordinate transformation:

a (x,y,z), b (x,y,z), c (x,y,z), d (x,y,z) ....

Hence, the permittivity, ε, and permeability, µ, is proportionally calibrated by a common factor. This implies that less precisely, the same occurs with the refractive index. Renormalized values of permittivity and permeability are applied in the new coordinate system. For the renormalization equations see ref. #.

Application to cloaking devices

Given the above parameters of operation, the system, a metamaterial, can now be shown to be able to conceal an object of arbitrary size. Its function is to manipulate incoming rays, which are about to strike the object. These incoming rays are instead electromagnetically steered around the object by the metamaterial, which then returns them to their original trajectory. As part of the design it can be assumed that no radiation leaves the concealed volume of space, and no radiation can enter the space. As illustrated by the function of the metamaterial, any radiation attempting to penetrate is steered around the space or the object within the space, returning to the initial direction. It appears to any observer that the concealed volume of space is empty, even with an object present there. An arbitrary object may be hidden because it remains untouched by external radiation.

A sphere with radius R₁ is chosen as the object to be hidden. The cloaking region is to be contained within the annulus R₁ < r < R₂. A simple transformation that achieves the desired result can be found by taking all fields in the region r < R₂ and compressing them into the region R₁ < r < R₂. The coordinate transformations do not alter Maxwell's equations. Only the values of ε′ and µ′ change over time.

Cloaking hurdles

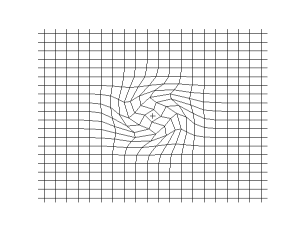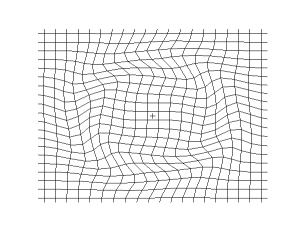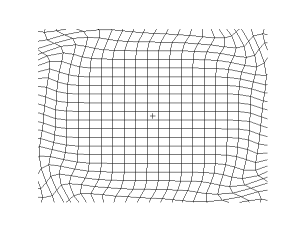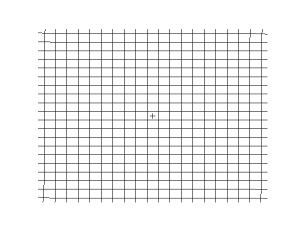
There are issues to be dealt with to achieve invisibility cloaking. One issue, related to ray tracing, is the anisotropic effects of the material on the electromagnetic rays entering the "system". Parallel bundles of rays, (see above image), headed directly for the center are abruptly curved and, along with neighboring rays, are forced into tighter and tighter arcs. This is due to rapid changes in the now shifting and transforming permittivity ε′ and permeability µ′. The second issue is that, while it has been discovered that the selected metamaterials are capable of working within the parameters of the anisotropic effects and the continual shifting of ε′ and µ′, the values for ε′ and µ′ cannot be very large or very small. The third issue is that the selected metamaterials are currently unable to achieve broad, frequency spectrum capabilities. This is because the rays must curve around the "concealed" sphere, and therefore have longer trajectories than traversing free space, or air. However, the rays must arrive around the other side of the sphere in phase with the beginning radiated light. If this is happening then the phase velocity exceeds the velocity of light in a vacuum, which is the speed limit of the universe. (Note, this does not violate the laws of physics). And, with a required absence of frequency dispersion, the group velocity will be identical with phase velocity. In the context of this experiment, group velocity can never exceed the velocity of light, hence the analytical parameters are effective for only one frequency.

Optical conformal mapping and ray tracing in transformation media

The goal then is to create no discernible difference between a concealed volume of space and the propagation of electromagnetic waves through empty space. It would appear that achieving a perfectly concealed (100%) hole, where an object could be placed and hidden from view, is not probable. The problem is the following: in order to carry images, light propagates in a continuous range of directions. The scattering data of electromagnetic waves, after bouncing off an object or hole, is unique compared to light propagating through empty space, and is therefore easily perceived. Light propagating through empty space is consistent only with empty space. This includes microwave frequencies.

Although mathematical reasoning shows that perfect concealment is not probable because of the wave nature of light, this problem does not apply to electromagnetic rays, i.e., the domain of geometrical optics. Imperfections can be made arbitrarily, and exponentially small for objects that are much larger than the wavelength of light.

Mathematically, this implies n < 1, because the rays follow the shortest path and hence in theory create a perfect concealment. In practice, a certain amount of acceptable visibility occurs, as noted above. The range of the refractive index of the dielectric (optical material) needs to be across a wide spectrum to achieve concealment, with the illusion created by wave propagation across empty space. These places where n < 1 would be the shortest path for the ray around the object without phase distortion. Artificial propagation of empty space could be reached in the microwave-to-terahertz range. In stealth technology, impedance matching could result in absorption of beamed electromagnetic waves rather than reflection, hence, evasion of detection by radar. These general principles can also be applied to sound waves, where the index n describes the ratio of the local phase velocity of the wave to the bulk value. Hence, it would be useful to protect a space from any sound sourced detection. This also implies protection from sonar. Furthermore, these general principles are applicable in diverse fields such as electrostatics, fluid mechanics, classical mechanics, and quantum chaos.

Mathematically, it can be shown that the wave propagation is indistinguishable from empty space where light rays propagate along straight lines. The medium performs an optical conformal mapping to empty space.

Microwave frequencies

The next step, then, is to actually conceal an object by controlling electromagnetic fields. Now, the demonstrated and theoretical ability for controlled electromagnetic fields has opened a new field, transformation optics. This nomenclature is derived from coordinate transformations used to create variable pathways for the propagation of light through a material. This demonstration is based on previous theoretical prescriptions, along with the accomplishment of the prism experiment. One possible application of transformation optics and materials is electromagnetic cloaking for the purpose of rendering a volume or object undetectable to incident radiation, including radiated probing.

This demonstration, for the first time, of actually concealing an object with electromagnetic fields, uses the method of purposely designed spatial variation. This is an effect of embedding purposely designed electromagnetic sources in the metamaterial.

As discussed earlier, the fields produced by the metamaterial are compressed into a shell (coordinate transformations) surrounding the now concealed volume. Earlier this was supported theory; this experiment demonstrated the effect actually occurs. Maxwell's equations are scalar when applying transformational coordinates, only the permittivity tensor and permeability tensor are affected, which then become spatially variant, and directionally dependent along different axes. The researchers state:

By implementing these complex material properties, the concealed volume plus the cloak appear to have the properties of free space when viewed externally. The cloak thus neither scatters waves nor imparts a shadow in the either of which would enable the cloak to be detected. Other approaches to invisibility either rely on the reduction of backscatter or make use of a resonance in which the properties of the cloaked object and the must be carefully matched. ...Advances in the development of [negative index metamaterials], especially with respect to gradient index lenses, have made the physical realization of the specified complex material properties feasible. We implemented a two-dimensional (2D) cloak because its fabrication and measurement requirements were simpler than those of a 3D cloak.

Before the actual demonstration, the experimental limits of the transformational fields were computationally determined, in addition to simulations, as both were used to determine the effectiveness of the cloak.

A month prior to this demonstration, the results of an experiment to spatially map the internal and external electromagnetic fields of negative refractive metamaterial was published in September 2006. This was innovative because prior to this the microwave fields were measured only externally. In this September experiment the permittivity and permeability of the microstructures (instead of external macrostructure) of the metamaterial samples were measured, as well as the scattering by the two-dimensional negative index metamaterials. This gave an average effective refractive index, which results in assuming homogeneous metamaterial.

Employing this technique for this experiment, spatial mapping of phases and amplitudes of the microwave radiations interacting with metamaterial samples was conducted. The performance of the cloak was confirmed by comparing the measured field maps to simulations.

For this demonstration, the concealed object was a conducting cylinder at the inner radius of the cloak. As the largest possible object designed for this volume of space, it has the most substantial scattering properties. The conducting cylinder was effectively concealed in two dimensions.

Infrared frequencies

The definition optical frequency, in metamaterials literature, ranges from far infrared, to near infrared, through the visible spectrum, and includes at least a portion of ultra-violet. To date when literature refers optical frequencies these are almost always frequencies in the infrared, which is below the visible spectrum. In 2009 a group of researchers announced cloaking at optical frequencies. In this case the cloaking frequency was centered at 1500 nm or 1.5 micrometers – the infrared.

Sonic frequencies

Main article: Acoustic metamaterials

A laboratory metamaterial device, applicable to ultra-sound waves was demonstrated in January 2011. It can be applied to sound wavelengths corresponding to frequencies from 40 to 80 kHz.

The metamaterial acoustic cloak is designed to hide objects submerged in water. The metamaterial cloaking mechanism bends and twists sound waves by intentional design.

The cloaking mechanism consists of 16 concentric rings in a cylindrical configuration. Each ring has acoustic circuits. It is intentionally designed to guide sound waves in two dimensions.

Each ring has a different index of refraction. This causes sound waves to vary their speed from ring to ring. "The sound waves propagate around the outer ring, guided by the channels in the circuits, which bend the waves to wrap them around the outer layers of the cloak". It forms an array of cavities that slow the speed of the propagating sound waves. An experimental cylinder was submerged and then disappeared from sonar. Other objects of various shape and density were also hidden from the sonar. The acoustic cloak demonstrated effectiveness for frequencies of 40 kHz to 80 kHz.

In 2014 researchers created a 3D acoustic cloak from stacked plastic sheets dotted with repeating patterns of holes. The pyramidal geometry of the stack and the hole placement provide the effect.

Invisibility in diffusive light scattering media

In 2014, scientists demonstrated good cloaking performance in murky water, demonstrating that an object shrouded in fog can disappear completely when appropriately coated with metamaterial. This is due to the random scattering of light, such as that which occurs in clouds, fog, milk, frosted glass, etc., combined with the properties of the metatmaterial coating. When light is diffused, a thin coat of metamaterial around an object can make it essentially invisible under a range of lighting conditions.

Cloaking attempts

Broadband ground-plane cloak

If a transformation to quasi-orthogonal coordinates is applied to Maxwell's equations in order to conceal a perturbation on a flat conducting plane rather than a singular point, as in the first demonstration of a transformation optics-based cloak, then an object can be hidden underneath the perturbation. This is sometimes referred to as a "carpet" cloak.

As noted above, the original cloak demonstrated utilized resonant metamaterial elements to meet the effective material constraints. Utilizing a quasi-conformal transformation in this case, rather than the non-conformal original transformation, changed the required material properties. Unlike the original (singular expansion) cloak, the "carpet" cloak required less extreme material values. The quasi-conformal carpet cloak required anisotropic, inhomogeneous materials which only varied in permittivity. Moreover, the permittivity was always positive. This allowed the use of non-resonant metamaterial elements to create the cloak, significantly increasing the bandwidth.

An automated process, guided by a set of algorithms, was used to construct a metamaterial consisting of thousands of elements, each with its own geometry. Developing the algorithm allowed the manufacturing process to be automated, which resulted in fabrication of the metamaterial in nine days. The previous device used in 2006 was rudimentary in comparison, and the manufacturing process required four months in order to create the device. These differences are largely due to the different form of transformation: the original 2006 cloak transformed a singular point, while the ground-plane version transforms a plane, and the transformation in the carpet cloak was quasi-conformal, rather than non-conformal.

Other theories of cloaking

Main article: Theories of cloaking

Other theories of cloaking discuss various science and research based theories for producing an electromagnetic cloak of invisibility. Theories presented employ transformation optics, event cloaking, dipolar scattering cancellation, tunneling light transmittance, sensors and active sources, and acoustic cloaking.

Institutional research

The research in the field of metamaterials has diffused out into the American government science research departments, including the US Naval Air Systems Command, US Air Force, and US Army. Many scientific institutions are involved including:

• California Institute of Technology
• Massachusetts Institute of Technology
• Colorado State University
• Pennsylvania State University
• Duke University
• Harvard University
• Aalto University
• Imperial College London
• Max Planck Society
• MSU Faculty of Physics
• National Institute of Standards and Technology
• Nederlandse Organisatie voor Wetenschappelijk Onderzoek
• University College London
• University of California, Berkeley
• University of California, Irvine
• University of California, Los Angeles
• University of California, San Diego
• University of Colorado
• University of Delaware
• University of Rochester

Funding for research into this technology is provided by the following American agencies:

• Air Force Research Laboratory
• Defense Advanced Research Projects Agency
• Director of Central Intelligence
• National Geospatial-Intelligence Agency
• Naval Air Systems Command
• Office of Naval Research

Through this research, it has been realized that developing a method for controlling electromagnetic fields can be applied to escape detection by radiated probing, or sonar technology, and to improve communications in the microwave range; that this method is relevant to superlens design and to the cloaking of objects within and from electromagnetic fields.

In the news

On October 20, 2006, the day after Duke University achieved enveloping and "disappearing" an object in the microwave range, the story was reported by Associated Press. Media outlets covering the story included USA Today, MSNBC's Countdown With Keith Olbermann: Sight Unseen, The New York Times with Cloaking Copper, Scientists Take Step Toward Invisibility, (London) The Times with Don't Look Now—Visible Gains in the Quest for Invisibility, Christian Science Monitor with Disappear Into Thin Air? Scientists Take Step Toward Invisibility, Australian Broadcasting, Reuters with Invisibility Cloak a Step Closer, and the (Raleigh) News & Observer with 'Invisibility Cloak a Step Closer.

On November 6, 2006, the Duke University research and development team was selected as part of the Scientific American best 50 articles of 2006.

In the month of November 2009, "research into designing and building unique 'metamaterials' has received a £4.9 million funding boost. Metamaterials can be used for invisibility 'cloaking' devices, sensitive security sensors that can detect tiny quantities of dangerous substances, and flat lenses that can be used to image tiny objects much smaller than the wavelength of light."

In November 2010, scientists at the University of St Andrews in Scotland reported the creation of a flexible cloaking material they call "Metaflex", which may bring industrial applications significantly closer.

In 2014, the world 's first 3D acoustic device was built by Duke engineers.