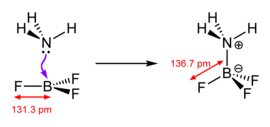Lewis acids and bases

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Lewis_acids_and_bases 

 

Diagram of some Lewis bases and acids

 

Acids and bases

A Lewis acid (named for the American physical chemist Gilbert N. Lewis) is a chemical species that contains an empty orbital which is capable of accepting an electron pair from a Lewis base to form a Lewis adduct. A Lewis base, then, is any species that has a filled orbital containing an electron pair which is not involved in bonding but may form a dative bond with a Lewis acid to form a Lewis adduct. For example, NH₃ is a Lewis base, because it can donate its lone pair of electrons. Trimethylborane (Me₃B) is a Lewis acid as it is capable of accepting a lone pair. In a Lewis adduct, the Lewis acid and base share an electron pair furnished by the Lewis base, forming a dative bond. In the context of a specific chemical reaction between NH₃ and Me₃B, a lone pair from NH₃ will form a dative bond with the empty orbital of Me₃B to form an adduct NH₃•BMe₃. The terminology refers to the contributions of Gilbert N. Lewis.

The terms nucleophile and electrophile are more or less interchangeable with Lewis base and Lewis acid, respectively. However, these terms, especially their abstract noun forms nucleophilicity and electrophilicity, emphasize the kinetic aspect of reactivity, while the Lewis basicity and Lewis acidity emphasize the thermodynamic aspect of Lewis adduct formation.

Depicting adducts

In many cases, the interaction between the Lewis base and Lewis acid in a complex is indicated by an arrow indicating the Lewis base donating electrons toward the Lewis acid using the notation of a dative bond — for example, Me₃B←NH₃. Some sources indicate the Lewis base with a pair of dots (the explicit electrons being donated), which allows consistent representation of the transition from the base itself to the complex with the acid:

Me₃B + :NH₃ → Me₃B:NH₃

A center dot may also be used to represent a Lewis adduct, such as Me₃B·NH₃. Another example is boron trifluoride diethyl etherate, BF₃·Et₂O. In a slightly different usage, the center dot is also used to represent hydrate coordination in various crystals, as in MgSO₄·7H₂O for hydrated magnesium sulfate, irrespective of whether the water forms a dative bond with the metal.

Although there have been attempts to use computational and experimental energetic criteria to distinguish dative bonding from non-dative covalent bonds, for the most part, the distinction merely makes note of the source of the electron pair, and dative bonds, once formed, behave simply as other covalent bonds do, though they typically have considerable polar character. Moreover, in some cases (e.g., sulfoxides and amine oxides as R₂S → O and R₃N → O), the use of the dative bond arrow is just a notational convenience for avoiding the drawing of formal charges. In general, however, the donor–acceptor bond is viewed as simply somewhere along a continuum between idealized covalent bonding and ionic bonding.

Lewis acids

Major structural changes accompany binding of the Lewis base to the coordinatively unsaturated, planar Lewis acid BF₃

Lewis acids are diverse and the term is used loosely. Simplest are those that react directly with the Lewis base, such as boron trihalides and the pentahalides of phosphorus, arsenic, and antimony.

In the same vein, CH₃⁺ can be considered to be the Lewis acid in methylation reactions. However, the methyl cation never occurs as a free species in the condensed phase, and methylation reactions by reagents like CH₃I take place through the simultaneous formation of a bond from the nucleophile to the carbon and cleavage of the bond between carbon and iodine (S_N2 reaction). Textbooks disagree on this point: some asserting that alkyl halides are electrophiles but not Lewis acids, while others describe alkyl halides (e.g. CH₃Br) as a type of Lewis acid. The IUPAC states that Lewis acids and Lewis bases react to form Lewis adducts, and defines electrophile as Lewis acids.

Simple Lewis acids

Some of the most studied examples of such Lewis acids are the boron trihalides and organoboranes:

BF₃ + F⁻ → BF₄⁻

In this adduct, all four fluoride centres (or more accurately, ligands) are equivalent.

BF₃ + OMe₂ → BF₃OMe₂

Both BF₄⁻ and BF₃OMe₂ are Lewis base adducts of boron trifluoride.

Many adducts violate the octet rule, such as the triiodide anion:

I₂ + I⁻ → I₃⁻

The variability of the colors of iodine solutions reflects the variable abilities of the solvent to form adducts with the Lewis acid I₂.

Some Lewis acids binding two Lewis bases, a famous example being the formation of hexafluorosilicate:

SiF₄ + 2 F⁻ → SiF₆²⁻

Complex Lewis acids

Most compounds considered to be Lewis acids require an activation step prior to formation of the adduct with the Lewis base. Complex compounds such as Et₃Al₂Cl₃ and AlCl₃ are treated as trigonal planar Lewis acids but exist as aggregates and polymers that must be degraded by the Lewis base. A simpler case is the formation of adducts of borane. Monomeric BH₃ does not exist appreciably, so the adducts of borane are generated by degradation of diborane:

B₂H₆ + 2 H⁻ → 2 BH₄⁻

In this case, an intermediate B₂H₇⁻ can be isolated.

Many metal complexes serve as Lewis acids, but usually only after dissociating a more weakly bound Lewis base, often water.

[Mg(H₂O)₆]²⁺ + 6 NH₃ → [Mg(NH₃)₆]²⁺ + 6 H₂O

H⁺ as Lewis acid

The proton (H⁺)  is one of the strongest but is also one of the most complicated Lewis acids. It is convention to ignore the fact that a proton is heavily solvated (bound to solvent). With this simplification in mind, acid-base reactions can be viewed as the formation of adducts:

• H⁺ + NH₃ → NH₄⁺
• H⁺ + OH⁻ → H₂O

Applications of Lewis acids

A typical example of a Lewis acid in action is in the Friedel–Crafts alkylation reaction. The key step is the acceptance by AlCl₃ of a chloride ion lone-pair, forming AlCl₄⁻ and creating the strongly acidic, that is, electrophilic, carbonium ion.

RCl +AlCl₃ → R⁺ + AlCl₄⁻

Lewis bases

A Lewis base is an atomic or molecular species where the highest occupied molecular orbital (HOMO) is highly localized. Typical Lewis bases are conventional amines such as ammonia and alkyl amines. Other common Lewis bases include pyridine and its derivatives. Some of the main classes of Lewis bases are

• amines of the formula NH_3−xR_x where R = alkyl or aryl. Related to these are pyridine and its derivatives.
• phosphines of the formula PR_3−xA_x, where R = alkyl, A = aryl.
• compounds of O, S, Se and Te in oxidation state -2, including water, ethers, ketones

The most common Lewis bases are anions. The strength of Lewis basicity correlates with the pK_a of the parent acid: acids with high pK_a's give good Lewis bases. As usual, a weaker acid has a stronger conjugate base.

• Examples of Lewis bases based on the general definition of electron pair donor include:
  • simple anions, such as H⁻ and F⁻
  • other lone-pair-containing species, such as H₂O, NH₃, HO⁻, and CH₃⁻
  • complex anions, such as sulfate
  • electron-rich π-system Lewis bases, such as ethyne, ethene, and benzene

The strength of Lewis bases have been evaluated for various Lewis acids, such as I₂, SbCl₅, and BF₃.

Lewis base	Donor atom	Enthalpy of complexation (kJ/mol)
quinuclidine	N	150
Et3N	N	135
pyridine	N	128
Acetonitrile	N	60
DMA	O	112
DMSO	O	105
THF	O	90.4
Et2O	O	78.8
acetone	O	76.0
EtOAc	O	75.5
Trimethylphosphine	P	97.3
Tetrahydrothiophene	S	51.6

Applications of Lewis bases

Main article: Homogeneous catalysis

Nearly all electron pair donors that form compounds by binding transition elements can be viewed as a collections of the Lewis bases—or ligands. Thus a large application of Lewis bases is to modify the activity and selectivity of metal catalysts. Chiral Lewis bases thus confer chirality on a catalyst, enabling asymmetric catalysis, which is useful for the production of pharmaceuticals.

Many Lewis bases are "multidentate," that is they can form several bonds to the Lewis acid. These multidentate Lewis bases are called chelating agents.

Hard and soft classification

Main article: HSAB theory

Lewis acids and bases are commonly classified according to their hardness or softness. In this context hard implies small and nonpolarizable and soft indicates larger atoms that are more polarizable.

• typical hard acids: H⁺, alkali/alkaline earth metal cations, boranes, Zn²⁺
• typical soft acids: Ag⁺, Mo(0), Ni(0), Pt²⁺
• typical hard bases: ammonia and amines, water, carboxylates, fluoride and chloride
• typical soft bases: organophosphines, thioethers, carbon monoxide, iodide

For example, an amine will displace phosphine from the adduct with the acid BF₃. In the same way, bases could be classified. For example, bases donating a lone pair from an oxygen atom are harder than bases donating through a nitrogen atom. Although the classification was never quantified it proved to be very useful in predicting the strength of adduct formation, using the key concepts that hard acid—hard base and soft acid—soft base interactions are stronger than hard acid—soft base or soft acid—hard base interactions. Later investigation of the thermodynamics of the interaction suggested that hard—hard interactions are enthalpy favored, whereas soft—soft are entropy favored.

Quantifying Lewis acidity

Many methods have been devised to evaluate and predict Lewis acidity. Many are based on spectroscopic signatures such as shifts NMR signals or IR bands e.g. the Gutmann-Beckett method and the Childs method.

The ECW model is a quantitative model that describes and predicts the strength of Lewis acid base interactions, −ΔH. The model assigned E and C parameters to many Lewis acids and bases. Each acid is characterized by an E_A and a C_A. Each base is likewise characterized by its own E_B and C_B. The E and C parameters refer, respectively, to the electrostatic and covalent contributions to the strength of the bonds that the acid and base will form. The equation is

−ΔH = E_AE_B + C_AC_B + W

The W term represents a constant energy contribution for acid–base reaction such as the cleavage of a dimeric acid or base. The equation predicts reversal of acids and base strengths. The graphical presentations of the equation show that there is no single order of Lewis base strengths or Lewis acid strengths, and that single property scales are limited to a smaller range of acids or bases.

History

MO diagram depicting the formation of a dative covalent bond between two atoms

The concept originated with Gilbert N. Lewis who studied chemical bonding. In 1923, Lewis wrote An acid substance is one which can employ an electron lone pair from another molecule in completing the stable group of one of its own atoms. The Brønsted–Lowry acid–base theory was published in the same year. The two theories are distinct but complementary. A Lewis base is also a Brønsted–Lowry base, but a Lewis acid doesn't need to be a Brønsted–Lowry acid. The classification into hard and soft acids and bases (HSAB theory) followed in 1963. The strength of Lewis acid-base interactions, as measured by the standard enthalpy of formation of an adduct can be predicted by the Drago–Wayland two-parameter equation.

Reformulation of Lewis theory

Lewis had suggested in 1916 that two atoms are held together in a chemical bond by sharing a pair of electrons. When each atom contributed one electron to the bond, it was called a covalent bond. When both electrons come from one of the atoms, it was called a dative covalent bond or coordinate bond. The distinction is not very clear-cut. For example, in the formation of an ammonium ion from ammonia and hydrogen the ammonia molecule donates a pair of electrons to the proton; the identity of the electrons is lost in the ammonium ion that is formed. Nevertheless, Lewis suggested that an electron-pair donor be classified as a base and an electron-pair acceptor be classified as acid.

A more modern definition of a Lewis acid is an atomic or molecular species with a localized empty atomic or molecular orbital of low energy. This lowest-energy molecular orbital (LUMO) can accommodate a pair of electrons.

Comparison with Brønsted–Lowry theory

A Lewis base is often a Brønsted–Lowry base as it can donate a pair of electrons to H⁺; the proton is a Lewis acid as it can accept a pair of electrons. The conjugate base of a Brønsted–Lowry acid is also a Lewis base as loss of H⁺ from the acid leaves those electrons which were used for the A—H bond as a lone pair on the conjugate base. However, a Lewis base can be very difficult to protonate, yet still react with a Lewis acid. For example, carbon monoxide is a very weak Brønsted–Lowry base but it forms a strong adduct with BF₃.

In another comparison of Lewis and Brønsted–Lowry acidity by Brown and Kanner, 2,6-di-t-butylpyridine reacts to form the hydrochloride salt with HCl but does not react with BF₃. This example demonstrates that steric factors, in addition to electron configuration factors, play a role in determining the strength of the interaction between the bulky di-t-butylpyridine and tiny proton.

Allotropes of carbon

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Allotropes_of_carbon 

 

Two familiar allotropes of carbon: graphite and diamond.

 

Eight allotropes of carbon: (a) diamond, (b) graphite, (c) lonsdaleite, (d) C₆₀ buckminsterfullerene, (e) C₅₄₀ fullerite (f) C₇₀ fullerene, (g) amorphous carbon, (h) zig-zag single-walled carbon nanotube. Missing: cyclocarbon, carbon nanobuds, schwarzites, glassy carbon, and linear acetylenic carbon (carbyne)

Carbon is capable of forming many allotropes (structurally different forms of the same element) due to its valency. Well-known forms of carbon include diamond and graphite. In recent decades, many more allotropes have been discovered and researched, including ball shapes such as buckminsterfullerene and sheets such as graphene. Larger-scale structures of carbon include nanotubes, nanobuds and nanoribbons. Other unusual forms of carbon exist at very high temperatures or extreme pressures. Around 500 hypothetical 3‑periodic allotropes of carbon are known at the present time, according to the Samara Carbon Allotrope Database (SACADA).

Diamond

Main article: Diamond

Diamond is a well-known allotrope of carbon. The hardness, extremely high refractive index, and high dispersion of light make diamond useful for industrial applications and for jewellery. Diamond is the hardest known natural mineral. This makes it an excellent abrasive and makes it hold polish and luster extremely well. No known naturally occurring substance can cut or scratch diamond, except another diamond. In diamond form, carbon is one of the costliest elements.

The crystal structure of diamond is a face-centred cubic lattice having eight atoms per unit cell to form a diamond cubic structure. Each carbon atom is covalently bonded to four other carbons in a tetrahedral geometry. These tetrahedrons together form a 3-dimensional network of six-membered carbon rings in the chair conformation, allowing for zero bond angle strain. The bonding occurs through sp³ hybridized orbitals to give a C-C bond length of 154 pm. This network of unstrained covalent bonds makes diamond extremely strong. Diamond is thermodynamically less stable than graphite at pressures below 1.7 GPa.

The dominant industrial use of diamond is cutting, drilling (drill bits), grinding (diamond edged cutters), and polishing. Most uses of diamonds in these technologies do not require large diamonds, and most diamonds that are not gem-quality can find an industrial use. Diamonds are embedded in drill tips and saw blades, or ground into a powder for use in grinding and polishing applications (due to its extraordinary hardness). Specialized applications include use in laboratories as containment for high pressure experiments (see diamond anvil), high-performance bearings, and specialized windows of technical apparatuses.

The market for industrial-grade diamonds operates much differently from its gem-grade counterpart. Industrial diamonds are valued mostly for their hardness and heat conductivity, making many of the gemological characteristics of diamond, including clarity and color, mostly irrelevant. This helps explain why 80% of mined diamonds (equal to about 100 million carats or 20 tonnes annually) are unsuitable for use as gemstones and known as bort, are destined for industrial use. In addition to mined diamonds, synthetic diamonds found industrial applications almost immediately after their invention in the 1950s; another 400 million carats (80 tonnes) of synthetic diamonds are produced annually for industrial use, which is nearly four times the mass of natural diamonds mined over the same period.

With the continuing advances being made in the production of synthetic diamond, future applications are beginning to become feasible. Garnering much excitement is the possible use of diamond as a semiconductor suitable to build microchips from, or the use of diamond as a heat sink in electronics. Significant research efforts in Japan, Europe, and the United States are under way to capitalize on the potential offered by diamond's unique material properties, combined with increased quality and quantity of supply starting to become available from synthetic diamond manufacturers.

Graphite

Main article: Graphite

Graphite, named by Abraham Gottlob Werner in 1789, from the Greek γράφειν (graphein, "to draw/write", for its use in pencils) is one of the most common allotropes of carbon. Unlike diamond, graphite is an electrical conductor. Thus, it can be used in, for instance, electrical arc lamp electrodes. Likewise, under standard conditions, graphite is the most stable form of carbon. Therefore, it is used in thermochemistry as the standard state for defining the heat of formation of carbon compounds.

Graphite conducts electricity, due to delocalization of the pi bond electrons above and below the planes of the carbon atoms. These electrons are free to move, so are able to conduct electricity. However, the electricity is only conducted along the plane of the layers. In diamond, all four outer electrons of each carbon atom are 'localized' between the atoms in covalent bonding. The movement of electrons is restricted and diamond does not conduct an electric current. In graphite, each carbon atom uses only 3 of its 4 outer energy level electrons in covalently bonding to three other carbon atoms in a plane. Each carbon atom contributes one electron to a delocalized system of electrons that is also a part of the chemical bonding. The delocalized electrons are free to move throughout the plane. For this reason, graphite conducts electricity along the planes of carbon atoms, but does not conduct electricity in a direction at right angles to the plane.

Graphite powder is used as a dry lubricant. Although it might be thought that this industrially important property is due entirely to the loose interlamellar coupling between sheets in the structure, in fact in a vacuum environment (such as in technologies for use in space), graphite was found to be a very poor lubricant. This fact led to the discovery that graphite's lubricity is due to adsorbed air and water between the layers, unlike other layered dry lubricants such as molybdenum disulfide. Recent studies suggest that an effect called superlubricity can also account for this effect.

When a large number of crystallographic defects (physical) bind these planes together, graphite loses its lubrication properties and becomes pyrolytic carbon, a useful material in blood-contacting implants such as prosthetic heart valves.

Graphite is the most stable allotrope of carbon. Contrary to popular belief, high-purity graphite does not readily burn, even at elevated temperatures. For this reason, it is used in nuclear reactors and for high-temperature crucibles for melting metals. At very high temperatures and pressures (roughly 2000 °C and 5 GPa), it can be transformed into diamond.

Natural and crystalline graphites are not often used in pure form as structural materials due to their shear-planes, brittleness and inconsistent mechanical properties.

In its pure glassy (isotropic) synthetic forms, pyrolytic graphite and carbon fiber graphite are extremely strong, heat-resistant (to 3000 °C) materials, used in reentry shields for missile nosecones, solid rocket engines, high temperature reactors, brake shoes and electric motor brushes.

Intumescent or expandable graphites are used in fire seals, fitted around the perimeter of a fire door. During a fire the graphite intumesces (expands and chars) to resist fire penetration and prevent the spread of fumes. A typical start expansion temperature (SET) is between 150 and 300 °C.

Density: Graphite's specific gravity is 2.3, which makes it lighter than diamond.

Chemical activity: it is slightly more reactive than diamond. This is because the reactants are able to penetrate between the hexagonal layers of carbon atoms in graphite. It is unaffected by ordinary solvents, dilute acids, or fused alkalis. However, chromic acid oxidizes it to carbon dioxide.

Graphene

Main article: Graphene

A single layer of graphite is called graphene and has extraordinary electrical, thermal, and physical properties. It can be produced by epitaxy on an insulating or conducting substrate or by mechanical exfoliation (repeated peeling) from graphite. Its applications may include replacing silicon in high-performance electronic devices. With two layers stacked, bilayer graphene results with different properties.

Lonsdaleite (hexagonal diamond)

Lonsdaleite is an allotrope sometimes called "hexagonal diamond", formed from graphite present in meteorites upon their impact on the earth. The great heat and pressure of the impact transforms the graphite into a denser form similar to diamond, but retaining graphite's hexagonal crystal lattice. "Hexagonal diamond" has also been synthesized in the laboratory, by compressing and heating graphite either in a static press or using explosives. It can also be produced by the thermal decomposition of a polymer, poly(hydridocarbyne), at atmospheric pressure, under inert gas atmosphere (e.g. argon, nitrogen), starting at temperature 110 °C (230 °F).

Graphenylene

Graphenylene is a single layer carbon material with biphenylene-like subunits as basis in its hexagonal lattice structure. It is also known as biphenylene-carbon.

Carbophene

Carbophene is a 2 dimensional covalent organic framework. 4-6 carbophene has been synthesized from 1-3-5 trihydroxybenzene. It consists of 4-carbon and 6-carbon rings in 1:1 ratio. The angles between the three σ-bonds of the orbitals are approximately 120°, 90°, and 150°.

AA'-graphite

AA'-graphite is an allotrope of carbon similar to graphite, but where the layers are positioned differently to each other as compared to the order in graphite.

Diamane

Diamane is a 2D form of diamond. It can be made via high pressures, but without that pressure, the material reverts to graphene. Another technique is to add hydrogen atoms but those bonds are weak. Using fluorine (xenon-difluoride) instead brings the layers closer together, strengthening the bonds. This is called f-diamane.

Amorphous carbon

Main article: Amorphous carbon

Amorphous carbon is the name used for carbon that does not have any crystalline structure. As with all glassy materials, some short-range order can be observed, but there is no long-range pattern of atomic positions. While entirely amorphous carbon can be produced, most amorphous carbon actually contains microscopic crystals of graphite-like, or even diamond-like carbon.

Coal and soot or carbon black are informally called amorphous carbon. However, they are products of pyrolysis (the process of decomposing a substance by the action of heat), which does not produce true amorphous carbon under normal conditions.

Nanocarbons

Buckminsterfullerenes

Main article: Fullerene

The buckminsterfullerenes, or usually just fullerenes or buckyballs for short, were discovered in 1985 by a team of scientists from Rice University and the University of Sussex, three of whom were awarded the 1996 Nobel Prize in Chemistry. They are named for the resemblance to the geodesic structures devised by Richard Buckminster "Bucky" Fuller. Fullerenes are positively curved molecules of varying sizes composed entirely of carbon, which take the form of a hollow sphere, ellipsoid, or tube.

As of the early twenty-first century, the chemical and physical properties of fullerenes are still under heavy study, in both pure and applied research labs. In April 2003, fullerenes were under study for potential medicinal use — binding specific antibiotics to the structure to target resistant bacteria and even target certain cancer cells such as melanoma.

Carbon nanotubes

Main article: Carbon nanotube

Carbon nanotubes, also called buckytubes, are cylindrical carbon molecules with novel properties that make them potentially useful in a wide variety of applications (e.g., nano-electronics, optics, materials applications, etc.). They exhibit extraordinary strength, unique electrical properties, and are efficient conductors of heat. Non-carbon nanotubes have also been synthesized. Carbon nanotubes are a members of the fullerene structural family, which also includes buckyballs. Whereas buckyballs are spherical in shape, a nanotube is cylindrical, with at least one end typically capped with a hemisphere of the buckyball structure. Their name is derived from their size, since the diameter of a nanotube is on the order of a few nanometers (approximately 50,000 times smaller than the width of a human hair), while they can be up to several centimeters in length. There are two main types of nanotubes: single-walled nanotubes (SWNTs) and multi-walled nanotubes (MWNTs).

Carbon nanobuds

Computer models of stable nanobud structures

 

Main article: Carbon nanobud

Carbon nanobuds are a newly discovered allotrope of carbon in which fullerene like "buds" are covalently attached to the outer sidewalls of the carbon nanotubes. This hybrid material has useful properties of both fullerenes and carbon nanotubes. For instance, they have been found to be exceptionally good field emitters.

Schwarzites

Schwarzites are negatively curved carbon surfaces originally proposed by decorating triply periodic minimal surfaces with carbon atoms. The geometric topology of the structure is determined by the presence of ring defects, such as heptagons and octagons, to graphene's hexagonal lattice. (Negative curvature bends surfaces outwards like a saddle rather than bending inwards like a sphere.)

Recent work has proposed zeolite-templated carbons (ZTCs) may be schwarzites. The name, ZTC, derives from their origin inside the pores of zeolites, crystalline silicon dioxide minerals. A vapor of carbon-containing molecules is injected into the zeolite, where the carbon gathers on the pores' walls, creating the negative curve. Dissolving the zeolite leaves the carbon. A team generated structures by decorating the pores of a zeolite with carbon through a Monte Carlo method. Some of the resulting models resemble schwarzite-like structures.

Glassy carbon

A large sample of glassy carbon.

 

Main article: Glassy carbon

Glassy carbon or vitreous carbon is a class of non-graphitizing carbon widely used as an electrode material in electrochemistry, as well as for high-temperature crucibles and as a component of some prosthetic devices.

It was first produced by Bernard Redfern in the mid-1950s at the laboratories of The Carborundum Company, Manchester, UK. He had set out to develop a polymer matrix to mirror a diamond structure and discovered a resole (phenolic) resin that would, with special preparation, set without a catalyst. Using this resin the first glassy carbon was produced.

The preparation of glassy carbon involves subjecting the organic precursors to a series of heat treatments at temperatures up to 3000 °C. Unlike many non-graphitizing carbons, they are impermeable to gases and are chemically extremely inert, especially those prepared at very high temperatures. It has been demonstrated that the rates of oxidation of certain glassy carbons in oxygen, carbon dioxide or water vapor are lower than those of any other carbon. They are also highly resistant to attack by acids. Thus, while normal graphite is reduced to a powder by a mixture of concentrated sulfuric and nitric acids at room temperature, glassy carbon is unaffected by such treatment, even after several months.

Atomic and diatomic carbon

Main articles: Atomic carbon and diatomic carbon

Under certain conditions, carbon can be found in its atomic form. It can be formed by vaporizing graphite, by passing large electric currents to form a carbon arc under very low pressures. It is extremely reactive, but it is an intermediate product used in the creation of carbenes.

Diatomic carbon can also be found under certain conditions. It is often detected via spectroscopy in extraterrestrial bodies, including comets and certain stars.

Carbon nanofoam

Main article: Carbon nanofoam

Carbon nanofoam is the fifth known allotrope of carbon, discovered in 1997 by Andrei V. Rode and co-workers at the Australian National University in Canberra. It consists of a low-density cluster-assembly of carbon atoms strung together in a loose three-dimensional web.

Each cluster is about 6 nanometers wide and consists of about 4000 carbon atoms linked in graphite-like sheets that are given negative curvature by the inclusion of heptagons among the regular hexagonal pattern. This is the opposite of what happens in the case of buckminsterfullerenes, in which carbon sheets are given positive curvature by the inclusion of pentagons.

The large-scale structure of carbon nanofoam is similar to that of an aerogel, but with 1% of the density of previously produced carbon aerogels – only a few times the density of air at sea level. Unlike carbon aerogels, carbon nanofoam is a poor electrical conductor.

Carbide-derived carbon

Main article: Carbide-derived carbon

Carbide-derived carbon (CDC) is a family of carbon materials with different surface geometries and carbon ordering that are produced via selective removal of metals from metal carbide precursors, such as TiC, SiC, Ti₃AlC₂, Mo₂C, etc. This synthesis is accomplished using chlorine treatment, hydrothermal synthesis, or high-temperature selective metal desorption under vacuum. Depending on the synthesis method, carbide precursor, and reaction parameters, multiple carbon allotropes can be achieved, including endohedral particles composed of predominantly amorphous carbon, carbon nanotubes, epitaxial graphene, nanocrystalline diamond, onion-like carbon, and graphitic ribbons, barrels, and horns. These structures exhibit high porosity and specific surface areas, with highly tunable pore diameters, making them promising materials for supercapacitor-based energy storage, water filtration and capacitive desalinization, catalyst support, and cytokine removal.

Linear acetylenic carbon

Main article: Linear acetylenic carbon

A one-dimensional carbon polymer with the structure —(C≡C)_n—.

Cyclocarbons

Main article: Cyclocarbon

Cyclo[18]carbon (C₁₈) was synthesised in 2019.

Other possible allotropes

Many other allotropes have been hypothesized but have yet to be synthesized.

• 

• Crystal structure of the proposed C₈ cubic form of carbon
  bcc-carbon: At ultrahigh pressures of above 1000 GPa, diamond is predicted to transform into a body-centred cubic structure. This phase has importance in astrophysics and deep interiors of planets like Uranus and Neptune. Various structures have been proposed. Superdense and superhard material resembling this phase was synthesized and published in 1979 and reported to have the Im3 space group with eight atoms per primitive unit cell (16 atoms per conventional unit cell). Claims were made that the so-called C₈ structure had been synthesized, having eight-carbon cubes similar to cubane in the Im3m space group, with eight atoms per primitive unit cell, or 16 atoms per conventional unit cell (also called supercubane, see illustration to the right). But a paper in 1988 claimed that a better theory was that the structure was the same as that of an allotrope of silicon called Si-III or γ-silicon, the so-called BC8 structure with space group Ia3 and 8 atoms per primitive unit cell (16 atoms per conventional unit cell). In 2008 it was reported that the cubane-like structure had been identified. A paper in 2012 considered four proposed structures, the supercubane structure, the BC8 structure, a structure with clusters of four carbon atoms in tetrahedra in space group I43m having four atoms per primitive unit cell (eight per conventional unit cell), and a structure the authors called "carbon sodalite". They found in favor of this carbon sodalite structure, with a calculated density of 2.927 g/cm³, shown in the upper left of the illustration under the abstract. This structure has just six atoms per primitive unit cell (twelve per conventional unit cell). The carbon atoms are in the same locations as the silicon and aluminum atoms of the mineral sodalite. The space group, I43m, is the same as the fully expanded form of sodalite would have if sodalite had just silicon or just aluminum.

• bct-carbon: Body-centered tetragonal carbon was proposed by theorists in 2010.
• Chaoite is a mineral believed to have been formed in meteorite impacts. It has been described as slightly harder than graphite with a reflection color of grey to white. However, the existence of carbyne phases is disputed – see the article on chaoite for details.
• D-carbon: D-carbon was proposed by theorists in 2018. D-carbon is an orthorhombic sp³ carbon allotrope (6 atoms per cell). Total-energy calculations demonstrate that D-carbon is energetically more favorable than the previously proposed T₆ structure (with 6 atoms per cell) as well as many others.
• Haeckelites: Ordered arrangements of pentagons, hexagons, and heptagons which can either be flat or tubular.

The K₄ crystal

• The Laves graph or K₄ crystal is a theoretically predicted three-dimensional crystalline metastable carbon structure in which each carbon atom is bonded to three others, at 120° angles (like graphite), but where the bond planes of adjacent layers lie at an angle of 70.5°, rather than coinciding.
• M-carbon: Monoclinic C-centered carbon is thought to have been first created in 1963 by compressing graphite at room temperature. Its structure was theorized in 2006, then in 2009 it was related to those experimental observations. Many structural candidates, including bct-carbon, were proposed to be equally compatible with experimental data available at the time, until in 2012 it was shown theoretically that this structure is kinetically the most likely to form from graphite. High-resolution data appeared shortly after, demonstrating that among all structure candidates only M-carbon is compatible with experiment.
• Metallic carbon: Theoretical studies have shown that there are regions in the phase diagram, at extremely high pressures, where carbon has metallic character. Laser shock experiments and theory indicate that above 600 GPa liquid carbon is metallic.
• Novamene: A combination of both hexagonal diamond and sp² hexagons as in graphene.
• Phagraphene: Graphene-like allotrope with distorted Dirac cones.
• Prismane C₈ is a theoretically predicted metastable carbon allotrope comprising an atomic cluster of eight carbon atoms, with the shape of an elongated triangular bipyramid—a six-atom triangular prism with two more atoms above and below its bases.
• Protomene: A hexagonal crystal structure with a fully relaxed primitive cell involving 48 atoms. Out of these, 12 atoms have the potential to switch hybridization between sp² and sp³, forming dimers.
• Q-carbon: Ferromagnetic carbon was discovered in 2015.
• T-carbon: Every carbon atom in diamond is replaced with a carbon tetrahedron (hence 'T-carbon'). This was proposed by theorists in 1985.
• There is evidence that white dwarf stars have a core of crystallized carbon and oxygen nuclei. The largest of these found in the universe so far, BPM 37093, is located 50 light-years (4.7×10¹⁴ km) away in the constellation Centaurus. A news release from the Harvard-Smithsonian Center for Astrophysics described the 2,500-mile (4,000 km)-wide stellar core as a diamond, and it was named as Lucy, after the Beatles' song "Lucy in the Sky With Diamonds"; however, it is more likely an exotic form of carbon. Penta-graphene is a predicted carbon allotrope that utilizes the Cairo pentagonal tiling.
• U carbon is predicted to consist of corrugated layers tiled with six- or 12-atom rings, linked by covalent bonds. Notably, it can be harder than steel, as conductive as stainless steel, highly reflective and ferromagnetic, behaving as a permanent magnet at temperatures up to 125 °C.

• Zayedene: A combination of linear sp carbon chains and sp3 bulk carbon. The structure of these crystalline carbon allotropes consists of sp chains inserted in cylindrical cavities periodically arranged in hexagonal diamond (lonsdaleite).

Variability of carbon

Diamond and graphite are two allotropes of carbon: pure forms of the same element that differ in structure.

The system of carbon allotropes spans an astounding range of extremes, considering that they are all merely structural formations of the same element.

Between diamond and graphite:

• Diamond crystallizes in the cubic system but graphite crystallizes in the hexagonal system.
• Diamond is clear and transparent, but graphite is black and opaque.
• Diamond is the hardest mineral known (10 on the Mohs scale), but graphite is one of the softest (1–2 on Mohs scale).
• Diamond is the ultimate abrasive, but graphite is soft and is a very good lubricant.
• Diamond is an excellent electrical insulator, but graphite is an excellent conductor.
• Diamond is an excellent thermal conductor, but some forms of graphite are used for thermal insulation (for example heat shields and firebreaks).
• At standard temperature and pressure, graphite is the thermodynamically stable form. Thus diamonds do not exist forever. The conversion from diamond to graphite, however, has a very high activation energy and is therefore extremely slow.

Despite the hardness of diamonds, the chemical bonds that hold the carbon atoms in diamonds together are actually weaker than those that hold together graphite. The difference is that in diamond, the bonds form an inflexible three-dimensional lattice. In graphite, the atoms are tightly bonded into sheets, but the sheets can slide easily over each other, making graphite soft.

Optical properties of carbon nanotubes

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Optical_properties_of_carbon_nanotubes

 

A sample of multiwalled carbon nanotubes with 3–15 walls, mean inner diameter 4 nm, mean outer diameter 13–16 nm, length 1-10+ micrometers.

 

The optical properties of carbon nanotubes are highly relevant for materials science. The way those materials interact with electromagnetic radiation is unique in many respects, as evidenced by their peculiar absorption, photoluminescence (fluorescence), and Raman spectra.

Carbon nanotubes are unique "one-dimensional" materials, whose hollow fibers (tubes) have a unique and highly ordered atomic and electronic structure, and can be made in a wide range of dimension. The diameter typically varies from 0.4 to 40 nm (i.e., a range of ~100 times). However, the length can reach 55.5 cm (21.9 in), implying a length-to-diameter ratio as high as 132,000,000:1; which is unequaled by any other material. Consequently, all the electronic, optical, electrochemical and mechanical properties of the carbon nanotubes are extremely anisotropic (directionally dependent) and tunable.

Applications of carbon nanotubes in optics and photonics are still less developed than in other fields. Some properties that may lead to practical use include tuneability and wavelength selectivity. Potential applications that have been demonstrated include light emitting diodes (LEDs), bolometers and optoelectronic memory.

Apart from direct applications, the optical properties of carbon nanotubes can be very useful in their manufacture and application to other fields. Spectroscopic methods offer the possibility of quick and non-destructive characterization of relatively large amounts of carbon nanotubes, yielding detailed measurements of non-tubular carbon content, tube type and chirality, structural defects, and many other properties that are relevant to those other applications.

Geometric structure

Main article: Carbon nanotube § Structure

Chiral angle

A single-walled carbon nanotubes (SWCNT) can be envisioned as strip of a graphene molecule (a single sheet of graphite) rolled and joined into a seamless cylinder. The structure of the nanotube can be characterized by the width of this hypothetical strip (that is, the circumference c or diameter d of the tube) and the angle α of the strip relative to the main symmetry axes of the hexagonal graphene lattice. This angle, which may vary from 0 to 30 degrees, is called the "chiral angle" of the tube.

The (n,m) notation

A "sliced and unrolled" representation of a carbon nanotube as a strip of a graphene molecule, overlaid on a diagram of the full molecule (faint background). The vector w (large blue arrow) connects corresponding positions on the two edges of the strip. Since w = 3u + 1v, the tube is said to be of type (3,1).

Alternatively, the structure can be described by two integer indices (n,m) that describe the width and direction of that hypothetical strip as coordinates in a fundamental reference frame of the graphene lattice. If the atoms around any 6-member ring of the graphene are numbered sequentially from 1 to 6, the two vectors u and v of that frame are the displacements from atom 1 to atoms 3 and 5, respectively. Those two vectors have the same length, and their directions are 60 degrees apart. The vector w = n u + m v is then interpreted as the circumference of the unrolled tube on the graphene lattice; it relates each point A1 on one edge of the strip to the point A2 on the other edge that will be identified with it as the strip is rolled up. The chiral angle α is then the angle between u and w.

The pairs (n,m) that describe distinct tube structures are those with 0 ≤ m ≤ n and n > 0. All geometric properties of the tube, such as diameter, chiral angle, and symmetries, can be computed from these indices.

The type also determines the electronic structure of the tube. Specifically, the tube behaves like a metal if |m–n| is a multiple of 3, and like a semiconductor otherwise.

Zigzag and armchair tubes

Tubes of type (n,m) with n=m (chiral angle = 30°) are called "armchair" and those with m=0 (chiral angle = 0°) "zigzag". These tubes have mirror symmetry, and can be viewed as stacks of simple closed paths ("zigzag" and "armchair" paths, respectively).

Armchair nanotube

Zigzag nanotube

Electronic structure

The optical properties of carbon nanotubes are largely determined by their unique electronic structure. The rolling up of the graphene lattice affects that structure in ways that depend strongly on the geometric structure type (n,m).

Van Hove singularities

A bulk 3D material (blue) has continuous DOS, but a 1D wire (green) has Van Hove singularities.

A characteristic feature of one-dimensional crystals is that their distribution of density of states (DOS) is not a continuous function of energy, but it descends gradually and then increases in a discontinuous spike. These sharp peaks are called Van Hove singularities. In contrast, three-dimensional materials have continuous DOS.

Van Hove singularities result in the following remarkable optical properties of carbon nanotubes:

• Optical transitions occur between the v₁ − c₁, v₂ − c₂, etc., states of semiconducting or metallic nanotubes and are traditionally labeled as S₁₁, S₂₂, M₁₁, etc., or, if the "conductivity" of the tube is unknown or unimportant, as E₁₁, E₂₂, etc. Crossover transitions c₁ − v₂, c₂ − v₁, etc., are dipole-forbidden and thus are extremely weak, but they were possibly observed using cross-polarized optical geometry.

• The energies between the Van Hove singularities depend on the nanotube structure. Thus by varying this structure, one can tune the optoelectronic properties of carbon nanotube. Such fine tuning has been experimentally demonstrated using UV illumination of polymer-dispersed CNTs.

• Optical transitions are rather sharp (~10 meV) and strong. Consequently, it is relatively easy to selectively excite nanotubes having certain (n, m) indices, as well as to detect optical signals from individual nanotubes.

Kataura plot

In this Kataura plot, the energy of an electronic transition decreases as the diameter of the nanotube increases.

The band structure of carbon nanotubes having certain (n, m) indexes can be easily calculated. A theoretical graph based on these calculations was designed in 1999 by Hiromichi Kataura to rationalize experimental findings. A Kataura plot relates the nanotube diameter and its bandgap energies for all nanotubes in a diameter range. The oscillating shape of every branch of the Kataura plot reflects the intrinsic strong dependence of the SWNT properties on the (n, m) index rather than on its diameter. For example, (10, 1) and (8, 3) tubes have almost the same diameter, but very different properties: the former is a metal, but the latter is a semiconductor.

Optical properties

Optical absorption

Optical absorption spectrum from dispersed single-wall carbon nanotubes

Optical absorption in carbon nanotubes differs from absorption in conventional 3D materials by presence of sharp peaks (1D nanotubes) instead of an absorption threshold followed by an absorption increase (most 3D solids). Absorption in nanotubes originates from electronic transitions from the v₂ to c₂ (energy E₂₂) or v₁ to c₁ (E₁₁) levels, etc. The transitions are relatively sharp and can be used to identify nanotube types. Note that the sharpness deteriorates with increasing energy, and that many nanotubes have very similar E₂₂ or E₁₁ energies, and thus significant overlap occurs in absorption spectra. This overlap is avoided in photoluminescence mapping measurements (see below), which instead of a combination of overlapped transitions identifies individual (E₂₂, E₁₁) pairs.

Interactions between nanotubes, such as bundling, broaden optical lines. While bundling strongly affects photoluminescence, it has much weaker effect on optical absorption and Raman scattering. Consequently, sample preparation for the latter two techniques is relatively simple.

Optical absorption is routinely used to quantify quality of the carbon nanotube powders.

The spectrum is analyzed in terms of intensities of nanotube-related peaks, background and pi-carbon peak; the latter two mostly originate from non-nanotube carbon in contaminated samples. However, it has been recently shown that by aggregating nearly single chirality semiconducting nanotubes into closely packed Van der Waals bundles the absorption background can be attributed to free carrier transition originating from intertube charge transfer.

Carbon nanotubes as a black body

An ideal black body should have emissivity or absorbance of 1.0, which is difficult to attain in practice, especially in a wide spectral range. Vertically aligned "forests" of single-wall carbon nanotubes can have absorbances of 0.98–0.99 from the far-ultraviolet (200 nm) to far-infrared (200 μm) wavelengths.

These SWNT forests (buckypaper) were grown by the super-growth CVD method to about 10 μm height. Two factors could contribute to strong light absorption by these structures: (i) a distribution of CNT chiralities resulted in various bandgaps for individual CNTs. Thus a compound material was formed with broadband absorption. (ii) Light might be trapped in those forests due to multiple reflections.

Reflectance measurements

	UV-to-near IR	Near-to-mid IR	Mid-to-far IR
Wavelength, μm	0.2-2	2–20	25–200
Incident angle, °	8	5	10
Reflection	Hemispherical-directional	Hemispherical-directional	Specular
Reference	White reflectance standard	Gold mirror	Aluminum mirror
Average reflectance	0.0160	0.0097	0.0017
Standard deviation	0.0048	0.0041	0.0027

Luminescence

Photoluminescence map from single-wall carbon nanotubes. (n, m) indexes identify certain semiconducting nanotubes. Note that PL measurements do not detect nanotubes with n = m or m = 0.

Photoluminescence (fluorescence)

Semiconducting single-walled carbon nanotubes emit near-infrared light upon photoexcitation, described interchangeably as fluorescence or photoluminescence (PL). The excitation of PL usually occurs as follows: an electron in a nanotube absorbs excitation light via S₂₂ transition, creating an electron-hole pair (exciton). Both electron and hole rapidly relax (via phonon-assisted processes) from c₂ to c₁ and from v₂ to v₁ states, respectively. Then they recombine through a c₁ − v₁ transition resulting in light emission.

No excitonic luminescence can be produced in metallic tubes. Their electrons can be excited, thus resulting in optical absorption, but the holes are immediately filled by other electrons out of the many available in the metal. Therefore, no excitons are produced.

Salient properties

• Photoluminescence from SWNT, as well as optical absorption and Raman scattering, is linearly polarized along the tube axis. This allows monitoring of the SWNTs orientation without direct microscopic observation.
• PL is quick: relaxation typically occurs within 100 picoseconds.
• PL efficiency was first found to be low (~0.01%), but later studies measured much higher quantum yields. By improving the structural quality and isolation of nanotubes, emission efficiency increased. A quantum yield of 1% was reported in nanotubes sorted by diameter and length through gradient centrifugation, and it was further increased to 20% by optimizing the procedure of isolating individual nanotubes in solution.
• The spectral range of PL is rather wide. Emission wavelength can vary between 0.8 and 2.1 micrometers depending on the nanotube structure.
• Excitons are apparently delocalized over several nanotubes in single chirality bundles as the photoluminescence spectrum displays a splitting consistent with intertube exciton tunneling.
• Interaction between nanotubes or between a nanotube and another material may quench or increase PL. No PL is observed in multi-walled carbon nanotubes. PL from double-wall carbon nanotubes strongly depends on the preparation method: CVD grown DWCNTs show emission both from inner and outer shells. However, DWCNTs produced by encapsulating fullerenes into SWNTs and annealing show PL only from the outer shells. Isolated SWNTs lying on the substrate show extremely weak PL which has been detected in few studies only. Detachment of the tubes from the substrate drastically increases PL.

• Position of the (S₂₂, S₁₁) PL peaks depends slightly (within 2%) on the nanotube environment (air, dispersant, etc.). However, the shift depends on the (n, m) index, and thus the whole PL map not only shifts, but also warps upon changing the CNT medium.

Raman scattering

Main article: Raman spectroscopy

 

Raman spectrum of single-wall carbon nanotubes

Raman spectroscopy has good spatial resolution (~0.5 micrometers) and sensitivity (single nanotubes); it requires only minimal sample preparation and is rather informative. Consequently, Raman spectroscopy is probably the most popular technique of carbon nanotube characterization. Raman scattering in SWNTs is resonant, i.e., only those tubes are probed which have one of the bandgaps equal to the exciting laser energy. Several scattering modes dominate the SWNT spectrum, as discussed below.

Similar to photoluminescence mapping, the energy of the excitation light can be scanned in Raman measurements, thus producing Raman maps. Those maps also contain oval-shaped features uniquely identifying (n, m) indices. Contrary to PL, Raman mapping detects not only semiconducting but also metallic tubes, and it is less sensitive to nanotube bundling than PL. However, requirement of a tunable laser and a dedicated spectrometer is a strong technical impediment.

Radial breathing mode

Radial breathing mode (RBM) corresponds to radial expansion-contraction of the nanotube. Therefore, its frequency ν_RBM (in cm⁻¹) depends on the nanotube diameter d as, ν_RBM= A/d + B (where A and B are constants dependent on the environment in which the nanotube is present. For example, B=0 for individual nanotubes.) (in nanometers) and can be estimated as ν_RBM = 234/d + 10 for SWNT or ν_RBM = 248/d for DWNT, which is very useful in deducing the CNT diameter from the RBM position. Typical RBM range is 100–350 cm⁻¹. If RBM intensity is particularly strong, its weak second overtone can be observed at double frequency.

Bundling mode

The bundling mode is a special form of RBM supposedly originating from collective vibration in a bundle of SWNTs.

G mode

Another very important mode is the G mode (G from graphite). This mode corresponds to planar vibrations of carbon atoms and is present in most graphite-like materials. G band in SWNT is shifted to lower frequencies relative to graphite (1580 cm⁻¹) and is split into several peaks. The splitting pattern and intensity depend on the tube structure and excitation energy; they can be used, though with much lower accuracy compared to RBM mode, to estimate the tube diameter and whether the tube is metallic or semiconducting.

D mode

D mode is present in all graphite-like carbons and originates from structural defects. Therefore, the ratio of the G/D modes is conventionally used to quantify the structural quality of carbon nanotubes. High-quality nanotubes have this ratio significantly higher than 100. At a lower functionalisation of the nanotube, the G/D ratio remains almost unchanged. This ratio gives an idea of the functionalisation of a nanotube.

G' mode

The name of this mode is misleading: it is given because in graphite, this mode is usually the second strongest after the G mode. However, it is actually the second overtone of the defect-induced D mode (and thus should logically be named D'). Its intensity is stronger than that of the D mode due to different selection rules. In particular, D mode is forbidden in the ideal nanotube and requires a structural defect, providing a phonon of certain angular momentum, to be induced. In contrast, G' mode involves a "self-annihilating" pair of phonons and thus does not require defects. The spectral position of G' mode depends on diameter, so it can be used roughly to estimate the SWNT diameter. In particular, G' mode is a doublet in double-wall carbon nanotubes, but the doublet is often unresolved due to line broadening.

Other overtones, such as a combination of RBM+G mode at ~1750 cm⁻¹, are frequently seen in CNT Raman spectra. However, they are less important and are not considered here.

Anti-Stokes scattering

All the above Raman modes can be observed both as Stokes and anti-Stokes scattering. As mentioned above, Raman scattering from CNTs is resonant in nature, i.e. only tubes whose band gap energy is similar to the laser energy are excited. The difference between those two energies, and thus the band gap of individual tubes, can be estimated from the intensity ratio of the Stokes/anti-Stokes lines. This estimate however relies on the temperature factor (Boltzmann factor), which is often miscalculated – a focused laser beam is used in the measurement, which can locally heat the nanotubes without changing the overall temperature of the studied sample.

Rayleigh scattering

Carbon nanotubes have very large aspect ratio, i.e., their length is much larger than their diameter. Consequently, as expected from the classical electromagnetic theory, elastic light scattering (or Rayleigh scattering) by straight CNTs has anisotropic angular dependence, and from its spectrum, the band gaps of individual nanotubes can be deduced.

Another manifestation of Rayleigh scattering is the "antenna effect", an array of nanotubes standing on a substrate has specific angular and spectral distributions of reflected light, and both those distributions depend on the nanotube length.

Applications

Light emitting diodes (LEDs) and photo-detectors based on a single nanotube have been produced in the lab. Their unique feature is not the efficiency, which is yet relatively low, but the narrow selectivity in the wavelength of emission and detection of light and the possibility of its fine tuning through the nanotube structure. In addition, bolometer and optoelectronic memory devices have been realised on ensembles of single-walled carbon nanotubes.

• Photoluminescence is used for characterization purposes to measure the quantities of semiconducting nanotube species in a sample. Nanotubes are isolated (dispersed) using an appropriate chemical agent ("dispersant") to reduce the intertube quenching. Then PL is measured, scanning both the excitation and emission energies and thereby producing a PL map. The ovals in the map define (S₂₂, S₁₁) pairs, which unique identify (n, m) index of a tube. The data of Weisman and Bachilo are conventionally used for the identification.

• Nanotube fluorescence has been investigated for the purposes of imaging and sensing in biomedical applications.

Sensitization

Optical properties, including the PL efficiency, can be modified by encapsulating organic dyes (carotene, lycopene, etc.) inside the tubes. Efficient energy transfer occurs between the encapsulated dye and nanotube — light is efficiently absorbed by the dye and without significant loss is transferred to the SWNT. Thus potentially, optical properties of a carbon nanotube can be controlled by encapsulating certain molecule inside it. Besides, encapsulation allows isolation and characterization of organic molecules which are unstable under ambient conditions. For example, Raman spectra are extremely difficult to measure from dyes because of their strong PL (efficiency close to 100%). However, encapsulation of dye molecules inside SWNTs completely quenches dye PL, thus allowing measurement and analysis of their Raman spectra.

Cathodoluminescence

Cathodoluminescence (CL) — light emission excited by electron beam — is a process commonly observed in TV screens. An electron beam can be finely focused and scanned across the studied material. This technique is widely used to study defects in semiconductors and nanostructures with nanometer-scale spatial resolution. It would be beneficial to apply this technique to carbon nanotubes. However, no reliable CL, i.e. sharp peaks assignable to certain (n, m) indices, has been detected from carbon nanotubes yet.

Electroluminescence

If appropriate electrical contacts are attached to a nanotube, electron-hole pairs (excitons) can be generated by injecting electrons and holes from the contacts. Subsequent exciton recombination results in electroluminescence (EL). Electroluminescent devices have been produced from single nanotubes and their macroscopic assemblies. Recombination appears to proceed via triplet-triplet annihilation giving distinct peaks corresponding to E₁₁ and E₂₂ transitions.

Multi-walled carbon nanotubes

Multi-walled carbon nanotubes (MWNT) may consist of several nested single-walled tubes, or of a single graphene strip rolled up multiple times, like a scroll. They are difficult to study because their properties are determined by contributions and interactions of all individual shells, which have different structures. Moreover, the methods used to synthesize them are poorly selective and result in higher incidence of defects.