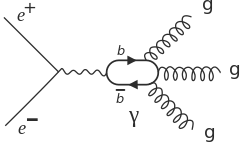
Diagram 1: In Feynman diagrams, emitted gluons are represented as helices. This diagram depicts the annihilation of an electron and positron. | |
| Composition | Elementary particle |
|---|---|
| Statistics | Bosonic |
| Family | Gauge boson |
| Interactions | Strong interaction |
| Symbol | g |
| Theorized | Murray Gell-Mann (1962) |
| Discovered | e+e− → Υ(9.46) → 3g: 1978 at DORIS (DESY) by PLUTO experiments (see diagram 2 and recollection) and |
| Types | 8 |
| Mass | 0 (theoretical value) < 1.3 MeV/ (experimental limit) |
| Electric charge | 0 e |
| Color charge | octet (8 linearly independent types) |
| Spin | 1 ħ |
| Parity | -1 |
A gluon (/ˈɡluːɒn/ GLOO-on) is a type of elementary particle that mediates the strong interaction between quarks, acting as the exchange particle for the interaction. Gluons are massless vector bosons, thereby having a spin of 1. Through the strong interaction, gluons bind quarks into groups according to quantum chromodynamics (QCD), forming hadrons such as protons and neutrons.
Gluons carry the color charge of the strong interaction, thereby participating in the strong interaction as well as mediating it. Because gluons carry the color charge, QCD is more difficult to analyze compared to quantum electrodynamics (QED) where the photon carries no electric charge.
Properties
The gluon is a vector boson, which means it has a spin of 1. While massive spin-1 particles have three polarization states, massless gauge bosons like the gluon have only two polarization states because gauge invariance requires the polarization to be transverse to the direction that the gluon is traveling. In quantum field theory, unbroken gauge invariance requires that gauge bosons have zero mass. Experiments limit the gluon's rest mass (if any) to less than a few MeV/c2. The gluon has negative intrinsic parity.
Counting gluons
Unlike the photon of QED or the three W and Z bosons of the weak interaction, there are eight independent types of gluons in QCD.
However, gluons are subject to the color charge phenomena (of which they have combinations of color and anticolor). Quarks carry three types of color charge; antiquarks carry three types of anticolor. Gluons may be thought of as carrying both color and anticolor. This gives nine possible combinations of color and anticolor in gluons. The following is a list of those combinations (and their schematic names):
- red–antired (), red–antigreen (), red–antiblue ()
- green–antired (), green–antigreen (), green–antiblue ()
- blue–antired (), blue–antigreen (), blue–antiblue ()
These are not the actual color states of observed gluons, but rather effective states. To correctly understand how they are combined, it is necessary to consider the mathematics of color charge in more detail.
Color singlet states
It is often said that the stable strongly interacting particles (such as hadrons like the proton and neutron) observed in nature are "colorless", but more precisely they are in a "color singlet" state, which is mathematically analogous to a spin singlet state. Such states allow interaction with other color singlets, but not with other color states; because long-range gluon interactions do not exist, this illustrates that gluons in the singlet state do not exist either.
The color singlet state is:
In other words, if one could measure the color of the state, there would be equal probabilities of it being red–antired, blue–antiblue, or green–antigreen.
Eight color states
There are eight remaining independent color states, which correspond to the "eight types" or "eight colors" of gluons. Because states can be mixed together as discussed above, there are many ways of presenting these states, which are known as the "color octet". One commonly used list is:
|
|
||
|
|
||
|
|
These are equivalent to the Gell-Mann matrices. The critical feature of these particular eight states is that they are linearly independent, and also independent of the singlet state, hence 32 − 1 or 23. There is no way to add any combination of these states to produce any other, and it is also impossible to add them to make rr, gg, or bb the forbidden singlet state. There are many other possible choices, but all are mathematically equivalent, at least equally complicated, and give the same physical results.
Group theory details
Formally, QCD is a gauge theory with SU(3) gauge symmetry. Quarks are introduced as spinors in Nf flavors, each in the fundamental representation (triplet, denoted 3) of the color gauge group, SU(3). The gluons are vectors in the adjoint representation (octets, denoted 8) of color SU(3). For a general gauge group, the number of force-carriers (like photons or gluons) is always equal to the dimension of the adjoint representation. For the simple case of SU(N), the dimension of this representation is N2 − 1.
In terms of group theory, the assertion that there are no color singlet gluons is simply the statement that quantum chromodynamics has an SU(3) rather than a U(3) symmetry. There is no known a priori reason for one group to be preferred over the other, but as discussed above, the experimental evidence supports SU(3). If the group were U(3), the ninth (colorless singlet) gluon would behave like a "second photon" and not like the other eight gluons.
Confinement
Since gluons themselves carry color charge, they participate in strong interactions. These gluon–gluon interactions constrain color fields to string-like objects called "flux tubes", which exert constant force when stretched. Due to this force, quarks are confined within composite particles called hadrons. This effectively limits the range of the strong interaction to 1×10−15 meters, roughly the size of a nucleon. Beyond a certain distance, the energy of the flux tube binding two quarks increases linearly. At a large enough distance, it becomes energetically more favorable to pull a quark–antiquark pair out of the vacuum rather than increase the length of the flux tube.
One consequence of the hadron-confinement property of gluons is that they are not directly involved in the nuclear forces between hadrons. The force mediators for these are other hadrons called mesons.
Although in the normal phase of QCD single gluons may not travel freely, it is predicted that there exist hadrons that are formed entirely of gluons — called glueballs. There are also conjectures about other exotic hadrons in which real gluons (as opposed to virtual ones found in ordinary hadrons) would be primary constituents. Beyond the normal phase of QCD (at extreme temperatures and pressures), quark–gluon plasma forms. In such a plasma there are no hadrons; quarks and gluons become free particles.
Experimental observations
Quarks and gluons (colored) manifest themselves by fragmenting into more quarks and gluons, which in turn hadronize into normal (colorless) particles, correlated in jets. As revealed in 1978 summer conferences, the PLUTO detector at the electron-positron collider DORIS (DESY) produced the first evidence that the hadronic decays of the very narrow resonance Υ(9.46) could be interpreted as three-jet event topologies produced by three gluons. Later, published analyses by the same experiment confirmed this interpretation and also the spin = 1 nature of the gluon (see also the recollection and PLUTO experiments).
In summer 1979, at higher energies at the electron-positron collider PETRA (DESY), again three-jet topologies were observed, now interpreted as qq gluon bremsstrahlung, now clearly visible, by TASSO, MARK-J and PLUTO experiments (later in 1980 also by JADE). The spin = 1 property of the gluon was confirmed in 1980 by TASSO and PLUTO experiments (see also the review). In 1991 a subsequent experiment at the LEP storage ring at CERN again confirmed this result.
The gluons play an important role in the elementary strong interactions between quarks and gluons, described by QCD and studied particularly at the electron-proton collider HERA at DESY. The number and momentum distribution of the gluons in the proton (gluon density) have been measured by two experiments, H1 and ZEUS, in the years 1996–2007. The gluon contribution to the proton spin has been studied by the HERMES experiment at HERA. The gluon density in the proton (when behaving hadronically) also has been measured.
Color confinement is verified by the failure of free quark searches (searches of fractional charges). Quarks are normally produced in pairs (quark + antiquark) to compensate the quantum color and flavor numbers; however at Fermilab single production of top quarks has been shown. No glueball has been demonstrated.
Deconfinement was claimed in 2000 at CERN SPS in heavy-ion collisions, and it implies a new state of matter: quark–gluon plasma, less interactive than in the nucleus, almost as in a liquid. It was found at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven in the years 2004–2010 by four contemporaneous experiments. A quark–gluon plasma state has been confirmed at the CERN Large Hadron Collider (LHC) by the three experiments ALICE, ATLAS and CMS in 2010.
Jefferson Lab's Continuous Electron Beam Accelerator Facility, in Newport News, Virginia, is one of 10 Department of Energy facilities doing research on gluons. The Virginia lab was competing with another facility – Brookhaven National Laboratory, on Long Island, New York – for funds to build a new electron-ion collider. In December 2019 the US Department of Energy selected the Brookhaven National Laboratory to host the electron-ion collider.



































![{\displaystyle {\begin{aligned}\left[\lambda _{a},\lambda _{b}\right]&=2i\sum _{c}f^{abc}\lambda _{c},\\\{\lambda _{a},\lambda _{b}\}&={\frac {4}{3}}\delta _{ab}I+2\sum _{c}d^{abc}\lambda _{c},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acb32747d25b81daa7467fc12a48c294ab249993)
![{\displaystyle {\begin{aligned}f^{abc}&=-{\frac {1}{4}}i\operatorname {tr} (\lambda _{a}[\lambda _{b},\lambda _{c}]),\\d^{abc}&={\frac {1}{4}}\operatorname {tr} (\lambda _{a}\{\lambda _{b},\lambda _{c}\}).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44b7489c8dbf3caea3b1edb82509883a29a2b013)



![{\displaystyle \lambda _{a}\lambda _{b}={\frac {1}{2}}([\lambda _{a},\lambda _{b}]+\{\lambda _{a},\lambda _{b}\})={\frac {2}{3}}\delta _{ab}I+\sum _{c}\left(d^{abc}+if^{abc}\right)\lambda _{c},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a39f164ff0301ad7a9be5ad96b5e999b357d97a2)









