Perfect number

From Wikipedia, the free encyclopedia

 

Illustration of the perfect number status of the number 6

In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself (also known as its aliquot sum). Equivalently, a perfect number is a number that is half the sum of all of its positive divisors (including itself) i.e. σ₁(n) = 2n.

This definition is ancient, appearing as early as Euclid's Elements (VII.22) where it is called τέλειος ἀριθμός (perfect, ideal, or complete number). Euclid also proved a formation rule (IX.36) whereby ${\displaystyle q(q+1)/2}$ is an even perfect number whenever ${\displaystyle q}$ is a prime of the form ${\displaystyle 2^{p}-1}$ for prime ${\displaystyle p}$—what is now called a Mersenne prime. Much later, Euler proved that all even perfect numbers are of this form. This is known as the Euclid–Euler theorem.

It is not known whether there are any odd perfect numbers, nor whether infinitely many perfect numbers exist.

Examples

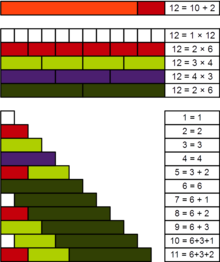
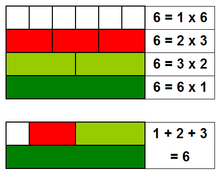
The first perfect number is 6. Its proper divisors are 1, 2, and 3, and 1 + 2 + 3 = 6. Equivalently, the number 6 is equal to half the sum of all its positive divisors: ( 1 + 2 + 3 + 6 ) ÷ 2 = 6. The next perfect number is 28: 28 = 1 + 2 + 4 + 7 + 14. This is followed by the perfect numbers 496 and 8128 (sequence A000396 in the OEIS).

History

In about 300 BC Euclid showed that if 2^p − 1 is prime then (2^p − 1)2^p−1 is perfect. The first four perfect numbers were the only ones known to early Greek mathematics, and the mathematician Nicomachus had noted 8128 as early as 100 AD. Philo of Alexandria in his first-century book "On the creation" mentions perfect numbers, claiming that the world was created in 6 days and the moon orbits in 28 days because 6 and 28 are perfect. Philo is followed by Origen, and by Didymus the Blind, who adds the observation that there are only four perfect numbers that are less than 10,000. (Commentary on Genesis 1. 14-19). St Augustine defines perfect numbers in City of God (Part XI, Chapter 30) in the early 5th century AD, repeating the claim that God created the world in 6 days because 6 is the smallest perfect number. The Egyptian mathematician Ismail ibn Fallūs (1194–1252) mentioned the next three perfect numbers (33,550,336; 8,589,869,056; and 137,438,691,328) and listed a few more which are now known to be incorrect. In a manuscript written between 1456 and 1461, an unknown mathematician recorded the earliest European reference to a fifth perfect number, with 33,550,336 being correctly identified for the first time. In 1588, the Italian mathematician Pietro Cataldi also identified the sixth (8,589,869,056) and the seventh (137,438,691,328) perfect numbers, and also proved that every perfect number obtained from Euclid's rule ends with a 6 or an 8.

Even perfect numbers

Euclid proved that 2^p−1(2^p − 1) is an even perfect number whenever 2^p − 1 is prime (Euclid, Prop. IX.36).

For example, the first four perfect numbers are generated by the formula 2^p−1(2^p − 1), with p a prime number, as follows:

for p = 2:   2¹(2² − 1) = 6

for p = 3:   2²(2³ − 1) = 28

for p = 5:   2⁴(2⁵ − 1) = 496

for p = 7:   2⁶(2⁷ − 1) = 8128.

Prime numbers of the form 2^p − 1 are known as Mersenne primes, after the seventeenth-century monk Marin Mersenne, who studied number theory and perfect numbers. For 2^p − 1 to be prime, it is necessary that p itself be prime. However, not all numbers of the form 2^p − 1 with a prime p are prime; for example, 2¹¹ − 1 = 2047 = 23 × 89 is not a prime number. In fact, Mersenne primes are very rare—of the 2,270,720 prime numbers p up to 37,156,667, 2^p − 1 is prime for only 45 of them.

Nicomachus (60–120 AD) conjectured that every perfect number is of the form 2^p−1(2^p − 1) where 2^p − 1 is prime. Ibn al-Haytham (Alhazen) circa 1000 AD conjectured that every even perfect number is of that form. It was not until the 18th century that Leonhard Euler proved that the formula 2^p−1(2^p − 1) will yield all the even perfect numbers. Thus, there is a one-to-one correspondence between even perfect numbers and Mersenne primes; each Mersenne prime generates one even perfect number, and vice versa. This result is often referred to as the Euclid–Euler theorem. As of January 2018, 50 Mersenne primes are known, and therefore 50 even perfect numbers (the largest of which is 2^77232916 × (2^77232917 − 1) with 46,498,850 digits).

An exhaustive search by the GIMPS distributed computing project has shown that the first 47 even perfect numbers are 2^p−1(2^p − 1) for

p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801, and 43112609 (sequence A000043 in the OEIS).

Three higher perfect numbers have also been discovered, namely those for which p = 57885161, 74207281, and 77232917, though there may be others within this range. It is not known whether there are infinitely many perfect numbers, nor whether there are infinitely many Mersenne primes.

As well as having the form 2^p−1(2^p − 1), each even perfect number is the (2^p − 1)th triangular number (and hence equal to the sum of the integers from 1 to 2^p − 1) and the 2^p−1th hexagonal number. Furthermore, each even perfect number except for 6 is the ((2^p + 1)/3)th centered nonagonal number and is equal to the sum of the first 2^(p−1)/2 odd cubes:

${\displaystyle {\begin{aligned}6&=2^{1}(2^{2}-1)&&=1+2+3,\\[8pt]28&=2^{2}(2^{3}-1)&&=1+2+3+4+5+6+7=1^{3}+3^{3},\\[8pt]496&=2^{4}(2^{5}-1)&&=1+2+3+\cdots +29+30+31\\&&&=1^{3}+3^{3}+5^{3}+7^{3},\\[8pt]8128&=2^{6}(2^{7}-1)&&=1+2+3+\cdots +125+126+127\\&&&=1^{3}+3^{3}+5^{3}+7^{3}+9^{3}+11^{3}+13^{3}+15^{3},\\[8pt]33550336&=2^{12}(2^{13}-1)&&=1+2+3+\cdots +8189+8190+8191\\&&&=1^{3}+3^{3}+5^{3}+\cdots +123^{3}+125^{3}+127^{3}.\end{aligned}}}$

Even perfect numbers (except 6) are of the form

${\displaystyle T_{2^{p}-1}=1+{\frac {(2^{p}-2)\times (2^{p}+1)}{2}}=1+9\times T_{(2^{p}-2)/3}}$

with each resulting triangular number (after subtracting 1 from the perfect number and dividing the result by 9) ending in 3 or 5, the sequence starting with 3, 55, 903, 3727815, ... This can be reformulated as follows: adding the digits of any even perfect number (except 6), then adding the digits of the resulting number, and repeating this process until a single digit (called the digital root) is obtained, always produces the number 1. For example, the digital root of 8128 is 1, because 8 + 1 + 2 + 8 = 19, 1 + 9 = 10, and 1 + 0 = 1. This works with all perfect numbers 2^p−1(2^p − 1) with odd prime p and, in fact, with all numbers of the form 2^m−1(2^m − 1) for odd integer (not necessarily prime) m.

Owing to their form, 2^p−1(2^p − 1), every even perfect number is represented in binary as p ones followed by p − 1  zeros; for example,

6₁₀ = 110₂

28₁₀ = 11100₂

496₁₀ = 111110000₂

and

8128₁₀ = 1111111000000₂.

Thus every even perfect number is a pernicious number.

Note that every even perfect number is also a practical number.

Odd perfect numbers

It is unknown whether there is any odd perfect number, though various results have been obtained. In 1496, Jacques Lefèvre stated that Euclid's rule gives all perfect numbers, thus implying that no odd perfect number exists. More recently, Carl Pomerance has presented a heuristic argument suggesting that indeed no odd perfect number should exist. All perfect numbers are also Ore's harmonic numbers, and it has been conjectured as well that there are no odd Ore's harmonic numbers other than 1.

Any odd perfect number N must satisfy the following conditions:

• N > 10¹⁵⁰⁰.
• N is not divisible by 105.
• N is of the form N ≡ 1 (mod 12), N ≡ 117 (mod 468), or N ≡ 81 (mod 324).
• N is of the form

${\displaystyle N=q^{\alpha }p_{1}^{2e_{1}}\cdots p_{k}^{2e_{k}},}$

where:

• q, p₁, ..., p_k are distinct primes (Euler).
• q ≡ α ≡ 1 (mod 4) (Euler).
• The smallest prime factor of N is less than (2k + 8) / 3.
• Either q^α > 10⁶², or p_j^2e_j  > 10⁶² for some j.^[20]
• N < 2^4k+1.
• ${\displaystyle \alpha +2e_{1}+2e_{2}+2e_{3}+\cdots +2e_{k}\geq (21k-18)/8}$ 

• The largest prime factor of N is greater than 10⁸.
• The second largest prime factor is greater than 10⁴, and the third largest prime factor is greater than 100.
• N has at least 101 prime factors and at least 10 distinct prime factors. If 3 is not one of the factors of N, then N has at least 12 distinct prime factors.

In 1888, Sylvester stated:

...a prolonged meditation on the subject has satisfied me that the existence of any one such [odd perfect number] — its escape, so to say, from the complex web of conditions which hem it in on all sides — would be little short of a miracle.

Euler stated: "Whether (...) there are any odd perfect numbers is a most difficult question".

Minor results

All even perfect numbers have a very precise form; odd perfect numbers either do not exist or are rare. There are a number of results on perfect numbers that are actually quite easy to prove but nevertheless superficially impressive; some of them also come under Richard Guy's strong law of small numbers:

• The only even perfect number of the form x³ + 1 is 28 (Makowski 1962).
• 28 is also the only even perfect number that is a sum of two positive cubes of integers (Gallardo 2010).
• The reciprocals of the divisors of a perfect number N must add up to 2 (to get this, take the definition of a perfect number, ${\displaystyle \sigma _{1}(n)=2n}$, and divide both sides by n):
  • For 6, we have ${\displaystyle 1/6+1/3+1/2+1/1=2}$;
  • For 28, we have ${\displaystyle 1/28+1/14+1/7+1/4+1/2+1/1=2}$, etc.
• The number of divisors of a perfect number (whether even or odd) must be even, because N cannot be a perfect square.
  • From these two results it follows that every perfect number is an Ore's harmonic number.
• The even perfect numbers are not trapezoidal numbers; that is, they cannot be represented as the difference of two positive non-consecutive triangular numbers. There are only three types of non-trapezoidal numbers: even perfect numbers, powers of two, and the numbers of the form ${\displaystyle 2^{n-1}(2^{n}+1)}$ formed as the product of a Fermat prime ${\displaystyle 2^{n}+1}$ with a power of two in a similar way to the construction of even perfect numbers from Mersenne primes.
• The number of perfect numbers less than n is less than ${\displaystyle c{\sqrt {n}}}$, where c > 0 is a constant. In fact it is ${\displaystyle o({\sqrt {n}})}$, using little-o notation.
• Every even perfect number ends in 6 or 28, base ten; and, with the only exception of 6, ends in 1, base 9. Therefore in particular the digital root of every even perfect number other than 6 is 1.
• The only square-free perfect number is 6.

Related concepts

The sum of proper divisors gives various other kinds of numbers. Numbers where the sum is less than the number itself are called deficient, and where it is greater than the number, abundant. These terms, together with perfect itself, come from Greek numerology. A pair of numbers which are the sum of each other's proper divisors are called amicable, and larger cycles of numbers are called sociable. A positive integer such that every smaller positive integer is a sum of distinct divisors of it is a practical number.

By definition, a perfect number is a fixed point of the restricted divisor function s(n) = σ(n) − n, and the aliquot sequence associated with a perfect number is a constant sequence. All perfect numbers are also ${\displaystyle {\mathcal {S}}}$-perfect numbers, or Granville numbers.

A semiperfect number is a natural number that is equal to the sum of all or some of its proper divisors. A semiperfect number that is equal to the sum of all its proper divisors is a perfect number. Most abundant numbers are also semiperfect; abundant numbers which are not semiperfect are called weird numbers.

Practical number

From Wikipedia, the free encyclopedia

 

Demonstration of the practicality of the number 12

In number theory, a practical number or panarithmic number is a positive integer n such that all smaller positive integers can be represented as sums of distinct divisors of n. For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.

The sequence of practical numbers (sequence A005153 in the OEIS) begins

1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90, 96, 100, 104, 108, 112, 120, 126, 128, 132, 140, 144, 150....

Practical numbers were used by Fibonacci in his Liber Abaci (1202) in connection with the problem of representing rational numbers as Egyptian fractions. Fibonacci does not formally define practical numbers, but he gives a table of Egyptian fraction expansions for fractions with practical denominators.

The name "practical number" is due to Srinivasan (1948). He noted that "the subdivisions of money, weights, and measures involve numbers like 4, 12, 16, 20 and 28 which are usually supposed to be so inconvenient as to deserve replacement by powers of 10." He rediscovered the number theoretical property of such numbers and was the first to attempt a classification of these numbers that was completed by Stewart (1954) and Sierpiński (1955). This characterization makes it possible to determine whether a number is practical by examining its prime factorization. Every even perfect number and every power of two is also a practical number.

Practical numbers have also been shown to be analogous with prime numbers in many of their properties.

Characterization of practical numbers

The original characterisation by Srinivasan (1948) stated that a practical number cannot be a deficient number, that is one of which the sum of all divisors (including 1 and itself) is less than twice the number unless the deficiency is one. If the ordered set of all divisors of the practical number ${\displaystyle n}$ is ${\displaystyle {d_{1},d_{2},...,d_{j}}}$ with ${\displaystyle d_{1}=1}$ and ${\displaystyle d_{j}=n}$, then Srinivasan's statement can be expressed by the inequality

${\displaystyle 2n\leq 1+\sum _{i=1}^{j}d_{i}}$.

In other words, the ordered sequence of all divisors ${\displaystyle {d_{1}$ of a practical number has to be a complete sub-sequence.

This partial characterization was extended and completed by Stewart (1954) and Sierpiński (1955) who showed that it is straightforward to determine whether a number is practical from its prime factorization. A positive integer greater than one with prime factorization ${\displaystyle n=p_{1}^{\alpha _{1}}...p_{k}^{\alpha _{k}}}$ (with the primes in sorted order ${\displaystyle p_{1}$) is practical if and only if each of its prime factors ${\displaystyle p_{i}}$ is small enough for ${\displaystyle p_{i}-1}$ to have a representation as a sum of smaller divisors. For this to be true, the first prime ${\displaystyle p_{1}}$ must equal 2 and, for every i from 2 to k, each successive prime ${\displaystyle p_{i}}$ must obey the inequality

${\displaystyle p_{i}\leq 1+\sigma (p_{1}^{\alpha _{1}}p_{2}^{\alpha _{2}}\dots p_{i-1}^{\alpha _{i-1}})=1+\prod _{j=1}^{i-1}{\frac {p_{j}^{\alpha _{j}+1}-1}{p_{j}-1}},}$

where ${\displaystyle \sigma (x)}$ denotes the sum of the divisors of x. For example, 2 × 3² × 29 × 823 = 429606 is practical, because the inequality above holds for each of its prime factors: 3 ≤ σ(2) + 1 = 4, 29 ≤ σ(2 × 3²) + 1 = 40, and 823 ≤ σ(2 × 3² × 29) + 1 = 1171.

The condition stated above is necessary and sufficient for a number to be practical. In one direction, this condition is necessary in order to be able to represent ${\displaystyle p_{i}-1}$ as a sum of divisors of n, because if the inequality failed to be true then even adding together all the smaller divisors would give a sum too small to reach ${\displaystyle p_{i}-1}$. In the other direction, the condition is sufficient, as can be shown by induction. More strongly, if the factorization of n satisfies the condition above, then any ${\displaystyle m\leq \sigma (n)}$ can be represented as a sum of divisors of n, by the following sequence of steps:

• Let ${\displaystyle q=\min\{\lfloor m/p_{k}^{\alpha _{k}}\rfloor ,\sigma (n/p_{k}^{\alpha _{k}})\}}$, and let ${\displaystyle r=m-qp_{k}^{\sigma _{k}}}$.
• Since ${\displaystyle q\leq \sigma (n/p_{k}^{\alpha _{k}})}$ and ${\displaystyle n/p_{k}^{\alpha _{k}}}$ can be shown by induction to be practical, we can find a representation of q as a sum of divisors of ${\displaystyle n/p_{k}^{\alpha _{k}}}$.
• Since ${\displaystyle r\leq \sigma (n)-p_{k}^{\alpha _{k}}\sigma (n/p_{k}^{\alpha _{k}})=\sigma (n/p_{k})}$, and since ${\displaystyle n/p_{k}}$ can be shown by induction to be practical, we can find a representation of r as a sum of divisors of ${\displaystyle n/p_{k}}$.
• The divisors representing r, together with ${\displaystyle p_{k}^{\alpha _{k}}}$ times each of the divisors representing q, together form a representation of m as a sum of divisors of n.

Properties

• The only odd practical number is 1, because if n > 2 is an odd number, then 2 cannot be expressed as the sum of distinct divisors of n. More strongly, Srinivasan (1948) observes that other than 1 and 2, every practical number is divisible by 4 or 6 (or both).
• The product of two practical numbers is also a practical number. More strongly the least common multiple of any two practical numbers is also a practical number. Equivalently, the set of all practical numbers is closed under multiplication.
• From the above characterization by Stewart and Sierpiński it can be seen that if n is a practical number and d is one of its divisors then n*d must also be a practical number.
• In the set of all practical numbers there is a primitive set of practical numbers. A primitive practical number is either practical and squarefree or practical and when divided by any of its prime factors whose factorization exponent is greater than 1 is no longer practical. The sequence of primitive practical numbers (sequence A267124 in the OEIS) begins

1, 2, 6, 20, 28, 30, 42, 66, 78, 88, 104, 140, 204, 210, 220, 228, 260, 272, 276, 304, 306, 308, 330, 340, 342, 348, 364, 368, 380, 390, 414, 460 ...

Relation to other classes of numbers

Several other notable sets of integers consist only of practical numbers:

• From the above properties with n a practical number and d one of its divisors (that is, d | n) then n*d must also be a practical number therefore six times every power of 3 must be a practical number as well as six times every power of 2.
• Every power of two is a practical number. Powers of two trivially satisfy the characterization of practical numbers in terms of their prime factorizations: the only prime in their factorizations, p₁, equals two as required.
• Every even perfect number is also a practical number. This follows from Leonhard Euler's result that an even perfect number must have the form 2^n − 1(2ⁿ − 1). The odd part of this factorization equals the sum of the divisors of the even part, so every odd prime factor of such a number must be at most the sum of the divisors of the even part of the number. Therefore, this number must satisfy the characterization of practical numbers.
• Every primorial (the product of the first i primes, for some i) is practical. For the first two primorials, two and six, this is clear. Each successive primorial is formed by multiplying a prime number p_i by a smaller primorial that is divisible by both two and the next smaller prime, p_i − 1. By Bertrand's postulate, p_i < 2p_i − 1, so each successive prime factor in the primorial is less than one of the divisors of the previous primorial. By induction, it follows that every primorial satisfies the characterization of practical numbers. Because a primorial is, by definition, squarefree it is also a primitive practical number.
• Generalizing the primorials, any number that is the product of nonzero powers of the first k primes must also be practical. This includes Ramanujan's highly composite numbers (numbers with more divisors than any smaller positive integer) as well as the factorial numbers.

Practical numbers and Egyptian fractions

If n is practical, then any rational number of the form m/n with m < n may be represented as a sum ∑d_i/n where each d_i is a distinct divisor of n. Each term in this sum simplifies to a unit fraction, so such a sum provides a representation of m/n as an Egyptian fraction. For instance,

${\displaystyle {\frac {13}{20}}={\frac {10}{20}}+{\frac {2}{20}}+{\frac {1}{20}}={\frac {1}{2}}+{\frac {1}{10}}+{\frac {1}{20}}.}$

Fibonacci, in his 1202 book Liber Abaci lists several methods for finding Egyptian fraction representations of a rational number. Of these, the first is to test whether the number is itself already a unit fraction, but the second is to search for a representation of the numerator as a sum of divisors of the denominator, as described above. This method is only guaranteed to succeed for denominators that are practical. Fibonacci provides tables of these representations for fractions having as denominators the practical numbers 6, 8, 12, 20, 24, 60, and 100.

Vose (1985) showed that every number x/y has an Egyptian fraction representation with ${\displaystyle \scriptstyle O({\sqrt {\log y}})}$ terms. The proof involves finding a sequence of practical numbers n_i with the property that every number less than n_i may be written as a sum of ${\displaystyle \scriptstyle O({\sqrt {\log n_{i-1}}})}$ distinct divisors of n_i. Then, i is chosen so that n_i − 1 < y ≤ n_i, and xn_i is divided by y giving quotient q and remainder r. It follows from these choices that ${\displaystyle \scriptstyle {\frac {x}{y}}={\frac {q}{n_{i}}}+{\frac {r}{yn_{i}}}}$. Expanding both numerators on the right hand side of this formula into sums of divisors of n_i results in the desired Egyptian fraction representation. Tenenbaum & Yokota (1990) use a similar technique involving a different sequence of practical numbers to show that every number x/y has an Egyptian fraction representation in which the largest denominator is ${\displaystyle \scriptstyle O({\frac {y\log ^{2}y}{\log \log y}})}$.
According to a September 2015 conjecture by Zhi-Wei Sun, every positive rational number has an Egyptian fraction representation in which every denominator is a practical number. There is a proof for the conjecture on David Eppstein's blog.

Analogies with prime numbers

One reason for interest in practical numbers is that many of their properties are similar to properties of the prime numbers. Indeed, theorems analogous to Goldbach's conjecture and the twin prime conjecture are known for practical numbers: every positive even integer is the sum of two practical numbers, and there exist infinitely many triples of practical numbers x − 2, x, x + 2. Melfi also showed that there are infinitely many practical Fibonacci numbers (sequence A124105 in the OEIS); the analogous question of the existence of infinitely many Fibonacci primes is open. Hausman & Shapiro (1984) showed that there always exists a practical number in the interval [x²,(x + 1)²] for any positive real x, a result analogous to Legendre's conjecture for primes.

Let p(x) count how many practical numbers are at most x. Margenstern (1991) conjectured that p(x) is asymptotic to cx/log x for some constant c, a formula which resembles the prime number theorem, strengthening the earlier claim of Erdős & Loxton (1979) that the practical numbers have density zero in the integers. Saias (1997) proved that for suitable constants c₁ and c₂:

${\displaystyle c_{1}{\frac {x}{\log x}}$

Finally Weingartner (2015) proved Margenstern's conjecture showing that

${\displaystyle p(x)={\frac {cx}{\log x}}\left(1+O\!\left({\frac {\log \log x}{\log x}}\right)\right),}$

for ${\displaystyle x\geq 3}$ and some constant ${\displaystyle c>0}$.