Tachyonic field

From Wikipedia, the free encyclopedia

A tachyonic field, or simply tachyon, is a field with an imaginary mass. Although tachyonic particles (particles that move faster than light) are a purely hypothetical concept that violate a number of essential physical principles, at least one field with imaginary mass is believed to exist. In general, tachyonic fields play an important role in physics and are discussed in popular books. Under no circumstances do any excitations of tachyonic fields ever propagate faster than light—the presence or absence of a tachyonic (imaginary) mass has no effect on the maximum velocity of signals, and so unlike faster-than-light particles there is no violation of causality.

The term "tachyon" was coined by Gerald Feinberg in a 1967 paper that studied quantum fields with imaginary mass. Feinberg believed such fields permitted faster than light propagation, but it was soon realized that Feinberg's model in fact did not allow for superluminal speeds. Instead, the imaginary mass creates an instability in the configuration: any configuration in which one or more field excitations are tachyonic will spontaneously decay, and the resulting configuration contains no physical tachyons. This process is known as tachyon condensation. A famous example is the condensation of the Higgs boson in the Standard Model of particle physics.

In modern physics, all fundamental particles are regarded as localized excitations of fields. Tachyons are unusual because the instability prevents any such localized excitations from existing. Any localized perturbation, no matter how small, starts an exponentially growing cascade that strongly affects physics everywhere inside the future light cone of the perturbation.

Interpretation

Overview of tachyonic condensation

Although the notion of a tachyonic imaginary mass might seem troubling because there is no classical interpretation of an imaginary mass, the mass is not quantized. Rather, the scalar field is; even for tachyonic quantum fields, the field operators at spacelike separated points still commute (or anticommute), thus preserving causality. Therefore, information still does not propagate faster than light, and solutions grow exponentially, but not superluminally (there is no violation of causality).

The "imaginary mass" really means that the system becomes unstable. The zero value field is at a local maximum rather than a local minimum of its potential energy, much like a ball at the top of a hill. A very small impulse (which will always happen due to quantum fluctuations) will lead the field to roll down with exponentially increasing amplitudes toward the local minimum. In this way, tachyon condensation drives a physical system that has reached a local limit and might naively be expected to produce physical tachyons, to an alternative stable state where no physical tachyons exist. Once the tachyonic field reaches the minimum of the potential, its quanta are not tachyons any more but rather are ordinary particles with a positive mass-squared, such as the Higgs boson.

Physical interpretation of a tachyonic field and signal propagation

There is a simple mechanical analogy that illustrates that tachyonic fields do not propagate faster than light, why they represent instabilities, and helps explain the meaning of imaginary mass (the mass squared being negative).

Consider a long line of pendulums, all pointing straight down. The mass on the end of each pendulum is connected to the masses of its two neighbors by springs. Wiggling one of the pendulums will create two ripples that propagate in both directions down the line. As the ripple passes, each pendulum in its turn oscillates a few times about the straight down position. The speed of propagation of these ripples is determined in a simple way by the tension of the springs and the inertial mass of the pendulum weights. Formally, these parameters can be chosen so that the propagation speed is the speed of light. In the limit of an infinite density of closely spaced pendulums, this model becomes identical to a relativistic field theory, where the ripples are the analog of particles. Displacing the pendulums from pointing straight down requires positive energy, which indicates that the squared mass of those particles is positive.

Now consider an initial condition where at time t=0, all the pendulums are pointing straight up. Clearly this is unstable, but at least in classical physics one can imagine that they are so carefully balanced they will remain pointing straight up indefinitely so long as they are not perturbed. Wiggling one of the upside-down pendulums will have a very different effect from before. The speed of propagation of the effects of the wiggle is identical to what it was before, since neither the spring tension nor the inertial mass have changed. However, the effects on the pendulums affected by the perturbation are dramatically different. Those pendulums that feel the effects of the perturbation will begin to topple over, and will pick up speed exponentially. Indeed, it is easy to show that any localized perturbation kicks off an exponentially growing instability that affects everything within its future "ripple cone" (a region of size equal to time multiplied by the ripple propagation speed). In the limit of infinite pendulum density, this model is a tachyonic field theory.

Importance in physics

Tachyonic fields play an important role in modern physics. Perhaps the most famous example of a tachyon is the Higgs boson of the Standard model of particle physics. In its uncondensed phase, the square of the mass of the Higgs field is negative, and therefore, the associated particle is a tachyon.

The phenomenon of spontaneous symmetry breaking, which is closely related to tachyon condensation, plays a central part in many aspects of theoretical physics, including the Ginzburg–Landau and BCS theories of superconductivity.

Other examples include the inflaton field in certain models of cosmic inflation (such as new inflation), and the tachyon of bosonic string theory.

Condensation

In quantum field theory, a tachyon is a quantum of a field—usually a scalar field—whose squared mass is negative, and is used to describe spontaneous symmetry breaking: The existence of such a field implies the instability of the field vacuum; the field is at a local maximum rather than a local minimum of its potential energy, much like a ball at the top of a hill. A very small impulse (which will always happen due to quantum fluctuations) will lead the field (ball) to roll down with exponentially increasing amplitudes: it will induce tachyon condensation. Once the tachyonic field reaches the minimum of the potential, its quanta are not tachyons any more but rather have a positive mass-squared. The Higgs boson of the standard model of particle physics is an example.

Technically, the squared mass is the second derivative of the effective potential. For a tachyonic field the second derivative is negative, meaning that the effective potential is at a local maximum rather than a local minimum. Therefore, this situation is unstable and the field will roll down the potential.

Because a tachyon's squared mass is negative, it formally has an imaginary mass. This is a special case of the general rule, where unstable massive particles are formally described as having a complex mass, with the real part being their mass in usual sense, and the imaginary part being the decay rate in natural units.

However, in quantum field theory, a particle (a "one-particle state") is roughly defined as a state which is constant over time; i.e., an eigenvalue of the Hamiltonian. An unstable particle is a state which is only approximately constant over time; If it exists long enough to be measured, it can be formally described as having a complex mass, with the real part of the mass greater than its imaginary part. If both parts are of the same magnitude, this is interpreted as a resonance appearing in a scattering process rather than particle, as it is considered not to exist long enough to be measured independently of the scattering process. In the case of a tachyon the real part of the mass is zero, and hence no concept of a particle can be attributed to it.

Even for tachyonic quantum fields, the field operators at space-like separated points still commute (or anticommute), thus preserving the principle of causality. For closely related reasons, the maximum velocity of signals sent with a tachyonic field is strictly bounded from above by the speed of light. Therefore, information never moves faster than light regardless of the presence or absence of tachyonic fields.

Examples for tachyonic fields are all cases of spontaneous symmetry breaking. In condensed matter physics a notable example is ferromagnetism; in particle physics the best known example is the Higgs mechanism in the standard model.

Tachyons in string theory

In string theory, tachyons have the same interpretation as in quantum field theory. However, string theory can, at least, in principle, not only describe the physics of tachyonic fields, but also predict whether such fields appear.

Tachyonic fields indeed arise in many versions of string theory. In general, string theory states that what we see as "particles" (electrons, photons, gravitons and so forth) are actually different vibrational states of the same underlying string. The mass of the particle can be deduced from the vibrations which the string exhibits; roughly speaking, the mass depends upon the "note" which the string sounds. Tachyons frequently appear in the spectrum of permissible string states, in the sense that some states have negative mass-squared, and therefore, imaginary mass. If the tachyon appears as a vibrational mode of an open string, this signals an instability of the underlying D-brane system to which the string is attached. The system will then decay to a state of closed strings and/or stable D-branes. If the tachyon is a closed string vibrational mode, this indicates an instability in spacetime itself. Generally, it is not known (or theorized) what this system will decay to. However, if the closed string tachyon is localized around a spacetime singularity, the endpoint of the decay process will often have the singularity resolved.

Mass

From Wikipedia, the free encyclopedia

Cast iron weight used for balances - Weight: 2 kg (4.44 lb) Height: 4.9 cm (1.9 in); Width: 9.2 cm (3.6 in).

Mass is both a property of a physical body and a measure of its resistance to acceleration (a change in its state of motion) when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies.

The basic SI unit of mass is the kilogram (kg). In physics, mass is not the same as weight, even though mass is often determined by measuring the object's weight using a spring scale, rather than balance scale comparing it directly with known masses. An object on the Moon would weigh less than it does on Earth because of the lower gravity, but it would still have the same mass. This is because weight is a force, while mass is the property that (along with gravity) determines the strength of this force.

Phenomena

There are several distinct phenomena which can be used to measure mass. Although some theorists have speculated that some of these phenomena could be independent of each other, current experiments have found no difference in results regardless of how it is measured:

• Inertial mass measures an object's resistance to being accelerated by a force (represented by the relationship F = ma).
• Active gravitational mass measures the gravitational force exerted by an object.
• Passive gravitational mass measures the gravitational force exerted on an object in a known gravitational field.

The mass of an object determines its acceleration in the presence of an applied force. The inertia and the inertial mass describe the same properties of physical bodies at the qualitative and quantitative level respectively, by other words, the mass quantitatively describes the inertia. According to Newton's second law of motion, if a body of fixed mass m is subjected to a single force F, its acceleration a is given by F/m. A body's mass also determines the degree to which it generates or is affected by a gravitational field. If a first body of mass m_A is placed at a distance r (center of mass to center of mass) from a second body of mass m_B, each body is subject to an attractive force F_g = Gm_Am_B/r², where G = 6.67×10⁻¹¹ N kg⁻² m² is the "universal gravitational constant". This is sometimes referred to as gravitational mass. Repeated experiments since the 17th century have demonstrated that inertial and gravitational mass are identical; since 1915, this observation has been entailed a priori in the equivalence principle of general relativity.

Units of mass

The kilogram is one of the seven SI base units and one of three which is defined ad hoc (i.e. without reference to another base unit).

The standard International System of Units (SI) unit of mass is the kilogram (kg). The kilogram is 1000 grams (g), first defined in 1795 as one cubic decimeter of water at the melting point of ice. However, because precise measurement of a decimeter of water at the proper temperature and pressure was difficult, in 1889 the kilogram was redefined as the mass of the international prototype kilogram of cast iron, and thus became independent of the meter and the properties of water.

However, the mass of the international prototype and its supposedly identical national copies have been found to be drifting over time. It is expected that the re-definition of the kilogram and several other units will occur on May 20, 2019, following a final vote by the CGPM in November 2018. The new definition will use only invariant quantities of nature: the speed of light, the caesium hyperfine frequency, and the Planck constant.

Other units are accepted for use in SI:

• the tonne (t) (or "metric ton") is equal to 1000 kg.
• the electronvolt (eV) is a unit of energy, but because of the mass–energy equivalence it can easily be converted to a unit of mass, and is often used like one. In this context, the mass has units of eV/c² (where c is the speed of light). The electronvolt and its multiples, such as the MeV (megaelectronvolt), are commonly used in particle physics.
• the atomic mass unit (u) is 1/12 of the mass of a carbon-12 atom, approximately 1.66×10⁻²⁷ kg. The atomic mass unit is convenient for expressing the masses of atoms and molecules.

Outside the SI system, other units of mass include:

• the slug (sl) is an Imperial unit of mass (about 14.6 kg).
• the pound (lb) is a unit of both mass and force, used mainly in the United States (about 0.45 kg or 4.5 N). In scientific contexts where pound (force) and pound (mass) need to be distinguished, SI units are usually used instead.
• the Planck mass (m_P) is the maximum mass of point particles (about 2.18×10⁻⁸ kg). It is used in particle physics.
• the solar mass (M_☉) is defined as the mass of the Sun. It is primarily used in astronomy to compare large masses such as stars or galaxies (≈1.99×10³⁰ kg).
• the mass of a very small particle may be identified by its inverse Compton wavelength (1 cm⁻¹ ≈ 3.52×10⁻⁴¹ kg).
• the mass of a very large star or black hole may be identified with its Schwarzschild radius (1 cm ≈ 6.73×10²⁴ kg).

Definitions of mass

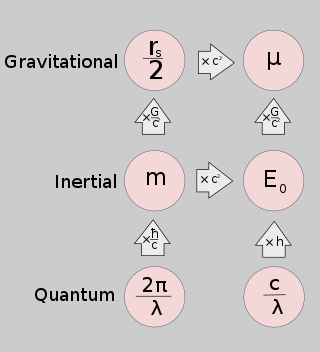
The relation between properties of mass and their associated physical constants. Every massive object is believed to exhibit all five properties. However, due to extremely large or extremely small constants, it is generally impossible to verify more than two or three properties for any object.

• The Schwarzschild radius (r_s) represents the ability of mass to cause curvature in space and time.
• The standard gravitational parameter (μ) represents the ability of a massive body to exert Newtonian gravitational forces on other bodies.
• Inertial mass (m) represents the Newtonian response of mass to forces.
• Rest energy (E₀) represents the ability of mass to be converted into other forms of energy.
• The Compton wavelength (λ) represents the quantum response of mass to local geometry.

In physical science, one may distinguish conceptually between at least seven different aspects of mass, or seven physical notions that involve the concept of mass. Every experiment to date has shown these seven values to be proportional, and in some cases equal, and this proportionality gives rise to the abstract concept of mass. There are a number of ways mass can be measured or operationally defined:

• Inertial mass is a measure of an object's resistance to acceleration when a force is applied. It is determined by applying a force to an object and measuring the acceleration that results from that force. An object with small inertial mass will accelerate more than an object with large inertial mass when acted upon by the same force. One says the body of greater mass has greater inertia.
• Active gravitational mass is a measure of the strength of an object's gravitational flux (gravitational flux is equal to the surface integral of gravitational field over an enclosing surface). Gravitational field can be measured by allowing a small "test object" to fall freely and measuring its free-fall acceleration. For example, an object in free fall near the Moon is subject to a smaller gravitational field, and hence accelerates more slowly, than the same object would if it were in free fall near the Earth. The gravitational field near the Moon is weaker because the Moon has less active gravitational mass.
• Passive gravitational mass is a measure of the strength of an object's interaction with a gravitational field. Passive gravitational mass is determined by dividing an object's weight by its free-fall acceleration. Two objects within the same gravitational field will experience the same acceleration; however, the object with a smaller passive gravitational mass will experience a smaller force (less weight) than the object with a larger passive gravitational mass.
• Energy also has mass according to the principle of mass–energy equivalence. This equivalence is exemplified in a large number of physical processes including pair production, nuclear fusion, and the gravitational bending of light. Pair production and nuclear fusion are processes in which measurable amounts of mass are converted to energy, or vice versa. In the gravitational bending of light, photons of pure energy are shown to exhibit a behavior similar to passive gravitational mass.
• Curvature of spacetime is a relativistic manifestation of the existence of mass. Such curvature is extremely weak and difficult to measure. For this reason, curvature was not discovered until after it was predicted by Einstein's theory of general relativity. Extremely precise atomic clocks on the surface of the Earth, for example, are found to measure less time (run slower) when compared to similar clocks in space. This difference in elapsed time is a form of curvature called gravitational time dilation. Other forms of curvature have been measured using the Gravity Probe B satellite.
• Quantum mass manifests itself as a difference between an object's quantum frequency and its wave number. The quantum mass of an electron, the Compton wavelength, can be determined through various forms of spectroscopy and is closely related to the Rydberg constant, the Bohr radius, and the classical electron radius. The quantum mass of larger objects can be directly measured using a Watt balance. In relativistic quantum mechanics, mass is one of the irreducible representation labels of the Poincaré group.

Weight vs. mass

In everyday usage, mass and "weight" are often used interchangeably. For instance, a person's weight may be stated as 75 kg. In a constant gravitational field, the weight of an object is proportional to its mass, and it is unproblematic to use the same unit for both concepts. But because of slight differences in the strength of the Earth's gravitational field at different places, the distinction becomes important for measurements with a precision better than a few percent, and for places far from the surface of the Earth, such as in space or on other planets. Conceptually, "mass" (measured in kilograms) refers to an intrinsic property of an object, whereas "weight" (measured in newtons) measures an object's resistance to deviating from its natural course of free fall, which can be influenced by the nearby gravitational field. No matter how strong the gravitational field, objects in free fall are weightless, though they still have mass.

The force known as "weight" is proportional to mass and acceleration in all situations where the mass is accelerated away from free fall. For example, when a body is at rest in a gravitational field (rather than in free fall), it must be accelerated by a force from a scale or the surface of a planetary body such as the Earth or the Moon. This force keeps the object from going into free fall. Weight is the opposing force in such circumstances, and is thus determined by the acceleration of free fall. On the surface of the Earth, for example, an object with a mass of 50 kilograms weighs 491 newtons, which means that 491 newtons is being applied to keep the object from going into free fall. By contrast, on the surface of the Moon, the same object still has a mass of 50 kilograms but weighs only 81.5 newtons, because only 81.5 newtons is required to keep this object from going into a free fall on the moon. Restated in mathematical terms, on the surface of the Earth, the weight W of an object is related to its mass m by W = mg, where g = 9.80665 m/s² is the acceleration due to Earth's gravitational field, (expressed as the acceleration experienced by a free-falling object).

For other situations, such as when objects are subjected to mechanical accelerations from forces other than the resistance of a planetary surface, the weight force is proportional to the mass of an object multiplied by the total acceleration away from free fall, which is called the proper acceleration. Through such mechanisms, objects in elevators, vehicles, centrifuges, and the like, may experience weight forces many times those caused by resistance to the effects of gravity on objects, resulting from planetary surfaces. In such cases, the generalized equation for weight W of an object is related to its mass m by the equation W = –ma, where a is the proper acceleration of the object caused by all influences other than gravity. (Again, if gravity is the only influence, such as occurs when an object falls freely, its weight will be zero).

Inertial vs. gravitational mass

Although inertial mass, passive gravitational mass and active gravitational mass are conceptually distinct, no experiment has ever unambiguously demonstrated any difference between them. In classical mechanics, Newton's third law implies that active and passive gravitational mass must always be identical (or at least proportional), but the classical theory offers no compelling reason why the gravitational mass has to equal the inertial mass. That it does is merely an empirical fact.

Albert Einstein developed his general theory of relativity starting with the assumption of the intentionality of correspondence between inertial and passive gravitational mass, and that no experiment will ever detect a difference between them, in essence the equivalence principle.

This particular equivalence often referred to as the "Galilean equivalence principle" or the "weak equivalence principle" has the most important consequence for freely falling objects. Suppose an object has inertial and gravitational masses m and M, respectively. If the only force acting on the object comes from a gravitational field g, the force on the object is:

${\displaystyle F=Mg.}$

Given this force, the acceleration of the object can be determined by Newton's second law:

${\displaystyle F=ma.}$

Putting these together, the gravitational acceleration is given by:

${\displaystyle a={\frac {M}{m}}g.}$

This says that the ratio of gravitational to inertial mass of any object is equal to some constant K if and only if all objects fall at the same rate in a given gravitational field. This phenomenon is referred to as the "universality of free-fall". In addition, the constant K can be taken as 1 by defining our units appropriately.

The first experiments demonstrating the universality of free-fall were—according to scientific ‘folklore’—conducted by Galileo obtained by dropping objects from the Leaning Tower of Pisa. This is most likely apocryphal: he is more likely to have performed his experiments with balls rolling down nearly frictionless inclined planes to slow the motion and increase the timing accuracy. Increasingly precise experiments have been performed, such as those performed by Loránd Eötvös, using the torsion balance pendulum, in 1889. As of 2008, no deviation from universality, and thus from Galilean equivalence, has ever been found, at least to the precision 10⁻¹². More precise experimental efforts are still being carried out.

The universality of free-fall only applies to systems in which gravity is the only acting force. All other forces, especially friction and air resistance, must be absent or at least negligible. For example, if a hammer and a feather are dropped from the same height through the air on Earth, the feather will take much longer to reach the ground; the feather is not really in free-fall because the force of air resistance upwards against the feather is comparable to the downward force of gravity. On the other hand, if the experiment is performed in a vacuum, in which there is no air resistance, the hammer and the feather should hit the ground at exactly the same time (assuming the acceleration of both objects towards each other, and of the ground towards both objects, for its own part, is negligible). This can easily be done in a high school laboratory by dropping the objects in transparent tubes that have the air removed with a vacuum pump. It is even more dramatic when done in an environment that naturally has a vacuum, as David Scott did on the surface of the Moon during Apollo 15.

A stronger version of the equivalence principle, known as the Einstein equivalence principle or the strong equivalence principle, lies at the heart of the general theory of relativity. Einstein's equivalence principle states that within sufficiently small regions of space-time, it is impossible to distinguish between a uniform acceleration and a uniform gravitational field. Thus, the theory postulates that the force acting on a massive object caused by a gravitational field is a result of the object's tendency to move in a straight line (in other words its inertia) and should therefore be a function of its inertial mass and the strength of the gravitational field.

Origin of mass

In theoretical physics, a mass generation mechanism is a theory which attempts to explain the origin of mass from the most fundamental laws of physics. To date, a number of different models have been proposed which advocate different views of the origin of mass. The problem is complicated by the fact that the notion of mass is strongly related to the gravitational interaction but a theory of the latter has not been yet reconciled with the currently popular model of particle physics, known as the Standard Model.

Pre-Newtonian concepts

Weight as an amount

Depiction of early balance scales in the Papyrus of Hunefer (dated to the 19th dynasty, ca. 1285 BC). The scene shows Anubis weighing the heart of Hunefer.

The concept of amount is very old and predates recorded history. Humans, at some early era, realized that the weight of a collection of similar objects was directly proportional to the number of objects in the collection:

${\displaystyle W_{n}\propto n,}$

where W is the weight of the collection of similar objects and n is the number of objects in the collection. Proportionality, by definition, implies that two values have a constant ratio:

${\displaystyle {\frac {W_{n}}{n}}={\frac {W_{m}}{m}}}$, or equivalently ${\displaystyle {\frac {W_{n}}{W_{m}}}={\frac {n}{m}}.}$

An early use of this relationship is a balance scale, which balances the force of one object's weight against the force of another object's weight. The two sides of a balance scale are close enough that the objects experience similar gravitational fields. Hence, if they have similar masses then their weights will also be similar. This allows the scale, by comparing weights, to also compare masses.

Consequently, historical weight standards were often defined in terms of amounts. The Romans, for example, used the carob seed (carat or siliqua) as a measurement standard. If an object's weight was equivalent to 1728 carob seeds, then the object was said to weigh one Roman pound. If, on the other hand, the object's weight was equivalent to 144 carob seeds then the object was said to weigh one Roman ounce (uncia). The Roman pound and ounce were both defined in terms of different sized collections of the same common mass standard, the carob seed. The ratio of a Roman ounce (144 carob seeds) to a Roman pound (1728 carob seeds) was:

${\displaystyle {\frac {\mathrm {ounce} }{\mathrm {pound} }}={\frac {W_{144}}{W_{1728}}}={\frac {144}{1728}}={\frac {1}{12}}.}$

Planetary motion

In 1600 AD, Johannes Kepler sought employment with Tycho Brahe, who had some of the most precise astronomical data available. Using Brahe's precise observations of the planet Mars, Kepler spent the next five years developing his own method for characterizing planetary motion. In 1609, Johannes Kepler published his three laws of planetary motion, explaining how the planets orbit the Sun. In Kepler's final planetary model, he described planetary orbits as following elliptical paths with the Sun at a focal point of the ellipse. Kepler discovered that the square of the orbital period of each planet is directly proportional to the cube of the semi-major axis of its orbit, or equivalently, that the ratio of these two values is constant for all planets in the Solar System.

On 25 August 1609, Galileo Galilei demonstrated his first telescope to a group of Venetian merchants, and in early January 1610, Galileo observed four dim objects near Jupiter, which he mistook for stars. However, after a few days of observation, Galileo realized that these "stars" were in fact orbiting Jupiter. These four objects (later named the Galilean moons in honor of their discoverer) were the first celestial bodies observed to orbit something other than the Earth or Sun. Galileo continued to observe these moons over the next eighteen months, and by the middle of 1611 he had obtained remarkably accurate estimates for their periods.

Galilean free fall

Galileo Galilei (1636)

Distance traveled by a freely falling ball is proportional to the square of the elapsed time

Sometime prior to 1638, Galileo turned his attention to the phenomenon of objects in free fall, attempting to characterize these motions. Galileo was not the first to investigate Earth's gravitational field, nor was he the first to accurately describe its fundamental characteristics. However, Galileo's reliance on scientific experimentation to establish physical principles would have a profound effect on future generations of scientists. It is unclear if these were just hypothetical experiments used to illustrate a concept, or if they were real experiments performed by Galileo, but the results obtained from these experiments were both realistic and compelling. A biography by Galileo's pupil Vincenzo Viviani stated that Galileo had dropped balls of the same material, but different masses, from the Leaning Tower of Pisa to demonstrate that their time of descent was independent of their mass. In support of this conclusion, Galileo had advanced the following theoretical argument: He asked if two bodies of different masses and different rates of fall are tied by a string, does the combined system fall faster because it is now more massive, or does the lighter body in its slower fall hold back the heavier body? The only convincing resolution to this question is that all bodies must fall at the same rate.

A later experiment was described in Galileo's Two New Sciences published in 1638. One of Galileo's fictional characters, Salviati, describes an experiment using a bronze ball and a wooden ramp. The wooden ramp was "12 cubits long, half a cubit wide and three finger-breadths thick" with a straight, smooth, polished groove. The groove was lined with "parchment, also smooth and polished as possible". And into this groove was placed "a hard, smooth and very round bronze ball". The ramp was inclined at various angles to slow the acceleration enough so that the elapsed time could be measured. The ball was allowed to roll a known distance down the ramp, and the time taken for the ball to move the known distance was measured. The time was measured using a water clock described as follows:

"a large vessel of water placed in an elevated position; to the bottom of this vessel was soldered a pipe of small diameter giving a thin jet of water, which we collected in a small glass during the time of each descent, whether for the whole length of the channel or for a part of its length; the water thus collected was weighed, after each descent, on a very accurate balance; the differences and ratios of these weights gave us the differences and ratios of the times, and this with such accuracy that although the operation was repeated many, many times, there was no appreciable discrepancy in the results."

Galileo found that for an object in free fall, the distance that the object has fallen is always proportional to the square of the elapsed time:

${\displaystyle {\text{Distance}}\propto {{\text{Time}}^{2}}}$

Galileo had shown that objects in free fall under the influence of the Earth’s gravitational field have a constant acceleration, and Galileo’s contemporary, Johannes Kepler, had shown that the planets follow elliptical paths under the influence of the Sun’s gravitational mass. However, Galileo’s free fall motions and Kepler’s planetary motions remained distinct during Galileo’s lifetime.

Newtonian mass

Isaac Newton 1689

Robert Hooke had published his concept of gravitational forces in 1674, stating that all celestial bodies have an attraction or gravitating power towards their own centers, and also attract all the other celestial bodies that are within the sphere of their activity. He further stated that gravitational attraction increases by how much nearer the body wrought upon is to their own center. In correspondence with Isaac Newton from 1679 and 1680, Hooke conjectured that gravitational forces might decrease according to the double of the distance between the two bodies. Hooke urged Newton, who was a pioneer in the development of calculus, to work through the mathematical details of Keplerian orbits to determine if Hooke's hypothesis was correct. Newton's own investigations verified that Hooke was correct, but due to personal differences between the two men, Newton chose not to reveal this to Hooke. Isaac Newton kept quiet about his discoveries until 1684, at which time he told a friend, Edmond Halley, that he had solved the problem of gravitational orbits, but had misplaced the solution in his office. After being encouraged by Halley, Newton decided to develop his ideas about gravity and publish all of his findings. In November 1684, Isaac Newton sent a document to Edmund Halley, now lost but presumed to have been titled De motu corporum in gyrum (Latin for "On the motion of bodies in an orbit"). Halley presented Newton's findings to the Royal Society of London, with a promise that a fuller presentation would follow. Newton later recorded his ideas in a three book set, entitled Philosophiæ Naturalis Principia Mathematica (Latin: Mathematical Principles of Natural Philosophy). The first was received by the Royal Society on 28 April 1685–6; the second on 2 March 1686–7; and the third on 6 April 1686–7. The Royal Society published Newton’s entire collection at their own expense in May 1686–7.


Iacceleration, resulting in the discovery of the following relationship which governed both of these:

${\displaystyle \mathbf {g} =-\mu {\frac {\hat {\mathbf {R} }}{|\mathbf {R} |^{2}}}}$

where g is the apparent acceleration of a body as it passes through a region of space where gravitational fields exist, μ is the gravitational mass (standard gravitational parameter) of the body causing gravitational fields, and R is the radial coordinate (the distance between the centers of the two bodies).

By finding the exact relationship between a body's gravitational mass and its gravitational field, Newton provided a second method for measuring gravitational mass. The mass of the Earth can be determined using Kepler's method (from the orbit of Earth's Moon), or it can be determined by measuring the gravitational acceleration on the Earth's surface, and multiplying that by the square of the Earth's radius. The mass of the Earth is approximately three millionths of the mass of the Sun. To date, no other accurate method for measuring gravitational mass has been discovered.

Newton's cannonball

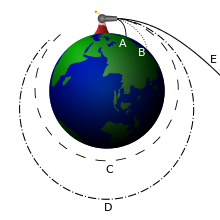
A cannon on top of a very high mountain shoots a cannonball horizontally. If the speed is low, the cannonball quickly falls back to Earth (A,B). At intermediate speeds, it will revolve around Earth along an elliptical orbit (C,D). At a sufficiently high speed, it will leave the Earth altogether (E).

Newton's cannonball was a thought experiment used to bridge the gap between Galileo's gravitational acceleration and Kepler's elliptical orbits. It appeared in Newton's 1728 book A Treatise of the System of the World. According to Galileo's concept of gravitation, a dropped stone falls with constant acceleration down towards the Earth. However, Newton explains that when a stone is thrown horizontally (meaning sideways or perpendicular to Earth's gravity) it follows a curved path. "For a stone projected is by the pressure of its own weight forced out of the rectilinear path, which by the projection alone it should have pursued, and made to describe a curve line in the air; and through that crooked way is at last brought down to the ground. And the greater the velocity is with which it is projected, the farther it goes before it falls to the Earth." Newton further reasons that if an object were "projected in an horizontal direction from the top of a high mountain" with sufficient velocity, "it would reach at last quite beyond the circumference of the Earth, and return to the mountain from which it was projected."

Universal gravitational mass

An apple experiences gravitational fields directed towards every part of the Earth; however, the sum total of these many fields produces a single gravitational field directed towards the Earth's center

In contrast to earlier theories (e.g. celestial spheres) which stated that the heavens were made of entirely different material, Newton's theory of mass was groundbreaking partly because it introduced universal gravitational mass: every object has gravitational mass, and therefore, every object generates a gravitational field. Newton further assumed that the strength of each object's gravitational field would decrease according to the square of the distance to that object. If a large collection of small objects were formed into a giant spherical body such as the Earth or Sun, Newton calculated the collection would create a gravitational field proportional to the total mass of the body, and inversely proportional to the square of the distance to the body's center.

For example, according to Newton's theory of universal gravitation, each carob seed produces a gravitational field. Therefore, if one were to gather an immense number of carob seeds and form them into an enormous sphere, then the gravitational field of the sphere would be proportional to the number of carob seeds in the sphere. Hence, it should be theoretically possible to determine the exact number of carob seeds that would be required to produce a gravitational field similar to that of the Earth or Sun. In fact, by unit conversion it is a simple matter of abstraction to realize that any traditional mass unit can theoretically be used to measure gravitational mass.

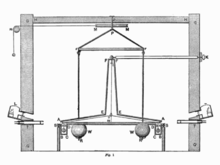
Vertical section drawing of Cavendish's torsion balance instrument including the building in which it was housed. The large balls were hung from a frame so they could be rotated into position next to the small balls by a pulley from outside. Figure 1 of Cavendish's paper.

Measuring gravitational mass in terms of traditional mass units is simple in principle, but extremely difficult in practice. According to Newton's theory all objects produce gravitational fields and it is theoretically possible to collect an immense number of small objects and form them into an enormous gravitating sphere. However, from a practical standpoint, the gravitational fields of small objects are extremely weak and difficult to measure. Newton's books on universal gravitation were published in the 1680s, but the first successful measurement of the Earth's mass in terms of traditional mass units, the Cavendish experiment, did not occur until 1797, over a hundred years later. Cavendish found that the Earth's density was 5.448 ± 0.033 times that of water. As of 2009, the Earth's mass in kilograms is only known to around five digits of accuracy, whereas its gravitational mass is known to over nine significant figures.

Given two objects A and B, of masses M_A and M_B, separated by a displacement R_AB, Newton's law of gravitation states that each object exerts a gravitational force on the other, of magnitude

${\displaystyle \mathbf {F} _{\text{AB}}=-GM_{\text{A}}M_{\text{B}}{\frac {{\hat {\mathbf {R} }}_{\text{AB}}}{|\mathbf {R} _{\text{AB}}|^{2}}}\ }$,

where G is the universal gravitational constant. The above statement may be reformulated in the following way: if g is the magnitude at a given location in a gravitational field, then the gravitational force on an object with gravitational mass M is

${\displaystyle F=Mg}$.

This is the basis by which masses are determined by weighing. In simple spring scales, for example, the force F is proportional to the displacement of the spring beneath the weighing pan, as per Hooke's law, and the scales are calibrated to take g into account, allowing the mass M to be read off. Assuming the gravitational field is equivalent on both sides of the balance, a balance measures relative weight, giving the relative gravitation mass of each object.

Inertial mass

Massmeter, a device for measuring the inertial mass of an astronaut in weightlessness. The mass is calculated via the oscillation period for a spring with the astronaut attached (Tsiolkovsky State Museum of the History of Cosmonautics)

Inertial mass is the mass of an object measured by its resistance to acceleration. This definition has been championed by Ernst Mach and has since been developed into the notion of operationalism by Percy W. Bridgman. The simple classical mechanics definition of mass is slightly different than the definition in the theory of special relativity, but the essential meaning is the same.

In classical mechanics, according to Newton's second law, we say that a body has a mass m if, at any instant of time, it obeys the equation of motion

${\displaystyle \mathbf {F} =m\mathbf {a} ,}$

where F is the resultant force acting on the body and a is the acceleration of the body's centre of mass. For the moment, we will put aside the question of what "force acting on the body" actually means.

This equation illustrates how mass relates to the inertia of a body. Consider two objects with different masses. If we apply an identical force to each, the object with a bigger mass will experience a smaller acceleration, and the object with a smaller mass will experience a bigger acceleration. We might say that the larger mass exerts a greater "resistance" to changing its state of motion in response to the force.

However, this notion of applying "identical" forces to different objects brings us back to the fact that we have not really defined what a force is. We can sidestep this difficulty with the help of Newton's third law, which states that if one object exerts a force on a second object, it will experience an equal and opposite force. To be precise, suppose we have two objects of constant inertial masses m₁ and m₂. We isolate the two objects from all other physical influences, so that the only forces present are the force exerted on m₁ by m₂, which we denote F₁₂, and the force exerted on m₂ by m₁, which we denote F₂₁. Newton's second law states that

${\displaystyle {\begin{aligned}\mathbf {F_{12}} &=m_{1}\mathbf {a} _{1},\\\mathbf {F_{21}} &=m_{2}\mathbf {a} _{2},\end{aligned}}}$

where a₁ and a₂ are the accelerations of m₁ and m₂, respectively. Suppose that these accelerations are non-zero, so that the forces between the two objects are non-zero. This occurs, for example, if the two objects are in the process of colliding with one another. Newton's third law then states that

${\displaystyle \mathbf {F} _{12}=-\mathbf {F} _{21};}$

and thus

${\displaystyle m_{1}=m_{2}{\frac {|\mathbf {a} _{2}|}{|\mathbf {a} _{1}|}}\!.}$

If |a₁| is non-zero, the fraction is well-defined, which allows us to measure the inertial mass of m₁. In this case, m₂ is our "reference" object, and we can define its mass m as (say) 1 kilogram. Then we can measure the mass of any other object in the universe by colliding it with the reference object and measuring the accelerations.

Additionally, mass relates a body's momentum p to its linear velocity v:

${\displaystyle \mathbf {p} =m\mathbf {v} }$,

and the body's kinetic energy K to its velocity:

${\displaystyle K={\dfrac {1}{2}}m|\mathbf {v} |^{2}}$.

The primary difficulty with Mach's definition of mass is that it fails to take into account the potential energy (or binding energy) needed to bring two masses sufficiently close to one another to perform the measurement of mass. This is most vividly demonstrated by comparing the mass of the proton in the nucleus of deuterium, to the mass of the proton in free space (which is greater by about 0.239% - this is due to the binding energy of deuterium.). Thus, for example, if the reference weight m₂ is taken to be the mass of the neutron in free space, and the relative accelerations for the proton and neutron in deuterium are computed, then the above formula over-estimates the mass m₁ (by 0.239%) for the proton in deuterium. At best, Mach's formula can only be used to obtain ratios of masses, that is, as m₁ /m₂ = |a₂| / |a₁|. An additional difficulty was pointed out by Henri Poincaré, which is that the measurement of instantaneous acceleration is impossible: unlike the measurement of time or distance, there is no way to measure acceleration with a single measurement; one must make multiple measurements (of position, time, etc.) and perform a computation to obtain the acceleration. Poincaré termed this to be an "insurmountable flaw" in the Mach definition of mass.

Atomic mass

Typically, the mass of objects is measured in relation to that of the kilogram, which is defined as the mass of the international prototype kilogram (IPK), a platinum alloy cylinder stored in an environmentally-monitored safe secured in a vault at the International Bureau of Weights and Measures in France. However, the IPK is not convenient for measuring the masses of atoms and particles of similar scale, as it contains trillions of trillions of atoms, and has most certainly lost or gained a little mass over time despite the best efforts to prevent this. It is much easier to precisely compare an atom's mass to that of another atom, thus scientists developed the atomic mass unit (or Dalton). By definition, 1 u is exactly one twelfth of the mass of a carbon-12 atom, and by extension a carbon-12 atom has a mass of exactly 12 u. This definition, however, might be changed by the proposed redefinition of SI base units, which will leave the Dalton very close to one, but no longer exactly equal to it.

Mass in relativity

Special relativity

In some frameworks of special relativity, physicists have used differing definitions of the term "mass". However, such usage is controversial and has fallen out of favor.

In these frameworks, two kinds of mass are defined: rest mass (invariant mass), and relativistic mass (which increases with velocity). Rest mass is the Newtonian mass as measured by an observer moving along with the object. Relativistic mass is the total quantity of energy in a body or system divided by c². The two are related by the following equation:

${\displaystyle m_{\mathrm {relative} }=\gamma (m_{\mathrm {rest} })\!}$

where ${\displaystyle \gamma }$ is the Lorentz factor:

${\displaystyle \gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}}$

The invariant mass of systems is the same for observers in all inertial frames, while the relativistic mass depends on the observer's frame of reference. In order to formulate the equations of physics such that mass values do not change between observers, it is convenient to use rest mass. The rest mass of a body is also related to its energy E and the magnitude of its momentum p by the relativistic energy-momentum equation:

${\displaystyle (m_{\mathrm {rest} })c^{2}={\sqrt {E_{\mathrm {total} }^{2}-(|\mathbf {p} |c)^{2}}}.\!}$

So long as the system is closed with respect to mass and energy, both kinds of mass are conserved in any given frame of reference. The conservation of mass holds even as some types of particles are converted to others. Matter particles (such as atoms) may be converted to non-matter particles (such as photons of light), but this does not affect the total amount of mass or energy. Although things like heat may not be matter, all types of energy still continue to exhibit mass. Thus, mass and energy do not change into one another in relativity; rather, both are names for the same thing, and neither mass nor energy appear without the other.

Both rest and relativistic mass can be expressed as an energy by applying the well-known relationship E = mc², yielding rest energy and "relativistic energy" (total system energy) respectively:

${\displaystyle E_{\mathrm {rest} }=(m_{\mathrm {rest} })c^{2}\!}$

${\displaystyle E_{\mathrm {total} }=(m_{\mathrm {relative} })c^{2}\!}$

The "relativistic" mass and energy concepts are related to their "rest" counterparts, but they do not have the same value as their rest counterparts in systems where there is a net momentum. Because the relativistic mass is proportional to the energy, it has gradually fallen into disuse among physicists. There is disagreement over whether the concept remains useful pedagogically.

In bound systems, the binding energy must often be subtracted from the mass of the unbound system, because binding energy commonly leaves the system at the time it is bound. The mass of the system changes in this process merely because the system was not closed during the binding process, so the energy escaped. For example, the binding energy of atomic nuclei is often lost in the form of gamma rays when the nuclei are formed, leaving nuclides which have less mass than the free particles (nucleons) of which they are composed.

Mass–energy equivalence also holds in macroscopic systems. For example, if one takes exactly one kilogram of ice, and applies heat, the mass of the resulting melt-water will be more than a kilogram: it will include the mass from the thermal energy (latent heat) used to melt the ice; this follows from the conservation of energy. This number is small but not negligible: about 3.7 nanograms. It is given by the latent heat of melting ice (334 kJ/kg) divided by the speed of light squared (c² = 9×10¹⁶ m²/s²).

General relativity

In general relativity, the equivalence principle is the equivalence of gravitational and inertial mass. At the core of this assertion is Albert Einstein's idea that the gravitational force as experienced locally while standing on a massive body (such as the Earth) is the same as the pseudo-force experienced by an observer in a non-inertial (i.e. accelerated) frame of reference.

However, it turns out that it is impossible to find an objective general definition for the concept of invariant mass in general relativity. At the core of the problem is the non-linearity of the Einstein field equations, making it impossible to write the gravitational field energy as part of the stress–energy tensor in a way that is invariant for all observers. For a given observer, this can be achieved by the stress–energy–momentum pseudotensor.

Mass in quantum physics

In classical mechanics, the inert mass of a particle appears in the Euler–Lagrange equation as a parameter m:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\ \left(\,{\frac {\partial L}{\partial {\dot {x}}_{i}}}\,\right)\ =\ m\,{\ddot {x}}_{i}}$.

After quantization, replacing the position vector x with a wave function, the parameter m appears in the kinetic energy operator:

${\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,\,t)=\left(-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} )\right)\Psi (\mathbf {r} ,\,t)}$.

In the ostensibly covariant (relativistically invariant) Dirac equation, and in natural units, this becomes:

${\displaystyle (-i\gamma ^{\mu }\partial _{\mu }+m)\psi =0\,}$

where the "mass" parameter m is now simply a constant associated with the quantum described by the wave function ψ.

In the Standard Model of particle physics as developed in the 1960s, this term arises from the coupling of the field ψ to an additional field Φ, the Higgs field. In the case of fermions, the Higgs mechanism results in the replacement of the term mψ in the Lagrangian with ${\displaystyle G_{\psi }{\overline {\psi }}\phi \psi }$. This shifts the explanandum of the value for the mass of each elementary particle to the value of the unknown couplings G_ψ.

Tachyonic particles and imaginary (complex) mass

A tachyonic field, or simply tachyon, is a quantum field with an imaginary mass. Although tachyons (particles that move faster than light) are a purely hypothetical concept not generally believed to exist, fields with imaginary mass have come to play an important role in modern physics and are discussed in popular books on physics. Under no circumstances do any excitations ever propagate faster than light in such theories – the presence or absence of a tachyonic mass has no effect whatsoever on the maximum velocity of signals (there is no violation of causality). While the field may have imaginary mass, any physical particles do not; the "imaginary mass" shows that the system becomes unstable, and sheds the instability by undergoing a type of phase transition called tachyon condensation (closely related to second order phase transitions) that results in symmetry breaking in current models of particle physics.

The term "tachyon" was coined by Gerald Feinberg in a 1967 paper, but it was soon realized that Feinberg's model in fact did not allow for superluminal speeds. Instead, the imaginary mass creates an instability in the configuration:- any configuration in which one or more field excitations are tachyonic will spontaneously decay, and the resulting configuration contains no physical tachyons. This process is known as tachyon condensation. Well known examples include the condensation of the Higgs boson in particle physics, and ferromagnetism in condensed matter physics.

Although the notion of a tachyonic imaginary mass might seem troubling because there is no classical interpretation of an imaginary mass, the mass is not quantized. Rather, the scalar field is; even for tachyonic quantum fields, the field operators at spacelike separated points still commute (or anticommute), thus preserving causality. Therefore, information still does not propagate faster than light, and solutions grow exponentially, but not superluminally (there is no violation of causality).  Tachyon condensation drives a physical system that has reached a local limit and might naively be expected to produce physical tachyons, to an alternate stable state where no physical tachyons exist. Once the tachyonic field reaches the minimum of the potential, its quanta are not tachyons any more but rather are ordinary particles with a positive mass-squared.

This is a special case of the general rule, where unstable massive particles are formally described as having a complex mass, with the real part being their mass in the usual sense, and the imaginary part being the decay rate in natural units. However, in quantum field theory, a particle (a "one-particle state") is roughly defined as a state which is constant over time; i.e., an eigenvalue of the Hamiltonian. An unstable particle is a state which is only approximately constant over time; If it exists long enough to be measured, it can be formally described as having a complex mass, with the real part of the mass greater than its imaginary part. If both parts are of the same magnitude, this is interpreted as a resonance appearing in a scattering process rather than a particle, as it is considered not to exist long enough to be measured independently of the scattering process. In the case of a tachyon the real part of the mass is zero, and hence no concept of a particle can be attributed to it.

In a Lorentz invariant theory, the same formulas that apply to ordinary slower-than-light particles (sometimes called "bradyons" in discussions of tachyons) must also apply to tachyons. In particular the energy–momentum relation:

${\displaystyle E^{2}=p^{2}c^{2}+m^{2}c^{4}\;}$

(where p is the relativistic momentum of the bradyon and m is its rest mass) should still apply, along with the formula for the total energy of a particle:

${\displaystyle E={\frac {mc^{2}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}.}$

This equation shows that the total energy of a particle (bradyon or tachyon) contains a contribution from its rest mass (the "rest mass–energy") and a contribution from its motion, the kinetic energy. When v is larger than c, the denominator in the equation for the energy is "imaginary", as the value under the radical is negative. Because the total energy must be real, the numerator must also be imaginary: i.e. the rest mass m must be imaginary, as a pure imaginary number divided by another pure imaginary number is a real number.

Exotic matter and negative mass

The negative mass exists in the model to describe dark energy (phantom energy) and radiation in negative-index metamaterial in a unified way.^[41] In this way, the negative mass is associated with negative momentum, negative pressure, negative kinetic energy and FTL (faster-than-light).