From Wikipedia, the free encyclopedia
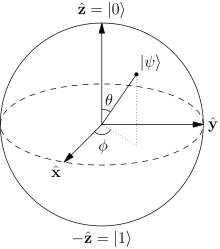
The Bloch sphere is a representation of a qubit, the fundamental building block of quantum computers.
Quantum computing studies theoretical computation systems (quantum computers) that make direct use of quantum-mechanical phenomena, such as superposition and entanglement, to perform operations on data.[1]
Quantum computers are different from digital computers based on transistors. Whereas digital computers require data to be encoded into binary digits (bits), each of which is always in one of two definite states (0 or 1), quantum computation uses qubits (quantum bits), which can be in superpositions of states. A quantum Turing machine is a theoretical model of such a computer, and is also known as the universal quantum computer. Quantum computers share theoretical similarities with non-deterministic and probabilistic computers. The field of quantum computing was initiated by the work of Yuri Manin in 1980,[2] Richard Feynman in 1982,[3] and David Deutsch.[4] A quantum computer with spins as quantum bits was also formulated for use as a quantum space–time in 1968.[5]
As of 2015[update], the development of actual quantum computers is still in its infancy, but experiments have been carried out in which quantum computational operations were executed on a very small number of qubits.[6][citation needed]
Both practical and theoretical research continues, and many national governments and military agencies are funding quantum computing research in an effort to develop quantum computers for civilian, business, trade, and national security purposes, such as cryptanalysis.[7]
Large-scale quantum computers will be able to solve certain problems much more quickly than any classical computers that use even the best currently known algorithms, like integer factorization using Shor's algorithm or the simulation of quantum many-body systems. There exist quantum algorithms, such as Simon's algorithm, that run faster than any possible probabilistic classical algorithm.[8] Given sufficient computational resources, however, a classical computer could be made to simulate any quantum algorithm, as quantum computation does not violate the Church–Turing thesis. [9]
Basis
A classical computer has a memory made up of bits, where each bit represents either a one or a zero. A quantum computer maintains a sequence of qubits. A single qubit can represent a one, a zero, or any quantum superposition of those two qubit states; a pair of qubits can be in any quantum superposition of 4 states, and three qubits in any superposition of 8 states. In general, a quantum computer with qubits can be in an arbitrary superposition of up to
qubits can be in an arbitrary superposition of up to 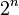 different states simultaneously (this compares to a normal computer that can only be in one of these
different states simultaneously (this compares to a normal computer that can only be in one of these 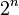 states at any one time). A quantum computer operates by setting the qubits in a controlled initial state that represents the problem at hand and by manipulating those qubits with a fixed sequence of quantum logic gates. The sequence of gates to be applied is called a quantum algorithm. The calculation ends with a measurement, collapsing the system of qubits into one of the
states at any one time). A quantum computer operates by setting the qubits in a controlled initial state that represents the problem at hand and by manipulating those qubits with a fixed sequence of quantum logic gates. The sequence of gates to be applied is called a quantum algorithm. The calculation ends with a measurement, collapsing the system of qubits into one of the 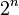 pure states, where each qubit is zero or one. The outcome can therefore be at most
pure states, where each qubit is zero or one. The outcome can therefore be at most  classical bits of information. Quantum algorithms are often non-deterministic, in that they provide the correct solution only with a certain known probability.
classical bits of information. Quantum algorithms are often non-deterministic, in that they provide the correct solution only with a certain known probability.An example of an implementation of qubits for a quantum computer could start with the use of particles with two spin states: "down" and "up" (typically written
 and
and  , or
, or 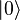 and
and  ). But in fact any system possessing an observable quantity A, which is conserved under time evolution such that A has at least two discrete and sufficiently spaced consecutive eigenvalues, is a suitable candidate for implementing a qubit. This is true because any such system can be mapped onto an effective spin-1/2 system.
). But in fact any system possessing an observable quantity A, which is conserved under time evolution such that A has at least two discrete and sufficiently spaced consecutive eigenvalues, is a suitable candidate for implementing a qubit. This is true because any such system can be mapped onto an effective spin-1/2 system.Mechanics
A quantum computer with a given number of qubits is fundamentally different from a classical computer composed of the same number of classical bits. For example, to represent the state of an n-qubit system on a classical computer would require the storage of 2n complex coefficients. Although this fact may seem to indicate that qubits can hold exponentially more information than their classical counterparts, care must be taken not to overlook the fact that the qubits are only in a probabilistic superposition of all of their states. This means that when the final state of the qubits is measured, they will only be found in one of the possible configurations they were in before measurement. Moreover, it is incorrect to think of the qubits as only being in one particular state before measurement since the fact that they were in a superposition of states before the measurement was made directly affects the possible outcomes of the computation.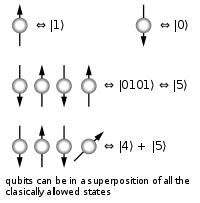
Qubits are made up of controlled particles and the means of control (e.g. devices that trap particles and switch them from one state to another).[10]
For example: Consider first a classical computer that operates on a three-bit register. The state of the computer at any time is a probability distribution over the
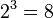 different three-bit strings 000, 001, 010, 011, 100, 101, 110, 111. If it is a deterministic computer, then it is in exactly one of these states with probability 1.
different three-bit strings 000, 001, 010, 011, 100, 101, 110, 111. If it is a deterministic computer, then it is in exactly one of these states with probability 1.However, if it is a probabilistic computer, then there is a possibility of it being in any one of a number of different states. We can describe this probabilistic state by eight nonnegative numbers A,B,C,D,E,F,G,H (where A = is the probability that the computer is in state 000, B = is the probability that the computer is in state 001, etc.). There is a restriction that these probabilities sum to 1.
The state of a three-qubit quantum computer is similarly described by an eight-dimensional vector (a,b,c,d,e,f,g,h), called a ket. Here, however, the coefficients can have complex values, and it is the sum of the squares of the coefficients' magnitudes,
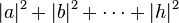 , that must equal 1. These squared magnitudes represent the probability of each of the given states. However, because a complex number encodes not just a magnitude but also a direction in the complex plane, the phase difference between any two coefficients (states) represents a meaningful parameter. This is a fundamental difference between quantum computing and probabilistic classical computing.[11]
, that must equal 1. These squared magnitudes represent the probability of each of the given states. However, because a complex number encodes not just a magnitude but also a direction in the complex plane, the phase difference between any two coefficients (states) represents a meaningful parameter. This is a fundamental difference between quantum computing and probabilistic classical computing.[11]If you measure the three qubits, you will observe a three-bit string. The probability of measuring a given string is the squared magnitude of that string's coefficient (i.e., the probability of measuring 000 =
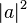 , the probability of measuring 001 =
, the probability of measuring 001 =  , etc..). Thus, measuring a quantum state described by complex coefficients (a,b,...,h) gives the classical probability distribution
, etc..). Thus, measuring a quantum state described by complex coefficients (a,b,...,h) gives the classical probability distribution  and we say that the quantum state "collapses" to a classical state as a result of making the measurement.
and we say that the quantum state "collapses" to a classical state as a result of making the measurement.Note that an eight-dimensional vector can be specified in many different ways depending on what basis is chosen for the space. The basis of bit strings (e.g., 000, 001, …, 111) is known as the computational basis. Other possible bases are unit-length, orthogonal vectors and the eigenvectors of the Pauli-x operator. Ket notation is often used to make the choice of basis explicit. For example, the state (a,b,c,d,e,f,g,h) in the computational basis can be written as:
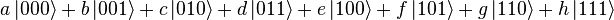
- where, e.g.,

 and
and 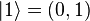 .
.Using the eigenvectors of the Pauli-x operator, a single qubit is
 and
and  .
.Operation
While a classical three-bit state and a quantum three-qubit state are both eight-dimensional vectors, they are manipulated quite differently for classical or quantum computation. For computing in either case, the system must be initialized, for example into the all-zeros string, , corresponding to the vector (1,0,0,0,0,0,0,0). In classical randomized computation, the system evolves according to the application of stochastic matrices, which preserve that the probabilities add up to one (i.e., preserve the L1 norm). In quantum computation, on the other hand, allowed operations are unitary matrices, which are effectively rotations (they preserve that the sum of the squares add up to one, the Euclidean or L2 norm). (Exactly what unitaries can be applied depend on the physics of the quantum device.) Consequently, since rotations can be undone by rotating backward, quantum computations are reversible. (Technically, quantum operations can be probabilistic combinations of unitaries, so quantum computation really does generalize classical computation. See quantum circuit for a more precise formulation.)
, corresponding to the vector (1,0,0,0,0,0,0,0). In classical randomized computation, the system evolves according to the application of stochastic matrices, which preserve that the probabilities add up to one (i.e., preserve the L1 norm). In quantum computation, on the other hand, allowed operations are unitary matrices, which are effectively rotations (they preserve that the sum of the squares add up to one, the Euclidean or L2 norm). (Exactly what unitaries can be applied depend on the physics of the quantum device.) Consequently, since rotations can be undone by rotating backward, quantum computations are reversible. (Technically, quantum operations can be probabilistic combinations of unitaries, so quantum computation really does generalize classical computation. See quantum circuit for a more precise formulation.)Finally, upon termination of the algorithm, the result needs to be read off. In the case of a classical computer, we sample from the probability distribution on the three-bit register to obtain one definite three-bit string, say 000.
Quantum mechanically, we measure the three-qubit state, which is equivalent to collapsing the quantum state down to a classical distribution (with the coefficients in the classical state being the squared magnitudes of the coefficients for the quantum state, as described above), followed by sampling from that distribution. Note that this destroys the original quantum state. Many algorithms will only give the correct answer with a certain probability. However, by repeatedly initializing, running and measuring the quantum computer's results, the probability of getting the correct answer can be increased.
For more details on the sequences of operations used for various quantum algorithms, see universal quantum computer, Shor's algorithm, Grover's algorithm, Deutsch–Jozsa algorithm, amplitude amplification, quantum Fourier transform, quantum gate, quantum adiabatic algorithm and quantum error correction.
Potential
Integer factorization is believed to be computationally infeasible with an ordinary computer for large integers if they are the product of few prime numbers (e.g., products of two 300-digit primes).[12] By comparison, a quantum computer could efficiently solve this problem using Shor's algorithm to find its factors. This ability would allow a quantum computer to decrypt many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem. In particular, most of the popular public key ciphers are based on the difficulty of factoring integers or the discrete logarithm problem, both of which can be solved by Shor's algorithm. In particular the RSA, Diffie-Hellman, and Elliptic curve Diffie-Hellman algorithms could be broken. These are used to protect secure Web pages, encrypted email, and many other types of data. Breaking these would have significant ramifications for electronic privacy and security.However, other cryptographic algorithms do not appear to be broken by those algorithms.[13][14] Some public-key algorithms are based on problems other than the integer factorization and discrete logarithm problems to which Shor's algorithm applies, like the McEliece cryptosystem based on a problem in coding theory.[13][15] Lattice-based cryptosystems are also not known to be broken by quantum computers, and finding a polynomial time algorithm for solving the dihedral hidden subgroup problem, which would break many lattice based cryptosystems, is a well-studied open problem.[16] It has been proven that applying Grover's algorithm to break a symmetric (secret key) algorithm by brute force requires time equal to roughly 2n/2 invocations of the underlying cryptographic algorithm, compared with roughly 2n in the classical case,[17] meaning that symmetric key lengths are effectively halved: AES-256 would have the same security against an attack using Grover's algorithm that AES-128 has against classical brute-force search (see Key size). Quantum cryptography could potentially fulfill some of the functions of public key cryptography.
Besides factorization and discrete logarithms, quantum algorithms offering a more than polynomial speedup over the best known classical algorithm have been found for several problems,[18] including the simulation of quantum physical processes from chemistry and solid state physics, the approximation of Jones polynomials, and solving Pell's equation. No mathematical proof has been found that shows that an equally fast classical algorithm cannot be discovered, although this is considered unlikely. For some problems, quantum computers offer a polynomial speedup. The most well-known example of this is quantum database search, which can be solved by Grover's algorithm using quadratically fewer queries to the database than are required by classical algorithms. In this case the advantage is provable. Several other examples of provable quantum speedups for query problems have subsequently been discovered, such as for finding collisions in two-to-one functions and evaluating NAND trees.
Consider a problem that has these four properties:
- The only way to solve it is to guess answers repeatedly and check them,
- The number of possible answers to check is the same as the number of inputs,
- Every possible answer takes the same amount of time to check, and
- There are no clues about which answers might be better: generating possibilities randomly is just as good as checking them in some special order.
For problems with all four properties, the time for a quantum computer to solve this will be proportional to the square root of the number of inputs. It can be used to attack symmetric ciphers such as Triple DES and AES by attempting to guess the secret key.[19]
Grover's algorithm can also be used to obtain a quadratic speed-up over a brute-force search for a class of problems known as NP-complete.
Since chemistry and nanotechnology rely on understanding quantum systems, and such systems are impossible to simulate in an efficient manner classically, many believe quantum simulation will be one of the most important applications of quantum computing.[20] Quantum simulation could also be used to simulate the behavior of atoms and particles at unusual conditions such as the reactions inside a collider.[21]
There are a number of technical challenges in building a large-scale quantum computer, and thus far quantum computers have yet to solve a problem faster than a classical computer. David DiVincenzo, of IBM, listed the following requirements for a practical quantum computer:[22]
- scalable physically to increase the number of qubits;
- qubits that can be initialized to arbitrary values;
- quantum gates that are faster than decoherence time;
- universal gate set;
- qubits that can be read easily.
Quantum decoherence
One of the greatest challenges is controlling or removing quantum decoherence. This usually means isolating the system from its environment as interactions with the external world cause the system to decohere. However, other sources of decoherence also exist. Examples include the quantum gates, and the lattice vibrations and background nuclear spin of the physical system used to implement the qubits. Decoherence is irreversible, as it is non-unitary, and is usually something that should be highly controlled, if not avoided. Decoherence times for candidate systems, in particular the transverse relaxation time T2 (for NMR and MRI technology, also called the dephasing time), typically range between nanoseconds and seconds at low temperature.[11] Currently, some quantum computers require their qubits to be cooled to 20 millikelvin in order to prevent significant decoherence.[23]These issues are more difficult for optical approaches as the timescales are orders of magnitude shorter and an often-cited approach to overcoming them is optical pulse shaping. Error rates are typically proportional to the ratio of operating time to decoherence time, hence any operation must be completed much more quickly than the decoherence time.
If the error rate is small enough, it is thought to be possible to use quantum error correction, which corrects errors due to decoherence, thereby allowing the total calculation time to be longer than the decoherence time. An often cited figure for required error rate in each gate is 10−4. This implies that each gate must be able to perform its task in one 10,000th of the decoherence time of the system.
Meeting this scalability condition is possible for a wide range of systems. However, the use of error correction brings with it the cost of a greatly increased number of required qubits. The number required to factor integers using Shor's algorithm is still polynomial, and thought to be between L and L2, where L is the number of bits in the number to be factored; error correction algorithms would inflate this figure by an additional factor of L. For a 1000-bit number, this implies a need for about 104 qubits without error correction.[24] With error correction, the figure would rise to about 107 qubits. Note that computation time is about L2 or about 107 steps and on 1 MHz, about 10 seconds.
A very different approach to the stability-decoherence problem is to create a topological quantum computer with anyons, quasi-particles used as threads and relying on braid theory to form stable logic gates.[25][26]
Developments
There are a number of quantum computing models, distinguished by the basic elements in which the computation is decomposed. The four main models of practical importance are:- Quantum gate array (computation decomposed into sequence of few-qubit quantum gates)
- One-way quantum computer (computation decomposed into sequence of one-qubit measurements applied to a highly entangled initial state or cluster state)
- Adiabatic quantum computer, based on Quantum annealing (computation decomposed into a slow continuous transformation of an initial Hamiltonian into a final Hamiltonian, whose ground states contains the solution)[27]
- Topological quantum computer[28] (computation decomposed into the braiding of anyons in a 2D lattice)
For physically implementing a quantum computer, many different candidates are being pursued, among them (distinguished by the physical system used to realize the qubits):
- Superconductor-based quantum computers (including SQUID-based quantum computers)[29][30] (qubit implemented by the state of small superconducting circuits (Josephson junctions))
- Trapped ion quantum computer (qubit implemented by the internal state of trapped ions)
- Optical lattices (qubit implemented by internal states of neutral atoms trapped in an optical lattice)
- Quantum dot computer, spin-based (e.g. the Loss-DiVincenzo quantum computer [31]) (qubit given by the spin states of trapped electrons)
- Quantum dot computer, spatial-based (qubit given by electron position in double quantum dot)[32]
- Nuclear magnetic resonance on molecules in solution (liquid-state NMR) (qubit provided by nuclear spins within the dissolved molecule)
- Solid-state NMR Kane quantum computers (qubit realized by the nuclear spin state of phosphorus donors in silicon)
- Electrons-on-helium quantum computers (qubit is the electron spin)
- Cavity quantum electrodynamics (CQED) (qubit provided by the internal state of trapped atoms coupled to high-finesse cavities)
- Molecular magnet[33] (qubit given by spin states)
- Fullerene-based ESR quantum computer (qubit based on the electronic spin of atoms or molecules encased in fullerenes)
- Linear optical quantum computer (qubits realized by processing states of different modes of light through linear elements e.g. mirrors, beam splitters and phase shifters)[34]
- Diamond-based quantum computer[35][36][37] (qubit realized by electronic or nuclear spin of nitrogen-vacancy centers in diamond)
- Bose–Einstein condensate-based quantum computer[38]
- Transistor-based quantum computer – string quantum computers with entrainment of positive holes using an electrostatic trap
- Rare-earth-metal-ion-doped inorganic crystal based quantum computers[39][40] (qubit realized by the internal electronic state of dopants in optical fibers)
Timeline
In 2001, researchers demonstrated Shor's algorithm to factor 15 using a 7-qubit NMR computer.[41]In 2005, researchers at the University of Michigan built a semiconductor chip ion trap. Such devices from standard lithography, may point the way to scalable quantum computing.[42]
In 2009, researchers at Yale University created the first solid-state quantum processor. The two-qubit superconducting chip had artificial atom qubits made of a billion aluminum atoms that acted like a single atom that could occupy two states.[43][44]
A team at the University of Bristol, also created a silicon chip based on quantum optics, able to run Shor's algorithm.[45] Further developments were made in 2010.[46] Springer publishes a journal (Quantum Information Processing) devoted to the subject.[47]
In April 2011, a team of scientists from Australia and Japan made a breakthrough in quantum teleportation. They successfully transferred a complex set of quantum data with full transmission integrity, without affecting the qubits superpositions.[48][49]

Photograph of a chip constructed by D-Wave Systems Inc., mounted and wire-bonded in a sample holder. The D-Wave processor is designed to use 128 superconducting logic elements that exhibit controllable and tunable coupling to perform operations.
In 2011, D-Wave Systems announced the first commercial quantum annealer, the D-Wave One, claiming a 128 qubit processor.[50] On May 25, 2011 Lockheed Martin agreed to purchase a D-Wave One system.[51] Lockheed and the University of Southern California (USC) will house the D-Wave One at the newly formed USC Lockheed Martin Quantum Computing Center.[52] D-Wave's engineers designed the chips with an empirical approach, focusing on solving particular problems. Investors liked this more than academics, who said D-Wave had not demonstrated they really had a quantum computer. Criticism softened after a D-Wave paper in Nature, that proved the chips have some quantum properties.[53][54] Experts remain skeptical of D-Waves claims. Two published papers have concluded that the D-Wave machine operates classically, not via quantum computing.[55][56]
During the same year, researchers at the University of Bristol created an all-bulk optics system that ran a version of Shor's algorithm to successfully factor 21.[57]
In September 2011 researchers proved quantum computers can be made with a Von Neumann architecture (separation of RAM).[58]
In November 2011 researchers factorized 143 using 4 qubits.[59]
In February 2012 IBM scientists said that they had made several breakthroughs in quantum computing with superconducting integrated circuits.[60]
In April 2012 a multinational team of researchers from the University of Southern California, Delft University of Technology, the Iowa State University of Science and Technology, and the University of California, Santa Barbara, constructed a two-qubit quantum computer on a doped diamond crystal that can easily be scaled up and is functional at room temperature. Two logical qubit directions of electron spin and nitrogen kernels spin were used, with microwave impulses. This computer ran Grover's algorithm generating the right answer from the first try in 95% of cases.[61]
In September 2012, Australian researchers at the University of New South Wales said the world's first quantum computer was just 5 to 10 years away, after announcing a global breakthrough enabling manufacture of its memory building blocks. A research team led by Australian engineers created the first working qubit based on a single atom in silicon, invoking the same technological platform that forms the building blocks of modern day computers.[62] [63]
In October 2012, Nobel Prizes were presented to David J. Wineland and Serge Haroche for their basic work on understanding the quantum world, which may help make quantum computing possible.[64][65]
In November 2012, the first quantum teleportation from one macroscopic object to another was reported.[66][67]
In December 2012, the first dedicated quantum computing software company, 1QBit was founded in Vancouver, BC.[68] 1QBit is the first company to focus exclusively on commercializing software applications for commercially available quantum computers, including the D-Wave Two. 1QBit's research demonstrated the ability of superconducting quantum annealing processors to solve real-world problems.[69]
In February 2013, a new technique, boson sampling, was reported by two groups using photons in an optical lattice that is not a universal quantum computer but may be good enough for practical problems. Science Feb 15, 2013
In May 2013, Google announced that it was launching the Quantum Artificial Intelligence Lab, hosted by NASA 's Ames Research Center, with a 512-qubit D-Wave quantum computer. The USRA (Universities Space Research Association) will invite researchers to share time on it with the goal of studying quantum computing for machine learning.[70]
In early 2014 it was reported, based on documents provided by former NSA contractor Edward Snowden, that the U.S. National Security Agency (NSA) is running a $79.7 million research program (titled "Penetrating Hard Targets") to develop a quantum computer capable of breaking vulnerable encryption.[71]
In 2014, a group of researchers from ETH Zürich, USC, Google and Microsoft reported a definition of quantum speedup, and were not able to measure quantum speedup with the D-Wave Two device, but did not explicitly rule it out.[72][73]
In 2014, researchers at University of New South Wales used silicon as a protectant shell around qubits, making them more accurate, increasing the length of time they will hold information and possibly made quantum computers easier to build.[74]
In April 2015 IBM scientists claimed two critical advances towards the realization of a practical quantum computer. They claimed the ability to detect and measure both kinds of quantum errors simultaneously, as well as a new, square quantum bit circuit design that could scale to larger dimensions. [75]
Relation to computational complexity theory
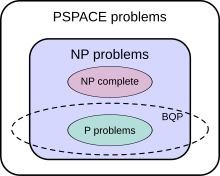
The suspected relationship of BQP to other problem spaces.[76]
The class of problems that can be efficiently solved by quantum computers is called BQP, for "bounded error, quantum, polynomial time". Quantum computers only run probabilistic algorithms, so BQP on quantum computers is the counterpart of BPP ("bounded error, probabilistic, polynomial time") on classical computers. It is defined as the set of problems solvable with a polynomial-time algorithm, whose probability of error is bounded away from one half.[77] A quantum computer is said to "solve" a problem if, for every instance, its answer will be right with high probability. If that solution runs in polynomial time, then that problem is in BQP.
BQP is contained in the complexity class #P (or more precisely in the associated class of decision problems P#P),[78] which is a subclass of PSPACE.
BQP is suspected to be disjoint from NP-complete and a strict superset of P, but that is not known. Both integer factorization and discrete log are in BQP. Both of these problems are NP problems suspected to be outside BPP, and hence outside P. Both are suspected to not be NP-complete. There is a common misconception that quantum computers can solve NP-complete problems in polynomial time. That is not known to be true, and is generally suspected to be false.[78]
The capacity of a quantum computer to accelerate classical algorithms has rigid limits—upper bounds of quantum computation's complexity. The overwhelming part of classical calculations cannot be accelerated on a quantum computer.[79] A similar fact takes place for particular computational tasks, like the search problem, for which Grover's algorithm is optimal.[80]
Although quantum computers may be faster than classical computers, those described above can't solve any problems that classical computers can't solve, given enough time and memory (however, those amounts might be practically infeasible). A Turing machine can simulate these quantum computers, so such a quantum computer could never solve an undecidable problem like the halting problem. The existence of "standard" quantum computers does not disprove the Church–Turing thesis.[81] It has been speculated that theories of quantum gravity, such as M-theory or loop quantum gravity, may allow even faster computers to be built. Currently, defining computation in such theories is an open problem due to the problem of time, i.e., there currently exists no obvious way to describe what it means for an observer to submit input to a computer and later receive output.[82]

 . For a more complicated case, consider
. For a more complicated case, consider 
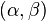 , with a length of one; that is, with
, with a length of one; that is, with
 and
and  are the
are the  and
and 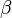 . A mixed state, in this case, is a
. A mixed state, in this case, is a  matrix that is
matrix that is 
 .
.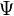 are part of
are part of 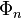 . A number
. A number 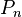 represents the probability of a randomly selected system being in the state
represents the probability of a randomly selected system being in the state  of an observable A is a statistical mean of measured values of the observable. It is this mean, and the distribution of probabilities, that is predicted by physical theories.
of an observable A is a statistical mean of measured values of the observable. It is this mean, and the distribution of probabilities, that is predicted by physical theories.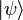 (where the "
(where the " " can be replaced by any other symbols, letters, numbers, or even words). This can be contrasted with the usual mathematical notation, where vectors are usually bold, lower-case letters, or letters with arrows on top.
" can be replaced by any other symbols, letters, numbers, or even words). This can be contrasted with the usual mathematical notation, where vectors are usually bold, lower-case letters, or letters with arrows on top. , which corresponds to the same physical quantum state. Technically, the bra is the
, which corresponds to the same physical quantum state. Technically, the bra is the  . (The phrase "bra-ket" is supposed to resemble "bracket".)
. (The phrase "bra-ket" is supposed to resemble "bracket".)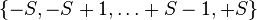


 is the spin of νth particle.
is the spin of νth particle.  for a particle that does not exhibit spin.
for a particle that does not exhibit spin. , any ket
, any ket 
 .
.

 and
and  are two kets corresponding to quantum states, the ket
are two kets corresponding to quantum states, the ket

 and
and 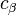 . In other words, for example, even though
. In other words, for example, even though  (for real θ) correspond to the same physical quantum state, they are not interchangeable, since for example
(for real θ) correspond to the same physical quantum state, they are not interchangeable, since for example  and
and 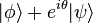 do not (in general) correspond to the same physical state. However,
do not (in general) correspond to the same physical state. However,  do correspond to the same physical state. This is sometimes described by saying that "global" phase factors are unphysical, but "relative" phase factors are physical and important.
do correspond to the same physical state. This is sometimes described by saying that "global" phase factors are unphysical, but "relative" phase factors are physical and important.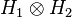 with an
with an  is inaccessible to the observer. The state of the part
is inaccessible to the observer. The state of the part  is expressed then as the
is expressed then as the 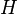 can be always represented as the partial trace of a pure quantum state (called a
can be always represented as the partial trace of a pure quantum state (called a  for a sufficiently large Hilbert space
for a sufficiently large Hilbert space 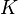 .
.
 is the fraction of the ensemble in each pure state
is the fraction of the ensemble in each pure state  The density matrix can be thought of as a way of using the one-particle
The density matrix can be thought of as a way of using the one-particle 
 are eigenkets and eigenvalues, respectively, for the operator A, and "tr" denotes trace. It is important to note that two types of averaging are occurring, one being a weighted quantum superposition over the basis kets
are eigenkets and eigenvalues, respectively, for the operator A, and "tr" denotes trace. It is important to note that two types of averaging are occurring, one being a weighted quantum superposition over the basis kets  of the pure states, and the other being a statistical (said incoherent) average with the probabilities ps of those states.
of the pure states, and the other being a statistical (said incoherent) average with the probabilities ps of those states.