Medical classification

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Medical_classification 

A medical classification is used to transform descriptions of medical diagnoses or procedures into standardized statistical code in a process known as clinical coding. Diagnosis classifications list diagnosis codes, which are used to track diseases and other health conditions, inclusive of chronic diseases such as diabetes mellitus and heart disease, and infectious diseases such as norovirus, the flu, and athlete's foot. Procedure classifications list procedure code, which are used to capture interventional data. These diagnosis and procedure codes are used by health care providers, government health programs, private health insurance companies, workers' compensation carriers, software developers, and others for a variety of applications in medicine, public health and medical informatics, including:

• statistical analysis of diseases and therapeutic actions
• reimbursement (e.g., to process claims in medical billing based on diagnosis-related groups)
• knowledge-based and decision support systems
• direct surveillance of epidemic or pandemic outbreaks

There are country specific standards and international classification systems.

Classification types

Many different medical classifications exist, though they occur into two main groupings: Statistical classifications and Nomenclatures.

A statistical classification brings together similar clinical concepts and groups them into categories. The number of categories is limited so that the classification does not become too big. An example of this is used by the International Statistical Classification of Diseases and Related Health Problems (known as ICD). ICD groups diseases of the circulatory system into one "chapter," known as Chapter IX, covering codes I00–I99. One of the codes in this chapter (I47.1) has the code title (rubric) Supraventricular tachycardia. However, there are several other clinical concepts that are also classified here. Among them are paroxysmal atrial tachycardia, paroxysmal junctional tachycardia, auricular tachycardia and nodal tachycardia.

Another feature of statistical classifications is the provision of residual categories for "other" and "unspecified" conditions that do not have a specific category in the particular classification.

In a nomenclature there is a separate listing and code for every clinical concept. So, in the previous example, each of the tachycardia listed would have its own code. This makes nomenclatures unwieldy for compiling health statistics.

Types of coding systems specific to health care include:

• Diagnostic codes
  • Are used to determine diseases, disorders, and symptoms
  • Can be used to measure morbidity and mortality
  • Examples: ICD-9-CM, ICD-10
• Procedural codes
  • They are numbers or alphanumeric codes used to identify specific health interventions taken by medical professionals.
  • Examples: CPT, HCPCS, ICPM, ICHI
• Pharmaceutical codes
  • Are used to identify medications
  • Examples: ATC, NDC
• Topographical codes
  • Are codes that indicate a specific location in the body
  • Examples :ICD-O, SNOMED

WHO Family of International Classifications

The World Health Organization (WHO) maintains several internationally endorsed classifications designed to facilitate the comparison of health related data within and across populations and over time as well as the compilation of nationally consistent data. This "Family of International Classifications" (FIC) include three main (or reference) classifications on basic parameters of health prepared by the organization and approved by the World Health Assembly for international use, as well as a number of derived and related classifications providing additional details. Some of these international standards have been revised and adapted by various countries for national use.

Reference classifications

• International Statistical Classification of Diseases and Related Health Problems (ICD)
  • ICD-10 (10th revision, in use by WHO since 1994)
  • ICD-11 (11th revision)
• International Classification of Functioning, Disability and Health (ICF)
• International Classification of Health Interventions (ICHI) (in development)

Derived classifications

Derived classifications are based on the WHO reference classifications (i.e. ICD and ICF). They include the following:

• International Classification of Diseases for Oncology, Third Edition (ICD-O-3)
• The ICD-10 Classification of Mental and Behavioural Disorders – This publication deals exclusively with Chapter V of ICD-10, and is available as two variants;
  • Clinical descriptions and diagnostic guidelines, also known as the blue book.
  • Diagnostic criteria for research, also known as the green book.
• Application of the International Classification of Diseases to Dentistry and Stomatology, 3rd Edition (ICD-DA)
• Application of the International Classification of Diseases to Neurology (ICD-10-NA)
• EUROCAT is an extension of the ICD-10 Chapter XVII, which covers congenital disorders.

National versions

See also: ICD-10 § National adoptions

Several countries have developed their own version of WHO-FIC publications, which go beyond a local language translation. Many of these are based on the ICD:

• ICD-9-CM was the US' adaptation of ICD-9 and was maintained for use until September 2015. Starting on October 1, 2015, the Centers for Medicare and Medicaid Services (CMMS) granted physicians a one-year grace period to begin using ICD-10-CM, or they would be denied Medicare Part B claims.
• ICD-10-CM was developed by the US' Centers for Medicare and Medicaid Services (CMS) and the National Center for Health Statistics (NCHS), and has been in use in the US since October 2015 – replacing ICD-9-CM.
• ICD-10-AM was published by Australia's National Centre for Classification in Health in 1998 and has since been adopted by a number of other countries.

Related classifications

Related classifications in the WHO-FIC are those that partially refer to the reference classifications, e.g. only at specific levels. They include:

• International Classification of Primary Care (ICPC)
  • ICPC-2 PLUS
• International Classification of External Causes of Injury (ICECI)
• Anatomical Therapeutic Chemical Classification System with Defined Daily Doses (ATC/DDD)
• Technical aids for persons with disabilities: Classification and terminology (ISO9999)
• International Classification for Nursing Practice (ICNP)

Historic FIC classifications

ICD versions before ICD-9 are not in use anywhere.

ICD-9 was published in 1977, and was superseded by ICD-10. (ICD-10 is due to be replaced by ICD-11 on 1 January 2022.) The International Classification of Procedures in Medicine (ICPM) is a procedural classification that has not updated since 1989, and will be replaced by ICHI. National adaptions of the ICPM includes OPS-301, which is the official German procedural classification.

Other medical classifications

Diagnosis

Main article: Diagnosis code § Diagnostic coding systems

The categories in a diagnosis classification classify diseases, disorders, symptoms and medical signs. In addition to the ICD and its national variants, they include:

• Diagnostic and Statistical Manual of Mental Disorders (DSM)
  • DSM-IV Codes
  • DSM-5
• International Classification of Headache Disorders 2nd Edition (ICHD-II)
• International Classification of Sleep Disorders (ICSD)
• Online Mendelian Inheritance in Man, database of genetic codes
• Orchard Sports Injury and Illness Classification System (OSIICS)
• Read codes
• SNOMED CT

Procedure

The categories in a procedure classification classify specific health interventions undertaken by health professionals. In addition to the ICHI and ICPC, they include:

• Australian Classification of Health Interventions (ACHI)
• Canadian Classification of Health Interventions (CCI)
• Current Procedural Terminology (CPT)
• Health Care Procedure Coding System (HCPCS)
• ICD-10 Procedure Coding System (ICD-10-PCS)
• OPCS Classification of Interventions and Procedures (OPCS-4)

Drugs

Drugs are often grouped into drug classes. Such classifications include:

• RxNorm
• Anatomical Therapeutic Chemical Classification System
• Medical Reference Terminology
• National Pharmaceutical Product Index

National Drug File-Reference Terminology (NDF-RT)

National Drug File-Reference Terminology was a terminology maintained by the Veterans Health Administration (VHA). It groups drug concepts into classes. It was part of RxNorm until March 2018.

Medication Reference Terminology (MED-RT)

Medication Reference Terminology (MED-RT) is a terminology created and maintained by Veterans Health Administration in the United States. In 2018, it replaced NDF-RT that was used during 2005–2017. Med-RT is not included in RxNorm but is included in National Library of Medicine's UMLS Metathesaurus. Prior 2017, NDF-RT was included in RxNorm. The first release of MED-RT was in the spring of 2018.

The United States Food and Drug Administration requires in its Manual of Policies and Procedures (MaPP) 7400.13 dated July 18, 2013 and updated on July 25, 2018 that MED-RT be used for selecting an established pharmacologic class (EPC) for the Highlights of Prescribing Information in drug labeling. Each EPC text phrase is associated with a term known as an EPC concept. EPC concepts use a standardized format derived from the U.S. Department of Veterans Affairs, Veterans Health Administration (VHA) Medication Reference Terminology (MED-RT). Each EPC concept also has a unique standardized alphanumeric identifier code, used as the machine-readable tag for the concept. These codes enable SPL indexing. The exact EPC text phrase used in INDICATIONS AND USAGE in Highlights might not be identical to the wording used to describe the EPC concept, because the standardized language used for the EPC concept might not be considered sufficiently clear to the readers of the labeling. Each active moiety also may be assigned MOA, PE, and CS standardized indexing concepts, which are also linked to unique standardized alphanumeric identifier codes. MOA, PE, and CS standardized indexing concepts may or may not be related to the therapeutic effect of the active moiety for a particular indication, but they should still be scientifically valid and clinically meaningful. Even if the MOA, PE, and CS standardized indexing concepts are not known with certainty to be related to the therapeutic effect, they may still be useful for identifying drug interactions and permitting other safety assessments for a moiety based upon appropriate and relevant considerations, such as enzyme inhibition and enzyme induction. MOA, PE, and CS concepts are maintained in a standardized format as part of the MED-RT hierarchy. https://www.fda.gov/media/86437/download

The United States Food and Drug Administration Study Data Technical Conformance Guide dated July 2020 states, “6.5 Pharmacologic Class 6.5.1 Medication Reference Terminology 6.5.1.1 General Considerations The Veterans Administration’s Medication Reference Terminology (MED-RT) should be used to identify the pharmacologic class(es) of all active investigational substances that are used in a study (either clinical or nonclinical). This information should be provided in the SDTM TS domain when a full TS is indicated. The information should be provided as one or more records in TS, where TSPARMCD= PCLAS. Pharmacologic class is a complex concept that is made up of one or more component concepts: mechanism of action (MOA), physiologic effect (PE), and chemical structure (CS).51 The established pharmacologic class is generally the MOA, PE, or CS term that is considered the most scientifically valid and clinically meaningful. Sponsors should include in TS (the full TS) the established pharmacologic class of all active moieties of investigational products used in a study. FDA maintains a list of established pharmacologic classes of approved moieties.52 If the established pharmacologic class is not available for an active moiety, then the sponsor should discuss the appropriate MOA, PE, and CS terms with the review division. For unapproved investigational active moieties where the pharmacologic class is unknown, the PCLAS record may not be available." https://www.fda.gov/media/136460/download

The United States Food and Drug Administration publishes a Data Standards Catalog that lists the data standards and terminologies that FDA supports for use in regulatory submissions to better enable the evaluation of safety, effectiveness, and quality of FDA-regulated products. In addition, the FDA has the statutory and regulatory authority to require certain standards and terminologies and these are identified in the Catalog with the date the requirement begins and, as needed, the date the requirement ends, and information sources. The submission of data using standards or terminologies not listed in the Catalog should be discussed with the Agency in advance. Where the Catalog expresses support for more than one standard or terminology for a specific use, the sponsor or applicant may select one to use or can discuss, as appropriate, with their review division. Version 7.0 of the FDA Data Standards Catalog dated 03-15-2021, specifies that MED-RT was a required terminology by the White House Consolidated Health Informatics Initiative in various Federal Register Notices beginning as early as May 6, 2004, for NDAs, ANDAs, and certain BLAs beginning on December 17, 2016, and for certain IND's beginning on December 17, 2017. https://www.fda.gov/media/85137/download

Medical Devices

• Global Medical Device Nomenclature (GMDN), the standard international naming system for medical devices.

Other

• Classification of Pharmaco-Therapeutic Referrals (CPR)
• Logical Observation Identifiers Names and Codes (LOINC), standard for identifying medical laboratory observations
• MEDCIN, point-of-care terminology, intended for use in Electronic Health Record (EHR) systems
• Medical Dictionary for Regulatory Activities (MedDRA)
• Medical Subject Headings (MeSH)
  • List of MeSH codes
• Nursing Interventions Classification (NIC)
• Nursing Outcomes Classification (NOC)
• TIME-ITEM, ontology of topics in medical education
• TNM Classification of Malignant Tumors
• Unified Medical Language System (UMLS)
• Victoria Ambulatory Coding System (VACS) / Queensland Ambulatory Coding System (QACS), Australia

Library classification that have medical components

• Dewey Decimal Classification and Universal Decimal Classification (section 610–620)
• National Library of Medicine classification

ICD, SNOMED and Electronic Health Record (EHR)

SNOMED

The Systematized Nomenclature of Medicine (SNOMED) is the most widely recognised nomenclature in healthcare. Its current version, SNOMED Clinical Terms (SNOMED CT), is intended to provide a set of concepts and relationships that offers a common reference point for comparison and aggregation of data about the health care process. SNOMED CT is often described as a reference terminology. SNOMED CT contains more than 311,000 active concepts with unique meanings and formal logic-based definitions organised into hierarchies. SNOMED CT can be used by anyone with an Affiliate License, 40 low income countries defined by the World Bank or qualifying research, humanitarian and charitable projects. SNOMED CT is designed to be managed by computer, and it is a complex relationship concepts.

ICD

The International Classification of Disease (ICD) is the most widely recognized medical classification. Maintained by the World Health Organization (WHO), its primary purpose is to categorise diseases for morbidity and mortality reporting. However the coded data is often used for other purposes too; including reimbursement practices such as medical billing. ICD has a hierarchical structure, and coding in this context, is the term applied when representations are assigned to the words they represent. Coding diagnoses and procedures is the assignment of codes from a code set that follows the rules of the underlying classification or other coding guidelines. The current version of the ICD, ICD-10, was endorsed by WHO in 1990. WHO Member states began using the ICD-10 classification system from 1994 for both morbidity and mortality reporting. The exception was the US, who only began using it for reporting mortality in 1999 whilst continuing to use ICD-9-CM for morbidity reporting. The US only adopted its version of ICD-10 in October 2015. The delay meant it was unable to compare US morbidity data with the rest of the world during this period. The next major version of the ICD, ICD-11, was ratified by the 72nd World Health Assembly on 25 May 2019, and member countries will be able to begin reporting data recorded using ICD-11 from 1 January 2022.

Comparison

SNOMED CT and ICD are designed for different purposes and each should be used for the purposes for which they were designed. As a core terminology for the EHR, SNOMED CT provides a common language that enables a consistent language that enables a consistent way of capturing, sharing, and aggregating health data across specialties and sites of care. It is highly detailed terminology designed for input not reporting. SNOMED is clinically-based, documents whatever is needed for patient care and has better clinical coverage than ICD. ICD's focus is statistical with less common diseases get lumped together in “catch-all” categories, which result in loss of information. SNOMED CT is used directly by healthcare providers during the process of care, whereas ICD is used by coding professionals after the episode of care. SNOMED CT has multiple hierarchy, whereas there is single hierarchy for ICD. SNOMED CT concepts are defined logically by their attributes, whereas only textual rules and definitions in ICD.

Data Mapping

SNOMED and ICD can be coordinated. The National Library of Medicine (NLM) maps ICD-9-CM, ICD-10-CM, ICD-10-PCS, and other classification systems to SNOMED. Data Mapping is the process of identifying relationships between two distinct data models.

Veterinary medical coding

Veterinary medical codes include the VeNom Coding Group, the U.S. Animal Hospital Codes, and the Veterinary Extension to SNOMED CT (VetSCT).

Memristor

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Memristor 

Memristor

Memristor developed by the University of Illinois at Urbana-Champaign and National Energy Technology Laboratory
Invented	Leon Chua (1971)
Electronic symbol

A memristor (/ˈmɛmrɪstər/; a portmanteau of memory resistor) is a non-linear two-terminal electrical component relating electric charge and magnetic flux linkage. It was described and named in 1971 by Leon Chua, completing a theoretical quartet of fundamental electrical components which comprises also the resistor, capacitor and inductor.

Chua and Kang later generalized the concept to memristive systems. Such a system comprises a circuit, of multiple conventional components, which mimics key properties of the ideal memristor component and is also commonly referred to as a memristor. Several such memristor system technologies have been developed, notably ReRAM.

The identification of memristive properties in electronic devices has attracted controversy. Experimentally, the ideal memristor has yet to be demonstrated.

As a fundamental electrical component

Conceptual symmetries of resistor, capacitor, inductor, and memristor.

Chua in his 1971 paper identified a theoretical symmetry between the non-linear resistor (voltage vs. current), non-linear capacitor (voltage vs. charge), and non-linear inductor (magnetic flux linkage vs. current). From this symmetry he inferred the characteristics of a fourth fundamental non-linear circuit element, linking magnetic flux and charge, which he called the memristor. In contrast to a linear (or non-linear) resistor the memristor has a dynamic relationship between current and voltage including a memory of past voltages or currents. Other scientists had proposed dynamic memory resistors such as the memistor of Bernard Widrow, but Chua introduced a mathematical generality.

Derivation and characteristics

The memristor was originally defined in terms of a non-linear functional relationship between magnetic flux linkage Φ_m(t) and the amount of electric charge that has flowed, q(t):

${\displaystyle f(\mathrm {\Phi } _{\mathrm {m} }(t),q(t))=0}$

The magnetic flux linkage, Φ_m, is generalized from the circuit characteristic of an inductor. It does not represent a magnetic field here. Its physical meaning is discussed below. The symbol Φ_m may be regarded as the integral of voltage over time.

In the relationship between Φ_m and q, the derivative of one with respect to the other depends on the value of one or the other, and so each memristor is characterized by its memristance function describing the charge-dependent rate of change of flux with charge.

${\displaystyle M(q)={\frac {\mathrm {d} \Phi _{\rm {m}}}{\mathrm {d} q}}}$

Substituting the flux as the time integral of the voltage, and charge as the time integral of current, the more convenient forms are;

${\displaystyle M(q(t))={\cfrac {\mathrm {d} \Phi _{\rm {}}/\mathrm {d} t}{\mathrm {d} q/\mathrm {d} t}}={\frac {V(t)}{I(t)}}}$

To relate the memristor to the resistor, capacitor, and inductor, it is helpful to isolate the term M(q), which characterizes the device, and write it as a differential equation.

Device	Characteristic property (units)	Differential equation
Resistor (R)	Resistance (V / A, or ohm, Ω)	R = dV / dI
Capacitor (C)	Capacitance (C / V, or farad)	C = dq / dV
Inductor (L)	Inductance (Wb / A, or henry)	L = dΦm / dI
Memristor (M)	Memristance (Wb / C, or ohm)	M = dΦm / dq

The above table covers all meaningful ratios of differentials of I, q, Φ_m, and V. No device can relate dI to dq, or dΦ_m to dV, because I is the derivative of q and Φ_m is the integral of V.

It can be inferred from this that memristance is charge-dependent resistance. If M(q(t)) is a constant, then we obtain Ohm's Law R(t) = V(t)/I(t). If M(q(t)) is nontrivial, however, the equation is not equivalent because q(t) and M(q(t)) can vary with time. Solving for voltage as a function of time produces

${\displaystyle V(t)=\ M(q(t))I(t)}$

This equation reveals that memristance defines a linear relationship between current and voltage, as long as M does not vary with charge. Nonzero current implies time varying charge. Alternating current, however, may reveal the linear dependence in circuit operation by inducing a measurable voltage without net charge movement—as long as the maximum change in q does not cause much change in M.

Furthermore, the memristor is static if no current is applied. If I(t) = 0, we find V(t) = 0 and M(t) is constant. This is the essence of the memory effect.

Analogously, we can define a ${\displaystyle W(\phi (t))}$ as menductance.

${\displaystyle i(t)=W(\phi (t))v(t)}$

The power consumption characteristic recalls that of a resistor, I²R.

${\displaystyle P(t)=\ I(t)V(t)=\ I^{2}(t)M(q(t))}$

As long as M(q(t)) varies little, such as under alternating current, the memristor will appear as a constant resistor. If M(q(t)) increases rapidly, however, current and power consumption will quickly stop.

M(q) is physically restricted to be positive for all values of q (assuming the device is passive and does not become superconductive at some q). A negative value would mean that it would perpetually supply energy when operated with alternating current.

Modelling and validation

In order to understand the nature of memristor function, some knowledge of fundamental circuit theoretic concepts is useful, starting with the concept of device modelling.

Engineers and scientists seldom analyze a physical system in its original form. Instead, they construct a model which approximates the behaviour of the system. By analyzing the behaviour of the model, they hope to predict the behaviour of the actual system. The primary reason for constructing models is that physical systems are usually too complex to be amenable to a practical analysis.

In the 20th century, work was done on devices where researchers did not recognize the memristive characteristics. This has raised the suggestion that such devices should be recognised as memristors. Pershin and Di Ventra have proposed a test that can help to resolve some of the long-standing controversies about whether an ideal memristor does actually exist or is a purely mathematical concept.

The rest of this article primarily addresses memristors as related to ReRAM devices, since the majority of work since 2008 has been concentrated in this area.

Superconducting memristor component

Dr. Paul Penfield, in a 1974 MIT technical report mentions the memristor in connection with Josephson junctions. This was an early use of the word "memristor" in the context of a circuit device.

One of the terms in the current through a Josephson junction is of the form:

${\displaystyle {\begin{aligned}i_{M}(v)&=\epsilon \cos(\phi _{0})v\\&=W(\phi _{0})v\end{aligned}}}$

where ${\displaystyle \epsilon }$ is a constant based on the physical superconducting materials, ${\displaystyle v}$ is the voltage across the junction and ${\displaystyle i_{M}}$ is the current through the junction.

Through the late 20th century, research regarding this phase-dependent conductance in Josephson junctions was carried out. A more comprehensive approach to extracting this phase-dependent conductance appeared with Peotta and DiVentra's seminal paper in 2014.

Memristor circuits

Due to the practical difficulty of studying the ideal memristor, we will discuss other electrical devices which can be modelled using memristors. For a mathematical description of a memristive device (systems), see Theory.

A discharge tube can be modelled as a memristive device, with resistance being a function of the number of conduction electrons ${\displaystyle n_{e}}$.

${\displaystyle {\begin{aligned}v_{M}&=R(n_{e})i_{M}\\{\frac {dn_{e}}{dt}}&=\beta n+\alpha R(n_{e})i_{M}^{2}\end{aligned}}}$

${\displaystyle v_{M}}$ is the voltage across the discharge tube, ${\displaystyle i_{M}}$ is the current flowing through it and ${\displaystyle n_{e}}$ is the number of conduction electrons. A simple memristance function is ${\displaystyle R(n_{e})={\frac {F}{n_{e}}}}$. ${\displaystyle \alpha ,\beta }$ and ${\displaystyle F}$ are parameters depending on the dimensions of the tube and the gas fillings. An experimental identification of memristive behaviour is the "pinched hysteresis loop" in the ${\displaystyle v-i}$ plane. For an experiment that shows such a characteristic for a common discharge tube, see "A physical memristor Lissajous figure" (YouTube). The video also illustrates how to understand deviations in the pinched hysteresis characteristics of physical memristors.

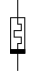
Thermistors can be modelled as memristive devices.

${\displaystyle {\begin{aligned}v&=R_{0}(T_{0})\exp \left[\beta \left({\frac {1}{T}}-{\frac {1}{T_{0}}}\right)\right]i\\&\equiv R(T)i\\{\frac {dT}{dt}}&={\frac {1}{C}}\left[-\delta \cdot (T-T_{0})+R(T)i^{2}\right]\end{aligned}}}$

${\displaystyle \beta }$ is a material constant, ${\displaystyle T}$ is the absolute body temperature of the thermistor, ${\displaystyle T_{0}}$ is the ambient temperature (both temperatures in Kelvin), ${\displaystyle R_{0}(T_{0})}$ denotes the cold temperature resistance at ${\displaystyle T=T_{0}}$, ${\displaystyle C}$ is the heat capacitance and ${\displaystyle \delta }$ is the dissipation constant for the thermistor.

A fundamental phenomenon that has hardly been studied is memristive behaviour in pn-junctions. The memristor plays a crucial role in mimicking the charge storage effect in the diode base, and is also responsible for the conductivity modulation phenomenon (that is so important during forward transients).

Criticisms

In 2008, a team at HP Labs claimed to have found Chua's missing memristor based on an analysis of a thin film of titanium dioxide, thus connecting the operation of ReRAM devices to the memristor concept. According to HP Labs, the memristor would operate in the following way: the memristor's electrical resistance is not constant but depends on the current that had previously flowed through the device, i.e., its present resistance depends on how much electric charge has previously flowed through it and in what direction; the device remembers its history—the so-called non-volatility property. When the electric power supply is turned off, the memristor remembers its most recent resistance until it is turned on again.

The HP Labs result was published in the scientific journal Nature. Following this claim, Leon Chua has argued that the memristor definition could be generalized to cover all forms of two-terminal non-volatile memory devices based on resistance switching effects. Chua also argued that the memristor is the oldest known circuit element, with its effects predating the resistor, capacitor, and inductor. There are, however, some serious doubts as to whether a genuine memristor can actually exist in physical reality. Additionally, some experimental evidence contradicts Chua's generalization since a non-passive nanobattery effect is observable in resistance switching memory. A simple test has been proposed by Pershin and Di Ventra to analyze whether such an ideal or generic memristor does actually exist or is a purely mathematical concept. Up to now, there seems to be no experimental resistance switching device (ReRAM) which can pass the test.

These devices are intended for applications in nanoelectronic memory devices, computer logic, and neuromorphic/neuromemristive computer architectures. In 2013, Hewlett-Packard CTO Martin Fink suggested that memristor memory may become commercially available as early as 2018. In March 2012, a team of researchers from HRL Laboratories and the University of Michigan announced the first functioning memristor array built on a CMOS chip.

An array of 17 purpose-built oxygen-depleted titanium dioxide memristors built at HP Labs, imaged by an atomic force microscope. The wires are about 50 nm, or 150 atoms, wide. Electric current through the memristors shifts the oxygen vacancies, causing a gradual and persistent change in electrical resistance.

According to the original 1971 definition, the memristor is the fourth fundamental circuit element, forming a non-linear relationship between electric charge and magnetic flux linkage. In 2011, Chua argued for a broader definition that includes all 2-terminal non-volatile memory devices based on resistance switching. Williams argued that MRAM, phase-change memory and ReRAM are memristor technologies. Some researchers argued that biological structures such as blood and skin fit the definition. Others argued that the memory device under development by HP Labs and other forms of ReRAM are not memristors, but rather part of a broader class of variable-resistance systems, and that a broader definition of memristor is a scientifically unjustifiable land grab that favored HP's memristor patents.

In 2011, Meuffels and Schroeder noted that one of the early memristor papers included a mistaken assumption regarding ionic conduction. In 2012, Meuffels and Soni discussed some fundamental issues and problems in the realization of memristors. They indicated inadequacies in the electrochemical modeling presented in the Nature article "The missing memristor found" because the impact of concentration polarization effects on the behavior of metal−TiO_2−x−metal structures under voltage or current stress was not considered. This critique was referred to by Valov et al. in 2013.

In a kind of thought experiment, Meuffels and Soni furthermore revealed a severe inconsistency: If a current-controlled memristor with the so-called non-volatility property exists in physical reality, its behavior would violate Landauer's principle, which places a limit on the minimum amount of energy required to change "information" states of a system. This critique was finally adopted by Di Ventra and Pershin in 2013.

Within this context, Meuffels and Soni pointed to a fundamental thermodynamic principle: Non-volatile information storage requires the existence of free-energy barriers that separate the distinct internal memory states of a system from each other; otherwise, one would be faced with an "indifferent" situation, and the system would arbitrarily fluctuate from one memory state to another just under the influence of thermal fluctuations. When unprotected against thermal fluctuations, the internal memory states exhibit some diffusive dynamics, which causes state degradation. The free-energy barriers must therefore be high enough to ensure a low bit-error probability of bit operation. Consequently, there is always a lower limit of energy requirement – depending on the required bit-error probability – for intentionally changing a bit value in any memory device.

In the general concept of memristive system the defining equations are (see Theory):

${\displaystyle {\begin{aligned}y(t)&=g(\mathbf {x} ,u,t)u(t),\\{\dot {\mathbf {x} }}&=f(\mathbf {x} ,u,t),\end{aligned}}}$

where u(t) is an input signal, and y(t) is an output signal. The vector x represents a set of n state variables describing the different internal memory states of the device. ẋ is the time-dependent rate of change of the state vector x with time.

When one wants to go beyond mere curve fitting and aims at a real physical modeling of non-volatile memory elements, e.g., resistive random-access memory devices, one has to keep an eye on the aforementioned physical correlations. To check the adequacy of the proposed model and its resulting state equations, the input signal u(t) can be superposed with a stochastic term ξ(t), which takes into account the existence of inevitable thermal fluctuations. The dynamic state equation in its general form then finally reads:

${\displaystyle {\dot {\mathbf {x} }}=f(\mathbf {x} ,u(t)+\xi (t),t),}$

where ξ(t) is, e.g., white Gaussian current or voltage noise. On base of an analytical or numerical analysis of the time-dependent response of the system towards noise, a decision on the physical validity of the modeling approach can be made, e.g., would the system be able to retain its memory states in power-off mode?

Such an analysis was performed by Di Ventra and Pershin with regard to the genuine current-controlled memristor. As the proposed dynamic state equation provides no physical mechanism enabling such a memristor to cope with inevitable thermal fluctuations, a current-controlled memristor would erratically change its state in course of time just under the influence of current noise. Di Ventra and Pershin thus concluded that memristors whose resistance (memory) states depend solely on the current or voltage history would be unable to protect their memory states against unavoidable Johnson–Nyquist noise and permanently suffer from information loss, a so-called "stochastic catastrophe". A current-controlled memristor can thus not exist as a solid-state device in physical reality.

The above-mentioned thermodynamic principle furthermore implies that the operation of 2-terminal non-volatile memory devices (e.g. "resistance-switching" memory devices (ReRAM)) cannot be associated with the memristor concept, i.e., such devices cannot by itself remember their current or voltage history. Transitions between distinct internal memory or resistance states are of probabilistic nature. The probability for a transition from state {i} to state {j} depends on the height of the free-energy barrier between both states. The transition probability can thus be influenced by suitably driving the memory device, i.e., by "lowering" the free-energy barrier for the transition {i} → {j} by means of, for example, an externally applied bias.

A "resistance switching" event can simply be enforced by setting the external bias to a value above a certain threshold value. This is the trivial case, i.e., the free-energy barrier for the transition {i} → {j} is reduced to zero. In case one applies biases below the threshold value, there is still a finite probability that the device will switch in course of time (triggered by a random thermal fluctuation), but – as one is dealing with probabilistic processes – it is impossible to predict when the switching event will occur. That is the basic reason for the stochastic nature of all observed resistance-switching (ReRAM) processes. If the free-energy barriers are not high enough, the memory device can even switch without having to do anything.

When a 2-terminal non-volatile memory device is found to be in a distinct resistance state {j}, there exists therefore no physical one-to-one relationship between its present state and its foregoing voltage history. The switching behavior of individual non-volatile memory devices thus cannot be described within the mathematical framework proposed for memristor/memristive systems.

An extra thermodynamic curiosity arises from the definition that memristors/memristive devices should energetically act like resistors. The instantaneous electrical power entering such a device is completely dissipated as Joule heat to the surrounding, so no extra energy remains in the system after it has been brought from one resistance state x_i to another one x_j. Thus, the internal energy of the memristor device in state x_i, U(V, T, x_i), would be the same as in state x_j, U(V, T, x_j), even though these different states would give rise to different device's resistances, which itself must be caused by physical alterations of the device's material.

Other researchers noted that memristor models based on the assumption of linear ionic drift do not account for asymmetry between set time (high-to-low resistance switching) and reset time (low-to-high resistance switching) and do not provide ionic mobility values consistent with experimental data. Non-linear ionic-drift models have been proposed to compensate for this deficiency.

A 2014 article from researchers of ReRAM concluded that Strukov's (HP's) initial/basic memristor modeling equations do not reflect the actual device physics well, whereas subsequent (physics-based) models such as Pickett's model or Menzel's ECM model (Menzel is a co-author of that article) have adequate predictability, but are computationally prohibitive. As of 2014, the search continues for a model that balances these issues; the article identifies Chang's and Yakopcic's models as potentially good compromises.

Martin Reynolds, an electrical engineering analyst with research outfit Gartner, commented that while HP was being sloppy in calling their device a memristor, critics were being pedantic in saying that it was not a memristor.

Experimental tests

Chua suggested experimental tests to determine if a device may properly be categorized as a memristor:

• The Lissajous curve in the voltage-current plane is a pinched hysteresis loop when driven by any bipolar periodic voltage or current without respect to initial conditions.
• The area of each lobe of the pinched hysteresis loop shrinks as the frequency of the forcing signal increases.
• As the frequency tends to infinity, the hysteresis loop degenerates to a straight line through the origin, whose slope depends on the amplitude and shape of the forcing signal.

According to Chua all resistive switching memories including ReRAM, MRAM and phase-change memory meet these criteria and are memristors. However, the lack of data for the Lissajous curves over a range of initial conditions or over a range of frequencies complicates assessments of this claim.

Experimental evidence shows that redox-based resistance memory (ReRAM) includes a nanobattery effect that is contrary to Chua's memristor model. This indicates that the memristor theory needs to be extended or corrected to enable accurate ReRAM modeling.

Theory

In 2008 researchers from HP Labs introduced a model for a memristance function based on thin films of titanium dioxide. For R_ON ≪ R_OFF the memristance function was determined to be

${\displaystyle M(q(t))=R_{\mathrm {OFF} }\cdot \left(1-{\frac {\mu _{v}R_{\mathrm {ON} }}{D^{2}}}q(t)\right)}$

where R_OFF represents the high resistance state, R_ON represents the low resistance state, μ_v represents the mobility of dopants in the thin film, and D represents the film thickness. The HP Labs group noted that "window functions" were necessary to compensate for differences between experimental measurements and their memristor model due to non-linear ionic drift and boundary effects.

Operation as a switch

For some memristors, applied current or voltage causes substantial change in resistance. Such devices may be characterized as switches by investigating the time and energy that must be spent to achieve a desired change in resistance. This assumes that the applied voltage remains constant. Solving for energy dissipation during a single switching event reveals that for a memristor to switch from R_on to R_off in time T_on to T_off, the charge must change by ΔQ = Q_on−Q_off.

${\displaystyle E_{\mathrm {switch} }=\ V^{2}\int _{T_{\mathrm {off} }}^{T_{\mathrm {on} }}{\frac {\mathrm {d} t}{M(q(t))}}=\ V^{2}\int _{Q_{\mathrm {off} }}^{Q_{\mathrm {on} }}{\frac {\mathrm {d} q}{I(q)M(q)}}=\ V^{2}\int _{Q_{\mathrm {off} }}^{Q_{\mathrm {on} }}{\frac {\mathrm {d} q}{V(q)}}=\ V\Delta Q}$

Substituting V = I(q)M(q), and then ∫dq/V = ∆Q/V for constant VTo produces the final expression. This power characteristic differs fundamentally from that of a metal oxide semiconductor transistor, which is capacitor-based. Unlike the transistor, the final state of the memristor in terms of charge does not depend on bias voltage.

The type of memristor described by Williams ceases to be ideal after switching over its entire resistance range, creating hysteresis, also called the "hard-switching regime". Another kind of switch would have a cyclic M(q) so that each off-on event would be followed by an on-off event under constant bias. Such a device would act as a memristor under all conditions, but would be less practical.

Memristive systems

In the more general concept of an n-th order memristive system the defining equations are

${\displaystyle {\begin{aligned}y(t)&=g({\textbf {x}},u,t)u(t),\\{\dot {\textbf {x}}}&=f({\textbf {x}},u,t)\end{aligned}}}$

where u(t) is an input signal, y(t) is an output signal, the vector x represents a set of n state variables describing the device, and g and f are continuous functions. For a current-controlled memristive system the signal u(t) represents the current signal i(t) and the signal y(t) represents the voltage signal v(t). For a voltage-controlled memristive system the signal u(t) represents the voltage signal v(t) and the signal y(t) represents the current signal i(t).

The pure memristor is a particular case of these equations, namely when x depends only on charge (x = q) and since the charge is related to the current via the time derivative dq/dt = i(t). Thus for pure memristors f (i.e. the rate of change of the state) must be equal or proportional to the current i(t) .

Pinched hysteresis

Example of pinched hysteresis curve, V versus I

One of the resulting properties of memristors and memristive systems is the existence of a pinched hysteresis effect. For a current-controlled memristive system, the input u(t) is the current i(t), the output y(t) is the voltage v(t), and the slope of the curve represents the electrical resistance. The change in slope of the pinched hysteresis curves demonstrates switching between different resistance states which is a phenomenon central to ReRAM and other forms of two-terminal resistance memory. At high frequencies, memristive theory predicts the pinched hysteresis effect will degenerate, resulting in a straight line representative of a linear resistor. It has been proven that some types of non-crossing pinched hysteresis curves (denoted Type-II) cannot be described by memristors.

Extended systems

Some researchers have raised the question of the scientific legitimacy of HP's memristor models in explaining the behavior of ReRAM. and have suggested extended memristive models to remedy perceived deficiencies.

One example attempts to extend the memristive systems framework by including dynamic systems incorporating higher-order derivatives of the input signal u(t) as a series expansion

${\displaystyle {\begin{aligned}y(t)&=g_{0}({\textbf {x}},u)u(t)+g_{1}({\textbf {x}},u){\operatorname {d} ^{2}u \over \operatorname {d} t^{2}}+g_{2}({\textbf {x}},u){\operatorname {d} ^{4}u \over \operatorname {d} t^{4}}+\ldots +g_{m}({\textbf {x}},u){\operatorname {d} ^{2m}u \over \operatorname {d} t^{2m}},\\{\dot {\textbf {x}}}&=f({\textbf {x}},u)\end{aligned}}}$

where m is a positive integer, u(t) is an input signal, y(t) is an output signal, the vector x represents a set of n state variables describing the device, and the functions g and f are continuous functions. This equation produces the same zero-crossing hysteresis curves as memristive systems but with a different frequency response than that predicted by memristive systems.

Another example suggests including an offset value ${\displaystyle a}$ to account for an observed nanobattery effect which violates the predicted zero-crossing pinched hysteresis effect.

${\displaystyle {\begin{aligned}y(t)&=g_{0}({\textbf {x}},u)(u(t)-a),\\{\dot {\textbf {x}}}&=f({\textbf {x}},u)\end{aligned}}}$

Implementations

Titanium dioxide memristor

Interest in the memristor revived when an experimental solid-state version was reported by R. Stanley Williams of Hewlett Packard in 2007. The article was the first to demonstrate that a solid-state device could have the characteristics of a memristor based on the behavior of nanoscale thin films. The device neither uses magnetic flux as the theoretical memristor suggested, nor stores charge as a capacitor does, but instead achieves a resistance dependent on the history of current.

Although not cited in HP's initial reports on their TiO₂ memristor, the resistance switching characteristics of titanium dioxide were originally described in the 1960s.

The HP device is composed of a thin (50 nm) titanium dioxide film between two 5 nm thick electrodes, one titanium, the other platinum. Initially, there are two layers to the titanium dioxide film, one of which has a slight depletion of oxygen atoms. The oxygen vacancies act as charge carriers, meaning that the depleted layer has a much lower resistance than the non-depleted layer. When an electric field is applied, the oxygen vacancies drift (see Fast ion conductor), changing the boundary between the high-resistance and low-resistance layers. Thus the resistance of the film as a whole is dependent on how much charge has been passed through it in a particular direction, which is reversible by changing the direction of current. Since the HP device displays fast ion conduction at nanoscale, it is considered a nanoionic device.

Memristance is displayed only when both the doped layer and depleted layer contribute to resistance. When enough charge has passed through the memristor that the ions can no longer move, the device enters hysteresis. It ceases to integrate q=∫I dt, but rather keeps q at an upper bound and M fixed, thus acting as a constant resistor until current is reversed.

Memory applications of thin-film oxides had been an area of active investigation for some time. IBM published an article in 2000 regarding structures similar to that described by Williams. Samsung has a U.S. patent for oxide-vacancy based switches similar to that described by Williams. Williams also has a U.S. patent application related to the memristor construction.

In April 2010, HP labs announced that they had practical memristors working at 1 ns (~1 GHz) switching times and 3 nm by 3 nm sizes, which bodes well for the future of the technology. At these densities it could easily rival the current sub-25 nm flash memory technology.

Polymeric memristor

In 2004, Krieger and Spitzer described dynamic doping of polymer and inorganic dielectric-like materials that improved the switching characteristics and retention required to create functioning nonvolatile memory cells. They used a passive layer between electrode and active thin films, which enhanced the extraction of ions from the electrode. It is possible to use fast ion conductor as this passive layer, which allows a significant reduction of the ionic extraction field.

In July 2008, Erokhin and Fontana claimed to have developed a polymeric memristor before the more recently announced titanium dioxide memristor.

In 2010, Alibart, Gamrat, Vuillaume et al. introduced a new hybrid organic/nanoparticle device (the NOMFET : Nanoparticle Organic Memory Field Effect Transistor), which behaves as a memristor and which exhibits the main behavior of a biological spiking synapse. This device, also called a synapstor (synapse transistor), was used to demonstrate a neuro-inspired circuit (associative memory showing a pavlovian learning).

In 2012, Crupi, Pradhan and Tozer described a proof of concept design to create neural synaptic memory circuits using organic ion-based memristors. The synapse circuit demonstrated long-term potentiation for learning as well as inactivity based forgetting. Using a grid of circuits, a pattern of light was stored and later recalled. This mimics the behavior of the V1 neurons in the primary visual cortex that act as spatiotemporal filters that process visual signals such as edges and moving lines.

Layered memristor

In 2014, Bessonov et al. reported a flexible memristive device comprising a MoO_x/MoS₂ heterostructure sandwiched between silver electrodes on a plastic foil. The fabrication method is entirely based on printing and solution-processing technologies using two-dimensional layered transition metal dichalcogenides (TMDs). The memristors are mechanically flexible, optically transparent and produced at low cost. The memristive behaviour of switches was found to be accompanied by a prominent memcapacitive effect. High switching performance, demonstrated synaptic plasticity and sustainability to mechanical deformations promise to emulate the appealing characteristics of biological neural systems in novel computing technologies.

Atomristor

Atomristor is defined as the electrical devices showing memristive behavior in atomically thin nanomaterials or atomic sheets. In 2018, Ge and Wu et al. first reported a universal memristive effect in single-layer TMD (MX₂, M = Mo, W; and X = S, Se) atomic sheets based on vertical metal-insulator-metal (MIM) device structure. These atomristors offer forming-free switching and both unipolar and bipolar operation. The switching behavior is found in single-crystalline and poly-crystalline films, with various metallic electrodes (gold, silver and graphene). Atomically thin TMD sheets are prepared via CVD/MOCVD, enabling low-cost fabrication. Afterwards, taking advantage of the low "on" resistance and large on/off ratio, a high-performance zero-power RF switch is proved based on MoS₂ atomristors, indicating a new application of memristors.

Ferroelectric memristor

The ferroelectric memristor is based on a thin ferroelectric barrier sandwiched between two metallic electrodes. Switching the polarization of the ferroelectric material by applying a positive or negative voltage across the junction can lead to a two order of magnitude resistance variation: R_OFF ≫ R_ON (an effect called Tunnel Electro-Resistance). In general, the polarization does not switch abruptly. The reversal occurs gradually through the nucleation and growth of ferroelectric domains with opposite polarization. During this process, the resistance is neither R_ON or R_OFF, but in between. When the voltage is cycled, the ferroelectric domain configuration evolves, allowing a fine tuning of the resistance value. The ferroelectric memristor's main advantages are that ferroelectric domain dynamics can be tuned, offering a way to engineer the memristor response, and that the resistance variations are due to purely electronic phenomena, aiding device reliability, as no deep change to the material structure is involved.

Carbon nanotube memristor

In 2013, Ageev, Blinov et al. reported observing memristor effect in structure based on vertically aligned carbon nanotubes studying bundles of CNT by scanning tunneling microscope.

Later it was found that CNT memristive switching is observed when a nanotube has a non-uniform elastic strain ΔL0. It was shown that the memristive switching mechanism of strained СNT is based on the formation and subsequent redistribution of non-uniform elastic strain and piezoelectric field Edef in the nanotube under the influence of an external electric field E(x,t).

Biomolecular memristor

Biomaterials have been evaluated for use in artificial synapses and have shown potential for application in neuromorphic systems. In particular, the feasibility of using a collagen‐based biomemristor as an artificial synaptic device has been investigated, whereas a synaptic device based on lignin demonstrated rising or lowering current with consecutive voltage sweeps depending on the sign of the voltage furthermore a natural silk fibroin demonstrated memristive properties; spin-memristive systems based on biomolecules are also being studied.

Spin memristive systems

Spintronic memristor

Chen and Wang, researchers at disk-drive manufacturer Seagate Technology described three examples of possible magnetic memristors. In one device resistance occurs when the spin of electrons in one section of the device points in a different direction from those in another section, creating a "domain wall", a boundary between the two sections. Electrons flowing into the device have a certain spin, which alters the device's magnetization state. Changing the magnetization, in turn, moves the domain wall and changes the resistance. The work's significance led to an interview by IEEE Spectrum. A first experimental proof of the spintronic memristor based on domain wall motion by spin currents in a magnetic tunnel junction was given in 2011.

Memristance in a magnetic tunnel junction

The magnetic tunnel junction has been proposed to act as a memristor through several potentially complementary mechanisms, both extrinsic (redox reactions, charge trapping/detrapping and electromigration within the barrier) and intrinsic (spin-transfer torque).

Extrinsic mechanism

Based on research performed between 1999 and 2003, Bowen et al. published experiments in 2006 on a magnetic tunnel junction (MTJ) endowed with bi-stable spin-dependent states (resistive switching). The MTJ consists in a SrTiO3 (STO) tunnel barrier that separates half-metallic oxide LSMO and ferromagnetic metal CoCr electrodes. The MTJ's usual two device resistance states, characterized by a parallel or antiparallel alignment of electrode magnetization, are altered by applying an electric field. When the electric field is applied from the CoCr to the LSMO electrode, the tunnel magnetoresistance (TMR) ratio is positive. When the direction of electric field is reversed, the TMR is negative. In both cases, large amplitudes of TMR on the order of 30% are found. Since a fully spin-polarized current flows from the half-metallic LSMO electrode, within the Julliere model, this sign change suggests a sign change in the effective spin polarization of the STO/CoCr interface. The origin to this multistate effect lies with the observed migration of Cr into the barrier and its state of oxidation. The sign change of TMR can originate from modifications to the STO/CoCr interface density of states, as well as from changes to the tunneling landscape at the STO/CoCr interface induced by CrOx redox reactions.

Reports on MgO-based memristive switching within MgO-based MTJs appeared starting in 2008 and 2009. While the drift of oxygen vacancies within the insulating MgO layer has been proposed to describe the observed memristive effects, another explanation could be charge trapping/detrapping on the localized states of oxygen vacancies and its impact on spintronics. This highlights the importance of understanding what role oxygen vacancies play in the memristive operation of devices that deploy complex oxides with an intrinsic property such as ferroelectricity or multiferroicity.

Intrinsic mechanism

The magnetization state of a MTJ can be controlled by Spin-transfer torque, and can thus, through this intrinsic physical mechanism, exhibit memristive behavior. This spin torque is induced by current flowing through the junction, and leads to an efficient means of achieving a MRAM. However, the length of time the current flows through the junction determines the amount of current needed, i.e., charge is the key variable.

The combination of intrinsic (spin-transfer torque) and extrinsic (resistive switching) mechanisms naturally leads to a second-order memristive system described by the state vector x = (x₁,x₂), where x₁ describes the magnetic state of the electrodes and x₂ denotes the resistive state of the MgO barrier. In this case the change of x₁ is current-controlled (spin torque is due to a high current density) whereas the change of x₂ is voltage-controlled (the drift of oxygen vacancies is due to high electric fields). The presence of both effects in a memristive magnetic tunnel junction led to the idea of a nanoscopic synapse-neuron system.

Spin memristive system

A fundamentally different mechanism for memristive behavior has been proposed by Pershin and Di Ventra. The authors show that certain types of semiconductor spintronic structures belong to a broad class of memristive systems as defined by Chua and Kang. The mechanism of memristive behavior in such structures is based entirely on the electron spin degree of freedom which allows for a more convenient control than the ionic transport in nanostructures. When an external control parameter (such as voltage) is changed, the adjustment of electron spin polarization is delayed because of the diffusion and relaxation processes causing hysteresis. This result was anticipated in the study of spin extraction at semiconductor/ferromagnet interfaces, but was not described in terms of memristive behavior. On a short time scale, these structures behave almost as an ideal memristor. This result broadens the possible range of applications of semiconductor spintronics and makes a step forward in future practical applications.

Self-directed channel memristor

In 2017, Dr Kris Campbell formally introduced the self-directed channel (SDC) memristor. The SDC device is the first memristive device available commercially to researchers, students and electronics enthusiast worldwide. The SDC device is operational immediately after fabrication. In the Ge₂Se₃ active layer, Ge-Ge homopolar bonds are found and switching occurs. The three layers consisting of Ge₂Se₃/Ag/Ge₂Se₃, directly below the top tungsten electrode, mix together during deposition and jointly form the silver-source layer. A layer of SnSe is between these two layers ensuring that the silver-source layer is not in direct contact with the active layer. Since silver does not migrate into the active layer at high temperatures, and the active layer maintains a high glass transition temperature of about 350 °C (662 °F), the device has significantly higher processing and operating temperatures at 250 °C (482 °F) and at least 150 °C (302 °F), respectively. These processing and operating temperatures are higher than most ion-conducting chalcogenide device types, including the S-based glasses (e.g. GeS) that need to be photodoped or thermally annealed. These factors allow the SDC device to operate over a wide range of temperatures, including long-term continuous operation at 150 °C (302 °F).

Potential applications

Memristors remain a laboratory curiosity, as yet made in insufficient numbers to gain any commercial applications. Despite this lack of mass availability, according to Allied Market Research the memristor market was worth $3.2 million in 2015 and will be worth $79.0 million by 2022.

A potential application of memristors is in analog memories for superconducting quantum computers.

Memristors can potentially be fashioned into non-volatile solid-state memory, which could allow greater data density than hard drives with access times similar to DRAM, replacing both components. HP prototyped a crossbar latch memory that can fit 100 gigabits in a square centimeter, and proposed a scalable 3D design (consisting of up to 1000 layers or 1 petabit per cm³). In May 2008 HP reported that its device reaches currently about one-tenth the speed of DRAM. The devices' resistance would be read with alternating current so that the stored value would not be affected. In May 2012, it was reported that the access time had been improved to 90 nanoseconds, which is nearly one hundred times faster than the contemporaneous Flash memory. At the same time, the energy consumption was just one percent of that consumed by Flash memory.

Memristor have applications in programmable logic, signal processing, Super-resolution imaging, physical neural networks, control systems, reconfigurable computing, brain–computer interfaces, and RFID. Memristive devices are potentially used for stateful logic implication, allowing a replacement for CMOS-based logic computation. Several early works have been reported in this direction.

In 2009, a simple electronic circuit consisting of an LC network and a memristor was used to model experiments on adaptive behavior of unicellular organisms. It was shown that subjected to a train of periodic pulses, the circuit learns and anticipates the next pulse similar to the behavior of slime molds Physarum polycephalum where the viscosity of channels in the cytoplasm responds to periodic environment changes. Applications of such circuits may include, e.g., pattern recognition. The DARPA SyNAPSE project funded HP Labs, in collaboration with the Boston University Neuromorphics Lab, has been developing neuromorphic architectures which may be based on memristive systems. In 2010, Versace and Chandler described the MoNETA (Modular Neural Exploring Traveling Agent) model. MoNETA is the first large-scale neural network model to implement whole-brain circuits to power a virtual and robotic agent using memristive hardware. Application of the memristor crossbar structure in the construction of an analog soft computing system was demonstrated by Merrikh-Bayat and Shouraki. In 2011, they showed how memristor crossbars can be combined with fuzzy logic to create an analog memristive neuro-fuzzy computing system with fuzzy input and output terminals. Learning is based on the creation of fuzzy relations inspired from Hebbian learning rule.

In 2013 Leon Chua published a tutorial underlining the broad span of complex phenomena and applications that memristors span and how they can be used as non-volatile analog memories and can mimic classic habituation and learning phenomena.

Derivative devices

Memistor and memtransistor

The memistor and memtransistor are transistor based devices which include memristor function.

Memcapacitors and meminductors

In 2009, Di Ventra, Pershin, and Chua extended the notion of memristive systems to capacitive and inductive elements in the form of memcapacitors and meminductors, whose properties depend on the state and history of the system, further extended in 2013 by Di Ventra and Pershin.

Memfractance and memfractor, 2nd- and 3rd-order memristor, memcapacitor and meminductor

In September 2014, Mohamed-Salah Abdelouahab, Rene Lozi, and Leon Chua published a general theory of 1st-, 2nd-, 3rd-, and nth-order memristive elements using fractional derivatives.

History

Precursors

Sir Humphry Davy is said by some to have performed the first experiments which can be explained by memristor effects as long ago as 1808. However the first device of a related nature to be constructed was the memistor (i.e. memory resistor), a term coined in 1960 by Bernard Widrow to describe a circuit element of an early artificial neural network called ADALINE. A few years later, in 1968, Argall published an article showing the resistance switching effects of TiO₂ which was later claimed by researchers from Hewlett Packard to be evidence of a memristor.

Theoretical description

Leon Chua postulated his new two-terminal circuit element in 1971. It was characterized by a relationship between charge and flux linkage as a fourth fundamental circuit element. Five years later he and his student Sung Mo Kang generalized the theory of memristors and memristive systems including a property of zero crossing in the Lissajous curve characterizing current vs. voltage behavior.

Twenty-first century

On May 1, 2008, Strukov, Snider, Stewart, and Williams published an article in Nature identifying a link between the 2-terminal resistance switching behavior found in nanoscale systems and memristors.

On January 23, 2009, Di Ventra, Pershin, and Chua extended the notion of memristive systems to capacitive and inductive elements, namely capacitors and inductors, whose properties depend on the state and history of the system.

In July 2014, the MeMOSat/LabOSat group (composed of researchers from Universidad Nacional de General San Martín (Argentina), INTI, CNEA, and CONICET) put memory devices into orbit for their study at LEO. Since then, seven missions with different devices are performing experiments in low orbit, onboard Satellogic's Ñu-Sat satellites.

On July 7, 2015 Knowm Inc announced Self Directed Channel (SDC) memristors commercially. These devices remain available in small numbers.

On July 13, 2018 MemSat (Memristor Satellite) was launched to fly a memristor evaluation payload.