Degenerate matter[1][2] in
physics is a collection of free, non-interacting particles with a
pressure and other physical characteristics determined by
quantum mechanical effects. It is the analogue of an
ideal gas in
classical mechanics. The degenerate state of matter, in the sense of deviant from an ideal gas, arises at extraordinarily high density (in
compact stars) or at extremely low temperatures in laboratories.
[3][4] It occurs for matter particles such as
electrons,
neutrons,
protons, and
fermions in general and is referred to as
electron-degenerate matter,
neutron-degenerate matter, etc. In a mixture of particles, such as
ions and electrons in
white dwarfs or
metals, the electrons may be degenerate, while the ions are not.
In a quantum mechanical description, free particles limited to a finite volume may take only a discrete set of energies, called quantum states. The
Pauli exclusion principle prevents identical fermions from occupying the same quantum state. At lowest total energy (when the thermal energy of the particles is negligible), all the lowest energy quantum states are filled. This state is referred to as full degeneracy. The pressure (called degeneracy pressure or Fermi pressure) remains nonzero even near absolute zero temperature.
[3][4] Adding particles or reducing the volume forces the particles into higher-energy quantum states. This requires a compression force, and is made manifest as a resisting pressure. The key feature is that this degeneracy pressure does not depend on the temperature and only on the density of the fermions. It keeps dense stars in equilibrium independent of the thermal structure of the star.
Degenerate matter is also called a
Fermi gas or a
degenerate gas. A degenerate state with velocities of the fermions close to the speed of light (particle energy larger than its
rest mass energy) is called
relativistic degenerate matter.
Degenerate matter was first described for a mixture of ions and electrons in 1926 by
Ralph H. Fowler,
[5] showing that at densities observed in
white dwarfs the electrons (obeying
Fermi–Dirac statistics, the term degenerate was not yet in use) have a pressure much higher than the
partial pressure of the ions.
Concept
Imagine that a
plasma is cooled and compressed repeatedly. Eventually, it will not be possible to compress the plasma any further, because the
Pauli exclusion principle states that two
fermions cannot share the same quantum state. When in this state, since there is no extra space for any particles, we can also say that a particle's location is extremely defined. Therefore, since (according to the Heisenberg
uncertainty principle)
ΔpΔx ≥ ħ/2 where Δ
p is the uncertainty in the particle's momentum and Δ
x is the uncertainty in position, then we must say that their momentum is extremely uncertain since the particles are located in a very confined space. Therefore,
even though the plasma is cold, the particles must be moving very fast on average. This leads to the conclusion that in order to compress an object into a very small space, tremendous force is required to control its particles' momentum.
Unlike a classical
ideal gas, whose pressure is proportional to its
temperature (
P = nkT/V, where
P is pressure,
V is the volume,
n is the number of particles—typically atoms or molecules—
k is
Boltzmann's constant, and
T is temperature), the pressure exerted by degenerate matter depends only weakly on its temperature. In particular, the pressure remains nonzero even at
absolute zero temperature. At relatively low densities, the pressure of a fully degenerate gas is given by
P = K(n/V)5/3, where
K depends on the properties of the particles making up the gas. At very high densities, where most of the particles are forced into quantum states with
relativistic energies, the pressure is given by
P = K′(n/V)4/3, where
K′ again depends on the properties of the particles making up the gas.
[6]
All matter experiences both normal thermal pressure and degeneracy pressure, but in commonly encountered gases, thermal pressure dominates so much that degeneracy pressure can be ignored. Likewise, degenerate matter still has normal thermal pressure, but at extremely high densities the degeneracy pressure usually dominates.
Exotic examples of degenerate matter include
neutronium,
strange matter,
metallic hydrogen and
white dwarf matter. Degeneracy pressure contributes to the pressure of conventional
solids, but these are not usually considered to be degenerate matter because a significant contribution to their pressure is provided by electrical repulsion of atomic
nuclei and the screening of nuclei from each other by electrons. In
metals it is useful to treat the
conduction electrons alone as a degenerate, free electron gas while the majority of the electrons are regarded as occupying bound quantum states. This contrasts with degenerate matter that forms the body of a white dwarf, where all the electrons would be treated as occupying free particle momentum states.
Degenerate gases
Degenerate gases are gases composed of
fermions that have a particular configuration that usually forms at high densities.
Fermions are particles with
half-integer spin. Their behavior is regulated by a set of quantum mechanical rules called the
Fermi–Dirac statistics. One particular rule is the
Pauli exclusion principle, which states that there can be only one fermion occupying each
quantum state, which also applies to electrons that are not bound to a nucleus but merely confined to a fixed volume, such as in the deep interior of a star. Such particles as electrons, protons, neutrons, and neutrinos are all fermions and obey Fermi–Dirac statistics.
A fermion gas in which all energy states below some energy level are filled is called a fully degenerate fermion gas. The difference between this energy level and the lowest energy level is known as the
Fermi energy. The electron gas in ordinary metals and in the interior of white dwarf stars constitute two examples of a degenerate electron gas. Most stars are supported against their own gravitation by normal thermal gas pressure.
White dwarf stars are supported by the degeneracy pressure of the electron gas in their interior, while for
neutron stars the degenerate particles are neutrons.
Electron degeneracy
In an ordinary fermion gas in which thermal effects dominate, most of the available electron energy levels are unfilled and the electrons are free to move to these states. As particle density is increased, electrons progressively fill the lower energy states and additional electrons are forced to occupy states of higher energy even at low temperatures. Degenerate gases strongly resist further compression because the electrons cannot move to already filled lower energy levels due to the
Pauli exclusion principle. Since electrons cannot give up energy by moving to lower energy states, no thermal energy can be extracted. The momentum of the fermions in the fermion gas nevertheless generates pressure, termed
degeneracy pressure.
Under high densities the matter becomes a degenerate gas when the electrons are all stripped from their parent atoms. In the core of a star, once hydrogen burning in
nuclear fusion reactions stops, it becomes a collection of positively charged
ions, largely helium and carbon nuclei, floating in a sea of electrons, which have been stripped from the nuclei. Degenerate gas is an almost perfect conductor of heat and does not obey the ordinary gas laws.
White dwarfs are luminous not because they are generating any energy but rather because they have trapped a large amount of heat which is gradually radiated away. Normal gas exerts higher pressure when it is heated and expands, but the pressure in a degenerate gas does not depend on the temperature. When gas becomes super-compressed, particles position right up against each other to produce degenerate gas that behaves more like a solid. In degenerate gases the
kinetic energies of electrons are quite high and the rate of collision between electrons and other particles is quite low, therefore degenerate electrons can travel great distances at velocities that approach the speed of light. Instead of temperature, the pressure in a degenerate gas depends only on the speed of the degenerate particles; however, adding heat does not increase the speed. Pressure is only increased by the mass of the particles, which increases the gravitational force pulling the particles closer together. Therefore, the phenomenon is the opposite of that normally found in matter where if the mass of the matter is increased, the object becomes bigger. In degenerate gas, when the mass is increased, the pressure is increased, and the particles become spaced closer together, so the object becomes smaller. Degenerate gas can be compressed to very high densities, typical values being in the range of 10,000 kilograms per cubic centimeter.
There is an upper limit to the mass of an electron-degenerate object, the
Chandrasekhar limit, beyond which electron degeneracy pressure cannot support the object against collapse. The limit is approximately 1.44
[7]solar masses for objects with compositions similar to the
sun. The mass cutoff changes with the chemical composition of the object, as this affects the ratio of mass to number of electrons present. Celestial objects below this limit are
white dwarf stars, formed by the collapse of the cores of
stars that run out of fuel. During collapse, an electron-degenerate gas forms in the core, providing sufficient degeneracy pressure as it is compressed to resist further collapse. Above this mass limit, a
neutron star (supported by neutron degeneracy pressure) or a
black hole may be formed instead.
Proton degeneracy
Sufficiently dense matter containing protons experiences proton degeneracy pressure, in a manner similar to the electron degeneracy pressure in electron-degenerate matter: protons confined to a sufficiently small volume have a large uncertainty in their momentum due to the Heisenberg uncertainty principle. Because protons are much more massive than electrons, the same momentum represents a much smaller velocity for protons than for electrons. As a result, in matter with approximately equal numbers of protons and electrons, proton degeneracy pressure is much smaller than electron degeneracy pressure, and proton degeneracy is usually modeled as a correction to the
equations of state of electron-degenerate matter.
Neutron degeneracy
Neutron degeneracy is analogous to electron degeneracy and is demonstrated in neutron stars, which are primarily supported by the pressure from a degenerate neutron gas.
[8] This happens when a stellar core above 1.44
[citation needed] solar masses, the
Chandrasekhar limit, collapses and is not halted by the degenerate electrons. As the star collapses, the
Fermi energy of the electrons increases to the point where it is energetically favorable for them to combine with protons to produce neutrons (via inverse
beta decay, also termed
electron capture and "neutralization"). The result of this collapse is an extremely compact star composed of
nuclear matter, which is predominantly a degenerate neutron gas, sometimes called
neutronium, with a small admixture of degenerate proton and electron gases.
Neutrons in a degenerate neutron gas are spaced much more closely than electrons in an electron-degenerate gas, because the more massive neutron has a much shorter
wavelength at a given energy. In the case of neutron stars and white dwarf stars, this is compounded by the fact that the pressures within neutron stars are much higher than those in white dwarfs. The pressure increase is caused by the fact that the compactness of a neutron star causes gravitational forces to be much higher than in a less compact body with similar mass. This results in a star with a diameter on the order of a thousandth that of a white dwarf.
There is an upper limit to the mass of a neutron-degenerate object, the
Tolman–Oppenheimer–Volkoff limit, which is analogous to the Chandrasekhar limit for electron-degenerate objects. The precise limit is unknown, as it depends on the
equations of state of nuclear matter, for which a highly accurate model is not yet available. Above this limit, a neutron star may collapse into a black hole, or into other, denser forms of degenerate matter (such as
quark matter) if these forms exist and have suitable properties (mainly related to degree of compressibility, or "stiffness", described by the equations of state).
Quark degeneracy
At densities greater than those supported by neutron degeneracy,
quark matter is expected to occur. Several variations of this have been proposed that represent quark-degenerate states.
Strange matter is a degenerate gas of quarks that is often assumed to contain
strange quarks in addition to the usual
up and
down quarks.
Color superconductor materials are degenerate gases of quarks in which quarks pair up in a manner similar to
Cooper pairing in electrical
superconductors. The equations of state for the various proposed forms of quark-degenerate matter vary widely, and are usually also poorly defined, due to the difficulty of modeling
strong force interactions.
Quark-degenerate matter may occur in the cores of neutron stars, depending on the equations of state of neutron-degenerate matter. It may also occur in hypothetical
quark stars, formed by the collapse of objects above the
Tolman–Oppenheimer–Volkoff mass limit for neutron-degenerate objects. Whether quark-degenerate matter forms at all in these situations depends on the equations of state of both neutron-degenerate matter and quark-degenerate matter, both of which are poorly known.
Preon degeneracy hypothesis
Preons are subatomic particles proposed to be the constituents of
quarks, which become composite particles in preon-based models. If preons exist, preon-degenerate matter might occur at densities greater than that which can be supported by quark-degenerate matter. The expected properties of preon-degenerate matter depend very strongly on the model chosen to describe preons, and the existence of preons is not assumed by the majority of the scientific community, due to conflicts between the preon models originally proposed and experimental data from particle accelerators.
Singularity
At densities greater than those supported by any degeneracy, gravity overwhelms all other forces. To the best of our current understanding, the body collapses to form a
black hole. In the frame of reference that is co-moving with the collapsing matter, all the matter ends up in an infinitely dense singularity at the center of the
event horizon. In the frame of reference of an observer at infinity, the collapse asymptotically approaches the event horizon.
As a consequence of relativity, the extreme gravitational field and orbital velocity experienced by infalling matter around a black hole would
"slow" time for that matter relative to a distant observer.
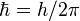 (reduced
(reduced  and the other in state
and the other in state  :
: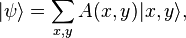


 . But this is equal to
. But this is equal to
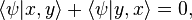




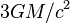 or less, then the photons may be
or less, then the photons may be 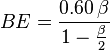

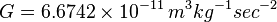



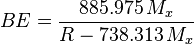



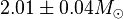 .
.