Field (physics)

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Field_(physics) 

 

Illustration of the electric field surrounding a positive (red) and a negative (blue) charge.

In physics, a field is a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time. For example, on a weather map, the surface temperature is described by assigning a number to each point on the map; the temperature can be considered at a certain point in time or over some interval of time, to study the dynamics of temperature change. A surface wind map, assigning an arrow to each point on a map that describes the wind speed and direction at that point, is an example of a vector field, i.e. a 1-dimensional (rank-1) tensor field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, while electrodynamics can be formulated in terms of two interacting vector fields at each point in spacetime, or as a single-rank 2-tensor field.

In the modern framework of the quantum theory of fields, even without referring to a test particle, a field occupies space, contains energy, and its presence precludes a classical "true vacuum". This has led physicists to consider electromagnetic fields to be a physical entity, making the field concept a supporting paradigm of the edifice of modern physics. "The fact that the electromagnetic field can possess momentum and energy makes it very real ... a particle makes a field, and a field acts on another particle, and the field has such familiar properties as energy content and momentum, just as particles can have." In practice, the strength of most fields diminishes with distance, eventually becoming undetectable. For instance the strength of many relevant classical fields, such as the gravitational field in Newton's theory of gravity or the electrostatic field in classical electromagnetism, is inversely proportional to the square of the distance from the source (i.e., they follow Gauss's law).

A field can be classified as a scalar field, a vector field, a spinor field or a tensor field according to whether the represented physical quantity is a scalar, a vector, a spinor, or a tensor, respectively. A field has a consistent tensorial character wherever it is defined: i.e. a field cannot be a scalar field somewhere and a vector field somewhere else. For example, the Newtonian gravitational field is a vector field: specifying its value at a point in spacetime requires three numbers, the components of the gravitational field vector at that point. Moreover, within each category (scalar, vector, tensor), a field can be either a classical field or a quantum field, depending on whether it is characterized by numbers or quantum operators respectively. In this theory an equivalent representation of field is a field particle, for instance a boson.

History

To Isaac Newton, his law of universal gravitation simply expressed the gravitational force that acted between any pair of massive objects. When looking at the motion of many bodies all interacting with each other, such as the planets in the Solar System, dealing with the force between each pair of bodies separately rapidly becomes computationally inconvenient. In the eighteenth century, a new quantity was devised to simplify the bookkeeping of all these gravitational forces. This quantity, the gravitational field, gave at each point in space the total gravitational acceleration which would be felt by a small object at that point. This did not change the physics in any way: it did not matter if all the gravitational forces on an object were calculated individually and then added together, or if all the contributions were first added together as a gravitational field and then applied to an object.

The development of the independent concept of a field truly began in the nineteenth century with the development of the theory of electromagnetism. In the early stages, André-Marie Ampère and Charles-Augustin de Coulomb could manage with Newton-style laws that expressed the forces between pairs of electric charges or electric currents. However, it became much more natural to take the field approach and express these laws in terms of electric and magnetic fields; in 1849 Michael Faraday became the first to coin the term "field".

The independent nature of the field became more apparent with James Clerk Maxwell's discovery that waves in these fields propagated at a finite speed. Consequently, the forces on charges and currents no longer just depended on the positions and velocities of other charges and currents at the same time, but also on their positions and velocities in the past.

Maxwell, at first, did not adopt the modern concept of a field as a fundamental quantity that could independently exist. Instead, he supposed that the electromagnetic field expressed the deformation of some underlying medium—the luminiferous aether—much like the tension in a rubber membrane. If that were the case, the observed velocity of the electromagnetic waves should depend upon the velocity of the observer with respect to the aether. Despite much effort, no experimental evidence of such an effect was ever found; the situation was resolved by the introduction of the special theory of relativity by Albert Einstein in 1905. This theory changed the way the viewpoints of moving observers were related to each other. They became related to each other in such a way that velocity of electromagnetic waves in Maxwell's theory would be the same for all observers. By doing away with the need for a background medium, this development opened the way for physicists to start thinking about fields as truly independent entities.

In the late 1920s, the new rules of quantum mechanics were first applied to the electromagnetic field. In 1927, Paul Dirac used quantum fields to successfully explain how the decay of an atom to a lower quantum state led to the spontaneous emission of a photon, the quantum of the electromagnetic field. This was soon followed by the realization (following the work of Pascual Jordan, Eugene Wigner, Werner Heisenberg, and Wolfgang Pauli) that all particles, including electrons and protons, could be understood as the quanta of some quantum field, elevating fields to the status of the most fundamental objects in nature. That said, John Wheeler and Richard Feynman seriously considered Newton's pre-field concept of action at a distance (although they set it aside because of the ongoing utility of the field concept for research in general relativity and quantum electrodynamics).

Classical fields

Main article: Classical field theory

There are several examples of classical fields. Classical field theories remain useful wherever quantum properties do not arise, and can be active areas of research. Elasticity of materials, fluid dynamics and Maxwell's equations are cases in point.

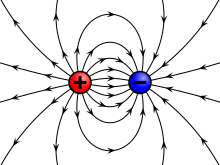
Some of the simplest physical fields are vector force fields. Historically, the first time that fields were taken seriously was with Faraday's lines of force when describing the electric field. The gravitational field was then similarly described.

Newtonian gravitation

In classical gravitation, mass is the source of an attractive gravitational field g.

A classical field theory describing gravity is Newtonian gravitation, which describes the gravitational force as a mutual interaction between two masses.

Any body with mass M is associated with a gravitational field g which describes its influence on other bodies with mass. The gravitational field of M at a point r in space corresponds to the ratio between force F that M exerts on a small or negligible test mass m located at r and the test mass itself:

${\displaystyle \mathbf {g} (\mathbf {r} )={\frac {\mathbf {F} (\mathbf {r} )}{m}}.}$

Stipulating that m is much smaller than M ensures that the presence of m has a negligible influence on the behavior of M.

According to Newton's law of universal gravitation, F(r) is given by

${\displaystyle \mathbf {F} (\mathbf {r} )=-{\frac {GMm}{r^{2}}}{\hat {\mathbf {r} }},}$

where ${\displaystyle {\hat {\mathbf {r} }}}$ is a unit vector lying along the line joining M and m and pointing from M to m. Therefore, the gravitational field of M is

${\displaystyle \mathbf {g} (\mathbf {r} )={\frac {\mathbf {F} (\mathbf {r} )}{m}}=-{\frac {GM}{r^{2}}}{\hat {\mathbf {r} }}.}$

The experimental observation that inertial mass and gravitational mass are equal to an unprecedented level of accuracy leads to the identity that gravitational field strength is identical to the acceleration experienced by a particle. This is the starting point of the equivalence principle, which leads to general relativity.

Because the gravitational force F is conservative, the gravitational field g can be rewritten in terms of the gradient of a scalar function, the gravitational potential Φ(r):

${\displaystyle \mathbf {g} (\mathbf {r} )=-\nabla \Phi (\mathbf {r} ).}$

Electromagnetism

Main article: Electromagnetism

Michael Faraday first realized the importance of a field as a physical quantity, during his investigations into magnetism. He realized that electric and magnetic fields are not only fields of force which dictate the motion of particles, but also have an independent physical reality because they carry energy.

These ideas eventually led to the creation, by James Clerk Maxwell, of the first unified field theory in physics with the introduction of equations for the electromagnetic field. The modern version of these equations is called Maxwell's equations.

Electrostatics

Main article: Electrostatics

A charged test particle with charge q experiences a force F based solely on its charge. We can similarly describe the electric field E so that F = qE. Using this and Coulomb's law tells us that the electric field due to a single charged particle is

${\displaystyle \mathbf {E} ={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{r^{2}}}{\hat {\mathbf {r} }}.}$

The electric field is conservative, and hence can be described by a scalar potential, V(r):

${\displaystyle \mathbf {E} (\mathbf {r} )=-\nabla V(\mathbf {r} ).}$

Magnetostatics

Main article: Magnetostatics

A steady current I flowing along a path ℓ will create a field B, that exerts a force on nearby moving charged particles that is quantitatively different from the electric field force described above. The force exerted by I on a nearby charge q with velocity v is

${\displaystyle \mathbf {F} (\mathbf {r} )=q\mathbf {v} \times \mathbf {B} (\mathbf {r} ),}$

where B(r) is the magnetic field, which is determined from I by the Biot–Savart law:

${\displaystyle \mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\int {\frac {Id{\boldsymbol {\ell }}\times {\hat {\mathbf {r} }}}{r^{2}}}.}$

The magnetic field is not conservative in general, and hence cannot usually be written in terms of a scalar potential. However, it can be written in terms of a vector potential, A(r):

${\displaystyle \mathbf {B} (\mathbf {r} )={\boldsymbol {\nabla }}\times \mathbf {A} (\mathbf {r} )}$

The E fields and B fields due to electric charges (black/white) and magnetic poles (red/blue). Top: E field due to an electric dipole moment d. Bottom left: B field due to a mathematical magnetic dipole m formed by two magnetic monopoles. Bottom right: B field due to a pure magnetic dipole moment m found in ordinary matter (not from monopoles).

Electrodynamics

Main article: Electrodynamics

In general, in the presence of both a charge density ρ(r, t) and current density J(r, t), there will be both an electric and a magnetic field, and both will vary in time. They are determined by Maxwell's equations, a set of differential equations which directly relate E and B to ρ and J.

Alternatively, one can describe the system in terms of its scalar and vector potentials V and A. A set of integral equations known as retarded potentials allow one to calculate V and A from ρ and J, and from there the electric and magnetic fields are determined via the relations

${\displaystyle \mathbf {E} =-{\boldsymbol {\nabla }}V-{\frac {\partial \mathbf {A} }{\partial t}}}$

${\displaystyle \mathbf {B} ={\boldsymbol {\nabla }}\times \mathbf {A} .}$

At the end of the 19th century, the electromagnetic field was understood as a collection of two vector fields in space. Nowadays, one recognizes this as a single antisymmetric 2nd-rank tensor field in spacetime.

The E fields and B fields due to electric charges (black/white) and magnetic poles (red/blue). E fields due to stationary electric charges and B fields due to stationary magnetic charges (note in nature N and S monopoles do not exist). In motion (velocity v), an electric charge induces a B field while a magnetic charge (not found in nature) would induce an E field. Conventional current is used.

Gravitation in general relativity

In general relativity, mass-energy warps space time (Einstein tensor G), and rotating asymmetric mass-energy distributions with angular momentum J generate GEM fields H

Einstein's theory of gravity, called general relativity, is another example of a field theory. Here the principal field is the metric tensor, a symmetric 2nd-rank tensor field in spacetime. This replaces Newton's law of universal gravitation.

Waves as fields

Waves can be constructed as physical fields, due to their finite propagation speed and causal nature when a simplified physical model of an isolated closed system is set. They are also subject to the inverse-square law.

For electromagnetic waves, there are optical fields, and terms such as near- and far-field limits for diffraction. In practice though, the field theories of optics are superseded by the electromagnetic field theory of Maxwell.

Quantum fields

Main article: Quantum field theory

It is now believed that quantum mechanics should underlie all physical phenomena, so that a classical field theory should, at least in principle, permit a recasting in quantum mechanical terms; success yields the corresponding quantum field theory. For example, quantizing classical electrodynamics gives quantum electrodynamics. Quantum electrodynamics is arguably the most successful scientific theory; experimental data confirm its predictions to a higher precision (to more significant digits) than any other theory. The two other fundamental quantum field theories are quantum chromodynamics and the electroweak theory.

Fields due to color charges, like in quarks (G is the gluon field strength tensor). These are "colorless" combinations. Top: Color charge has "ternary neutral states" as well as binary neutrality (analogous to electric charge). Bottom: The quark/antiquark combinations.

In quantum chromodynamics, the color field lines are coupled at short distances by gluons, which are polarized by the field and line up with it. This effect increases within a short distance (around 1 fm from the vicinity of the quarks) making the color force increase within a short distance, confining the quarks within hadrons. As the field lines are pulled together tightly by gluons, they do not "bow" outwards as much as an electric field between electric charges.

These three quantum field theories can all be derived as special cases of the so-called standard model of particle physics. General relativity, the Einsteinian field theory of gravity, has yet to be successfully quantized. However an extension, thermal field theory, deals with quantum field theory at finite temperatures, something seldom considered in quantum field theory.

In BRST theory one deals with odd fields, e.g. Faddeev–Popov ghosts. There are different descriptions of odd classical fields both on graded manifolds and supermanifolds.

As above with classical fields, it is possible to approach their quantum counterparts from a purely mathematical view using similar techniques as before. The equations governing the quantum fields are in fact PDEs (specifically, relativistic wave equations (RWEs)). Thus one can speak of Yang–Mills, Dirac, Klein–Gordon and Schrödinger fields as being solutions to their respective equations. A possible problem is that these RWEs can deal with complicated mathematical objects with exotic algebraic properties (e.g. spinors are not tensors, so may need calculus for spinor fields), but these in theory can still be subjected to analytical methods given appropriate mathematical generalization.

Field theory

Field theory usually refers to a construction of the dynamics of a field, i.e. a specification of how a field changes with time or with respect to other independent physical variables on which the field depends. Usually this is done by writing a Lagrangian or a Hamiltonian of the field, and treating it as a classical or quantum mechanical system with an infinite number of degrees of freedom. The resulting field theories are referred to as classical or quantum field theories.

The dynamics of a classical field are usually specified by the Lagrangian density in terms of the field components; the dynamics can be obtained by using the action principle.

It is possible to construct simple fields without any prior knowledge of physics using only mathematics from several variable calculus, potential theory and partial differential equations (PDEs). For example, scalar PDEs might consider quantities such as amplitude, density and pressure fields for the wave equation and fluid dynamics; temperature/concentration fields for the heat/diffusion equations. Outside of physics proper (e.g., radiometry and computer graphics), there are even light fields. All these previous examples are scalar fields. Similarly for vectors, there are vector PDEs for displacement, velocity and vorticity fields in (applied mathematical) fluid dynamics, but vector calculus may now be needed in addition, being calculus for vector fields (as are these three quantities, and those for vector PDEs in general). More generally problems in continuum mechanics may involve for example, directional elasticity (from which comes the term tensor, derived from the Latin word for stretch), complex fluid flows or anisotropic diffusion, which are framed as matrix-tensor PDEs, and then require matrices or tensor fields, hence matrix or tensor calculus. The scalars (and hence the vectors, matrices and tensors) can be real or complex as both are fields in the abstract-algebraic/ring-theoretic sense.

In a general setting, classical fields are described by sections of fiber bundles and their dynamics is formulated in the terms of jet manifolds (covariant classical field theory).

In modern physics, the most often studied fields are those that model the four fundamental forces which one day may lead to the Unified Field Theory.

Symmetries of fields

A convenient way of classifying a field (classical or quantum) is by the symmetries it possesses. Physical symmetries are usually of two types:

Spacetime symmetries

Main articles: Global symmetry and Spacetime symmetries

Fields are often classified by their behaviour under transformations of spacetime. The terms used in this classification are:

• scalar fields (such as temperature) whose values are given by a single variable at each point of space. This value does not change under transformations of space.
• vector fields (such as the magnitude and direction of the force at each point in a magnetic field) which are specified by attaching a vector to each point of space. The components of this vector transform between themselves contravariantly under rotations in space. Similarly, a dual (or co-) vector field attaches a dual vector to each point of space, and the components of each dual vector transform covariantly.
• tensor fields, (such as the stress tensor of a crystal) specified by a tensor at each point of space. Under rotations in space, the components of the tensor transform in a more general way which depends on the number of covariant indices and contravariant indices.
• spinor fields (such as the Dirac spinor) arise in quantum field theory to describe particles with spin which transform like vectors except for the one of their components; in other words, when one rotates a vector field 360 degrees around a specific axis, the vector field turns to itself; however, spinors would turn to their negatives in the same case.

Internal symmetries

Main article: Internal symmetry

Fields may have internal symmetries in addition to spacetime symmetries. In many situations, one needs fields which are a list of spacetime scalars: (φ₁, φ₂, ... φ_N). For example, in weather prediction these may be temperature, pressure, humidity, etc. In particle physics, the color symmetry of the interaction of quarks is an example of an internal symmetry, that of the strong interaction. Other examples are isospin, weak isospin, strangeness and any other flavour symmetry.

If there is a symmetry of the problem, not involving spacetime, under which these components transform into each other, then this set of symmetries is called an internal symmetry. One may also make a classification of the charges of the fields under internal symmetries.

Statistical field theory

Main article: Statistical field theory

Statistical field theory attempts to extend the field-theoretic paradigm toward many-body systems and statistical mechanics. As above, it can be approached by the usual infinite number of degrees of freedom argument.

Much like statistical mechanics has some overlap between quantum and classical mechanics, statistical field theory has links to both quantum and classical field theories, especially the former with which it shares many methods. One important example is mean field theory.

Continuous random fields

Classical fields as above, such as the electromagnetic field, are usually infinitely differentiable functions, but they are in any case almost always twice differentiable. In contrast, generalized functions are not continuous. When dealing carefully with classical fields at finite temperature, the mathematical methods of continuous random fields are used, because thermally fluctuating classical fields are nowhere differentiable. Random fields are indexed sets of random variables; a continuous random field is a random field that has a set of functions as its index set. In particular, it is often mathematically convenient to take a continuous random field to have a Schwartz space of functions as its index set, in which case the continuous random field is a tempered distribution.

We can think about a continuous random field, in a (very) rough way, as an ordinary function that is ${\displaystyle \pm \infty }$ almost everywhere, but such that when we take a weighted average of all the infinities over any finite region, we get a finite result. The infinities are not well-defined; but the finite values can be associated with the functions used as the weight functions to get the finite values, and that can be well-defined. We can define a continuous random field well enough as a linear map from a space of functions into the real numbers.

Interactome

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Interactome 

In molecular biology, an interactome is the whole set of molecular interactions in a particular cell. The term specifically refers to physical interactions among molecules (such as those among proteins, also known as protein–protein interactions, PPIs; or between small molecules and proteins) but can also describe sets of indirect interactions among genes (genetic interactions).

Part of the DISC1 interactome with genes represented by text in boxes and interactions noted by lines between the genes. From Hennah and Porteous, 2009.

The word "interactome" was originally coined in 1999 by a group of French scientists headed by Bernard Jacq. Mathematically, interactomes are generally displayed as graphs. Though interactomes may be described as biological networks, they should not be confused with other networks such as neural networks or food webs.

Molecular interaction networks

Molecular interactions can occur between molecules belonging to different biochemical families (proteins, nucleic acids, lipids, carbohydrates, etc.) and also within a given family. Whenever such molecules are connected by physical interactions, they form molecular interaction networks that are generally classified by the nature of the compounds involved. Most commonly, interactome refers to protein–protein interaction (PPI) network (PIN) or subsets thereof. For instance, the Sirt-1 protein interactome and Sirt family second order interactome is the network involving Sirt-1 and its directly interacting proteins where as second order interactome illustrates interactions up to second order of neighbors (Neighbors of neighbors). Another extensively studied type of interactome is the protein–DNA interactome, also called a gene-regulatory network, a network formed by transcription factors, chromatin regulatory proteins, and their target genes. Even metabolic networks can be considered as molecular interaction networks: metabolites, i.e. chemical compounds in a cell, are converted into each other by enzymes, which have to bind their substrates physically.

In fact, all interactome types are interconnected. For instance, protein interactomes contain many enzymes which in turn form biochemical networks. Similarly, gene regulatory networks overlap substantially with protein interaction networks and signaling networks.

Size

Estimates of the yeast protein interactome. From Uetz P. & Grigoriev A, 2005.

It has been suggested that the size of an organism's interactome correlates better than genome size with the biological complexity of the organism. Although protein–protein interaction maps containing several thousand binary interactions are now available for several species, none of them is presently complete and the size of interactomes is still a matter of debate.

Yeast

The yeast interactome, i.e. all protein–protein interactions among proteins of Saccharomyces cerevisiae, has been estimated to contain between 10,000 and 30,000 interactions. A reasonable estimate may be on the order of 20,000 interactions. Larger estimates often include indirect or predicted interactions, often from affinity purification/mass spectrometry (AP/MS) studies.

Genetic interaction networks

Main article: Genetic interaction network

Genes interact in the sense that they affect each other's function. For instance, a mutation may be harmless, but when it is combined with another mutation, the combination may turn out to be lethal. Such genes are said to "interact genetically". Genes that are connected in such a way form genetic interaction networks. Some of the goals of these networks are: develop a functional map of a cell's processes, drug target identification using chemoproteomics, and to predict the function of uncharacterized genes.

In 2010, the most "complete" gene interactome produced to date was compiled from about 5.4 million two-gene comparisons to describe "the interaction profiles for ~75% of all genes in the budding yeast", with ~170,000 gene interactions. The genes were grouped based on similar function so as to build a functional map of the cell's processes. Using this method the study was able to predict known gene functions better than any other genome-scale data set as well as adding functional information for genes that hadn't been previously described. From this model genetic interactions can be observed at multiple scales which will assist in the study of concepts such as gene conservation. Some of the observations made from this study are that there were twice as many negative as positive interactions, negative interactions were more informative than positive interactions, and genes with more connections were more likely to result in lethality when disrupted.

Interactomics

Interactomics is a discipline at the intersection of bioinformatics and biology that deals with studying both the interactions and the consequences of those interactions between and among proteins, and other molecules within a cell. Interactomics thus aims to compare such networks of interactions (i.e., interactomes) between and within species in order to find how the traits of such networks are either preserved or varied.

Interactomics is an example of "top-down" systems biology, which takes an overhead, as well as overall, view of a biosystem or organism. Large sets of genome-wide and proteomic data are collected, and correlations between different molecules are inferred. From the data new hypotheses are formulated about feedbacks between these molecules. These hypotheses can then be tested by new experiments.

Experimental methods to map interactomes

The study of interactomes is called interactomics. The basic unit of a protein network is the protein–protein interaction (PPI). While there are numerous methods to study PPIs, there are relatively few that have been used on a large scale to map whole interactomes.

The yeast two hybrid system (Y2H) is suited to explore the binary interactions among two proteins at a time. Affinity purification and subsequent mass spectrometry is suited to identify a protein complex. Both methods can be used in a high-throughput (HTP) fashion. Yeast two hybrid screens allow false positive interactions between proteins that are never expressed in the same time and place; affinity capture mass spectrometry does not have this drawback, and is the current gold standard. Yeast two-hybrid data better indicates non-specific tendencies towards sticky interactions rather while affinity capture mass spectrometry better indicates functional in vivo protein–protein interactions.

Computational methods to study interactomes

Once an interactome has been created, there are numerous ways to analyze its properties. However, there are two important goals of such analyses. First, scientists try to elucidate the systems properties of interactomes, e.g. the topology of its interactions. Second, studies may focus on individual proteins and their role in the network. Such analyses are mainly carried out using bioinformatics methods and include the following, among many others:

Validation

First, the coverage and quality of an interactome has to be evaluated. Interactomes are never complete, given the limitations of experimental methods. For instance, it has been estimated that typical Y2H screens detect only 25% or so of all interactions in an interactome. The coverage of an interactome can be assessed by comparing it to benchmarks of well-known interactions that have been found and validated by independent assays. Other methods filter out false positives calculating the similarity of known annotations of the proteins involved or define a likelihood of interaction using the subcellular localization of these proteins.

Predicting PPIs

Schizophrenia PPI.

Using experimental data as a starting point, homology transfer is one way to predict interactomes. Here, PPIs from one organism are used to predict interactions among homologous proteins in another organism ("interologs"). However, this approach has certain limitations, primarily because the source data may not be reliable (e.g. contain false positives and false negatives). In addition, proteins and their interactions change during evolution and thus may have been lost or gained. Nevertheless, numerous interactomes have been predicted, e.g. that of Bacillus licheniformis.

Some algorithms use experimental evidence on structural complexes, the atomic details of binding interfaces and produce detailed atomic models of protein–protein complexes as well as other protein–molecule interactions. Other algorithms use only sequence information, thereby creating unbiased complete networks of interaction with many mistakes.

Some methods use machine learning to distinguish how interacting protein pairs differ from non-interacting protein pairs in terms of pairwise features such as cellular colocalization, gene co-expression, how closely located on a DNA are the genes that encode the two proteins, and so on. Random Forest has been found to be most-effective machine learning method for protein interaction prediction. Such methods have been applied for discovering protein interactions on human interactome, specifically the interactome of Membrane proteins and the interactome of Schizophrenia-associated proteins.

Text mining of PPIs

Some efforts have been made to extract systematically interaction networks directly from the scientific literature. Such approaches range in terms of complexity from simple co-occurrence statistics of entities that are mentioned together in the same context (e.g. sentence) to sophisticated natural language processing and machine learning methods for detecting interaction relationships.

Protein function prediction

Protein interaction networks have been used to predict the function of proteins of unknown functions. This is usually based on the assumption that uncharacterized proteins have similar functions as their interacting proteins (guilt by association). For example, YbeB, a protein of unknown function was found to interact with ribosomal proteins and later shown to be involved in bacterial and eukaryotic (but not archaeal) translation. Although such predictions may be based on single interactions, usually several interactions are found. Thus, the whole network of interactions can be used to predict protein functions, given that certain functions are usually enriched among the interactors. The term hypothome has been used to denote an interactome wherein at least one of the genes or proteins is a hypothetical protein.

Perturbations and disease

Main article: Network medicine

The topology of an interactome makes certain predictions how a network reacts to the perturbation (e.g. removal) of nodes (proteins) or edges (interactions). Such perturbations can be caused by mutations of genes, and thus their proteins, and a network reaction can manifest as a disease. A network analysis can identify drug targets and biomarkers of diseases.

Network structure and topology

Interaction networks can be analyzed using the tools of graph theory. Network properties include the degree distribution, clustering coefficients, betweenness centrality, and many others. The distribution of properties among the proteins of an interactome has revealed that the interactome networks often have scale-free topology where functional modules within a network indicate specialized subnetworks. Such modules can be functional, as in a signaling pathway, or structural, as in a protein complex. In fact, it is a formidable task to identify protein complexes in an interactome, given that a network on its own does not directly reveal the presence of a stable complex.

Studied interactomes

Viral interactomes

Viral protein interactomes consist of interactions among viral or phage proteins. They were among the first interactome projects as their genomes are small and all proteins can be analyzed with limited resources. Viral interactomes are connected to their host interactomes, forming virus-host interaction networks. Some published virus interactomes include

Bacteriophage

• Escherichia coli bacteriophage lambda
• Escherichia coli bacteriophage T7
• Streptococcus pneumoniae bacteriophage Dp-1
• Streptococcus pneumoniae bacteriophage Cp-1

The lambda and VZV interactomes are not only relevant for the biology of these viruses but also for technical reasons: they were the first interactomes that were mapped with multiple Y2H vectors, proving an improved strategy to investigate interactomes more completely than previous attempts have shown.

Human (mammalian) viruses

• Human varicella zoster virus (VZV)
• Chandipura virus
• Epstein-Barr virus (EBV)
• Hepatitis C virus (HPC), Human-HCV interactions
• Hepatitis E virus (HEV)
• Herpes simplex virus 1 (HSV-1)
• Kaposi's sarcoma-associated herpesvirus (KSHV)
• Murine cytomegalovirus (mCMV)

Bacterial interactomes

Relatively few bacteria have been comprehensively studied for their protein–protein interactions. However, none of these interactomes are complete in the sense that they captured all interactions. In fact, it has been estimated that none of them covers more than 20% or 30% of all interactions, primarily because most of these studies have only employed a single method, all of which discover only a subset of interactions. Among the published bacterial interactomes (including partial ones) are

Species	proteins total	interactions	type
Helicobacter pylori	1,553	~3,004	Y2H
Campylobacter jejuni	1,623	11,687	Y2H
Treponema pallidum	1,040	3,649	Y2H
Escherichia coli	4,288	(5,993)	AP/MS
Escherichia coli	4,288	2,234	Y2H
Mesorhizobium loti	6,752	3,121	Y2H
Mycobacterium tuberculosis	3,959	>8000	B2H
Mycoplasma genitalium	482		AP/MS
Synechocystis sp. PCC6803	3,264	3,236	Y2H
Staphylococcus aureus (MRSA)	2,656	13,219	AP/MS

The E. coli and Mycoplasma interactomes have been analyzed using large-scale protein complex affinity purification and mass spectrometry (AP/MS), hence it is not easily possible to infer direct interactions. The others have used extensive yeast two-hybrid (Y2H) screens. The Mycobacterium tuberculosis interactome has been analyzed using a bacterial two-hybrid screen (B2H).

Note that numerous additional interactomes have been predicted using computational methods (see section above).

Eukaryotic interactomes

There have been several efforts to map eukaryotic interactomes through HTP methods. While no biological interactomes have been fully characterized, over 90% of proteins in Saccharomyces cerevisiae have been screened and their interactions characterized, making it the best-characterized interactome. Species whose interactomes have been studied in some detail include

• Schizosaccharomyces pombe
• Caenorhabditis elegans
• Drosophila melanogaster
• Homo sapiens

Recently, the pathogen-host interactomes of Hepatitis C Virus/Human (2008), Epstein Barr virus/Human (2008), Influenza virus/Human (2009) were delineated through HTP to identify essential molecular components for pathogens and for their host's immune system.

Predicted interactomes

As described above, PPIs and thus whole interactomes can be predicted. While the reliability of these predictions is debatable, they are providing hypotheses that can be tested experimentally. Interactomes have been predicted for a number of species, e.g.

• Human (Homo sapiens)
• Rice (Oryza sativa)
• Xanthomonas oryzae
• Arabidopsis thaliana
• Tomato (Solanum lycopersicum)
• Field mustard (Brassica rapa)
• Maize, corn (Zea mays)
• Poplar (Populus trichocarpa)
• SARS-CoV-2

Representation of the predicted SARS-CoV-2/Human interactome

Network properties

Protein interaction networks can be analyzed with the same tool as other networks. In fact, they share many properties with biological or social networks. Some of the main characteristics are as follows.

The Treponema pallidum protein interactome.

Degree distribution

The degree distribution describes the number of proteins that have a certain number of connections. Most protein interaction networks show a scale-free (power law) degree distribution where the connectivity distribution P(k) ~ k^−γ with k being the degree. This relationship can also be seen as a straight line on a log-log plot since, the above equation is equal to log(P(k)) ~ —y•log(k). One characteristic of such distributions is that there are many proteins with few interactions and few proteins that have many interactions, the latter being called "hubs".

Hubs

Highly connected nodes (proteins) are called hubs. Han et al. have coined the term "party hub" for hubs whose expression is correlated with its interaction partners. Party hubs also connect proteins within functional modules such as protein complexes. In contrast, "date hubs" do not exhibit such a correlation and appear to connect different functional modules. Party hubs are found predominantly in AP/MS data sets, whereas date hubs are found predominantly in binary interactome network maps. Note that the validity of the date hub/party hub distinction was disputed. Party hubs generally consist of multi-interface proteins whereas date hubs are more frequently single-interaction interface proteins. Consistent with a role for date-hubs in connecting different processes, in yeast the number of binary interactions of a given protein is correlated to the number of phenotypes observed for the corresponding mutant gene in different physiological conditions.

Modules

Nodes involved in the same biochemical process are highly interconnected.

Evolution

The evolution of interactome complexity is delineated in a study published in Nature. In this study it is first noted that the boundaries between prokaryotes, unicellular eukaryotes and multicellular eukaryotes are accompanied by orders-of-magnitude reductions in effective population size, with concurrent amplifications of the effects of random genetic drift. The resultant decline in the efficiency of selection seems to be sufficient to influence a wide range of attributes at the genomic level in a nonadaptive manner. The Nature study shows that the variation in the power of random genetic drift is also capable of influencing phylogenetic diversity at the subcellular and cellular levels. Thus, population size would have to be considered as a potential determinant of the mechanistic pathways underlying long-term phenotypic evolution. In the study it is further shown that a phylogenetically broad inverse relation exists between the power of drift and the structural integrity of protein subunits. Thus, the accumulation of mildly deleterious mutations in populations of small size induces secondary selection for protein–protein interactions that stabilize key gene functions, mitigating the structural degradation promoted by inefficient selection. By this means, the complex protein architectures and interactions essential to the genesis of phenotypic diversity may initially emerge by non-adaptive mechanisms.

Criticisms, challenges, and responses

Kiemer and Cesareni raise the following concerns with the state (circa 2007) of the field especially with the comparative interactomic: The experimental procedures associated with the field are error prone leading to "noisy results". This leads to 30% of all reported interactions being artifacts. In fact, two groups using the same techniques on the same organism found less than 30% interactions in common. However, some authors have argued that such non-reproducibility results from the extraordinary sensitivity of various methods to small experimental variation. For instance, identical conditions in Y2H assays result in very different interactions when different Y2H vectors are used.

Techniques may be biased, i.e. the technique determines which interactions are found. In fact, any method has built in biases, especially protein methods. Because every protein is different no method can capture the properties of each protein. For instance, most analytical methods that work fine with soluble proteins deal poorly with membrane proteins. This is also true for Y2H and AP/MS technologies.

Interactomes are not nearly complete with perhaps the exception of S. cerevisiae. This is not really a criticism as any scientific area is "incomplete" initially until the methodologies have been improved. Interactomics in 2015 is where genome sequencing was in the late 1990s, given that only a few interactome datasets are available (see table above).

While genomes are stable, interactomes may vary between tissues, cell types, and developmental stages. Again, this is not a criticism, but rather a description of the challenges in the field.

It is difficult to match evolutionarily related proteins in distantly related species. While homologous DNA sequences can be found relatively easily, it is much more difficult to predict homologous interactions ("interologs") because the homologs of two interacting proteins do not need to interact. For instance, even within a proteome two proteins may interact but their paralogs may not.

Each protein–protein interactome may represent only a partial sample of potential interactions, even when a supposedly definitive version is published in a scientific journal. Additional factors may have roles in protein interactions that have yet to be incorporated in interactomes. The binding strength of the various protein interactors, microenvironmental factors, sensitivity to various procedures, and the physiological state of the cell all impact protein–protein interactions, yet are usually not accounted for in interactome studies.

Condorcet paradox

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Condorcet_paradox

The Condorcet paradox (also known as the voting paradox or the paradox of voting) in social choice theory is a situation noted by the Marquis de Condorcet in the late 18th century, in which collective preferences can be cyclic, even if the preferences of individual voters are not cyclic. This is paradoxical, because it means that majority wishes can be in conflict with each other: Suppose majorities prefer, for example, candidate A over B, B over C, and yet C over A. When this occurs, it is because the conflicting majorities are each made up of different groups of individuals.

Thus an expectation that transitivity on the part of all individuals' preferences should result in transitivity of societal preferences is an example of a fallacy of composition.

The paradox was independently discovered by Lewis Carroll and Edward J. Nanson, but its significance was not recognized until popularized by Duncan Black in the 1940s.

Example

Voters (blue) and candidates (red) plotted in a 2-dimensional preference space. Each voter prefers a closer candidate over a farther. Arrows show the order in which voters prefer the candidates.

Suppose we have three candidates, A, B, and C, and that there are three voters with preferences as follows (candidates being listed left-to-right for each voter in decreasing order of preference):

Voter	First preference	Second preference	Third preference
Voter 1	A	B	C
Voter 2	B	C	A
Voter 3	C	A	B

If C is chosen as the winner, it can be argued that B should win instead, since two voters (1 and 2) prefer B to C and only one voter (3) prefers C to B. However, by the same argument A is preferred to B, and C is preferred to A, by a margin of two to one on each occasion. Thus the society's preferences show cycling: A is preferred over B which is preferred over C which is preferred over A. A paradoxical feature of relations between the voters' preferences described above is that although the majority of voters agree that A is preferable to B, B to C, and C to A, all three coefficients of rank correlation between the preferences of any two voters are negative (namely, –.5), as calculated with Spearman's rank correlation coefficient formula designed by Charles Spearman much later.

Cardinal ratings

Notice that in Score voting, a voter's power is reduced in certain pairwise matchups relative to Condorcet. This guarantees that a cyclical social preference can never occur.

Note that in the graphical example, the voters and candidates are not symmetrical, but the ranked voting system "flattens" their preferences into a symmetrical cycle. Cardinal voting systems provide more information than rankings, allowing a winner to be found. For instance, under score voting, the ballots might be:

	A	B	C
1	6	3	0
2	0	6	1
3	5	0	6
Total:	11	9	7

Candidate A gets the largest score, and is the winner, as A is the nearest to all voters. However, a majority of voters have an incentive to give A a 0 and C a 10, allowing C to beat A, which they prefer, at which point, a majority will then have an incentive to give C a 0 and B a 10, to make B win, etc. (In this particular example, though, the incentive is weak, as those who prefer C to A only score C 1 point above A; in a ranked Condorcet method, it's quite possible they would simply equally rank A and C because of how weak their preference is, in which case a Condorcet cycle wouldn't have formed in the first place, and A would've been the Condorcet winner). So though the cycle doesn't occur in any given set of votes, it can appear through iterated elections with strategic voters with cardinal ratings.

Necessary condition for the paradox

Suppose that x is the fraction of voters who prefer A over B and that y is the fraction of voters who prefer B over C. It has been shown that the fraction z of voters who prefer A over C is always at least (x + y – 1). Since the paradox (a majority preferring C over A) requires z < 1/2, a necessary condition for the paradox is that

${\displaystyle x+y-1\leq z<{\frac {1}{2}}\quad {\text{and hence}}\quad x+y<{\frac {3}{2}}.}$

Likelihood of the paradox

It is possible to estimate the probability of the paradox by extrapolating from real election data, or using mathematical models of voter behavior, though the results depend strongly on which model is used. In particular, Andranik Tangian has proved that the probability of Condorcet paradox is negligible in a large society.

Impartial culture model

We can calculate the probability of seeing the paradox for the special case where voter preferences are uniformly distributed among the candidates. (This is the "impartial culture" model, which is known to be unrealistic, so, in practice, a Condorcet paradox may be more or less likely than this calculation.)

For ${\displaystyle n}$ voters providing a preference list of three candidates A, B, C, we write ${\displaystyle X_{n}}$ (resp. ${\displaystyle Y_{n}}$, ${\displaystyle Z_{n}}$) the random variable equal to the number of voters who placed A in front of B (respectively B in front of C, C in front of A). The sought probability is ${\displaystyle p_{n}=2P(X_{n}>n/2,Y_{n}>n/2,Z_{n}>n/2)}$ (we double because there is also the symmetric case A> C> B> A). We show that, for odd ${\displaystyle n}$, ${\displaystyle p_{n}=3q_{n}-1/2}$ where ${\displaystyle q_{n}=P(X_{n}>n/2,Y_{n}>n/2)}$ which makes one need to know only the joint distribution of ${\displaystyle X_{n}}$ and ${\displaystyle Y_{n}}$.

If we put ${\displaystyle p_{n,i,j}=P(X_{n}=i,Y_{n}=j)}$, we show the relation which makes it possible to compute this distribution by recurrence: ${\displaystyle p_{n+1,i,j}={1 \over 6}p_{n,i,j}+{1 \over 3}p_{n,i-1,j}+{1 \over 3}p_{n,i,j-1}+{1 \over 6}p_{n,i-1,j-1}}$.

The following results are then obtained:

${\displaystyle n}$	3	101	201	301	401	501	601
${\displaystyle p_{n}}$	5.556%	8.690%	8.732%	8.746%	8.753%	8.757%	8.760%

The sequence seems to be tending towards a finite limit.

Using the Central-Limit Theorem, we show that ${\displaystyle q_{n}}$ tends to ${\displaystyle q={1 \over 4}P(|T|>{{\sqrt {2}} \over 4})}$ where ${\displaystyle T}$ is a variable following a Cauchy distribution, which gives ${\displaystyle q={\dfrac {1}{2\pi }}\int _{{\sqrt {2}}/4}^{+\infty }{\frac {dt}{1+t^{2}}}={\dfrac {\arctan 2{\sqrt {2}}}{2\pi }}={\dfrac {\arccos {\frac {1}{3}}}{2\pi }}}$ (constant quoted in the OEIS).

The asymptotic probability of encountering the Condorcet paradox is therefore ${\displaystyle {{3\arccos {1 \over 3}} \over {2\pi }}-{1 \over 2}={\arcsin {{\sqrt {6}} \over 9} \over \pi }}$ which gives the value 8.77%.

Some results for the case of more than three objects have been calculated.

The likelihood of a Condorcet cycle for related models approach these values for large electorates:

• Impartial anonymous culture (IAC): 6.25%
• Uniform culture (UC): 6.25%
• Maximal culture condition (MC): 9.17%

All of these models are unrealistic, and are investigated to establish an upper bound on the likelihood of a cycle.

Group coherence models

When modeled with more realistic voter preferences, Condorcet paradoxes in elections with a small number of candidates and a large number of voters become very rare.

Spatial model

A study of three-candidate elections analyzed 12 different models of voter behavior, and found the spatial model of voting to be the most accurate to real-world ranked-ballot election data. Analyzing this spatial model, they found the likelihood of a cycle to decrease to zero as the number of voters increases, with likelihoods of 5% for 100 voters, 0.5% for 1000 voters, and 0.06% for 10,000 voters.

Empirical studies

Many attempts have been made at finding empirical examples of the paradox. Empirical identification of a Condorcet paradox presupposes extensive data on the decision-makers' preferences over all alternatives—something that is only very rarely available.

A summary of 37 individual studies, covering a total of 265 real-world elections, large and small, found 25 instances of a Condorcet paradox, for a total likelihood of 9.4% (and this may be a high estimate, since cases of the paradox are more likely to be reported on than cases without).

An analysis of 883 three-candidate elections extracted from 84 real-world ranked-ballot elections of the Electoral Reform Society found a Condorcet cycle likelihood of 0.7%. These derived elections had between 350 and 1,957 voters. A similar analysis of data from the 1970–2004 American National Election Studies thermometer scale surveys found a Condorcet cycle likelihood of 0.4%. These derived elections had between 759 and 2,521 "voters".

While examples of the paradox seem to occur occasionally in small settings (e.g., parliaments) very few examples have been found in larger groups (e.g. electorates), although some have been identified.

Implications

When a Condorcet method is used to determine an election, the voting paradox of cyclical societal preferences implies that the election has no Condorcet winner: no candidate who can win a one-on-one election against each other candidate. There will still be a smallest group of candidates, known as the Smith set, such that each candidate in the group can win a one-on-one election against each of the candidates outside the group. The several variants of the Condorcet method differ on how they resolve such ambiguities when they arise to determine a winner. The Condorcet methods which always elect someone from the Smith set when there is no Condorcet winner are known as Smith-efficient. Note that using only rankings, there is no fair and deterministic resolution to the trivial example given earlier because each candidate is in an exactly symmetrical situation.

Situations having the voting paradox can cause voting mechanisms to violate the axiom of independence of irrelevant alternatives—the choice of winner by a voting mechanism could be influenced by whether or not a losing candidate is available to be voted for.

Two-stage voting processes

One important implication of the possible existence of the voting paradox in a practical situation is that in a two-stage voting process, the eventual winner may depend on the way the two stages are structured. For example, suppose the winner of A versus B in the open primary contest for one party's leadership will then face the second party's leader, C, in the general election. In the earlier example, A would defeat B for the first party's nomination, and then would lose to C in the general election. But if B were in the second party instead of the first, B would defeat C for that party's nomination, and then would lose to A in the general election. Thus the structure of the two stages makes a difference for whether A or C is the ultimate winner.

Likewise, the structure of a sequence of votes in a legislature can be manipulated by the person arranging the votes, to ensure a preferred outcome.

The structure of the Condorcet paradox can be reproduced in mechanical devices demonstrating intransitivity of relations such as "to rotate faster than", "to lift and be not lifted", "to be stronger than" in some geometrical constructions.