From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Franck-Condon_principle
The Franck–Condon principle is a rule in spectroscopy and quantum chemistry that explains the intensity of vibronic transitions. Vibronic transitions are the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon of the appropriate energy. The principle states that during an electronic transition, a change from one vibrational energy level to another will be more likely to happen if the two vibrational wave functions overlap more significantly.
Overview
The Franck–Condon principle has a well-established semiclassical interpretation based on the original contributions of James Franck. Electronic transitions are relatively instantaneous compared with the time scale of nuclear motions, therefore if the molecule is to move to a new vibrational level during the electronic transition, this new vibrational level must be instantaneously compatible with the nuclear positions and momenta of the vibrational level of the molecule in the originating electronic state. In the semiclassical picture of vibrations (oscillations) of a simple harmonic oscillator, the necessary conditions can occur at the turning points, where the momentum is zero.
Classically, the Franck–Condon principle is the approximation that an electronic transition is most likely to occur without changes in the positions of the nuclei in the molecular entity and its environment. The resulting state is called a Franck–Condon state, and the transition involved, a vertical transition. The quantum mechanical formulation of this principle is that the intensity of a vibronic transition is proportional to the square of the overlap integral between the vibrational wavefunctions of the two states that are involved in the transition.
— IUPAC Compendium of Chemical Terminology, 2nd Edition (1997)
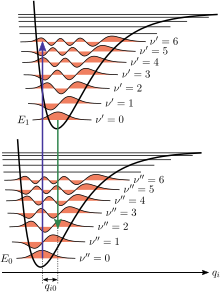
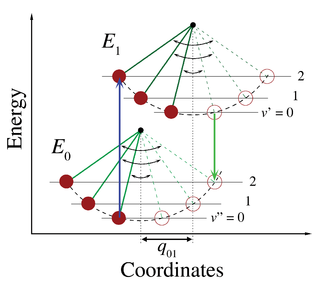
In the quantum mechanical picture, the vibrational levels and vibrational wavefunctions are those of quantum harmonic oscillators, or of more complex approximations to the potential energy of molecules, such as the Morse potential. Figure 1 illustrates the Franck–Condon principle for vibronic transitions in a molecule with Morse-like potential energy functions in both the ground and excited electronic states. In the low temperature approximation, the molecule starts out in the v = 0 vibrational level of the ground electronic state and upon absorbing a photon of the necessary energy, makes a transition to the excited electronic state. The electron configuration of the new state may result in a shift of the equilibrium position of the nuclei constituting the molecule. In the figure this shift in nuclear coordinates between the ground and the first excited state is labeled as q 01. In the simplest case of a diatomic molecule the nuclear coordinates axis refers to the internuclear separation. The vibronic transition is indicated by a vertical arrow due to the assumption of constant nuclear coordinates during the transition. The probability that the molecule can end up in any particular vibrational level is proportional to the square of the (vertical) overlap of the vibrational wavefunctions of the original and final state (see Quantum mechanical formulation section below). In the electronic excited state molecules quickly relax to the lowest vibrational level of the lowest electronic excitation state (Kasha's rule), and from there can decay to the electronic ground state via photon emission. The Franck–Condon principle is applied equally to absorption and to fluorescence.
The applicability of the Franck–Condon principle in both absorption and fluorescence, along with Kasha's rule leads to an approximate mirror symmetry shown in Figure 2. The vibrational structure of molecules in a cold, sparse gas is most clearly visible due to the absence of inhomogeneous broadening of the individual transitions. Vibronic transitions are drawn in Figure 2 as narrow, equally spaced Lorentzian lineshapes. Equal spacing between vibrational levels is only the case for the parabolic potential of simple harmonic oscillators, in more realistic potentials, such as those shown in Figure 1, energy spacing decreases with increasing vibrational energy. Electronic transitions to and from the lowest vibrational states are often referred to as 0–0 (zero zero) transitions and have the same energy in both absorption and fluorescence.
Development of the principle
In a report published in 1926 in Transactions of the Faraday Society, James Franck was concerned with the mechanisms of photon-induced chemical reactions. The presumed mechanism was the excitation of a molecule by a photon, followed by a collision with another molecule during the short period of excitation. The question was whether it was possible for a molecule to break into photoproducts in a single step, the absorption of a photon, and without a collision. In order for a molecule to break apart, it must acquire from the photon a vibrational energy exceeding the dissociation energy, that is, the energy to break a chemical bond. However, as was known at the time, molecules will only absorb energy corresponding to allowed quantum transitions, and there are no vibrational levels above the dissociation energy level of the potential well. High-energy photon absorption leads to a transition to a higher electronic state instead of dissociation. In examining how much vibrational energy a molecule could acquire when it is excited to a higher electronic level, and whether this vibrational energy could be enough to immediately break apart the molecule, he drew three diagrams representing the possible changes in binding energy between the lowest electronic state and higher electronic states.
Diagram I. shows a great weakening of the binding on a transition from the normal state n to the excited states a and a'. Here we have D > D' and D' > D". At the same time the equilibrium position of the nuclei moves with the excitation to greater values of r. If we go from the equilibrium position (the minimum of potential energy) of the n curve vertically [emphasis added] upwards to the a curves in Diagram I. the particles will have a potential energy greater than D' and will fly apart. In this case we have a very great change in the oscillation energy on excitation by light...
— James Franck, 1926
James Franck recognized that changes in vibrational levels could be a consequence of the instantaneous nature of excitation to higher electronic energy levels and a new equilibrium position for the nuclear interaction potential. Edward Condon extended this insight beyond photoreactions in a 1926 Physical Review article titled "A Theory of Intensity Distribution in Band Systems". Here he formulates the semiclassical formulation in a manner quite similar to its modern form. The first joint reference to both Franck and Condon in regards to the new principle appears in the same 1926 issue of Physical Review in an article on the band structure of carbon monoxide by Raymond Birge.
Quantum mechanical formulation
Consider an electrical dipole transition from the initial vibrational state (υ) of the ground electronic level (ε), , to some vibrational state (υ′) of an excited electronic state (ε′), (see bra–ket notation). The molecular dipole operator μ is determined by the charge (−e) and locations (ri) of the electrons as well as the charges (+Zje) and locations (Rj) of the nuclei:
The probability amplitude P for the transition between these two states is given by
where and are, respectively, the overall wavefunctions of the initial and final state. The overall wavefunctions are the product of the individual vibrational (depending on spatial coordinates of the nuclei) and electronic space and spin wavefunctions:
This separation of the electronic and vibrational wavefunctions is an expression of the Born–Oppenheimer approximation and is the fundamental assumption of the Franck–Condon principle. Combining these equations leads to an expression for the probability amplitude in terms of separate electronic space, spin and vibrational contributions:
The spin-independent part of the initial integral is here approximated as a product of two integrals:
This factorization would be exact if the integral over the spatial coordinates of the electrons would not depend on the nuclear coordinates. However, in the Born–Oppenheimer approximation and do depend (parametrically) on the nuclear coordinates, so that the integral (a so-called transition dipole surface) is a function of nuclear coordinates. Since the dependence is usually rather smooth it is neglected (i.e., the assumption that the transition dipole surface is independent of nuclear coordinates, called the Condon approximation is often allowed).
The first integral after the plus sign is equal to zero because electronic wavefunctions of different states are orthogonal. Remaining is the product of three integrals. The first integral is the vibrational overlap integral, also called the Franck–Condon factor. The remaining two integrals contributing to the probability amplitude determine the electronic spatial and spin selection rules.
The Franck–Condon principle is a statement on allowed vibrational transitions between two different electronic states; other quantum mechanical selection rules may lower the probability of a transition or prohibit it altogether. Rotational selection rules have been neglected in the above derivation. Rotational contributions can be observed in the spectra of gases but are strongly suppressed in liquids and solids.
It should be clear that the quantum mechanical formulation of the Franck–Condon principle is the result of a series of approximations, principally the electrical dipole transition assumption and the Born–Oppenheimer approximation. Weaker magnetic dipole and electric quadrupole electronic transitions along with the incomplete validity of the factorization of the total wavefunction into nuclear, electronic spatial and spin wavefunctions means that the selection rules, including the Franck–Condon factor, are not strictly observed. For any given transition, the value of P is determined by all of the selection rules, however spin selection is the largest contributor, followed by electronic selection rules. The Franck–Condon factor only weakly modulates the intensity of transitions, i.e., it contributes with a factor on the order of 1 to the intensity of bands whose order of magnitude is determined by the other selection rules. The table below gives the range of extinction coefficients for the possible combinations of allowed and forbidden spin and orbital selection rules.
| Range of extinction coefficient (ε) values (mol−1 cm−1) | |
|---|---|
| Spin and orbitally allowed | 103 to 105 |
| Spin allowed but orbitally forbidden | 100 to 103 |
| Spin forbidden but orbitally allowed | 10−5 to 100 |
Franck–Condon metaphors in spectroscopy
The Franck–Condon principle, in its canonical form, applies only to changes in the vibrational levels of a molecule in the course of a change in electronic levels by either absorption or emission of a photon. The physical intuition of this principle is anchored by the idea that the nuclear coordinates of the atoms constituting the molecule do not have time to change during the very brief amount of time involved in an electronic transition. However, this physical intuition can be, and is indeed, routinely extended to interactions between light-absorbing or emitting molecules (chromophores) and their environment. Franck–Condon metaphors are appropriate because molecules often interact strongly with surrounding molecules, particularly in liquids and solids, and these interactions modify the nuclear coordinates of the chromophore in ways closely analogous to the molecular vibrations considered by the Franck–Condon principle.
Franck–Condon principle for phonons
The closest Franck–Condon analogy is due to the interaction of phonons (quanta of lattice vibrations) with the electronic transitions of chromophores embedded as impurities in the lattice. In this situation, transitions to higher electronic levels can take place when the energy of the photon corresponds to the purely electronic transition energy or to the purely electronic transition energy plus the energy of one or more lattice phonons. In the low-temperature approximation, emission is from the zero-phonon level of the excited state to the zero-phonon level of the ground state or to higher phonon levels of the ground state. Just like in the Franck–Condon principle, the probability of transitions involving phonons is determined by the overlap of the phonon wavefunctions at the initial and final energy levels. For the Franck–Condon principle applied to phonon transitions, the label of the horizontal axis of Figure 1 is replaced in Figure 6 with the configurational coordinate for a normal mode. The lattice mode potential energy in Figure 6 is represented as that of a harmonic oscillator, and the spacing between phonon levels () is determined by lattice parameters. Because the energy of single phonons is generally quite small, zero- or few-phonon transitions can only be observed at temperatures below about 40 kelvins.
- See Zero-phonon line and phonon sideband for further details and references.
Franck–Condon principle in solvation
Franck–Condon considerations can also be applied to the electronic transitions of chromophores dissolved in liquids. In this use of the Franck–Condon metaphor, the vibrational levels of the chromophores, as well as interactions of the chromophores with phonons in the liquid, continue to contribute to the structure of the absorption and emission spectra, but these effects are considered separately and independently.
Consider chromophores surrounded by solvent molecules. These surrounding molecules may interact with the chromophores, particularly if the solvent molecules are polar. This association between solvent and solute is referred to as solvation and is a stabilizing interaction, that is, the solvent molecules can move and rotate until the energy of the interaction is minimized. The interaction itself involves electrostatic and van der Waals forces and can also include hydrogen bonds. Franck–Condon principles can be applied when the interactions between the chromophore and the surrounding solvent molecules are different in the ground and in the excited electronic state. This change in interaction can originate, for example, due to different dipole moments in these two states. If the chromophore starts in its ground state and is close to equilibrium with the surrounding solvent molecules and then absorbs a photon that takes it to the excited state, its interaction with the solvent will be far from equilibrium in the excited state. This effect is analogous to the original Franck–Condon principle: the electronic transition is very fast compared with the motion of nuclei—the rearrangement of solvent molecules in the case of solvation. We now speak of a vertical transition, but now the horizontal coordinate is solvent-solute interaction space. This coordinate axis is often labeled as "Solvation Coordinate" and represents, somewhat abstractly, all of the relevant dimensions of motion of all of the interacting solvent molecules.
In the original Franck–Condon principle, after the electronic transition, the molecules which end up in higher vibrational states immediately begin to relax to the lowest vibrational state. In the case of solvation, the solvent molecules will immediately try to rearrange themselves in order to minimize the interaction energy. The rate of solvent relaxation depends on the viscosity of the solvent. Assuming the solvent relaxation time is short compared with the lifetime of the electronic excited state, emission will be from the lowest solvent energy state of the excited electronic state. For small-molecule solvents such as water or methanol at ambient temperature, solvent relaxation time is on the order of some tens of picoseconds whereas chromophore excited state lifetimes range from a few picoseconds to a few nanoseconds. Immediately after the transition to the ground electronic state, the solvent molecules must also rearrange themselves to accommodate the new electronic configuration of the chromophore. Figure 7 illustrates the Franck–Condon principle applied to solvation. When the solution is illuminated by light corresponding to the electronic transition energy, some of the chromophores will move to the excited state. Within this group of chromophores there will be a statistical distribution of solvent-chromophore interaction energies, represented in the figure by a Gaussian distribution function. The solvent-chromophore interaction is drawn as a parabolic potential in both electronic states. Since the electronic transition is essentially instantaneous on the time scale of solvent motion (vertical arrow), the collection of excited state chromophores is immediately far from equilibrium. The rearrangement of the solvent molecules according to the new potential energy curve is represented by the curved arrows in Figure 7. Note that while the electronic transitions are quantized, the chromophore-solvent interaction energy is treated as a classical continuum due to the large number of molecules involved. Although emission is depicted as taking place from the minimum of the excited state chromophore-solvent interaction potential, significant emission can take place before equilibrium is reached when the viscosity of the solvent is high or the lifetime of the excited state is short. The energy difference between absorbed and emitted photons depicted in Figure 7 is the solvation contribution to the Stokes shift.

























![{\displaystyle K_{\ce {c}}={\frac {[{\ce {S}}]^{\sigma }[{\ce {T}}]^{\tau }}{[{\ce {A}}]^{\alpha }[{\ce {B}}]^{\beta }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2ac61ea07e9614e7c3e261d737d856396c1b178)























![{\displaystyle K={\frac {[\mathrm {S} ]^{\sigma }[\mathrm {T} ]^{\tau }...}{[\mathrm {A} ]^{\alpha }[\mathrm {B} ]^{\beta }...}}\times {\frac {{\gamma _{\mathrm {S} }}^{\sigma }{\gamma _{\mathrm {T} }}^{\tau }...}{{\gamma _{\mathrm {A} }}^{\alpha }{\gamma _{\mathrm {B} }}^{\beta }...}}=K_{\mathrm {c} }\Gamma }](https://wikimedia.org/api/rest_v1/media/math/render/svg/160fbc88403a037161d2c9a44d10cd44746215e8)



![{\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} }{\mathrm {[{CH_{3}CO_{2}H}][{H_{2}O}]} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53b93bf6dae8354f02ab3e935fca63b9bd4a16c4)
![{\displaystyle K={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} }{\mathrm {[{CH_{3}CO_{2}H}]} }}=K_{\mathrm {c} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/472d349477dcf83e95cb3c3423e8ba247ff1d23a)
![{\displaystyle K_{\mathrm {w} }=\mathrm {[H^{+}][OH^{-}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/02e72380cadad70b38e1a6f42ce8b217618bc11f)
![{\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[CO_{2}]} }{\mathrm {[CO]^{2}} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7ff1e7f45707791cfd9dd8e697fe5695e94f60)
![{\displaystyle {\begin{array}{rl}{\ce {H2A <=> HA^- + H+}}:&K_{1}={\frac {{\ce {[HA-][H+]}}}{{\ce {[H2A]}}}}\\{\ce {HA- <=> A^2- + H+}}:&K_{2}={\frac {{\ce {[A^{2-}][H+]}}}{{\ce {[HA-]}}}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/964f444d4c5ff73dc96c30e9eca7e742a64c7cbc)

![{\displaystyle \beta _{{\ce {D}}}={\frac {{\ce {[A^{2-}][H^+]^2}}}{{\ce {[H_2A]}}}}=K_{1}K_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c204101410770f2cc038f6d29c1a7a0da1d363a1)
![{\displaystyle {\begin{array}{ll}{\ce {A^2- + H+ <=> HA-}}:&\beta _{1}={\frac {{\ce {[HA^-]}}}{{\ce {[A^{2-}][H+]}}}}\\{\ce {A^2- + 2H+ <=> H2A}}:&\beta _{2}={\frac {{\ce {[H2A]}}}{{\ce {[A^{2-}][H+]^2}}}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/266ddb8f43fb05b0d3a3195274e597a4fd3d6f37)


![{\displaystyle T_{\mathrm {A} }=\mathrm {[A]+[HA]+[H_{2}A]} \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4caf4ff0552bd0430f4b305b3b92c05aef15aa2)
![{\displaystyle T_{\mathrm {H} }=\mathrm {[H]+[HA]+2[H_{2}A]-[OH]} \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/094ecf5d3e87ba5a02d744835486f24086804cfc)
![{\displaystyle T_{\mathrm {A} }=\mathrm {[A]} +\beta _{1}\mathrm {[A][H]} +\beta _{2}\mathrm {[A][H]} ^{2}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6ae376d767bfb698f8d771a8aa374366c647255)
![{\displaystyle T_{\mathrm {H} }=\mathrm {[H]} +\beta _{1}\mathrm {[A][H]} +2\beta _{2}\mathrm {[A][H]} ^{2}-K_{w}[\mathrm {H} ]^{-1}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25502da2d24e51d7cb6c53782a5392673c4b0819)
![{\displaystyle T_{\mathrm {A} }=[\mathrm {A} ]+\sum _{i}p_{i}\beta _{i}[\mathrm {A} ]^{p_{i}}[\mathrm {B} ]^{q_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de4c20306740d1b3f30387f17ac264b500d313b8)
![{\displaystyle T_{\mathrm {B} }=[\mathrm {B} ]+\sum _{i}q_{i}\beta _{i}[\mathrm {A} ]^{p_{i}}[\mathrm {B} ]^{q_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c9dea321370bf3d5b01364cfed9dbe3c941ce31)