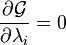From Wikipedia, the free encyclopedia
In physics, a virtual particle is an explanatory conceptual entity that is found in mathematical calculations about quantum field theory. It refers to mathematical terms that have some appearance of representing particles inside a subatomic process such as a collision. Virtual particles, however, do not appear directly amongst the observable and detectable input and output quantities of those calculations, which refer only to actual, as distinct from virtual, particles. Virtual particle terms represent "particles" that are said to be 'off mass shell'. For example, they can progress backwards in time, can have apparent mass very different from their regular particle namesake's[dubious ], and can travel faster than light. That is to say, when looked at individually, they appear to be able to violate basic laws of physics. Regular particles of course never do so. On the other hand, any particle that is actually observed never precisely satisfies the conditions theoretically imposed on regular particles. Virtual particles occur in combinations that mutually more or less nearly cancel from the actual output quantities, so that no actual violation of the laws of physics occurs in completed processes. Often the virtual-particle virtual "events" appear to occur close to one another in time, for example within the time scale of a collision, so that they are virtually and apparently "short-lived". If the mathematical terms that are interpreted as representing virtual particles are omitted from the calculations, the result is an approximation that may or may not be near the correct and accurate answer obtained from the proper full calculation.[1][2][3]
Quantum theory is different from classical theory. The difference is in accounting for the inner workings of subatomic processes. Classical physics cannot account for such. It was pointed out by Heisenberg that what "actually" or "really" occurs inside such subatomic processes as collisions is not directly observable and no unique and physically definite visualization is available for it. Quantum mechanics has the specific merit of by-passing speculation about such inner workings. It restricts itself to what is actually observable and detectable. Virtual particles are conceptual devices that in a sense try to by-pass Heisenberg's insight, by offering putative or virtual explanatory visualizations for the inner workings of subatomic processes.
A virtual particle does not necessarily appear to carry the same mass as the corresponding real particle. This is because it appears as "short-lived" and "transient", so that the uncertainty principle allows it to appear not to conserve energy and momentum. The longer a virtual particle appears to "live", the closer its characteristics come to those of an actual particle.
Virtual particles appear in many processes, including particle scattering and Casimir forces. In quantum field theory, even classical forces — such as the electromagnetic repulsion or attraction between two charges — can be thought of as due to the exchange of many virtual photons between the charges.
Virtual particles appear in calculations of subatomic interactions, but never as asymptotic states or indices to the scattering matrix. A subatomic process involving virtual particles is schematically representable by a Feynman diagram in which they are represented by internal lines.
Antiparticles and quasiparticles should not be confused with virtual particles or virtual antiparticles.
Many physicists believe that, because of its intrinsically perturbative character, the concept of virtual particles is often confusing and misleading, and is thus best avoided.[4][5]
A virtual particle does not precisely obey the energy–momentum relation m2c4 = E2 − p2c2. Its kinetic energy may not have the usual relationship to velocity–indeed, it can be negative.[7]:110 This is expressed by the phrase off mass shell.[6]:119 The probability amplitude for a virtual particle to exist tends to be canceled out by destructive interference over longer distances and times. Quantum tunnelling may be considered a manifestation of virtual particle exchanges.[8]:235 The range of forces carried by virtual particles is limited by the uncertainty principle, which regards energy and time as conjugate variables; thus, virtual particles of larger mass have more limited range.[9]
Written in the usual mathematical notations, in the equations of physics, there is no mark of the distinction between virtual and actual particles. The amplitude that a virtual particle exists interferes with the amplitude for its non-existence, whereas for an actual particle the cases of existence and non-existence cease to be coherent with each other and do not interfere any more. In the quantum field theory view, actual particles are viewed as being detectable excitations of underlying quantum fields. Virtual particles are also viewed as excitations of the underlying fields, but appear only as forces, not as detectable particles. They are "temporary" in the sense that they appear in calculations, but are not detected as single particles. Thus, in mathematical terms, they never appear as indices to the scattering matrix, which is to say, they never appear as the observable inputs and outputs of the physical process being modelled.
There are two principal ways in which the notion of virtual particles appears in modern physics. They appear as intermediate terms in Feynman diagrams; that is, as terms in a perturbative calculation. They also appear as an infinite set of states to be summed or integrated over in the calculation of a semi-non-perturbative effect. In the latter case, it is sometimes said that virtual particles contribute to a mechanism that mediates the effect, or that the effect occurs through the virtual particles.[6]:118
Some field interactions which may be seen in terms of virtual particles are:
The calculation of scattering amplitudes in theoretical particle physics requires the use of some rather large and complicated integrals over a large number of variables. These integrals do, however, have a regular structure, and may be represented as Feynman diagrams. The appeal of the Feynman diagrams is strong, as it allows for a simple visual presentation of what would otherwise be a rather arcane and abstract formula. In particular, part of the appeal is that the outgoing legs of a Feynman diagram can be associated with actual, on-shell particles. Thus, it is natural to associate the other lines in the diagram with particles as well, called the "virtual particles". In mathematical terms, they correspond to the propagators appearing in the diagram.
In the image to the right, the solid lines correspond to actual particles (of momentum p1 and so on), while the dotted line corresponds to a virtual particle carrying momentum k. For example, if the solid lines were to correspond to electrons interacting by means of the electromagnetic interaction, the dotted line would correspond to the exchange of a virtual photon. In the case of interacting nucleons, the dotted line would be a virtual pion. In the case of quarks interacting by means of the strong force, the dotted line would be a virtual gluon, and so on.
Virtual particles may be mesons or vector bosons, as in the example above; they may also be fermions. However, in order to preserve quantum numbers, most simple diagrams involving fermion exchange are prohibited. The image to the right shows an allowed diagram, a one-loop diagram. The solid lines correspond to a fermion propagator, the wavy lines to bosons.
An important example of the "presence" of virtual particles in a vacuum is the Casimir effect.[13] Here, the explanation of the effect requires that the total energy of all of the virtual particles in a vacuum can be added together. Thus, although the virtual particles themselves are not directly observable in the laboratory, they do leave an observable effect: Their zero-point energy results in forces acting on suitably arranged metal plates or dielectrics.[14] On the other hand, the Casimir effect can be interpreted as the relativistic van der Waals force.[15]
This may occur in one of two ways. In an accelerating frame of reference, the virtual particles may appear to be actual to the accelerating observer; this is known as the Unruh effect. In short, the vacuum of a stationary frame appears, to the accelerated observer, to be a warm gas of actual particles in thermodynamic equilibrium.
Another example is pair production in very strong electric fields, sometimes called vacuum decay. If, for example, a pair of atomic nuclei are merged to very briefly form a nucleus with a charge greater than about 140, (that is, larger than about the inverse of the fine structure constant, which is a dimensionless quantity), the strength of the electric field will be such that it will be energetically favorable to create positron-electron pairs out of the vacuum or Dirac sea, with the electron attracted to the nucleus to annihilate the positive charge. This pair-creation amplitude was first calculated by Julian Schwinger in 1951.
However, all particles have a finite lifetime, as they are created and eventually destroyed by some processes. As such, there is no absolute distinction between "real" and "virtual" particles. In practice, the lifetime of "ordinary" particles is far longer than the lifetime of the virtual particles that contribute to processes in particle physics, and as such the distinction is useful to make.
Quantum theory is different from classical theory. The difference is in accounting for the inner workings of subatomic processes. Classical physics cannot account for such. It was pointed out by Heisenberg that what "actually" or "really" occurs inside such subatomic processes as collisions is not directly observable and no unique and physically definite visualization is available for it. Quantum mechanics has the specific merit of by-passing speculation about such inner workings. It restricts itself to what is actually observable and detectable. Virtual particles are conceptual devices that in a sense try to by-pass Heisenberg's insight, by offering putative or virtual explanatory visualizations for the inner workings of subatomic processes.
A virtual particle does not necessarily appear to carry the same mass as the corresponding real particle. This is because it appears as "short-lived" and "transient", so that the uncertainty principle allows it to appear not to conserve energy and momentum. The longer a virtual particle appears to "live", the closer its characteristics come to those of an actual particle.
Virtual particles appear in many processes, including particle scattering and Casimir forces. In quantum field theory, even classical forces — such as the electromagnetic repulsion or attraction between two charges — can be thought of as due to the exchange of many virtual photons between the charges.
Virtual particles appear in calculations of subatomic interactions, but never as asymptotic states or indices to the scattering matrix. A subatomic process involving virtual particles is schematically representable by a Feynman diagram in which they are represented by internal lines.
Antiparticles and quasiparticles should not be confused with virtual particles or virtual antiparticles.
Many physicists believe that, because of its intrinsically perturbative character, the concept of virtual particles is often confusing and misleading, and is thus best avoided.[4][5]
Properties
The concept of virtual particles arises in the perturbation theory of quantum field theory, an approximation scheme in which interactions (in essence, forces) between actual particles are calculated in terms of exchanges of virtual particles. Such calculations are often performed using schematic representations known as Feynman diagrams, in which virtual particles appear as internal lines. By expressing the interaction in terms of the exchange of a virtual particle with four-momentum q, where q is given by the difference between the four-momenta of the particles entering and leaving the interaction vertex, both momentum and energy are conserved at the interaction vertices of the Feynman diagram.[6]:119A virtual particle does not precisely obey the energy–momentum relation m2c4 = E2 − p2c2. Its kinetic energy may not have the usual relationship to velocity–indeed, it can be negative.[7]:110 This is expressed by the phrase off mass shell.[6]:119 The probability amplitude for a virtual particle to exist tends to be canceled out by destructive interference over longer distances and times. Quantum tunnelling may be considered a manifestation of virtual particle exchanges.[8]:235 The range of forces carried by virtual particles is limited by the uncertainty principle, which regards energy and time as conjugate variables; thus, virtual particles of larger mass have more limited range.[9]
Written in the usual mathematical notations, in the equations of physics, there is no mark of the distinction between virtual and actual particles. The amplitude that a virtual particle exists interferes with the amplitude for its non-existence, whereas for an actual particle the cases of existence and non-existence cease to be coherent with each other and do not interfere any more. In the quantum field theory view, actual particles are viewed as being detectable excitations of underlying quantum fields. Virtual particles are also viewed as excitations of the underlying fields, but appear only as forces, not as detectable particles. They are "temporary" in the sense that they appear in calculations, but are not detected as single particles. Thus, in mathematical terms, they never appear as indices to the scattering matrix, which is to say, they never appear as the observable inputs and outputs of the physical process being modelled.
There are two principal ways in which the notion of virtual particles appears in modern physics. They appear as intermediate terms in Feynman diagrams; that is, as terms in a perturbative calculation. They also appear as an infinite set of states to be summed or integrated over in the calculation of a semi-non-perturbative effect. In the latter case, it is sometimes said that virtual particles contribute to a mechanism that mediates the effect, or that the effect occurs through the virtual particles.[6]:118
Manifestations
There are many observable physical phenomena that arise in interactions involving virtual particles. For bosonic particles that exhibit rest mass when they are free and actual, virtual interactions are characterized by the relatively short range of the force interaction produced by particle exchange.[citation needed] Examples of such short-range interactions are the strong and weak forces, and their associated field bosons. For the gravitational and electromagnetic forces, the zero rest-mass of the associated boson particle permits long-range forces to be mediated by virtual particles. However, in the case of photons, power and information transfer by virtual particles is a relatively short-range phenomenon (existing only within a few wavelengths of the field-disturbance, which carries information or transferred power), as for example seen in the characteristically short range of inductive and capacitative effects in the near field zone of coils and antennas.[citation needed]Some field interactions which may be seen in terms of virtual particles are:
- The Coulomb force (static electric force) between electric charges. It is caused by the exchange of virtual photons. In symmetric 3-dimensional space this exchange results in the inverse square law for electric force. Since the photon has no mass, the coulomb potential has an infinite range.
- The magnetic field between magnetic dipoles. It is caused by the exchange of virtual photons. In symmetric 3-dimensional space this exchange results in the inverse cube law for magnetic force. Since the photon has no mass, the magnetic potential has an infinite range.
- Electromagnetic induction. This phenomenon transfers energy to and from a magnetic coil via a changing (electro)magnetic field.
- The strong nuclear force between quarks is the result of interaction of virtual gluons. The residual of this force outside of quark triplets (neutron and proton) holds neutrons and protons together in nuclei, and is due to virtual mesons such as the pi meson and rho meson.
- The weak nuclear force - it is the result of exchange by virtual W and Z bosons.
- The spontaneous emission of a photon during the decay of an excited atom or excited nucleus; such a decay is prohibited by ordinary quantum mechanics and requires the quantization of the electromagnetic field for its explanation.
- The Casimir effect, where the ground state of the quantized electromagnetic field causes attraction between a pair of electrically neutral metal plates.
- The van der Waals force, which is partly due to the Casimir effect between two atoms.
- Vacuum polarization, which involves pair production or the decay of the vacuum, which is the spontaneous production of particle-antiparticle pairs (such as electron-positron).
- Lamb shift of positions of atomic levels.
- Hawking radiation, where the gravitational field is so strong that it causes the spontaneous production of photon pairs (with black body energy distribution) and even of particle pairs.
- Much of the so-called near-field of radio antennas, where the magnetic and electric effects of the changing current in the antenna wire and the charge effects of the wire's capacitive charge may be (and usually are) important contributors to the total EM field close to the source, but both of which effects are dipole effects that decay with increasing distance from the antenna much more quickly than do the influence of "conventional" electromagnetic waves that are "far" from the source. ["Far" in terms of ratio of antenna length or diameter, to wavelength]. These far-field waves, for which E is (in the limit of long distance) equal to cB, are composed of actual photons. It should be noted that actual and virtual photons are mixed near an antenna, with the virtual photons responsible only for the "extra" magnetic-inductive and transient electric-dipole effects, which cause any imbalance between E and cB. As distance from the antenna grows, the near-field effects (as dipole fields) die out more quickly, and only the "radiative" effects that are due to actual photons remain as important effects. Although virtual effects extend to infinity, they drop off in field strength as 1/r2 rather than the field of EM waves composed of actual photons, which drop 1/r (the powers, respectively, decrease as 1/r4 and 1/r2). See near and far field for a more detailed discussion. See near field communication for practical communications applications of near fields.
History
Paul Dirac was the first to propose that empty space (a vacuum) can be visualized as consisting of a sea of electrons with negative energy, known as the Dirac sea. The Dirac sea has a direct analog to the electronic band structure in crystalline solids as described in solid state physics. Here, particles correspond to conduction electrons, and antiparticles to holes. A variety of interesting phenomena can be attributed to this structure. The development of quantum field theory (QFT) in the 1930s made it possible to reformulate the Dirac equation in a way that treats the positron as a "real" particle rather than the absence of a particle, and makes the vacuum the state in which no particles exist instead of an infinite sea of particles.Feynman diagrams
The calculation of scattering amplitudes in theoretical particle physics requires the use of some rather large and complicated integrals over a large number of variables. These integrals do, however, have a regular structure, and may be represented as Feynman diagrams. The appeal of the Feynman diagrams is strong, as it allows for a simple visual presentation of what would otherwise be a rather arcane and abstract formula. In particular, part of the appeal is that the outgoing legs of a Feynman diagram can be associated with actual, on-shell particles. Thus, it is natural to associate the other lines in the diagram with particles as well, called the "virtual particles". In mathematical terms, they correspond to the propagators appearing in the diagram.
In the image to the right, the solid lines correspond to actual particles (of momentum p1 and so on), while the dotted line corresponds to a virtual particle carrying momentum k. For example, if the solid lines were to correspond to electrons interacting by means of the electromagnetic interaction, the dotted line would correspond to the exchange of a virtual photon. In the case of interacting nucleons, the dotted line would be a virtual pion. In the case of quarks interacting by means of the strong force, the dotted line would be a virtual gluon, and so on.
Virtual particles may be mesons or vector bosons, as in the example above; they may also be fermions. However, in order to preserve quantum numbers, most simple diagrams involving fermion exchange are prohibited. The image to the right shows an allowed diagram, a one-loop diagram. The solid lines correspond to a fermion propagator, the wavy lines to bosons.
Vacuums
In formal terms, a particle is considered to be an eigenstate of the particle number operator a†a, where a is the particle annihilation operator and a† the particle creation operator (sometimes collectively called ladder operators). In many cases, the particle number operator does not commute with the Hamiltonian for the system. This implies the number of particles in an area of space is not a well-defined quantity but, like other quantum observables, is represented by a probability distribution. Since these particles do not have a permanent existence,[clarification needed] they are called virtual particles or vacuum fluctuations of vacuum energy. In a certain sense, they can be understood to be a manifestation of the time-energy uncertainty principle in a vacuum.[12]An important example of the "presence" of virtual particles in a vacuum is the Casimir effect.[13] Here, the explanation of the effect requires that the total energy of all of the virtual particles in a vacuum can be added together. Thus, although the virtual particles themselves are not directly observable in the laboratory, they do leave an observable effect: Their zero-point energy results in forces acting on suitably arranged metal plates or dielectrics.[14] On the other hand, the Casimir effect can be interpreted as the relativistic van der Waals force.[15]
Pair production
Virtual particles are often popularly described as coming in pairs, a particle and antiparticle, which can be of any kind. These pairs exist for an extremely short time, and then mutually annihilate. In some cases, however, it is possible to boost the pair apart using external energy so that they avoid annihilation and become actual particles.This may occur in one of two ways. In an accelerating frame of reference, the virtual particles may appear to be actual to the accelerating observer; this is known as the Unruh effect. In short, the vacuum of a stationary frame appears, to the accelerated observer, to be a warm gas of actual particles in thermodynamic equilibrium.
Another example is pair production in very strong electric fields, sometimes called vacuum decay. If, for example, a pair of atomic nuclei are merged to very briefly form a nucleus with a charge greater than about 140, (that is, larger than about the inverse of the fine structure constant, which is a dimensionless quantity), the strength of the electric field will be such that it will be energetically favorable to create positron-electron pairs out of the vacuum or Dirac sea, with the electron attracted to the nucleus to annihilate the positive charge. This pair-creation amplitude was first calculated by Julian Schwinger in 1951.
Actual and virtual particles compared
As a consequence of quantum mechanical uncertainty, any object or process that exists for a limited time or in a limited volume cannot have a precisely defined energy or momentum. This is the reason that virtual particles — which exist only temporarily as they are exchanged between ordinary particles — do not necessarily obey the mass-shell relation. However, the longer a virtual particle exists, the more closely it adheres to the mass-shell relation. A "virtual" particle that exists for an arbitrarily long time is simply an ordinary particle.However, all particles have a finite lifetime, as they are created and eventually destroyed by some processes. As such, there is no absolute distinction between "real" and "virtual" particles. In practice, the lifetime of "ordinary" particles is far longer than the lifetime of the virtual particles that contribute to processes in particle physics, and as such the distinction is useful to make.





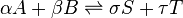
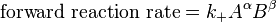





![K_c=\frac{[S]^\sigma [T]^\tau } {[A]^\alpha [B]^\beta}](http://upload.wikimedia.org/math/a/f/6/af61c8307fbde1f9595004610ce90563.png)
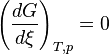 : equilibrium
: equilibrium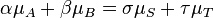
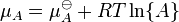 , (
, (  is the standard chemical potential ).
is the standard chemical potential ). .
. into the above equation gives a
into the above equation gives a 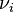 ) and a differential that denotes the reaction occurring once (
) and a differential that denotes the reaction occurring once (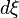 ). At constant pressure and temperature the above equations can be written as
). At constant pressure and temperature the above equations can be written as which is the "Gibbs free energy change for the reaction .
which is the "Gibbs free energy change for the reaction . .
.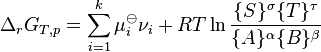
 : which is the standard Gibbs energy change for the reaction that can be calculated using thermodynamical tables.
: which is the standard Gibbs energy change for the reaction that can be calculated using thermodynamical tables.




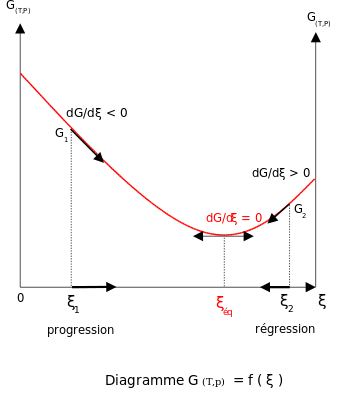
 ;
;  .
.


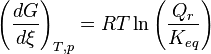
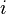 increases
increases , the reaction quotient decreases.
, the reaction quotient decreases. and
and 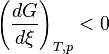 : The reaction will shift to the right (i.e. in the forward direction, and thus more products will form).
: The reaction will shift to the right (i.e. in the forward direction, and thus more products will form). increases
increases and
and  : The reaction will shift to the left (i.e. in the reverse direction, and thus less products will form).
: The reaction will shift to the left (i.e. in the reverse direction, and thus less products will form).![K=\frac{{[S]} ^\sigma {[T]}^\tau ... } {{[A]}^\alpha {[B]}^\beta ...}
\times \frac{{\gamma_S} ^\sigma {\gamma_T}^\tau ... } {{\gamma_A}^\alpha {\gamma_B}^\beta ...} = K_c \Gamma](http://upload.wikimedia.org/math/e/a/3/ea34698e710811edf7462f812d3e2bcd.png)



 2SO3
2SO3![K_c=\frac{[{CH_3CO_2}^-][{H_3O}^+]} {[{CH_3CO_2H}][{H_2O}]}](http://upload.wikimedia.org/math/3/0/7/307fe3fe38fb84bace20e2b8ba8eeebd.png)
![K=\frac{[{CH_3CO_2}^-][{H_3O}^+]} {[{CH_3CO_2H}]} = K_c](http://upload.wikimedia.org/math/3/e/8/3e83ebbc3fca08dba0b87020d4dda461.png) .
.
![K_w = [H^+][OH^-]\,](http://upload.wikimedia.org/math/0/4/7/04751982906d78616e59229017e70bc8.png)
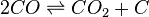
![K_c=\frac{[CO_2]} {[CO]^2}](http://upload.wikimedia.org/math/6/d/3/6d35112295d85580245a93dbd6cfd011.png)
![H_2A \rightleftharpoons HA^- + H^+ :K_1=\frac{[HA^-][H^+]} {[H_2A]}](http://upload.wikimedia.org/math/6/8/9/689ba8b4100e2ca021e92cc57c87829b.png)
![HA^- \rightleftharpoons A^{2-} + H^+ :K_2=\frac{[A^{2-}][H^+]} {[HA^-]}](http://upload.wikimedia.org/math/5/0/8/508c0a5e1a5b68608b549a390a6c28f4.png)
 , is product of the stepwise constants.
, is product of the stepwise constants.![H_2A \rightleftharpoons A^{2-} + 2H^+ :\beta_D = \frac{[A^{2-}][H^+]^2} {[H_2A]}=K_1K_2](http://upload.wikimedia.org/math/d/a/b/dabc558f3d7d75d148f9bea2e83f842e.png)
![A^{2-} + H^+ \rightleftharpoons HA^- :\beta_1=\frac {[HA^-]} {[A^{2-}][H^+]}](http://upload.wikimedia.org/math/d/3/8/d387e931f865d551b3f7b992b1f638f3.png)
![A^{2-} + 2H^+ \rightleftharpoons H_2A :\beta_2=\frac {[H_2A]} {[A^{2-}][H^+]^2}](http://upload.wikimedia.org/math/8/f/b/8fbf2ccc028a357fbf558f2c87b02c38.png)



![T_A = [A] + [HA] +[H_2A] \,](http://upload.wikimedia.org/math/b/a/a/baa30fecb1f077660b02981ea3e2165d.png)
![T_H = [H] + [HA] + 2[H_2A] - [OH] \,](http://upload.wikimedia.org/math/a/f/0/af0c187ac39ffc5a18d3091fa7d4579d.png)
![T_A = [A] + \beta_1[A][H] + \beta_2[A][H]^2 \,](http://upload.wikimedia.org/math/2/7/6/27647add7a20346a578e0a31316af783.png)
![T_H = [H] + \beta_1[A][H] + 2\beta_2[A][H]^2 - K_w[H]^{-1} \,](http://upload.wikimedia.org/math/4/3/f/43fc06f15ea67771c7a47b911db13a31.png)
![T_A=[A]+\sum_i{p_i \beta_i[A]^{p_i}[B]^{q_i}}](http://upload.wikimedia.org/math/a/6/6/a6688b731e5c97ba006bd88e5260263b.png)
![T_B=[B]+\sum_i{q_i \beta_i[A]^{p_i}[B]^{q_i}}](http://upload.wikimedia.org/math/6/8/9/68978139960014c7dc00450e0d8e562e.png)



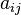 is the number of atoms of element i in molecule j and bi0 is the total number of atoms of element i, which is a constant, since the system is closed. If there are a total of k types of atoms in the system, then there will be k such equations.
is the number of atoms of element i in molecule j and bi0 is the total number of atoms of element i, which is a constant, since the system is closed. If there are a total of k types of atoms in the system, then there will be k such equations.
 are the Lagrange multipliers, one for each element. This allows each of the
are the Lagrange multipliers, one for each element. This allows each of the  to be treated independently, and it can be shown using the tools of
to be treated independently, and it can be shown using the tools of 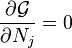 and
and