| Function |
|---|
| x ↦ f (x) |
| Examples of domains and codomains |
| Classes/properties |
| Constructions |
| Generalizations |
In mathematical analysis, and applications in geometry, applied mathematics, engineering, and natural sciences, a function of a real variable is a function whose domain is the real numbers , or a subset of that contains an interval of positive length. Most real functions that are considered and studied are differentiable in some interval. The most widely considered such functions are the real functions, which are the real-valued functions of a real variable, that is, the functions of a real variable whose codomain is the set of real numbers.
Nevertheless, the codomain of a function of a real variable may be any set. However, it is often assumed to have a structure of -vector space over the reals. That is, the codomain may be a Euclidean space, a coordinate vector, the set of matrices of real numbers of a given size, or an -algebra, such as the complex numbers or the quaternions. The structure -vector space of the codomain induces a structure of -vector space on the functions. If the codomain has a structure of -algebra, the same is true for the functions.
The image of a function of a real variable is a curve in the codomain. In this context, a function that defines curve is called a parametric equation of the curve.
When the codomain of a function of a real variable is a finite-dimensional vector space, the function may be viewed as a sequence of real functions. This is often used in applications.
Real function
A real function is a function from a subset of to where denotes as usual the set of real numbers. That is, the domain of a real function is a subset , and its codomain is It is generally assumed that the domain contains an interval of positive length.
Basic examples
For many commonly used real functions, the domain is the whole set of real numbers, and the function is continuous and differentiable at every point of the domain. One says that these functions are defined, continuous and differentiable everywhere. This is the case of:
- All polynomial functions, including constant functions and linear functions
- Sine and cosine functions
- Exponential function
Some functions are defined everywhere, but not continuous at some points. For example
- The Heaviside step function is defined everywhere, but not continuous at zero.
Some functions are defined and continuous everywhere, but not everywhere differentiable. For example
- The absolute value is defined and continuous everywhere, and is differentiable everywhere, except for zero.
- The cubic root is defined and continuous everywhere, and is differentiable everywhere, except for zero.
Many common functions are not defined everywhere, but are continuous and differentiable everywhere where they are defined. For example:
- A rational function is a quotient of two polynomial functions, and is not defined at the zeros of the denominator.
- The tangent function is not defined for where k is any integer.
- The logarithm function is defined only for positive values of the variable.
Some functions are continuous in their whole domain, and not differentiable at some points. This is the case of:
- The square root is defined only for nonnegative values of the variable, and not differentiable at 0 (it is differentiable for all positive values of the variable).
General definition
A real-valued function of a real variable is a function that takes as input a real number, commonly represented by the variable x, for producing another real number, the value of the function, commonly denoted f(x). For simplicity, in this article a real-valued function of a real variable will be simply called a function. To avoid any ambiguity, the other types of functions that may occur will be explicitly specified.
Some functions are defined for all real values of the variables (one says that they are everywhere defined), but some other functions are defined only if the value of the variable is taken in a subset X of ℝ, the domain of the function, which is always supposed to contain an interval of positive length. In other words, a real-valued function of a real variable is a function
such that its domain X is a subset of ℝ that contains an interval of positive length.
A simple example of a function in one variable could be:
which is the square root of x.
Image
The image of a function is the set of all values of f when the variable x runs in the whole domain of f. For a continuous (see below for a definition) real-valued function with a connected domain, the image is either an interval or a single value. In the latter case, the function is a constant function.
The preimage of a given real number y is the set of the solutions of the equation y = f(x).
Domain
The domain of a function of several real variables is a subset of ℝ that is sometimes explicitly defined. In fact, if one restricts the domain X of a function f to a subset Y ⊂ X, one gets formally a different function, the restriction of f to Y, which is denoted f|Y. In practice, it is often not harmful to identify f and f|Y, and to omit the subscript |Y.
Conversely, it is sometimes possible to enlarge naturally the domain of a given function, for example by continuity or by analytic continuation. This means that it is not worthy to explicitly define the domain of a function of a real variable.
Algebraic structure
The arithmetic operations may be applied to the functions in the following way:
- For every real number r, the constant function , is everywhere defined.
- For every real number r and every function f, the function has the same domain as f (or is everywhere defined if r = 0).
- If f and g are two functions of respective domains X and Y such that X∩Y contains an open subset of ℝ, then and are functions that have a domain containing X∩Y.
It follows that the functions of n variables that are everywhere defined and the functions of n variables that are defined in some neighbourhood of a given point both form commutative algebras over the reals (ℝ-algebras).
One may similarly define which is a function only if the set of the points (x) in the domain of f such that f(x) ≠ 0 contains an open subset of ℝ. This constraint implies that the above two algebras are not fields.
Continuity and limit
Until the second part of 19th century, only continuous functions were considered by mathematicians. At that time, the notion of continuity was elaborated for the functions of one or several real variables a rather long time before the formal definition of a topological space and a continuous map between topological spaces. As continuous functions of a real variable are ubiquitous in mathematics, it is worth defining this notion without reference to the general notion of continuous maps between topological space.
For defining the continuity, it is useful to consider the distance function of ℝ, which is an everywhere defined function of 2 real variables:
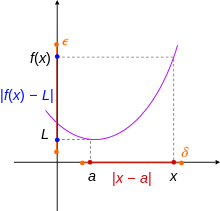
A function f is continuous at a point which is interior to its domain, if, for every positive real number ε, there is a positive real number φ such that for all such that In other words, φ may be chosen small enough for having the image by f of the interval of radius φ centered at contained in the interval of length 2ε centered at A function is continuous if it is continuous at every point of its domain.
The limit of a real-valued function of a real variable is as follows.[1] Let a be a point in topological closure of the domain X of the function f. The function, f has a limit L when x tends toward a, denoted
if the following condition is satisfied: For every positive real number ε > 0, there is a positive real number δ > 0 such that
for all x in the domain such that
If the limit exists, it is unique. If a is in the interior of the domain, the limit exists if and only if the function is continuous at a. In this case, we have
When a is in the boundary of the domain of f, and if f has a limit at a, the latter formula allows to "extend by continuity" the domain of f to a.
Calculus
One can collect a number of functions each of a real variable, say
into a vector parametrized by x:
The derivative of the vector y is the vector derivatives of fi(x) for i = 1, 2, ..., n:
One can also perform line integrals along a space curve parametrized by x, with position vector r = r(x), by integrating with respect to the variable x:
where · is the dot product, and x = a and x = b are the start and endpoints of the curve.
Theorems
With the definitions of integration and derivatives, key theorems can be formulated, including the fundamental theorem of calculus integration by parts, and Taylor's theorem. Evaluating a mixture of integrals and derivatives can be done by using theorem differentiation under the integral sign.
Implicit functions
A real-valued implicit function of a real variable is not written in the form "y = f(x)". Instead, the mapping is from the space ℝ2 to the zero element in ℝ (just the ordinary zero 0):
and
is an equation in the variables. Implicit functions are a more general way to represent functions, since if:
then we can always define:
but the converse is not always possible, i.e. not all implicit functions have the form of this equation.
One-dimensional space curves in ℝn
Formulation
Given the functions r1 = r1(t), r2 = r2(t), ..., rn = rn(t) all of a common variable t, so that:
or taken together:
then the parametrized n-tuple,
describes a one-dimensional space curve.
Tangent line to curve
At a point r(t = c) = a = (a1, a2, ..., an) for some constant t = c, the equations of the one-dimensional tangent line to the curve at that point are given in terms of the ordinary derivatives of r1(t), r2(t), ..., rn(t), and r with respect to t:
Normal plane to curve
The equation of the n-dimensional hyperplane normal to the tangent line at r = a is:
or in terms of the dot product:
where p = (p1, p2, ..., pn) are points in the plane, not on the space curve.
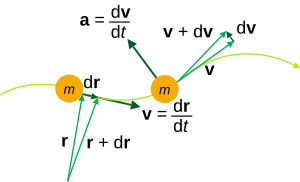
Relation to kinematics
The physical and geometric interpretation of dr(t)/dt is the "velocity" of a point-like particle moving along the path r(t), treating r as the spatial position vector coordinates parametrized by time t, and is a vector tangent to the space curve for all t in the instantaneous direction of motion. At t = c, the space curve has a tangent vector dr(t)/dt|t = c, and the hyperplane normal to the space curve at t = c is also normal to the tangent at t = c. Any vector in this plane (p − a) must be normal to dr(t)/dt|t = c.
Similarly, d2r(t)/dt2 is the "acceleration" of the particle, and is a vector normal to the curve directed along the radius of curvature.
Matrix valued functions
A matrix can also be a function of a single variable. For example, the rotation matrix in 2d:
is a matrix valued function of rotation angle of about the origin. Similarly, in special relativity, the Lorentz transformation matrix for a pure boost (without rotations):
is a function of the boost parameter β = v/c, in which v is the relative velocity between the frames of reference (a continuous variable), and c is the speed of light, a constant.
Banach and Hilbert spaces and quantum mechanics
Generalizing the previous section, the output of a function of a real variable can also lie in a Banach space or a Hilbert space. In these spaces, division and multiplication and limits are all defined, so notions such as derivative and integral still apply. This occurs especially often in quantum mechanics, where one takes the derivative of a ket or an operator. This occurs, for instance, in the general time-dependent Schrödinger equation:
where one takes the derivative of a wave function, which can be an element of several different Hilbert spaces.
Complex-valued function of a real variable
A complex-valued function of a real variable may be defined by relaxing, in the definition of the real-valued functions, the restriction of the codomain to the real numbers, and allowing complex values.
If f(x) is such a complex valued function, it may be decomposed as
- f(x) = g(x) + ih(x),
where g and h are real-valued functions. In other words, the study of the complex valued functions reduces easily to the study of the pairs of real valued functions.
Cardinality of sets of functions of a real variable
The cardinality of the set of real-valued functions of a real variable, , is , which is strictly larger than the cardinality of the continuum (i.e., set of all real numbers). This fact is easily verified by cardinal arithmetic:
Furthermore, if is a set such that , then the cardinality of the set is also , since
However, the set of continuous functions has a strictly smaller cardinality, the cardinality of the continuum, . This follows from the fact that a continuous function is completely determined by its value on a dense subset of its domain.[2] Thus, the cardinality of the set of continuous real-valued functions on the reals is no greater than the cardinality of the set of real-valued functions of a rational variable. By cardinal arithmetic:
On the other hand, since there is a clear bijection between and the set of constant functions , which forms a subset of , must also hold. Hence, .
































![{\mathbf {y}}=(y_{1},y_{2},\ldots ,y_{n})=[f_{1}(x),f_{2}(x),\ldots ,f_{n}(x)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf6094665fed0f442aec3c0137dc30dfb7fa100d)









![{\mathbf {r}}(t)=[r_{1}(t),r_{2}(t),\ldots ,r_{n}(t)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c51b92c84d7efdb07ec33ed3cf518567b78de696)