Real analysis

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Real_analysis 

In mathematics, real analysis is the branch of mathematical analysis that studies the behavior of real numbers, sequences and series of real numbers, and real functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.

Real analysis is distinguished from complex analysis, which deals with the study of complex numbers and their functions.

Scope

Construction of the real numbers

Main article: Construction of the real numbers

The theorems of real analysis rely on the properties of the real number system, which must be established. The real number system consists of an uncountable set (${\displaystyle \mathbb {R} }$), together with two binary operations denoted + and ⋅, and an order denoted <. The operations make the real numbers a field, and, along with the order, an ordered field. The real number system is the unique complete ordered field, in the sense that any other complete ordered field is isomorphic to it. Intuitively, completeness means that there are no 'gaps' in the real numbers. This property distinguishes the real numbers from other ordered fields (e.g., the rational numbers ${\displaystyle \mathbb {Q} }$) and is critical to the proof of several key properties of functions of the real numbers. The completeness of the reals is often conveniently expressed as the least upper bound property (see below).

Order properties of the real numbers

The real numbers have various lattice-theoretic properties that are absent in the complex numbers. Also, the real numbers form an ordered field, in which sums and products of positive numbers are also positive. Moreover, the ordering of the real numbers is total, and the real numbers have the least upper bound property:

Every nonempty subset of ${\displaystyle \mathbb {R} }$ that has an upper bound has a least upper bound that is also a real number.

These order-theoretic properties lead to a number of fundamental results in real analysis, such as the monotone convergence theorem, the intermediate value theorem and the mean value theorem.

However, while the results in real analysis are stated for real numbers, many of these results can be generalized to other mathematical objects. In particular, many ideas in functional analysis and operator theory generalize properties of the real numbers – such generalizations include the theories of Riesz spaces and positive operators. Also, mathematicians consider real and imaginary parts of complex sequences, or by pointwise evaluation of operator sequences.

Topological properties of the real numbers

Many of the theorems of real analysis are consequences of the topological properties of the real number line. The order properties of the real numbers described above are closely related to these topological properties. As a topological space, the real numbers has a standard topology, which is the order topology induced by order ${\displaystyle <}$. Alternatively, by defining the metric or distance function ${\displaystyle d:\mathbb {R} \times \mathbb {R} \to \mathbb {R} _{\geq 0}}$ using the absolute value function as ${\displaystyle d(x,y)=|x-y|}$, the real numbers become the prototypical example of a metric space. The topology induced by metric ${\displaystyle d}$ turns out to be identical to the standard topology induced by order ${\displaystyle <}$. Theorems like the intermediate value theorem that are essentially topological in nature can often be proved in the more general setting of metric or topological spaces rather than in ${\displaystyle \mathbb {R} }$ only. Often, such proofs tend to be shorter or simpler compared to classical proofs that apply direct methods.

Sequences

Main article: Sequence

A sequence is a function whose domain is a countable, totally ordered set. The domain is usually taken to be the natural numbers, although it is occasionally convenient to also consider bidirectional sequences indexed by the set of all integers, including negative indices.

Of interest in real analysis, a real-valued sequence, here indexed by the natural numbers, is a map ${\displaystyle a:\mathbb {N} \to \mathbb {R} :n\mapsto a_{n}}$. Each ${\displaystyle a(n)=a_{n}}$ is referred to as a term (or, less commonly, an element) of the sequence. A sequence is rarely denoted explicitly as a function; instead, by convention, it is almost always notated as if it were an ordered ∞-tuple, with individual terms or a general term enclosed in parentheses:

$${\displaystyle (a_{n})=(a_{n})_{n\in \mathbb {N} }=(a_{1},a_{2},a_{3},\dots ).}$$

A sequence that tends to a limit (i.e., ${\textstyle \lim _{n\to \infty }a_{n}}$ exists) is said to be convergent; otherwise it is divergent. (See the section on limits and convergence for details.) A real-valued sequence ${\displaystyle (a_{n})}$ is bounded if there exists ${\displaystyle M\in \mathbb {R} }$ such that ${\displaystyle |a_{n}|<M}$ for all ${\displaystyle n\in \mathbb {N} }$. A real-valued sequence ${\displaystyle (a_{n})}$ is monotonically increasing or decreasing if

$${\displaystyle a_{1}\leq a_{2}\leq a_{3}\leq \cdots }$$

or

$${\displaystyle a_{1}\geq a_{2}\geq a_{3}\geq \cdots }$$

holds, respectively. If either holds, the sequence is said to be monotonic. The monotonicity is strict if the chained inequalities still hold with ${\displaystyle \leq }$ or ${\displaystyle \geq }$ replaced by < or >.

Given a sequence ${\displaystyle (a_{n})}$, another sequence ${\displaystyle (b_{k})}$ is a subsequence of ${\displaystyle (a_{n})}$ if ${\displaystyle b_{k}=a_{n_{k}}}$ for all positive integers ${\displaystyle k}$ and ${\displaystyle (n_{k})}$ is a strictly increasing sequence of natural numbers.

Limits and convergence

Main article: Limit (mathematics)

Roughly speaking, a limit is the value that a function or a sequence "approaches" as the input or index approaches some value. (This value can include the symbols ${\displaystyle \pm \infty }$ when addressing the behavior of a function or sequence as the variable increases or decreases without bound.) The idea of a limit is fundamental to calculus (and mathematical analysis in general) and its formal definition is used in turn to define notions like continuity, derivatives, and integrals. (In fact, the study of limiting behavior has been used as a characteristic that distinguishes calculus and mathematical analysis from other branches of mathematics.)

The concept of limit was informally introduced for functions by Newton and Leibniz, at the end of the 17th century, for building infinitesimal calculus. For sequences, the concept was introduced by Cauchy, and made rigorous, at the end of the 19th century by Bolzano and Weierstrass, who gave the modern ε-δ definition, which follows.

Definition. Let ${\displaystyle f}$ be a real-valued function defined on ${\displaystyle E\subset \mathbb {R} }$. We say that ${\displaystyle f(x)}$ tends to ${\displaystyle L}$ as ${\displaystyle x}$ approaches ${\displaystyle x_{0}}$, or that the limit of ${\displaystyle f(x)}$ as ${\displaystyle x}$ approaches ${\displaystyle x_{0}}$ is ${\displaystyle L}$ if, for any ${\displaystyle \varepsilon >0}$, there exists ${\displaystyle \delta >0}$ such that for all ${\displaystyle x\in E}$, ${\displaystyle 0<|x-x_{0}|<\delta }$ implies that ${\displaystyle |f(x)-L|<\varepsilon }$. We write this symbolically as

$${\displaystyle f(x)\to L\ \ {\text{as}}\ \ x\to x_{0},}$$

or as

$${\displaystyle \lim _{x\to x_{0}}f(x)=L.}$$

Intuitively, this definition can be thought of in the following way: We say that ${\displaystyle f(x)\to L}$ as ${\displaystyle x\to x_{0}}$, when, given any positive number ${\displaystyle \varepsilon }$, no matter how small, we can always find a ${\displaystyle \delta }$, such that we can guarantee that ${\displaystyle f(x)}$ and ${\displaystyle L}$ are less than ${\displaystyle \varepsilon }$ apart, as long as ${\displaystyle x}$ (in the domain of ${\displaystyle f}$) is a real number that is less than ${\displaystyle \delta }$ away from ${\displaystyle x_{0}}$ but distinct from ${\displaystyle x_{0}}$. The purpose of the last stipulation, which corresponds to the condition ${\displaystyle 0<|x-x_{0}|}$ in the definition, is to ensure that ${\textstyle \lim _{x\to x_{0}}f(x)=L}$ does not imply anything about the value of ${\displaystyle f(x_{0})}$ itself. Actually, ${\displaystyle x_{0}}$ does not even need to be in the domain of ${\displaystyle f}$ in order for ${\textstyle \lim _{x\to x_{0}}f(x)}$ to exist.

In a slightly different but related context, the concept of a limit applies to the behavior of a sequence ${\displaystyle (a_{n})}$ when ${\displaystyle n}$ becomes large.

Definition. Let ${\displaystyle (a_{n})}$ be a real-valued sequence. We say that ${\displaystyle (a_{n})}$ converges to ${\displaystyle a}$ if, for any ${\displaystyle \varepsilon >0}$, there exists a natural number ${\displaystyle N}$ such that ${\displaystyle n\geq N}$ implies that ${\displaystyle |a-a_{n}|<\varepsilon }$. We write this symbolically as

$${\displaystyle a_{n}\to a\ \ {\text{as}}\ \ n\to \infty ,}$$

or as

$${\displaystyle \lim _{n\to \infty }a_{n}=a;}$$

if ${\displaystyle (a_{n})}$ fails to converge, we say that ${\displaystyle (a_{n})}$ diverges.

Generalizing to a real-valued function of a real variable, a slight modification of this definition (replacement of sequence ${\displaystyle (a_{n})}$ and term ${\displaystyle a_{n}}$ by function ${\displaystyle f}$ and value ${\displaystyle f(x)}$ and natural numbers ${\displaystyle N}$ and ${\displaystyle n}$ by real numbers ${\displaystyle M}$ and ${\displaystyle x}$, respectively) yields the definition of the limit of ${\displaystyle f(x)}$ as ${\displaystyle x}$ increases without bound, notated ${\textstyle \lim _{x\to \infty }f(x)}$. Reversing the inequality ${\displaystyle x\geq M}$ to ${\displaystyle x\leq M}$ gives the corresponding definition of the limit of ${\displaystyle f(x)}$ as ${\displaystyle x}$ decreases without bound, ${\textstyle \lim _{x\to -\infty }f(x)}$.

Sometimes, it is useful to conclude that a sequence converges, even though the value to which it converges is unknown or irrelevant. In these cases, the concept of a Cauchy sequence is useful.

Definition. Let ${\displaystyle (a_{n})}$ be a real-valued sequence. We say that ${\displaystyle (a_{n})}$ is a Cauchy sequence if, for any ${\displaystyle \varepsilon >0}$, there exists a natural number ${\displaystyle N}$ such that ${\displaystyle m,n\geq N}$ implies that ${\displaystyle |a_{m}-a_{n}|<\varepsilon }$.

It can be shown that a real-valued sequence is Cauchy if and only if it is convergent. This property of the real numbers is expressed by saying that the real numbers endowed with the standard metric, ${\displaystyle (\mathbb {R} ,|\cdot |)}$, is a complete metric space. In a general metric space, however, a Cauchy sequence need not converge.

In addition, for real-valued sequences that are monotonic, it can be shown that the sequence is bounded if and only if it is convergent.

Uniform and pointwise convergence for sequences of functions

Main article: Uniform convergence

In addition to sequences of numbers, one may also speak of sequences of functions on ${\displaystyle E\subset \mathbb {R} }$, that is, infinite, ordered families of functions ${\displaystyle f_{n}:E\to \mathbb {R} }$, denoted ${\displaystyle (f_{n})_{n=1}^{\infty }}$, and their convergence properties. However, in the case of sequences of functions, there are two kinds of convergence, known as pointwise convergence and uniform convergence, that need to be distinguished.

Roughly speaking, pointwise convergence of functions ${\displaystyle f_{n}}$ to a limiting function ${\displaystyle f:E\to \mathbb {R} }$, denoted ${\displaystyle f_{n}\rightarrow f}$, simply means that given any ${\displaystyle x\in E}$, ${\displaystyle f_{n}(x)\to f(x)}$ as ${\displaystyle n\to \infty }$. In contrast, uniform convergence is a stronger type of convergence, in the sense that a uniformly convergent sequence of functions also converges pointwise, but not conversely. Uniform convergence requires members of the family of functions, ${\displaystyle f_{n}}$, to fall within some error ${\displaystyle \varepsilon >0}$ of ${\displaystyle f}$ for every value of ${\displaystyle x\in E}$, whenever ${\displaystyle n\geq N}$, for some integer ${\displaystyle N}$. For a family of functions to uniformly converge, sometimes denoted ${\displaystyle f_{n}\rightrightarrows f}$, such a value of ${\displaystyle N}$ must exist for any ${\displaystyle \varepsilon >0}$ given, no matter how small. Intuitively, we can visualize this situation by imagining that, for a large enough ${\displaystyle N}$, the functions ${\displaystyle f_{N},f_{N+1},f_{N+2},\ldots }$ are all confined within a 'tube' of width ${\displaystyle 2\varepsilon }$ about ${\displaystyle f}$ (that is, between ${\displaystyle f-\varepsilon }$ and ${\displaystyle f+\varepsilon }$) for every value in their domain ${\displaystyle E}$.

The distinction between pointwise and uniform convergence is important when exchanging the order of two limiting operations (e.g., taking a limit, a derivative, or integral) is desired: in order for the exchange to be well-behaved, many theorems of real analysis call for uniform convergence. For example, a sequence of continuous functions (see below) is guaranteed to converge to a continuous limiting function if the convergence is uniform, while the limiting function may not be continuous if convergence is only pointwise. Karl Weierstrass is generally credited for clearly defining the concept of uniform convergence and fully investigating its implications.

Compactness

Main article: Compactness

Compactness is a concept from general topology that plays an important role in many of the theorems of real analysis. The property of compactness is a generalization of the notion of a set being closed and bounded. (In the context of real analysis, these notions are equivalent: a set in Euclidean space is compact if and only if it is closed and bounded.) Briefly, a closed set contains all of its boundary points, while a set is bounded if there exists a real number such that the distance between any two points of the set is less than that number. In ${\displaystyle \mathbb {R} }$, sets that are closed and bounded, and therefore compact, include the empty set, any finite number of points, closed intervals, and their finite unions. However, this list is not exhaustive; for instance, the set ${\displaystyle \{1/n:n\in \mathbb {N} \}\cup \{0}\}$ is a compact set; the Cantor ternary set ${\displaystyle {\mathcal {C}}\subset [0,1]}$ is another example of a compact set. On the other hand, the set ${\displaystyle \{1/n:n\in \mathbb {N} \}}$ is not compact because it is bounded but not closed, as the boundary point 0 is not a member of the set. The set ${\displaystyle [0,\infty )}$ is also not compact because it is closed but not bounded.

For subsets of the real numbers, there are several equivalent definitions of compactness.

Definition. A set ${\displaystyle E\subset \mathbb {R} }$ is compact if it is closed and bounded.

This definition also holds for Euclidean space of any finite dimension, ${\displaystyle \mathbb {R} ^{n}}$, but it is not valid for metric spaces in general. The equivalence of the definition with the definition of compactness based on subcovers, given later in this section, is known as the Heine-Borel theorem.

A more general definition that applies to all metric spaces uses the notion of a subsequence (see above).

Definition. A set ${\displaystyle E}$ in a metric space is compact if every sequence in ${\displaystyle E}$ has a convergent subsequence.

This particular property is known as subsequential compactness. In ${\displaystyle \mathbb {R} }$, a set is subsequentially compact if and only if it is closed and bounded, making this definition equivalent to the one given above. Subsequential compactness is equivalent to the definition of compactness based on subcovers for metric spaces, but not for topological spaces in general.

The most general definition of compactness relies on the notion of open covers and subcovers, which is applicable to topological spaces (and thus to metric spaces and ${\displaystyle \mathbb {R} }$ as special cases). In brief, a collection of open sets ${\displaystyle U_{\alpha }}$ is said to be an open cover of set ${\displaystyle X}$ if the union of these sets is a superset of ${\displaystyle X}$. This open cover is said to have a finite subcover if a finite subcollection of the ${\displaystyle U_{\alpha }}$ could be found that also covers ${\displaystyle X}$.

Definition. A set ${\displaystyle X}$ in a topological space is compact if every open cover of ${\displaystyle X}$ has a finite subcover.

Compact sets are well-behaved with respect to properties like convergence and continuity. For instance, any Cauchy sequence in a compact metric space is convergent. As another example, the image of a compact metric space under a continuous map is also compact.

Continuity

Main article: Continuous function

A function from the set of real numbers to the real numbers can be represented by a graph in the Cartesian plane; such a function is continuous if, roughly speaking, the graph is a single unbroken curve with no "holes" or "jumps".

There are several ways to make this intuition mathematically rigorous. Several definitions of varying levels of generality can be given. In cases where two or more definitions are applicable, they are readily shown to be equivalent to one another, so the most convenient definition can be used to determine whether a given function is continuous or not. In the first definition given below, ${\displaystyle f:I\to \mathbb {R} }$ is a function defined on a non-degenerate interval ${\displaystyle I}$ of the set of real numbers as its domain. Some possibilities include ${\displaystyle I=\mathbb {R} }$, the whole set of real numbers, an open interval ${\displaystyle I=(a,b)=\{x\in \mathbb {R} \mid a<x<b\},}$ or a closed interval ${\displaystyle I=[a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}.}$ Here, ${\displaystyle a}$ and ${\displaystyle b}$ are distinct real numbers, and we exclude the case of ${\displaystyle I}$ being empty or consisting of only one point, in particular.

Definition. If ${\displaystyle I\subset \mathbb {R} }$ is a non-degenerate interval, we say that ${\displaystyle f:I\to \mathbb {R} }$ is continuous at ${\displaystyle p\in I}$ if ${\textstyle \lim _{x\to p}f(x)=f(p)}$. We say that ${\displaystyle f}$ is a continuous map if ${\displaystyle f}$ is continuous at every ${\displaystyle p\in I}$.

In contrast to the requirements for ${\displaystyle f}$ to have a limit at a point ${\displaystyle p}$, which do not constrain the behavior of ${\displaystyle f}$ at ${\displaystyle p}$ itself, the following two conditions, in addition to the existence of ${\textstyle \lim _{x\to p}f(x)}$, must also hold in order for ${\displaystyle f}$ to be continuous at ${\displaystyle p}$: (i) ${\displaystyle f}$ must be defined at ${\displaystyle p}$, i.e., ${\displaystyle p}$ is in the domain of ${\displaystyle f}$; and (ii) ${\displaystyle f(x)\to f(p)}$ as ${\displaystyle x\to p}$. The definition above actually applies to any domain ${\displaystyle E}$ that does not contain an isolated point, or equivalently, ${\displaystyle E}$ where every ${\displaystyle p\in E}$ is a limit point of ${\displaystyle E}$. A more general definition applying to ${\displaystyle f:X\to \mathbb {R} }$ with a general domain ${\displaystyle X\subset \mathbb {R} }$ is the following:

Definition. If ${\displaystyle X}$ is an arbitrary subset of ${\displaystyle \mathbb {R} }$, we say that ${\displaystyle f:X\to \mathbb {R} }$ is continuous at ${\displaystyle p\in X}$ if, for any ${\displaystyle \varepsilon >0}$, there exists ${\displaystyle \delta >0}$ such that for all ${\displaystyle x\in X}$, ${\displaystyle |x-p|<\delta }$ implies that ${\displaystyle |f(x)-f(p)|<\varepsilon }$. We say that ${\displaystyle f}$ is a continuous map if ${\displaystyle f}$ is continuous at every ${\displaystyle p\in X}$.

A consequence of this definition is that ${\displaystyle f}$ is trivially continuous at any isolated point ${\displaystyle p\in X}$. This somewhat unintuitive treatment of isolated points is necessary to ensure that our definition of continuity for functions on the real line is consistent with the most general definition of continuity for maps between topological spaces (which includes metric spaces and ${\displaystyle \mathbb {R} }$ in particular as special cases). This definition, which extends beyond the scope of our discussion of real analysis, is given below for completeness.

Definition. If ${\displaystyle X}$ and ${\displaystyle Y}$ are topological spaces, we say that ${\displaystyle f:X\to Y}$ is continuous at ${\displaystyle p\in X}$ if ${\displaystyle f^{-1}(V)}$ is a neighborhood of ${\displaystyle p}$ in ${\displaystyle X}$ for every neighborhood ${\displaystyle V}$ of ${\displaystyle f(p)}$ in ${\displaystyle Y}$. We say that ${\displaystyle f}$ is a continuous map if ${\displaystyle f^{-1}(U)}$ is open in ${\displaystyle X}$ for every ${\displaystyle U}$ open in ${\displaystyle Y}$.

(Here, ${\displaystyle f^{-1}(S)}$ refers to the preimage of ${\displaystyle S\subset Y}$ under ${\displaystyle f}$.)

Uniform continuity

Main article: Uniform continuity

Definition. If ${\displaystyle X}$ is a subset of the real numbers, we say a function ${\displaystyle f:X\to \mathbb {R} }$ is uniformly continuous on ${\displaystyle X}$ if, for any ${\displaystyle \varepsilon >0}$, there exists a ${\displaystyle \delta >0}$ such that for all ${\displaystyle x,y\in X}$, ${\displaystyle |x-y|<\delta }$ implies that ${\displaystyle |f(x)-f(y)|<\varepsilon }$.

Explicitly, when a function is uniformly continuous on ${\displaystyle X}$, the choice of ${\displaystyle \delta }$ needed to fulfill the definition must work for all of ${\displaystyle X}$ for a given ${\displaystyle \varepsilon }$. In contrast, when a function is continuous at every point ${\displaystyle p\in X}$ (or said to be continuous on ${\displaystyle X}$), the choice of ${\displaystyle \delta }$ may depend on both ${\displaystyle \varepsilon }$ and ${\displaystyle p}$. In contrast to simple continuity, uniform continuity is a property of a function that only makes sense with a specified domain; to speak of uniform continuity at a single point ${\displaystyle p}$ is meaningless.

On a compact set, it is easily shown that all continuous functions are uniformly continuous. If ${\displaystyle E}$ is a bounded noncompact subset of ${\displaystyle \mathbb {R} }$, then there exists ${\displaystyle f:E\to \mathbb {R} }$ that is continuous but not uniformly continuous. As a simple example, consider ${\displaystyle f:(0,1)\to \mathbb {R} }$ defined by ${\displaystyle f(x)=1/x}$. By choosing points close to 0, we can always make ${\displaystyle |f(x)-f(y)|>\varepsilon }$ for any single choice of ${\displaystyle \delta >0}$, for a given ${\displaystyle \varepsilon >0}$.

Absolute continuity

Main article: Absolute continuity

Definition. Let ${\displaystyle I\subset \mathbb {R} }$ be an interval on the real line. A function ${\displaystyle f:I\to \mathbb {R} }$ is said to be absolutely continuous on ${\displaystyle I}$ if for every positive number ${\displaystyle \varepsilon }$, there is a positive number ${\displaystyle \delta }$ such that whenever a finite sequence of pairwise disjoint sub-intervals ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2}),\ldots ,(x_{n},y_{n})}$ of ${\displaystyle I}$ satisfies

${\displaystyle \sum _{k=1}^{n}(y_{k}-x_{k})<\delta }$

then

${\displaystyle \sum _{k=1}^{n}|f(y_{k})-f(x_{k})|<\varepsilon .}$

Absolutely continuous functions are continuous: consider the case n = 1 in this definition. The collection of all absolutely continuous functions on I is denoted AC(I). Absolute continuity is a fundamental concept in the Lebesgue theory of integration, allowing the formulation of a generalized version of the fundamental theorem of calculus that applies to the Lebesgue integral.

Differentiation

Main articles: Derivative and Differential calculus

The notion of the derivative of a function or differentiability originates from the concept of approximating a function near a given point using the "best" linear approximation. This approximation, if it exists, is unique and is given by the line that is tangent to the function at the given point ${\displaystyle a}$, and the slope of the line is the derivative of the function at ${\displaystyle a}$.

A function ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ is differentiable at ${\displaystyle a}$ if the limit

${\displaystyle f'(a)=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}}$

exists. This limit is known as the derivative of ${\displaystyle f}$ at ${\displaystyle a}$, and the function ${\displaystyle f'}$, possibly defined on only a subset of ${\displaystyle \mathbb {R} }$, is the derivative (or derivative function) of ${\displaystyle f}$. If the derivative exists everywhere, the function is said to be differentiable.

As a simple consequence of the definition, ${\displaystyle f}$ is continuous at ${\displaystyle a}$ if it is differentiable there. Differentiability is therefore a stronger regularity condition (condition describing the "smoothness" of a function) than continuity, and it is possible for a function to be continuous on the entire real line but not differentiable anywhere (see Weierstrass's nowhere differentiable continuous function). It is possible to discuss the existence of higher-order derivatives as well, by finding the derivative of a derivative function, and so on.

One can classify functions by their differentiability class. The class ${\displaystyle C^{0}}$ (sometimes ${\displaystyle C^{0}([a,b])}$ to indicate the interval of applicability) consists of all continuous functions. The class ${\displaystyle C^{1}}$ consists of all differentiable functions whose derivative is continuous; such functions are called continuously differentiable. Thus, a ${\displaystyle C^{1}}$ function is exactly a function whose derivative exists and is of class ${\displaystyle C^{0}}$. In general, the classes ${\displaystyle C^{k}}$ can be defined recursively by declaring ${\displaystyle C^{0}}$ to be the set of all continuous functions and declaring ${\displaystyle C^{k}}$ for any positive integer ${\displaystyle k}$ to be the set of all differentiable functions whose derivative is in ${\displaystyle C^{k-1}}$. In particular, ${\displaystyle C^{k}}$ is contained in ${\displaystyle C^{k-1}}$ for every ${\displaystyle k}$, and there are examples to show that this containment is strict. Class ${\displaystyle C^{\infty }}$ is the intersection of the sets ${\displaystyle C^{k}}$ as ${\displaystyle k}$ varies over the non-negative integers, and the members of this class are known as the smooth functions. Class ${\displaystyle C^{\omega }}$ consists of all analytic functions, and is strictly contained in ${\displaystyle C^{\infty }}$ (see bump function for a smooth function that is not analytic).

Series

Main article: Series (mathematics)

A series formalizes the imprecise notion of taking the sum of an endless sequence of numbers. The idea that taking the sum of an "infinite" number of terms can lead to a finite result was counterintuitive to the ancient Greeks and led to the formulation of a number of paradoxes by Zeno and other philosophers. The modern notion of assigning a value to a series avoids dealing with the ill-defined notion of adding an "infinite" number of terms. Instead, the finite sum of the first ${\displaystyle n}$ terms of the sequence, known as a partial sum, is considered, and the concept of a limit is applied to the sequence of partial sums as ${\displaystyle n}$ grows without bound. The series is assigned the value of this limit, if it exists.

Given an (infinite) sequence ${\displaystyle (a_{n})}$, we can define an associated series as the formal mathematical object ${\textstyle a_{1}+a_{2}+a_{3}+\cdots =\sum _{n=1}^{\infty }a_{n}}$, sometimes simply written as ${\textstyle \sum a_{n}}$. The partial sums of a series ${\textstyle \sum a_{n}}$ are the numbers ${\textstyle s_{n}=\sum _{j=1}^{n}a_{j}}$. A series ${\textstyle \sum a_{n}}$ is said to be convergent if the sequence consisting of its partial sums, ${\displaystyle (s_{n})}$, is convergent; otherwise it is divergent. The sum of a convergent series is defined as the number ${\textstyle s=\lim _{n\to \infty }s_{n}}$.

The word "sum" is used here in a metaphorical sense as a shorthand for taking the limit of a sequence of partial sums and should not be interpreted as simply "adding" an infinite number of terms. For instance, in contrast to the behavior of finite sums, rearranging the terms of an infinite series may result in convergence to a different number (see the article on the Riemann rearrangement theorem for further discussion).

An example of a convergent series is a geometric series which forms the basis of one of Zeno's famous paradoxes:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{2^{n}}}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+\cdots =1.}$

In contrast, the harmonic series has been known since the Middle Ages to be a divergent series:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots =\infty .}$

(Here, "${\displaystyle =\infty }$" is merely a notational convention to indicate that the partial sums of the series grow without bound.)

A series ${\textstyle \sum a_{n}}$ is said to converge absolutely if ${\textstyle \sum |a_{n}|}$ is convergent. A convergent series ${\textstyle \sum a_{n}}$ for which ${\textstyle \sum |a_{n}|}$ diverges is said to converge non-absolutely. It is easily shown that absolute convergence of a series implies its convergence. On the other hand, an example of a series that converges non-absolutely is

${\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\cdots =\ln 2.}$

Taylor series

Main article: Taylor series

The Taylor series of a real or complex-valued function ƒ(x) that is infinitely differentiable at a real or complex number a is the power series

${\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f^{(3)}(a)}{3!}}(x-a)^{3}+\cdots .}$

which can be written in the more compact sigma notation as

${\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}\,(x-a)^{n}}$

where n! denotes the factorial of n and ƒ ⁽ⁿ⁾(a) denotes the nth derivative of ƒ evaluated at the point a. The derivative of order zero ƒ is defined to be ƒ itself and (x − a)⁰ and 0! are both defined to be 1. In the case that a = 0, the series is also called a Maclaurin series.

A Taylor series of f about point a may diverge, converge at only the point a, converge for all x such that ${\displaystyle |x-a|<R}$ (the largest such R for which convergence is guaranteed is called the radius of convergence), or converge on the entire real line. Even a converging Taylor series may converge to a value different from the value of the function at that point. If the Taylor series at a point has a nonzero radius of convergence, and sums to the function in the disc of convergence, then the function is analytic. The analytic functions have many fundamental properties. In particular, an analytic function of a real variable extends naturally to a function of a complex variable. It is in this way that the exponential function, the logarithm, the trigonometric functions and their inverses are extended to functions of a complex variable.

Fourier series

Main article: Fourier series

 

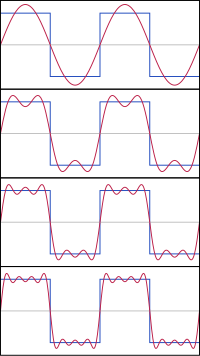
The first four partial sums of the Fourier series for a square wave. Fourier series are an important tool in real analysis.

Fourier series decomposes periodic functions or periodic signals into the sum of a (possibly infinite) set of simple oscillating functions, namely sines and cosines (or complex exponentials). The study of Fourier series typically occurs and is handled within the branch mathematics > mathematical analysis > Fourier analysis.

Integration

Integration is a formalization of the problem of finding the area bound by a curve and the related problems of determining the length of a curve or volume enclosed by a surface. The basic strategy to solving problems of this type was known to the ancient Greeks and Chinese, and was known as the method of exhaustion. Generally speaking, the desired area is bounded from above and below, respectively, by increasingly accurate circumscribing and inscribing polygonal approximations whose exact areas can be computed. By considering approximations consisting of a larger and larger ("infinite") number of smaller and smaller ("infinitesimal") pieces, the area bound by the curve can be deduced, as the upper and lower bounds defined by the approximations converge around a common value.

The spirit of this basic strategy can easily be seen in the definition of the Riemann integral, in which the integral is said to exist if upper and lower Riemann (or Darboux) sums converge to a common value as thinner and thinner rectangular slices ("refinements") are considered. Though the machinery used to define it is much more elaborate compared to the Riemann integral, the Lebesgue integral was defined with similar basic ideas in mind. Compared to the Riemann integral, the more sophisticated Lebesgue integral allows area (or length, volume, etc.; termed a "measure" in general) to be defined and computed for much more complicated and irregular subsets of Euclidean space, although there still exist "non-measurable" subsets for which an area cannot be assigned.

Riemann integration

Main article: Riemann integral

The Riemann integral is defined in terms of Riemann sums of functions with respect to tagged partitions of an interval. Let ${\displaystyle [a,b]}$ be a closed interval of the real line; then a tagged partition ${\displaystyle {\cal {P}}}$ of ${\displaystyle [a,b]}$ is a finite sequence

${\displaystyle a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!}$

This partitions the interval ${\displaystyle [a,b]}$ into ${\displaystyle n}$ sub-intervals ${\displaystyle [x_{i-1},x_{i}]}$ indexed by ${\displaystyle i=1,\ldots ,n}$, each of which is "tagged" with a distinguished point ${\displaystyle t_{i}\in [x_{i-1},x_{i}]}$. For a function ${\displaystyle f}$ bounded on ${\displaystyle [a,b]}$, we define the Riemann sum of ${\displaystyle f}$ with respect to tagged partition ${\displaystyle {\cal {P}}}$ as

${\displaystyle \sum _{i=1}^{n}f(t_{i})\Delta _{i},}$

where ${\displaystyle \Delta _{i}=x_{i}-x_{i-1}}$ is the width of sub-interval ${\displaystyle i}$. Thus, each term of the sum is the area of a rectangle with height equal to the function value at the distinguished point of the given sub-interval, and width the same as the sub-interval width. The mesh of such a tagged partition is the width of the largest sub-interval formed by the partition, ${\textstyle \|\Delta _{i}\|=\max _{i=1,\ldots ,n}\Delta _{i}}$. We say that the Riemann integral of ${\displaystyle f}$ on ${\displaystyle [a,b]}$ is ${\displaystyle S}$ if for any ${\displaystyle \varepsilon >0}$ there exists ${\displaystyle \delta >0}$ such that, for any tagged partition ${\displaystyle {\cal {P}}}$ with mesh ${\displaystyle \|\Delta _{i}\|<\delta }$, we have

${\displaystyle \left|S-\sum _{i=1}^{n}f(t_{i})\Delta _{i}\right|<\varepsilon .}$

This is sometimes denoted ${\textstyle {\mathcal {R}}\int _{a}^{b}f=S}$. When the chosen tags give the maximum (respectively, minimum) value of each interval, the Riemann sum is known as the upper (respectively, lower) Darboux sum. A function is Darboux integrable if the upper and lower Darboux sums can be made to be arbitrarily close to each other for a sufficiently small mesh. Although this definition gives the Darboux integral the appearance of being a special case of the Riemann integral, they are, in fact, equivalent, in the sense that a function is Darboux integrable if and only if it is Riemann integrable, and the values of the integrals are equal. In fact, calculus and real analysis textbooks often conflate the two, introducing the definition of the Darboux integral as that of the Riemann integral, due to the slightly easier to apply definition of the former.

The fundamental theorem of calculus asserts that integration and differentiation are inverse operations in a certain sense.

Lebesgue integration and measure

Main article: Lebesgue integral

Lebesgue integration is a mathematical construction that extends the integral to a larger class of functions; it also extends the domains on which these functions can be defined. The concept of a measure, an abstraction of length, area, or volume, is central to Lebesgue integral probability theory.

Distributions

Main article: Distribution (mathematics)

Distributions (or generalized functions) are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative.

Relation to complex analysis

Real analysis is an area of analysis that studies concepts such as sequences and their limits, continuity, differentiation, integration and sequences of functions. By definition, real analysis focuses on the real numbers, often including positive and negative infinity to form the extended real line. Real analysis is closely related to complex analysis, which studies broadly the same properties of complex numbers. In complex analysis, it is natural to define differentiation via holomorphic functions, which have a number of useful properties, such as repeated differentiability, expressibility as power series, and satisfying the Cauchy integral formula.

In real analysis, it is usually more natural to consider differentiable, smooth, or harmonic functions, which are more widely applicable, but may lack some more powerful properties of holomorphic functions. However, results such as the fundamental theorem of algebra are simpler when expressed in terms of complex numbers.

Techniques from the theory of analytic functions of a complex variable are often used in real analysis – such as evaluation of real integrals by residue calculus.

Important results

Important results include the Bolzano–Weierstrass and Heine–Borel theorems, the intermediate value theorem and mean value theorem, Taylor's theorem, the fundamental theorem of calculus, the Arzelà-Ascoli theorem, the Stone-Weierstrass theorem, Fatou's lemma, and the monotone convergence and dominated convergence theorems.

Generalizations and related areas of mathematics

Various ideas from real analysis can be generalized from the real line to broader or more abstract contexts. These generalizations link real analysis to other disciplines and subdisciplines. For instance, generalization of ideas like continuous functions and compactness from real analysis to metric spaces and topological spaces connects real analysis to the field of general topology, while generalization of finite-dimensional Euclidean spaces to infinite-dimensional analogs led to the concepts of Banach spaces and Hilbert spaces and, more generally to functional analysis. Georg Cantor's investigation of sets and sequence of real numbers, mappings between them, and the foundational issues of real analysis gave birth to naive set theory. The study of issues of convergence for sequences of functions eventually gave rise to Fourier analysis as a subdiscipline of mathematical analysis. Investigation of the consequences of generalizing differentiability from functions of a real variable to ones of a complex variable gave rise to the concept of holomorphic functions and the inception of complex analysis as another distinct subdiscipline of analysis. On the other hand, the generalization of integration from the Riemann sense to that of Lebesgue led to the formulation of the concept of abstract measure spaces, a fundamental concept in measure theory. Finally, the generalization of integration from the real line to curves and surfaces in higher dimensional space brought about the study of vector calculus, whose further generalization and formalization played an important role in the evolution of the concepts of differential forms and smooth (differentiable) manifolds in differential geometry and other closely related areas of geometry and topology.

Kessler syndrome

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Kessler_syndrome

Space debris populations seen from outside geosynchronous orbit (GSO). There are two primary debris fields: the ring of objects in GSO and the cloud of objects in low Earth orbit (LEO).

The Kessler syndrome (also called the Kessler effect, collisional cascading, or ablation cascade), proposed by NASA scientist Donald J. Kessler in 1978, is a scenario in which the density of objects in low Earth orbit (LEO) due to space pollution is high enough that collisions between objects could cause a cascade in which each collision generates space debris that increases the likelihood of further collisions. In 2009 Kessler wrote that modeling results had concluded that the debris environment was already unstable, "such that any attempt to achieve a growth-free small debris environment by eliminating sources of past debris will likely fail because fragments from future collisions will be generated faster than atmospheric drag will remove them". One implication is that the distribution of debris in orbit could render space activities and the use of satellites in specific orbital ranges difficult for many generations.

History

NORAD, Gabbard and Kessler

Willy Ley predicted in 1960 that "In time, a number of such accidentally too-lucky shots will accumulate in space and will have to be removed when the era of manned space flight arrives". After the launch of Sputnik 1 in 1957, the North American Aerospace Defense Command (NORAD) began compiling a database (the Space Object Catalog) of all known rocket launches and objects reaching orbit: satellites, protective shields and upper- and lower-stage booster rockets. NASA later published modified versions of the database in two-line element set, and during the early 1980s the CelesTrak bulletin board system re-published them.

Gabbard diagram of almost 300 pieces of debris from the disintegration of the five-month-old third stage of the Chinese Long March 4 booster on 11 March 2000

The trackers who fed the database were aware of other objects in orbit, many of which were the result of in-orbit explosions. Some were deliberately caused during the 1960s anti-satellite weapon (ASAT) testing, and others were the result of rocket stages blowing up in orbit as leftover propellant expanded and ruptured their tanks. To improve tracking, NORAD employee John Gabbard kept a separate database. Studying the explosions, Gabbard developed a technique for predicting the orbital paths of their products, and Gabbard diagrams (or plots) are now widely used. These studies were used to improve the modeling of orbital evolution and decay.

When the NORAD database became publicly available during the 1970s, NASA scientist Donald J. Kessler applied the technique developed for the asteroid-belt study to the database of known objects. In June 1978, Kessler and Burton Cour-Palais co-authored "Collision Frequency of Artificial Satellites: The Creation of a Debris Belt", demonstrating that the process controlling asteroid evolution would cause a similar collision process in LEO in decades rather than billions of years. They concluded that by about 2000, space debris would outpace micrometeoroids as the primary ablative risk to orbiting spacecraft.

At the time, it was widely thought that drag from the upper atmosphere would de-orbit debris faster than it was created. However, Gabbard was aware that the number and type of objects in space were under-represented in the NORAD data and was familiar with its behavior. In an interview shortly after the publication of the 1978 paper, Gabbard coined the term Kessler syndrome to refer to the accumulation of debris; it became widely used after its appearance in a 1982 Popular Science article, which won the Aviation-Space Writers Association 1982 National Journalism Award.

Follow-up studies

Baker–Nunn cameras were widely used to study space debris.

The lack of hard data about space debris prompted a series of studies to better characterize the LEO environment. In October 1979, NASA provided Kessler with funding for further studies. Several approaches were used by these studies.

Optical telescopes and short-wavelength radar were used to measure the number and size of space objects, and these measurements demonstrated that the published population count was at least 50% too low. Before this, it was believed that the NORAD database accounted for the majority of large objects in orbit. Some objects (typically, US military spacecraft) were found to be omitted from the NORAD list, and others were not included because they were considered unimportant. The list could not easily account for objects under 20 cm (8 in) in size—in particular, debris from exploding rocket stages and several 1960s anti-satellite tests.

Returned spacecraft were microscopically examined for small impacts, and sections of Skylab and the Apollo Command/Service Module which were recovered were found to be pitted. Each study indicated that the debris flux was higher than expected and debris was the primary source of micrometeoroids and orbital debris collisions in space. LEO already demonstrated the Kessler syndrome.

In 1978, Kessler found that 42 percent of cataloged debris was the result of 19 events, primarily explosions of spent rocket stages (especially US Delta rockets). He discovered this by first identifying those launches that were described as having a large number of objects associated with a payload, then researching the literature to determine the rockets used in the launch. In 1979, this finding resulted in establishment of the NASA Orbital Debris Program after a briefing to NASA senior management, overturning the previously held belief that most unknown debris was from old ASAT tests, not from US upper stage rocket explosions that could seemingly be easily managed by depleting the unused fuel from the upper stage Delta rocket following the payload injection. Beginning in 1986, when it was discovered that other international agencies were possibly experiencing the same type of problem, NASA expanded its program to include international agencies, the first being the European Space Agency. A number of other Delta components in orbit (Delta was a workhorse of the US space program) had not yet exploded.

A new Kessler syndrome

During the 1980s, the US Air Force (USAF) conducted an experimental program to determine what would happen if debris collided with satellites or other debris. The study demonstrated that the process differed from micrometeoroid collisions, with large chunks of debris created which would become collision threats.

In 1991, Kessler published "Collisional cascading: The limits of population growth in low Earth orbit" with the best data then available. Citing the USAF conclusions about creation of debris, he wrote that although almost all debris objects (such as paint flecks) were lightweight, most of its mass was in debris about 1 kg (2 lb 3 oz) or heavier. This mass could destroy a spacecraft on impact, creating more debris in the critical-mass area. According to the National Academy of Sciences:

A 1 kg object impacting at 10 km/s, for example, is probably capable of catastrophically breaking up a 1,000 kg spacecraft if it strikes a high-density element in the spacecraft. In such a breakup, numerous fragments larger than 1 kg would be created.

Kessler's analysis divided the problem into three parts. With a low-enough density, the addition of debris by impacts is slower than their decay rate and the problem is not significant. Beyond that is a critical density, where additional debris leads to additional collisions. At densities beyond this critical mass production exceeds decay, leading to a cascading chain reaction reducing the orbiting population to small objects (several centimeters in size) and increasing the hazard of space activity. This chain reaction is known as the Kessler syndrome.

In an early 2009 historical overview, Kessler summed up the situation:

Aggressive space activities without adequate safeguards could significantly shorten the time between collisions and produce an intolerable hazard to future spacecraft. Some of the most environmentally dangerous activities in space include large constellations such as those initially proposed by the Strategic Defense Initiative in the mid-1980s, large structures such as those considered in the late-1970s for building solar power stations in Earth orbit, and anti-satellite warfare using systems tested by the USSR, the US, and China over the past 30 years. Such aggressive activities could set up a situation where a single satellite failure could lead to cascading failures of many satellites in a period much shorter than years.

Anti-satellite missile tests

Main article: Anti-satellite weapon

In 1985, the first anti-satellite (ASAT) missile was used in the destruction of a satellite. The American 1985 ASM-135 ASAT test was carried out, in which the Solwind P78-1 satellite flying at an altitude of 555 kilometres was struck by the 14 kilogram payload at a velocity of 24,000 kilometres per hour (15,000 mph; 6.7 km/s). When NASA learned of U.S. Air Force plans for the Solwind ASAT test, they modeled the effects of the test and determined that debris produced by the collision would still be in orbit late into the 1990s. It would force NASA to enhance debris shielding for its planned space station.

On 11 January 2007, China conducted an anti-satellite missile test in which one of their FY-1C weather satellites was chosen as the target. The collision occurred at an altitude of 865 kilometres, when the satellite with a mass of 750 kilograms was struck in a head-on-collision by a kinetic payload traveling with a speed of 8 km/s (18,000 mph) in the opposite direction. The resulting debris orbits the Earth with a mean altitude above 850 kilometres, and will likely remain in orbit for decades or centuries.

The destruction of the Kosmos 1408 satellite by a Russian ASAT missile on November 15, 2021, has created a large debris cloud, with 1500 pieces of debris being tracked and an estimated hundreds of thousands of pieces too small to track. Since the satellite was in a polar orbit, and its debris has spread out between the altitudes of 300 km and 1000 km, it could potentially collide with any LEO satellite, including the International Space Station and the Chinese Space Station (Tiangong).

Debris generation and destruction

Main article: Space debris

Every satellite, space probe, and crewed mission has the potential to produce space debris. The theoretical cascading Kessler syndrome becomes more likely as satellites in orbit increase in number. As of 2014, there were about 2,000 commercial and government satellites orbiting the earth, and as of 2021 more than 4000. It is estimated that there are 600,000 pieces of space junk ranging from 1 to 10 cm (1⁄2 to 4 in), and 23,000 larger than that. On average one satellite is destroyed by collision with space junk each year. As of 2009 there had been four collisions between catalogued objects, including a collision between two satellites in 2009.

Orbital decay is much slower at altitudes where atmospheric drag is insignificant. Slight atmospheric drag, lunar perturbation, and solar wind drag can gradually bring debris down to lower altitudes where fragments finally re-enter, but this process can take millennia at very high altitudes.

Implications

Image made from models used to track debris in Earth orbit as of July 2009

The Kessler syndrome is troublesome because of the domino effect and feedback runaway wherein impacts between objects of sizable mass spall off debris from the force of the collision. The fragments can then hit other objects, producing even more space debris: if a large enough collision or explosion were to occur, such as between a space station and a defunct satellite, or as the result of hostile actions in space, then the resulting debris cascade could make prospects for long-term viability of satellites in particular low Earth orbits extremely low. However, even a catastrophic Kessler scenario at LEO would pose minimal risk for launches continuing past LEO, or satellites travelling at medium Earth orbit (MEO) or geosynchronous orbit (GEO). The catastrophic scenarios predict an increase in the number of collisions per year, as opposed to a physically impassable barrier to space exploration that occurs in higher orbits.

Avoidance and reduction

Designers of a new vehicle or satellite are frequently required by the ITU to demonstrate that it can be safely disposed of at the end of its life, for example by use of a controlled atmospheric reentry system or a boost into a graveyard orbit. For US launches or satellites that will have broadcast to US territories—in order to obtain a license to provide telecommunications services in the United States—the Federal Communications Commission (FCC) required all geostationary satellites launched after 18 March 2002 to commit to moving to a graveyard orbit at the end of their operational life. US government regulations similarly require a plan to dispose of satellites after the end of their mission: atmospheric re-entry, movement to a storage orbit, or direct retrieval.

A proposed energy-efficient means of deorbiting a spacecraft from MEO is to shift it to an orbit in an unstable resonance with the Sun or Moon that speeds up orbital decay.

One technology proposed to help deal with fragments from 1 to 10 cm (1⁄2 to 4 in) in size is the laser broom, a proposed multimegawatt land-based laser that could deorbit debris: the side of the debris hit by the laser would ablate and create a thrust that would change the eccentricity of the remains of the fragment until it would re-enter and be destroyed harmlessly.

Potential triggers

The Envisat satellite is a large, inactive satellite with a mass of 8,211 kg (18,102 lb) that orbits at 785 km (488 mi), an altitude where the debris environment is the greatest—two catalogued objects can be expected to pass within about 200 m (660 ft) of Envisat every year—and likely to increase. Don Kessler predicted in 2012 that it could easily become a major debris contributor from a collision during the next 150 years that it will remain in orbit.

SpaceX's Starlink program raises concern among many experts about significantly worsening the possibility of Kessler Syndrome due to the large number of satellites the program aims to place in LEO, as the program's goal will more than double the satellites currently in LEO. In response to these concerns, SpaceX said that a large part of Starlink satellites are launched at a lower altitude of 550 km to achieve lower latency (versus 1,150 kilometers as originally planned), and failed satellites or debris are thus expected to deorbit within five years even without propulsion, due to atmospheric drag. 

In fiction

• Manga and anime Planetes is about the crew of Space Debris Section, whose purpose is to prevent the damage or destruction of satellites, space stations and spacecraft from collision with debris.
• The 2013 film Gravity features a Kessler syndrome catastrophe as the inciting incident of the story, when Russia shoots down an old satellite.
• Neal Stephenson's 2015 novel Seveneves begins with the unexplained explosion of the Moon into seven large pieces, the subsequent creation of a cloud of debris by Kessler syndrome collisions, and the eventual bombardment of Earth's surface by lunar meteoroids.
• In Ace Combat 7: Skies Unknown, the protagonist's homeland of Osea and its enemy Erusea coincidentally launch simultaneous antisatellite attacks during a mission to attack the enemy capital; the resulting debris creates a cascading disruption of communications that causes chaos on the continent Erusea is on.
• In Battlefield 2042, a Kessler syndrome leads to the destruction of many satellites orbiting earth, precipitating the conflicts of the game.