
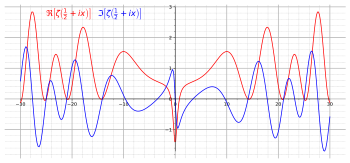

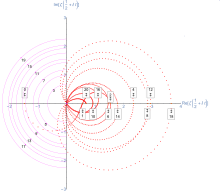
The curve starts for t = -30 at ζ(1/2 - 30 i) = -0.12 + 0.58 i, and end symmetrically below the starting point at ζ(1/2 + 30 i) = -0.12 - 0.58 i.
Six zeros of ζ(s) are found along the trajectory when the origin (0,0) is traversed, corresponding to imaginary parts Im(s) = ±14.135, ±21.022 and ±25.011.
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics.[2] It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann (1859), after whom it is named.
The Riemann hypothesis and some of its generalizations, along with Goldbach's conjecture and the twin prime conjecture, make up Hilbert's eighth problem in David Hilbert's list of twenty-three unsolved problems; it is also one of the Clay Mathematics Institute's Millennium Prize Problems, which offers a million dollars to anyone who solves any of them. The name is also used for some closely related analogues, such as the Riemann hypothesis for curves over finite fields.
The Riemann zeta function ζ(s) is a function whose argument s may be any complex number other than 1, and whose values are also complex. It has zeros at the negative even integers; that is, ζ(s) = 0 when s is one of −2, −4, −6, .... These are called its trivial zeros. The zeta function is also zero for other values of s, which are called nontrivial zeros. The Riemann hypothesis is concerned with the locations of these nontrivial zeros, and states that:
The real part of every nontrivial zero of the Riemann zeta function is 1/2.
Thus, if the hypothesis is correct, all the nontrivial zeros lie on the critical line consisting of the complex numbers 1/2 + i t, where t is a real number and i is the imaginary unit.
Riemann zeta function
The Riemann zeta function is defined for complex s with real part greater than 1 by the absolutely convergent infinite series
Leonhard Euler already considered this series in the 1730s for real values of s, in conjunction with his solution to the Basel problem. He also proved that it equals the Euler product
where the infinite product extends over all prime numbers p.[3]
The Riemann hypothesis discusses zeros outside the region of convergence of this series and Euler product. To make sense of the hypothesis, it is necessary to analytically continue the function to obtain a form that is valid for all complex s. Because the zeta function is meromorphic, all choices of how to perform this analytic continuation will lead to the same result, by the identity theorem. A first step in this continuation observes that the series for the zeta function and the Dirichlet eta function satisfy the relation
within the region of convergence for both series. However, the zeta function series on the right converges not just when the real part of s is greater than one, but more generally whenever s has positive real part. Thus, the zeta function can be redefined as , extending it from Re(s) > 1 to a larger domain: Re(s) > 0, except for the points where is zero. These are the points where can be any nonzero integer; the zeta function can be extended to these values too by taking limits (see Dirichlet eta function § Landau's problem with ζ(s) = η(s)/0 and solutions), giving a finite value for all values of s with positive real part except for the simple pole at s = 1.
In the strip 0 < Re(s) < 1 this extension of the zeta function satisfies the functional equation
One may then define ζ(s) for all remaining nonzero complex numbers s (Re(s) ≤ 0 and s ≠ 0) by applying this equation outside the strip, and letting ζ(s) equal the right-hand side of the equation whenever s has non-positive real part (and s ≠ 0).
If s is a negative even integer then ζ(s) = 0 because the factor sin(πs/2) vanishes; these are the trivial zeros of the zeta function. (If s is a positive even integer this argument does not apply because the zeros of the sine function are cancelled by the poles of the gamma function as it takes negative integer arguments.)
The value ζ(0) = −1/2 is not determined by the functional equation, but is the limiting value of ζ(s) as s approaches zero. The functional equation also implies that the zeta function has no zeros with negative real part other than the trivial zeros, so all non-trivial zeros lie in the critical strip where s has real part between 0 and 1.
Origin
... es ist sehr wahrscheinlich, dass alle Wurzeln reell sind. Hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrlich schien.
... it is very probable that all roots are real. Of course one would wish for a rigorous proof here; I have for the time being, after some fleeting vain attempts, provisionally put aside the search for this, as it appears dispensable for the immediate objective of my investigation.— Riemann's statement of the Riemann hypothesis, from (Riemann 1859). (He was discussing a version of the zeta function, modified so that its roots (zeros) are real rather than on the critical line.)
At the death of Riemann, a note was found among his papers, saying "These properties of ζ(s) (the function in question) are deduced from an expression of it which, however, I did not succeed in simplifying enough to publish it." We still have not the slightest idea of what the expression could be. As to the properties he simply enunciated, some thirty years elapsed before I was able to prove all of them but one [the Riemann Hypothesis itself].
— Jacques Hadamard, The Mathematician's Mind, VIII. Paradoxical Cases of Intuition
Riemann's original motivation for studying the zeta function and its zeros was their occurrence in his explicit formula for the number of primes π(x) less than or equal to a given number x, which he published in his 1859 paper "On the Number of Primes Less Than a Given Magnitude". His formula was given in terms of the related function
which counts the primes and prime powers up to x, counting a prime power pn as 1⁄n. The number of primes can be recovered from this function by using the Möbius inversion formula,
where μ is the Möbius function. Riemann's formula is then
where the sum is over the nontrivial zeros of the zeta function and where Π0 is a slightly modified version of Π that replaces its value at its points of discontinuity by the average of its upper and lower limits:
The summation in Riemann's formula is not absolutely convergent, but may be evaluated by taking the zeros ρ in order of the absolute value of their imaginary part. The function li occurring in the first term is the (unoffset) logarithmic integral function given by the Cauchy principal value of the divergent integral
The terms li(xρ) involving the zeros of the zeta function need some care in their definition as li has branch points at 0 and 1, and are defined (for x > 1) by analytic continuation in the complex variable ρ in the region Re(ρ) > 0, i.e. they should be considered as Ei(ρ log x). The other terms also correspond to zeros: the dominant term li(x) comes from the pole at s = 1, considered as a zero of multiplicity −1, and the remaining small terms come from the trivial zeros. For some graphs of the sums of the first few terms of this series see Riesel & Göhl (1970) or Zagier (1977).
This formula says that the zeros of the Riemann zeta function control the oscillations of primes around their "expected" positions. Riemann knew that the non-trivial zeros of the zeta function were symmetrically distributed about the line s = 1/2 + it, and he knew that all of its non-trivial zeros must lie in the range 0 ≤ Re(s) ≤ 1. He checked that a few of the zeros lay on the critical line with real part 1/2 and suggested that they all do; this is the Riemann hypothesis.
The result has caught the imagination of most mathematicians because it is so unexpected, connecting two seemingly unrelated areas in mathematics; namely, number theory, which is the study of the discrete, and complex analysis, which deals with continuous processes. (Burton 2006, p. 376)
Consequences
The practical uses of the Riemann hypothesis include many propositions known to be true under the Riemann hypothesis, and some that can be shown to be equivalent to the Riemann hypothesis.
Distribution of prime numbers
Riemann's explicit formula for the number of primes less than a given number in terms of a sum over the zeros of the Riemann zeta function says that the magnitude of the oscillations of primes around their expected position is controlled by the real parts of the zeros of the zeta function. In particular the error term in the prime number theorem is closely related to the position of the zeros. For example, if β is the upper bound of the real parts of the zeros, then It is already known that 1/2 ≤ β ≤ 1.
Von Koch (1901) proved that the Riemann hypothesis implies the "best possible" bound for the error of the prime number theorem. A precise version of Koch's result, due to Schoenfeld (1976), says that the Riemann hypothesis implies
where is the prime-counting function, is the logarithmic integral function, and is the natural logarithm of x.
Schoenfeld (1976) also showed that the Riemann hypothesis implies
where is Chebyshev's second function.
Dudek (2014) proved that the Riemann hypothesis implies that for all there is a prime satisfying
- .
This is an explicit version of a theorem of Cramér.
Growth of arithmetic functions
The Riemann hypothesis implies strong bounds on the growth of many other arithmetic functions, in addition to the primes counting function above.
One example involves the Möbius function μ. The statement that the equation
is valid for every s with real part greater than 1/2, with the sum on the right hand side converging, is equivalent to the Riemann hypothesis. From this we can also conclude that if the Mertens function is defined by
then the claim that
for every positive ε is equivalent to the Riemann hypothesis (J. E. Littlewood, 1912; see for instance: paragraph 14.25 in Titchmarsh (1986)). (For the meaning of these symbols, see Big O notation.) The determinant of the order n Redheffer matrix is equal to M(n), so the Riemann hypothesis can also be stated as a condition on the growth of these determinants. Littlewood's result has been improved several times since then, by Edmund Landau, Edward Charles Titchmarsh, Helmut Maier and Hugh Montgomery, and Kannan Soundararajan. Soundararajan's result is that
The Riemann hypothesis puts a rather tight bound on the growth of M, since Odlyzko & te Riele (1985) disproved the slightly stronger Mertens conjecture
Another closely related result is due to Björner (2011), that the Riemann hypothesis is equivalent to the statement that the Euler characteristic of the simplicial complex determined by the lattice of integers under divisibility is for all (see incidence algebra).
The Riemann hypothesis is equivalent to many other conjectures about the rate of growth of other arithmetic functions aside from μ(n). A typical example is Robin's theorem, which states that if σ(n) is the sigma function, given by
then
for all n > 5040 if and only if the Riemann hypothesis is true, where γ is the Euler–Mascheroni constant.
A related bound was given by Jeffrey Lagarias in 2002, who proved that the Riemann hypothesis is equivalent to the statement that:
for every natural number n > 1, where is the nth harmonic number.
The Riemann hypothesis is also true if and only if the inequality
is true for all n ≥ p120569# where φ(n) is Euler's totient function and p120569# is the product of the first 120569 primes.
Another example was found by Jérôme Franel, and extended by Landau (see Franel & Landau (1924)). The Riemann hypothesis is equivalent to several statements showing that the terms of the Farey sequence are fairly regular. One such equivalence is as follows: if Fn is the Farey sequence of order n, beginning with 1/n and up to 1/1, then the claim that for all ε > 0
is equivalent to the Riemann hypothesis. Here
is the number of terms in the Farey sequence of order n.
For an example from group theory, if g(n) is Landau's function given by the maximal order of elements of the symmetric group Sn of degree n, then Massias, Nicolas & Robin (1988) showed that the Riemann hypothesis is equivalent to the bound
for all sufficiently large n.
Lindelöf hypothesis and growth of the zeta function
The Riemann hypothesis has various weaker consequences as well; one is the Lindelöf hypothesis on the rate of growth of the zeta function on the critical line, which says that, for any ε > 0,
as .
The Riemann hypothesis also implies quite sharp bounds for the growth rate of the zeta function in other regions of the critical strip. For example, it implies that
so the growth rate of ζ(1+it) and its inverse would be known up to a factor of 2.
Large prime gap conjecture
The prime number theorem implies that on average, the gap between the prime p and its successor is log p. However, some gaps between primes may be much larger than the average. Cramér proved that, assuming the Riemann hypothesis, every gap is O(√p log p). This is a case in which even the best bound that can be proved using the Riemann hypothesis is far weaker than what seems true: Cramér's conjecture implies that every gap is O((log p)2), which, while larger than the average gap, is far smaller than the bound implied by the Riemann hypothesis. Numerical evidence supports Cramér's conjecture.
Analytic criteria equivalent to the Riemann hypothesis
Many statements equivalent to the Riemann hypothesis have been found, though so far none of them have led to much progress in proving (or disproving) it. Some typical examples are as follows. (Others involve the divisor function σ(n).)
The Riesz criterion was given by Riesz (1916), to the effect that the bound
holds for all ε > 0 if and only if the Riemann hypothesis holds. See also the Hardy–Littlewood criterion.
Nyman (1950) proved that the Riemann hypothesis is true if and only if the space of functions of the form
where ρ(z) is the fractional part of z, 0 ≤ θν ≤ 1, and
- ,
is dense in the Hilbert space L2(0,1) of square-integrable functions on the unit interval. Beurling (1955) extended this by showing that the zeta function has no zeros with real part greater than 1/p if and only if this function space is dense in Lp(0,1). This Nyman-Beurling criterion was strengthened by Baez-Duarte to the case where .
Salem (1953) showed that the Riemann hypothesis is true if and only if the integral equation
has no non-trivial bounded solutions for .
Weil's criterion is the statement that the positivity of a certain function is equivalent to the Riemann hypothesis. Related is Li's criterion, a statement that the positivity of a certain sequence of numbers is equivalent to the Riemann hypothesis.
Speiser (1934) proved that the Riemann hypothesis is equivalent to the statement that , the derivative of , has no zeros in the strip
That has only simple zeros on the critical line is equivalent to its derivative having no zeros on the critical line.
The Farey sequence provides two equivalences, due to Jerome Franel and Edmund Landau in 1924.
The de Bruijn–Newman constant denoted by Λ and named after Nicolaas Govert de Bruijn and Charles M. Newman, is defined as the unique real number such that the function
- ,
that is parametrised by a real parameter λ, has a complex variable z and is defined using a super-exponentially decaying function
- .
has only real zeros if and only if λ ≥ Λ. Since the Riemann hypothesis is equivalent to the claim that all the zeroes of H(0, z) are real, the Riemann hypothesis is equivalent to the conjecture that . Brad Rodgers and Terence Tao discovered the equivalence is actually by proving zero to be the lower bound of the constant. Proving zero is also the upper bound would therefore prove the Riemann hypothesis. As of April 2020 the upper bound is .
Consequences of the generalized Riemann hypothesis
Several applications use the generalized Riemann hypothesis for Dirichlet L-series or zeta functions of number fields rather than just the Riemann hypothesis. Many basic properties of the Riemann zeta function can easily be generalized to all Dirichlet L-series, so it is plausible that a method that proves the Riemann hypothesis for the Riemann zeta function would also work for the generalized Riemann hypothesis for Dirichlet L-functions. Several results first proved using the generalized Riemann hypothesis were later given unconditional proofs without using it, though these were usually much harder. Many of the consequences on the following list are taken from Conrad (2010).
- In 1913, Grönwall showed that the generalized Riemann hypothesis implies that Gauss's list of imaginary quadratic fields with class number 1 is complete, though Baker, Stark and Heegner later gave unconditional proofs of this without using the generalized Riemann hypothesis.
- In 1917, Hardy and Littlewood showed that the generalized Riemann hypothesis implies a conjecture of Chebyshev that which says that primes 3 mod 4 are more common than primes 1 mod 4 in some sense. (For related results, see Prime number theorem § Prime number race.)
- In 1923, Hardy and Littlewood showed that the generalized Riemann hypothesis implies a weak form of the Goldbach conjecture for odd numbers: that every sufficiently large odd number is the sum of three primes, though in 1937 Vinogradov gave an unconditional proof. In 1997 Deshouillers, Effinger, te Riele, and Zinoviev showed that the generalized Riemann hypothesis implies that every odd number greater than 5 is the sum of three primes. In 2013 Harald Helfgott proved the ternary Goldbach conjecture without the GRH dependence, subject to some extensive calculations completed with the help of David J. Platt.
- In 1934, Chowla showed that the generalized Riemann hypothesis implies that the first prime in the arithmetic progression a mod m is at most Km2log(m)2 for some fixed constant K.
- In 1967, Hooley showed that the generalized Riemann hypothesis implies Artin's conjecture on primitive roots.
- In 1973, Weinberger showed that the generalized Riemann hypothesis implies that Euler's list of idoneal numbers is complete.
- Weinberger (1973) showed that the generalized Riemann hypothesis for the zeta functions of all algebraic number fields implies that any number field with class number 1 is either Euclidean or an imaginary quadratic number field of discriminant −19, −43, −67, or −163.
- In 1976, G. Miller showed that the generalized Riemann hypothesis implies that one can test if a number is prime in polynomial time via the Miller test. In 2002, Manindra Agrawal, Neeraj Kayal and Nitin Saxena proved this result unconditionally using the AKS primality test.
- Odlyzko (1990) discussed how the generalized Riemann hypothesis can be used to give sharper estimates for discriminants and class numbers of number fields.
- Ono & Soundararajan (1997) showed that the generalized Riemann hypothesis implies that Ramanujan's integral quadratic form x2 + y2 + 10z2 represents all integers that it represents locally, with exactly 18 exceptions.
- In 2021, Alexander (Alex) Dunn and Maksym Radziwill proved Patterson's conjecture under the assumption of the GRH.
Excluded middle
Some consequences of the RH are also consequences of its negation, and are thus theorems. In their discussion of the Hecke, Deuring, Mordell, Heilbronn theorem, Ireland & Rosen (1990, p. 359) say
The method of proof here is truly amazing. If the generalized Riemann hypothesis is true, then the theorem is true. If the generalized Riemann hypothesis is false, then the theorem is true. Thus, the theorem is true!! (punctuation in original)
Care should be taken to understand what is meant by saying the generalized Riemann hypothesis is false: one should specify exactly which class of Dirichlet series has a counterexample.
Littlewood's theorem
This concerns the sign of the error in the prime number theorem. It has been computed that π(x) < li(x) for all x ≤ 1025 (see this table), and no value of x is known for which π(x) > li(x).
In 1914 Littlewood proved that there are arbitrarily large values of x for which
and that there are also arbitrarily large values of x for which
Thus the difference π(x) − li(x) changes sign infinitely many times. Skewes' number is an estimate of the value of x corresponding to the first sign change.
Littlewood's proof is divided into two cases: the RH is assumed false (about half a page of Ingham 1932, Chapt. V), and the RH is assumed true (about a dozen pages). Stanisław Knapowski (1962) followed this up with a paper on the number of times changes sign in the interval .
Gauss's class number conjecture
This is the conjecture (first stated in article 303 of Gauss's Disquisitiones Arithmeticae) that there are only finitely many imaginary quadratic fields with a given class number. One way to prove it would be to show that as the discriminant D → −∞ the class number h(D) → ∞.
The following sequence of theorems involving the Riemann hypothesis is described in Ireland & Rosen 1990, pp. 358–361:
Theorem (Hecke; 1918) — Let D < 0 be the discriminant of an imaginary quadratic number field K. Assume the generalized Riemann hypothesis for L-functions of all imaginary quadratic Dirichlet characters. Then there is an absolute constant C such that
Theorem (Deuring; 1933) — If the RH is false then h(D) > 1 if |D| is sufficiently large.
Theorem (Mordell; 1934) — If the RH is false then h(D) → ∞ as D → −∞.
Theorem (Heilbronn; 1934) — If the generalized RH is false for the L-function of some imaginary quadratic Dirichlet character then h(D) → ∞ as D → −∞.
(In the work of Hecke and Heilbronn, the only L-functions that occur are those attached to imaginary quadratic characters, and it is only for those L-functions that GRH is true or GRH is false is intended; a failure of GRH for the L-function of a cubic Dirichlet character would, strictly speaking, mean GRH is false, but that was not the kind of failure of GRH that Heilbronn had in mind, so his assumption was more restricted than simply GRH is false.)
In 1935, Carl Siegel later strengthened the result without using RH or GRH in any way.
Growth of Euler's totient
In 1983 J. L. Nicolas proved that
Generalizations and analogs
Dirichlet L-series and other number fields
The Riemann hypothesis can be generalized by replacing the Riemann zeta function by the formally similar, but much more general, global L-functions. In this broader setting, one expects the non-trivial zeros of the global L-functions to have real part 1/2. It is these conjectures, rather than the classical Riemann hypothesis only for the single Riemann zeta function, which account for the true importance of the Riemann hypothesis in mathematics.
The generalized Riemann hypothesis extends the Riemann hypothesis to all Dirichlet L-functions. In particular it implies the conjecture that Siegel zeros (zeros of L-functions between 1/2 and 1) do not exist.
The extended Riemann hypothesis extends the Riemann hypothesis to all Dedekind zeta functions of algebraic number fields. The extended Riemann hypothesis for abelian extension of the rationals is equivalent to the generalized Riemann hypothesis. The Riemann hypothesis can also be extended to the L-functions of Hecke characters of number fields.
The grand Riemann hypothesis extends it to all automorphic zeta functions, such as Mellin transforms of Hecke eigenforms.
Function fields and zeta functions of varieties over finite fields
Artin (1924) introduced global zeta functions of (quadratic) function fields and conjectured an analogue of the Riemann hypothesis for them, which has been proved by Hasse in the genus 1 case and by Weil (1948) in general. For instance, the fact that the Gauss sum, of the quadratic character of a finite field of size q (with q odd), has absolute value is actually an instance of the Riemann hypothesis in the function field setting. This led Weil (1949) to conjecture a similar statement for all algebraic varieties; the resulting Weil conjectures were proved by Pierre Deligne (1974, 1980).
Arithmetic zeta functions of arithmetic schemes and their L-factors
Arithmetic zeta functions generalise the Riemann and Dedekind zeta functions as well as the zeta functions of varieties over finite fields to every arithmetic scheme or a scheme of finite type over integers. The arithmetic zeta function of a regular connected equidimensional arithmetic scheme of Kronecker dimension n can be factorized into the product of appropriately defined L-factors and an auxiliary factor Jean-Pierre Serre (1969–1970). Assuming a functional equation and meromorphic continuation, the generalized Riemann hypothesis for the L-factor states that its zeros inside the critical strip lie on the central line. Correspondingly, the generalized Riemann hypothesis for the arithmetic zeta function of a regular connected equidimensional arithmetic scheme states that its zeros inside the critical strip lie on vertical lines and its poles inside the critical strip lie on vertical lines . This is known for schemes in positive characteristic and follows from Pierre Deligne (1974, 1980), but remains entirely unknown in characteristic zero.
Selberg zeta functions
Selberg (1956) introduced the Selberg zeta function of a Riemann surface. These are similar to the Riemann zeta function: they have a functional equation, and an infinite product similar to the Euler product but taken over closed geodesics rather than primes. The Selberg trace formula is the analogue for these functions of the explicit formulas in prime number theory. Selberg proved that the Selberg zeta functions satisfy the analogue of the Riemann hypothesis, with the imaginary parts of their zeros related to the eigenvalues of the Laplacian operator of the Riemann surface.
Ihara zeta functions
The Ihara zeta function of a finite graph is an analogue of the Selberg zeta function, which was first introduced by Yasutaka Ihara in the context of discrete subgroups of the two-by-two p-adic special linear group. A regular finite graph is a Ramanujan graph, a mathematical model of efficient communication networks, if and only if its Ihara zeta function satisfies the analogue of the Riemann hypothesis as was pointed out by T. Sunada.
Montgomery's pair correlation conjecture
Montgomery (1973) suggested the pair correlation conjecture that the correlation functions of the (suitably normalized) zeros of the zeta function should be the same as those of the eigenvalues of a random hermitian matrix. Odlyzko (1987) showed that this is supported by large-scale numerical calculations of these correlation functions.
Montgomery showed that (assuming the Riemann hypothesis) at least 2/3 of all zeros are simple, and a related conjecture is that all zeros of the zeta function are simple (or more generally have no non-trivial integer linear relations between their imaginary parts). Dedekind zeta functions of algebraic number fields, which generalize the Riemann zeta function, often do have multiple complex zeros. This is because the Dedekind zeta functions factorize as a product of powers of Artin L-functions, so zeros of Artin L-functions sometimes give rise to multiple zeros of Dedekind zeta functions. Other examples of zeta functions with multiple zeros are the L-functions of some elliptic curves: these can have multiple zeros at the real point of their critical line; the Birch-Swinnerton-Dyer conjecture predicts that the multiplicity of this zero is the rank of the elliptic curve.
Other zeta functions
There are many other examples of zeta functions with analogues of the Riemann hypothesis, some of which have been proved. Goss zeta functions of function fields have a Riemann hypothesis, proved by Sheats (1998). The main conjecture of Iwasawa theory, proved by Barry Mazur and Andrew Wiles for cyclotomic fields, and Wiles for totally real fields, identifies the zeros of a p-adic L-function with the eigenvalues of an operator, so can be thought of as an analogue of the Hilbert–Pólya conjecture for p-adic L-functions.
Attempted proofs
Several mathematicians have addressed the Riemann hypothesis, but none of their attempts has yet been accepted as a proof. Watkins (2021) lists some incorrect solutions.
Operator theory
Hilbert and Pólya suggested that one way to derive the Riemann hypothesis would be to find a self-adjoint operator, from the existence of which the statement on the real parts of the zeros of ζ(s) would follow when one applies the criterion on real eigenvalues. Some support for this idea comes from several analogues of the Riemann zeta functions whose zeros correspond to eigenvalues of some operator: the zeros of a zeta function of a variety over a finite field correspond to eigenvalues of a Frobenius element on an étale cohomology group, the zeros of a Selberg zeta function are eigenvalues of a Laplacian operator of a Riemann surface, and the zeros of a p-adic zeta function correspond to eigenvectors of a Galois action on ideal class groups.
Odlyzko (1987) showed that the distribution of the zeros of the Riemann zeta function shares some statistical properties with the eigenvalues of random matrices drawn from the Gaussian unitary ensemble. This gives some support to the Hilbert–Pólya conjecture.
In 1999, Michael Berry and Jonathan Keating conjectured that there is some unknown quantization of the classical Hamiltonian H = xp so that
The analogy with the Riemann hypothesis over finite fields suggests that the Hilbert space containing eigenvectors corresponding to the zeros might be some sort of first cohomology group of the spectrum Spec (Z) of the integers. Deninger (1998) described some of the attempts to find such a cohomology theory.
Zagier (1981) constructed a natural space of invariant functions on the upper half plane that has eigenvalues under the Laplacian operator that correspond to zeros of the Riemann zeta function—and remarked that in the unlikely event that one could show the existence of a suitable positive definite inner product on this space, the Riemann hypothesis would follow. Cartier (1982) discussed a related example, where due to a bizarre bug a computer program listed zeros of the Riemann zeta function as eigenvalues of the same Laplacian operator.
Schumayer & Hutchinson (2011) surveyed some of the attempts to construct a suitable physical model related to the Riemann zeta function.
Lee–Yang theorem
The Lee–Yang theorem states that the zeros of certain partition functions in statistical mechanics all lie on a "critical line" with their real part equals to 0, and this has led to some speculation about a relationship with the Riemann hypothesis.
Turán's result
Pál Turán (1948) showed that if the functions
Noncommutative geometry
Connes (1999, 2000) has described a relationship between the Riemann hypothesis and noncommutative geometry, and showed that a suitable analog of the Selberg trace formula for the action of the idèle class group on the adèle class space would imply the Riemann hypothesis. Some of these ideas are elaborated in Lapidus (2008).
Hilbert spaces of entire functions
Louis de Branges (1992) showed that the Riemann hypothesis would follow from a positivity condition on a certain Hilbert space of entire functions. However Conrey & Li (2000) showed that the necessary positivity conditions are not satisfied. Despite this obstacle, de Branges has continued to work on an attempted proof of the Riemann hypothesis along the same lines, but this has not been widely accepted by other mathematicians.
Quasicrystals
The Riemann hypothesis implies that the zeros of the zeta function form a quasicrystal, a distribution with discrete support whose Fourier transform also has discrete support. Dyson (2009) suggested trying to prove the Riemann hypothesis by classifying, or at least studying, 1-dimensional quasicrystals.
Arithmetic zeta functions of models of elliptic curves over number fields
When one goes from geometric dimension one, e.g. an algebraic number field, to geometric dimension two, e.g. a regular model of an elliptic curve over a number field, the two-dimensional part of the generalized Riemann hypothesis for the arithmetic zeta function of the model deals with the poles of the zeta function. In dimension one the study of the zeta integral in Tate's thesis does not lead to new important information on the Riemann hypothesis. Contrary to this, in dimension two work of Ivan Fesenko on two-dimensional generalisation of Tate's thesis includes an integral representation of a zeta integral closely related to the zeta function. In this new situation, not possible in dimension one, the poles of the zeta function can be studied via the zeta integral and associated adele groups. Related conjecture of Fesenko (2010) on the positivity of the fourth derivative of a boundary function associated to the zeta integral essentially implies the pole part of the generalized Riemann hypothesis. Suzuki (2011) proved that the latter, together with some technical assumptions, implies Fesenko's conjecture.
Multiple zeta functions
Deligne's proof of the Riemann hypothesis over finite fields used the zeta functions of product varieties, whose zeros and poles correspond to sums of zeros and poles of the original zeta function, in order to bound the real parts of the zeros of the original zeta function. By analogy, Kurokawa (1992) introduced multiple zeta functions whose zeros and poles correspond to sums of zeros and poles of the Riemann zeta function. To make the series converge he restricted to sums of zeros or poles all with non-negative imaginary part. So far, the known bounds on the zeros and poles of the multiple zeta functions are not strong enough to give useful estimates for the zeros of the Riemann zeta function.
Location of the zeros
Number of zeros
The functional equation combined with the argument principle implies that the number of zeros of the zeta function with imaginary part between 0 and T is given by
for s=1/2+iT, where the argument is defined by varying it continuously along the line with Im(s)=T, starting with argument 0 at ∞+iT. This is the sum of a large but well understood term
and a small but rather mysterious term
So the density of zeros with imaginary part near T is about log(T)/2π, and the function S describes the small deviations from this. The function S(t) jumps by 1 at each zero of the zeta function, and for t ≥ 8 it decreases monotonically between zeros with derivative close to −log t.
Trudgian (2014) proved that, if , then
- .
Karatsuba (1996) proved that every interval (T, T+H] for contains at least
points where the function S(t) changes sign.
Selberg (1946) showed that the average moments of even powers of S are given by
This suggests that S(T)/(log log T)1/2 resembles a Gaussian random variable with mean 0 and variance 2π2 (Ghosh (1983) proved this fact). In particular |S(T)| is usually somewhere around (log log T)1/2, but occasionally much larger. The exact order of growth of S(T) is not known. There has been no unconditional improvement to Riemann's original bound S(T)=O(log T), though the Riemann hypothesis implies the slightly smaller bound S(T)=O(log T/log log T). The true order of magnitude may be somewhat less than this, as random functions with the same distribution as S(T) tend to have growth of order about log(T)1/2. In the other direction it cannot be too small: Selberg (1946) showed that S(T) ≠ o((log T)1/3/(log log T)7/3), and assuming the Riemann hypothesis Montgomery showed that S(T) ≠ o((log T)1/2/(log log T)1/2).
Numerical calculations confirm that S grows very slowly: |S(T)| < 1 for T < 280, |S(T)| < 2 for T < 6800000, and the largest value of |S(T)| found so far is not much larger than 3.
Riemann's estimate S(T) = O(log T) implies that the gaps between zeros are bounded, and Littlewood improved this slightly, showing that the gaps between their imaginary parts tend to 0.
Theorem of Hadamard and de la Vallée-Poussin
Hadamard (1896) and de la Vallée-Poussin (1896) independently proved that no zeros could lie on the line Re(s) = 1. Together with the functional equation and the fact that there are no zeros with real part greater than 1, this showed that all non-trivial zeros must lie in the interior of the critical strip 0 < Re(s) < 1. This was a key step in their first proofs of the prime number theorem.
Both the original proofs that the zeta function has no zeros with real part 1 are similar, and depend on showing that if ζ(1+it) vanishes, then ζ(1+2it) is singular, which is not possible. One way of doing this is by using the inequality
for σ > 1, t real, and looking at the limit as σ → 1. This inequality follows by taking the real part of the log of the Euler product to see that
where the sum is over all prime powers pn, so that
which is at least 1 because all the terms in the sum are positive, due to the inequality
Zero-free regions
The most extensive computer search by Platt and Trudgian for counter examples of the Riemann hypothesis has verified it for . Beyond that zero-free regions are known as inequalities concerning σ + i t, which can be zeroes. The oldest version is from De la Vallée-Poussin (1899–1900), who proved there is a region without zeroes that satisfies 1 − σ ≥ C/log(t) for some positive constant C. In other words, zeros cannot be too close to the line σ = 1: there is a zero-free region close to this line. This has been enlarged by several authors using methods such as Vinogradov's mean-value theorem.
The most recent paper by Mossinghoff, Trudgian and Yang is from December 2022 and provides four zero-free regions that improved the previous results of Kevin Ford from 2002, Mossinghoff and Trudgian themselves from 2015 and Pace Nielsen's slight improvement of Ford from October 2022:
- whenever ,
- whenever (largest known region in the bound ),
- whenever (largest known region in the bound ) and
- whenever (largest known region in its own bound)
The paper also has a improvement to the second zero-free region, whose bounds are unknown on account of being merely assumed to be "sufficiently large" to fulfill the requirements of the paper's proof. This region is
.
Zeros on the critical line
Hardy (1914) and Hardy & Littlewood (1921) showed there are infinitely many zeros on the critical line, by considering moments of certain functions related to the zeta function. Selberg (1942) proved that at least a (small) positive proportion of zeros lie on the line. Levinson (1974) improved this to one-third of the zeros by relating the zeros of the zeta function to those of its derivative, and Conrey (1989) improved this further to two-fifths. In 2020, this estimate was extended to five-twelfths by Pratt, Robles, Zaharescu and Zeindler by considering extended mollifiers that can accommodate higher order derivatives of the zeta function and their associated Kloosterman sums.
Most zeros lie close to the critical line. More precisely, Bohr & Landau (1914) showed that for any positive ε, the number of zeroes with real part at least 1/2+ε and imaginary part at between -T and T is . Combined with the facts that zeroes on the critical strip are symmetric about the critical line and that the total number of zeroes in the critical strip is , almost all non-trivial zeroes are within a distance ε of the critical line. Ivić (1985) gives several more precise versions of this result, called zero density estimates, which bound the number of zeros in regions with imaginary part at most T and real part at least 1/2+ε.
Hardy–Littlewood conjectures
In 1914 Godfrey Harold Hardy proved that has infinitely many real zeros.
The next two conjectures of Hardy and John Edensor Littlewood on the distance between real zeros of and on the density of zeros of on the interval for sufficiently large , and and with as small as possible value of , where is an arbitrarily small number, open two new directions in the investigation of the Riemann zeta function:
- For any there exists a lower bound such that for and the interval contains a zero of odd order of the function .
Let be the total number of real zeros, and be the total number of zeros of odd order of the function lying on the interval .
- For any there exists and some , such that for and the inequality is true.
Selberg's zeta function conjecture
Atle Selberg (1942) investigated the problem of Hardy–Littlewood 2 and proved that for any ε > 0 there exists such and c = c(ε) > 0, such that for and the inequality is true. Selberg conjectured that this could be tightened to . A. A. Karatsuba (1984a, 1984b, 1985) proved that for a fixed ε satisfying the condition 0 < ε < 0.001, a sufficiently large T and , , the interval (T, T+H) contains at least cH log(T) real zeros of the Riemann zeta function and therefore confirmed the Selberg conjecture. The estimates of Selberg and Karatsuba can not be improved in respect of the order of growth as T → ∞.
Karatsuba (1992) proved that an analog of the Selberg conjecture holds for almost all intervals (T, T+H], , where ε is an arbitrarily small fixed positive number. The Karatsuba method permits to investigate zeros of the Riemann zeta function on "supershort" intervals of the critical line, that is, on the intervals (T, T+H], the length H of which grows slower than any, even arbitrarily small degree T. In particular, he proved that for any given numbers ε, satisfying the conditions almost all intervals (T, T+H] for contain at least zeros of the function . This estimate is quite close to the one that follows from the Riemann hypothesis.
Numerical calculations
The function
has the same zeros as the zeta function in the critical strip, and is real on the critical line because of the functional equation, so one can prove the existence of zeros exactly on the real line between two points by checking numerically that the function has opposite signs at these points. Usually one writes
where Hardy's Z function and the Riemann–Siegel theta function θ are uniquely defined by this and the condition that they are smooth real functions with θ(0)=0. By finding many intervals where the function Z changes sign one can show that there are many zeros on the critical line. To verify the Riemann hypothesis up to a given imaginary part T of the zeros, one also has to check that there are no further zeros off the line in this region. This can be done by calculating the total number of zeros in the region using Turing's method and checking that it is the same as the number of zeros found on the line. This allows one to verify the Riemann hypothesis computationally up to any desired value of T (provided all the zeros of the zeta function in this region are simple and on the critical line).
These calculations can also be used to estimate for finite ranges of . For example, using the latest result from 2020 (zeros up to height ), it has been shown that
In general, this inequality holds if
- and
where is the largest known value such that the Riemann hypothesis is true for all zeros with .
Some calculations of zeros of the zeta function are listed below, where the "height" of a zero is the magnitude of its imaginary part, and the height of the nth zero is denoted by γn. So far all zeros that have been checked are on the critical line and are simple. (A multiple zero would cause problems for the zero finding algorithms, which depend on finding sign changes between zeros.) For tables of the zeros, see Haselgrove & Miller (1960) or Odlyzko.
| Year | Number of zeros | Author |
|---|---|---|
| 1859? | 3 | B. Riemann used the Riemann–Siegel formula (unpublished, but reported in Siegel 1932). |
| 1903 | 15 | J. P. Gram (1903) used Euler–Maclaurin formula and discovered Gram's law. He showed that all 10 zeros with imaginary part at most 50 range lie on the critical line with real part 1/2 by computing the sum of the inverse 10th powers of the roots he found. |
| 1914 | 79 (γn ≤ 200) | R. J. Backlund (1914) introduced a better method of checking all the zeros up to that point are on the line, by studying the argument S(T) of the zeta function. |
| 1925 | 138 (γn ≤ 300) | J. I. Hutchinson (1925) found the first failure of Gram's law, at the Gram point g126. |
| 1935 | 195 | E. C. Titchmarsh (1935) used the recently rediscovered Riemann–Siegel formula, which is much faster than Euler–Maclaurin summation. It takes about O(T3/2+ε) steps to check zeros with imaginary part less than T, while the Euler–Maclaurin method takes about O(T2+ε) steps. |
| 1936 | 1041 | E. C. Titchmarsh (1936) and L. J. Comrie were the last to find zeros by hand. |
| 1953 | 1104 | A. M. Turing (1953) found a more efficient way to check that all zeros up to some point are accounted for by the zeros on the line, by checking that Z has the correct sign at several consecutive Gram points and using the fact that S(T) has average value 0. This requires almost no extra work because the sign of Z at Gram points is already known from finding the zeros, and is still the usual method used. This was the first use of a digital computer to calculate the zeros. |
| 1956 | 15000 | D. H. Lehmer (1956) discovered a few cases where the zeta function has zeros that are "only just" on the line: two zeros of the zeta function are so close together that it is unusually difficult to find a sign change between them. This is called "Lehmer's phenomenon", and first occurs at the zeros with imaginary parts 7005.063 and 7005.101, which differ by only .04 while the average gap between other zeros near this point is about 1. |
| 1956 | 25000 | D. H. Lehmer |
| 1958 | 35337 | N. A. Meller |
| 1966 | 250000 | R. S. Lehman |
| 1968 | 3500000 | Rosser, Yohe & Schoenfeld (1969) stated Rosser's rule (described below). |
| 1977 | 40000000 | R. P. Brent |
| 1979 | 81000001 | R. P. Brent |
| 1982 | 200000001 | R. P. Brent, J. van de Lune, H. J. J. te Riele, D. T. Winter |
| 1983 | 300000001 | J. van de Lune, H. J. J. te Riele |
| 1986 | 1500000001 | van de Lune, te Riele & Winter (1986) gave some statistical data about the zeros and give several graphs of Z at places where it has unusual behavior. |
| 1987 | A few of large (~1012) height | A. M. Odlyzko (1987) computed smaller numbers of zeros of much larger height, around 1012, to high precision to check Montgomery's pair correlation conjecture. |
| 1992 | A few of large (~1020) height | A. M. Odlyzko (1992) computed a 175 million zeros of heights around 1020 and a few more of heights around 2×1020, and gave an extensive discussion of the results. |
| 1998 | 10000 of large (~1021) height | A. M. Odlyzko (1998) computed some zeros of height about 1021 |
| 2001 | 10000000000 | J. van de Lune (unpublished) |
| 2004 | ~900000000000 | S. Wedeniwski (ZetaGrid distributed computing) |
| 2004 | 10000000000000 and a few of large (up to ~1024) heights | X. Gourdon (2004) and Patrick Demichel used the Odlyzko–Schönhage algorithm. They also checked two billion zeros around heights 1013, 1014, ..., 1024. |
| 2020 | 12363153437138 up to height 3000175332800 | Platt & Trudgian (2021).
They also verified the work of Gourdon (2004) and others. |
Gram points
A Gram point is a point on the critical line 1/2 + it where the zeta function is real and non-zero. Using the expression for the zeta function on the critical line, ζ(1/2 + it) = Z(t)e − iθ(t), where Hardy's function, Z, is real for real t, and θ is the Riemann–Siegel theta function, we see that zeta is real when sin(θ(t)) = 0. This implies that θ(t) is an integer multiple of π, which allows for the location of Gram points to be calculated fairly easily by inverting the formula for θ. They are usually numbered as gn for n = 0, 1, ..., where gn is the unique solution of θ(t) = nπ.
Gram observed that there was often exactly one zero of the zeta function between any two Gram points; Hutchinson called this observation Gram's law. There are several other closely related statements that are also sometimes called Gram's law: for example, (−1)nZ(gn) is usually positive, or Z(t) usually has opposite sign at consecutive Gram points. The imaginary parts γn of the first few zeros (in blue) and the first few Gram points gn are given in the following table
|
|
|
g−1 | γ1 | g0 | γ2 | g1 | γ3 | g2 | γ4 | g3 | γ5 | g4 | γ6 | g5 |
| 0 | 3.436 | 9.667 | 14.135 | 17.846 | 21.022 | 23.170 | 25.011 | 27.670 | 30.425 | 31.718 | 32.935 | 35.467 | 37.586 | 38.999 |
The first failure of Gram's law occurs at the 127th zero and the Gram point g126, which are in the "wrong" order.
| g124 | γ126 | g125 | g126 | γ127 | γ128 | g127 | γ129 | g128 |
|---|---|---|---|---|---|---|---|---|
| 279.148 | 279.229 | 280.802 | 282.455 | 282.465 | 283.211 | 284.104 | 284.836 | 285.752 |
A Gram point t is called good if the zeta function is positive at 1/2 + it. The indices of the "bad" Gram points where Z has the "wrong" sign are 126, 134, 195, 211, ... (sequence A114856 in the OEIS). A Gram block is an interval bounded by two good Gram points such that all the Gram points between them are bad. A refinement of Gram's law called Rosser's rule due to Rosser, Yohe & Schoenfeld (1969) says that Gram blocks often have the expected number of zeros in them (the same as the number of Gram intervals), even though some of the individual Gram intervals in the block may not have exactly one zero in them. For example, the interval bounded by g125 and g127 is a Gram block containing a unique bad Gram point g126, and contains the expected number 2 of zeros although neither of its two Gram intervals contains a unique zero. Rosser et al. checked that there were no exceptions to Rosser's rule in the first 3 million zeros, although there are infinitely many exceptions to Rosser's rule over the entire zeta function.
Gram's rule and Rosser's rule both say that in some sense zeros do not stray too far from their expected positions. The distance of a zero from its expected position is controlled by the function S defined above, which grows extremely slowly: its average value is of the order of (log log T)1/2, which only reaches 2 for T around 1024. This means that both rules hold most of the time for small T but eventually break down often. Indeed, Trudgian (2011) showed that both Gram's law and Rosser's rule fail in a positive proportion of cases. To be specific, it is expected that in about 66% one zero is enclosed by two successive Gram points, but in 17% no zero and in 17% two zeros are in such a Gram-interval on the long run Hanga (2020).
Arguments for and against the Riemann hypothesis
Mathematical papers about the Riemann hypothesis tend to be cautiously noncommittal about its truth. Of authors who express an opinion, most of them, such as Riemann (1859) and Bombieri (2000), imply that they expect (or at least hope) that it is true. The few authors who express serious doubt about it include Ivić (2008), who lists some reasons for skepticism, and Littlewood (1962), who flatly states that he believes it false, that there is no evidence for it and no imaginable reason it would be true. The consensus of the survey articles (Bombieri 2000, Conrey 2003, and Sarnak 2005) is that the evidence for it is strong but not overwhelming, so that while it is probably true there is reasonable doubt.
Some of the arguments for and against the Riemann hypothesis are listed by Sarnak (2005), Conrey (2003), and Ivić (2008), and include the following:
- Several analogues of the Riemann hypothesis have already been proved. The proof of the Riemann hypothesis for varieties over finite fields by Deligne (1974) is possibly the single strongest theoretical reason in favor of the Riemann hypothesis. This provides some evidence for the more general conjecture that all zeta functions associated with automorphic forms satisfy a Riemann hypothesis, which includes the classical Riemann hypothesis as a special case. Similarly Selberg zeta functions satisfy the analogue of the Riemann hypothesis, and are in some ways similar to the Riemann zeta function, having a functional equation and an infinite product expansion analogous to the Euler product expansion. But there are also some major differences; for example, they are not given by Dirichlet series. The Riemann hypothesis for the Goss zeta function was proved by Sheats (1998). In contrast to these positive examples, some Epstein zeta functions do not satisfy the Riemann hypothesis even though they have an infinite number of zeros on the critical line. These functions are quite similar to the Riemann zeta function, and have a Dirichlet series expansion and a functional equation, but the ones known to fail the Riemann hypothesis do not have an Euler product and are not directly related to automorphic representations.
- At first, the numerical verification that many zeros lie on the line seems strong evidence for it. But analytic number theory has had many conjectures supported by substantial numerical evidence that turned out to be false. See Skewes number for a notorious example, where the first exception to a plausible conjecture related to the Riemann hypothesis probably occurs around 10316; a counterexample to the Riemann hypothesis with imaginary part this size would be far beyond anything that can currently be computed using a direct approach. The problem is that the behavior is often influenced by very slowly increasing functions such as log log T, that tend to infinity, but do so so slowly that this cannot be detected by computation. Such functions occur in the theory of the zeta function controlling the behavior of its zeros; for example the function S(T) above has average size around (log log T)1/2. As S(T) jumps by at least 2 at any counterexample to the Riemann hypothesis, one might expect any counterexamples to the Riemann hypothesis to start appearing only when S(T) becomes large. It is never much more than 3 as far as it has been calculated, but is known to be unbounded, suggesting that calculations may not have yet reached the region of typical behavior of the zeta function.
- Denjoy's probabilistic argument for the Riemann hypothesis is based on the observation that if μ(x) is a random sequence of "1"s and "−1"s then, for every ε > 0, the partial sums (the values of which are positions in a simple random walk) satisfy the boundwith probability 1. The Riemann hypothesis is equivalent to this bound for the Möbius function μ and the Mertens function M derived in the same way from it. In other words, the Riemann hypothesis is in some sense equivalent to saying that μ(x) behaves like a random sequence of coin tosses. When μ(x) is nonzero its sign gives the parity of the number of prime factors of x, so informally the Riemann hypothesis says that the parity of the number of prime factors of an integer behaves randomly. Such probabilistic arguments in number theory often give the right answer, but tend to be very hard to make rigorous, and occasionally give the wrong answer for some results, such as Maier's theorem.
- The calculations in Odlyzko (1987) show that the zeros of the zeta function behave very much like the eigenvalues of a random Hermitian matrix, suggesting that they are the eigenvalues of some self-adjoint operator, which would imply the Riemann hypothesis. All attempts to find such an operator have failed.
- There are several theorems, such as Goldbach's weak conjecture for sufficiently large odd numbers, that were first proved using the generalized Riemann hypothesis, and later shown to be true unconditionally. This could be considered as weak evidence for the generalized Riemann hypothesis, as several of its "predictions" are true.
- Lehmer's phenomenon, where two zeros are sometimes very close, is sometimes given as a reason to disbelieve the Riemann hypothesis. But one would expect this to happen occasionally by chance even if the Riemann hypothesis is true, and Odlyzko's calculations suggest that nearby pairs of zeros occur just as often as predicted by Montgomery's conjecture.
- Patterson suggests that the most compelling reason for the Riemann hypothesis for most mathematicians is the hope that primes are distributed as regularly as possible.










































































































![(T,T+H]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a7f206ba185f5e71e82482b52823f9cab4a9d99)











![{\displaystyle (0,T]~}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32185e31a7ceddedfbd8767e0dd79a6afbb0582c)





















![{\displaystyle \Im {\left(\rho \right)}\in \left(0,T\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/386ca464716d11155c40348b352a968faf05bbc8)






















