From Wikipedia, the free encyclopedia
In physics, the Lorentz transformation (or transformations) is named after the Dutch physicist Hendrik Lorentz. It was the result of attempts by Lorentz and others to explain how the speed of light was observed to be independent of the reference frame, and to understand the symmetries of the laws of electromagnetism. The Lorentz transformation is in accordance with special relativity, but was derived before special relativity.
The transformations describe how measurements of space and time by two observers are related. They reflect the fact that observers moving at different velocities may measure different distances, elapsed times, and even different orderings of events. They supersede the Galilean transformation of Newtonian physics, which assumes an absolute space and time (see Galilean relativity). The Galilean transformation is a good approximation only at relative speeds much smaller than the speed of light.
The Lorentz transformation is a linear transformation. It may include a rotation of space; a rotation-free Lorentz transformation is called a Lorentz boost.
In Minkowski space, the Lorentz transformations preserve the spacetime interval between any two events. They describe only the transformations in which the spacetime event at the origin is left fixed, so they can be considered as a hyperbolic rotation of Minkowski space. The more general set of transformations that also includes translations is known as the Poincaré group.
History
Many physicists, including Woldemar Voigt, George FitzGerald, Joseph Larmor, and Hendrik Lorentz himself had been discussing the physics implied by these equations since 1887.[1]Early in 1889, Oliver Heaviside had shown from Maxwell's equations that the electric field surrounding a spherical distribution of charge should cease to have spherical symmetry once the charge is in motion relative to the ether. FitzGerald then conjectured that Heaviside’s distortion result might be applied to a theory of intermolecular forces. Some months later, FitzGerald published the conjecture that bodies in motion are being contracted, in order to explain the baffling outcome of the 1887 ether-wind experiment of Michelson and Morley. In 1892, Lorentz independently presented the same idea in a more detailed manner, which was subsequently called FitzGerald–Lorentz contraction hypothesis.[2] Their explanation was widely known before 1905.[3]
Lorentz (1892–1904) and Larmor (1897–1900), who believed the luminiferous ether hypothesis, were also seeking the transformation under which Maxwell's equations are invariant when transformed from the ether to a moving frame. They extended the FitzGerald–Lorentz contraction hypothesis and found out that the time coordinate has to be modified as well ("local time"). Henri Poincaré gave a physical interpretation to local time (to first order in v/c) as the consequence of clock synchronization, under the assumption that the speed of light is constant in moving frames.[4] Larmor is credited to have been the first to understand the crucial time dilation property inherent in his equations.[5]
In 1905, Poincaré was the first to recognize that the transformation has the properties of a mathematical group, and named it after Lorentz.[6] Later in the same year Albert Einstein published what is now called special relativity, by deriving the Lorentz transformation under the assumptions of the principle of relativity and the constancy of the speed of light in any inertial reference frame, and by abandoning the mechanical aether.[7]
Lorentz transformation for frames in standard configuration
Consider two observers O and O′, each using their own Cartesian coordinate system to measure space and time intervals. O uses (t, x, y, z) and O′ uses (t′, x′, y′, z′). Assume further that the coordinate systems are oriented so that, in 3 dimensions, the x-axis and the x′-axis are collinear, the y-axis is parallel to the y′-axis, and the z-axis parallel to the z′-axis. The relative velocity between the two observers is v along the common x-axis; O measures O′ to move at velocity v along the coincident xx′ axes, while O′ measures O to move at velocity −v along the coincident xx′ axes. Also assume that the origins of both coordinate systems are the same, that is, coincident times and positions. If all these hold, then the coordinate systems are said to be in standard configuration.The inverse of a Lorentz transformation relates the coordinates the other way round; from the coordinates O′ measures (t′, x′, y′, z′) to the coordinates O measures (t, x, y, z), so t, x, y, z are in terms of t′, x′, y′, z′. The mathematical form is nearly identical to the original transformation; the only difference is the negation of the uniform relative velocity (from v to −v), and exchange of primed and unprimed quantities, because O′ moves at velocity v relative to O, and equivalently, O moves at velocity −v relative to O′. This symmetry makes it effortless to find the inverse transformation (carrying out the exchange and negation saves a lot of rote algebra), although more fundamentally; it highlights that all physical laws should remain unchanged under a Lorentz transformation.[8]
Below, the Lorentz transformations are called "boosts" in the stated directions.
Boost in the x-direction

The spacetime coordinates of an event, as measured by each observer in their inertial reference frame (in standard configuration) are shown in the speech bubbles.
Top: frame F′ moves at velocity v along the x-axis of frame F.
Bottom: frame F moves at velocity −v along the x′-axis of frame F′.[9]
Top: frame F′ moves at velocity v along the x-axis of frame F.
Bottom: frame F moves at velocity −v along the x′-axis of frame F′.[9]
These are the simplest forms. The Lorentz transformation for frames in standard configuration can be shown to be (see for example [10] and [11]):
- v is the relative velocity between frames in the x-direction,
- c is the speed of light,
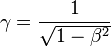 is the Lorentz factor (Greek lowercase gamma),
is the Lorentz factor (Greek lowercase gamma),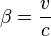 is the velocity coefficient (Greek lowercase beta), again for the x-direction.
is the velocity coefficient (Greek lowercase beta), again for the x-direction.
Boost in the y or z directions
The above collection of equations apply only for a boost in the x-direction. The standard configuration works equally well in the y or z directions instead of x, and so the results are similar.For the y-direction:
For the z-direction:
The Lorentz or boost matrix is usually denoted by Λ (Greek capital lambda). Above the transformations have been applied to the four-position X,
Boost in any direction
Vector form
For a boost in an arbitrary direction with velocity v, that is, O observes O′ to move in direction v in the F coordinate frame, while O′ observes O to move in direction −v in the F′ coordinate frame, it is convenient to decompose the spatial vector r into components perpendicular and parallel to v: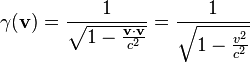 .
.
 into r′:
into r′:- v/v is a dimensionless unit vector pointing in the same direction as r‖,
- r‖ = (r • v)/v is the projection of r into the direction of v,
Matrix forms
These equations can be expressed in block matrix form asNote that this transformation is only the "boost," i.e., a transformation between two frames whose x, y, and z axis are parallel and whose spacetime origins coincide. The most general proper Lorentz transformation also contains a rotation of the three axes, because the composition of two boosts is not a pure boost but is a boost followed by a rotation. The rotation gives rise to Thomas precession. The boost is given by a symmetric matrix, but the general Lorentz transformation matrix need not be symmetric.
Composition of two boosts
The composition of two Lorentz boosts B(u) and B(v) of velocities u and v is given by:[14][15]![B(\mathbf{u})B(\mathbf{v})=B\left ( \mathbf{u}\oplus\mathbf{v} \right )\mathrm{Gyr}\left [ \mathbf{u},\mathbf{v}\right ]=\mathrm{Gyr}\left [\mathbf{u},\mathbf{v} \right ]B \left ( \mathbf{v}\oplus\mathbf{u} \right )](//upload.wikimedia.org/math/d/2/b/d2bc92820ed87642d3e19f9160655e55.png) ,
,
- B(v) is the 4 × 4 matrix that uses the components of v, i.e. v1, v2, v3 in the entries of the matrix, or rather the components of v/c in the representation that is used above,
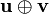 is the velocity-addition,
is the velocity-addition,- Gyr[u,v] (capital G) is the rotation arising from the composition. If the 3 × 3 matrix form of the rotation applied to spatial coordinates is given by gyr[u,v], then the 4 × 4 matrix rotation applied to 4-coordinates is given by:[14]
- gyr (lower case g) is the gyrovector space abstraction of the gyroscopic Thomas precession, defined as an operator on a velocity w in terms of velocity addition:
-
- for all w.
Visualizing the transformations in Minkowski space
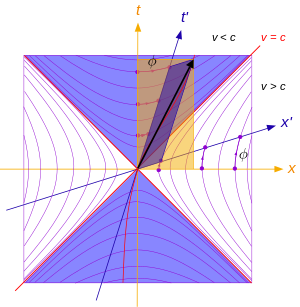
Lorentz transformations can be depicted on the Minkowski light cone spacetime diagram.
The momentarily co-moving inertial frames along the world line of a rapidly accelerating observer (center). The vertical direction indicates time, while the horizontal indicates distance, the dashed line is the spacetime trajectory ("world line") of the observer. The small dots are specific events in spacetime. If one imagines these events to be the flashing of a light, then the events that pass the two diagonal lines in the bottom half of the image (the past light cone of the observer in the origin) are the events visible to the observer. The slope of the world line (deviation from being vertical) gives the relative velocity to the observer. Note how the momentarily co-moving inertial frame changes when the observer accelerates.
Particle travelling at constant velocity (straight worldline coincident with time t′ axis).
Accelerating particle (curved worldline).
Lorentz transformations on the Minkowski light cone spacetime diagram, for one space and one time dimension.
The yellow axes are the rest frame of an observer, the blue axes correspond to the frame of a moving observer
The red lines are world lines, a continuous sequence of events: straight for an object travelling at constant velocity, curved for an object accelerating. Worldlines of light form the boundary of the light cone.
The purple hyperbolae indicate this is a hyperbolic rotation, the hyperbolic angle ϕ is called rapidity (see below). The greater the relative speed between the reference frames, the more "warped" the axes become. The relative velocity cannot exceed c.
The black arrow is a displacement four-vector between two events (not necessarily on the same world line), showing that in a Lorentz boost; time dilation (fewer time intervals in moving frame) and length contraction (shorter lengths in moving frame) occur. The axes in the moving frame are orthogonal (even though they do not look so).
Rapidity
The Lorentz transformation can be cast into another useful form by defining a parameter ϕ called the rapidity (an instance of hyperbolic angle) such thatHyperbolic expressions
From the above expressions for eφ and e−φHyperbolic rotation of coordinates
Substituting these expressions into the matrix form of the transformation, it is evident thatThis transformation is sometimes illustrated with a Minkowski diagram, as displayed above.
This 4-by-4 boost matrix can thus be written compactly as a Matrix exponential,
Transformation of other physical quantities
The transformation matrix is universal for all four-vectors, not just 4-dimensional spacetime coordinates. If Z is any four-vector, then:[13]More generally, the transformation of any tensor quantity T is given by:[17]
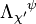 is the inverse matrix of
is the inverse matrix of 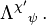
Special relativity
The crucial insight of Einstein's clock-setting method is the idea that time is relative. In essence, each observer's frame of reference is associated with a unique set of clocks, the result being that time as measured for a location passes at different rates for different observers.[18] This was a direct result of the Lorentz transformations and is called time dilation. We can also clearly see from the Lorentz "local time" transformation that the concept of the relativity of simultaneity and of the relativity of length contraction are also consequences of that clock-setting hypothesis.[19]Transformation of the electromagnetic field
Lorentz transformations can also be used to prove that magnetic and electric fields are simply different aspects of the same force — the electromagnetic force, as a consequence of relative motion between electric charges and observers.[20] The fact that the electromagnetic field shows relativistic effects becomes clear by carrying out a simple thought experiment:[21]- Consider an observer measuring a charge at rest in a reference frame F. The observer will detect a static electric field. As the charge is stationary in this frame, there is no electric current, so the observer will not observe any magnetic field.
- Consider another observer in frame F′ moving at relative velocity v (relative to F and the charge). This observer will see a different electric field because the charge is moving at velocity −v in their rest frame. Further, in frame F′ the moving charge constitutes an electric current, and thus the observer in frame F′ will also see a magnetic field.
The correspondence principle
For relative speeds much less than the speed of light, the Lorentz transformations reduce to the Galilean transformation in accordance with the correspondence principle.The correspondence limit is usually stated mathematically as: as v → 0, c → ∞. In words: as velocity approaches 0, the speed of light (seems to) approach infinity. Hence, it is sometimes said that nonrelativistic physics is a physics of "instantaneous action at a distance".[18]
Spacetime interval
In a given coordinate system xμ, if two events A and B are separated byTaking the determinant of
- Proper Lorentz transformations have det(Λμν) = +1, and form a subgroup called the special orthogonal group SO(1,3).
- Improper Lorentz transformations are det(Λμν) = −1, which do not form a subgroup, as the product of any two improper Lorentz transformations will be a proper Lorentz transformation.
A quantity invariant under Lorentz transformations is known as a Lorentz scalar.
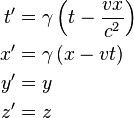
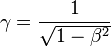 is the
is the 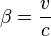 is the velocity coefficient (
is the velocity coefficient (



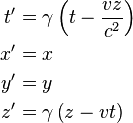

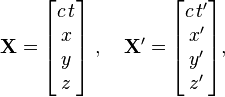


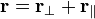
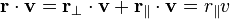

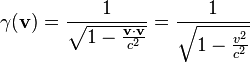 .
.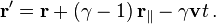
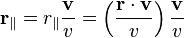


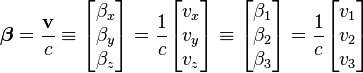
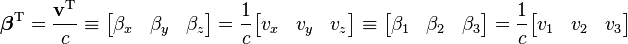


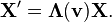

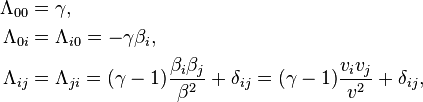
![B(\mathbf{u})B(\mathbf{v})=B\left ( \mathbf{u}\oplus\mathbf{v} \right )\mathrm{Gyr}\left [ \mathbf{u},\mathbf{v}\right ]=\mathrm{Gyr}\left [\mathbf{u},\mathbf{v} \right ]B \left ( \mathbf{v}\oplus\mathbf{u} \right )](http://upload.wikimedia.org/math/d/2/b/d2bc92820ed87642d3e19f9160655e55.png) ,
,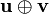 is the
is the ![\mathrm{Gyr}[\mathbf{u},\mathbf{v}]=
\begin{pmatrix}
1 & 0 \\
0 & \mathrm{gyr}[\mathbf{u},\mathbf{v}]
\end{pmatrix}\,,](http://upload.wikimedia.org/math/a/b/7/ab7771e0f086cf79d006e720540dff64.png)
![\text{gyr}[\mathbf{u},\mathbf{v}]\mathbf{w}=\ominus(\mathbf{u} \oplus \mathbf{v}) \oplus (\mathbf{u} \oplus (\mathbf{v} \oplus \mathbf{w}))](http://upload.wikimedia.org/math/7/5/5/7558d528e4c138a4b33c2220ddde9651.png)
![L(\mathbf{u},U)L(\mathbf{v},V)=L(\mathbf{u}\oplus U\mathbf{v}, \mathrm{gyr}[\mathbf{u},U\mathbf{v}]UV)](http://upload.wikimedia.org/math/9/e/1/9e1df3b4dbc3302216b6d7fc95079fa6.png)

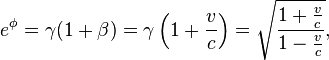

![\phi = \ln \left[\gamma(1+\beta)\right] = -\ln \left[\gamma(1-\beta)\right] \,](http://upload.wikimedia.org/math/4/0/5/4059316ea27f6c51c310306cc1753299.png)



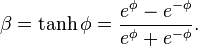
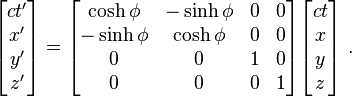
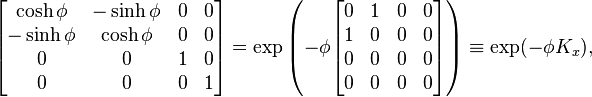
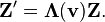
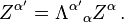
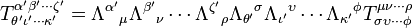
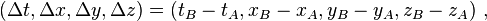
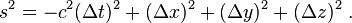
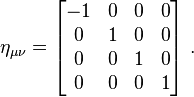
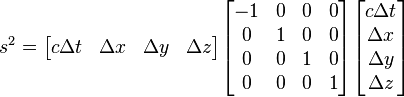
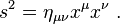
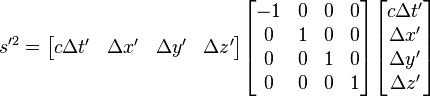
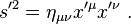
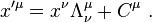
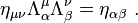
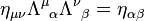
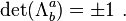
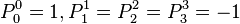
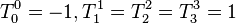


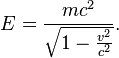
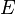 approaches zero when
approaches zero when  approaches infinity. (For ordinary
approaches infinity. (For ordinary 


