From Wikipedia, the free encyclopedia

Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics.
Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918.[1] The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.
Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.
Basic illustrations and background
As an illustration, if a physical system behaves the same regardless of how it is oriented in space, its Lagrangian is rotationally symmetric: from this symmetry, Noether's theorem dictates that the angular momentum of the system be conserved, as a consequence of its laws of motion. The physical system itself need not be symmetric; a jagged asteroid tumbling in space conserves angular momentum despite its asymmetry — it is the laws of its motion that are symmetric.As another example, if a physical process exhibits the same outcomes regardless of place or time, then its Lagrangian is symmetric under continuous translations in space and time: by Noether's theorem, these symmetries account for the conservation laws of linear momentum and energy within this system, respectively.
Noether's theorem is important, both because of the insight it gives into conservation laws, and also as a practical calculational tool. It allows investigators to determine the conserved quantities (invariants) from the observed symmetries of a physical system. Conversely, it allows researchers to consider whole classes of hypothetical Lagrangians with given invariants, to describe a physical system. As an illustration, suppose that a new field is discovered that conserves a quantity X. Using Noether's theorem, the types of Lagrangians that conserve X through a continuous symmetry may be determined, and their fitness judged by further criteria.
There are numerous versions of Noether's theorem, with varying degrees of generality. The original version only applied to ordinary differential equations (particles) and not partial differential equations (fields). The original versions also assume that the Lagrangian only depends upon the first derivative, while later versions generalize the theorem to Lagrangians depending on the nth derivative.[disputed ] There are natural quantum counterparts of this theorem, expressed in the Ward–Takahashi identities. Generalizations of Noether's theorem to superspaces are also available.
Informal statement of the theorem
All fine technical points aside, Noether's theorem can be stated informallyIf a system has a continuous symmetry property, then there are corresponding quantities whose values are conserved in time.[2]A more sophisticated version of the theorem involving fields states that:
To every differentiable symmetry generated by local actions, there corresponds a conserved current.The word "symmetry" in the above statement refers more precisely to the covariance of the form that a physical law takes with respect to a one-dimensional Lie group of transformations satisfying certain technical criteria. The conservation law of a physical quantity is usually expressed as a continuity equation.
The formal proof of the theorem utilizes the condition of invariance to derive an expression for a current associated with a conserved physical quantity. In modern (since ca. 1980[3]) terminology, the conserved quantity is called the Noether charge, while the flow carrying that charge is called the Noether current. The Noether current is defined up to a solenoidal (divergenceless) vector field.
In the context of gravitation, Felix Klein's statement of Noether's theorem for action I stipulates for the invariants:[4]
If an integral I is invariant under a continuous group Gρ with ρ parameters, then ρ linearly independent combinations of the Lagrangian expressions are divergences.
Historical context
A conservation law states that some quantity X in the mathematical description of a system's evolution remains constant throughout its motion — it is an invariant. Mathematically, the rate of change of X (its derivative with respect to time) vanishes,The earliest constants of motion discovered were momentum and energy, which were proposed in the 17th century by René Descartes and Gottfried Leibniz on the basis of collision experiments, and refined by subsequent researchers. Isaac Newton was the first to enunciate the conservation of momentum in its modern form, and showed that it was a consequence of Newton's third law. According to general relativity, the conservation laws of linear momentum, energy and angular momentum are only exactly true globally when expressed in terms of the sum of the stress–energy tensor (non-gravitational stress–energy) and the Landau–Lifshitz stress–energy–momentum pseudotensor (gravitational stress–energy). The local conservation of non-gravitational linear momentum and energy in a free-falling reference frame is expressed by the vanishing of the covariant divergence of the stress–energy tensor. Another important conserved quantity, discovered in studies of the celestial mechanics of astronomical bodies, is the Laplace–Runge–Lenz vector.
In the late 18th and early 19th centuries, physicists developed more systematic methods for discovering invariants. A major advance came in 1788 with the development of Lagrangian mechanics, which is related to the principle of least action. In this approach, the state of the system can be described by any type of generalized coordinates q; the laws of motion need not be expressed in a Cartesian coordinate system, as was customary in Newtonian mechanics. The action is defined as the time integral I of a function known as the Lagrangian L
Thus, the absence of the ignorable coordinate qk from the Lagrangian implies that the Lagrangian is unaffected by changes or transformations of qk; the Lagrangian is invariant, and is said to exhibit a symmetry under such transformations. This is the seed idea generalized in Noether's theorem.
Several alternative methods for finding conserved quantities were developed in the 19th century, especially by William Rowan Hamilton. For example, he developed a theory of canonical transformations which allowed changing coordinates so that some coordinates disappeared from the Lagrangian, as above, resulting in conserved canonical momenta. Another approach, and perhaps the most efficient for finding conserved quantities, is the Hamilton–Jacobi equation.
Mathematical expression
Simple form using perturbations
The essence of Noether's theorem is generalizing the ignorable coordinates outlined.Imagine that the action I defined above is invariant under small perturbations (warpings) of the time variable t and the generalized coordinates q; in a notation commonly used in physics,
Then the resultant perturbation can be written as a linear sum of the individual types of perturbations,
- generator Tr of time evolution, and
- generator Qr of the generalized coordinates.
Using these definitions, Noether showed that the N quantities
Examples
- Time invariance
- Translational invariance
- Rotational invariance
If n is arbitrary, i.e., if the system is insensitive to any rotation, then every component of L is conserved; in short, angular momentum is conserved.
Field theory version
Although useful in its own right, the version of Noether's theorem just given is a special case of the general version derived in 1915. To give the flavor of the general theorem, a version of the Noether theorem for continuous fields in four-dimensional space–time is now given. Since field theory problems are more common in modern physics than mechanics problems, this field theory version is the most commonly used version (or most often implemented) of Noether's theorem.Let there be a set of differentiable fields φ defined over all space and time; for example, the temperature T(x, t) would be representative of such a field, being a number defined at every place and time. The principle of least action can be applied to such fields, but the action is now an integral over space and time
Let the action be invariant under certain transformations of the space–time coordinates xμ and the fields φ
For illustration, consider a physical system of fields that behaves the same under translations in time and space, as considered above; in other words,
 is constant in its third argument. In that case, N = 4, one for each dimension of space and time. Since only the positions in space–time are being warped, not the fields, the Ψ are all zero and the Xμν equal the Kronecker delta δμν, where we have used μ instead of r for the index. In that case, Noether's theorem corresponds to the conservation law for the stress–energy tensor Tμν[7]
is constant in its third argument. In that case, N = 4, one for each dimension of space and time. Since only the positions in space–time are being warped, not the fields, the Ψ are all zero and the Xμν equal the Kronecker delta δμν, where we have used μ instead of r for the index. In that case, Noether's theorem corresponds to the conservation law for the stress–energy tensor Tμν[7]Derivations
One independent variable
Consider the simplest case, a system with one independent variable, time. Suppose the dependent variables q are such that the action integral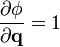 and so the conserved quantity simplifies to
and so the conserved quantity simplifies toField-theoretic derivation
Noether's theorem may also be derived for tensor fields φA where the index A ranges over the various components of the various tensor fields. These field quantities are functions defined over a four-dimensional space whose points are labeled by coordinates xμ where the index μ ranges over time (μ = 0) and three spatial dimensions (μ = 1, 2, 3). These four coordinates are the independent variables; and the values of the fields at each event are the dependent variables. Under an infinitesimal transformation, the variation in the coordinates is writtenNoether's theorem begins with the assumption that a specific transformation of the coordinates and field variables does not change the action, which is defined as the integral of the Lagrangian density over the given region of spacetime. Expressed mathematically, this assumption may be written as
 is the Lie derivative of φA in the Xμ direction. When φA is a scalar or
is the Lie derivative of φA in the Xμ direction. When φA is a scalar or  ,
,Manifold/fiber bundle derivation
Suppose we have an n-dimensional oriented Riemannian manifold, M and a target manifold T. Let be the configuration space of smooth functions from M to T. (More generally, we can have smooth sections of a fiber bundle over M.)
be the configuration space of smooth functions from M to T. (More generally, we can have smooth sections of a fiber bundle over M.)Examples of this M in physics include:
- In classical mechanics, in the Hamiltonian formulation, M is the one-dimensional manifold R, representing time and the target space is the cotangent bundle of space of generalized positions.
- In field theory, M is the spacetime manifold and the target space is the set of values the fields can take at any given point. For example, if there are m real-valued scalar fields,
 , then the target manifold is Rm. If the field is a real vector field, then the target manifold is isomorphic to R3.
, then the target manifold is Rm. If the field is a real vector field, then the target manifold is isomorphic to R3.
To get to the usual version of Noether's theorem, we need additional restrictions on the action. We assume
![\mathcal{S}[\phi]](http://upload.wikimedia.org/math/3/6/f/36f42f8d4b11565941f7d147eb293ed6.png) is the integral over M of a function
is the integral over M of a function
 consisting of functions φ such that all functional derivatives of
consisting of functions φ such that all functional derivatives of 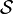 at φ are zero, that is:
at φ are zero, that is:Now, suppose we have an infinitesimal transformation on
 , generated by a functional derivation, Q such that
, generated by a functional derivation, Q such thatNow, for any N, because of the Euler–Lagrange theorem, on shell (and only on-shell), we have
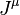 defined by:[10]
defined by:[10]Comments
Noether's theorem is an on shell theorem: it relies on use of the equations of motion—the classical path. It reflects the relation between the boundary conditions and the variational principle. Assuming no boundary terms in the action, Noether's theorem implies thatGeneralization to Lie algebras
Suppose say we have two symmetry derivations Q1 and Q2. Then, [Q1, Q2] is also a symmetry derivation. Let's see this explicitly. Let's sayGeneralization of the proof
This applies to any local symmetry derivation Q satisfying QS ≈ 0, and also to more general local functional differentiable actions, including ones where the Lagrangian depends on higher derivatives of the fields. Let ε be any arbitrary smooth function of the spacetime (or time) manifold such that the closure of its support is disjoint from the boundary. ε is a test function. Then, because of the variational principle (which does not apply to the boundary, by the way), the derivation distribution q generated by q[ε][Φ(x)] = ε(x)Q[Φ(x)] satisfies q[ε][S] ≈ 0 for every ε, or more compactly, q(x)[S] ≈ 0 for all x not on the boundary (but remember that q(x) is a shorthand for a derivation distribution, not a derivation parametrized by x in general). This is the generalization of Noether's theorem.To see how the generalization is related to the version given above, assume that the action is the spacetime integral of a Lagrangian that only depends on φ and its first derivatives. Also, assume
More generally, if the Lagrangian depends on higher derivatives, then
Examples
Example 1: Conservation of energy
Looking at the specific case of a Newtonian particle of mass m, coordinate x, moving under the influence of a potential V, coordinatized by time t. The action, S, is:![Q[x(t)]=\dot{x}(t)](http://upload.wikimedia.org/math/e/b/3/eb370d10596af1f1eef7750ee1fadc8d.png) . Note that x has an explicit dependence on time, whilst V does not; consequently:
. Note that x has an explicit dependence on time, whilst V does not; consequently: (i.e. the principle of conservation of energy is a consequence of invariance under time translations).
(i.e. the principle of conservation of energy is a consequence of invariance under time translations).More generally, if the Lagrangian does not depend explicitly on time, the quantity
Example 2: Conservation of center of momentum
Still considering 1-dimensional time, letFor
 , let's consider the generator of Galilean transformations (i.e. a change in the frame of reference). In other words,
, let's consider the generator of Galilean transformations (i.e. a change in the frame of reference). In other words, so we can set
so we can set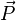 is the total momentum, M is the total mass and
is the total momentum, M is the total mass and  is the center of mass. Noether's theorem states:
is the center of mass. Noether's theorem states:Example 3: Conformal transformation
Both examples 1 and 2 are over a 1-dimensional manifold (time). An example involving spacetime is a conformal transformation of a massless real scalar field with a quartic potential in (3 + 1)-Minkowski spacetime.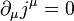 (as one may explicitly check by substituting the Euler–Lagrange equations into the left hand side).
(as one may explicitly check by substituting the Euler–Lagrange equations into the left hand side).(Aside: If one tries to find the Ward–Takahashi analog of this equation, one runs into a problem because of anomalies.)
Applications
Application of Noether's theorem allows physicists to gain powerful insights into any general theory in physics, by just analyzing the various transformations that would make the form of the laws involved invariant. For example:- the invariance of physical systems with respect to spatial translation (in other words, that the laws of physics do not vary with locations in space) gives the law of conservation of linear momentum;
- invariance with respect to rotation gives the law of conservation of angular momentum;
- invariance with respect to time translation gives the well-known law of conservation of energy
The Noether charge is also used in calculating the entropy of stationary black holes.[11]







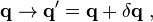
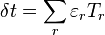










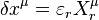

![j^\nu_r =
- \left( \frac{\partial L}{\partial \phi_{,\nu}} \right) \cdot \Psi_r +
\left[ \left( \frac{\partial L}{\partial \phi_{,\nu}} \right) \cdot\phi_{,\sigma} - L \delta^{\nu}_{\sigma} \right] X_{r}^{\sigma}](http://upload.wikimedia.org/math/6/7/3/673d2742b9843ee956ad0330812892ea.png)
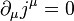
![T_\mu{}^\nu =
\left[ \left( \frac{\partial L}{\partial \phi_{,\nu}} \right) \cdot\phi_{,\sigma} - L\,\delta^\nu_\sigma \right] \delta_\mu^\sigma =
\left( \frac{\partial L}{\partial\phi_{,\nu}} \right) \cdot\phi_{,\mu} - L\,\delta_\mu^\nu](http://upload.wikimedia.org/math/3/1/7/3172a373ca2a3c76a135239f42e69b75.png)
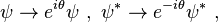


![I = \int_{t_1}^{t_2} L [\mathbf{q} [t], \dot{\mathbf{q}} [t], t] \, dt](http://upload.wikimedia.org/math/8/a/5/8a5e18371361c8ae6182ed4ff639f03b.png)
![\frac{d}{dt} \frac{\partial L}{\partial \dot{\mathbf{q}}} [t] = \frac{\partial L}{\partial \mathbf{q}} [t].](http://upload.wikimedia.org/math/d/c/8/dc8dd82908c3e68d23a3ed2ac78edc0e.png)

![\mathbf{q} [t] \rightarrow \mathbf{q}' [t'] = \phi [\mathbf{q} [t], \varepsilon] = \phi [\mathbf{q} [t' - \varepsilon T], \varepsilon]](http://upload.wikimedia.org/math/f/5/c/f5c325aef4ab97a62257df4e2f36a5ca.png)
![\dot{\mathbf{q}} [t] \rightarrow \dot{\mathbf{q}}' [t'] = \frac{d}{dt} \phi [\mathbf{q} [t], \varepsilon] = \frac{\partial \phi}{\partial \mathbf{q}} [\mathbf{q} [t' - \varepsilon T], \varepsilon] \dot{\mathbf{q}} [t' - \varepsilon T]
.](http://upload.wikimedia.org/math/4/d/7/4d71e81f00bd6a7a041f0b469bdef3e8.png)
![\begin{align}
I' [\varepsilon] & = \int_{t_1 + \varepsilon T}^{t_2 + \varepsilon T} L [\mathbf{q}'[t'], \dot{\mathbf{q}}' [t'], t'] \, dt' \\[6pt]
& = \int_{t_1 + \varepsilon T}^{t_2 + \varepsilon T} L [\phi [\mathbf{q} [t' - \varepsilon T], \varepsilon], \frac{\partial \phi}{\partial \mathbf{q}} [\mathbf{q} [t' - \varepsilon T], \varepsilon] \dot{\mathbf{q}} [t' - \varepsilon T], t'] \, dt'
\end{align}](http://upload.wikimedia.org/math/d/1/7/d17b6217f2e1be10a5a45d6002b87d86.png)
![\begin{align}
0 & = \frac{d I'}{d \varepsilon} [0] = L [\mathbf{q} [t_2], \dot{\mathbf{q}} [t_2], t_2] T - L [\mathbf{q} [t_1], \dot{\mathbf{q}} [t_1], t_1] T \\[6pt]
& {} + \int_{t_1}^{t_2} \frac{\partial L}{\partial \mathbf{q}} \left( - \frac{\partial \phi}{\partial \mathbf{q}} \dot{\mathbf{q}} T + \frac{\partial \phi}{\partial \varepsilon} \right) + \frac{\partial L}{\partial \dot{\mathbf{q}}} \left( - \frac{\partial^2 \phi}{(\partial \mathbf{q})^2} {\dot{\mathbf{q}}}^2 T + \frac{\partial^2 \phi}{\partial \varepsilon \partial \mathbf{q}} \dot{\mathbf{q}} -
\frac{\partial \phi}{\partial \mathbf{q}} \ddot{\mathbf{q}} T \right) \, dt.
\end{align}](http://upload.wikimedia.org/math/1/1/5/1155d56f7761429a8997ecc0e8c484bf.png)
![\begin{align}
\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{\mathbf{q}}} \frac{\partial \phi}{\partial \mathbf{q}} \dot{\mathbf{q}} T \right)
& = \left( \frac{d}{dt} \frac{\partial L}{\partial \dot{\mathbf{q}}} \right) \frac{\partial \phi}{\partial \mathbf{q}} \dot{\mathbf{q}} T + \frac{\partial L}{\partial \dot{\mathbf{q}}} \left( \frac{d}{dt} \frac{\partial \phi}{\partial \mathbf{q}} \right) \dot{\mathbf{q}} T + \frac{\partial L}{\partial \dot{\mathbf{q}}} \frac{\partial \phi}{\partial \mathbf{q}} \ddot{\mathbf{q}} \, T \\[6pt]
& = \frac{\partial L}{\partial \mathbf{q}} \frac{\partial \phi}{\partial \mathbf{q}} \dot{\mathbf{q}} T + \frac{\partial L}{\partial \dot{\mathbf{q}}} \left( \frac{\partial^2 \phi}{(\partial \mathbf{q})^2} \dot{\mathbf{q}} \right) \dot{\mathbf{q}} T + \frac{\partial L}{\partial \dot{\mathbf{q}}} \frac{\partial \phi}{\partial \mathbf{q}} \ddot{\mathbf{q}} \, T.
\end{align}](http://upload.wikimedia.org/math/d/9/d/d9d5e33b142622220aab264dafac337d.png)
![\begin{align}
0 & = \frac{d I'}{d \varepsilon} [0] = L [\mathbf{q} [t_2], \dot{\mathbf{q}} [t_2], t_2] T - L [\mathbf{q} [t_1], \dot{\mathbf{q}} [t_1], t_1] T - \frac{\partial L}{\partial \dot{\mathbf{q}}} \frac{\partial \phi}{\partial \mathbf{q}} \dot{\mathbf{q}} [t_2] T + \frac{\partial L}{\partial \dot{\mathbf{q}}} \frac{\partial \phi}{\partial \mathbf{q}} \dot{\mathbf{q}} [t_1] T \\[6pt]
& {} + \int_{t_1}^{t_2} \frac{\partial L}{\partial \mathbf{q}} \frac{\partial \phi}{\partial \varepsilon} + \frac{\partial L}{\partial \dot{\mathbf{q}}} \frac{\partial^2 \phi}{\partial \varepsilon \partial \mathbf{q}} \dot{\mathbf{q}} \, dt.
\end{align}](http://upload.wikimedia.org/math/5/d/3/5d34e512fef2ce66e101a79bd186b5c9.png)
![\begin{align}
0 & = L [\mathbf{q} [t_2], \dot{\mathbf{q}} [t_2], t_2] T - L [\mathbf{q} [t_1], \dot{\mathbf{q}} [t_1], t_1] T - \frac{\partial L}{\partial \dot{\mathbf{q}}} \frac{\partial \phi}{\partial \mathbf{q}} \dot{\mathbf{q}} [t_2] T + \frac{\partial L}{\partial \dot{\mathbf{q}}} \frac{\partial \phi}{\partial \mathbf{q}} \dot{\mathbf{q}} [t_1] T \\[6pt]
& {} + \frac{\partial L}{\partial \dot{\mathbf{q}}} \frac{\partial \phi}{\partial \varepsilon} [t_2] - \frac{\partial L}{\partial \dot{\mathbf{q}}} \frac{\partial \phi}{\partial \varepsilon} [t_1].
\end{align}](http://upload.wikimedia.org/math/3/7/e/37e8ceac9bf1368e59ba37ee2b6e93eb.png)
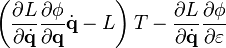
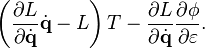

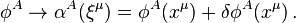






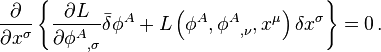





![j^\sigma =
\left[\frac{\partial L}{\partial {\phi^A}_{,\sigma}} \mathcal{L}_X \phi^A - L \, X^\sigma\right]
- \left(\frac{\partial L}{\partial {\phi^A}_{,\sigma}} \right) \Psi^A\,.](http://upload.wikimedia.org/math/4/4/d/44ddf7dc6ad22e80d3583e3a51e86510.png)
 , then the target manifold is Rm. If the field is a real vector field, then the target manifold is
, then the target manifold is Rm. If the field is a real vector field, then the target manifold is 
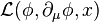
![\mathcal{S}[\phi]\,=\,\int_M \mathcal{L}[\phi(x),\partial_\mu\phi(x),x] \mathrm{d}^nx.](http://upload.wikimedia.org/math/c/2/5/c254f5efb8dbaa229990eebe6944d725.png)
![\frac{\delta \mathcal{S}[\phi]}{\delta \phi(x)}\approx 0](http://upload.wikimedia.org/math/1/5/a/15a9155583ac4337f36aa1a6ff3a6154.png)
![Q \left[ \int_N \mathcal{L} \, \mathrm{d}^n x \right] \approx \int_{\partial N} f^\mu [\phi(x),\partial\phi,\partial\partial\phi,\ldots] \, \mathrm{d}s_\mu](http://upload.wikimedia.org/math/a/0/a/a0a5797bc38b0444a8078b5ca8484d01.png)
![Q[\mathcal{L}(x)]\approx\partial_\mu f^\mu(x)](http://upload.wikimedia.org/math/4/6/e/46e611c92744d66d240a38e2e692f836.png)
![\mathcal{L}(x)=\mathcal{L}[\phi(x), \partial_\mu \phi(x),x].\](http://upload.wikimedia.org/math/6/5/e/65ef98213e3f023adf0ed1c866e99491.png)
![Q\left[\int_N \mathcal{L} \, \mathrm{d}^nx \right]](http://upload.wikimedia.org/math/9/6/c/96c7fef93bf3a13ee9350399e967fab5.png)
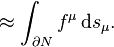
![\partial_\mu\left[\frac{\partial\mathcal{L}}{\partial(\partial_\mu\phi)}Q[\phi]-f^\mu\right]\approx 0.](http://upload.wikimedia.org/math/b/a/8/ba81243cac6c2b4e67ba18b3e2552d3a.png)
![J^\mu\,=\,\frac{\partial\mathcal{L}}{\partial(\partial_\mu\phi)}Q[\phi]-f^\mu,](http://upload.wikimedia.org/math/f/8/c/f8c883b8dd18e74ebe57bbc9d585a2ad.png)
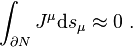
![Q_1[\mathcal{L}]\approx\partial_\mu f_1^\mu](http://upload.wikimedia.org/math/7/5/6/756487075fff546ecd5184def8efd44f.png)
![Q_2[\mathcal{L}]\approx\partial_\mu f_2^\mu](http://upload.wikimedia.org/math/f/f/e/ffe719678676321957cc8289a2c5bf54.png)
![[Q_1,Q_2][\mathcal{L}]=Q_1[Q_2[\mathcal{L}]]-Q_2[Q_1[\mathcal{L}]]\approx\partial_\mu f_{12}^\mu](http://upload.wikimedia.org/math/d/f/8/df8613fb4c5fd1d33b11f9797c159c57.png)
![j_{12}^\mu=\left(\frac{\partial}{\partial (\partial_\mu\phi)}\mathcal{L}\right)(Q_1[Q_2[\phi]]-Q_2[Q_1[\phi]])-f_{12}^\mu.](http://upload.wikimedia.org/math/e/2/c/e2cf8359a187cfbd228ca4ca0cc8ae74.png)
![Q[\mathcal{L}]\approx\partial_\mu f^\mu](http://upload.wikimedia.org/math/1/b/5/1b5c80503ceefac861f3d738a2149118.png)
![\begin{align}
q[\varepsilon][\mathcal{S}] & = \int q[\varepsilon][\mathcal{L}] \, \mathrm{d}^n x \\
& = \int \left\{ \left(\frac{\partial}{\partial \phi}\mathcal{L}\right) \varepsilon Q[\phi]+ \left[\frac{\partial}{\partial (\partial_\mu \phi)}\mathcal{L}\right]\partial_\mu(\varepsilon Q[\phi]) \right\} \, \mathrm{d}^n x \\
& = \int \left\{ \varepsilon Q[\mathcal{L}] + \partial_{\mu}\varepsilon \left[\frac{\partial}{\partial \left( \partial_\mu \phi\right)} \mathcal{L} \right] Q[\phi] \right\} \, \mathrm{d}^n x \\
& \approx \int \varepsilon \partial_\mu \left\{f^\mu-\left[\frac{\partial}{\partial (\partial_\mu\phi)}\mathcal{L}\right]Q[\phi]\right\} \, \mathrm{d}^n x
\end{align}](http://upload.wikimedia.org/math/7/9/c/79cf910baf3550d0968e9673c3907af2.png)
![\begin{align}
\mathcal{S}[x] & = \int L[x(t),\dot{x}(t)] \, dt \\
& = \int \left(\frac{m}{2}\sum_{i=1}^3\dot{x}_i^2-V(x(t))\right) \, dt.
\end{align}](http://upload.wikimedia.org/math/7/b/e/7be178316994bd30411b814b9afd7b69.png)
![Q[L]=m \sum_i\dot{x}_i\ddot{x}_i-\sum_i\frac{\partial V(x)}{\partial x_i}\dot{x}_i = \frac{d}{dt}\left[\frac{m}{2}\sum_i\dot{x}_i^2-V(x)\right]](http://upload.wikimedia.org/math/5/c/f/5cff0476366293b4668457847650e3f8.png)

![\begin{align}
j & = \sum_{i=1}^3\frac{\partial L}{\partial \dot{x}_i}Q[x_i]-f \\
& = m \sum_i\dot{x}_i^2 -\left[\frac{m}{2}\sum_i\dot{x}_i^2 -V(x)\right] \\
& = \frac{m}{2}\sum_i\dot{x}_i^2+V(x).
\end{align}](http://upload.wikimedia.org/math/e/8/8/e883bfc378039d069e6a28282d3bf4e7.png)

![\begin{align}
\mathcal{S}[\vec{x}] & = \int \mathcal{L}[\vec{x}(t),\dot{\vec{x}}(t)] \, \mathrm{d}t \\
& = \int \left [\sum^N_{\alpha=1} \frac{m_\alpha}{2}(\dot{\vec{x}}_\alpha)^2 -\sum_{\alpha<\beta} V_{\alpha\beta}(\vec{x}_\beta-\vec{x}_\alpha)\right] \, \mathrm{d}t
\end{align}](http://upload.wikimedia.org/math/b/2/0/b208b60bfc58b82d8e3c305944271af2.png)
![Q_i[x^j_\alpha(t)]=t \delta^j_i. \,](http://upload.wikimedia.org/math/1/9/a/19ad54603acce5b63020eb53c5a0e8c9.png)
![\begin{align}
Q_i[\mathcal{L}] & = \sum_\alpha m_\alpha \dot{x}_\alpha^i-\sum_{\alpha<\beta}\partial_i V_{\alpha\beta}(\vec{x}_\beta-\vec{x}_\alpha)(t-t) \\
& = \sum_\alpha m_\alpha \dot{x}_\alpha^i.
\end{align}](http://upload.wikimedia.org/math/5/2/f/52fbe41dee1c10f779057843009fcf83.png)

![\vec{j}=\sum_\alpha \left(\frac{\partial}{\partial \dot{\vec{x}}_\alpha}\mathcal{L}\right)\cdot\vec{Q}[\vec{x}_\alpha]-\vec{f}](http://upload.wikimedia.org/math/7/2/3/72378e7c90a2534d994fdffc72eab3e7.png)

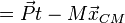
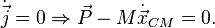
![\mathcal{S}[\phi]\,](http://upload.wikimedia.org/math/b/7/e/b7e3b1082fdde7d0599c6d1adf686bff.png)
![=\int \mathcal{L}[\phi (x),\partial_\mu \phi (x)] \, \mathrm{d}^4x](http://upload.wikimedia.org/math/2/1/0/2104e4252432104224b78dbb4e728bd4.png)
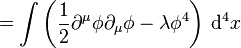
![Q[\phi(x)]=x^\mu\partial_\mu \phi(x)+\phi(x). \!](http://upload.wikimedia.org/math/e/3/a/e3a97d1d6748273dcdbf99df3a7954eb.png)
![Q[\mathcal{L}]=\partial^\mu\phi\left(\partial_\mu\phi+x^\nu\partial_\mu\partial_\nu\phi+\partial_\mu\phi\right)-4\lambda\phi^3\left(x^\mu\partial_\mu\phi+\phi\right).](http://upload.wikimedia.org/math/7/d/8/7d831f48aacd4dc53b1967e6e5a66ca4.png)
![\partial_\mu\left[\frac{1}{2}x^\mu\partial^\nu\phi\partial_\nu\phi-\lambda x^\mu \phi^4 \right] = \partial_\mu\left(x^\mu\mathcal{L}\right)](http://upload.wikimedia.org/math/1/e/2/1e27310e90848d15d418e410e9aaaf6a.png)

![j^\mu=\left[\frac{\partial}{\partial
(\partial_\mu\phi)}\mathcal{L}\right]Q[\phi]-f^\mu](http://upload.wikimedia.org/math/3/6/c/36cbe1cc7a9883228802af41dc8b82f6.png)




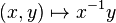
 as a parameter, this group can be
as a parameter, this group can be 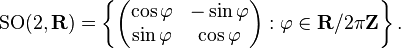
 Thus the Lie bracket on
Thus the Lie bracket on  is given explicitly by [v, w] = [v^, w^]e.
is given explicitly by [v, w] = [v^, w^]e. be a Lie group homomorphism and let
be a Lie group homomorphism and let  be its
be its 
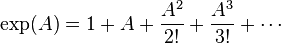


 is a Lie group homomorphism and
is a Lie group homomorphism and  the induced map on the corresponding Lie algebras, then for all
the induced map on the corresponding Lie algebras, then for all 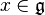 we have
we have

 is equal to the group of area preserving diffeomorphisms of a torus.
is equal to the group of area preserving diffeomorphisms of a torus.