In celestial mechanics, the Roche limit, also called Roche radius, is the distance in which a celestial body, held together only by its own gravity, will disintegrate due to a second celestial body's tidal forces exceeding the first body's gravitational self-attraction.[1] Inside the Roche limit, orbiting material disperses and forms rings whereas outside the limit material tends to coalesce. The term is named after Édouard Roche (pronounced [ʁɔʃ] (French), /rɔːʃ/ rawsh (English)), who is the French astronomer who first calculated this theoretical limit in 1848.[2]
Explanation
Comet Shoemaker-Levy 9 was disintegrated by the tidal forces of Jupiter into a string of smaller bodies in 1992, before colliding with the planet in 1994.
Typically, the Roche limit applies to a satellite's disintegrating due to tidal forces induced by its primary, the body about which it orbits. Parts of the satellite that are closer to the primary are attracted more strongly by gravity from the primary than parts that are farther away; this disparity effectively pulls the near and far parts of the satellite apart from each other, and if the disparity (combined with any centrifugal effects due to the object's spin) is larger than the force of gravity holding the satellite together, it can pull the satellite apart. Some real satellites, both natural and artificial, can orbit within their Roche limits because they are held together by forces other than gravitation. Objects resting on the surface of such a satellite would be lifted away by tidal forces. A weaker satellite, such as a comet, could be broken up when it passes within its Roche limit.
Since, within the Roche limit, tidal forces overwhelm the gravitational forces that might otherwise hold the satellite together, no satellite can gravitationally coalesce out of smaller particles within that limit. Indeed, almost all known planetary rings are located within their Roche limit, Saturn's E-Ring and Phoebe ring being notable exceptions. They could either be remnants from the planet's proto-planetary accretion disc that failed to coalesce into moonlets, or conversely have formed when a moon passed within its Roche limit and broke apart.
The Roche limit is not the only factor that causes comets to break apart. Splitting by thermal stress, internal gas pressure and rotational splitting are other ways for a comet to split under stress.
Selected examples
The table below shows the mean density and the equatorial radius for selected objects in the Solar System.| Primary | Density (kg/m3) | Radius (m) |
|---|---|---|
| Sun | 1,408 | 696,000,000 |
| Earth | 5,513 | 6,378,137 |
| Moon | 3,346 | 1,737,100 |
| Jupiter | 1,326 | 71,493,000 |
| Saturn | 687 | 60,267,000 |
| Uranus | 1,318 | 25,557,000 |
| Neptune | 1,638 | 24,766,000 |
The equations for the Roche limits relate the minimum sustainable orbital radius to the ratio of the two objects' densities and the Radius of the primary body. Hence, using the data above, the Roche limits for these objects can be calculated. This has been done twice for each, assuming the extremes of the rigid and fluid body cases. The average density of comets is taken to be around 500 kg/m³.
The table below gives the Roche limits expressed in kilometres and in primary radii. The mean radius of the orbit can be compared with the Roche limits. For convenience, the table lists the mean radius of the orbit for each, excluding the comets, whose orbits are extremely variable and eccentric.
| Body | Satellite | Roche limit (rigid) | Roche limit (fluid) | Mean orbital radius (km) | ||
|---|---|---|---|---|---|---|
| Distance (km) | R | Distance (km) | R | |||
| Earth | Moon | 9,492 | 1.49 | 18,381 | 2.88 | 384,399 |
| Earth | average comet | 17,887 | 2.80 | 34,638 | 5.43 | N/A |
| Sun | Earth | 556,397 | 0.80 | 1,077,467 | 1.55 | 149,597,890 |
| Sun | Jupiter | 894,677 | 1.29 | 1,732,549 | 2.49 | 778,412,010 |
| Sun | Moon | 657,161 | 0.94 | 1,272,598 | 1.83 | 149,597,890 Approx |
| Sun | average comet | 1,238,390 | 1.78 | 2,398,152 | 3.45 | N/A |
These bodies are well outside their Roche limits by various factors, from 21 for the Moon (over its fluid-body Roche limit) as part of the Earth–Moon system, upwards to hundreds for Earth and Jupiter.
The table below gives each satellite's closest approach in its orbit divided by its own Roche limit. Again, both rigid and fluid body calculations are given. Note that Pan, Cordelia and Naiad, in particular, may be quite close to their actual break-up points.
In practice, the densities of most of the inner satellites of giant planets are not known. In these cases, shown in italics, likely values have been assumed, but their actual Roche limit can vary from the value shown.
| Primary | Satellite | Orbital Radius / Roche limit | |
|---|---|---|---|
| (rigid) | (fluid) | ||
| Sun | Mercury | 104:1 | 54:1 |
| Earth | Moon | 41:1 | 21:1 |
| Mars | Phobos | 172% | 89% |
| Deimos | 451% | 234% | |
| Jupiter | Metis | ~186% | ~94% |
| Adrastea | ~188% | ~95% | |
| Amalthea | 175% | 88% | |
| Thebe | 254% | 128% | |
| Saturn | Pan | 142% | 70% |
| Atlas | 156% | 78% | |
| Prometheus | 162% | 80% | |
| Pandora | 167% | 83% | |
| Epimetheus | 200% | 99% | |
| Janus | 195% | 97% | |
| Uranus | Cordelia | ~154% | ~79% |
| Ophelia | ~166% | ~86% | |
| Bianca | ~183% | ~94% | |
| Cressida | ~191% | ~98% | |
| Desdemona | ~194% | ~100% | |
| Juliet | ~199% | ~102% | |
| Neptune | Naiad | ~139% | ~72% |
| Thalassa | ~145% | ~75% | |
| Despina | ~152% | ~78% | |
| Galatea | 153% | 79% | |
| Larissa | ~218% | ~113% | |
| Pluto | Charon | 12.5:1 | 6.5:1 |
Determination
The limiting distance to which a satellite can approach without breaking up depends on the rigidity of the satellite. At one extreme, a completely rigid satellite will maintain its shape until tidal forces break it apart. At the other extreme, a highly fluid satellite gradually deforms leading to increased tidal forces, causing the satellite to elongate, further compounding the tidal forces and causing it to break apart more readily.Most real satellites would lie somewhere between these two extremes, with tensile strength rendering the satellite neither perfectly rigid nor perfectly fluid. For example, a rubble-pile asteroid will behave more like a fluid than a solid rocky one; an icy body will behave quite rigidly at first but become more fluid as tidal heating accumulates and its ices begin to melt.
But note that, as defined above, the Roche limit refers to a body held together solely by the gravitational forces which cause otherwise unconnected particles to coalesce, thus forming the body in question. The Roche limit is also usually calculated for the case of a circular orbit, although it is straightforward to modify the calculation to apply to the case (for example) of a body passing the primary on a parabolic or hyperbolic trajectory.
Rigid-satellite calculation
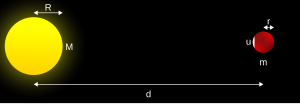
The rigid-body Roche limit is a simplified calculation for a spherical satellite. Irregular shapes such as those of tidal deformation on the body or the primary it orbits are neglected. It is assumed to be in hydrostatic equilibrium. These assumptions, although unrealistic, greatly simplify calculations.The Roche limit for a rigid spherical satellite is the distance,
 ,
from the primary at which the gravitational force on a test mass at the
surface of the object is exactly equal to the tidal force pulling the
mass away from the object:[3][4]
,
from the primary at which the gravitational force on a test mass at the
surface of the object is exactly equal to the tidal force pulling the
mass away from the object:[3][4] is the radius of the primary,
is the radius of the primary,  is the density of the primary, and
is the density of the primary, and  is the density of the satellite. This can be equivalently written as
is the density of the satellite. This can be equivalently written as is the radius of the secondary,
is the radius of the secondary,  is the mass of the primary, and
is the mass of the primary, and  is the mass of the secondary.
is the mass of the secondary.This does not depend on the size of the objects, but on the ratio of densities. This is the orbital distance inside of which loose material (e.g. regolith) on the surface of the satellite closest to the primary would be pulled away, and likewise material on the side opposite the primary will also be pulled away from, rather than toward, the satellite.
Note that this is an approximate result as inertia force and rigid structure are ignored in its derivation.
Derivation of the formula
Derivation of the Roche limit
In order to determine the Roche limit, consider a small mass
 on the surface of the satellite closest to the primary. There are two forces on this mass
on the surface of the satellite closest to the primary. There are two forces on this mass  : the gravitational pull towards the satellite and the gravitational pull towards the primary. Assume that the satellite is in free fall around the primary and that the tidal force
is the only relevant term of the gravitational attraction of the
primary. This assumption is a simplification as free-fall only truly
applies to the planetary center, but will suffice for this derivation.[5]
: the gravitational pull towards the satellite and the gravitational pull towards the primary. Assume that the satellite is in free fall around the primary and that the tidal force
is the only relevant term of the gravitational attraction of the
primary. This assumption is a simplification as free-fall only truly
applies to the planetary center, but will suffice for this derivation.[5]The gravitational pull
 on the mass
on the mass  towards the satellite with mass
towards the satellite with mass  and radius
and radius  can be expressed according to Newton's law of gravitation.
can be expressed according to Newton's law of gravitation. on the mass
on the mass  towards the primary with radius
towards the primary with radius  and mass
and mass  , at a distance
, at a distance  between the centers of the two bodies, can be expressed approximately as
between the centers of the two bodies, can be expressed approximately as.
 and
and  , it can be said that the
, it can be said that the  in the numerator and every term with
in the numerator and every term with  in the denominator goes to zero, which gives us:
in the denominator goes to zero, which gives us:,
 , as
, asFor a sphere the mass
 can be written as
can be written aswhere
is the radius of the primary.
where
is the radius of the satellite.
 gives
gives,
.
A more accurate formula
Since a close satellite will likely be orbiting in a nearly-circular orbit with synchronous rotation, consider how the centrifugal force from rotation will affect the results. That force is.......... (1)
 .......... (2)
.......... (2)Use
 (where
(where  is the radius of the satellite) to replace
is the radius of the satellite) to replace  in formula(1), we can have a third formula:
in formula(1), we can have a third formula:.......... (3)
Roche limit, Hill sphere and radius of the planet
Consider a planet with a density of and a radius of
and a radius of  , orbiting a star with a mass of M in a distant of R,
, orbiting a star with a mass of M in a distant of R,Let's place the planet on its Roche limit:
![R_{{{\mathrm {Roche}}}}={\sqrt[ {3}]{{\frac {9M}{4\pi \rho _{m}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59a740a9c4621892a6d59709e68a275a609fbc59)
Hill sphere of the planet here is around L1(or L2):
![R_{{{\mathrm {Hill}}}}=R_{{{\mathrm {Roche}}}}{\sqrt[ {3}]{{\frac {m}{3M}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c08102a73acb81669f492abf5d4e1c8667623d51) , Hill sphere ..........(4)
, Hill sphere ..........(4)![l={\sqrt[ {3}]{{\frac {9M}{4\pi \rho _{m}}}.{\frac {m}{3M}}}}=r](https://wikimedia.org/api/rest_v1/media/math/render/svg/02dd2c3bed69c3bce8063a93f7fd1d00f7632c20)
the surface of the planet coincide with the Roche lobe(or the planet fill full the Roche lobe)!
Celestial body cannot absorb any little thing or further more, lose its material.This is the physical meaning of Roche limit, Roche lobe and Hill sphere.
Formula(2) can be described as:
![R_{{{\text{Roche}}}}=R_{{{\text{Hill}}}}{\sqrt[ {3}]{{\frac {3M}{m}}}}=R_{{\text{secondary}}}{\sqrt[ {3}]{{\frac {3M}{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1714f4e75850812ae3341eba865677431e396822) , a perfect mathematical symmetry.
, a perfect mathematical symmetry.This is the astronomical significance of Roche limit and Hill sphere.
Fluid satellites
A more accurate approach for calculating the Roche limit takes the deformation of the satellite into account. An extreme example would be a tidally locked liquid satellite orbiting a planet, where any force acting upon the satellite would deform it into a prolate spheroid.The calculation is complex and its result cannot be represented in an exact algebraic formula. Roche himself derived the following approximate solution for the Roche limit:
 is the oblateness of the primary. The numerical factor is calculated with the aid of a computer.
is the oblateness of the primary. The numerical factor is calculated with the aid of a computer.The fluid solution is appropriate for bodies that are only loosely held together, such as a comet. For instance, comet Shoemaker–Levy 9's decaying orbit around Jupiter passed within its Roche limit in July 1992, causing it to fragment into a number of smaller pieces. On its next approach in 1994 the fragments crashed into the planet. Shoemaker–Levy 9 was first observed in 1993, but its orbit indicated that it had been captured by Jupiter a few decades prior.[6]
Derivation of the formula
As the fluid satellite case is more delicate than the rigid one, the satellite is described with some simplifying assumptions. First, assume the object consists of incompressible fluid that has constant density and volume
and volume  that do not depend on external or internal forces.
that do not depend on external or internal forces.Second, assume the satellite moves in a circular orbit and it remains in synchronous rotation. This means that the angular speed
 at which it rotates around its center of mass is the same as the angular speed at which it moves around the overall system barycenter.
at which it rotates around its center of mass is the same as the angular speed at which it moves around the overall system barycenter.The angular speed
 is given by Kepler's third law:
is given by Kepler's third law:Given these assumptions, the following forces should be taken into account:
- The force of gravitation due to the main body;
- the centrifugal force in the rotary reference system; and
- the self-gravitation field of the satellite.
Radial distance of one point on the surface of the ellipsoid to the center of mass
As the orbit has been assumed circular, the total gravitational force and orbital centrifugal force acting on the main body cancel. That leaves two forces: the tidal force and the rotational centrifugal force. The tidal force depends on the position with respect to the center of mass, already considered in the rigid model. For small bodies, the distance of the liquid particles from the center of the body is small in relation to the distance d to the main body. Thus the tidal force can be linearized, resulting in the same formula for FT as given above.
While this force in the rigid model depends only on the radius r of the satellite, in the fluid case, all the points on the surface must be considered, and the tidal force depends on the distance Δd from the center of mass to a given particle projected on the line joining the satellite and the main body. We call Δd the radial distance. Since the tidal force is linear in Δd, the related potential is proportional to the square of the variable and for
 we have
we have .
.We want to determine the shape of the satellite for which the sum of the self-gravitation potential and VT + VC is constant on the surface of the body. In general, such a problem is very difficult to solve, but in this particular case, it can be solved by a skillful guess due to the square dependence of the tidal potential on the radial distance Δd To a first approximation, we can ignore the centrifugal potential VC and consider only the tidal potential VT.
Since the potential VT changes only in one direction, i.e. the direction toward the main body, the satellite can be expected to take an axially symmetric form. More precisely, we may assume that it takes a form of a solid of revolution. The self-potential on the surface of such a solid of revolution can only depend on the radial distance to the center of mass. Indeed, the intersection of the satellite and a plane perpendicular to the line joining the bodies is a disc whose boundary by our assumptions is a circle of constant potential. Should the difference between the self-gravitation potential and VT be constant, both potentials must depend in the same way on Δd. In other words, the self-potential has to be proportional to the square of Δd. Then it can be shown that the equipotential solution is an ellipsoid of revolution. Given a constant density and volume the self-potential of such body depends only on the eccentricity ε of the ellipsoid:
 is the constant self-potential on the intersection of the circular edge
of the body and the central symmetry plane given by the equation Δd=0.
is the constant self-potential on the intersection of the circular edge
of the body and the central symmetry plane given by the equation Δd=0.The dimensionless function f is to be determined from the accurate solution for the potential of the ellipsoid
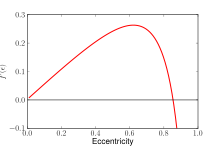
The graph of the dimensionless function f which indicates how the strength of the tidal potential depends on the eccentricity ε of the ellipsoid.
Although the explicit form of the function f looks complicated, it is clear that we may and do choose the value of ε so that the potential VT is equal to VS plus a constant independent of the variable Δd. By inspection, this occurs when
The derivative of f determines the maximal eccentricity. This gives the Roche limit.
More precisely, the Roche limit is determined by the fact that the function f, which can be regarded as a nonlinear measure of the force squeezing the ellipsoid towards a spherical shape, is bounded so that there is an eccentricity at which this contracting force becomes maximal. Since the tidal force increases when the satellite approaches the main body, it is clear that there is a critical distance at which the ellipsoid is torn up.
The maximal eccentricity can be calculated numerically as the zero of the derivative of f'. One obtains
























![{\displaystyle f(\epsilon )={\frac {1-\epsilon ^{2}}{\epsilon ^{3}}}\cdot \left[\left(3-\epsilon ^{2}\right)\cdot \operatorname {artanh} \epsilon -3\epsilon \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d1ede01bd864ef31d67fe4f82eb43d9028f5132)



![d \approx 2{.}423 \cdot R \cdot \sqrt[3]{ \frac {\rho_M} {\rho_m} } \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/adf67a6033e5be6374b2fc5aaff7408aef194ea6)
![d \approx 2{.}455 \cdot R \cdot \sqrt[3]{ \frac {\rho_M} {\rho_m} } \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/2acb36cc10937bd46bfa70894d73800e1f7b088c)



