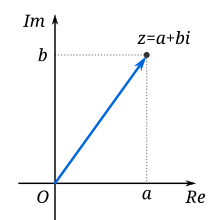
A complex number can be visually represented as a pair of numbers (a, b) forming a vector on a diagram called an Argand diagram, representing the complex plane. "Re" is the real axis, "Im" is the imaginary axis, and i satisfies i2 = −1.
A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is a solution of the equation x2 = −1. Because no real number satisfies this equation, i is called an imaginary number. For the complex number a + bi, a is called the real part, and b is called the imaginary part. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers, and are fundamental in many aspects of the scientific description of the natural world.[1][2]
The complex number system can be defined as the algebraic extension of the ordinary real numbers by an imaginary number i.[3] This means that complex numbers can be added, subtracted, and multiplied, as polynomials in the variable i, with the rule i2 = −1 imposed. Furthermore, complex numbers can also be divided by nonzero complex numbers. Overall, the complex number system is a field.
Most importantly the complex numbers give rise to the fundamental theorem of algebra: every non-constant polynomial equation with complex coefficients has a complex solution. This property is true of the complex numbers, but not the reals. The 16th century Italian mathematician Gerolamo Cardano is credited with introducing complex numbers in his attempts to find solutions to cubic equations.[4]
Geometrically, complex numbers extend the concept of the one-dimensional number line to the two-dimensional complex plane by using the horizontal axis for the real part and the vertical axis for the imaginary part. The complex number a + bi can be identified with the point (a, b) in the complex plane. A complex number whose real part is zero is said to be purely imaginary; the points for these numbers lie on the vertical axis of the complex plane. A complex number whose imaginary part is zero can be viewed as a real number; its point lies on the horizontal axis of the complex plane. Complex numbers can also be represented in polar form, which associates each complex number with its distance from the origin (its magnitude) and with a particular angle known as the argument of this complex number.
Overview
Complex numbers allow solutions to certain equations that have no solutions in real numbers. For example, the equationDefinition
An illustration of the complex plane. The real part of a complex number z = x + iy is x, and its imaginary part is y.
A complex number is a number of the form a + bi, where a and b are real numbers and i is an indeterminate satisfying i2 = −1. For example, 2 + 3i is a complex number.[5]
A complex number may therefore be defined as a polynomial in the single indeterminate i, with the relation i2 + 1 = 0 imposed. From this definition, complex numbers can be added or multiplied, using the addition and multiplication for polynomials. Formally, the set of complex numbers is the quotient ring of the polynomial ring in the indeterminate i, by the ideal generated by the polynomial i2 + 1 (see below).[6] The set of all complex numbers is denoted by
 (upright bold) or
(upright bold) or  (blackboard bold).
(blackboard bold).The real number a is called the real part of the complex number a + bi; the real number b is called the imaginary part of a + bi. By this convention, the imaginary part does not include a factor of i: hence b, not bi, is the imaginary part.[7][8] The real part of a complex number z is denoted by Re(z) or ℜ(z); the imaginary part of a complex number z is denoted by Im(z) or ℑ(z). For example,
Cartesian form and definition via ordered pairs
A complex number can thus be identified with an ordered pair (Re(z),Im(z)) in the Cartesian plane, an identification sometimes known as the Cartesian form of z. In fact, a complex number can be defined as an ordered pair (a,b), but then rules for addition and multiplication must also be included as part of the definition (see below).[9] William Rowan Hamilton introduced this approach to define the complex number system.[10]Complex plane
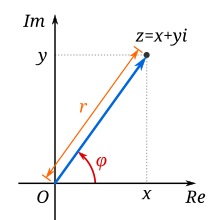
Figure 1: A complex number z, plotted as a point (red) and position vector (blue) on an Argand diagram; a+bi is its rectangular expression.
A complex number can be viewed as a point or position vector in a two-dimensional Cartesian coordinate system called the complex plane or Argand diagram (see Pedoe 1988 and Solomentsev 2001), named after Jean-Robert Argand. The numbers are conventionally plotted using the real part as the horizontal component, and imaginary part as vertical (see Figure 1). These two values used to identify a given complex number are therefore called its Cartesian, rectangular, or algebraic form.
A position vector may also be defined in terms of its magnitude and direction relative to the origin. These are emphasized in a complex number's polar form. Using the polar form of the complex number in calculations may lead to a more intuitive interpretation of mathematical results. Notably, the operations of addition and multiplication take on a very natural geometric character when complex numbers are viewed as position vectors: addition corresponds to vector addition while multiplication corresponds to multiplying their magnitudes and adding their arguments (i.e. the angles they make with the x axis). Viewed in this way the multiplication of a complex number by i corresponds to rotating the position vector counterclockwise by a quarter turn (90°) about the origin: (a+bi)i = ai+bi2 = -b+ai.
History in brief
The solution in radicals (without trigonometric functions) of a general cubic equation contains the square roots of negative numbers when all three roots are real numbers, a situation that cannot be rectified by factoring aided by the rational root test if the cubic is irreducible (the so-called casus irreducibilis). This conundrum led Italian mathematician Gerolamo Cardano to conceive of complex numbers in around 1545,[11] though his understanding was rudimentary.Work on the problem of general polynomials ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation of degree one or higher. Complex numbers thus form an algebraically closed field, where any polynomial equation has a root.
Many mathematicians contributed to the full development of complex numbers. The rules for addition, subtraction, multiplication, and division of complex numbers were developed by the Italian mathematician Rafael Bombelli.[12] A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton, who extended this abstraction to the theory of quaternions.
Notation
Because it is a polynomial in the indeterminate i, a + ib may be written instead of a + bi, which is often expedient when b is a radical.[13] In some disciplines, in particular electromagnetism and electrical engineering, j is used instead of i,[14] since i is frequently used for electric current. In these cases complex numbers are written as a + bj or a + jb.Equality and order relations
Two complex numbers are equal if and only if both their real and imaginary parts are equal. That is, complex numbers and
and  are equal if and only if
are equal if and only if  and
and  .
If the complex numbers are written in polar form, they are equal if and
only if they have the same argument and the same magnitude.
.
If the complex numbers are written in polar form, they are equal if and
only if they have the same argument and the same magnitude.Because complex numbers are naturally thought of as existing on a two-dimensional plane, there is no natural linear ordering on the set of complex numbers. Furthermore, there is no linear ordering on the complex numbers that is compatible with addition and multiplication – the complex numbers cannot have the structure of an ordered field. This is because any square in an ordered field is at least 0, but i2 = −1.
Elementary operations
Conjugate
Geometric representation of z and its conjugate  in the complex plane
in the complex plane
 in the complex plane
in the complex planeThe complex conjugate of the complex number z = x + yi is defined to be x − yi. It is denoted by either
 or z*.[15]
or z*.[15]Geometrically,
 is the "reflection" of z about the real axis. Conjugating twice gives the original complex number:
is the "reflection" of z about the real axis. Conjugating twice gives the original complex number:  .
.The real and imaginary parts of a complex number z can be extracted using the conjugate:
Conjugation distributes over the standard arithmetic operations:
Addition and subtraction
Addition of two complex numbers can be done geometrically by constructing a parallelogram.
Complex numbers are added by separately adding the real and imaginary parts of the summands. That is to say:
Multiplication and division
The multiplication of two complex numbers is defined by the following formula:(distributive property)
-
(commutative property of addition—the order of the summands can be changed)
(commutative and distributive properties)
(fundamental property of i).
-
Reciprocal
The reciprocal of a nonzero complex number z = x + yi is given bySquare root
The square roots of a + bi (with b ≠ 0) are , where
, where
 to obtain a + bi.[16][17] Here
to obtain a + bi.[16][17] Here  is called the modulus of a + bi, and the square root sign indicates the square root with non-negative real part, called the principal square root; also
is called the modulus of a + bi, and the square root sign indicates the square root with non-negative real part, called the principal square root; also  , where
, where  .[18]
.[18]Polar form
Figure 2: The argument φ and modulus r locate a point on an Argand diagram;  or
or  are polar expressions of the point.
are polar expressions of the point.
 or
or  are polar expressions of the point.
are polar expressions of the point.Absolute value and argument
An alternative way of defining a point P in the complex plane, other than using the x- and y-coordinates, is to use the distance of the point from O, the point whose coordinates are (0, 0) (the origin), together with the angle subtended between the positive real axis and the line segment OP in a counterclockwise direction. This idea leads to the polar form of complex numbers.The absolute value (or modulus or magnitude) of a complex number z = x + yi is[19]
By Pythagoras' theorem, the absolute value of complex number is the distance to the origin of the point representing the complex number in the complex plane.
The square of the absolute value is
 is the complex conjugate of
is the complex conjugate of  .
.The argument of z (in many applications referred to as the "phase") is the angle of the radius OP with the positive real axis, and is written as
 . As with the modulus, the argument can be found from the rectangular form
. As with the modulus, the argument can be found from the rectangular form  :[20]
:[20]
Visualisation of the square to sixth roots of a complex number z, in polar form reiφ where φ = arg z and r = |z | – if z is real, φ = 0 or π. Principal roots are in black.
Normally, as given above, the principal value in the interval (−π,π] is chosen. Values in the range [0,2π) are obtained by adding 2π if the value is negative. The value of φ is expressed in radians in this article. It can increase by any integer multiple of 2π and still give the same angle. Hence, the arg function is sometimes considered as multivalued. The polar angle for the complex number 0 is indeterminate, but arbitrary choice of the angle 0 is common.
The value of φ equals the result of atan2:
Multiplication and division in polar form
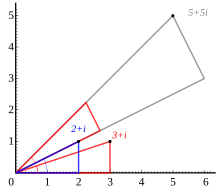
Multiplication of 2 + i (blue triangle) and 3 + i (red triangle). The red triangle is rotated to match the vertex of the blue one and stretched by √5, the length of the hypotenuse of the blue triangle.
Formulas for multiplication, division and exponentiation are simpler in polar form than the corresponding formulas in Cartesian coordinates. Given two complex numbers z1 = r1(cos φ1 + i sin φ1) and z2 = r2(cos φ2 + i sin φ2), because of the well-known trigonometric identities
Similarly, division is given by
Exponentiation
Euler's formula
Euler's formula states that, for any real number x,,
Natural logarithm
It follows from Euler's formula that, for any complex number z written in polar form, , so both
, so both  and
and  are two possible values for the natural logarithm of
are two possible values for the natural logarithm of  .
.To deal with the existence of more than one possible value for a given input, the complex logarithm may be considered a multi-valued function, with
Integer and fractional exponents
We may use the identityProperties
Field structure
The set C of complex numbers is a field.[22] Briefly, this means that the following facts hold: first, any two complex numbers can be added and multiplied to yield another complex number. Second, for any complex number z, its additive inverse −z is also a complex number; and third, every nonzero complex number has a reciprocal complex number. Moreover, these operations satisfy a number of laws, for example the law of commutativity of addition and multiplication for any two complex numbers z1 and z2:Unlike the reals, C is not an ordered field, that is to say, it is not possible to define a relation z1 < z2 that is compatible with the addition and multiplication. In fact, in any ordered field, the square of any element is necessarily positive, so i2 = −1 precludes the existence of an ordering on C.[23]
When the underlying field for a mathematical topic or construct is the field of complex numbers, the topic's name is usually modified to reflect that fact. For example: complex analysis, complex matrix, complex polynomial, and complex Lie algebra.
Solutions of polynomial equations
Given any complex numbers (called coefficients) a0, …, an, the equationThere are various proofs of this theorem, either by analytic methods such as Liouville's theorem, or topological ones such as the winding number, or a proof combining Galois theory and the fact that any real polynomial of odd degree has at least one real root.
Because of this fact, theorems that hold for any algebraically closed field, apply to C. For example, any non-empty complex square matrix has at least one (complex) eigenvalue.
Algebraic characterization
The field C has the following three properties: first, it has characteristic 0. This means that 1 + 1 + ⋯ + 1 ≠ 0 for any number of summands (all of which equal one). Second, its transcendence degree over Q, the prime field of C, is the cardinality of the continuum. Third, it is algebraically closed (see above). It can be shown that any field having these properties is isomorphic (as a field) to C. For example, the algebraic closure of Qp also satisfies these three properties, so these two fields are isomorphic (as fields, but not as topological fields).[25] Also, C is isomorphic to the field of complex Puiseux series. However, specifying an isomorphism requires the axiom of choice. Another consequence of this algebraic characterization is that C contains many proper subfields that are isomorphic to C.Characterization as a topological field
The preceding characterization of C describes only the algebraic aspects of C. That is to say, the properties of nearness and continuity, which matter in areas such as analysis and topology, are not dealt with. The following description of C as a topological field (that is, a field that is equipped with a topology, which allows the notion of convergence) does take into account the topological properties. C contains a subset P (namely the set of positive real numbers) of nonzero elements satisfying the following three conditions:- P is closed under addition, multiplication and taking inverses.
- If x and y are distinct elements of P, then either x − y or y − x is in P.
- If S is any nonempty subset of P, then S + P = x + P for some x in C.
Any field F with these properties can be endowed with a topology by taking the sets B(x, p) = { y | p − (y − x)(y − x)* ∈ P } as a base, where x ranges over the field and p ranges over P. With this topology F is isomorphic as a topological field to C.
The only connected locally compact topological fields are R and C. This gives another characterization of C as a topological field, since C can be distinguished from R because the nonzero complex numbers are connected, while the nonzero real numbers are not.[26]
Formal construction
Construction as ordered pairs
The set C of complex numbers can be defined as the set R2 of ordered pairs (a, b) of real numbers, in which the following rules for addition and multiplication are imposed:[27]Construction as a quotient field
Though this low-level construction does accurately describe the structure of the complex numbers, the following equivalent definition reveals the algebraic nature of C more immediately. This characterization relies on the notion of fields and polynomials. A field is a set endowed with addition, subtraction, multiplication and division operations that behave as is familiar from, say, rational numbers. For example, the distributive law,
The set of complex numbers is defined as the quotient ring R[X]/(X 2 + 1).[28] This extension field contains two square roots of −1, namely (the cosets of) X and −X, respectively. (The cosets of) 1 and X form a basis of R[X]/(X 2 + 1) as a real vector space, which means that each element of the extension field can be uniquely written as a linear combination in these two elements. Equivalently, elements of the extension field can be written as ordered pairs (a, b) of real numbers. The quotient ring is a field, because the (X2 + 1) is a prime ideal in R[X], a principal ideal domain, and therefore is a maximal ideal.
The formulas for addition and multiplication in the ring R[X], modulo the relation (X2 = 1 correspond to the formulas for addition and multiplication of complex numbers defined as ordered pairs. So the two definitions of the field C are isomorphic (as fields).
Accepting that C is algebraically closed, since it is an algebraic extension of R in this approach, C is therefore the algebraic closure of R.
Matrix representation of complex numbers
Complex numbers a + bi can also be represented by 2 × 2 matrices that have the following form: corresponds to the transpose of the matrix.
corresponds to the transpose of the matrix.Though this representation of complex numbers with matrices is the most common, many other representations arise from matrices other than
 that square to the negative of the identity matrix. See the article on 2 × 2 real matrices for other representations of complex numbers.
that square to the negative of the identity matrix. See the article on 2 × 2 real matrices for other representations of complex numbers.Complex analysis
Color wheel graph of sin(1/z). Black parts inside refer to numbers having large absolute values.
The study of functions of a complex variable is known as complex analysis and has enormous practical use in applied mathematics as well as in other branches of mathematics. Often, the most natural proofs for statements in real analysis or even number theory employ techniques from complex analysis (see prime number theorem for an example). Unlike real functions, which are commonly represented as two-dimensional graphs, complex functions have four-dimensional graphs and may usefully be illustrated by color-coding a three-dimensional graph to suggest four dimensions, or by animating the complex function's dynamic transformation of the complex plane.
The notions of convergent series and continuous functions in (real) analysis have natural analogs in complex analysis. A sequence of complex numbers is said to converge if and only if its real and imaginary parts do. This is equivalent to the (ε, δ)-definition of limits, where the absolute value of real numbers is replaced by the one of complex numbers. From a more abstract point of view, C, endowed with the metric
Like in real analysis, this notion of convergence is used to construct a number of elementary functions: the exponential function exp(z), also written ez, is defined as the infinite series
Euler's formula states:
Complex exponentiation zω is defined as
 is an integer. For ω = 1 / n, for some natural number n, this recovers the non-uniqueness of nth roots mentioned above.
is an integer. For ω = 1 / n, for some natural number n, this recovers the non-uniqueness of nth roots mentioned above.Complex numbers, unlike real numbers, do not in general satisfy the unmodified power and logarithm identities, particularly when naïvely treated as single-valued functions; see failure of power and logarithm identities. For example, they do not satisfy
Holomorphic functions
A function f : C → C is called holomorphic if it satisfies the Cauchy–Riemann equations. For example, any R-linear map C → C can be written in the form is real-differentiable, but does not satisfy the Cauchy–Riemann equations.
is real-differentiable, but does not satisfy the Cauchy–Riemann equations.Complex analysis shows some features not apparent in real analysis. For example, any two holomorphic functions f and g that agree on an arbitrarily small open subset of C necessarily agree everywhere. Meromorphic functions, functions that can locally be written as f(z)/(z − z0)n with a holomorphic function f, still share some of the features of holomorphic functions. Other functions have essential singularities, such as sin(1/z) at z = 0.
Applications
Complex numbers have essential concrete applications in a variety of scientific and related areas such as signal processing, control theory, electromagnetism, fluid dynamics, quantum mechanics, cartography, and vibration analysis. Some applications of complex numbers are:Control theory
In control theory, systems are often transformed from the time domain to the frequency domain using the Laplace transform. The system's zeros and poles are then analyzed in the complex plane. The root locus, Nyquist plot, and Nichols plot techniques all make use of the complex plane.In the root locus method, it is important whether zeros and poles are in the left or right half planes, i.e. have real part greater than or less than zero. If a linear, time-invariant (LTI) system has poles that are
- in the right half plane, it will be unstable,
- all in the left half plane, it will be stable,
- on the imaginary axis, it will have marginal stability.
Improper integrals
In applied fields, complex numbers are often used to compute certain real-valued improper integrals, by means of complex-valued functions. Several methods exist to do this; see methods of contour integration.Fluid dynamics
In fluid dynamics, complex functions are used to describe potential flow in two dimensions.Dynamic equations
In differential equations, it is common to first find all complex roots r of the characteristic equation of a linear differential equation or equation system and then attempt to solve the system in terms of base functions of the form f(t) = ert. Likewise, in difference equations, the complex roots r of the characteristic equation of the difference equation system are used, to attempt to solve the system in terms of base functions of the form f(t) = rt.Electromagnetism and electrical engineering
In electrical engineering, the Fourier transform is used to analyze varying voltages and currents. The treatment of resistors, capacitors, and inductors can then be unified by introducing imaginary, frequency-dependent resistances for the latter two and combining all three in a single complex number called the impedance. This approach is called phasor calculus.In electrical engineering, the imaginary unit is denoted by j, to avoid confusion with I, which is generally in use to denote electric current, or, more particularly, i, which is generally in use to denote instantaneous electric current.
Since the voltage in an AC circuit is oscillating, it can be represented as
 is called the analytic representation of the real-valued, measurable signal
is called the analytic representation of the real-valued, measurable signal  . [29]
. [29]Signal analysis
Complex numbers are used in signal analysis and other fields for a convenient description for periodically varying signals. For given real functions representing actual physical quantities, often in terms of sines and cosines, corresponding complex functions are considered of which the real parts are the original quantities. For a sine wave of a given frequency, the absolute value | z | of the corresponding z is the amplitude and the argument arg(z) is the phase.If Fourier analysis is employed to write a given real-valued signal as a sum of periodic functions, these periodic functions are often written as complex valued functions of the form
This use is also extended into digital signal processing and digital image processing, which utilize digital versions of Fourier analysis (and wavelet analysis) to transmit, compress, restore, and otherwise process digital audio signals, still images, and video signals.
Another example, relevant to the two side bands of amplitude modulation of AM radio, is:
Quantum mechanics
The complex number field is intrinsic to the mathematical formulations of quantum mechanics, where complex Hilbert spaces provide the context for one such formulation that is convenient and perhaps most standard. The original foundation formulas of quantum mechanics—the Schrödinger equation and Heisenberg's matrix mechanics—make use of complex numbers.Relativity
In special and general relativity, some formulas for the metric on spacetime become simpler if one takes the time component of the spacetime continuum to be imaginary. (This approach is no longer standard in classical relativity, but is used in an essential way in quantum field theory.) Complex numbers are essential to spinors, which are a generalization of the tensors used in relativity.Geometry
Fractals
Certain fractals are plotted in the complex plane, e.g. the Mandelbrot set and Julia sets.Triangles
Every triangle has a unique Steiner inellipse—an ellipse inside the triangle and tangent to the midpoints of the three sides of the triangle. The foci of a triangle's Steiner inellipse can be found as follows, according to Marden's theorem:[30][31] Denote the triangle's vertices in the complex plane as a = xA + yAi, b = xB + yBi, and c = xC + yCi. Write the cubic equation , take its derivative, and equate the (quadratic) derivative to zero. Marden's Theorem
says that the solutions of this equation are the complex numbers
denoting the locations of the two foci of the Steiner inellipse.
, take its derivative, and equate the (quadratic) derivative to zero. Marden's Theorem
says that the solutions of this equation are the complex numbers
denoting the locations of the two foci of the Steiner inellipse.Algebraic number theory
Construction of a regular pentagon using straightedge and compass.
As mentioned above, any nonconstant polynomial equation (in complex coefficients) has a solution in C. A fortiori, the same is true if the equation has rational coefficients. The roots of such equations are called algebraic numbers – they are a principal object of study in algebraic number theory. Compared to Q, the algebraic closure of Q, which also contains all algebraic numbers, C has the advantage of being easily understandable in geometric terms. In this way, algebraic methods can be used to study geometric questions and vice versa. With algebraic methods, more specifically applying the machinery of field theory to the number field containing roots of unity, it can be shown that it is not possible to construct a regular nonagon using only compass and straightedge – a purely geometric problem.
Another example are Gaussian integers, that is, numbers of the form x + iy, where x and y are integers, which can be used to classify sums of squares.
Analytic number theory
Analytic number theory studies numbers, often integers or rationals, by taking advantage of the fact that they can be regarded as complex numbers, in which analytic methods can be used. This is done by encoding number-theoretic information in complex-valued functions. For example, the Riemann zeta function ζ(s) is related to the distribution of prime numbers.History
The earliest fleeting reference to square roots of negative numbers can perhaps be said to occur in the work of the Greek mathematician Hero of Alexandria in the 1st century AD, where in his Stereometrica he considers, apparently in error, the volume of an impossible frustum of a pyramid to arrive at the term in his calculations, although negative quantities were not conceived of in Hellenistic mathematics and Heron merely replaced it by its positive (
in his calculations, although negative quantities were not conceived of in Hellenistic mathematics and Heron merely replaced it by its positive ( ).[32]
).[32]The impetus to study complex numbers as a topic in itself first arose in the 16th century when algebraic solutions for the roots of cubic and quartic polynomials were discovered by Italian mathematicians (see Niccolò Fontana Tartaglia, Gerolamo Cardano). It was soon realized that these formulas, even if one was only interested in real solutions, sometimes required the manipulation of square roots of negative numbers. As an example, Tartaglia's formula for a cubic equation of the form
 [33] gives the solution to the equation x3 = x as
[33] gives the solution to the equation x3 = x as and
and  . Substituting these in turn for
. Substituting these in turn for  in Tartaglia's cubic formula and simplifying, one gets 0, 1 and −1 as the solutions of x3 − x = 0.
Of course this particular equation can be solved at sight but it does
illustrate that when general formulas are used to solve cubic equations
with real roots then, as later mathematicians showed rigorously, the use
of complex numbers is unavoidable. Rafael Bombelli
was the first to explicitly address these seemingly paradoxical
solutions of cubic equations and developed the rules for complex
arithmetic trying to resolve these issues.
in Tartaglia's cubic formula and simplifying, one gets 0, 1 and −1 as the solutions of x3 − x = 0.
Of course this particular equation can be solved at sight but it does
illustrate that when general formulas are used to solve cubic equations
with real roots then, as later mathematicians showed rigorously, the use
of complex numbers is unavoidable. Rafael Bombelli
was the first to explicitly address these seemingly paradoxical
solutions of cubic equations and developed the rules for complex
arithmetic trying to resolve these issues.The term "imaginary" for these quantities was coined by René Descartes in 1637, although he was at pains to stress their imaginary nature[34]
[...] sometimes only imaginary, that is one can imagine as many as I said in each equation, but sometimes there exists no quantity that matches that which we imagine.A further source of confusion was that the equation
([...] quelquefois seulement imaginaires c’est-à-dire que l’on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu’il n’y a quelquefois aucune quantité qui corresponde à celle qu’on imagine.)
 seemed to be capriciously inconsistent with the algebraic identity
seemed to be capriciously inconsistent with the algebraic identity  , which is valid for non-negative real numbers a and b, and which was also used in complex number calculations with one of a, b positive and the other negative. The incorrect use of this identity (and the related identity
, which is valid for non-negative real numbers a and b, and which was also used in complex number calculations with one of a, b positive and the other negative. The incorrect use of this identity (and the related identity  ) in the case when both a and b are negative even bedeviled Euler. This difficulty eventually led to the convention of using the special symbol i in place of √−1 to guard against this mistake.[citation needed]
Even so, Euler considered it natural to introduce students to complex
numbers much earlier than we do today. In his elementary algebra text
book, Elements of Algebra, he introduces these numbers almost at once and then uses them in a natural way throughout.
) in the case when both a and b are negative even bedeviled Euler. This difficulty eventually led to the convention of using the special symbol i in place of √−1 to guard against this mistake.[citation needed]
Even so, Euler considered it natural to introduce students to complex
numbers much earlier than we do today. In his elementary algebra text
book, Elements of Algebra, he introduces these numbers almost at once and then uses them in a natural way throughout.In the 18th century complex numbers gained wider use, as it was noticed that formal manipulation of complex expressions could be used to simplify calculations involving trigonometric functions. For instance, in 1730 Abraham de Moivre noted that the complicated identities relating trigonometric functions of an integer multiple of an angle to powers of trigonometric functions of that angle could be simply re-expressed by the following well-known formula which bears his name, de Moivre's formula:
The idea of a complex number as a point in the complex plane (above) was first described by Caspar Wessel in 1799, although it had been anticipated as early as 1685 in Wallis's De Algebra tractatus.
Wessel's memoir appeared in the Proceedings of the Copenhagen Academy but went largely unnoticed. In 1806 Jean-Robert Argand independently issued a pamphlet on complex numbers and provided a rigorous proof of the fundamental theorem of algebra. Carl Friedrich Gauss had earlier published an essentially topological proof of the theorem in 1797 but expressed his doubts at the time about "the true metaphysics of the square root of −1". It was not until 1831 that he overcame these doubts and published his treatise on complex numbers as points in the plane, largely establishing modern notation and terminology. In the beginning of the 19th century, other mathematicians discovered independently the geometrical representation of the complex numbers: Buée, Mourey, Warren, Français and his brother, Bellavitis.[35]
The English mathematician G. H. Hardy remarked that Gauss was the first mathematician to use complex numbers in 'a really confident and scientific way' although mathematicians such as Niels Henrik Abel and Carl Gustav Jacob Jacobi were necessarily using them routinely before Gauss published his 1831 treatise.[36] Augustin Louis Cauchy and Bernhard Riemann together brought the fundamental ideas of complex analysis to a high state of completion, commencing around 1825 in Cauchy's case.
The common terms used in the theory are chiefly due to the founders. Argand called
 the direction factor, and
the direction factor, and  the modulus; Cauchy (1828) called
the modulus; Cauchy (1828) called  the reduced form (l'expression réduite) and apparently introduced the term argument; Gauss used i for
the reduced form (l'expression réduite) and apparently introduced the term argument; Gauss used i for  , introduced the term complex number for a + bi, and called a2 + b2 the norm. The expression direction coefficient, often used for
, introduced the term complex number for a + bi, and called a2 + b2 the norm. The expression direction coefficient, often used for  , is due to Hankel (1867), and absolute value, for modulus, is due to Weierstrass.
, is due to Hankel (1867), and absolute value, for modulus, is due to Weierstrass.Later classical writers on the general theory include Richard Dedekind, Otto Hölder, Felix Klein, Henri Poincaré, Hermann Schwarz, Karl Weierstrass and many others.
The process of extending the field R of reals to C is known as the Cayley–Dickson construction. It can be carried further to higher dimensions, yielding the quaternions H and octonions O which (as a real vector space) are of dimension 4 and 8, respectively. In this context the complex numbers have been called the binarions.[37]
However, just as applying the construction to reals loses the property of ordering, more properties familiar from real and complex numbers vanish with increasing dimension. The quaternions are not commutative, i.e. for some x, y: x·y ≠ y·x for two quaternions. The multiplication of octonions fails (in addition to not being commutative) to be associative: for some x, y, z: (x·y)·z ≠ x·(y·z).
Reals, complex numbers, quaternions and octonions are all normed division algebras over R. However, by Hurwitz's theorem they are the only ones. The next step in the Cayley–Dickson construction, the sedenions, in fact fails to have this structure.
The Cayley–Dickson construction is closely related to the regular representation of C, thought of as an R-algebra (an R-vector space with a multiplication), with respect to the basis (1, i). This means the following: the R-linear map
Hypercomplex numbers also generalize R, C, H, and O. For example, this notion contains the split-complex numbers, which are elements of the ring R[x]/(x2 − 1) (as opposed to R[x]/(x2 + 1)). In this ring, the equation a2 = 1 has four solutions.
The field R is the completion of Q, the field of rational numbers, with respect to the usual absolute value metric. Other choices of metrics on Q lead to the fields Qp of p-adic numbers (for any prime number p), which are thereby analogous to R. There are no other nontrivial ways of completing Q than R and Qp, by Ostrowski's theorem. The algebraic closures
 of Qp still carry a norm, but (unlike C) are not complete with respect to it. The completion
of Qp still carry a norm, but (unlike C) are not complete with respect to it. The completion  of
of  turns out to be algebraically closed. This field is called p-adic complex numbers by analogy.
turns out to be algebraically closed. This field is called p-adic complex numbers by analogy.The fields R and Qp and their finite field extensions, including C, are local fields.






































![{\begin{aligned}e^{ix}&{}=1+ix+{\frac {(ix)^{2}}{2!}}+{\frac {(ix)^{3}}{3!}}+{\frac {(ix)^{4}}{4!}}+{\frac {(ix)^{5}}{5!}}+{\frac {(ix)^{6}}{6!}}+{\frac {(ix)^{7}}{7!}}+{\frac {(ix)^{8}}{8!}}+\cdots \\[8pt]&{}=1+ix-{\frac {x^{2}}{2!}}-{\frac {ix^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {ix^{5}}{5!}}-{\frac {x^{6}}{6!}}-{\frac {ix^{7}}{7!}}+{\frac {x^{8}}{8!}}+\cdots \\[8pt]&{}=\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+{\frac {x^{8}}{8!}}-\cdots \right)+i\left(x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \right)\\[8pt]&{}=\cos x+i\sin x\ .\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7d453ec298973d3dc0c734240525d1d3a0bbb58)






![{\sqrt[{n}]{z}}={\sqrt[{n}]{r}}\left(\cos \left({\frac {\varphi +2k\pi }{n}}\right)+i\sin \left({\frac {\varphi +2k\pi }{n}}\right)\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e5d6cb7a2f49d4c58bcfe75e7da5886a3bd9562)
![{\sqrt[{n}]{z^{n}}}=z](https://wikimedia.org/api/rest_v1/media/math/render/svg/22d19cc956fb6ef528720b6290a93f6232f54ec9)




















![v(t)=\mathrm {Re} (V)=\mathrm {Re} \left[V_{0}e^{j\omega t}\right]=V_{0}\cos \omega t.](https://wikimedia.org/api/rest_v1/media/math/render/svg/b66155dd3cd373aba4b6b5513fc702b0d6274408)



























