Hypothetical types of biochemistry

From Wikipedia, the free encyclopedia

 

False-color Cassini radar mosaic of Titan's north polar region; the blue areas are lakes of liquid hydrocarbons

"The existence of lakes of liquid hydrocarbons on Titan opens up the possibility for solvents and energy sources that are alternatives to those in our biosphere and that might support novel life forms altogether different from those on Earth."—NASA Astrobiology Roadmap 2008^[1]

Hypothetical types of biochemistry are forms of biochemistry speculated to be scientifically viable but not proven to exist at this time. The kinds of living organisms currently known on Earth all use carbon compounds for basic structural and metabolic functions, water as a solvent, and DNA or RNA to define and control their form. If life exists on other planets or moons, it may be chemically similar; it is also possible that there are organisms with quite different chemistries—for instance, involving other classes of carbon compounds, compounds of another element, or another solvent in place of water.

The possibility of life-forms being based on "alternative" biochemistries is the topic of an ongoing scientific discussion, informed by what is known about extraterrestrial environments and about the chemical behaviour of various elements and compounds. It is also a common subject in science fiction.

The element silicon has been much discussed as a hypothetical alternative to carbon. Silicon is in the same group as carbon on the periodic table and, like carbon, it is tetravalent, although the silicon analogs of organic compounds are generally less stable. Hypothetical alternatives to water include ammonia, which, like water, is a polar molecule, and cosmically abundant; and non-polar hydrocarbon solvents such as methane and ethane, which are known to exist in liquid form on the surface of Titan.

Shadow biosphere

The Arecibo message (1974) sent information into space about basic chemistry of Earth life.

A shadow biosphere is a hypothetical microbial biosphere of Earth that uses radically different biochemical and molecular processes than currently known life.^[4][5] Although life on Earth is relatively well-studied, the shadow biosphere may still remain unnoticed because the exploration of the microbial world targets primarily the biochemistry of the macro-organisms.

Alternative-chirality biomolecules

Perhaps the least unusual alternative biochemistry would be one with differing chirality of its biomolecules. In known Earth-based life, amino acids are almost universally of the L form and sugars are of the D form. Molecules of opposite chirality have identical chemical properties to their mirrored forms, so life that used D amino acids or L sugars may be possible; molecules of such a chirality, however, would be incompatible with organisms using the opposing chirality molecules. Amino acids whose chirality is opposite to the norm are found on Earth, and these substances are generally thought to result from decay of organisms of normal chirality. However, physicist Paul Davies speculates that some of them might be products of "anti-chiral" life.^[6]

It is questionable, however, whether such a biochemistry would be truly alien. Although it would certainly be an alternative stereochemistry, molecules that are overwhelmingly found in one enantiomer throughout the vast majority of organisms can nonetheless often be found in another enantiomer in different (often basal) organisms such as in comparisons between members of Archaea and other domains,^{[citation needed]} making it an open topic whether an alternative stereochemistry is truly novel.

Non-carbon-based biochemistries

On Earth, all known living things have a carbon-based structure and system. Scientists have speculated about the pros and cons of using atoms other than carbon to form the molecular structures necessary for life, but no one has proposed a theory employing such atoms to form all the necessary structures. However, as Carl Sagan argued, it is very difficult to be certain whether a statement that applies to all life on Earth will turn out to apply to all life throughout the universe.^[7] Sagan used the term "carbon chauvinism" for such an assumption.^[8] He regarded silicon and germanium as conceivable alternatives to carbon;^[8] but, on the other hand, he noted that carbon does seem more chemically versatile and is more abundant in the cosmos.^[9]

Silicon biochemistry

Structure of silane, analog of methane.

 

Structure of the silicone polydimethylsiloxane (PDMS).

 

Marine diatoms—carbon-based organisms that extract silicon from sea water, in the form of its oxide (silica) and incorporate it into their cell walls

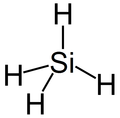
The silicon atom has been much discussed as the basis for an alternative biochemical system, because silicon has many chemical properties similar to those of carbon and is in the same group of the periodic table, the carbon group. Like carbon, silicon can create molecules that are sufficiently large to carry biological information.^[10]

However, silicon has several drawbacks as an alternative to carbon. Silicon, unlike carbon, lacks the ability to form chemical bonds with diverse types of atoms as is necessary for the chemical versatility required for metabolism. Elements creating organic functional groups with carbon include hydrogen, oxygen, nitrogen, phosphorus, sulfur, and metals such as iron, magnesium, and zinc. Silicon, on the other hand, interacts with very few other types of atoms.^[10] Moreover, where it does interact with other atoms, silicon creates molecules that have been described as "monotonous compared with the combinatorial universe of organic macromolecules".^[10] This is because silicon atoms are much bigger, having a larger mass and atomic radius, and so have difficulty forming double bonds (the double bonded carbon is part of the carbonyl group, a fundamental motif of bio-organic chemistry).

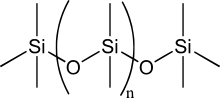
Silanes, which are chemical compounds of hydrogen and silicon that are analogous to the alkane hydrocarbons, are highly reactive with water, and long-chain silanes spontaneously decompose. Molecules incorporating polymers of alternating silicon and oxygen atoms instead of direct bonds between silicon, known collectively as silicones, are much more stable. It has been suggested that silicone-based chemicals would be more stable than equivalent hydrocarbons in a sulfuric-acid-rich environment, as is found in some extraterrestrial locations.^[11]

Of the varieties of molecules identified in the interstellar medium as of 1998, 84 are based on carbon while only 8 are based on silicon.^[12] Moreover, of those 8 compounds, four also include carbon within them. The cosmic abundance of carbon to silicon is roughly 10 to 1. This may suggest a greater variety of complex carbon compounds throughout the cosmos, providing less of a foundation on which to build silicon-based biologies, at least under the conditions prevalent on the surface of planets. Also, even though Earth and other terrestrial planets are exceptionally silicon-rich and carbon-poor (the relative abundance of silicon to carbon in Earth's crust is roughly 925:1), terrestrial life is carbon-based. The fact that carbon is used instead of silicon, may be evidence that silicon is poorly suited for biochemistry on Earth-like planets. Reasons for which may be that silicon is less versatile than carbon in forming compounds, that the compounds formed by silicon are unstable, and that it blocks the flow of heat.^[13]

Even so, biogenic silica is used by some Earth life, such as the silicate skeletal structure of diatoms. According to the clay hypothesis of A. G. Cairns-Smith, silicate minerals in water played a crucial role in abiogenesis: they replicated their crystal structures, interacted with carbon compounds, and were the precursors of carbon-based life.

Although not observed in nature, carbon–silicon bonds have been added to biochemistry by using directed evolution (artificial selection). A heme containing cytochrome c protein from Rhodothermus marinus has been engineered using directed evolution to catalyze the formation of new carbon–silicon bonds between hydrosilanes and diazo compounds.^[16]

Silicon compounds may possibly be biologically useful under temperatures or pressures different from the surface of a terrestrial planet, either in conjunction with or in a role less directly analogous to carbon. Polysilanols, the silicon compounds corresponding to sugars, are soluble in liquid nitrogen, suggesting that they could play a role in very low temperature biochemistry.

In cinematic and literary science fiction, at a moment when man-made machines cross from nonliving to living, it is often posited, this new form would be the first example of non-carbon-based life. Since the advent of the microprocessor in the late 1960s, these machines are often classed as computers (or computer-guided robots) and filed under "silicon-based life", even though the silicon backing matrix of these processors is not nearly as fundamental to their operation as carbon is for "wet life".

Other exotic element-based biochemistries

• Boranes are dangerously explosive in Earth's atmosphere, but would be more stable in a reducing environment. However, boron's low cosmic abundance makes it less likely as a base for life than carbon.
• Various metals, together with oxygen, can form very complex and thermally stable structures rivaling those of organic compounds;^{[citation needed]} the heteropoly acids are one such family. Some metal oxides are also similar to carbon in their ability to form both nanotube structures and diamond-like crystals (such as cubic zirconia). Titanium, aluminium, magnesium, and iron are all more abundant in the Earth's crust than carbon. Metal-oxide-based life could therefore be a possibility under certain conditions, including those (such as high temperatures) at which carbon-based life would be unlikely. The Cronin group at Glasgow University reported self-assembly of tungsten polyoxometalates into cell-like spheres.^[19] By modifying their metal oxide content, the spheres can acquire holes that act as porous membrane, selectively allowing chemicals in and out of the sphere according to size.^[19]
• Sulfur is also able to form long-chain molecules, but suffers from the same high-reactivity problems as phosphorus and silanes. The biological use of sulfur as an alternative to carbon is purely hypothetical, especially because sulfur usually forms only linear chains rather than branched ones. (The biological use of sulfur as an electron acceptor is widespread and can be traced back 3.5 billion years on Earth, thus predating the use of molecular oxygen.^[20] Sulfur-reducing bacteria can utilize elemental sulfur instead of oxygen, reducing sulfur to hydrogen sulfide.)

Arsenic as an alternative to phosphorus

Arsenic, which is chemically similar to phosphorus, while poisonous for most life forms on Earth, is incorporated into the biochemistry of some organisms.^[21] Some marine algae incorporate arsenic into complex organic molecules such as arsenosugars and arsenobetaines. Fungi and bacteria can produce volatile methylated arsenic compounds. Arsenate reduction and arsenite oxidation have been observed in microbes (Chrysiogenes arsenatis).^[22] Additionally, some prokaryotes can use arsenate as a terminal electron acceptor during anaerobic growth and some can utilize arsenite as an electron donor to generate energy.
It has been speculated that the earliest life forms on Earth may have used arsenic in place of phosphorus in the structure of their DNA.^[23] A common objection to this scenario is that arsenate esters are so much less stable to hydrolysis than corresponding phosphate esters that arsenic is poorly suited for this function.^[24]

The authors of a 2010 geomicrobiology study, supported in part by NASA, have postulated that a bacterium, named GFAJ-1, collected in the sediments of Mono Lake in eastern California, can employ such 'arsenic DNA' when cultured without phosphorus.^[25][26] They proposed that the bacterium may employ high levels of poly-β-hydroxybutyrate or other means to reduce the effective concentration of water and stabilize its arsenate esters.^[26] This claim was heavily criticized almost immediately after publication for the perceived lack of appropriate controls.^[27][28] Science writer Carl Zimmer contacted several scientists for an assessment: "I reached out to a dozen experts ... Almost unanimously, they think the NASA scientists have failed to make their case".^[29] Other authors were unable to reproduce their results and showed that the study had issues with phosphate contamination, suggesting that the low amounts present could sustain extremophile lifeforms.^[30] Alternatively, it was suggested that GFAJ-1 cells grow by recycling phosphate from degraded ribosomes, rather than by replacing it with arsenate.^[31]

Non-water solvents

Carl Sagan speculated alien life might use ammonia, hydrocarbons or hydrogen fluoride instead of water.

In addition to carbon compounds, all currently known terrestrial life also requires water as a solvent. This has led to discussions about whether water is the only liquid capable of filling that role. The idea that an extraterrestrial life-form might be based on a solvent other than water has been taken seriously in recent scientific literature by the biochemist Steven Benner,^[32] and by the astrobiological committee chaired by John A. Baross.^[33] Solvents discussed by the Baross committee include ammonia,^[34] sulfuric acid,^[35] formamide,^[36] hydrocarbons,^[36] and (at temperatures much lower than Earth's) liquid nitrogen, or hydrogen in the form of a supercritical fluid.

Carl Sagan once described himself as both a carbon chauvinist and a water chauvinist;^[38] however on another occasion he said he was a carbon chauvinist but "not that much of a water chauvinist".^[39] He speculated on hydrocarbons,^[39]:11 hydrofluoric acid,^[40] and ammonia^[39][40] as possible alternatives to water.

Some of the properties of water that are important for life processes include a large temperature range over which it is liquid, a high heat capacity (useful for temperature regulation), a large heat of vaporization, and the ability to dissolve a wide variety of compounds. Water is also amphoteric, meaning it can donate and accept an H⁺ ion, allowing it to act as an acid or a base. This property is crucial in many organic and biochemical reactions, where water serves as a solvent, a reactant, or a product. There are other chemicals with similar properties that have sometimes been proposed as alternatives. Additionally, water has the unusual property of being less dense as a solid (ice) than as a liquid. This is why bodies of water freeze over but do not freeze solid (from the bottom up). If ice were denser than liquid water (as is true for nearly all other compounds), then large bodies of liquid would slowly freeze solid, which would not be conducive to the formation of life. Water as a compound is cosmically abundant, although much of it is in the form of vapour or ice. Subsurface liquid water is considered likely or possible on several of the outer moons: Enceladus (where geysers have been observed), Europa, Titan, and Ganymede. Earth and Titan are the only worlds currently known to have stable bodies of liquid on their surfaces.

Not all properties of water are necessarily advantageous for life, however.^[41] For instance, water ice has a high albedo,^[41] meaning that it reflects a significant quantity of light and heat from the Sun. During ice ages, as reflective ice builds up over the surface of the water, the effects of global cooling are increased.^[41]

There are some properties that make certain compounds and elements much more favorable than others as solvents in a successful biosphere. The solvent must be able to exist in liquid equilibrium over a range of temperatures the planetary object would normally encounter. Because boiling points vary with the pressure, the question tends not to be does the prospective solvent remain liquid, but at what pressure. For example, hydrogen cyanide has a narrow liquid phase temperature range at 1 atmosphere, but in an atmosphere with the pressure of Venus, with 92 bars (91 atm) of pressure, it can indeed exist in liquid form over a wide temperature range.

Ammonia

Artist's conception of how a planet with ammonia-based life might look.

The ammonia molecule (NH₃), like the water molecule, is abundant in the universe, being a compound of hydrogen (the simplest and most common element) with another very common element, nitrogen.^[42] The possible role of liquid ammonia as an alternative solvent for life is an idea that goes back at least to 1954, when J.B.S. Haldane raised the topic at a symposium about life's origin.^[43]

Numerous chemical reactions are possible in an ammonia solution, and liquid ammonia has chemical similarities with water.^[42][44] Ammonia can dissolve most organic molecules at least as well as water does and, in addition, it is capable of dissolving many elemental metals. Haldane made the point that various common water-related organic compounds have ammonia-related analogs; for instance the ammonia-related amine group (-NH₂) is analogous to the water-related hydroxyl group (-OH).^[44]

Ammonia, like water, can either accept or donate an H⁺ ion. When ammonia accepts an H⁺, it forms the ammonium cation (NH₄⁺), analogous to hydronium (H₃O⁺). When it donates an H⁺ ion, it forms the amide anion (NH₂⁻), analogous to the hydroxide anion (OH⁻).^[34] Compared to water, however, ammonia is more inclined to accept an H⁺ ion, and less inclined to donate one; it is a stronger nucleophile.^[34] Ammonia added to water functions as Arrhenius base: it increases the concentration of the anion hydroxide. Conversely, using a solvent system definition of acidity and basicity, water added to liquid ammonia functions as an acid, because it increases the concentration of the cation ammonium.^[44] The carbonyl group (C=O), which is much used in terrestrial biochemistry, would not be stable in ammonia solution, but the analogous imine group (C=NH) could be used instead.^[34]

However, ammonia has some problems as a basis for life. The hydrogen bonds between ammonia molecules are weaker than those in water, causing ammonia's heat of vaporization to be half that of water, its surface tension to be a third, and reducing its ability to concentrate non-polar molecules through a hydrophobic effect. Gerald Feinberg and Robert Shapiro have questioned whether ammonia could hold prebiotic molecules together well enough to allow the emergence of a self-reproducing system.^[45] Ammonia is also flammable in oxygen, and could not exist sustainably in an environment suitable for aerobic metabolism.

Titan's theorized internal structure, subsurface ocean shown blue.

A biosphere based on ammonia would likely exist at temperatures or air pressures that are extremely unusual in relation to life on Earth. Life on Earth usually exists within the melting point and boiling point of water at normal pressure, between 0 °C (273 K) and 100 °C (373 K); at normal pressure ammonia's melting and boiling points are between −78 °C (195 K) and −33 °C (240 K). Chemical reactions generally proceed more slowly at a lower temperature. Therefore, ammonia-based life, if it exists, might metabolize more slowly and evolve more slowly than life on Earth.^[46] On the other hand, lower temperatures could also enable living systems to use chemical species that would be too unstable at Earth temperatures to be useful.^[42]

Ammonia could be a liquid at Earth-like temperatures, but at much higher pressures; for example, at 60 atm, ammonia melts at −77 °C (196 K) and boils at 98 °C (371 K).^[34]

Ammonia and ammonia–water mixtures remain liquid at temperatures far below the freezing point of pure water, so such biochemistries might be well suited to planets and moons orbiting outside the water-based habitability zone. Such conditions could exist, for example, under the surface of Saturn's largest moon Titan.^[47]

Methane and other hydrocarbons

Methane (CH₄) is a simple hydrocarbon: that is, a compound of two of the most common elements in the cosmos, hydrogen and carbon. It has a cosmic abundance comparable with ammonia.^[42] Hydrocarbons could act as a solvent over a wide range of temperatures, but would lack polarity. Isaac Asimov, the biochemist and science fiction writer, suggested in 1981 that poly-lipids could form a substitute for proteins in a non-polar solvent such as methane.^[42] Lakes composed of a mixture of hydrocarbons, including methane and ethane, have been detected on the surface of Titan by the Cassini spacecraft.

There is debate about the effectiveness of methane and other hydrocarbons as a solvent for life compared to water or ammonia.^[48][49][50] Water is a stronger solvent than the hydrocarbons, enabling easier transport of substances in a cell.^[51] However, water is also more chemically reactive, and can break down large organic molecules through hydrolysis.^[48] A life-form whose solvent was a hydrocarbon would not face the threat of its biomolecules being destroyed in this way.^[48] Also, the water molecule's tendency to form strong hydrogen bonds can interfere with internal hydrogen bonding in complex organic molecules.^[41] Life with a hydrocarbon solvent could make more use of hydrogen bonds within its biomolecules.^[48] Moreover, the strength of hydrogen bonds within biomolecules would be appropriate to a low-temperature biochemistry.^[48]

Astrobiologist Chris McKay has argued, on thermodynamic grounds, that if life does exist on Titan's surface, using hydrocarbons as a solvent, it is likely also to use the more complex hydrocarbons as an energy source by reacting them with hydrogen, reducing ethane and acetylene to methane.^[52] Possible evidence for this form of life on Titan was identified in 2010 by Darrell Strobel of Johns Hopkins University; a greater abundance of molecular hydrogen in the upper atmospheric layers of Titan compared to the lower layers, arguing for a downward diffusion at a rate of roughly 10²⁵ molecules per second and disappearance of hydrogen near Titan's surface. As Strobel noted, his findings were in line with the effects Chris McKay had predicted if methanogenic life-forms were present.^[51][52][53] The same year, another study showed low levels of acetylene on Titan's surface, which were interpreted by Chris McKay as consistent with the hypothesis of organisms reducing acetylene to methane.^[51] While restating the biological hypothesis, McKay cautioned that other explanations for the hydrogen and acetylene findings are to be considered more likely: the possibilities of yet unidentified physical or chemical processes (e.g. a non-living surface catalyst enabling acetylene to react with hydrogen), or flaws in the current models of material flow.^[54] He noted that even a non-biological catalyst effective at 95 K would in itself be a startling discovery.^[54]

Azotosome

A hypothetical cell membrane termed an azotosome capable of functioning in liquid methane in Titan conditions was computer-modeled in a paper published in February 2015. Composed of acrylonitrile, a small molecule containing carbon, hydrogen, and nitrogen, it is predicted to have stability and flexibility in liquid methane comparable to that of a phospholipid bilayer (the type of cell membrane possessed by all life on Earth) in liquid water.^[55][56] An analysis of data obtained using the Atacama Large Millimeter / submillimeter Array (ALMA), completed in 2017, confirmed substantial amounts of acrylonitrile in Titan's atmosphere.^[57][58]

Hydrogen fluoride

Hydrogen fluoride (HF), like water, is a polar molecule, and due to its polarity it can dissolve many ionic compounds. Its melting point is −84 °C and its boiling point is 19.54 °C (at atmospheric pressure); the difference between the two is a little more than 100 K. HF also makes hydrogen bonds with its neighbor molecules, as do water and ammonia. It has been considered as a possible solvent for life by scientists such as Peter Sneath^[59] and Carl Sagan.^[40]

HF is dangerous to the systems of molecules that Earth-life is made of, but certain other organic compounds, such as paraffin waxes, are stable with it.^[40] Like water and ammonia, liquid hydrogen fluoride supports an acid-base chemistry. Using a solvent system definition of acidity and basicity, nitric acid functions as a base when it is added to liquid HF.^[60]

However, hydrogen fluoride is cosmically rare, unlike water, ammonia, and methane.^[61]

Hydrogen sulfide

Hydrogen sulfide is the closest chemical analog to water,^[62] but is less polar and a weaker inorganic solvent.^[63] Hydrogen sulfide is quite plentiful on Jupiter's moon Io, and may be in liquid form a short distance below the surface; and astrobiologist Dirk Schulze-Makuch has suggested it as a possible solvent for life there.^[64] On a planet with hydrogen-sulfide oceans the source of the hydrogen sulfide could come from volcanos, in which case it could be mixed in with a bit of hydrogen fluoride, which could help dissolve minerals. Hydrogen sulfide life might use a mixture of carbon monoxide and carbon dioxide as their carbon source. They might produce and live off of sulfur monoxide, which is analogous to oxygen (O₂). Hydrogen sulfide, like hydrogen cyanide and ammonia, suffers from the small temperature range where it is liquid, though that, like that of hydrogen cyanide and ammonia, increases with increasing pressure.

Silicon dioxide and silicates

Silicon dioxide, also known as glass, silica, or quartz, is very abundant in the universe and has a large temperature range where it is liquid. However, its melting point is 1,600 to 1,725 °C (2,912 to 3,137 °F), so it would be impossible to make organic compounds in that temperature, because all of them would decompose. Silicates are similar to silicon dioxide and some could have lower boiling points than silica. Gerald Feinberg and Robert Shapiro have suggested that molten silicate rock could serve as a liquid medium for organisms with a chemistry based on silicon, oxygen, and other elements such as aluminium.^[65]

Other solvents or cosolvents

Sulfuric acid (H₂SO₄).

Other solvents sometimes proposed:

• Supercritical fluids: supercritical carbon dioxide and supercritical hydrogen^[66]
• Simple hydrogen compounds: hydrogen chloride^[67]
• More complex compounds: sulfuric acid,^[35] formamide,^[36] methanol^[67]
• Very-low-temperature fluids: liquid nitrogen,^[37] and hydrogen^[37]
• High-temperature liquids: sodium chloride^[68]

Sulfuric acid in liquid form is strongly polar. It remains liquid at higher temperatures than water, its liquid range being 10 °C to 337 °C at a pressure of 1 atm, although above 300 °C it will slowly decompose. Sulfuric acid is known to be abundant in the clouds of Venus, in the form of aerosol droplets. In a biochemistry that used sulfuric acid as a solvent, the alkene group (C=C), with two carbon atoms joined by a double bond, could function analogously to the carbonyl group (C=O) in water-based biochemistry.^[35]

A proposal has been made that life on Mars may exist and be using a mixture of water and hydrogen peroxide as its solvent.^[69] A 61.2% (by weight) mix of water and hydrogen peroxide has a freezing point of −56.5 °C, and also tends to super-cool rather than crystallize. It is also hygroscopic, an advantage in a water-scarce environment.^[70][71]

Supercritical carbon dioxide has been proposed as a candidate for alternative biochemistry due to its ability to selectively dissolve organic compounds and assist the functioning of enzymes and because "super-Earth"- or "super-Venus"-type planets with dense high-pressure atmospheres may be common.^[66]

Other speculations

Non-green photosynthesizers

Physicists have noted that, although photosynthesis on Earth generally involves green plants, a variety of other-colored plants could also support photosynthesis, essential for most life on Earth, and that other colors might be preferred in places that receive a different mix of stellar radiation than Earth.^[72][73] These studies indicate that, although blue photosynthetic plants would be less likely, yellow or red plants are plausible.^[73]

Variable environments

Many Earth plants and animals undergo major biochemical changes during their life cycles as a response to changing environmental conditions, for example, by having a spore or hibernation state that can be sustained for years or even millennia between more active life stages.^[74] Thus, it would be biochemically possible to sustain life in environments that are only periodically consistent with life as we know it.

For example, frogs in cold climates can survive for extended periods of time with most of their body water in a frozen state,^[74] whereas desert frogs in Australia can become inactive and dehydrate in dry periods, losing up to 75% of their fluids, yet return to life by rapidly rehydrating in wet periods.^[75] Either type of frog would appear biochemically inactive (i.e. not living) during dormant periods to anyone lacking a sensitive means of detecting low levels of metabolism.

Nonplanetary life

Dust and plasma-based

In 2007, Vadim N. Tsytovich and colleagues proposed that lifelike behaviors could be exhibited by dust particles suspended in a plasma, under conditions that might exist in space.^[76][77] Computer models showed that, when the dust became charged, the particles could self-organize into microscopic helical structures, and the authors offer "a rough sketch of a possible model of the helical grain structure reproduction".

Scientists who have published on this topic

Scientists who have considered possible alternatives to carbon-water biochemistry include:

• Isaac Asimov (1920–1992), biochemist and science fiction writer.^[42]
• William Bains, Cambridge biologist, a contributor to the journal Astrobiology.^[78]
• John Baross, oceanographer and astrobiologist, who chaired a committee of scientists under the United States National Research Council that published a report on life's limiting conditions in 2007.^[79] The report addresses the concern that a space agency might conduct a well-resourced search for life on other worlds "and then fail to recognize it if it is encountered".^[80]
• Gerald Feinberg (1933–1992), physicist and Robert Shapiro (1935–2011), chemist, co-authors of the book Life Beyond Earth.^[81][82]
• V.Axel Firsoff (1910–1981), British astronomer.^[83]
• Robert A. Freitas Jr. (1952–present), specialist in nano-technology and nano-medicine; author of the book Xenology.^[84][85]
• J. B. S. Haldane (1892–1964), a geneticist noted for his work on abiogenesis.^[43]
• George Pimentel (1922–1989), American chemist, University of California, Berkeley.^[86]
• Carl Sagan (1934–1996), astronomer,^[86] science popularizer, and SETI proponent.
• Peter Sneath (1923–2011), microbiologist, author of the book Planets and Life.^[59]
• Jonathan Lunine, (b. 1959) American planetary scientist and physicist

In fiction

• Alternate chirality: In Arthur C. Clarke's short story "Technical Error", there is an example of differing chirality.
• The concept of reversed chirality also figured prominently in the plot of James Blish's Star Trek novel Spock Must Die!, where a transporter experiment gone awry ends up creating a duplicate Spock who turns out to be a perfect mirror-image of the original all the way down to the atomic level.
• The eponymous organism in Michael Crichton's The Andromeda Strain is described as reproducing via the direct conversion of energy into matter.
• Silicoids: John Clark, in the introduction to the 1952 shared-world anthology The Petrified Planet, outlined the biologies of the planet Uller, with a mixture of siloxane and silicone life, and of Niflheim, where metabolism is based on hydrofluoric acid and carbon tetrafluoride.
• In the original Star Trek episode "The Devil in the Dark", a highly intelligent silicon-based creature called Horta, made almost entirely of pure rock, with eggs which take the form of silicon nodules scattered throughout the caverns and tunnels of its home planet. Subsequently, in the non-canonical Star Trek book 'The Romulan Way', another Horta is a junior officer in Starfleet.
• In Star Trek: The Next Generation, the Crystalline Entity appeared in two episodes, "Datalore" and "Silicon Avatar". This was an enormous spacefaring crystal lattice that had taken thousands of lives in its quest for energy. It was destroyed before communications could be established.
• In the Star Trek: The Next Generation episode "Home Soil" the Enterprise investigates the sabotage of a planetary terraforming station and the death of one of its members; these events are finally attributed to a completely non-organic, solar powered, saline thriving sentient life form.
• In the Star Trek: Enterprise episode "Observer Effect" Ensign Sato and Commander Tucker are infected by a silicon-based virus, while being observed by a non-physical life forms called Organians testing humanity if they are intelligent enough to engage in first contact. A reference to The Andromeda Strain (film) was also made in this episode.
• In the 1994 The X-Files episode "Firewalker", Mulder and Scully investigate a death in a remote research base and discover that a new silicon-based fungus found in the area may be affecting and killing the researchers.
• The Orion's Arm Universe Project, an online collaborative science-fiction project, includes a number of extraterrestrial species with exotic biochemistries, including organisms based on low-temperature carbohydrate chemistry, organisms that consume and live within sulfuric acid, and organisms composed of structured magnetic flux tubes within neutron stars or gas giant cores.

Dynamical system

From Wikipedia, the free encyclopedia

The Lorenz attractor arises in the study of the Lorenz Oscillator, a dynamical system.

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a lake.

At any given time, a dynamical system has a state given by a tuple of real numbers (a vector) that can be represented by a point in an appropriate state space (a geometrical manifold). The evolution rule of the dynamical system is a function that describes what future states follow from the current state. Often the function is deterministic, that is, for a given time interval only one future state follows from the current state.^[1][2] However, some systems are stochastic, in that random events also affect the evolution of the state variables.

In physics, a dynamical system is described as a "particle or ensemble of particles whose state varies over time and thus obeys differential equations involving time derivatives." In order to make a prediction about the system’s future behavior, an analytical solution of such equations or their integration over time through computer simulation is realized.

The study of dynamical systems is the focus of dynamical systems theory, which has applications to a wide variety of fields such as mathematics, physics, biology, chemistry, engineering, economics, and medicine. Dynamical systems are a fundamental part of chaos theory, logistic map dynamics, bifurcation theory, the self-assembly process, and the edge of chaos concept.

Overview

The concept of a dynamical system has its origins in Newtonian mechanics. There, as in other natural sciences and engineering disciplines, the evolution rule of dynamical systems is an implicit relation that gives the state of the system for only a short time into the future. (The relation is either a differential equation, difference equation or other time scale.) To determine the state for all future times requires iterating the relation many times—each advancing time a small step. The iteration procedure is referred to as solving the system or integrating the system. If the system can be solved, given an initial point it is possible to determine all its future positions, a collection of points known as a trajectory or orbit.

Before the advent of computers, finding an orbit required sophisticated mathematical techniques and could be accomplished only for a small class of dynamical systems. Numerical methods implemented on electronic computing machines have simplified the task of determining the orbits of a dynamical system.

For simple dynamical systems, knowing the trajectory is often sufficient, but most dynamical systems are too complicated to be understood in terms of individual trajectories. The difficulties arise because:

• The systems studied may only be known approximately—the parameters of the system may not be known precisely or terms may be missing from the equations. The approximations used bring into question the validity or relevance of numerical solutions. To address these questions several notions of stability have been introduced in the study of dynamical systems, such as Lyapunov stability or structural stability. The stability of the dynamical system implies that there is a class of models or initial conditions for which the trajectories would be equivalent. The operation for comparing orbits to establish their equivalence changes with the different notions of stability.
• The type of trajectory may be more important than one particular trajectory. Some trajectories may be periodic, whereas others may wander through many different states of the system. Applications often require enumerating these classes or maintaining the system within one class. Classifying all possible trajectories has led to the qualitative study of dynamical systems, that is, properties that do not change under coordinate changes. Linear dynamical systems and systems that have two numbers describing a state are examples of dynamical systems where the possible classes of orbits are understood.
• The behavior of trajectories as a function of a parameter may be what is needed for an application. As a parameter is varied, the dynamical systems may have bifurcation points where the qualitative behavior of the dynamical system changes. For example, it may go from having only periodic motions to apparently erratic behavior, as in the transition to turbulence of a fluid.
• The trajectories of the system may appear erratic, as if random. In these cases it may be necessary to compute averages using one very long trajectory or many different trajectories. The averages are well defined for ergodic systems and a more detailed understanding has been worked out for hyperbolic systems. Understanding the probabilistic aspects of dynamical systems has helped establish the foundations of statistical mechanics and of chaos.

History

Many people regard Henri Poincaré as the founder of dynamical systems.^[9] Poincaré published two now classical monographs, "New Methods of Celestial Mechanics" (1892–1899) and "Lectures on Celestial Mechanics" (1905–1910). In them, he successfully applied the results of their research to the problem of the motion of three bodies and studied in detail the behavior of solutions (frequency, stability, asymptotic, and so on). These papers included the Poincaré recurrence theorem, which states that certain systems will, after a sufficiently long but finite time, return to a state very close to the initial state.

Aleksandr Lyapunov developed many important approximation methods. His methods, which he developed in 1899, make it possible to define the stability of sets of ordinary differential equations. He created the modern theory of the stability of a dynamic system.

In 1913, George David Birkhoff proved Poincaré's "Last Geometric Theorem", a special case of the three-body problem, a result that made him world-famous. In 1927, he published his Dynamical SystemsBirkhoff's most durable result has been his 1931 discovery of what is now called the ergodic theorem. Combining insights from physics on the ergodic hypothesis with measure theory, this theorem solved, at least in principle, a fundamental problem of statistical mechanics. The ergodic theorem has also had repercussions for dynamics.

Stephen Smale made significant advances as well. His first contribution is the Smale horseshoe that jumpstarted significant research in dynamical systems. He also outlined a research program carried out by many others.

Oleksandr Mykolaiovych Sharkovsky developed Sharkovsky's theorem on the periods of discrete dynamical systems in 1964. One of the implications of the theorem is that if a discrete dynamical system on the real line has a periodic point of period 3, then it must have periodic points of every other period.

Basic definitions

A dynamical system is a manifold M called the phase (or state) space endowed with a family of smooth evolution functions Φ^t that for any element of t ∈ T, the time, map a point of the phase space back into the phase space. The notion of smoothness changes with applications and the type of manifold. There are several choices for the set T. When T is taken to be the reals, the dynamical system is called a flow; and if T is restricted to the non-negative reals, then the dynamical system is a semi-flow. When T is taken to be the integers, it is a cascade or a map; and the restriction to the non-negative integers is a semi-cascade.

Examples

The evolution function Φ ^t is often the solution of a differential equation of motion

${\displaystyle {\dot {x}}=v(x).}$

The equation gives the time derivative, represented by the dot, of a trajectory x(t) on the phase space starting at some point x₀. The vector field v(x) is a smooth function that at every point of the phase space M provides the velocity vector of the dynamical system at that point. (These vectors are not vectors in the phase space M, but in the tangent space T_xM of the point x.) Given a smooth Φ ^t, an autonomous vector field can be derived from it.

There is no need for higher order derivatives in the equation, nor for time dependence in v(x) because these can be eliminated by considering systems of higher dimensions. Other types of differential equations can be used to define the evolution rule:

${\displaystyle G(x,{\dot {x}})=0}$

is an example of an equation that arises from the modeling of mechanical systems with complicated constraints.

The differential equations determining the evolution function Φ ^t are often ordinary differential equations; in this case the phase space M is a finite dimensional manifold. Many of the concepts in dynamical systems can be extended to infinite-dimensional manifolds—those that are locally Banach spaces—in which case the differential equations are partial differential equations. In the late 20th century the dynamical system perspective to partial differential equations started gaining popularity.

Further examples

• Logistic map
• Complex quadratic polynomial
• Dyadic transformation
• Tent map
• Double pendulum
• Arnold's cat map
• Horseshoe map
• Baker's map is an example of a chaotic piecewise linear map
• Billiards and outer billiards
• Hénon map
• Lorenz system
• Circle map
• Rössler map
• Kaplan–Yorke map
• List of chaotic maps
• Swinging Atwood's machine
• Quadratic map simulation system
• Bouncing ball dynamics

Linear dynamical systems

Linear dynamical systems can be solved in terms of simple functions and the behavior of all orbits classified. In a linear system the phase space is the N-dimensional Euclidean space, so any point in phase space can be represented by a vector with N numbers. The analysis of linear systems is possible because they satisfy a superposition principle: if u(t) and w(t) satisfy the differential equation for the vector field (but not necessarily the initial condition), then so will u(t) + w(t).

Flows

For a flow, the vector field Φ(x) is an affine function of the position in the phase space, that is,

${\displaystyle {\dot {x}}=\phi (x)=Ax+b,}$

with A a matrix, b a vector of numbers and x the position vector. The solution to this system can be found by using the superposition principle (linearity). The case b ≠ 0 with A = 0 is just a straight line in the direction of b:

${\displaystyle \Phi ^{t}(x_{1})=x_{1}+bt.}$

When b is zero and A ≠ 0 the origin is an equilibrium (or singular) point of the flow, that is, if x₀ = 0, then the orbit remains there. For other initial conditions, the equation of motion is given by the exponential of a matrix: for an initial point x₀,

${\displaystyle \Phi ^{t}(x_{0})=e^{tA}x_{0}.}$

When b = 0, the eigenvalues of A determine the structure of the phase space. From the eigenvalues and the eigenvectors of A it is possible to determine if an initial point will converge or diverge to the equilibrium point at the origin.

The distance between two different initial conditions in the case A ≠ 0 will change exponentially in most cases, either converging exponentially fast towards a point, or diverging exponentially fast. Linear systems display sensitive dependence on initial conditions in the case of divergence. For nonlinear systems this is one of the (necessary but not sufficient) conditions for chaotic behavior.

Linear vector fields and a few trajectories.

Maps

A discrete-time, affine dynamical system has the form of a matrix difference equation:

${\displaystyle x_{n+1}=Ax_{n}+b,}$

with A a matrix and b a vector. As in the continuous case, the change of coordinates x → x + (1 − A) ^–1b removes the term b from the equation. In the new coordinate system, the origin is a fixed point of the map and the solutions are of the linear system A ⁿx₀. The solutions for the map are no longer curves, but points that hop in the phase space. The orbits are organized in curves, or fibers, which are collections of points that map into themselves under the action of the map.

As in the continuous case, the eigenvalues and eigenvectors of A determine the structure of phase space. For example, if u₁ is an eigenvector of A, with a real eigenvalue smaller than one, then the straight lines given by the points along α u₁, with α ∈ R, is an invariant curve of the map. Points in this straight line run into the fixed point.

There are also many other discrete dynamical systems.

Local dynamics

The qualitative properties of dynamical systems do not change under a smooth change of coordinates (this is sometimes taken as a definition of qualitative): a singular point of the vector field (a point where v(x) = 0) will remain a singular point under smooth transformations; a periodic orbit is a loop in phase space and smooth deformations of the phase space cannot alter it being a loop. It is in the neighborhood of singular points and periodic orbits that the structure of a phase space of a dynamical system can be well understood. In the qualitative study of dynamical systems, the approach is to show that there is a change of coordinates (usually unspecified, but computable) that makes the dynamical system as simple as possible.

Rectification

A flow in most small patches of the phase space can be made very simple. If y is a point where the vector field v(y) ≠ 0, then there is a change of coordinates for a region around y where the vector field becomes a series of parallel vectors of the same magnitude. This is known as the rectification theorem.

The rectification theorem says that away from singular points the dynamics of a point in a small patch is a straight line. The patch can sometimes be enlarged by stitching several patches together, and when this works out in the whole phase space M the dynamical system is integrable. In most cases the patch cannot be extended to the entire phase space. There may be singular points in the vector field (where v(x) = 0); or the patches may become smaller and smaller as some point is approached. The more subtle reason is a global constraint, where the trajectory starts out in a patch, and after visiting a series of other patches comes back to the original one. If the next time the orbit loops around phase space in a different way, then it is impossible to rectify the vector field in the whole series of patches.

Near periodic orbits

In general, in the neighborhood of a periodic orbit the rectification theorem cannot be used. Poincaré developed an approach that transforms the analysis near a periodic orbit to the analysis of a map. Pick a point x₀ in the orbit γ and consider the points in phase space in that neighborhood that are perpendicular to v(x₀). These points are a Poincaré section S(γ, x₀), of the orbit. The flow now defines a map, the Poincaré map F : S → S, for points starting in S and returning to S. Not all these points will take the same amount of time to come back, but the times will be close to the time it takes x₀.

The intersection of the periodic orbit with the Poincaré section is a fixed point of the Poincaré map F. By a translation, the point can be assumed to be at x = 0. The Taylor series of the map is F(x) = J · x + O(x²), so a change of coordinates h can only be expected to simplify F to its linear part

${\displaystyle h^{-1}\circ F\circ h(x)=J\cdot x.}$

This is known as the conjugation equation. Finding conditions for this equation to hold has been one of the major tasks of research in dynamical systems. Poincaré first approached it assuming all functions to be analytic and in the process discovered the non-resonant condition. If λ₁, ..., λ_ν are the eigenvalues of J they will be resonant if one eigenvalue is an integer linear combination of two or more of the others. As terms of the form λ_i – ∑ (multiples of other eigenvalues) occurs in the denominator of the terms for the function h, the non-resonant condition is also known as the small divisor problem.

Conjugation results

The results on the existence of a solution to the conjugation equation depend on the eigenvalues of J and the degree of smoothness required from h. As J does not need to have any special symmetries, its eigenvalues will typically be complex numbers. When the eigenvalues of J are not in the unit circle, the dynamics near the fixed point x₀ of F is called hyperbolic and when the eigenvalues are on the unit circle and complex, the dynamics is called elliptic.

In the hyperbolic case, the Hartman–Grobman theorem gives the conditions for the existence of a continuous function that maps the neighborhood of the fixed point of the map to the linear map J · x. The hyperbolic case is also structurally stable. Small changes in the vector field will only produce small changes in the Poincaré map and these small changes will reflect in small changes in the position of the eigenvalues of J in the complex plane, implying that the map is still hyperbolic.

The Kolmogorov–Arnold–Moser (KAM) theorem gives the behavior near an elliptic point.

Bifurcation theory

When the evolution map Φ^t (or the vector field it is derived from) depends on a parameter μ, the structure of the phase space will also depend on this parameter. Small changes may produce no qualitative changes in the phase space until a special value μ₀ is reached. At this point the phase space changes qualitatively and the dynamical system is said to have gone through a bifurcation.
Bifurcation theory considers a structure in phase space (typically a fixed point, a periodic orbit, or an invariant torus) and studies its behavior as a function of the parameter μ. At the bifurcation point the structure may change its stability, split into new structures, or merge with other structures. By using Taylor series approximations of the maps and an understanding of the differences that may be eliminated by a change of coordinates, it is possible to catalog the bifurcations of dynamical systems.

The bifurcations of a hyperbolic fixed point x₀ of a system family F_μ can be characterized by the eigenvalues of the first derivative of the system DF_μ(x₀) computed at the bifurcation point. For a map, the bifurcation will occur when there are eigenvalues of DF_μ on the unit circle. For a flow, it will occur when there are eigenvalues on the imaginary axis. For more information, see the main article on Bifurcation theory.

Some bifurcations can lead to very complicated structures in phase space. For example, the Ruelle–Takens scenario describes how a periodic orbit bifurcates into a torus and the torus into a strange attractor. In another example, Feigenbaum period-doubling describes how a stable periodic orbit goes through a series of period-doubling bifurcations.

Ergodic systems

In many dynamical systems, it is possible to choose the coordinates of the system so that the volume (really a ν-dimensional volume) in phase space is invariant. This happens for mechanical systems derived from Newton's laws as long as the coordinates are the position and the momentum and the volume is measured in units of (position) × (momentum). The flow takes points of a subset A into the points Φ ^t(A) and invariance of the phase space means that

${\displaystyle \mathrm {vol} (A)=\mathrm {vol} (\Phi ^{t}(A)).}$

In the Hamiltonian formalism, given a coordinate it is possible to derive the appropriate (generalized) momentum such that the associated volume is preserved by the flow. The volume is said to be computed by the Liouville measure.

In a Hamiltonian system, not all possible configurations of position and momentum can be reached from an initial condition. Because of energy conservation, only the states with the same energy as the initial condition are accessible. The states with the same energy form an energy shell Ω, a sub-manifold of the phase space. The volume of the energy shell, computed using the Liouville measure, is preserved under evolution.

For systems where the volume is preserved by the flow, Poincaré discovered the recurrence theorem: Assume the phase space has a finite Liouville volume and let F be a phase space volume-preserving map and A a subset of the phase space. Then almost every point of A returns to A infinitely often. The Poincaré recurrence theorem was used by Zermelo to object to Boltzmann's derivation of the increase in entropy in a dynamical system of colliding atoms.

One of the questions raised by Boltzmann's work was the possible equality between time averages and space averages, what he called the ergodic hypothesis. The hypothesis states that the length of time a typical trajectory spends in a region A is vol(A)/vol(Ω).

The ergodic hypothesis turned out not to be the essential property needed for the development of statistical mechanics and a series of other ergodic-like properties were introduced to capture the relevant aspects of physical systems. Koopman approached the study of ergodic systems by the use of functional analysis. An observable a is a function that to each point of the phase space associates a number (say instantaneous pressure, or average height). The value of an observable can be computed at another time by using the evolution function φ ^t. This introduces an operator U ^t, the transfer operator,

${\displaystyle (U^{t}a)(x)=a(\Phi ^{-t}(x)).}$

By studying the spectral properties of the linear operator U it becomes possible to classify the ergodic properties of Φ ^t. In using the Koopman approach of considering the action of the flow on an observable function, the finite-dimensional nonlinear problem involving Φ ^t gets mapped into an infinite-dimensional linear problem involving U.

The Liouville measure restricted to the energy surface Ω is the basis for the averages computed in equilibrium statistical mechanics. An average in time along a trajectory is equivalent to an average in space computed with the Boltzmann factor exp(−βH). This idea has been generalized by Sinai, Bowen, and Ruelle (SRB) to a larger class of dynamical systems that includes dissipative systems. SRB measures replace the Boltzmann factor and they are defined on attractors of chaotic systems.

Nonlinear dynamical systems and chaos

Simple nonlinear dynamical systems and even piecewise linear systems can exhibit a completely unpredictable behavior, which might seem to be random, despite the fact that they are fundamentally deterministic. This seemingly unpredictable behavior has been called chaos. Hyperbolic systems are precisely defined dynamical systems that exhibit the properties ascribed to chaotic systems. In hyperbolic systems the tangent space perpendicular to a trajectory can be well separated into two parts: one with the points that converge towards the orbit (the stable manifold) and another of the points that diverge from the orbit (the unstable manifold).
This branch of mathematics deals with the long-term qualitative behavior of dynamical systems. Here, the focus is not on finding precise solutions to the equations defining the dynamical system (which is often hopeless), but rather to answer questions like "Will the system settle down to a steady state in the long term, and if so, what are the possible attractors?" or "Does the long-term behavior of the system depend on its initial condition?"

Note that the chaotic behavior of complex systems is not the issue. Meteorology has been known for years to involve complex—even chaotic—behavior. Chaos theory has been so surprising because chaos can be found within almost trivial systems. The logistic map is only a second-degree polynomial; the horseshoe map is piecewise linear.

Geometrical definition

A dynamical system is the tuple ${\displaystyle \langle {\mathcal {M}},f,{\mathcal {T}}\rangle }$, with ${\displaystyle {\mathcal {M}}}$ a manifold (locally a Banach space or Euclidean space), ${\displaystyle {\mathcal {T}}}$ the domain for time (non-negative reals, the integers, ...) and f an evolution rule t → f ^t (with ${\displaystyle t\in {\mathcal {T}}}$) such that f ^t is a diffeomorphism of the manifold to itself. So, f is a mapping of the time-domain ${\displaystyle {\mathcal {T}}}$ into the space of diffeomorphisms of the manifold to itself. In other terms, f(t) is a diffeomorphism, for every time t in the domain ${\displaystyle {\mathcal {T}}}$ .

Measure theoretical definition

A dynamical system may be defined formally, as a measure-preserving transformation of a sigma-algebra, the quadruplet (X, Σ, μ, τ). Here, X is a set, and Σ is a sigma-algebra on X, so that the pair (X, Σ) is a measurable space. μ is a finite measure on the sigma-algebra, so that the triplet (X, Σ, μ) is a probability space. A map τ: X → X is said to be Σ-measurable if and only if, for every σ ∈ Σ, one has ${\displaystyle \tau ^{-1}\sigma \in \Sigma }$. A map τ is said to preserve the measure if and only if, for every σ ∈ Σ, one has ${\displaystyle \mu (\tau ^{-1}\sigma )=\mu (\sigma )}$. Combining the above, a map τ is said to be a measure-preserving transformation of X , if it is a map from X to itself, it is Σ-measurable, and is measure-preserving. The quadruple (X, Σ, μ, τ), for such a τ, is then defined to be a dynamical system.

The map τ embodies the time evolution of the dynamical system. Thus, for discrete dynamical systems the iterates ${\displaystyle \tau ^{n}=\tau \circ \tau \circ \cdots \circ \tau }$ for integer n are studied. For continuous dynamical systems, the map τ is understood to be a finite time evolution map and the construction is more complicated.

Examples of dynamical systems

• Arnold's cat map
• Baker's map is an example of a chaotic piecewise linear map
• Circle map
• Double pendulum
• Billiards and Outer billiards
• Hénon map
• Horseshoe map
• Irrational rotation
• List of chaotic maps
• Logistic map
• Lorenz system
• Rossler map

Multidimensional generalization

Dynamical systems are defined over a single independent variable, usually thought of as time. A more general class of systems are defined over multiple independent variables and are therefore called multidimensional systems. Such systems are useful for modeling, for example, image processing.

Self-replication

From Wikipedia, the free encyclopedia

Molecular structure of DNA

Self-replication is any behavior of a dynamical system that yields construction of an identical copy of itself. Biological cells, given suitable environments, reproduce by cell division. During cell division, DNA is replicated and can be transmitted to offspring during reproduction. Biological viruses can replicate, but only by commandeering the reproductive machinery of cells through a process of infection. Harmful prion proteins can replicate by converting normal proteins into rogue forms. Computer viruses reproduce using the hardware and software already present on computers. Self-replication in robotics has been an area of research and a subject of interest in science fiction. Any self-replicating mechanism which does not make a perfect copy will experience genetic variation and will create variants of itself. These variants will be subject to natural selection, since some will be better at surviving in their current environment than others and will out-breed them.

Overview

Theory

Early research by John von Neumann^[2] established that replicators have several parts:

• A coded representation of the replicator
• A mechanism to copy the coded representation
• A mechanism for effecting construction within the host environment of the replicator

Exceptions to this pattern are possible. For example, scientists have come close to constructing RNA that copies itself in an "environment" that is a solution of RNA monomers and transcriptase. In this case, the body is the genome, and the specialized copy mechanisms are external.
However, the simplest possible case is that only a genome exists. Without some specification of the self-reproducing steps, a genome-only system is probably better characterized as something like a crystal.

Classes of self-replication

Recent research^[3] has begun to categorize replicators, often based on the amount of support they require.

• Natural replicators have all or most of their design from nonhuman sources. Such systems include natural life forms.
• Autotrophic replicators can reproduce themselves "in the wild". They mine their own materials. It is conjectured that non-biological autotrophic replicators could be designed by humans, and could easily accept specifications for human products.
• Self-reproductive systems are conjectured systems which would produce copies of themselves from industrial feedstocks such as metal bar and wire.
• Self-assembling systems assemble copies of themselves from finished, delivered parts. Simple examples of such systems have been demonstrated at the macro scale.

The design space for machine replicators is very broad. A comprehensive study^[4] to date by Robert Freitas and Ralph Merkle has identified 137 design dimensions grouped into a dozen separate categories, including: (1) Replication Control, (2) Replication Information, (3) Replication Substrate, (4) Replicator Structure, (5) Passive Parts, (6) Active Subunits, (7) Replicator Energetics, (8) Replicator Kinematics, (9) Replication Process, (10) Replicator Performance, (11) Product Structure, and (12) Evolvability.

A self-replicating computer program

In computer science a quine is a self-reproducing computer program that, when executed, outputs its own code. For example, a quine in the Python programming language is:

a='a=%r;print a%%a';print a%a

A more trivial approach is to write a program that will make a copy of any stream of data that it is directed to, and then direct it at itself. In this case the program is treated as both executable code, and as data to be manipulated. This approach is common in most self-replicating systems, including biological life, and is simpler as it does not require the program to contain a complete description of itself.

In many programming languages an empty program is legal, and executes without producing errors or other output. The output is thus the same as the source code, so the program is trivially self-reproducing.

Self-replicating tiling

In geometry a self-replicating tiling is a tiling pattern in which several congruent tiles may be joined together to form a larger tile that is similar to the original. This is an aspect of the field of study known as tessellation. The "sphinx" hexiamond is the only known self-replicating pentagon.^[5] For example, four such concave pentagons can be joined together to make one with twice the dimensions.^[6] Solomon W. Golomb coined the term rep-tiles for self-replicating tilings.
In 2012, Lee Sallows identified rep-tiles as a special instance of a self-tiling tile set or setiset. A setiset of order n is a set of n shapes that can be assembled in n different ways so as to form larger replicas of themselves. Setisets in which every shape is distinct are called 'perfect'. A rep-n rep-tile is just a setiset composed of n identical pieces.

Four 'sphinx' hexiamonds can be put together to form another sphinx.

 

A perfect setiset of order 4

Applications

It is a long-term goal of some engineering sciences to achieve a clanking replicator, a material device that can self-replicate. The usual reason is to achieve a low cost per item while retaining the utility of a manufactured good. Many authorities say that in the limit, the cost of self-replicating items should approach the cost-per-weight of wood or other biological substances, because self-replication avoids the costs of labor, capital and distribution in conventional manufactured goods.

A fully novel artificial replicator is a reasonable near-term goal. A NASA study recently placed the complexity of a clanking replicator at approximately that of Intel's Pentium 4 CPU.^[7] That is, the technology is achievable with a relatively small engineering group in a reasonable commercial time-scale at a reasonable cost.

Given the currently keen interest in biotechnology and the high levels of funding in that field, attempts to exploit the replicative ability of existing cells are timely, and may easily lead to significant insights and advances.

A variation of self replication is of practical relevance in compiler construction, where a similar bootstrapping problem occurs as in natural self replication. A compiler (phenotype) can be applied on the compiler's own source code (genotype) producing the compiler itself. During compiler development, a modified (mutated) source is used to create the next generation of the compiler. This process differs from natural self-replication in that the process is directed by an engineer, not by the subject itself.

Mechanical self-replication

An activity in the field of robots is the self-replication of machines. Since all robots (at least in modern times) have a fair number of the same features, a self-replicating robot (or possibly a hive of robots) would need to do the following:

• Obtain construction materials
• Manufacture new parts including its smallest parts and thinking apparatus
• Provide a consistent power source
• Program the new members
• error correct any mistakes in the offspring

On a nano scale, assemblers might also be designed to self-replicate under their own power. This, in turn, has given rise to the "grey goo" version of Armageddon, as featured in such science fiction novels as Bloom, Prey, and Recursion.

The Foresight Institute has published guidelines for researchers in mechanical self-replication.^[8] The guidelines recommend that researchers use several specific techniques for preventing mechanical replicators from getting out of control, such as using a broadcast architecture.

For a detailed article on mechanical reproduction as it relates to the industrial age see mass production.

Fields

Research has occurred in the following areas:

• Biology studies natural replication and replicators, and their interaction. These can be an important guide to avoid design difficulties in self-replicating machinery.
• In Chemistry self-replication studies are typically about how a specific set of molecules can act together to replicate each other within the set ^[9] (often part of Systems chemistry field).
• Memetics studies ideas and how they propagate in human culture. Memes require only small amounts of material, and therefore have theoretical similarities to viruses and are often described as viral.
• Nanotechnology or more precisely, molecular nanotechnology is concerned with making nano scale assemblers. Without self-replication, capital and assembly costs of molecular machines become impossibly large.
• Space resources: NASA has sponsored a number of design studies to develop self-replicating mechanisms to mine space resources. Most of these designs include computer-controlled machinery that copies itself.
• Computer security: Many computer security problems are caused by self-reproducing computer programs that infect computers — computer worms and computer viruses.
• In parallel computing, it takes a long time to manually load a new program on every node of a large computer cluster or distributed computing system. Automatically loading new programs using mobile agents can save the system administrator a lot of time and give users their results much quicker, as long as they don't get out of control.

In industry

Space exploration and manufacturing

The goal of self-replication in space systems is to exploit large amounts of matter with a low launch mass. For example, an autotrophic self-replicating machine could cover a moon or planet with solar cells, and beam the power to the Earth using microwaves. Once in place, the same machinery that built itself could also produce raw materials or manufactured objects, including transportation systems to ship the products. Another model of self-replicating machine would copy itself through the galaxy and universe, sending information back.

In general, since these systems are autotrophic, they are the most difficult and complex known replicators. They are also thought to be the most hazardous, because they do not require any inputs from human beings in order to reproduce.

A classic theoretical study of replicators in space is the 1980 NASA study of autotrophic clanking replicators, edited by Robert Freitas.^[10]

Much of the design study was concerned with a simple, flexible chemical system for processing lunar regolith, and the differences between the ratio of elements needed by the replicator, and the ratios available in regolith. The limiting element was Chlorine, an essential element to process regolith for Aluminium. Chlorine is very rare in lunar regolith, and a substantially faster rate of reproduction could be assured by importing modest amounts.

The reference design specified small computer-controlled electric carts running on rails. Each cart could have a simple hand or a small bull-dozer shovel, forming a basic robot.

Power would be provided by a "canopy" of solar cells supported on pillars. The other machinery could run under the canopy.

A "casting robot" would use a robotic arm with a few sculpting tools to make plaster molds. Plaster molds are easy to make, and make precise parts with good surface finishes. The robot would then cast most of the parts either from non-conductive molten rock (basalt) or purified metals. An electric oven melted the materials.

A speculative, more complex "chip factory" was specified to produce the computer and electronic systems, but the designers also said that it might prove practical to ship the chips from Earth as if they were "vitamins".

Molecular manufacturing

Nanotechnologists in particular believe that their work will likely fail to reach a state of maturity until human beings design a self-replicating assembler of nanometer dimensions [1].
These systems are substantially simpler than autotrophic systems, because they are provided with purified feedstocks and energy. They do not have to reproduce them. This distinction is at the root of some of the controversy about whether molecular manufacturing is possible or not. Many authorities who find it impossible are clearly citing sources for complex autotrophic self-replicating systems. Many of the authorities who find it possible are clearly citing sources for much simpler self-assembling systems, which have been demonstrated. In the meantime, a Lego-built autonomous robot able to follow a pre-set track and assemble an exact copy of itself, starting from four externally provided components, was demonstrated experimentally in 2003 [2].

Merely exploiting the replicative abilities of existing cells is insufficient, because of limitations in the process of protein biosynthesis (also see the listing for RNA). What is required is the rational design of an entirely novel replicator with a much wider range of synthesis capabilities.

In 2011, New York University scientists have developed artificial structures that can self-replicate, a process that has the potential to yield new types of materials. They have demonstrated that it is possible to replicate not just molecules like cellular DNA or RNA, but discrete structures that could in principle assume many different shapes, have many different functional features, and be associated with many different types of chemical species.^[11][12]

For a discussion of other chemical bases for hypothetical self-replicating systems, see alternative biochemistry.