In theoretical physics and mathematical physics, analytical mechanics, or theoretical mechanics is a collection of closely related alternative formulations of classical mechanics. It was developed by many scientists and mathematicians during the 18th century and onward, after Newtonian mechanics. Since Newtonian mechanics considers vector quantities of motion, particularly accelerations, momenta, forces, of the constituents of the system, an alternative name for the mechanics governed by Newton's laws and Euler's laws is vectorial mechanics.
By contrast, analytical mechanics uses scalar properties of motion representing the system as a whole—usually its total kinetic energy and potential energy—not Newton's vectorial forces of individual particles. A scalar is a quantity, whereas a vector is represented by quantity and direction. The equations of motion are derived from the scalar quantity by some underlying principle about the scalar's variation.
Analytical mechanics takes advantage of a system's constraints to solve problems. The constraints limit the degrees of freedom the system can have, and can be used to reduce the number of coordinates needed to solve for the motion. The formalism is well suited to arbitrary choices of coordinates, known in the context as generalized coordinates. The kinetic and potential energies of the system are expressed using these generalized coordinates or momenta, and the equations of motion can be readily set up, thus analytical mechanics allows numerous mechanical problems to be solved with greater efficiency than fully vectorial methods. It does not always work for non-conservative forces or dissipative forces like friction, in which case one may revert to Newtonian mechanics or use the Udwadia–Kalaba equation.
Two dominant branches of analytical mechanics are Lagrangian mechanics (using generalized coordinates and corresponding generalized velocities in configuration space) and Hamiltonian mechanics (using coordinates and corresponding momenta in phase space). Both formulations are equivalent by a Legendre transformation on the generalized coordinates, velocities and momenta, therefore both contain the same information for describing the dynamics of a system. There are other formulations such as Hamilton–Jacobi theory, Routhian mechanics, and Appell's equation of motion. All equations of motion for particles and fields, in any formalism, can be derived from the widely applicable result called the principle of least action. One result is Noether's theorem, a statement which connects conservation laws to their associated symmetries.
Analytical mechanics does not introduce new physics and is not more general than Newtonian mechanics. Rather it is a collection of equivalent formalisms which have broad application. In fact the same principles and formalisms can be used in relativistic mechanics and general relativity, and with some modification, quantum mechanics and quantum field theory.
Analytical mechanics is used widely, from fundamental physics to applied mathematics, particularly chaos theory.
The methods of analytical mechanics apply to discrete particles, each with a finite number of degrees of freedom. They can be modified to describe continuous fields or fluids, which have infinite degrees of freedom. The definitions and equations have a close analogy with those of mechanics.
By contrast, analytical mechanics uses scalar properties of motion representing the system as a whole—usually its total kinetic energy and potential energy—not Newton's vectorial forces of individual particles. A scalar is a quantity, whereas a vector is represented by quantity and direction. The equations of motion are derived from the scalar quantity by some underlying principle about the scalar's variation.
Analytical mechanics takes advantage of a system's constraints to solve problems. The constraints limit the degrees of freedom the system can have, and can be used to reduce the number of coordinates needed to solve for the motion. The formalism is well suited to arbitrary choices of coordinates, known in the context as generalized coordinates. The kinetic and potential energies of the system are expressed using these generalized coordinates or momenta, and the equations of motion can be readily set up, thus analytical mechanics allows numerous mechanical problems to be solved with greater efficiency than fully vectorial methods. It does not always work for non-conservative forces or dissipative forces like friction, in which case one may revert to Newtonian mechanics or use the Udwadia–Kalaba equation.
Two dominant branches of analytical mechanics are Lagrangian mechanics (using generalized coordinates and corresponding generalized velocities in configuration space) and Hamiltonian mechanics (using coordinates and corresponding momenta in phase space). Both formulations are equivalent by a Legendre transformation on the generalized coordinates, velocities and momenta, therefore both contain the same information for describing the dynamics of a system. There are other formulations such as Hamilton–Jacobi theory, Routhian mechanics, and Appell's equation of motion. All equations of motion for particles and fields, in any formalism, can be derived from the widely applicable result called the principle of least action. One result is Noether's theorem, a statement which connects conservation laws to their associated symmetries.
Analytical mechanics does not introduce new physics and is not more general than Newtonian mechanics. Rather it is a collection of equivalent formalisms which have broad application. In fact the same principles and formalisms can be used in relativistic mechanics and general relativity, and with some modification, quantum mechanics and quantum field theory.
Analytical mechanics is used widely, from fundamental physics to applied mathematics, particularly chaos theory.
The methods of analytical mechanics apply to discrete particles, each with a finite number of degrees of freedom. They can be modified to describe continuous fields or fluids, which have infinite degrees of freedom. The definitions and equations have a close analogy with those of mechanics.
Intrinsic motion
- Generalized coordinates and constraints
These are known as generalized coordinates, denoted qi (i = 1, 2, 3...).
Difference between curvillinear and generalized coordinates
Generalized coordinates incorporate constraints on the system. There is one generalized coordinate qi for each degree of freedom (for convenience labelled by an index i = 1, 2...N), i.e. each way the system can change its configuration; as curvilinear lengths or angles of rotation. Generalized coordinates are not the same as curvilinear coordinates. The number of curvilinear coordinates equals the dimension of the position space in question (usually 3 for 3d space), while the number of generalized coordinates is not necessarily equal to this dimension; constraints can reduce the number of degrees of freedom (hence the number of generalized coordinates required to define the configuration of the system), following the general rule:
- [dimension of position space (usually 3)] × [number of constituents of system ("particles")] − (number of constraints)
- = (number of degrees of freedom) = (number of generalized coordinates)
- .
This principle states that infinitesimal virtual work done by a force across reversible displacements is zero, which is the work done by a force consistent with ideal constraints of the system. The idea of a constraint is useful - since this limits what the system can do, and can provide steps to solving for the motion of the system. The equation for D'Alembert's principle is:
Holonomic constraints
If the curvilinear coordinate system is defined by the standard position vector r, and if the position vector can be written in terms of the generalized coordinates q and time t in the form:
Lagrangian mechanics
Lagrangian and Euler–Lagrange equationsThe introduction of generalized coordinates and the fundamental Lagrangian function:
This formulation identifies the actual path followed by the motion as a selection of the path over which the time integral of kinetic energy is least, assuming the total energy to be fixed, and imposing no conditions on the time of transit.
Configuration space
The Lagrangian formulation uses the configuration space of the system, the set of all possible generalized coordinates:
Hamiltonian mechanics
Hamiltonian and Hamilton's equationsThe Legendre transformation of the Lagrangian replaces the generalized coordinates and velocities (q, q̇) with (q, p); the generalized coordinates and the generalized momenta conjugate to the generalized coordinates:
Analogous to the configuration space, the set of all momenta is the momentum space (technically in this context; generalized momentum space):
Phase space
The set of all positions and momenta form the phase space;
A particular solution to Hamilton's equations is called a phase path, a particular curve (q(t),p(t)) subject to the required initial conditions. The set of all phase paths, the general solution to the differential equations, is the phase portrait:
- The Poisson bracket
Properties of the Lagrangian and Hamiltonian functions
Following are overlapping properties between the Lagrangian and Hamiltonian functions.- All the individual generalized coordinates qi(t), velocities q̇i(t) and momenta pi(t) for every degree of freedom are mutually independent. Explicit time-dependence of a function means the function actually includes time t as a variable in addition to the q(t), p(t), not simply as a parameter through q(t) and p(t), which would mean explicit time-independence.
- The Lagrangian is invariant under addition of the total time derivative of any function of q and t, that is:
- so each Lagrangian L and L' describe exactly the same motion. In other words, the Lagrangian of a system is not unique.
- Analogously, the Hamiltonian is invariant under addition of the partial time derivative of any function of q, p and t, that is:
- (K is a frequently used letter in this case). This property is used in canonical transformations (see below).
- If the Lagrangian is independent of some generalized coordinates, then the generalized momenta conjugate to those coordinates are constants of the motion, i.e. are conserved, this immediately follows from Lagrange's equations:
- Such coordinates are "cyclic" or "ignorable". It can be shown that the Hamiltonian is also cyclic in exactly the same generalized coordinates.
- If the Lagrangian is time-independent the Hamiltonian is also time-independent (i.e. both are constant in time).
- If the kinetic energy is a homogeneous function of degree 2 of the generalized velocities, and the Lagrangian is explicitly time-independent, then:
- where λ is a constant, then the Hamiltonian will be the total conserved energy, equal to the total kinetic and potential energies of the system:
- This is the basis for the Schrödinger equation, inserting quantum operators directly obtains it.
Principle of least action
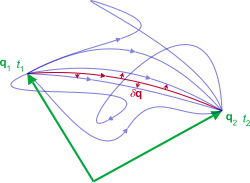
As the system evolves, q traces a path through configuration space (only some are shown). The path taken by the system (red) has a stationary action (δS = 0) under small changes in the configuration of the system (δq).
Action is another quantity in analytical mechanics defined as a functional of the Lagrangian:
From this principle, all equations of motion in classical mechanics can be derived. This approach can be extended to fields rather than a system of particles (see below), and underlies the path integral formulation of quantum mechanics, and is used for calculating geodesic motion in general relativity.
Hamiltonian-Jacobi mechanics
The invariance of the Hamiltonian (under addition of the partial time derivative of an arbitrary function of p, q, and t) allows the Hamiltonian in one set of coordinates q and momenta p to be transformed into a new set Q = Q(q, p, t) and P = P(q, p, t), in four possible ways:The choice of Q and P is completely arbitrary, but not every choice leads to a canonical transformation. One simple criterion for a transformation q → Q and p → P to be canonical is the Poisson bracket be unity,
By setting the canonically transformed Hamiltonian K = 0, and the type-2 generating function equal to Hamilton's principal function (also the action ) plus an arbitrary constant C:
The study of the solutions of the Hamilton–Jacobi equations leads naturally to the study of symplectic manifolds and symplectic topology. In this formulation, the solutions of the Hamilton–Jacobi equations are the integral curves of Hamiltonian vector fields.
Routhian mechanics
Routhian mechanics is a hybrid formulation of Lagrangian and Hamiltonian mechanics, not often used but especially useful for removing cyclic coordinates. If the Lagrangian of a system has s cyclic coordinates q = q1, q2, ... qs with conjugate momenta p = p1, p2, ... ps, with the rest of the coordinates non-cyclic and denoted ζ = ζ1, ζ1, ..., ζN − s, they can be removed by introducing the Routhian:The coordinates q do not have to be cyclic, the partition between which coordinates enter the Hamiltonian equations and those which enter the Lagrangian equations is arbitrary. It is simply convenient to let the Hamiltonian equations remove the cyclic coordinates, leaving the non cyclic coordinates to the Lagrangian equations of motion.
Appellian mechanics
Appell's equation of motion involve generalized accelerations, the second time derivatives of the generalized coordinates:Extensions to classical field theory
Generalized coordinates apply to discrete particles. For N scalar fields φi(r, t) where i = 1, 2, ... N, the Lagrangian density is a function of these fields and their space and time derivatives, and possibly the space and time coordinates themselves:and the Euler–Lagrange equations have an analogue for fields:
This scalar field formulation can be extended to vector fields, tensor fields, and spinor fields.
The Lagrangian is the volume integral of the Lagrangian density:
The corresponding "momentum" field densities conjugate to the N scalar fields φi(r, t) are:
Again, the volume integral of the Hamiltonian density is the Hamiltonian
Symmetry, conservation, and Noether's theorem
- Symmetry transformations in classical space and time
| Transformation | Operator | Position | Momentum |
|---|---|---|---|
| Translational symmetry | |||
| Time translation | |||
| Rotational invariance | |||
| Galilean transformations | |||
| Parity | |||
| T-symmetry |
where R(n̂, θ) is the rotation matrix about an axis defined by the unit vector n̂ and angle θ.
Noether's theorem states that a continuous symmetry transformation of the action corresponds to a conservation law, i.e. the action (and hence the Lagrangian) doesn't change under a transformation parameterized by a parameter s:






















![\{A,B\}\rightarrow {\frac {1}{i\hbar }}[{\hat {A}},{\hat {B}}]\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/0990f0c0d756e9d159c393f67053ba88f848789e)
















































![L[q(s,t),{\dot {q}}(s,t)]=L[q(t),{\dot {q}}(t)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a306c98f32aae1bd3da6bef5e96de807c6343bb)








