Determinant

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Determinant

In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It allows characterizing some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants (the preceding property is a corollary of this one). The determinant of a matrix A is denoted det(A), det A, or |A|.

In the case of a 2 × 2 matrix the determinant can be defined as

${\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.\end{aligned}}}$

Similarly, for a 3 × 3 matrix A, its determinant is

${\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\[3pt]&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}}$

Each determinant of a 2 × 2 matrix in this equation is called a minor of the matrix A. This procedure can be extended to give a recursive definition for the determinant of an n × n matrix, known as Laplace expansion.

Determinants occur throughout mathematics. For example, a matrix is often used to represent the coefficients in a system of linear equations, and determinants can be used to solve these equations (Cramer's rule), although other methods of solution are computationally much more efficient. Determinants are used for defining the characteristic polynomial of a matrix, whose roots are the eigenvalues. In geometry, the signed n-dimensional volume of a n-dimensional parallelepiped is expressed by a determinant. This is used in calculus with exterior differential forms and the Jacobian determinant, in particular for changes of variables in multiple integrals.

2 × 2 matrices

The determinant of a 2 × 2 matrix ${\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$ is denoted either by "det" or by vertical bars around the matrix, and is defined as

${\displaystyle \det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.}$

For example,

${\displaystyle \det {\begin{pmatrix}3&7\\1&-4\end{pmatrix}}={\begin{vmatrix}3&7\\1&{-4}\end{vmatrix}}=3\cdot (-4)-7\cdot 1=-19.}$

First properties

The determinant has several key properties that can be proved by direct evaluation of the definition for ${\displaystyle 2\times 2}$-matrices, and that continue to hold for determinants of larger matrices. They are as follows: first, the determinant of the identity matrix ${\displaystyle {\begin{pmatrix}1&0\\0&1\end{pmatrix}}}$ is 1. Second, the determinant is zero if two rows are the same:

${\displaystyle {\begin{vmatrix}a&b\\a&b\end{vmatrix}}=ab-ba=0.}$

This holds similarly if the two columns are the same. Moreover,

${\displaystyle {\begin{vmatrix}a&b+b'\\c&d+d'\end{vmatrix}}=a(d+d')-(b+b')c={\begin{vmatrix}a&b\\c&d\end{vmatrix}}+{\begin{vmatrix}a&b'\\c&d'\end{vmatrix}}.}$

Finally, if any column is multiplied by some number ${\displaystyle r}$ (i.e., all entries in that column are multiplied by that number), the determinant is also multiplied by that number:

${\displaystyle {\begin{vmatrix}r\cdot a&b\\r\cdot c&d\end{vmatrix}}=rad-brc=r(ad-bc)=r\cdot {\begin{vmatrix}a&b\\c&d\end{vmatrix}}.}$

Geometric meaning

The area of the parallelogram is the absolute value of the determinant of the matrix formed by the vectors representing the parallelogram's sides.

If the matrix entries are real numbers, the matrix A can be used to represent two linear maps: one that maps the standard basis vectors to the rows of A, and one that maps them to the columns of A. In either case, the images of the basis vectors form a parallelogram that represents the image of the unit square under the mapping. The parallelogram defined by the rows of the above matrix is the one with vertices at (0, 0), (a, b), (a + c, b + d), and (c, d), as shown in the accompanying diagram.

The absolute value of ad − bc is the area of the parallelogram, and thus represents the scale factor by which areas are transformed by A. (The parallelogram formed by the columns of A is in general a different parallelogram, but since the determinant is symmetric with respect to rows and columns, the area will be the same.)

The absolute value of the determinant together with the sign becomes the oriented area of the parallelogram. The oriented area is the same as the usual area, except that it is negative when the angle from the first to the second vector defining the parallelogram turns in a clockwise direction (which is opposite to the direction one would get for the identity matrix).

To show that ad − bc is the signed area, one may consider a matrix containing two vectors u ≡ (a, b) and v ≡ (c, d) representing the parallelogram's sides. The signed area can be expressed as |u| |v| sin θ for the angle θ between the vectors, which is simply base times height, the length of one vector times the perpendicular component of the other. Due to the sine this already is the signed area, yet it may be expressed more conveniently using the cosine of the complementary angle to a perpendicular vector, e.g. u^⊥ = (−b, a), so that |u^⊥| |v| cos θ′, which can be determined by the pattern of the scalar product to be equal to ad − bc:

${\displaystyle {\text{Signed area}}=|{\boldsymbol {u}}|\,|{\boldsymbol {v}}|\,\sin \,\theta =\left|{\boldsymbol {u}}^{\perp }\right|\,\left|{\boldsymbol {v}}\right|\,\cos \,\theta '={\begin{pmatrix}-b\\a\end{pmatrix}}\cdot {\begin{pmatrix}c\\d\end{pmatrix}}=ad-bc.}$

The volume of this parallelepiped is the absolute value of the determinant of the matrix formed by the columns constructed from the vectors r1, r2, and r3.

Thus the determinant gives the scaling factor and the orientation induced by the mapping represented by A. When the determinant is equal to one, the linear mapping defined by the matrix is equi-areal and orientation-preserving.

The object known as the bivector is related to these ideas. In 2D, it can be interpreted as an oriented plane segment formed by imagining two vectors each with origin (0, 0), and coordinates (a, b) and (c, d). The bivector magnitude (denoted by (a, b) ∧ (c, d)) is the signed area, which is also the determinant ad − bc.

If an n × n real matrix A is written in terms of its column vectors ${\displaystyle A=\left[{\begin{array}{c|c|c|c}\mathbf {a} _{1}&\mathbf {a} _{2}&\cdots &\mathbf {a} _{n}\end{array}}\right]}$, then

${\displaystyle A{\begin{pmatrix}1\\0\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{1},\quad A{\begin{pmatrix}0\\1\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{2},\quad \ldots ,\quad A{\begin{pmatrix}0\\0\\\vdots \\1\end{pmatrix}}=\mathbf {a} _{n}.}$

This means that ${\displaystyle A}$ maps the unit n-cube to the n-dimensional parallelotope defined by the vectors ${\displaystyle \mathbf {a} _{1},\mathbf {a} _{2},\ldots ,\mathbf {a} _{n},}$ the region ${\displaystyle P=\left\{c_{1}\mathbf {a} _{1}+\cdots +c_{n}\mathbf {a} _{n}\mid 0\leq c_{i}\leq 1\ \forall i\right\}.}$

The determinant gives the signed n-dimensional volume of this parallelotope, ${\displaystyle \det(A)=\pm {\text{vol}}(P),}$ and hence describes more generally the n-dimensional volume scaling factor of the linear transformation produced by A. (The sign shows whether the transformation preserves or reverses orientation.) In particular, if the determinant is zero, then this parallelotope has volume zero and is not fully n-dimensional, which indicates that the dimension of the image of A is less than n. This means that A produces a linear transformation which is neither onto nor one-to-one, and so is not invertible.

Definition

In the sequel, A is a square matrix with n rows and n columns, so that it can be written as

${\displaystyle A={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{bmatrix}}.}$

The entries ${\displaystyle a_{1,1}}$ etc. are, for many purposes, real or complex numbers. As discussed below, the determinant is also defined for matrices whose entries are elements in more abstract algebraic structures known as commutative rings.

The determinant of A is denoted by det(A), or it can be denoted directly in terms of the matrix entries by writing enclosing bars instead of brackets:

${\displaystyle {\begin{vmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{vmatrix}}.}$

There are various equivalent ways to define the determinant of a square matrix A, i.e. one with the same number of rows and columns: the determinant can be defined via the Leibniz formula, an explicit formula involving sums of products of certain entries of the matrix. The determinant can also be characterized as the unique function depending on the entries of the matrix satisfying certain properties. This approach can also be used to compute determinants by simplifying the matrices in question.

Leibniz formula

Main article: Leibniz formula for determinants

The Leibniz formula for the determinant of a 3 × 3 matrix is the following:

${\displaystyle {\begin{aligned}{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a(ei-fh)-b(di-fg)+c(dh-eg)\\&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}}$

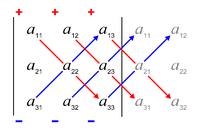
The rule of Sarrus is a mnemonic for this formula: the sum of the products of three diagonal north-west to south-east lines of matrix elements, minus the sum of the products of three diagonal south-west to north-east lines of elements, when the copies of the first two columns of the matrix are written beside it as in the illustration:

This scheme for calculating the determinant of a 3 × 3 matrix does not carry over into higher dimensions.

n × n matrices

The Leibniz formula expresses the determinant of an ${\displaystyle n\times n}$-matrix in a manner which is consistent across higher dimensions.

It is an expression involving the notion of permutations and their signature. A permutation of the set ${\displaystyle \{1,2,\dots ,n\}}$ is a function ${\displaystyle \sigma }$ that reorders this set of integers. The value in the ${\displaystyle i}$-th position after the reordering ${\displaystyle \sigma }$ is denoted by ${\displaystyle \sigma _{i}}$. The set of all such permutations, called the symmetric group, is denoted ${\displaystyle S_{n}}$. The signature of ${\displaystyle \sigma }$ is defined to be ${\displaystyle +1}$ whenever the reordering given by ${\displaystyle \sigma }$ can be achieved by successively interchanging two entries an even number of times, and ${\displaystyle -1}$ whenever it can be achieved by an odd number of such interchanges.

Given a permutation ${\displaystyle \sigma }$ and an ${\displaystyle n\times n}$-matrix ${\displaystyle A}$, where ${\displaystyle a_{i,j}}$ denotes the element in the ${\displaystyle i}$-th row and ${\displaystyle j}$-th column of ${\displaystyle A}$, the product

${\displaystyle a_{1,\sigma _{1}}\cdot a_{2,\sigma _{2}}\cdot \dots \cdot a_{n,\sigma _{n}}}$,

also written more briefly using Pi notation as

${\displaystyle \prod _{i=1}^{n}a_{i,\sigma _{i}}}$,

is used to define the determinant using the Leibniz formula:

${\displaystyle \det(A)=\sum _{\sigma \in S_{n}}\left(\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}\right)}$.

The following table unwinds these terms in the case ${\displaystyle n=3}$. In the first column, a permutation is listed according to its values. For example, in the second row, the permutation ${\displaystyle \sigma }$ satisfies ${\displaystyle \sigma _{1}=1,\sigma _{2}=3,\sigma _{3}=2}$. It can be obtained from the standard order (1, 2, 3) by a single exchange (exchanging the second and third entry), so that its signature is ${\displaystyle \operatorname {sgn}(\sigma )=-1}$.

Permutations of ${\displaystyle \{1,2,3\}}$ and their contribution to the determinant

Permutation ${\displaystyle \sigma }$	${\displaystyle \operatorname {sgn}(\sigma )}$	${\displaystyle \operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}}$
1, 2, 3	${\displaystyle +1}$	${\displaystyle +a_{1,1}a_{2,2}a_{3,3}}$
1, 3, 2	${\displaystyle -1}$	${\displaystyle -a_{1,1}a_{2,3}a_{3,2}}$
3, 1, 2	${\displaystyle +1}$	${\displaystyle +a_{1,3}a_{2,1}a_{3,2}}$
3, 2, 1	${\displaystyle -1}$	${\displaystyle -a_{1,3}a_{2,2}a_{3,1}}$
2, 3, 1	${\displaystyle +1}$	${\displaystyle +a_{1,2}a_{2,3}a_{3,1}}$
2, 1, 3	${\displaystyle -1}$	${\displaystyle -a_{1,2}a_{2,1}a_{3,3}}$

The sum of the six terms in the third column then reads

${\displaystyle \sum _{\sigma \in S_{3}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}=a_{1,1}a_{2,2}a_{3,3}-a_{1,1}a_{2,3}a_{3,2}+a_{1,3}a_{2,1}a_{3,2}-a_{1,3}a_{2,2}a_{3,1}+a_{1,2}a_{2,3}a_{3,1}-a_{1,2}a_{2,1}a_{3,3}.}$

This gives back the formula for ${\displaystyle 3\times 3}$-matrices above. For a general ${\displaystyle n\times n}$-matrix, the Leibniz formula involves ${\displaystyle n!}$ (n factorial) summands, each of which is a product of n entries of the matrix.

The Leibniz formula can also be expressed using a summation in which not only permutations, but all sequences of ${\displaystyle n}$ indices in the range ${\displaystyle 1,\dots ,n}$ occur. To do this, one uses the Levi-Civita symbol ${\displaystyle \varepsilon _{i_{1},\cdots ,i_{n}}}$ instead of the sign of a permutation

${\displaystyle \det(A)=\sum _{i_{1},i_{2},\ldots ,i_{n}=1}^{n}\varepsilon _{i_{1}\cdots i_{n}}a_{1,i_{1}}\cdots a_{n,i_{n}},}$

This gives back the formula above since the Levi-Civita symbol is zero if the indices ${\displaystyle i_{1},\dots ,i_{n}}$ do not form a permutation.

Properties of the determinant

Characterization of the determinant

The determinant can be characterized by the following three key properties. To state these, it is convenient to regard an ${\displaystyle n\times n}$-matrix A as being composed of its ${\displaystyle n}$ columns, so denoted as

${\displaystyle A={\big (}a_{1},\dots ,a_{n}{\big )},}$

where the column vector ${\displaystyle a_{i}}$ (for each i) is composed of the entries of the matrix in the i-th column.

1. ${\displaystyle \det \left(I\right)=1}$, where ${\displaystyle I}$ is an identity matrix.
2. The determinant is multilinear: if the jth column of a matrix ${\displaystyle A}$ is written as a linear combination ${\displaystyle a_{j}=r\cdot v+w}$ of two column vectors v and w and a number r, then the determinant of A is expressible as a similar linear combination:

   ${\displaystyle {\begin{aligned}|A|&={\big |}a_{1},\dots ,a_{j-1},r\cdot v+w,a_{j+1},\dots ,a_{n}|\\&=r\cdot |a_{1},\dots ,v,\dots a_{n}|+|a_{1},\dots ,w,\dots ,a_{n}|\end{aligned}}}$

3. The determinant is alternating: whenever two columns of a matrix are identical, its determinant is 0:

   ${\displaystyle |a_{1},\dots ,v,\dots ,v,\dots ,a_{n}|=0.}$

If the determinant is defined using the Leibniz formula as above, these three properties can be proved by direct inspection of that formula. Some authors also approach the determinant directly using these three properties: it can be shown that there is exactly one function that assigns to any ${\displaystyle n\times n}$-matrix A a number that satisfies these three properties.^[6] This also shows that this more abstract approach to the determinant yields the same definition as the one using the Leibniz formula.

To see this it suffices to expand the determinant by multi-linearity in the columns into a (huge) linear combination of determinants of matrices in which each column is a standard basis vector. These determinants are either 0 (by property 9) or else ±1 (by properties 1 and 12 below), so the linear combination gives the expression above in terms of the Levi-Civita symbol. While less technical in appearance, this characterization cannot entirely replace the Leibniz formula in defining the determinant, since without it the existence of an appropriate function is not clear.

Immediate consequences

These rules have several further consequences:

• The determinant is a homogeneous function, i.e.,
  $${\displaystyle \det(cA)=c^{n}\det(A)}$$

  
  (for an ${\displaystyle n\times n}$ matrix ${\displaystyle A}$).
• Interchanging any pair of columns of a matrix multiplies its determinant by −1. This follows from the determinant being multilinear and alternating (properties 2 and 3 above):
  $${\displaystyle |a_{1},\dots ,a_{j},\dots a_{i},\dots ,a_{n}|=-|a_{1},\dots ,a_{i},\dots ,a_{j},\dots ,a_{n}|.}$$

  
  This formula can be applied iteratively when several columns are swapped. For example
  $${\displaystyle |a_{3},a_{1},a_{2},a_{4}\dots ,a_{n}|=-|a_{1},a_{3},a_{2},a_{4},\dots ,a_{n}|=|a_{1},a_{2},a_{3},a_{4},\dots ,a_{n}|.}$$

  
  Yet more generally, any permutation of the columns multiplies the determinant by the sign of the permutation.
• If some column can be expressed as a linear combination of the other columns (i.e. the columns of the matrix form a linearly dependent set), the determinant is 0. As a special case, this includes: if some column is such that all its entries are zero, then the determinant of that matrix is 0.
• Adding a scalar multiple of one column to another column does not change the value of the determinant. This is a consequence of multilinearity and being alternative: by multilinearity the determinant changes by a multiple of the determinant of a matrix with two equal columns, which determinant is 0, since the determinant is alternating.
• If ${\displaystyle A}$ is a triangular matrix, i.e. ${\displaystyle a_{ij}=0}$, whenever ${\displaystyle i>j}$ or, alternatively, whenever ${\displaystyle i<j}$, then its determinant equals the product of the diagonal entries:
  $${\displaystyle \det(A)=a_{11}a_{22}\cdots a_{nn}=\prod _{i=1}^{n}a_{ii}.}$$

  
  Indeed, such a matrix can be reduced, by appropriately adding multiples of the columns with fewer nonzero entries to those with more entries, to a diagonal matrix (without changing the determinant). For such a matrix, using the linearity in each column reduces to the identity matrix, in which case the stated formula holds by the very first characterizing property of determinants. Alternatively, this formula can also be deduced from the Leibniz formula, since the only permutation ${\displaystyle \sigma }$ which gives a non-zero contribution is the identity permutation.

Example

These characterizing properties and their consequences listed above are both theoretically significant, but can also be used to compute determinants for concrete matrices. In fact, Gaussian elimination can be applied to bring any matrix into upper triangular form, and the steps in this algorithm affect the determinant in a controlled way. The following concrete example illustrates the computation of the determinant of the matrix ${\displaystyle A}$ using that method:

${\displaystyle A={\begin{bmatrix}-2&-1&2\\2&1&4\\-3&3&-1\end{bmatrix}}.}$

Computation of the determinant of matrix ${\displaystyle A}$

Matrix	${\displaystyle B={\begin{bmatrix}-3&-1&2\\3&1&4\\0&3&-1\end{bmatrix}}}$	${\displaystyle C={\begin{bmatrix}-3&5&2\\3&13&4\\0&0&-1\end{bmatrix}}}$	${\displaystyle D={\begin{bmatrix}5&-3&2\\13&3&4\\0&0&-1\end{bmatrix}}}$	${\displaystyle E={\begin{bmatrix}18&-3&2\\0&3&4\\0&0&-1\end{bmatrix}}}$
Obtained by	add the second column to the first	add 3 times the third column to the second	swap the first two columns	add ${\displaystyle -{\frac {13}{3}}}$ times the second column to the first
Determinant	${\displaystyle |A|=|B|}$	${\displaystyle |B|=|C|}$	${\displaystyle |D|=-|C|}$	${\displaystyle |E|=|D|}$

Combining these equalities gives ${\displaystyle |A|=-|E|=-(18\cdot 3\cdot (-1))=54.}$

Transpose

The determinant of the transpose of ${\displaystyle A}$ equals the determinant of A:

${\displaystyle \det \left(A^{\textsf {T}}\right)=\det(A)}$.

This can be proven by inspecting the Leibniz formula. This implies that in all the properties mentioned above, the word "column" can be replaced by "row" throughout. For example, viewing an n × n matrix as being composed of n rows, the determinant is an n-linear function.

Multiplicativity and matrix groups

Thus the determinant is a multiplicative map, i.e., for square matrices ${\displaystyle A}$ and ${\displaystyle B}$ of equal size, the determinant of a matrix product equals the product of their determinants:

${\displaystyle \det(AB)=\det(A)\det(B)}$

This key fact can be proven by observing that, for a fixed matrix ${\displaystyle B}$, both sides of the equation are alternating and multilinear as a function depending on the columns of ${\displaystyle A}$. Moreover, they both take the value ${\displaystyle \det B}$ when ${\displaystyle A}$ is the identity matrix. The above-mentioned unique characterization of alternating multilinear maps therefore shows this claim.

A matrix ${\displaystyle A}$ is invertible precisely if its determinant is nonzero. This follows from the multiplicativity of ${\displaystyle \det }$ and the formula for the inverse involving the adjugate matrix mentioned below. In this event, the determinant of the inverse matrix is given by

${\displaystyle \det \left(A^{-1}\right)={\frac {1}{\det(A)}}=[\det(A)]^{-1}}$.

In particular, products and inverses of matrices with non-zero determinant (respectively, determinant one) still have this property. Thus, the set of such matrices (of fixed size ${\displaystyle n}$) forms a group known as the general linear group ${\displaystyle \operatorname {GL} _{n}}$ (respectively, a subgroup called the special linear group ${\displaystyle \operatorname {SL} _{n}\subset \operatorname {GL} _{n}}$. More generally, the word "special" indicates the subgroup of another matrix group of matrices of determinant one. Examples include the special orthogonal group (which if n is 2 or 3 consists of all rotation matrices), and the special unitary group.

The Cauchy–Binet formula is a generalization of that product formula for rectangular matrices. This formula can also be recast as a multiplicative formula for compound matrices whose entries are the determinants of all quadratic submatrices of a given matrix.

Laplace expansion

Laplace expansion expresses the determinant of a matrix ${\displaystyle A}$ in terms of determinants of smaller matrices, known as its minors. The minor ${\displaystyle M_{i,j}}$ is defined to be the determinant of the ${\displaystyle (n-1)\times (n-1)}$-matrix that results from ${\displaystyle A}$ by removing the ${\displaystyle i}$-th row and the ${\displaystyle j}$-th column. The expression ${\displaystyle (-1)^{i+j}M_{i,j}}$ is known as a cofactor. For every ${\displaystyle i}$, one has the equality

${\displaystyle \det(A)=\sum _{j=1}^{n}(-1)^{i+j}a_{ij}M_{ij},}$

which is called the Laplace expansion along the ith row. For example, the Laplace expansion along the first row (${\displaystyle i=1}$) gives the following formula:

${\displaystyle {\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=a{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c{\begin{vmatrix}d&e\\g&h\end{vmatrix}}}$

Unwinding the determinants of these ${\displaystyle 2\times 2}$-matrices gives back the Leibniz formula mentioned above. Similarly, the Laplace expansion along the ${\displaystyle j}$-th column is the equality

${\displaystyle \det(A)=\sum _{i=1}^{n}(-1)^{i+j}a_{ij}M_{ij}.}$

Laplace expansion can be used iteratively for computing determinants, but this approach is inefficient for large matrices. However, it is useful for computing the determinants of highly symmetric matrix such as the Vandermonde matrix

$${\displaystyle {\begin{vmatrix}1&1&1&\cdots &1\\x_{1}&x_{2}&x_{3}&\cdots &x_{n}\\x_{1}^{2}&x_{2}^{2}&x_{3}^{2}&\cdots &x_{n}^{2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{1}^{n-1}&x_{2}^{n-1}&x_{3}^{n-1}&\cdots &x_{n}^{n-1}\end{vmatrix}}=\prod _{1\leq i<j\leq n}\left(x_{j}-x_{i}\right).}$$

This determinant has been applied, for example, in the proof of Baker's theorem in the theory of transcendental numbers.

Adjugate matrix

The adjugate matrix ${\displaystyle \operatorname {adj} (A)}$ is the transpose of the matrix of the cofactors, that is,

${\displaystyle (\operatorname {adj} (A))_{ij}=(-1)^{i+j}M_{ji}.}$

For every matrix, one has

${\displaystyle (\det A)I=A\operatorname {adj} A=(\operatorname {adj} A)\,A.}$

Thus the adjugate matrix can be used for expressing the inverse of a nonsingular matrix:

${\displaystyle A^{-1}={\frac {1}{\det A}}\operatorname {adj} A.}$

Block matrices

The formula for the determinant of a ${\displaystyle 2\times 2}$-matrix above continues to hold, under appropriate further assumptions, for a block matrix, i.e., a matrix composed of four submatrices ${\displaystyle A,B,C,D}$ of dimension ${\displaystyle n\times n}$, ${\displaystyle n\times m}$, ${\displaystyle m\times n}$ and ${\displaystyle m\times m}$, respectively. The easiest such formula, which can be proven using either the Leibniz formula or a factorization involving the Schur complement, is

${\displaystyle \det {\begin{pmatrix}A&0\\C&D\end{pmatrix}}=\det(A)\det(D)=\det {\begin{pmatrix}A&B\\0&D\end{pmatrix}}.}$

If ${\displaystyle A}$ is invertible (and similarly if ${\displaystyle D}$ is invertible), one has

${\displaystyle \det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(A)\det \left(D-CA^{-1}B\right).}$

If ${\displaystyle D}$ is a ${\displaystyle 1\times 1}$-matrix, this simplifies to ${\displaystyle \det(A)(D-CA^{-1}B)}$.

If the blocks are square matrices of the same size further formulas hold. For example, if ${\displaystyle C}$ and ${\displaystyle D}$ commute (i.e., ${\displaystyle CD=DC}$), then there holds 

${\displaystyle \det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(AD-BC).}$

This formula has been generalized to matrices composed of more than ${\displaystyle 2\times 2}$ blocks, again under appropriate commutativity conditions among the individual blocks.

For ${\displaystyle A=D}$ and ${\displaystyle B=C}$, the following formula holds (even if ${\displaystyle A}$ and ${\displaystyle B}$ do not commute)

${\displaystyle \det {\begin{pmatrix}A&B\\B&A\end{pmatrix}}=\det(A-B)\det(A+B).}$

Sylvester's determinant theorem

Sylvester's determinant theorem states that for A, an m × n matrix, and B, an n × m matrix (so that A and B have dimensions allowing them to be multiplied in either order forming a square matrix):

${\displaystyle \det \left(I_{\mathit {m}}+AB\right)=\det \left(I_{\mathit {n}}+BA\right),}$

where I_m and I_n are the m × m and n × n identity matrices, respectively.

From this general result several consequences follow.

1. For the case of column vector c and row vector r, each with m components, the formula allows quick calculation of the determinant of a matrix that differs from the identity matrix by a matrix of rank 1:

   ${\displaystyle \det \left(I_{\mathit {m}}+cr\right)=1+rc.}$

2. More generally, for any invertible m × m matrix X,
   ${\displaystyle \det(X+AB)=\det(X)\det \left(I_{\mathit {n}}+BX^{-1}A\right),}$
3. For a column and row vector as above:
   ${\displaystyle \det(X+cr)=\det(X)\det \left(1+rX^{-1}c\right)=\det(X)+r\,\operatorname {adj} (X)\,c.}$
4. For square matrices ${\displaystyle A}$ and ${\displaystyle B}$ of the same size, the matrices ${\displaystyle AB}$ and ${\displaystyle BA}$ have the same characteristic polynomials (hence the same eigenvalues).

Sum

The determinant of the sum ${\displaystyle A+B}$ of two square matrices of the same size is not in general expressible in terms of the determinants of A and of B. However, for positive semidefinite matrices ${\displaystyle A}$, ${\displaystyle B}$ and ${\displaystyle C}$ of equal size,

$${\displaystyle \det(A+B+C)+\det(C)\geq \det(A+C)+\det(B+C){\text{,}}}$$

with the corollary

$${\displaystyle \det(A+B)\geq \det(A)+\det(B){\text{.}}}$$

Conversely, if ${\displaystyle A}$ and ${\displaystyle B}$ are Hermitian, positive-definite, and size ${\displaystyle n\times n}$, then the determinant has concave ${\displaystyle n}$^th root; this implies

$${\displaystyle {\sqrt[{n}]{\det {\!(A+B)}}}\leq {\sqrt[{n}]{\det {\!(A)}}}+{\sqrt[{n}]{\det {\!(B)}}}}$$

by homogeneity.

Properties of the determinant in relation to other notions

Eigenvalues and characteristic polynomial

The determinant is closely related to two other central concepts in linear algebra, the eigenvalues and the characteristic polynomial of a matrix. Let ${\displaystyle A}$ be an ${\displaystyle n\times n}$-matrix with complex entries with eigenvalues ${\displaystyle \lambda _{1},\lambda _{2},\ldots ,\lambda _{n}}$. (Here it is understood that an eigenvalue with algebraic multiplicity μ occurs μ times in this list.) Then the determinant of A is the product of all eigenvalues,

${\displaystyle \det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.}$

The product of all non-zero eigenvalues is referred to as pseudo-determinant.

The characteristic polynomial is defined as

${\displaystyle \chi _{A}(t)=\det(t\cdot I-A).}$

Here, ${\displaystyle t}$ is the indeterminate of the polynomial and ${\displaystyle I}$ is the identity matrix of the same size as ${\displaystyle A}$. By means of this polynomial, determinants can be used to find the eigenvalues of the matrix ${\displaystyle A}$: they are precisely the roots of this polynomial, i.e., those complex numbers ${\displaystyle \lambda }$ such that

${\displaystyle \chi _{A}(\lambda )=0.}$

A Hermitian matrix is positive definite if all its eigenvalues are positive. Sylvester's criterion asserts that this is equivalent to the determinants of the submatrices

${\displaystyle A_{k}:={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,k}\\a_{2,1}&a_{2,2}&\cdots &a_{2,k}\\\vdots &\vdots &\ddots &\vdots \\a_{k,1}&a_{k,2}&\cdots &a_{k,k}\end{bmatrix}}}$

being positive, for all ${\displaystyle k}$ between ${\displaystyle 1}$ and ${\displaystyle n}$.

Trace

The trace tr(A) is by definition the sum of the diagonal entries of A and also equals the sum of the eigenvalues. Thus, for complex matrices A,

${\displaystyle \det(\exp(A))=\exp(\operatorname {tr} (A))}$

or, for real matrices A,

${\displaystyle \operatorname {tr} (A)=\log(\det(\exp(A))).}$

Here exp(A) denotes the matrix exponential of A, because every eigenvalue λ of A corresponds to the eigenvalue exp(λ) of exp(A). In particular, given any logarithm of A, that is, any matrix L satisfying

${\displaystyle \exp(L)=A}$

the determinant of A is given by

${\displaystyle \det(A)=\exp(\operatorname {tr} (L)).}$

For example, for n = 2, n = 3, and n = 4, respectively,

${\displaystyle {\begin{aligned}\det(A)&={\frac {1}{2}}\left(\left(\operatorname {tr} (A)\right)^{2}-\operatorname {tr} \left(A^{2}\right)\right),\\\det(A)&={\frac {1}{6}}\left(\left(\operatorname {tr} (A)\right)^{3}-3\operatorname {tr} (A)~\operatorname {tr} \left(A^{2}\right)+2\operatorname {tr} \left(A^{3}\right)\right),\\\det(A)&={\frac {1}{24}}\left(\left(\operatorname {tr} (A)\right)^{4}-6\operatorname {tr} \left(A^{2}\right)\left(\operatorname {tr} (A)\right)^{2}+3\left(\operatorname {tr} \left(A^{2}\right)\right)^{2}+8\operatorname {tr} \left(A^{3}\right)~\operatorname {tr} (A)-6\operatorname {tr} \left(A^{4}\right)\right).\end{aligned}}}$

cf. Cayley-Hamilton theorem. Such expressions are deducible from combinatorial arguments, Newton's identities, or the Faddeev–LeVerrier algorithm. That is, for generic n, detA = (−1)ⁿc₀ the signed constant term of the characteristic polynomial, determined recursively from

${\displaystyle c_{n}=1;~~~c_{n-m}=-{\frac {1}{m}}\sum _{k=1}^{m}c_{n-m+k}\operatorname {tr} \left(A^{k}\right)~~(1\leq m\leq n)~.}$

In the general case, this may also be obtained from

${\displaystyle \det(A)=\sum _{\begin{array}{c}k_{1},k_{2},\ldots ,k_{n}\geq 0\\k_{1}+2k_{2}+\cdots +nk_{n}=n\end{array}}\prod _{l=1}^{n}{\frac {(-1)^{k_{l}+1}}{l^{k_{l}}k_{l}!}}\operatorname {tr} \left(A^{l}\right)^{k_{l}},}$

where the sum is taken over the set of all integers k_l ≥ 0 satisfying the equation

${\displaystyle \sum _{l=1}^{n}lk_{l}=n.}$

The formula can be expressed in terms of the complete exponential Bell polynomial of n arguments s_l = −(l – 1)! tr(A^l) as

${\displaystyle \det(A)={\frac {(-1)^{n}}{n!}}B_{n}(s_{1},s_{2},\ldots ,s_{n}).}$

This formula can also be used to find the determinant of a matrix A^I_J with multidimensional indices I = (i₁, i₂, …, i_r) and J = (j₁, j₂, …, j_r). The product and trace of such matrices are defined in a natural way as

${\displaystyle (AB)_{J}^{I}=\sum _{K}A_{K}^{I}B_{J}^{K},\operatorname {tr} (A)=\sum _{I}A_{I}^{I}.}$

An important arbitrary dimension n identity can be obtained from the Mercator series expansion of the logarithm when the expansion converges. If every eigenvalue of A is less than 1 in absolute value,

${\displaystyle \det(I+A)=\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,}$

where I is the identity matrix. More generally, if

${\displaystyle \sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}s^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,}$

is expanded as a formal power series in s then all coefficients of s^m for m > n are zero and the remaining polynomial is det(I + sA).

Upper and lower bounds

For a positive definite matrix A, the trace operator gives the following tight lower and upper bounds on the log determinant

${\displaystyle \operatorname {tr} \left(I-A^{-1}\right)\leq \log \det(A)\leq \operatorname {tr} (A-I)}$

with equality if and only if A = I. This relationship can be derived via the formula for the KL-divergence between two multivariate normal distributions.

Also,

${\displaystyle {\frac {n}{\operatorname {tr} \left(A^{-1}\right)}}\leq \det(A)^{\frac {1}{n}}\leq {\frac {1}{n}}\operatorname {tr} (A)\leq {\sqrt {{\frac {1}{n}}\operatorname {tr} \left(A^{2}\right)}}.}$

These inequalities can be proved by expressing the traces and the determinant in terms of the eigenvalues. As such, they represent the well-known fact that the harmonic mean is less than the geometric mean, which is less than the arithmetic mean, which is, in turn, less than the root mean square.

Derivative

The Leibniz formula shows that the determinant of real (or analogously for complex) square matrices is a polynomial function from ${\displaystyle \mathbf {R} ^{n\times n}}$ to ${\displaystyle \mathbf {R} }$. In particular, it is everywhere differentiable. Its derivative can be expressed using Jacobi's formula:

${\displaystyle {\frac {d\det(A)}{d\alpha }}=\operatorname {tr} \left(\operatorname {adj} (A){\frac {dA}{d\alpha }}\right).}$

where ${\displaystyle \operatorname {adj} (A)}$ denotes the adjugate of ${\displaystyle A}$. In particular, if ${\displaystyle A}$ is invertible, we have

${\displaystyle {\frac {d\det(A)}{d\alpha }}=\det(A)\operatorname {tr} \left(A^{-1}{\frac {dA}{d\alpha }}\right).}$

Expressed in terms of the entries of ${\displaystyle A}$, these are

${\displaystyle {\frac {\partial \det(A)}{\partial A_{ij}}}=\operatorname {adj} (A)_{ji}=\det(A)\left(A^{-1}\right)_{ji}.}$

Yet another equivalent formulation is

${\displaystyle \det(A+\epsilon X)-\det(A)=\operatorname {tr} (\operatorname {adj} (A)X)\epsilon +O\left(\epsilon ^{2}\right)=\det(A)\operatorname {tr} \left(A^{-1}X\right)\epsilon +O\left(\epsilon ^{2}\right)}$,

using big O notation. The special case where ${\displaystyle A=I}$, the identity matrix, yields

${\displaystyle \det(I+\epsilon X)=1+\operatorname {tr} (X)\epsilon +O\left(\epsilon ^{2}\right).}$

This identity is used in describing Lie algebras associated to certain matrix Lie groups. For example, the special linear group ${\displaystyle \operatorname {SL} _{n}}$ is defined by the equation ${\displaystyle \det A=1}$. The above formula shows that its Lie algebra is the special linear Lie algebra ${\displaystyle {\mathfrak {sl}}_{n}}$ consisting of those matrices having trace zero.

Writing a ${\displaystyle 3\times 3}$-matrix as ${\displaystyle A={\begin{bmatrix}a&b&c\end{bmatrix}}}$ where ${\displaystyle a,b,c}$ are column vectors of length 3, then the gradient over one of the three vectors may be written as the cross product of the other two:

${\displaystyle {\begin{aligned}\nabla _{\mathbf {a} }\det(A)&=\mathbf {b} \times \mathbf {c} \\\nabla _{\mathbf {b} }\det(A)&=\mathbf {c} \times \mathbf {a} \\\nabla _{\mathbf {c} }\det(A)&=\mathbf {a} \times \mathbf {b} .\end{aligned}}}$

History

Historically, determinants were used long before matrices: A determinant was originally defined as a property of a system of linear equations. The determinant "determines" whether the system has a unique solution (which occurs precisely if the determinant is non-zero). In this sense, determinants were first used in the Chinese mathematics textbook The Nine Chapters on the Mathematical Art (九章算術, Chinese scholars, around the 3rd century BCE). In Europe, solutions of linear systems of two equations were expressed by Cardano in 1545 by a determinant-like entity.

Determinants proper originated from the work of Seki Takakazu in 1683 in Japan and parallelly of Leibniz in 1693. Cramer (1750) stated, without proof, Cramer's rule. Both Cramer and also Bezout (1779) were led to determinants by the question of plane curves passing through a given set of points.

Vandermonde (1771) first recognized determinants as independent functions. Laplace (1772) gave the general method of expanding a determinant in terms of its complementary minors: Vandermonde had already given a special case. Immediately following, Lagrange (1773) treated determinants of the second and third order and applied it to questions of elimination theory; he proved many special cases of general identities.

Gauss (1801) made the next advance. Like Lagrange, he made much use of determinants in the theory of numbers. He introduced the word "determinant" (Laplace had used "resultant"), though not in the present signification, but rather as applied to the discriminant of a quantic. Gauss also arrived at the notion of reciprocal (inverse) determinants, and came very near the multiplication theorem.

The next contributor of importance is Binet (1811, 1812), who formally stated the theorem relating to the product of two matrices of m columns and n rows, which for the special case of m = n reduces to the multiplication theorem. On the same day (November 30, 1812) that Binet presented his paper to the Academy, Cauchy also presented one on the subject. (See Cauchy–Binet formula.) In this he used the word "determinant" in its present sense, summarized and simplified what was then known on the subject, improved the notation, and gave the multiplication theorem with a proof more satisfactory than Binet's. With him begins the theory in its generality.

(Jacobi 1841) used the functional determinant which Sylvester later called the Jacobian. In his memoirs in Crelle's Journal for 1841 he specially treats this subject, as well as the class of alternating functions which Sylvester has called alternants. About the time of Jacobi's last memoirs, Sylvester (1839) and Cayley began their work. Cayley 1841 introduced the modern notation for the determinant using vertical bars.

The study of special forms of determinants has been the natural result of the completion of the general theory. Axisymmetric determinants have been studied by Lebesgue, Hesse, and Sylvester; persymmetric determinants by Sylvester and Hankel; circulants by Catalan, Spottiswoode, Glaisher, and Scott; skew determinants and Pfaffians, in connection with the theory of orthogonal transformation, by Cayley; continuants by Sylvester; Wronskians (so called by Muir) by Christoffel and Frobenius; compound determinants by Sylvester, Reiss, and Picquet; Jacobians and Hessians by Sylvester; and symmetric gauche determinants by Trudi. Of the textbooks on the subject Spottiswoode's was the first. In America, Hanus (1886), Weld (1893), and Muir/Metzler (1933) published treatises.

Applications

Cramer's rule

Determinants can be used to describe the solutions of a linear system of equations, written in matrix form as ${\displaystyle Ax=b}$. This equation has a unique solution ${\displaystyle x}$ if and only if ${\displaystyle \det(A)}$ is nonzero. In this case, the solution is given by Cramer's rule:

${\displaystyle x_{i}={\frac {\det(A_{i})}{\det(A)}}\qquad i=1,2,3,\ldots ,n}$

where ${\displaystyle A_{i}}$ is the matrix formed by replacing the ${\displaystyle i}$-th column of ${\displaystyle A}$ by the column vector ${\displaystyle b}$. This follows immediately by column expansion of the determinant, i.e.

${\displaystyle \det(A_{i})=\det {\begin{bmatrix}a_{1}&\ldots &b&\ldots &a_{n}\end{bmatrix}}=\sum _{j=1}^{n}x_{j}\det {\begin{bmatrix}a_{1}&\ldots &a_{i-1}&a_{j}&a_{i+1}&\ldots &a_{n}\end{bmatrix}}=x_{i}\det(A)}$

where the vectors ${\displaystyle a_{j}}$ are the columns of A. The rule is also implied by the identity

${\displaystyle A\,\operatorname {adj} (A)=\operatorname {adj} (A)\,A=\det(A)\,I_{n}.}$

Cramer's rule can be implemented in ${\displaystyle \operatorname {O} (n^{3})}$ time, which is comparable to more common methods of solving systems of linear equations, such as LU, QR, or singular value decomposition.

Linear independence

Determinants can be used to characterize linearly dependent vectors: ${\displaystyle \det A}$ is zero if and only if the column vectors (or, equivalently, the row vectors) of the matrix ${\displaystyle A}$ are linearly dependent. For example, given two linearly independent vectors ${\displaystyle v_{1},v_{2}\in \mathbf {R} ^{3}}$, a third vector ${\displaystyle v_{3}}$ lies in the plane spanned by the former two vectors exactly if the determinant of the ${\displaystyle 3\times 3}$-matrix consisting of the three vectors is zero. The same idea is also used in the theory of differential equations: given functions ${\displaystyle f_{1}(x),\dots ,f_{n}(x)}$ (supposed to be ${\displaystyle n-1}$ times differentiable), the Wronskian is defined to be

${\displaystyle W(f_{1},\ldots ,f_{n})(x)={\begin{vmatrix}f_{1}(x)&f_{2}(x)&\cdots &f_{n}(x)\\f_{1}'(x)&f_{2}'(x)&\cdots &f_{n}'(x)\\\vdots &\vdots &\ddots &\vdots \\f_{1}^{(n-1)}(x)&f_{2}^{(n-1)}(x)&\cdots &f_{n}^{(n-1)}(x)\end{vmatrix}}.}$

It is non-zero (for some ${\displaystyle x}$) in a specified interval if and only if the given functions and all their derivatives up to order ${\displaystyle n-1}$ are linearly independent. If it can be shown that the Wronskian is zero everywhere on an interval then, in the case of analytic functions, this implies the given functions are linearly dependent. See the Wronskian and linear independence. Another such use of the determinant is the resultant, which gives a criterion when two polynomials have a common root.

Orientation of a basis

Main article: Orientation (vector space)

The determinant can be thought of as assigning a number to every sequence of n vectors in Rⁿ, by using the square matrix whose columns are the given vectors. For instance, an orthogonal matrix with entries in Rⁿ represents an orthonormal basis in Euclidean space. The determinant of such a matrix determines whether the orientation of the basis is consistent with or opposite to the orientation of the standard basis. If the determinant is +1, the basis has the same orientation. If it is −1, the basis has the opposite orientation.

More generally, if the determinant of A is positive, A represents an orientation-preserving linear transformation (if A is an orthogonal 2 × 2 or 3 × 3 matrix, this is a rotation), while if it is negative, A switches the orientation of the basis.

Volume and Jacobian determinant

As pointed out above, the absolute value of the determinant of real vectors is equal to the volume of the parallelepiped spanned by those vectors. As a consequence, if ${\displaystyle f:\mathbf {R} ^{n}\to \mathbf {R} ^{n}}$ is the linear map given by multiplication with a matrix ${\displaystyle A}$, and ${\displaystyle S\subset \mathbf {R} ^{n}}$ is any measurable subset, then the volume of ${\displaystyle f(S)}$ is given by ${\displaystyle |\det(A)|}$ times the volume of ${\displaystyle S}$. More generally, if the linear map ${\displaystyle f:\mathbf {R} ^{n}\to \mathbf {R} ^{m}}$ is represented by the ${\displaystyle m\times n}$-matrix ${\displaystyle A}$, then the ${\displaystyle n}$-dimensional volume of ${\displaystyle f(S)}$ is given by:

${\displaystyle \operatorname {volume} (f(S))={\sqrt {\det \left(A^{\textsf {T}}A\right)}}\operatorname {volume} (S).}$

By calculating the volume of the tetrahedron bounded by four points, they can be used to identify skew lines. The volume of any tetrahedron, given its vertices ${\displaystyle a,b,c,d}$, ${\displaystyle {\frac {1}{6}}\cdot |\det(a-b,b-c,c-d)|}$, or any other combination of pairs of vertices that form a spanning tree over the vertices.

A nonlinear map ${\displaystyle f\colon \mathbf {R} ^{2}\to \mathbf {R} ^{2}}$ sends a small square (left, in red) to a distorted parallelogram (right, in red). The Jacobian at a point gives the best linear approximation of the distorted parallelogram near that point (right, in translucent white), and the Jacobian determinant gives the ratio of the area of the approximating parallelogram to that of the original square.

For a general differentiable function, much of the above carries over by considering the Jacobian matrix of f. For

${\displaystyle f:\mathbf {R} ^{n}\rightarrow \mathbf {R} ^{n},}$

the Jacobian matrix is the n × n matrix whose entries are given by the partial derivatives

${\displaystyle D(f)=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{1\leq i,j\leq n}.}$

Its determinant, the Jacobian determinant, appears in the higher-dimensional version of integration by substitution: for suitable functions f and an open subset U of Rⁿ (the domain of f), the integral over f(U) of some other function φ : Rⁿ → R^m is given by

${\displaystyle \int _{f(U)}\phi (\mathbf {v} )\,d\mathbf {v} =\int _{U}\phi (f(\mathbf {u} ))\left|\det(\operatorname {D} f)(\mathbf {u} )\right|\,d\mathbf {u} .}$

The Jacobian also occurs in the inverse function theorem.

When applied to the field of Cartography, the determinant can be used to measure the rate of expansion of a map near the poles. 

Abstract algebraic aspects

Determinant of an endomorphism

The above identities concerning the determinant of products and inverses of matrices imply that similar matrices have the same determinant: two matrices A and B are similar, if there exists an invertible matrix X such that A = X⁻¹BX. Indeed, repeatedly applying the above identities yields

${\displaystyle \det(A)=\det(X)^{-1}\det(B)\det(X)=\det(B)\det(X)^{-1}\det(X)=\det(B).}$

The determinant is therefore also called a similarity invariant. The determinant of a linear transformation

${\displaystyle T:V\to V}$

for some finite-dimensional vector space V is defined to be the determinant of the matrix describing it, with respect to an arbitrary choice of basis in V. By the similarity invariance, this determinant is independent of the choice of the basis for V and therefore only depends on the endomorphism T.

Square matrices over commutative rings

The above definition of the determinant using the Leibniz rule holds works more generally when the entries of the matrix are elements of a commutative ring ${\displaystyle R}$, such as the integers ${\displaystyle \mathbf {Z} }$, as opposed to the field of real or complex numbers. Moreover, the characterization of the determinant as the unique alternating multilinear map that satisfies ${\displaystyle \det(I)=1}$ still holds, as do all the properties that result from that characterization.

A matrix ${\displaystyle A\in \operatorname {Mat} _{n\times n}(R)}$ is invertible (in the sense that there is an inverse matrix whose entries are in ${\displaystyle R}$) if and only if its determinant is an invertible element in ${\displaystyle R}$. For ${\displaystyle R=\mathbf {Z} }$, this means that the determinant is +1 or −1. Such a matrix is called unimodular.

The determinant being multiplicative, it defines a group homomorphism

${\displaystyle \operatorname {GL} _{n}(R)\rightarrow R^{\times },}$

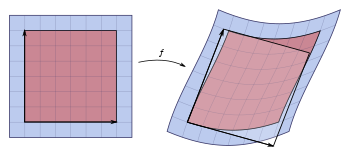
between the general linear group (the group of invertible ${\displaystyle n\times n}$-matrices with entries in ${\displaystyle R}$) and the multiplicative group of units in ${\displaystyle R}$. Since it respects the multiplication in both groups, this map is a group homomorphism.

The determinant is a natural transformation.

Given a ring homomorphism ${\displaystyle f:R\to S}$, there is a map ${\displaystyle \operatorname {GL} _{n}(f):\operatorname {GL} _{n}(R)\to \operatorname {GL} _{n}(S)}$ given by replacing all entries in ${\displaystyle R}$ by their images under ${\displaystyle f}$. The determinant respects these maps, i.e., the identity

${\displaystyle f(\det((a_{i,j})))=\det((f(a_{i,j})))}$

holds. In other words, the displayed commutative diagram commutes.

For example, the determinant of the complex conjugate of a complex matrix (which is also the determinant of its conjugate transpose) is the complex conjugate of its determinant, and for integer matrices: the reduction modulo ${\displaystyle m}$ of the determinant of such a matrix is equal to the determinant of the matrix reduced modulo ${\displaystyle m}$ (the latter determinant being computed using modular arithmetic). In the language of category theory, the determinant is a natural transformation between the two functors ${\displaystyle \operatorname {GL} _{n}}$ and ${\displaystyle (-)^{\times }}$. Adding yet another layer of abstraction, this is captured by saying that the determinant is a morphism of algebraic groups, from the general linear group to the multiplicative group,

${\displaystyle \det :\operatorname {GL} _{n}\to \mathbb {G} _{m}.}$

Exterior algebra

See also: Exterior algebra § Linear algebra

The determinant of a linear transformation ${\displaystyle T:V\to V}$ of an ${\displaystyle n}$-dimensional vector space ${\displaystyle V}$ or, more generally a free module of (finite) rank ${\displaystyle n}$ over a commutative ring ${\displaystyle R}$ can be formulated in a coordinate-free manner by considering the ${\displaystyle n}$-th exterior power ${\displaystyle \bigwedge ^{n}V}$ of ${\displaystyle V}$. The map ${\displaystyle T}$ induces a linear map

${\displaystyle {\begin{aligned}\bigwedge ^{n}T:\bigwedge ^{n}V&\rightarrow \bigwedge ^{n}V\\v_{1}\wedge v_{2}\wedge \dots \wedge v_{n}&\mapsto Tv_{1}\wedge Tv_{2}\wedge \dots \wedge Tv_{n}.\end{aligned}}}$

As ${\displaystyle \bigwedge ^{n}V}$ is one-dimensional, the map ${\displaystyle \bigwedge ^{n}T}$ is given by multiplying with some scalar, i.e., an element in ${\displaystyle R}$. Some authors such as (Bourbaki 1998) use this fact to define the determinant to be the element in ${\displaystyle R}$ satisfying the following identity (for all ${\displaystyle v_{i}\in V}$):

${\displaystyle \left(\bigwedge ^{n}T\right)\left(v_{1}\wedge \dots \wedge v_{n}\right)=\det(T)\cdot v_{1}\wedge \dots \wedge v_{n}.}$

This definition agrees with the more concrete coordinate-dependent definition. This can be shown using the unicity of a multilinear alternating form on ${\displaystyle n}$-tuples of vectors in ${\displaystyle R^{n}}$. For this reason, the highest non-zero exterior power ${\displaystyle \bigwedge ^{n}V}$ (as opposed to the determinant associated to an endomorphism) is sometimes also called the determinant of ${\displaystyle V}$ and similarly for more involved objects such as vector bundles or chain complexes of vector spaces. Minors of a matrix can also be cast in this setting, by considering lower alternating forms ${\displaystyle \bigwedge ^{k}V}$ with ${\displaystyle k<n}$.

Generalizations and related notions

Determinants as treated above admit several variants: the permanent of a matrix is defined as the determinant, except that the factors ${\displaystyle \operatorname {sgn}(\sigma )}$ occurring in Leibniz's rule are omitted. The immanant generalizes both by introducing a character of the symmetric group ${\displaystyle S_{n}}$ in Leibniz's rule.

Determinants for finite-dimensional algebras

For any associative algebra ${\displaystyle A}$ that is finite-dimensional as a vector space over a field ${\displaystyle F}$, there is a determinant map 

${\displaystyle \det :A\to F.}$

This definition proceeds by establishing the characteristic polynomial independently of the determinant, and defining the determinant as the lowest order term of this polynomial. This general definition recovers the determinant for the matrix algebra ${\displaystyle A=\operatorname {Mat} _{n\times n}(F)}$, but also includes several further cases including the determinant of a quaternion,

${\displaystyle \det(a+ib+jc+kd)=a^{2}+b^{2}+c^{2}+d^{2}}$,

the norm ${\displaystyle N_{L/F}:L\to F}$ of a field extension, as well as the Pfaffian of a skew-symmetric matrix and the reduced norm of a central simple algebra, also arise as special cases of this construction.

Infinite matrices

For matrices with an infinite number of rows and columns, the above definitions of the determinant do not carry over directly. For example, in the Leibniz formula, an infinite sum (all of whose terms are infinite products) would have to be calculated. Functional analysis provides different extensions of the determinant for such infinite-dimensional situations, which however only work for particular kinds of operators.

The Fredholm determinant defines the determinant for operators known as trace class operators by an appropriate generalization of the formula

${\displaystyle \det(I+A)=\exp(\operatorname {tr} (\log(I+A))).}$

Another infinite-dimensional notion of determinant is the functional determinant.

Operators in von Neumann algebras

For operators in a finite factor, one may define a positive real-valued determinant called the Fuglede−Kadison determinant using the canonical trace. In fact, corresponding to every tracial state on a von Neumann algebra there is a notion of Fuglede−Kadison determinant.

Related notions for non-commutative rings

For matrices over non-commutative rings, multilinearity and alternating properties are incompatible for n ≥ 2, so there is no good definition of the determinant in this setting.

For square matrices with entries in a non-commutative ring, there are various difficulties in defining determinants analogously to that for commutative rings. A meaning can be given to the Leibniz formula provided that the order for the product is specified, and similarly for other definitions of the determinant, but non-commutativity then leads to the loss of many fundamental properties of the determinant, such as the multiplicative property or that the determinant is unchanged under transposition of the matrix. Over non-commutative rings, there is no reasonable notion of a multilinear form (existence of a nonzero bilinear form with a regular element of R as value on some pair of arguments implies that R is commutative). Nevertheless, various notions of non-commutative determinant have been formulated that preserve some of the properties of determinants, notably quasideterminants and the Dieudonné determinant. For some classes of matrices with non-commutative elements, one can define the determinant and prove linear algebra theorems that are very similar to their commutative analogs. Examples include the q-determinant on quantum groups, the Capelli determinant on Capelli matrices, and the Berezinian on supermatrices (i.e., matrices whose entries are elements of ${\displaystyle \mathbb {Z} _{2}}$-graded rings). Manin matrices form the class closest to matrices with commutative elements.

Calculation

Determinants are mainly used as a theoretical tool. They are rarely calculated explicitly in numerical linear algebra, where for applications like checking invertibility and finding eigenvalues the determinant has largely been supplanted by other techniques. Computational geometry, however, does frequently use calculations related to determinants.

While the determinant can be computed directly using the Leibniz rule this approach is extremely inefficient for large matrices, since that formula requires calculating ${\displaystyle n!}$ (${\displaystyle n}$ factorial) products for an ${\displaystyle n\times n}$-matrix. Thus, the number of required operations grows very quickly: it is of order ${\displaystyle n!}$. The Laplace expansion is similarly inefficient. Therefore, more involved techniques have been developed for calculating determinants.

Decomposition methods

Some methods compute ${\displaystyle \det(A)}$ by writing the matrix as a product of matrices whose determinants can be more easily computed. Such techniques are referred to as decomposition methods. Examples include the LU decomposition, the QR decomposition or the Cholesky decomposition (for positive definite matrices). These methods are of order ${\displaystyle \operatorname {O} (n^{3})}$, which is a significant improvement over ${\displaystyle \operatorname {O} (n!)}$.

For example, LU decomposition expresses ${\displaystyle A}$ as a product

${\displaystyle A=PLU.}$

of a permutation matrix ${\displaystyle P}$ (which has exactly a single ${\displaystyle 1}$ in each column, and otherwise zeros), a lower triangular matrix ${\displaystyle L}$ and an upper triangular matrix ${\displaystyle U}$. The determinants of the two triangular matrices ${\displaystyle L}$ and ${\displaystyle U}$ can be quickly calculated, since they are the products of the respective diagonal entries. The determinant of ${\displaystyle P}$ is just the sign ${\displaystyle \varepsilon }$ of the corresponding permutation (which is ${\displaystyle +1}$ for an even number of permutations and is ${\displaystyle -1}$ for an odd number of permutations). Once such a LU decomposition is known for ${\displaystyle A}$, its determinant is readily computed as

${\displaystyle \det(A)=\varepsilon \det(L)\cdot \det(U).}$

Further methods

The order ${\displaystyle \operatorname {O} (n^{3})}$ reached by decomposition methods has been improved by different methods. If two matrices of order ${\displaystyle n}$ can be multiplied in time ${\displaystyle M(n)}$, where ${\displaystyle M(n)\geq n^{a}}$ for some ${\displaystyle a>2}$, then there is an algorithm computing the determinant in time ${\displaystyle O(M(n))}$. This means, for example, that an ${\displaystyle \operatorname {O} (n^{2.376})}$ algorithm exists based on the Coppersmith–Winograd algorithm. This exponent has been further lowered, as of 2016, to 2.373.

In addition to the complexity of the algorithm, further criteria can be used to compare algorithms. Especially for applications concerning matrices over rings, algorithms that compute the determinant without any divisions exist. (By contrast, Gauss elimination requires divisions.) One such algorithm, having complexity ${\displaystyle \operatorname {O} (n^{4})}$ is based on the following idea: one replaces permutations (as in the Leibniz rule) by so-called closed ordered walks, in which several items can be repeated. The resulting sum has more terms than in the Leibniz rule, but in the process several of these products can be reused, making it more efficient than naively computing with the Leibniz rule. Algorithms can also be assessed according to their bit complexity, i.e., how many bits of accuracy are needed to store intermediate values occurring in the computation. For example, the Gaussian elimination (or LU decomposition) method is of order ${\displaystyle \operatorname {O} (n^{3})}$, but the bit length of intermediate values can become exponentially long. By comparison, the Bareiss Algorithm, is an exact-division method (so it does use division, but only in cases where these divisions can be performed without remainder) is of the same order, but the bit complexity is roughly the bit size of the original entries in the matrix times ${\displaystyle n}$.

If the determinant of A and the inverse of A have already been computed, the matrix determinant lemma allows rapid calculation of the determinant of A + uv^T, where u and v are column vectors.

Charles Dodgson (i.e. Lewis Carroll of Alice's Adventures in Wonderland fame) invented a method for computing determinants called Dodgson condensation. Unfortunately this interesting method does not always work in its original form.

Plateau principle

From Wikipedia, the free encyclopedia

The plateau principle is a mathematical model or scientific law originally developed to explain the time course of drug action (pharmacokinetics). The principle has wide applicability in pharmacology, physiology, nutrition, biochemistry, and system dynamics. It applies whenever a drug or nutrient is infused or ingested at a relatively constant rate and when a constant fraction is eliminated during each time interval. Under these conditions, any change in the rate of infusion leads to an exponential increase or decrease until a new level is achieved. This behavior is also called an approach to steady state because rather than causing an indefinite increase or decrease, a natural balance is achieved when the rate of infusion or production is balanced by the rate of loss.

An especially important use of the plateau principle is to study the renewal of tissue constituents in the human and animal body. In adults, daily synthesis of tissue constituents is nearly constant, and most constituents are removed with a first-order reaction rate. Applicability of the plateau principle was recognized during radioactive tracer studies of protein turnover in the 1940s by Rudolph Schoenheimer and David Rittenberg. Unlike the case with drugs, the initial amount of tissue or tissue protein is not zero because daily synthesis offsets daily elimination. In this case, the model is also said to approach a steady state with exponential or logarithmic kinetics. Constituents that change in this manner are said to have a biological half-life.

A practical application of the plateau principle is that most people have experienced "plateauing" during regimens for weight management or training for sports. After a few weeks of progress, one seems unable to continue gaining in ability or losing weight. This outcome results from the same underlying quantitative model. This entry will describe the popular concepts as well as development of the plateau principle as a scientific, mathematical model.

In the sciences, the broadest application of the plateau principle is creating realistic time signatures for change in kinetic models (see Mathematical model). One example of this principle is the long time required to effectively change human body composition. Theoretical studies have shown that many months of consistent physical training and food restriction are needed to bring about permanent weight stability in people who were previously overweight.

The plateau principle in pharmacokinetics

Most drugs are eliminated from the blood plasma with first-order kinetics. For this reason, when a drug is introduced into the body at a constant rate by intravenous therapy, it approaches a new steady concentration in the blood at a rate defined by its half-life. Similarly, when the intravenous infusion is ended, the drug concentration decreases exponentially and reaches an undetectable level after 5–6 half-lives have passed. If the same drug is administered as a bolus (medicine) with a single injection, peak concentration is achieved almost immediately and then the concentration declines exponentially.

Most drugs are taken by mouth. In this case, the assumption of constant infusion is only approximated as doses are repeated over the course of several days. The plateau principle still applies but more complex models are required to account for the route of administration.

Equations for the approach to steady state

Derivation of equations that describe the time course of change for a system with zero-order input and first-order elimination are presented in the articles Exponential decay and Biological half-life, and in scientific literature.

${\displaystyle C_{t}=C_{0}e^{-k_{e}t}\,}$

• C_t is concentration after time t
• C₀ is the initial concentration (t = 0)
• k_e is the elimination rate constant

The relationship between the elimination rate constant and half-life is given by the following equation:

${\displaystyle k_{e}={\frac {\ln 2}{t_{1/2}}}\,}$

Because ln 2 equals 0.693, the half-life is readily calculated from the elimination rate constant. Half-life has units of time, and the elimination rate constant has units of 1/time, e.g., per hour or per day.

An equation can be used to forecast the concentration of a compound at any future time when the fractional degration rate and steady state concentration are known:

${\displaystyle C_{t}=C_{0}+(C_{ss}-C_{0})(1-e^{-k_{e}t})\,}$

• C_ss is concentration after the steady state has been achieved.

The exponential function in parentheses corresponds to the fraction of total change that has been achieved as time passes and the difference between C_ss and C₀ equals the total amount of change. Finally, at steady state, the concentration is expected to equal the rate of synthesis, production or infusion divided by the first-order elimination constant.

${\displaystyle C_{ss}={\frac {k_{s}}{k_{e}}}\,}$

• k_s is the rate of synthesis or infusion

Although these equations were derived to assist with predicting the time course of drug action, the same equation can be used for any substance or quantity that is being produced at a measurable rate and degraded with first-order kinetics. Because the equation applies in many instances of mass balance, it has very broad applicability in addition to pharmacokinetics. The most important inference derived from the steady state equation and the equation for fractional change over time is that the elimination rate constant (k_e) or the sum of rate constants that apply in a model determine the time course for change in mass when a system is perturbed (either by changing the rate of inflow or production, or by changing the elimination rate(s)).

Estimating values for kinetic rate parameters

When experimental data are available, the normal procedure for estimating rate parameters such as k_e and C_ss is to minimize the sum of squares of differences between observed data and values predicted based on initial estimates of the rate constant and steady state value. This can be done using any software package that contains a curve fitting routine. An example of this methodology implemented with spreadsheet software has been reported. The same article reports a method that requires only 3 equally spaced data points to obtain estimates for kinetic parameters. Spreadsheets that compare these methods are available.

The plateau principle in nutrition

Dr. Wilbur O. Atwater, who developed the first database of food composition in the United States, recognized that the response to excessive or insufficient nutrient intake included an adjustment in efficiency that would result in a plateau. He observed: "It has been found by numerous experiments that when the nutrients are fed in large excess, the body may continue for a time to store away part of the extra material, but after it has accumulated a certain amount, it refuses to take on more, and the daily consumption equals the supply even when this involves great waste."

In general, no essential nutrient is produced in the body. Nutrient kinetics therefore follow the plateau principle with the distinction that most are ingested by mouth and the body must contain an amount adequate for health. The plateau principle is important in determining how much time is needed to produce a deficiency when intake is insufficient. Because of this, pharmacokinetic considerations should be part of the information needed to set a dietary reference intake for essential nutrients.

Vitamin C

The blood plasma concentration of vitamin C or ascorbic acid as a function of dose attains a plateau with a half-life of about 2 weeks. Bioavailability of vitamin C is highest at dosages below 200 mg per day. Above 500 mg, nearly all of excess vitamin C is excreted through urine.

Vitamin D

Vitamin D metabolism is complex because the provitamin can be formed in the skin by ultraviolet irradiation or obtained from the diet. Once hydroxylated, the vitamin has a half-life of about 2 months. Various studies have suggested that current intakes are inadequate for optimum bone health and much current research is aimed at determining recommendations for obtaining adequate circulating vitamin D₃ and calcium while also minimizing potential toxicity.

Phytochemicals in foods and beverages

Many healthful qualities of foods and beverages may be related to the content of phytochemicals (see List of phytochemicals in food). Prime examples are flavonoids found in green tea, berries, cocoa, and spices as well as in the skins and seeds of apples, onions, and grapes.

Investigations into healthful benefits of phytochemicals follow exactly the same principles of pharmacokinetics that are required to study drug therapy. The initial concentration of any non-nutritive phytochemical in the blood plasma is zero unless a person has recently ingested a food or beverage. For example, as increasing amounts of green tea extract are consumed, a graded increase in plasma catechin can be measured, and the major compound is eliminated with a half-life of about 5 hours. Other considerations that must be evaluated include whether the ingested compound interacts favorably or unfavorably with other nutrients or drugs, and whether there is evidence for a threshold or toxicity at higher levels of intake.

Transitions in body composition

Plateaus during dieting and weight loss

It is especially common for people who are trying to lose weight to experience plateaus after several weeks of successful weight reduction. The plateau principle suggests that this leveling off is a sign of success. Basically, as one loses weight, less food energy is required to maintain the resting metabolic rate, which makes the initial regimen less effective. The idea of weight plateaus has been discussed for subjects who are participating in a calorie restriction experiment. Food energy is expended largely through work done against gravity (see Joule), so weight reduction lessens the effectiveness of a given workout. In addition, a trained person has greater skill and therefore greater efficiency during a workout. Remedies include increasing the workout intensity or length and reducing portion sizes of meals more than may have been done initially.

The fact that weight loss and dieting reduce the metabolic rate is supported by research. In one study, heat production was reduced 30% in obese men after a weight loss program, and this led to resistance to further lose body weight. Whether body mass increases or decreases, adjustments in the thermic effect of food, resting energy expenditure, and non-resting energy expenditure all oppose further change.

Plateaus during strength training

Any athlete who has trained for a sport has probably experienced plateaus, and this has given rise to various strategies to continue improving. Voluntary skeletal muscle is in balance between the amount of muscle synthesized or renewed each day and the amount that is degraded. Muscle fibers respond to repetition and load, and increased training causes the quantity of exercised muscle fiber to increase exponentially (simply meaning that the greatest gains are seen during the first weeks of training). Successful training produces hypertrophy of muscle fibers as an adaptation to the training regimen. In order to make further gains, greater workout intensity is required with heavier loads and more repetitions, although improvement in skill can contribute to gains in ability.

When a bodily constituent adjusts exponentially over time, it usually attains a new stable level as a result of the plateau principle. The new level may be higher than the initial level (hypertrophy) in the case of strength training or lower in the case of dieting or disuse atrophy. This adjustment contributes to homeostasis but does not require feedback regulation. Gradual, asymptotic approach to a new balance between synthesis and degradation produces a stable level. Because of this, the plateau principle is sometimes called the stability principle. Mathematically, the result is linear dynamics despite the fact that most biological processes are non-linear (see Nonlinear system) if considered over a very broad range of inputs.

Changes in body composition when food is restricted

Data from the Minnesota Starvation Experiment by Ancel Keys and others demonstrate that during food restriction, total body mass, fat mass and lean body mass follow an exponential approach to a new steady state. The observation that body mass changes exponentially during partial or complete starvation seems to be a general feature of adaptation to energy restriction.

The plateau principle in biochemistry

Each cell produces thousands of different kinds of protein and enzymes. One of the key methods of cellular regulation is to change the rate of transcription of messenger RNA, which gives rise to a change in the rate of synthesis for the protein that the messenger RNA encodes. The plateau principle explains why the concentration of different enzymes increases at unique rates in response to a single hormone. Because each enzyme is degraded with at a unique rate (each has a different half-life), the rate of change differs even when the same stimulus is applied. This principle has been demonstrated for the response of liver enzymes that degrade amino acids to cortisone, which is a catabolic hormone.

The method of approach to steady state has also been used to analyze the change in messenger RNA levels when synthesis or degradation changes, and a model has also been reported in which the plateau principle is used to connect the change in messenger RNA synthesis to the expected change in protein synthesis and concentration as a function of time.

The plateau principle in physiology

Excessive gain in body weight contributes to the metabolic syndrome, which may include elevated fasting blood sugar (or glucose), resistance to the action of insulin, elevated low-density lipoprotein (LDL cholesterol) or decreased high-density lipoprotein (HDL cholesterol), and elevated blood pressure. Obesity was designated as a disease in 2013 by the American Medical Association. It is defined as a chronic, relapsing, multi-factorial, neurobehavioral disease, wherein an increase in body fat promotes adipose tissue dysfunction and abnormal fat mass physical forces, resulting in adverse metabolic, biomechanical, and psychosocial health consequences. Because body mass, fat mass and fat free mass all change exponentially during weight reduction, it is a reasonable hypothesis to expect that symptoms of metabolic syndrome will also adjust exponentially towards normal values.

The plateau principle in compartmental modeling

Scientists have evaluated turnover of bodily constituents using radioactive tracers and stable isotope tracers. If given orally, the tracers are absorbed and move into the blood plasma, and are then distributed throughout the bodily tissues. In such studies, a multi-compartment model is required to analyze turnover by isotopic labeling. The isotopic marker is called a tracer and the material being analyzed is the tracee.

In studies with humans, blood plasma is the only tissue that can be easily sampled. A common procedure is to analyze the dynamics by assuming that changes can be attributed to a sum of exponentials. A single mathematical compartment is usually assumed to follow first-order kinetics in accord with the plateau principle. There are many examples of this kind of analysis in nutrition, for example, in the study of metabolism of zinc, and carotenoids.

The commonest assumption in compartmental modeling is that material in a homogeneous compartment behaves exponentially. However, this assumption is sometimes modified to include a saturable response that follows Michaelis–Menten kinetics or a related model called a Hill equation. When the material in question is present at a concentration near the K_M, it often behaves with pseudo first-order kinetics (see Rate equation) and the plateau principle applies despite the fact that the model is non-linear.

The plateau principle in system dynamics

Compartmental modeling in biomedical sciences primarily originated from the need to study metabolism by using tracers. In contrast, System dynamics originated as a simple method of developing mathematical models by Jay Wright Forrester and colleagues. System dynamics represents a compartment or pool as a stock and movement among compartments as flows. In general, the rate of flow depends on the amount of material in the stock to which it is connected. It is common to represent this dependence as a constant proportion (or first-order) using a connector element in the model.

System dynamics is one application of the field of control theory. In the biomedical field, one of the strongest advocates for computer-based analysis of physiological problems was Dr. Arthur Guyton. For example, system dynamics has been used to analyze the problem of body weight regulation. Similar methods have been used to study the spread of epidemics (see Compartmental models in epidemiology).

Software that solves systems of equations required for compartmental modeling and system dynamics makes use of finite difference methods to represent a set of ordinary differential equations. An expert appraisal of the different types of dynamic behavior that can be developed by application of the plateau principle to the field of system dynamics has been published.

Maggot therapy

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Maggot_therapy 

 

Maggot therapy
Maggot debridement therapy on a wound from a diabetic foot

Other names	maggot debridement therapy (MDT), larval therapy, larva therapy, larvae therapy, biodebridement, biosurgery

Maggot therapy (also known as larval therapy) is a type of biotherapy involving the introduction of live, disinfected maggots (fly larvae) into non-healing skin and soft-tissue wounds of a human or other animal for the purpose of cleaning out the necrotic (dead) tissue within a wound, (debridement) and disinfection.

There is evidence that maggot therapy may help with wound healing.

Medical uses

Maggots in medical packaging

Maggot therapy improves healing in chronic ulcers. In diabetic foot ulcers there is tentative evidence of benefit. A Cochrane review of methods for the debridement of venous leg ulcers found maggot therapy to be broadly as effective as most other methods, but the study also noted that the quality of data was poor.

In 2004, the United States Food and Drug Administration (FDA) cleared maggots from common green bottle fly for use as a "medical device" in the US for the purpose of treatment of:

• Non-healing necrotic skin and soft tissue wounds
• Pressure ulcers
• Venous stasis ulcers
• Neuropathic foot ulcers
• Non-healing traumatic or post-surgical wounds

Limitations

The wound must be of a type that can benefit from the application of maggot therapy. A moist, exudating wound with sufficient oxygen supply is a prerequisite. Not all wound-types are suitable: wounds which are dry, or open wounds of body cavities do not provide a good environment for maggots to feed. In some cases it may be possible to make a dry wound suitable for larval therapy by moistening it with saline soaks.

Patients and doctors may find maggots distasteful, although studies have shown that this does not cause patients to refuse the offer of maggot therapy. Maggots can be enclosed in opaque polymer bags to hide them from sight. Dressings must be designed to prevent any maggots from escaping, while allowing air to get to the maggots. Dressings are also designed to minimize the uncomfortable tickling sensation that the maggots often cause.

Mechanisms of action

The maggots have four principal actions:

• Debridement
• Disinfection of the wound
• Stimulation of healing
• Biofilm inhibition and eradication

Debridement

In maggot therapy, large numbers of small maggots consume necrotic tissue far more precisely than is possible in a normal surgical operation, and can debride a wound in a day or two. The area of a wound's surface is typically increased with the use of maggots due to the undebrided surface not revealing the actual underlying size of the wound. They derive nutrients through a process known as "extracorporeal digestion" by secreting a broad spectrum of proteolytic enzymes that liquefy necrotic tissue, and absorb the semi-liquid result within a few days. In an optimum wound environment maggots molt twice, increasing in length from about 2 mm to about 10 mm, and in girth, within a period of 48–72 hours by ingesting necrotic tissue, leaving a clean wound free of necrotic tissue when they are removed.

Disinfection

Secretions from maggots believed to have broad-spectrum antimicrobial activity include allantoin, urea, phenylacetic acid, phenylacetaldehyde, calcium carbonate, proteolytic enzymes, and many others. In vitro studies have shown that maggots inhibit and destroy a wide range of pathogenic bacteria including methicillin-resistant Staphylococcus aureus (MRSA), group A and B streptococci, and Gram-positive aerobic and anaerobic strains. Other bacteria like Pseudomonas aeruginosa, E. coli or Proteus spp. are not attacked by maggots, and in case of Pseudomonas even the maggots are in danger.

Biology of maggots

Lucilia sericata, Green Bottle Fly

 

Protophormia terraenovae, Northern blowfly

Those flies whose larvae feed on dead animals will sometimes lay their eggs on the dead parts (necrotic or gangrenous tissue) of living animals. The infestation by maggots of live animals is called myiasis. Some maggots will feed only on dead tissue, some only on live tissue, and some on live or dead tissue. The flies used most often for the purpose of maggot therapy are blow flies of the Calliphoridae: the blow fly species used most commonly is Lucilia sericata, the common green bottle fly. Another important species, Protophormia terraenovae, is also notable for its feeding secretions, which combat infection by Streptococcus pyogenes and S. pneumoniae.

History

Written records have documented that maggots have been used since antiquity as a wound treatment. There are reports of the use of maggots for wound healing by Maya, Native Americans, and Aboriginal tribes in Australia. Maggot treatment was reported in Renaissance times. Military physicians observed that soldiers whose wounds had become colonized with maggots experienced significantly less morbidity and mortality than soldiers whose wounds had not become colonized. These physicians included Napoleon’s general surgeon, Baron Dominique Larrey. Larrey reported during France's Egyptian campaign in Syria (1798–1801) that certain species of fly consumed only dead tissue and helped wounds to heal.

Joseph Jones, a ranking Confederate medical officer during the American Civil War, stated:

I have frequently seen neglected wounds ... filled with maggots ... as far as my experience extends, these worms eat only dead tissues, and do not injure specifically the well parts."

The first documented therapeutic use of maggots in the United States is credited to a second Confederate medical officer Dr. J.F. Zacharias, who reported during the American Civil War that:

"Maggots in a single day would clean a wound much better than any agents we had at our command ... I am sure I saved many lives by their use."

He recorded a high survival rate in patients he treated with maggots.

During World War I, orthopedic surgeon William S. Baer recorded the case of a soldier left for several days on the battlefield who had sustained compound fractures of the femur and large flesh wounds. The soldier arrived at the hospital with maggots infesting his wounds but had no fever or other signs of infection and survived his injuries, which would normally have been fatal. After the war, Baer began using maggot therapy at Boston Children's Hospital in Massachusetts.

There were reports that American prisoners of war of the Japanese in World War II resorted to maggot therapy to treat severe wounds.

A survey of US Army doctors published in 2013 found that 10% of them had used maggot therapy.

Regulation

In January 2004, the FDA granted permission to produce and market maggots for use in humans or animals as a prescription-only medical device for the following indications: "For debriding non-healing necrotic skin and soft tissue wounds, including pressure ulcers, venous stasis ulcers, neuropathic foot ulcers, and non-healing traumatic or post-surgical wounds."

Veterinary use

The use of maggots to clean dead tissue from animal wounds is part of folk medicine in many parts of the world. It is particularly helpful with chronic osteomyelitis, chronic ulcers, and other pus-producing infections that are frequently caused by chafing due to work equipment. Maggot therapy for horses in the United States was re-introduced after a study published in 2003 by veterinarian Dr. Scott Morrison. This therapy is used in horses for conditions such as osteomyelitis secondary to laminitis, sub-solar abscesses leading to osteomyelitis, post-surgical treatment of street-nail procedure for puncture wounds infecting the navicular bursa, canker, non-healing ulcers on the frog, and post-surgical site cleaning for keratoma removal.

However, there have not been many case studies done with maggot debridement therapy on animals, and as such it can be difficult to accurately assess how successful it is.