In
quantum physics,
quantum state refers to the state of a
quantum system.
A quantum state can be either
pure or
mixed. A pure quantum state is represented by a vector, called a
state vector, in a
Hilbert space. For example, when dealing with the energy spectrum of the
electron in a
hydrogen atom, the relevant state vectors are identified by the
principal quantum number, written
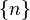
. For a more complicated case, consider
Bohm's formulation of the
EPR experiment, where the state vector

involves
superposition of joint
spin states for two particles. Mathematically, a pure quantum state is represented by a state vector in a
Hilbert space over
complex numbers, which is a generalization of our more usual three-dimensional space.
[1] If this Hilbert space is represented as a
function space, then its elements are called
wave functions.
A mixed quantum state corresponds to a probabilistic mixture of pure states; however, different distributions of pure states can generate equivalent (i.e., physically indistinguishable) mixed states. Mixed states are described by so-called
density matrices. A pure state can also be recast as a density matrix; in this way, pure states can be represented as a subset of the more general mixed states.
For example, if the spin of an electron is measured in any direction, e.g. with a
Stern–Gerlach experiment, there are two possible results: up or down. The Hilbert space for the electron's spin is therefore two-dimensional. A pure state here is represented by a two-dimensional
complex vector
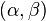
, with a length of one; that is, with

where

and

are the
absolute values of

and

. A mixed state, in this case, is a
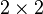
matrix that is
Hermitian,
positive-definite, and has
trace 1.
Before a particular
measurement is performed on a quantum system, the theory usually gives only a
probability distribution for the outcome, and the form that this distribution takes is completely determined by the quantum state and the
observable describing the measurement. These probability distributions arise for both mixed states and pure states: it is impossible in quantum mechanics (unlike classical mechanics) to prepare a state in which all properties of the system are fixed and certain. This is exemplified by the
uncertainty principle, and reflects a core difference between
classical and quantum physics. Even in quantum theory, however, for every observable there are some states that have an exact and determined value for that observable.
[2][3]
Conceptual description
Pure states
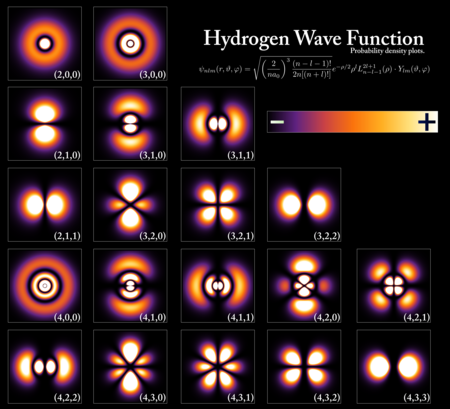
Probability densities for the electron of a hydrogen atom in different quantum states.
In the
mathematical formulation of quantum mechanics, pure quantum states correspond to
vectors in a
Hilbert space, while each observable quantity (such as the energy or momentum of a
particle) is associated with a mathematical
operator. The operator serves as a
linear function which acts on the states of the system. The
eigenvalues of the operator correspond to the possible values of the observable, i.e. it is possible to observe a particle with a momentum of 1 kg⋅m/s if and only if one of the eigenvalues of the momentum operator is 1 kg⋅m/s.
The corresponding
eigenvector (which physicists call an
eigenstate) with eigenvalue 1 kg⋅m/s would be a quantum state with a definite, well-defined value of momentum of 1 kg⋅m/s, with no
quantum uncertainty. If its momentum were measured, the result is guaranteed to be 1 kg⋅m/s.
On the other hand, a system in a
linear combination of multiple different eigenstates
does in general have quantum uncertainty for the given observable. We can represent this linear combination of eigenstates as:
 .
.
The coefficient which corresponds to a particular state in the linear combination is complex thus allowing interference effects between states. The coefficients are time dependent. How a quantum system changes in time is governed by the
time evolution operator. The symbols "|" and "
⟩"
[4] surrounding the
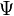
are part of
bra–ket notation.
Statistical mixtures of states are different from a linear combination. A statistical mixture of states is a
statistical ensemble of independent systems. Statistical mixtures represent the degree of knowledge whilst the uncertainty within quantum mechanics is fundamental. Mathematically, a statistical mixture is not a combination using complex coefficients, but rather a combination using real-valued, positive probabilities of different states
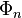
. A number
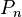
represents the probability of a randomly selected system being in the state
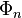
. Unlike the linear combination case each system is in a definite eigenstate.
[5][6]
The expectation value

of an observable
A is a statistical mean of measured values of the observable. It is this mean, and the distribution of probabilities, that is predicted by physical theories.
There is no state which is simultaneously an eigenstate for
all observables. For example, we cannot prepare a state such that both the position measurement
Q(
t) and the momentum measurement
P(
t) (at the same time
t) are known exactly; at least one of them will have a range of possible values.
[a] This is the content of the
Heisenberg uncertainty relation.
Moreover, in contrast to classical mechanics, it is unavoidable that
performing a measurement on the system generally changes its state[clarification needed] More precisely: After measuring an observable
A, the system will be in an eigenstate of
A; thus the state has changed, unless the system was already in that eigenstate. This expresses a kind of logical consistency: If we measure
A twice in the same run of the experiment, the measurements being directly consecutive
[clarification needed] in time, then they will produce the same results. This has some strange consequences, however, as follows.
Consider two observables,
A and
B, where
A corresponds to a measurement earlier in time than
B.
[7] Suppose that the system is in an eigenstate of
B at the experiment's begin. If we measure only
B, we will not notice statistical
[clarification needed] behaviour. If we measure first
A and then
B in the same run of the experiment, the system will transfer to an eigenstate of
A after the first measurement, and we will generally notice that the results of
B are statistical. Thus:
Quantum mechanical measurements influence one another, and it is important in which order they are performed.
Another feature of quantum states becomes relevant if we consider a physical system that consists of multiple subsystems; for example, an experiment with two particles rather than one. Quantum physics allows for certain states, called
entangled states, that show certain statistical correlations between measurements on the two particles which cannot be explained by classical theory. For details, see
entanglement. These entangled states lead to experimentally testable properties (
Bell's theorem) that allow us to distinguish between quantum theory and alternative classical (non-quantum) models.
Schrödinger picture vs. Heisenberg picture
One can take the observables to be dependent on time, while the state
σ was fixed once at the beginning of the experiment. This approach is called the
Heisenberg picture. (This approach was taken in the later part of the discussion above, with time-varying observables
P(
t),
Q(
t).) One can, equivalently, treat the observables as fixed, while the state of the system depends on time; that is known as the
Schrödinger picture. (This approach was taken in the earlier part of the discussion above, with a time-varying state

.) Conceptually (and mathematically), the two approaches are equivalent; choosing one of them is a matter of convention.
Both viewpoints are used in quantum theory. While non-relativistic
quantum mechanics is usually formulated in terms of the Schrödinger picture, the Heisenberg picture is often preferred in a relativistic context, that is, for
quantum field theory. Compare with
Dirac picture.
[8]
Formalism in quantum physics
Pure states as rays in a Hilbert space
Quantum physics is most commonly formulated in terms of
linear algebra, as follows. Any given system is identified with some finite- or infinite-dimensional
Hilbert space. The pure states correspond to vectors of
norm 1. Thus the set of all pure states corresponds to the
unit sphere in the Hilbert space.
Multiplying a pure state by a scalar is physically inconsequential (as long as the state is considered by itself). If one vector is obtained from the other by multiplying by a scalar of unit magnitude, the two vectors are said to correspond to the same "ray" in Hilbert space
[9] and also to the same point in the
projective Hilbert space.
Bra–ket notation
Calculations in quantum mechanics make frequent use of
linear operators,
inner products,
dual spaces and
Hermitian conjugation. In order to make such calculations flow smoothly, and to obviate the need (in some contexts) to fully understand the underlying linear algebra,
Paul Dirac invented a notation to describe quantum states, known as
bra-ket notation. Although the details of this are beyond the scope of this article (see the article
bra–ket notation), some consequences of this are:
- The expression used to denote a state vector (which corresponds to a pure quantum state) takes the form
 (where the "
(where the "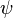 " can be replaced by any other symbols, letters, numbers, or even words). This can be contrasted with the usual mathematical notation, where vectors are usually bold, lower-case letters, or letters with arrows on top.
" can be replaced by any other symbols, letters, numbers, or even words). This can be contrasted with the usual mathematical notation, where vectors are usually bold, lower-case letters, or letters with arrows on top.
- Instead of vector, the term ket is used synonymously.
- Each ket
 is uniquely associated with a so-called bra, denoted
is uniquely associated with a so-called bra, denoted  , which corresponds to the same physical quantum state. Technically, the bra is the adjoint of the ket. It is an element of the dual space, and related to the ket by the Riesz representation theorem. In a finite-dimensional space with a chosen basis, writing
, which corresponds to the same physical quantum state. Technically, the bra is the adjoint of the ket. It is an element of the dual space, and related to the ket by the Riesz representation theorem. In a finite-dimensional space with a chosen basis, writing  as a column vector,
as a column vector,  is a row vector; to obtain it just take the transpose and entry-wise complex conjugate of
is a row vector; to obtain it just take the transpose and entry-wise complex conjugate of  .
.
- Inner products (also called brackets) are written so as to look like a bra and ket next to each other:
 . (The phrase "bra-ket" is supposed to resemble "bracket".)
. (The phrase "bra-ket" is supposed to resemble "bracket".)
Spin
The
angular momentum has the same dimension as the
Planck constant and, at quantum scale, behaves as a
discrete degree of freedom. Most particles possess a kind of intrinsic angular momentum that does not appear at all in classical mechanics and arises from Dirac's relativistic generalization of the theory. Mathematically it is described with
spinors. In non-relativistic quantum mechanics the
group representations of the
Lie group SU(2) are used to describe this additional freedom. For a given particle, the choice of representation (and hence the range of possible values of the spin observable) is specified by a non-negative number
S that, in units of
Planck's reduced constant ħ, is either an
integer (0, 1, 2 ...) or a
half-integer (1/2, 3/2, 5/2 ...). For a
massive particle with spin
S, its
spin quantum number m always assumes one of the 2
S + 1 possible values in the set
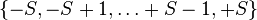
As a consequence, the quantum state of a particle with spin is described by a
vector-valued wave function with values in
C2S+1. Equivalently, it is represented by a
complex-valued function of four variables: one discrete
quantum number variable (for the spin) is added to the usual three continuous variables (for the position in space).
Many-body states and particle statistics
The quantum state of a system of
N particles, each potentially with spin, is described by a complex-valued function with four variables per particle, e.g.

Here, the spin variables
mν assume values from the set
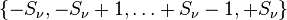
where

is the spin of
νth particle.

for a particle that does not exhibit spin.
The treatment of
identical particles is very different for
bosons (particles with integer spin) versus
fermions (particles with half-integer spin). The above
N-particle function must either be symmetrized (in the bosonic case) or anti-symmetrized (in the fermionic case) with respect to the particle numbers. If not all
N particles are identical, but some of them are, then the function must be (anti)symmetrized separately over the variables corresponding to each group of identical variables, according to its statistics (bosonic or fermionic).
Electrons are fermions with
S = 1/2,
photons (quanta of light) are bosons with
S = 1 (although in the
vacuum they are
massless and can't be described with Schrödingerian mechanics).
When symmetrization or anti-symmetrization is unnecessary,
N-particle spaces of states can be obtained simply by
tensor products of one-particle spaces, to which we will return later.
Basis states of one-particle systems
As with any
Hilbert space, if a
basis is chosen for the Hilbert space of a system, then any ket can be expanded as a
linear combination of those basis elements. Symbolically, given basis kets

, any ket

can be written

where
ci are
complex numbers. In physical terms, this is described by saying that

has been expressed as a
quantum superposition of the states

. If the basis kets are chosen to be
orthonormal (as is often the case), then

.
One property worth noting is that the
normalized states

are characterized by

Expansions of this sort play an important role in measurement in quantum mechanics. In particular, if the

are
eigenstates (with
eigenvalues ki) of an observable, and that observable is measured on the normalized state

, then the probability that the result of the measurement is
ki is |
ci|
2. (The normalization condition above mandates that the total sum of probabilities is equal to one.)
A particularly important example is the
position basis, which is the basis consisting of eigenstates of the observable which corresponds to measuring position. If these eigenstates are nondegenerate (for example, if the system is a single,
spinless particle), then any ket

is associated with a complex-valued function of three-dimensional space:
[clarification needed]

This function is called the
wavefunction corresponding to

.
Superposition of pure states
One aspect of quantum states, mentioned above, is that
superpositions of them can be formed. If
and

are two kets corresponding to quantum states, the ket

is a different quantum state (possibly not normalized). Note that
which quantum state it is depends on both the amplitudes and phases (arguments) of

and
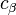
. In other words, for example, even though

and
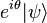
(for real
θ) correspond to the same physical quantum state, they are
not interchangeable, since for example

and
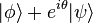
do
not (in general) correspond to the same physical state. However,

and
 do
do correspond to the same physical state. This is sometimes described by saying that "global" phase factors are unphysical, but "relative" phase factors are physical and important.
One example of a quantum interference phenomenon that arises from superposition is the
double-slit experiment. The
photon state is a superposition of two different states, one of which corresponds to the photon having passed through the left slit, and the other corresponding to passage through the right slit. The relative phase of those two states has a value which depends on the distance from each of the two slits. Depending on what that phase is, the interference is constructive at some locations and destructive in others, creating the interference pattern. By the analogy with
coherence in other wave phenomena, a superposed state can be referred to as a
coherent superposition.
Another example of the importance of relative phase in quantum superposition is
Rabi oscillations, where the relative phase of two states varies in time due to the
Schrödinger equation. The resulting superposition ends up oscillating back and forth between two different states.
Mixed states
A
pure quantum state is a state which can be described by a single ket vector, as described above. A
mixed quantum state is a
statistical ensemble of pure states (see
quantum statistical mechanics). Mixed states inevitably arise from pure states when, for a composite quantum system
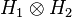
with an
entangled state on it, the part
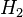
is inaccessible to the observer. The state of the part

is expressed then as the
partial trace over
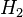
.
A mixed state
cannot be described as a ket vector. Instead, it is described by its associated
density matrix (or
density operator), usually denoted
ρ. Note that density matrices can describe both mixed
and pure states, treating them on the same footing. Moreover, a mixed quantum state on a given quantum system described by a Hilbert space

can be always represented as the partial trace of a pure quantum state (called a
purification) on a larger bipartite system

for a sufficiently large Hilbert space

.
The density matrix describing a mixed state is defined to be an operator of the form
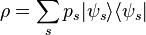
where

is the fraction of the ensemble in each pure state
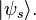
The density matrix can be thought of as a way of using the one-particle
formalism to describe the behavior of many similar particles by giving a probability distribution (or ensemble) of states that these particles can be found in.
A simple criterion for checking whether a density matrix is describing a pure or mixed state is that the
trace of
ρ2 is equal to 1 if the state is pure, and less than 1 if the state is mixed.
[10] Another, equivalent, criterion is that the
von Neumann entropy is 0 for a pure state, and strictly positive for a mixed state.
The rules for measurement in quantum mechanics are particularly simple to state in terms of density matrices. For example, the ensemble average (
expectation value) of a measurement corresponding to an observable
A is given by

where

are eigenkets and eigenvalues, respectively, for the operator
A, and "tr" denotes trace. It is important to note that two types of averaging are occurring, one being a weighted quantum superposition over the basis kets

of the pure states, and the other being a statistical (said
incoherent) average with the probabilities
ps of those states.
According to Wigner,
[11] the concept of mixture was put forward by Landau.
[12][13]
Interpretation
Although theoretically, for a given quantum system, a state vector provides the full information about its evolution, it is not easy to understand what information about the "real world" it carries. Due to the uncertainty principle, a state, even if it has the value of one observable exactly defined (i.e. the observable has this state as an
eigenstate), cannot exactly define values of
all observables.
For state vectors (pure states),
probability amplitudes offer a
probabilistic interpretation. It can be generalized for all states (including mixed), for instance, as expectation values mentioned
above.
Mathematical generalizations
States can be formulated in terms of observables, rather than as vectors in a vector space. These are
positive normalized linear functionals on a
C*-algebra, or sometimes other classes of algebras of observables. See
State on a C*-algebra and
Gelfand–Naimark–Segal construction for more details.
 and
and  (pronounced "ket 0" and "ket 1").
(pronounced "ket 0" and "ket 1"). and
and  :
: is
is 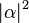 and the probability of outcome
and the probability of outcome  is
is  . Because the absolute squares of the amplitudes equate to probabilities, it follows that α and β must be constrained by the equation
. Because the absolute squares of the amplitudes equate to probabilities, it follows that α and β must be constrained by the equation and
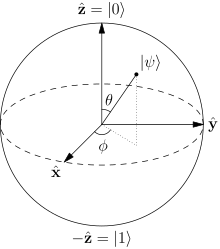
and  are respectively. The rest of the surface of the sphere is inaccessible to a classical bit, but a pure qubit state can be represented by any point on the surface. For example, the pure qubit state
are respectively. The rest of the surface of the sphere is inaccessible to a classical bit, but a pure qubit state can be represented by any point on the surface. For example, the pure qubit state  would lie on the equator of the sphere, on the positive y axis.
would lie on the equator of the sphere, on the positive y axis.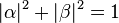 . Another, the overall phase of the state, has no physically observable consequences, so we can arbitrarily choose α to be real, leaving just two degrees of freedom.
. Another, the overall phase of the state, has no physically observable consequences, so we can arbitrarily choose α to be real, leaving just two degrees of freedom. and
and  , as well as the length r of the vector that represents the mixed state.
, as well as the length r of the vector that represents the mixed state. , with probability
, with probability 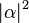 , or
, or  , with probability
, with probability  . Measurement of the state of the qubit alters the values of α and β. For instance, if the result of the measurement is
. Measurement of the state of the qubit alters the values of α and β. For instance, if the result of the measurement is  , α is changed to 1 (up to phase) and β is changed to 0. Note that a measurement of a qubit state entangled with another quantum system transforms a pure state into a mixed state.
, α is changed to 1 (up to phase) and β is changed to 0. Note that a measurement of a qubit state entangled with another quantum system transforms a pure state into a mixed state.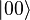 or
or 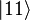 , as
, as  .
. or
or  . Because of the qubits' entanglement, Bob must now get exactly the same measurement as Alice; i.e., if she measures a
. Because of the qubits' entanglement, Bob must now get exactly the same measurement as Alice; i.e., if she measures a  , Bob must measure the same, as
, Bob must measure the same, as 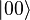 is the only state where Alice's qubit is a
is the only state where Alice's qubit is a  . Entanglement also allows multiple states (such as the Bell state mentioned above) to be acted on simultaneously, unlike classical bits that can only have one value at a time. Entanglement is a necessary ingredient of any quantum computation that cannot be done efficiently on a classical computer. Many of the successes of quantum computation and communication, such as quantum teleportation and superdense coding, make use of entanglement, suggesting that entanglement is a resource that is unique to quantum computation.
. Entanglement also allows multiple states (such as the Bell state mentioned above) to be acted on simultaneously, unlike classical bits that can only have one value at a time. Entanglement is a necessary ingredient of any quantum computation that cannot be done efficiently on a classical computer. Many of the successes of quantum computation and communication, such as quantum teleportation and superdense coding, make use of entanglement, suggesting that entanglement is a resource that is unique to quantum computation.

 and
and 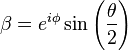 .
.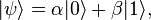
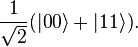
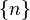 . For a more complicated case, consider
. For a more complicated case, consider 
 , with a length of one; that is, with
, with a length of one; that is, with
 and
and  are the
are the  and
and  . A mixed state, in this case, is a
. A mixed state, in this case, is a 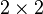 matrix that is
matrix that is 
 .
.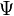 are part of
are part of 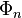 . A number
. A number 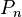 represents the probability of a randomly selected system being in the state
represents the probability of a randomly selected system being in the state  of an observable A is a statistical mean of measured values of the observable. It is this mean, and the distribution of probabilities, that is predicted by physical theories.
of an observable A is a statistical mean of measured values of the observable. It is this mean, and the distribution of probabilities, that is predicted by physical theories. (where the "
(where the "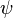 " can be replaced by any other symbols, letters, numbers, or even words). This can be contrasted with the usual mathematical notation, where vectors are usually bold, lower-case letters, or letters with arrows on top.
" can be replaced by any other symbols, letters, numbers, or even words). This can be contrasted with the usual mathematical notation, where vectors are usually bold, lower-case letters, or letters with arrows on top. , which corresponds to the same physical quantum state. Technically, the bra is the
, which corresponds to the same physical quantum state. Technically, the bra is the  . (The phrase "bra-ket" is supposed to resemble "bracket".)
. (The phrase "bra-ket" is supposed to resemble "bracket".)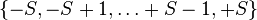

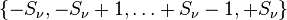
 is the spin of νth particle.
is the spin of νth particle.  for a particle that does not exhibit spin.
for a particle that does not exhibit spin. , any ket
, any ket 
 .
.

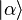 and
and  are two kets corresponding to quantum states, the ket
are two kets corresponding to quantum states, the ket

 and
and 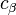 . In other words, for example, even though
. In other words, for example, even though 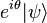 (for real θ) correspond to the same physical quantum state, they are not interchangeable, since for example
(for real θ) correspond to the same physical quantum state, they are not interchangeable, since for example  and
and 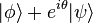 do not (in general) correspond to the same physical state. However,
do not (in general) correspond to the same physical state. However,  do correspond to the same physical state. This is sometimes described by saying that "global" phase factors are unphysical, but "relative" phase factors are physical and important.
do correspond to the same physical state. This is sometimes described by saying that "global" phase factors are unphysical, but "relative" phase factors are physical and important.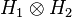 with an
with an 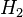 is inaccessible to the observer. The state of the part
is inaccessible to the observer. The state of the part  is expressed then as the
is expressed then as the  can be always represented as the partial trace of a pure quantum state (called a
can be always represented as the partial trace of a pure quantum state (called a  for a sufficiently large Hilbert space
for a sufficiently large Hilbert space  .
.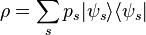
 is the fraction of the ensemble in each pure state
is the fraction of the ensemble in each pure state 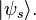 The density matrix can be thought of as a way of using the one-particle
The density matrix can be thought of as a way of using the one-particle 
 are eigenkets and eigenvalues, respectively, for the operator A, and "tr" denotes trace. It is important to note that two types of averaging are occurring, one being a weighted quantum superposition over the basis kets
are eigenkets and eigenvalues, respectively, for the operator A, and "tr" denotes trace. It is important to note that two types of averaging are occurring, one being a weighted quantum superposition over the basis kets  of the pure states, and the other being a statistical (said incoherent) average with the probabilities ps of those states.
of the pure states, and the other being a statistical (said incoherent) average with the probabilities ps of those states.