From Wikipedia, the free encyclopedia
In
physics,
relativistic mechanics refers to
mechanics compatible with
special relativity (SR) and
general relativity (GR). It provides a non-
quantum mechanical description of a system of particles, or of a
fluid, in cases where the
velocities of moving objects are comparable to the
speed of light c. As a result,
classical mechanics is extended correctly to particles traveling at high velocities and energies, and provides a consistent inclusion of
electromagnetism
with the mechanics of particles. This was not possible in Galilean
relativity, where it would be permitted for particles and light to
travel at
any speed, including faster than light. The foundations of relativistic mechanics are the
postulates of special relativity and general relativity. The unification of SR with quantum mechanics is
relativistic quantum mechanics, while attempts for that of GR is
quantum gravity, an
unsolved problem in physics.
As with classical mechanics, the subject can be divided into "
kinematics"; the description of motion by specifying
positions, velocities and
accelerations, and "
dynamics"; a full description by considering
energies,
momenta, and
angular momenta and their
conservation laws, and
forces
acting on particles or exerted by particles. There is however a
subtlety; what appears to be "moving" and what is "at rest"—which is
termed by "
statics" in classical mechanics—depends on the relative motion of
observers who measure in
frames of reference.
Although some definitions and concepts from classical mechanics do carry over to SR, such as force as the
time derivative of momentum (
Newton's second law), the
work done by a particle as the
line integral of force exerted on the particle along a path, and
power
as the time derivative of work done, there are a number of significant
modifications to the remaining definitions and formulae. SR states that
motion is relative and the laws of physics are the same for all
experimenters irrespective of their
inertial reference frames. In addition to modifying notions of
space and time, SR forces one to reconsider the concepts of
mass,
momentum, and
energy all of which are important constructs in
Newtonian mechanics.
SR shows that these concepts are all different aspects of the same
physical quantity in much the same way that it shows space and time to
be interrelated. Consequently, another modification is the concept of
the
center of mass of a system, which is straightforward to define in classical mechanics but much less obvious in relativity – see
relativistic center of mass for details.
The equations become more complicated in the more familiar
three-dimensional vector calculus formalism, due to the
nonlinearity in the
Lorentz factor, which accurately accounts for relativistic velocity dependence and the
speed limit of all particles and fields. However, they have a simpler and elegant form in
four-dimensional
spacetime, which includes flat
Minkowski space (SR) and
curved spacetime (GR), because three-dimensional vectors derived from space and scalars derived from time can be collected into
four vectors, or four-dimensional
tensors.
However, the six component angular momentum tensor is sometimes called a
bivector because in the 3D viewpoint it is two vectors (one of these,
the conventional angular momentum, being an
axial vector).
Relativistic kinematics
The relativistic four-velocity, that is the four-vector representing velocity in relativity, is defined as follows:

In the above, τ is the
proper time of the path through
spacetime, called the world-line, followed by the object velocity the above represents, and

is the
four-position; the coordinates of an
event. Due to
time dilation,
the proper time is the time between two events in a frame of reference
where they take place at the same location. The proper time is related
to
coordinate time t by:

where γ(
v) is the
Lorentz factor:

(either version may be quoted) so it follows:

The first three terms, excepting the factor of γ(
v), is the velocity as seen by the observer in their own reference frame. The γ(
v) is determined by the velocity
v
between the observer's reference frame and the object's frame, which is
the frame in which its proper time is measured. This quantity is
invariant under Lorentz transformation, so to check to see what an
observer in a different reference frame sees, one simply multiplies the
velocity four-vector by the Lorentz transformation matrix between the
two reference frames.
Relativistic dynamics
Relativistic energy and momentum
There are a couple of (equivalent) ways to define momentum and energy in SR. One method uses
conservation laws. If these laws are to remain valid in SR they must be true in every possible reference frame. However, if one does some simple
thought experiments
using the Newtonian definitions of momentum and energy, one sees that
these quantities are not conserved in SR. One can rescue the idea of
conservation by making some small modifications to the definitions to
account for
relativistic velocities. It is these new definitions which are taken as the correct ones for momentum and energy in SR.
The
four-momentum of an object is straightforward, identical in form to the classical momentum, but replacing 3-vectors with 4-vectors:

The energy and momentum of an object with
invariant mass m0 (also called
rest mass), moving with
velocity v with respect to a given frame of reference, are respectively given by

The factor of γ(
v) comes from the definition of the
four-velocity described above. The appearance of the γ factor has an
alternative way of being stated, explained in the next section.
The kinetic energy,
K, is defined as

And the speed as a function of kinetic energy is given by

Rest mass and relativistic mass
The quantity

is often called the
relativistic mass of the object in the given frame of reference.
[1]
This makes the relativistic relation between the spatial velocity and
the spatial momentum look identical. However, this can be misleading,
as it is
not appropriate in special relativity in
all
circumstances. For instance, kinetic energy and force in special
relativity can not be written exactly like their classical analogues by
only replacing the mass with the relativistic mass. Moreover, under
Lorentz transformations, this relativistic mass is not invariant, while
the rest mass is. For this reason many people find it easier use the
rest mass (thereby introduce γ through the 4-velocity or coordinate
time), and discard the concept of relativistic mass.
Lev B. Okun suggested that "this terminology ... has no rational justification today", and should no longer be taught.
[2]
Other physicists, including
Wolfgang Rindler and
T. R. Sandin, have argued that relativistic mass is a useful concept and there is little reason to stop using it.
[3] See
mass in special relativity for more information on this debate.
Some authors use
m for relativistic mass and
m0 for rest mass,
[4] others simply use
m for rest mass. This article uses the former convention for clarity.
The energy and momentum of an object with invariant mass
m0 are related by the formulas


The first is referred to as the
relativistic energy–momentum relation. It can be derived by considering that

can be written as

where the denominator can be written as

. Now, gamma can be replaced in the expression of energy. While the energy
E and the momentum
p depend on the frame of reference in which they are measured, the quantity
E2 − (
pc)
2 is invariant, and arises as −
c2 times the squared magnitude of the
4-momentum vector which is −(
m0c)
2.
It should be noted that the invariant mass of a system

is different from the sum of the rest masses of the particles of
which it is composed due to kinetic energy and binding energy. Rest mass
is not a conserved quantity in special relativity unlike the situation
in Newtonian physics. However, even if an object is changing internally,
so long as it does not exchange energy with surroundings, then its rest
mass will not change, and can be calculated with the same result in any
frame of reference.
A particle whose rest mass is zero is called
massless.
Photons and
gravitons are thought to be massless; and
neutrinos are nearly so.
Mass–energy equivalence
The relativistic energy–momentum equation holds for all particles, even for
massless particles for which
m0 = 0. In this case:

When substituted into
Ev =
c2p, this gives
v =
c: massless particles (such as
photons) always travel at the speed of light.
Notice that the rest mass of a composite system will generally be
slightly different from the sum of the rest masses of its parts since,
in its rest frame, their kinetic energy will increase its mass and their
(negative) binding energy will decrease its mass. In particular, a
hypothetical "box of light" would have rest mass even though made of
particles which do not since their momenta would cancel.
Looking at the above formula for invariant mass of a system, one sees that, when a single massive object is at rest (
v =
0,
p =
0), there is a non-zero mass remaining:
m0 =
E/
c2.
The corresponding energy, which is also the total energy when a single
particle is at rest, is referred to as "rest energy". In systems of
particles which are seen from a moving inertial frame, total energy
increases and so does momentum. However, for single particles the rest
mass remains constant, and for systems of particles the invariant mass
remain constant, because in both cases, the energy and momentum
increases subtract from each other, and cancel. Thus, the invariant mass
of systems of particles is a calculated constant for all observers, as
is the rest mass of single particles.
The mass of systems and conservation of invariant mass
For systems of particles, the energy–momentum equation requires summing the momentum vectors of the particles:

The inertial frame in which the momenta of all particles sums to zero is called the
center of momentum frame. In this special frame, the relativistic energy–momentum equation has
p = 0, and thus gives the invariant mass of the system as merely the total energy of all parts of the system, divided by
c2

This is the invariant mass of any system which is measured in a frame
where it has zero total momentum, such as a bottle of hot gas on a
scale. In such a system, the mass which the scale weighs is the
invariant mass, and it depends on the total energy of the system. It is
thus more than the sum of the rest masses of the molecules, but also
includes all the totaled energies in the system as well. Like energy and
momentum, the invariant mass of isolated systems cannot be changed so
long as the system remains totally closed (no mass or energy allowed in
or out), because the total relativistic energy of the system remains
constant so long as nothing can enter or leave it.
An increase in the energy of such a system which is caused by translating the system to an inertial frame which is not the
center of momentum frame, causes an increase in energy and momentum without an increase in invariant mass.
E =
m0c2, however, applies only to isolated systems in their center-of-momentum frame where momentum sums to zero.
Taking this formula at face value, we see that in relativity, mass is
simply energy by another name (and measured in different units). In
1927 Einstein remarked about special relativity, "Under this theory mass
is not an unalterable magnitude, but a magnitude dependent on (and,
indeed, identical with) the amount of energy."
[5]
Closed (isolated) systems
In a "totally-closed" system (i.e.,
isolated system)
the total energy, the total momentum, and hence the total invariant
mass are conserved. Einstein's formula for change in mass translates to
its simplest Δ
E = Δ
mc2 form, however, only in
non-closed systems in which energy is allowed to escape (for example, as
heat and light), and thus invariant mass is reduced. Einstein's
equation shows that such systems must lose mass, in accordance with the
above formula, in proportion to the energy they lose to the
surroundings. Conversely, if one can measure the differences in mass
between a system before it undergoes a reaction which releases heat and
light, and the system after the reaction when heat and light have
escaped, one can estimate the amount of energy which escapes the system.
Chemical and nuclear reactions
In
both nuclear and chemical reactions, such energy represents the
difference in binding energies of electrons in atoms (for chemistry) or
between nucleons in nuclei (in atomic reactions). In both cases, the
mass difference between reactants and (cooled) products measures the
mass of heat and light which will escape the reaction, and thus (using
the equation) give the equivalent energy of heat and light which may be
emitted if the reaction proceeds.
In chemistry, the mass differences associated with the emitted energy are around 10
−9 of the molecular mass.
[6]
However, in nuclear reactions the energies are so large that they are
associated with mass differences, which can be estimated in advance, if
the products and reactants have been weighed (atoms can be weighed
indirectly by using atomic masses, which are always the same for each
nuclide).
Thus, Einstein's formula becomes important when one has measured the
masses of different atomic nuclei. By looking at the difference in
masses, one can predict which nuclei have stored energy that can be
released by certain
nuclear reactions, providing important information which was useful in the development of nuclear energy and, consequently, the
nuclear bomb. Historically, for example,
Lise Meitner
was able to use the mass differences in nuclei to estimate that there
was enough energy available to make nuclear fission a favorable process.
The implications of this special form of Einstein's formula have thus
made it one of the most famous equations in all of science.
Center of momentum frame
The equation
E =
m0c2 applies only to isolated systems in their
center of momentum frame. It has been popularly misunderstood to mean that mass may be
converted to energy, after which the
mass
disappears. However, popular explanations of the equation as applied to
systems include open (non-isolated) systems for which heat and light
are allowed to escape, when they otherwise would have contributed to the
mass (
invariant mass) of the system.
Historically, confusion about mass being "converted" to energy has been aided by confusion between mass and "
matter", where matter is defined as
fermion
particles. In such a definition, electromagnetic radiation and kinetic
energy (or heat) are not considered "matter". In some situations, matter
may indeed be converted to non-matter forms of energy (see above), but
in all these situations, the matter and non-matter forms of energy still
retain their original mass.
For isolated systems (closed to all mass and energy exchange), mass
never disappears in the center of momentum frame, because energy cannot
disappear. Instead, this equation, in context, means only that when any
energy is added to, or escapes from, a system in the center-of-momentum
frame, the system will be measured as having gained or lost mass, in
proportion to energy added or removed. Thus, in theory, if an atomic
bomb were placed in a box strong enough to hold its blast, and detonated
upon a scale, the mass of this closed system would not change, and the
scale would not move. Only when a transparent "window" was opened in the
super-strong plasma-filled box, and light and heat were allowed to
escape in a beam, and the bomb components to cool, would the system lose
the mass associated with the energy of the blast. In a 21 kiloton bomb,
for example, about a gram of light and heat is created. If this heat
and light were allowed to escape, the remains of the bomb would lose a
gram of mass, as it cooled. In this thought-experiment, the light and
heat carry away the gram of mass, and would therefore deposit this gram
of mass in the objects that absorb them.
[7]
Angular momentum
In relativistic mechanics, the time-varying mass moment

and orbital 3-angular momentum

of a point-like particle are combined into a four-dimensional
bivector in terms of the 4-position
X and the 4-momentum
P of the particle:
[8][9]

where ∧ denotes the
exterior product.
This tensor is additive: the total angular momentum of a system is the
sum of the angular momentum tensors for each constituent of the system.
So, for an assembly of discrete particles one sums the angular momentum
tensors over the particles, or integrates the density of angular
momentum over the extent of a continuous mass distribution.
Each of the six components forms a conserved quantity when aggregated
with the corresponding components for other objects and fields.
Force
In special relativity,
Newton's second law does not hold in the form
F =
ma, but it does if it is expressed as

where
p = γ(
v)
m0v is the momentum as defined above and
m0 is the
invariant mass. Thus, the force is given by

Consequently, in some old texts, γ(
v)
3m0 is referred to as the
longitudinal mass, and γ(
v)
m0 is referred to as the
transverse mass, which is numerically the same as the
relativistic mass. See
mass in special relativity.
If one inverts this to calculate acceleration from force, one gets

The force described in this section is the classical 3-D force which is not a
four-vector. This 3-D force is the appropriate concept of force since it is the force which obeys
Newton's third law of motion. It should not be confused with the so-called
four-force
which is merely the 3-D force in the comoving frame of the object
transformed as if it were a four-vector. However, the density of 3-D
force (linear momentum transferred per unit
four-volume)
is a four-vector (
density of weight +1) when combined with the negative of the density of power transferred.
Torque
The
torque acting on a point-like particle is defined as the derivative of
the angular momentum tensor given above with respect to proper time:
[10][11]

or in tensor components:

where
F is the 4d force acting on the particle at the event
X. As with angular momentum, torque is additive, so for an extended object one sums or integrates over the distribution of mass.
Kinetic energy
The
work-energy theorem says
[12] the change in
kinetic energy is equal to the work done on the body. In special relativity:
![{\begin{aligned}\Delta K=W=[\gamma _{1}-\gamma _{0}]m_{0}c^{2}.\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc89ae0cb8f161d560e2900fbe6968467fc8742a)
If in the initial state the body was at rest, so
v0 = 0 and γ
0(
v0) = 1, and in the final state it has speed
v1 =
v, setting γ
1(
v1) = γ(
v), the kinetic energy is then;
![K=[\gamma (v)-1]m_{0}c^{2}\,,](https://wikimedia.org/api/rest_v1/media/math/render/svg/e46c795b5262cc66c64992a6ccdaf1f71cdbe677)
a result that can be directly obtained by subtracting the rest energy
m0c2 from the total relativistic energy γ(
v)
m0c2.
Newtonian limit
The Lorentz factor γ(
v) can be expanded into a
Taylor series or
binomial series for (
v/
c)
2 < 1, obtaining:

and consequently


For velocities much smaller than that of light, one can neglect the terms with
c2 and higher in the denominator. These formulas then reduce to the standard definitions of Newtonian
kinetic energy and momentum. This is as it should be, for special relativity must agree with Newtonian mechanics at low velocities.
 (ordinate) is equal to
(ordinate) is equal to  but as
but as  the
the  goes to infinity.
goes to infinity. (ordinate) is equal to
(ordinate) is equal to  but as
but as  the
the  goes to infinity.
goes to infinity. are the electron rest mass, velocity of the electron, and speed of light
respectively. The figure at the right illustrates the relativistic
effects on the mass of an electron as a function of its velocity.
are the electron rest mass, velocity of the electron, and speed of light
respectively. The figure at the right illustrates the relativistic
effects on the mass of an electron as a function of its velocity. ) which is given by
) which is given by is the reduced Planck's constant and α is the fine-structure constant (a relativistic correction for the Bohr model).
is the reduced Planck's constant and α is the fine-structure constant (a relativistic correction for the Bohr model). is the principal quantum number and Z is an integer for the atomic number. From quantum mechanics the angular momentum is given as
is the principal quantum number and Z is an integer for the atomic number. From quantum mechanics the angular momentum is given as  . Substituting into the equation above and solving for
. Substituting into the equation above and solving for  gives
gives and a high value of
and a high value of  that
that  .
This fits with intuition: electrons with lower principal quantum
numbers will have a higher probability density of being nearer to the
nucleus. A nucleus with a large charge will cause an electron to have a
high velocity. A higher electron velocity means an increased electron
relativistic mass, as a result the electrons will be near the nucleus
more of the time and thereby contract the radius for small principal
quantum numbers.[10]
.
This fits with intuition: electrons with lower principal quantum
numbers will have a higher probability density of being nearer to the
nucleus. A nucleus with a large charge will cause an electron to have a
high velocity. A higher electron velocity means an increased electron
relativistic mass, as a result the electrons will be near the nucleus
more of the time and thereby contract the radius for small principal
quantum numbers.[10]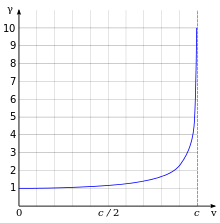






































![{\begin{aligned}\Delta K=W=[\gamma _{1}-\gamma _{0}]m_{0}c^{2}.\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc89ae0cb8f161d560e2900fbe6968467fc8742a)
![K=[\gamma (v)-1]m_{0}c^{2}\,,](https://wikimedia.org/api/rest_v1/media/math/render/svg/e46c795b5262cc66c64992a6ccdaf1f71cdbe677)



