Chemical equilibrium

From Wikipedia, the free encyclopedia

In a chemical reaction, chemical equilibrium is the state in which both reactants and products are present in concentrations which have no further tendency to change with time.^[1] Usually, this state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but equal. Thus, there are no net changes in the concentrations of the reactant(s) and product(s). Such a state is known as dynamic equilibrium.^[2][3]

Historical introduction

Burette, a common laboratory apparatus for carrying out titration, an important experimental technique in equilibrium and analytical chemistry.

The concept of chemical equilibrium was developed after Berthollet (1803) found that some chemical reactions are reversible. For any reaction mixture to exist at equilibrium, the rates of the forward and backward (reverse) reactions are equal. In the following chemical equation with arrows pointing both ways to indicate equilibrium, A and B are reactant chemical species, S and T are product species, and α, β, σ, and τ are the stoichiometric coefficients of the respective reactants and products:

α A + β B ⇌ σ S + τ T

The equilibrium concentration position of a reaction is said to lie "far to the right" if, at equilibrium, nearly all the reactants are consumed. Conversely the equilibrium position is said to be "far to the left" if hardly any product is formed from the reactants.

Guldberg and Waage (1865), building on Berthollet’s ideas, proposed the law of mass action:

${\displaystyle {\mbox{forward reaction rate}}=k_{+}\mathrm {A} ^{\alpha }\mathrm {B} ^{\beta }\,\!}$

${\displaystyle {\mbox{backward reaction rate}}=k_{-}\mathrm {S} ^{\sigma }\mathrm {T} ^{\tau }\,\!}$

where A, B, S and T are active masses and k₊ and k₋ are rate constants. Since at equilibrium forward and backward rates are equal:

${\displaystyle k_{+}\left\{\mathrm {A} \right\}^{\alpha }\left\{\mathrm {B} \right\}^{\beta }=k_{-}\left\{\mathrm {S} \right\}^{\sigma }\left\{\mathrm {T} \right\}^{\tau }\,}$

and the ratio of the rate constants is also a constant, now known as an equilibrium constant.

${\displaystyle K_{c}={\frac {k_{+}}{k_{-}}}={\frac {\{\mathrm {S} \}^{\sigma }\{\mathrm {T} \}^{\tau }}{\{\mathrm {A} \}^{\alpha }\{\mathrm {B} \}^{\beta }}}}$

By convention the products form the numerator. However, the law of mass action is valid only for concerted one-step reactions that proceed through a single transition state and is not valid in general because rate equations do not, in general, follow the stoichiometry of the reaction as Guldberg and Waage had proposed (see, for example, nucleophilic aliphatic substitution by S_N1 or reaction of hydrogen and bromine to form hydrogen bromide). Equality of forward and backward reaction rates, however, is a necessary condition for chemical equilibrium, though it is not sufficient to explain why equilibrium occurs.

Despite the failure of this derivation, the equilibrium constant for a reaction is indeed a constant, independent of the activities of the various species involved, though it does depend on temperature as observed by the van 't Hoff equation. Adding a catalyst will affect both the forward reaction and the reverse reaction in the same way and will not have an effect on the equilibrium constant. The catalyst will speed up both reactions thereby increasing the speed at which equilibrium is reached.^[2][4]

Although the macroscopic equilibrium concentrations are constant in time, reactions do occur at the molecular level. For example, in the case of acetic acid dissolved in water and forming acetate and hydronium ions,

CH₃CO₂H + H₂O ⇌ CH
3CO−
2 + H₃O⁺

a proton may hop from one molecule of acetic acid on to a water molecule and then on to an acetate anion to form another molecule of acetic acid and leaving the number of acetic acid molecules unchanged. This is an example of dynamic equilibrium. Equilibria, like the rest of thermodynamics, are statistical phenomena, averages of microscopic behavior.

Le Châtelier's principle (1884) gives an idea of the behavior of an equilibrium system when changes to its reaction conditions occur. If a dynamic equilibrium is disturbed by changing the conditions, the position of equilibrium moves to partially reverse the change. For example, adding more S from the outside will cause an excess of products, and the system will try to counteract this by increasing the reverse reaction and pushing the equilibrium point backward (though the equilibrium constant will stay the same).

If mineral acid is added to the acetic acid mixture, increasing the concentration of hydronium ion, the amount of dissociation must decrease as the reaction is driven to the left in accordance with this principle. This can also be deduced from the equilibrium constant expression for the reaction:

${\displaystyle K={\frac {\ce {\{CH3CO2^{-}\}\{H3O+\}}}{\ce {\{CH3CO2H\}}}}}$

If {H₃O⁺} increases {CH₃CO₂H} must increase and CH
3CO−
2 must decrease. The H₂O is left out, as it is the solvent and its concentration remains high and nearly constant.

A quantitative version is given by the reaction quotient.

J. W. Gibbs suggested in 1873 that equilibrium is attained when the Gibbs free energy of the system is at its minimum value (assuming the reaction is carried out at constant temperature and pressure). What this means is that the derivative of the Gibbs energy with respect to reaction coordinate (a measure of the extent of reaction that has occurred, ranging from zero for all reactants to a maximum for all products) vanishes, signalling a stationary point. This derivative is called the reaction Gibbs energy (or energy change) and corresponds to the difference between the chemical potentials of reactants and products at the composition of the reaction mixture.^[1] This criterion is both necessary and sufficient. If a mixture is not at equilibrium, the liberation of the excess Gibbs energy (or Helmholtz energy at constant volume reactions) is the "driving force" for the composition of the mixture to change until equilibrium is reached. The equilibrium constant can be related to the standard Gibbs free energy change for the reaction by the equation

${\displaystyle \Delta _{r}G^{\ominus }=-RT\ln K_{\mathrm {eq} }}$

where R is the universal gas constant and T the temperature.

When the reactants are dissolved in a medium of high ionic strength the quotient of activity coefficients may be taken to be constant. In that case the concentration quotient, K_c,

${\displaystyle K_{\mathrm {c} }={\frac {[\mathrm {S} ]^{\sigma }[\mathrm {T} ]^{\tau }}{[\mathrm {A} ]^{\alpha }[\mathrm {B} ]^{\beta }}}}$

where [A] is the concentration of A, etc., is independent of the analytical concentration of the reactants. For this reason, equilibrium constants for solutions are usually determined in media of high ionic strength. K_c varies with ionic strength, temperature and pressure (or volume). Likewise K_p for gases depends on partial pressure. These constants are easier to measure and encountered in high-school chemistry courses.

Thermodynamics

At constant temperature and pressure, one must consider the Gibbs free energy, G, while at constant temperature and volume, one must consider the Helmholtz free energy: A, for the reaction; and at constant internal energy and volume, one must consider the entropy for the reaction: S.

The constant volume case is important in geochemistry and atmospheric chemistry where pressure variations are significant. Note that, if reactants and products were in standard state (completely pure), then there would be no reversibility and no equilibrium. Indeed, they would necessarily occupy disjoint volumes of space. The mixing of the products and reactants contributes a large entropy (known as entropy of mixing) to states containing equal mixture of products and reactants. The standard Gibbs energy change, together with the Gibbs energy of mixing, determine the equilibrium state.^[5][6]

In this article only the constant pressure case is considered. The relation between the Gibbs free energy and the equilibrium constant can be found by considering chemical potentials.^[1]

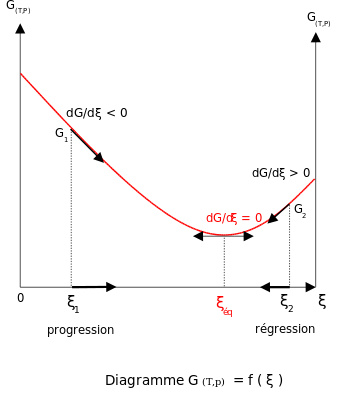
At constant temperature and pressure, the Gibbs free energy, G, for the reaction depends only on the extent of reaction: ξ (Greek letter xi), and can only decrease according to the second law of thermodynamics. It means that the derivative of G with ξ must be negative if the reaction happens; at the equilibrium the derivative being equal to zero.

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=0~}$:     equilibrium

In order to meet the thermodynamic condition for equilibrium, the Gibbs energy must be stationary, meaning that the derivative of G with respect to the extent of reaction: ξ, must be zero. It can be shown that in this case, the sum of chemical potentials of the products is equal to the sum of those corresponding to the reactants. Therefore, the sum of the Gibbs energies of the reactants must be the equal to the sum of the Gibbs energies of the products.

${\displaystyle \alpha \mu _{\mathrm {A} }+\beta \mu _{\mathrm {B} }=\sigma \mu _{\mathrm {S} }+\tau \mu _{\mathrm {T} }\,}$

where μ is in this case a partial molar Gibbs energy, a chemical potential. The chemical potential of a reagent A is a function of the activity, {A} of that reagent.

${\displaystyle \mu _{\mathrm {A} }=\mu _{A}^{\ominus }+RT\ln\{\mathrm {A} \}\,}$

(where μo
A is the standard chemical potential).

The definition of the Gibbs energy equation interacts with the fundamental thermodynamic relation to produce

${\displaystyle dG=Vdp-SdT+\sum _{i=1}^{k}\mu _{i}dN_{i}}$.

Inserting dN_i = ν_i dξ into the above equation gives a Stoichiometric coefficient (${\displaystyle \nu _{i}~}$) and a differential that denotes the reaction occurring once (dξ). At constant pressure and temperature the above equations can be written as

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\sum _{i=1}^{k}\mu _{i}\nu _{i}=\Delta _{\mathrm {r} }G_{T,p}}$ which is the "Gibbs free energy change for the reaction .

This results in:

${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=\sigma \mu _{\mathrm {S} }+\tau \mu _{\mathrm {T} }-\alpha \mu _{\mathrm {A} }-\beta \mu _{\mathrm {B} }\,}$.

By substituting the chemical potentials:

${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=(\sigma \mu _{\mathrm {S} }^{\ominus }+\tau \mu _{\mathrm {T} }^{\ominus })-(\alpha \mu _{\mathrm {A} }^{\ominus }+\beta \mu _{\mathrm {B} }^{\ominus })+(\sigma RT\ln\{\mathrm {S} \}+\tau RT\ln\{\mathrm {T} \})-(\alpha RT\ln\{\mathrm {A} \}+\beta RT\ln\{\mathrm {B} \})}$,

the relationship becomes:

${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=\sum _{i=1}^{k}\mu _{i}^{\ominus }\nu _{i}+RT\ln {\frac {\{\mathrm {S} \}^{\sigma }\{\mathrm {T} \}^{\tau }}{\{\mathrm {A} \}^{\alpha }\{\mathrm {B} \}^{\beta }}}}$

${\displaystyle \sum _{i=1}^{k}\mu _{i}^{\ominus }\nu _{i}=\Delta _{\mathrm {r} }G^{\ominus }}$:

which is the standard Gibbs energy change for the reaction that can be calculated using thermodynamical tables. The reaction quotient is defined as:

${\displaystyle Q_{\mathrm {r} }={\frac {\{\mathrm {S} \}^{\sigma }\{\mathrm {T} \}^{\tau }}{\{\mathrm {A} \}^{\alpha }\{\mathrm {B} \}^{\beta }}}}$

Therefore,

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G_{T,p}=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln Q_{\mathrm {r} }}$

At equilibrium:

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G_{T,p}=0}$

leading to:

${\displaystyle 0=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln K_{\mathrm {eq} }}$

and

${\displaystyle \Delta _{\mathrm {r} }G^{\ominus }=-RT\ln K_{\mathrm {eq} }}$

Obtaining the value of the standard Gibbs energy change, allows the calculation of the equilibrium constant.

Addition of reactants or products

For a reactional system at equilibrium: Q_r = K_eq; ξ = ξ_eq.

• If are modified activities of constituents, the value of the reaction quotient changes and becomes different from the equilibrium constant: Q_r ≠ K_eq

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln Q_{\mathrm {r} }~}$

and

${\displaystyle \Delta _{\mathrm {r} }G^{\ominus }=-RT\ln K_{eq}~}$

then

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=RT\ln \left({\frac {Q_{\mathrm {r} }}{K_{\mathrm {eq} }}}\right)~}$

• If activity of a reagent i increases

${\displaystyle Q_{\mathrm {r} }={\frac {\prod (a_{j})^{\nu _{j}}}{\prod (a_{i})^{\nu _{i}}}}~}$, the reaction quotient decreases.

then

${\displaystyle Q_{\mathrm {r} }$     and     ${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}<0 annotation="">$

The reaction will shift to the right (i.e. in the forward direction, and thus more products will form).

• If activity of a product j increases

then

${\displaystyle Q_{\mathrm {r} }>K_{\mathrm {eq} }~}$     and     ${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}>0~}$

The reaction will shift to the left (i.e. in the reverse direction, and thus less products will form).

Note that activities and equilibrium constants are dimensionless numbers.

Treatment of activity

The expression for the equilibrium constant can be rewritten as the product of a concentration quotient, K_c and an activity coefficient quotient, Γ.

${\displaystyle K={\frac {[\mathrm {S} ]^{\sigma }[\mathrm {T} ]^{\tau }...}{[\mathrm {A} ]^{\alpha }[\mathrm {B} ]^{\beta }...}}\times {\frac {{\gamma _{\mathrm {S} }}^{\sigma }{\gamma _{\mathrm {T} }}^{\tau }...}{{\gamma _{\mathrm {A} }}^{\alpha }{\gamma _{\mathrm {B} }}^{\beta }...}}=K_{\mathrm {c} }\Gamma }$

[A] is the concentration of reagent A, etc. It is possible in principle to obtain values of the activity coefficients, γ. For solutions, equations such as the Debye–Hückel equation or extensions such as Davies equation^[7] Specific ion interaction theory or Pitzer equations^[8] may be used.^{Software (below)}. However this is not always possible. It is common practice to assume that Γ is a constant, and to use the concentration quotient in place of the thermodynamic equilibrium constant. It is also general practice to use the term equilibrium constant instead of the more accurate concentration quotient. This practice will be followed here.

For reactions in the gas phase partial pressure is used in place of concentration and fugacity coefficient in place of activity coefficient. In the real world, for example, when making ammonia in industry, fugacity coefficients must be taken into account. Fugacity, f, is the product of partial pressure and fugacity coefficient. The chemical potential of a species in the gas phase is given by

${\displaystyle \mu =\mu ^{\ominus }+RT\ln \left({\frac {f}{\mathrm {bar} }}\right)=\mu ^{\ominus }+RT\ln \left({\frac {p}{\mathrm {bar} }}\right)+RT\ln \gamma }$

so the general expression defining an equilibrium constant is valid for both solution and gas phases.

Concentration quotients

In aqueous solution, equilibrium constants are usually determined in the presence of an "inert" electrolyte such as sodium nitrate NaNO₃ or potassium perchlorate KClO₄. The ionic strength of a solution is given by

${\displaystyle I={\frac {1}{2}}\sum _{i=1}^{N}c_{i}z_{i}^{2}}$

where c_i and z_i stand for the concentration and ionic charge of ion type i, and the sum is taken over all the N types of charged species in solution. When the concentration of dissolved salt is much higher than the analytical concentrations of the reagents, the ions originating from the dissolved salt determine the ionic strength, and the ionic strength is effectively constant. Since activity coefficients depend on ionic strength the activity coefficients of the species are effectively independent of concentration. Thus, the assumption that Γ is constant is justified. The concentration quotient is a simple multiple of the equilibrium constant.^[9]

${\displaystyle K_{\mathrm {c} }={\frac {K}{\Gamma }}}$

However, K_c will vary with ionic strength. If it is measured at a series of different ionic strengths the value can be extrapolated to zero ionic strength.^[8] The concentration quotient obtained in this manner is known, paradoxically, as a thermodynamic equilibrium constant.

To use a published value of an equilibrium constant in conditions of ionic strength different from the conditions used in its determination, the value should be adjusted^{Software (below)}.

Metastable mixtures

A mixture may appear to have no tendency to change, though it is not at equilibrium. For example, a mixture of SO₂ and O₂ is metastable as there is a kinetic barrier to formation of the product, SO₃.

2 SO₂ + O₂ ⇌ 2 SO₃

The barrier can be overcome when a catalyst is also present in the mixture as in the contact process, but the catalyst does not affect the equilibrium concentrations.

Likewise, the formation of bicarbonate from carbon dioxide and water is very slow under normal conditions

CO₂ + 2 H₂O ⇌ HCO−
3 + H₃O⁺

but almost instantaneous in the presence of the catalytic enzyme carbonic anhydrase.

Pure substances

When pure substances (liquids or solids) are involved in equilibria their activities do not appear in the equilibrium constant^[10] because their numerical values are considered one.

Applying the general formula for an equilibrium constant to the specific case of a dilute solution of acetic acid in water one obtains

CH₃CO₂H + H₂O ⇌ CH₃CO₂⁻ + H₃O⁺

${\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} }{\mathrm {[{CH_{3}CO_{2}H}][{H_{2}O}]} }}}$

For all but very concentrated solutions, the water can be considered a "pure" liquid, and therefore it has an activity of one. The equilibrium constant expression is therefore usually written as

${\displaystyle K={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} }{\mathrm {[{CH_{3}CO_{2}H}]} }}=K_{\mathrm {c} }}$.

A particular case is the self-ionization of water itself

2 H₂O ⇌ H₃O⁺ + OH⁻

Because water is the solvent, and has an activity of one, the self-ionization constant of water is defined as

${\displaystyle K_{\mathrm {w} }=\mathrm {[H^{+}][OH^{-}]} }$

It is perfectly legitimate to write [H⁺] for the hydronium ion concentration, since the state of solvation of the proton is constant (in dilute solutions) and so does not affect the equilibrium concentrations. K_w varies with variation in ionic strength and/or temperature.

The concentrations of H⁺ and OH⁻ are not independent quantities. Most commonly [OH⁻] is replaced by K_w[H⁺]⁻¹ in equilibrium constant expressions which would otherwise include hydroxide ion.

Solids also do not appear in the equilibrium constant expression, if they are considered to be pure and thus their activities taken to be one. An example is the Boudouard reaction:^[10]

2 CO ⇌ CO₂ + C

for which the equation (without solid carbon) is written as:

${\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[CO_{2}]} }{\mathrm {[CO]^{2}} }}}$

Multiple equilibria

Consider the case of a dibasic acid H₂A. When dissolved in water, the mixture will contain H₂A, HA⁻ and A²⁻. This equilibrium can be split into two steps in each of which one proton is liberated.

${\displaystyle {\begin{array}{rl}{\ce {H2A<=>{HA^{-}}+{H+}}}:&K_{1}={\frac {\ce {[HA-][H+]}}{\ce {[H2A]}}}\\{\ce {HA-<=>{A^{2-}}+{H+}}}:&K_{2}={\frac {\ce {[A^{2-}][H+]}}{\ce {[HA-]}}}\end{array}}}$

K₁ and K₂ are examples of stepwise equilibrium constants. The overall equilibrium constant, β_D, is product of the stepwise constants.

${\displaystyle {\ce {{H2A}<=>{A^{2-}}+{2H+}}}}$:     ${\displaystyle \beta _{\ce {D}}={\frac {\ce {[A^{2-}][H^{+}]^{2}}}{\ce {[H_{2}A]}}}=K_{1}K_{2}}$

Note that these constants are dissociation constants because the products on the right hand side of the equilibrium expression are dissociation products. In many systems, it is preferable to use association constants.

${\displaystyle {\begin{array}{ll}{\ce {{A^{2-}}+{H+}<=>HA-}}:&\beta _{1}={\frac {\ce {[HA^{-}]}}{\ce {[A^{2-}][H+]}}}\\{\ce {{A^{2-}}+{2H+}<=>H2A}}:&\beta _{2}={\frac {\ce {[H2A]}}{\ce {[A^{2-}][H+]^{2}}}}\end{array}}}$

β₁ and β₂ are examples of association constants. Clearly β₁ = 1/K₂ and β₂ = 1/β_D; log β₁ = pK₂ and log β₂ = pK₂ + pK₁^[11] For multiple equilibrium systems, also see: theory of Response reactions.

Effect of temperature

The effect of changing temperature on an equilibrium constant is given by the van 't Hoff equation

${\displaystyle {\frac {d\ln K}{dT}}={\frac {\Delta H_{\mathrm {m} }^{\ominus }}{RT^{2}}}}$

Thus, for exothermic reactions (ΔH is negative), K decreases with an increase in temperature, but, for endothermic reactions, (ΔH is positive) K increases with an increase temperature. An alternative formulation is

${\displaystyle {\frac {d\ln K}{d(T^{-1})}}=-{\frac {\Delta H_{\mathrm {m} }^{\ominus }}{R}}}$

At first sight this appears to offer a means of obtaining the standard molar enthalpy of the reaction by studying the variation of K with temperature. In practice, however, the method is unreliable because error propagation almost always gives very large errors on the values calculated in this way.

Effect of electric and magnetic fields

The effect of electric field on equilibrium has been studied by Manfred Eigen^{[citation needed]} among others.

Types of equilibrium

Haber–Bosch process

1. N₂ (g) ⇌ N₂ (adsorbed)
2. N₂ (adsorbed) ⇌ 2 N (adsorbed)
3. H₂ (g) ⇌ H₂ (adsorbed)
4. H₂ (adsorbed) ⇌ 2 H (adsorbed)
5. N (adsorbed) + 3 H(adsorbed) ⇌ NH₃ (adsorbed)
6. NH₃ (adsorbed) ⇌ NH₃ (g)

• In the gas phase: rocket engines^[12]
• The industrial synthesis such as ammonia in the Haber–Bosch process (depicted right) takes place through a succession of equilibrium steps including adsorption processes
• Atmospheric chemistry
• Seawater and other natural waters: chemical oceanography
• Distribution between two phases
  • log D distribution coefficient: important for pharmaceuticals where lipophilicity is a significant property of a drug
  • Liquid–liquid extraction, Ion exchange, Chromatography
  • Solubility product
  • Uptake and release of oxygen by haemoglobin in blood
• Acid–base equilibria: acid dissociation constant, hydrolysis, buffer solutions, indicators, acid–base homeostasis
• Metal–ligand complexation: sequestering agents, chelation therapy, MRI contrast reagents, Schlenk equilibrium
• Adduct formation: host–guest chemistry, supramolecular chemistry, molecular recognition, dinitrogen tetroxide
• In certain oscillating reactions, the approach to equilibrium is not asymptotically but in the form of a damped oscillation .^[10]
• The related Nernst equation in electrochemistry gives the difference in electrode potential as a function of redox concentrations.
• When molecules on each side of the equilibrium are able to further react irreversibly in secondary reactions, the final product ratio is determined according to the Curtin–Hammett principle.

In these applications, terms such as stability constant, formation constant, binding constant, affinity constant, association/dissociation constant are used. In biochemistry, it is common to give units for binding constants, which serve to define the concentration units used when the constant’s value was determined.

Composition of a mixture

When the only equilibrium is that of the formation of a 1:1 adduct as the composition of a mixture, there are any number of ways that the composition of a mixture can be calculated. For example, see ICE table for a traditional method of calculating the pH of a solution of a weak acid.

There are three approaches to the general calculation of the composition of a mixture at equilibrium.

1. The most basic approach is to manipulate the various equilibrium constants until the desired concentrations are expressed in terms of measured equilibrium constants (equivalent to measuring chemical potentials) and initial conditions.
2. Minimize the Gibbs energy of the system.^[13][14]
3. Satisfy the equation of mass balance. The equations of mass balance are simply statements that demonstrate that the total concentration of each reactant must be constant by the law of conservation of mass.

Mass-balance equations

In general, the calculations are rather complicated or complex. For instance, in the case of a dibasic acid, H₂A dissolved in water the two reactants can be specified as the conjugate base, A²⁻, and the proton, H⁺. The following equations of mass-balance could apply equally well to a base such as 1,2-diaminoethane, in which case the base itself is designated as the reactant A:

${\displaystyle T_{\mathrm {A} }=\mathrm {[A]+[HA]+[H_{2}A]} \,}$

${\displaystyle T_{\mathrm {H} }=\mathrm {[H]+[HA]+2[H_{2}A]-[OH]} \,}$

With T_A the total concentration of species A. Note that it is customary to omit the ionic charges when writing and using these equations.

When the equilibrium constants are known and the total concentrations are specified there are two equations in two unknown "free concentrations" [A] and [H]. This follows from the fact that [HA] = β₁[A][H], [H₂A] = β₂[A][H]² and [OH] = K_w[H]⁻¹

${\displaystyle T_{\mathrm {A} }=\mathrm {[A]} +\beta _{1}\mathrm {[A][H]} +\beta _{2}\mathrm {[A][H]} ^{2}\,}$

${\displaystyle T_{\mathrm {H} }=\mathrm {[H]} +\beta _{1}\mathrm {[A][H]} +2\beta _{2}\mathrm {[A][H]} ^{2}-K_{w}[\mathrm {H} ]^{-1}\,}$

so the concentrations of the "complexes" are calculated from the free concentrations and the equilibrium constants. General expressions applicable to all systems with two reagents, A and B would be

${\displaystyle T_{\mathrm {A} }=[\mathrm {A} ]+\sum _{i}p_{i}\beta _{i}[\mathrm {A} ]^{p_{i}}[\mathrm {B} ]^{q_{i}}}$

${\displaystyle T_{\mathrm {B} }=[\mathrm {B} ]+\sum _{i}q_{i}\beta _{i}[\mathrm {A} ]^{p_{i}}[\mathrm {B} ]^{q_{i}}}$

It is easy to see how this can be extended to three or more reagents.

Polybasic acids

Species concentrations during hydrolysis of the aluminium.

The composition of solutions containing reactants A and H is easy to calculate as a function of p[H]. When [H] is known, the free concentration [A] is calculated from the mass-balance equation in A.

The diagram alongside, shows an example of the hydrolysis of the aluminium Lewis acid Al³⁺_(aq)^[15] shows the species concentrations for a 5 × 10⁻⁶ M solution of an aluminium salt as a function of pH. Each concentration is shown as a percentage of the total aluminium.

Solution and precipitation

The diagram above illustrates the point that a precipitate that is not one of the main species in the solution equilibrium may be formed. At pH just below 5.5 the main species present in a 5 μM solution of Al³⁺ are aluminium hydroxides Al(OH)²⁺, AlOH+
2 and Al
13(OH)7+
32, but on raising the pH Al(OH)₃ precipitates from the solution. This occurs because Al(OH)₃ has a very large lattice energy. As the pH rises more and more Al(OH)₃ comes out of solution. This is an example of Le Châtelier's principle in action: Increasing the concentration of the hydroxide ion causes more aluminium hydroxide to precipitate, which removes hydroxide from the solution. When the hydroxide concentration becomes sufficiently high the soluble aluminate, Al(OH)−
4, is formed.

Another common instance where precipitation occurs is when a metal cation interacts with an anionic ligand to form an electrically neutral complex. If the complex is hydrophobic, it will precipitate out of water. This occurs with the nickel ion Ni²⁺ and dimethylglyoxime, (dmgH₂): in this case the lattice energy of the solid is not particularly large, but it greatly exceeds the energy of solvation of the molecule Ni(dmgH)₂.

Minimization of Gibbs energy

At equilibrium, at a specified temperature and pressure, the Gibbs energy G is at a minimum:

${\displaystyle dG=\sum _{j=1}^{m}\mu _{j}\,dN_{j}=0}$

For a closed system, no particles may enter or leave, although they may combine in various ways. The total number of atoms of each element will remain constant. This means that the minimization above must be subjected to the constraints:

${\displaystyle \sum _{j=1}^{m}a_{ij}N_{j}=b_{i}^{0}}$

where a_ij is the number of atoms of element i in molecule j and b0
i is the total number of atoms of element i, which is a constant, since the system is closed. If there are a total of k types of atoms in the system, then there will be k such equations. If ions are involved, an additional row is added to the a_ij matrix specifying the respective charge on each molecule which will sum to zero.

This is a standard problem in optimisation, known as constrained minimisation. The most common method of solving it is using the method of Lagrange multipliers, also known as undetermined multipliers (though other methods may be used).

Define:

${\displaystyle {\mathcal {G}}=G+\sum _{i=1}^{k}\lambda _{i}\left(\sum _{j=1}^{m}a_{ij}N_{j}-b_{i}^{0}\right)=0}$

where the λ_i are the Lagrange multipliers, one for each element. This allows each of the N_j and λ_j to be treated independently, and it can be shown using the tools of multivariate calculus that the equilibrium condition is given by

${\displaystyle 0={\frac {\partial {\mathcal {G}}}{\partial N_{j}}}=\mu _{j}+\sum _{i=1}^{k}\lambda _{i}a_{ij}}$

${\displaystyle 0={\frac {\partial {\mathcal {G}}}{\partial \lambda _{i}}}=\sum _{j=1}^{m}a_{ij}N_{j}-b_{i}^{0}}$

(For proof see Lagrange multipliers.) This is a set of (m + k) equations in (m + k) unknowns (the N_j and the λ_i) and may, therefore, be solved for the equilibrium concentrations N_j as long as the chemical potentials are known as functions of the concentrations at the given temperature and pressure. (See Thermodynamic databases for pure substances.) Note that the second equation is just the initial constraints for minimization.

This method of calculating equilibrium chemical concentrations is useful for systems with a large number of different molecules. The use of k atomic element conservation equations for the mass constraint is straightforward, and replaces the use of the stoichiometric coefficient equations.^[12]. The results are consistent with those specified by chemical equations. For example, if equilibrium is specified by a single chemical equation: ^[16],

${\displaystyle \sum _{j=0}^{m}\nu _{j}R_{j}=0}$

where ν_j is the stochiometric coefficient for the j th molecule (negative for reactants, positive for products) and R_j is the symbol for the j th molecule, a properly balanced equation will obey:

${\displaystyle \sum _{j=1}^{m}a_{ij}\nu _{j}=0}$

Multiplying the first equilibrium condition by ν_j yields

${\displaystyle 0=\sum _{j=1}^{m}\nu _{j}\mu _{j}+\sum _{j=1}^{m}\sum _{i=1}^{k}\nu _{j}\lambda _{i}a_{ij}=\sum _{j=1}^{m}\nu _{j}\mu _{j}}$

As above, defining ΔG

${\displaystyle \Delta G=\sum _{j=1}^{m}\nu _{j}\mu _{j}=\sum _{j=1}^{m}\nu _{j}(\mu _{j}^{\ominus }+RT\ln(\{R_{j}\}))=\Delta G^{\ominus }+RT\ln \left(\prod _{j=1}^{m}\{R_{j}\}^{\nu _{j}}\right)=\Delta G^{\ominus }+RT\ln(K_{eq})}$

which will be zero at equilibrium.

Electromagnetic absorption by water

From Wikipedia, the free encyclopedia

 

Absorption spectrum (attenuation coefficient vs. wavelength) of liquid water (red),^[1][2][3] atmospheric water vapor (green)^{[4][5][6][4][7]} and ice (blue line)^[8][9][10] between 667 nm and 200 μm.^[11] The plot for vapor is a transformation of data Synthetic spectrum for gas mixture 'Pure H₂O' (296K, 1 atm) retrieved from Hitran on the Web Information System.^[6]

Liquid water absorption spectrum across a wide wavelength range.

The absorption of electromagnetic radiation by water depends on the state of the water.

The absorption in the gas phase occurs in three regions of the spectrum. Rotational transitions are responsible for absorption in the microwave and far-infrared, vibrational transitions in the mid-infrared and near-infrared. Vibrational bands have rotational fine structure. Electronic transitions occur in the vacuum ultraviolet regions.

Liquid water has no rotational spectrum but does absorb in the microwave region.

Overview

The water molecule, in the gaseous state, has three types of transition that can give rise to absorption of electromagnetic radiation

• Rotational transitions, in which the molecule gains a quantum of rotational energy. Atmospheric water vapour at ambient temperature and pressure gives rise to absorption in the far-infrared region of the spectrum, from about 200 cm⁻¹ (50 μm) to longer wavelengths towards the microwave region.
• Vibrational transitions in which a molecule gains a quantum of vibrational energy. The fundamental transitions give rise to absorption in the mid-infrared in the regions around 1650 cm⁻¹ (μ band, 6 μm) and 3500 cm⁻¹ (so-called X band, 2.9 μm)
• Electronic transitions in which a molecule is promoted to an excited electronic state. The lowest energy transition of this type is in the vacuum ultraviolet region.

In reality, vibrations of molecules in the gaseous state are accompanied by rotational transitions, giving rise to a vibration-rotation spectrum. Furthermore, vibrational overtones and combination bands occur in the near-infrared region. The HITRAN spectroscopy database lists more than 37,000 spectral lines for gaseous H₂¹⁶O, ranging from the microwave region to the visible spectrum.^[5][12]

In liquid water the rotational transitions are effectively quenched, but absorption bands are affected by hydrogen bonding. In crystalline ice the vibrational spectrum is also affected by hydrogen bonding and there are lattice vibrations causing absorption in the far-infrared. Electronic transitions of gaseous molecules will show both vibrational and rotational fine structure.

Units

Infrared absorption band positions may be given either in wavelength (usually in micrometers, μm) or wavenumber (usually in reciprocal centimeters, cm⁻¹) scale.

Rotational spectrum

Rotating water molecule

The water molecule is an asymmetric top, that is, it has three independent moments of inertia. Consequently, the rotational spectrum has no obvious structure. A large number of transitions can be observed; lines due to atmospheric water vapor can easily be observed from about 50 μm (200 cm⁻¹) to longer wavelengths. Measurements of microwave spectra have provided a very precise value for the O−H bond length, 95.84 ± 0.05 pm and H−O−H bond angle, 104.5 ± 0.3°.^[13]

Part of the pure rotation (microwave) spectrum of water vapour between 1000 GHz (33 cm⁻¹, 300 μm) and 3000 GHz (100 cm⁻¹, 100 μm)

Vibrational spectrum

The three fundamental vibrations of the water molecule

ν₁,O-H symmetric stretching
3657 cm⁻¹ (2.734 μm)

ν₂, H-O-H bending
1595 cm⁻¹ (6.269 μm)

ν₃, O-H asymmetric stretching
3756 cm⁻¹ (2.662 μm)

The water molecule has three fundamental molecular vibrations. The O-H stretching vibrations give rise to absorption bands with band origins at 3657 cm⁻¹ (ν₁, 2.734 μm) and 3756 cm⁻¹ (ν₃, 2.662 μm) in the gas phase. The asymmetric stretching vibration, of B₂ symmetry in the point group C_2v is a normal vibration. The H-O-H bending mode origin is at 1595 cm⁻¹ (ν₂, 6.269 μm). Both symmetric stretching and bending vibrations have A₁ symmetry, but the frequency difference between them is so large that mixing is effectively zero. In the gas phase all three bands show extensive rotational fine structure.^[14] ν₃ has a series of overtones at wavenumbers somewhat less than n ν₃, n=2,3,4,5... Combination bands, such as ν₂ + ν₃ are also easily observed in the near infrared region.^[15][16] The presence of water vapor in the atmosphere is important for atmospheric chemistry especially as the infrared and near infrared spectra are easy to observe. Standard (atmospheric optical) codes are assigned to absorption bands as follows. 0.718 μm (visible): α, 0.810 μm: μ, 0.935 μm: ρστ, 1.13 μm: φ, 1.38 μm: ψ, 1.88 μm: Ω, 2.68 μm: X. The gaps between the bands define the infrared window in the Earth's atmosphere.^[17]

The infrared spectrum of liquid water is dominated by the intense absorption due to the fundamental O-H stretching vibrations. Because of the high intensity, very short path lengths, usually less than 50 μm, are needed to record the spectra of aqueous solutions. There is no rotational fine structure, but the absorption band are broader than might be expected, because of hydrogen bonding.^[18] Peak maxima for liquid water are observed at 3450 cm⁻¹ (2.898 μm), 3615 cm⁻¹ (2.766 μm) and 1640 cm ⁻¹ (6.097 μm).^[14] Direct measurement of the infrared spectra of aqueous solutions requires that the cuvette windows be made of substances such as calcium fluoride which are water-insoluble. This difficulty can be overcome by using an attenuated total reflectance (ATR) device.

In the near-infrared range liquid water has absorption bands around 1950 nm (5128 cm⁻¹), 1450 nm (6896 cm⁻¹), 1200 nm (8333 cm⁻¹) and 970 nm, (10300 cm⁻¹).^[19][20][15] The regions between these bands can be used in near-infrared spectroscopy to measure the spectra of aqueous solutions, with the advantage that glass is transparent in this region, so glass cuvettes can be used. The absorption intensity is weaker than for the fundamental vibrations, but this is not important as longer path-length cuvettes are used. The absorption band at 698 nm (14300 cm⁻¹) is a 3rd overtone (n=4). It tails off onto the visible region and is responsible for the intrinsic blue color of water. This can be observed with a standard UV/vis spectrophotometer, using a 10 cm path-length. The colour can be seen by eye by looking through a column of water about 10m in length; the water must be passed through an ultrafilter to eliminate color due to Rayleigh scattering which also can make water appear blue.^[16][21][22] In both liquid water and ice cluster vibrations occur, which involve the stretching (TS) or bending (TB) of intermolecular hydrogen bonds (O–H . . . O). Bands at wavelengths λ = 50-55 μm (44 μm in ice) have been attributed to TS, intermolecular stretch, and 200 μm (166 μm in ice), to TB, intermolecular bend^[11]

The spectrum of ice is similar to that of liquid water, with peak maxima at 3400 cm⁻¹ (2.941 μm), 3220 cm⁻¹ (3.105 μm) and 1620 cm⁻¹ (6.17 μm)^[14]

Visible region

Predicted wavelengths of overtones and combination bands of liquid water in the visible region^[16]

ν1, ν3	ν2	wavelength /nm
4	0	742
4	1	662
5	0	605
5	1	550
6	0	514
6	1	474
7	0	449
7	1	418
8	0	401
8	1	376

Absorption coefficients for 200 nm and 900 nm are almost equal at 6.9 m⁻¹ (attenuation length of 14.5 cm). Very weak light absorption, in the visible region, by liquid water has been measured using an integrating cavity absorption meter (ICAM).^[16] The absorption was attributed to a sequence of overtone and combination bands whose intensity decreases at each step, giving rise to an absolute minimum at 418 nm, at which wavelength the attenuation coefficient is about 0.0044 m⁻¹, which is an attenuation length of about 227 meters. These values correspond to pure absorption without scattering effects. The attenuation of, e.g., a laser beam would be slightly stronger.

Visible light absorption spectrum of pure water (absorption coefficient vs. wavelength).^[16][21][22]

Electronic spectrum

The electronic transitions of the water molecule lie in the vacuum ultraviolet region. For water vapor the bands have been assigned as follows.^[11]

• 65 nm band - many different electronic transitions, photo-ionization, photodissociation
• discrete features between 115 and 180 nm
  • set of narrow bands between 115 and 125 nm
    Rydberg series: 1b₁ (n₂) → many different Rydberg states and 3a₁ (n₁) → 3sa₁ Rydberg state
  • 128 nm band
    Rydberg series: 3a₁ (n₁) → 3sa₁ Rydberg state and 1b₁ (n₂) → 3sa₁ Rydberg state
  • 166.5 nm band
    1b₁ (n₂) → 4a₁ (σ₁*-like orbital)

At least some of these transitions result in photodissociation of water into H+OH. Among them the best known is that at 166.5 nm.

Microwaves and radio waves

Dielectric permittivity and dielectric loss of water between 0°C and 100°C, the arrows showing the effect of increasing temperature.^[23]

The pure rotation spectrum of water vapor extends into the microwave region.

Liquid water has a broad absorption spectrum in the microwave region, which has been explained in terms of changes in the hydrogen bond network giving rise to a broad, featureless, microwave spectrum.^[24] The absorption (equivalent to dielectric loss) is used in microwave ovens to heat food that contains water molecules. A frequency of 2.45 GHz, wavelength 122 mm, is commonly used.

Radiocommunication at GHz frequencies is very difficult in fresh waters and even more so in salt waters.^[11]

Atmospheric effects

Synthetic stick absorption spectrum of a simple gas mixture corresponding to the Earth's atmosphere composition based on HITRAN data^[5] created using Hitran on the Web system.^[6] Green color - water vapor, WN – wavenumber (caution: lower wavelengths on the right, higher on the left). Water vapor concentration for this gas mixture is 0.4%

Water vapor is a greenhouse gas in the Earth's atmosphere, responsible for 70% of the known absorption of incoming sunlight, particularly in the infrared region, and about 60% of the atmospheric absorption of thermal radiation by the Earth known as the greenhouse effect.^[25] It is also an important factor in multispectral imaging and hyperspectral imaging used in remote sensing^[12] because water vapor absorbs radiation differently in different spectral bands. Its effects are also an important consideration in infrared astronomy and radio astronomy in the microwave or millimeter wave bands. The South Pole Telescope was constructed in Antarctica in part because the elevation and low temperatures there mean there is very little water vapor in the atmosphere.^[26]

Similarly, carbon dioxide absorption bands occur around 1400, 1600 and 2000 nm,^[27] but its presence in the Earth's atmosphere accounts for just 26% of the greenhouse effect.^[25] Carbon dioxide gas absorbs energy in some small segments of the thermal infrared spectrum that water vapor misses. This extra absorption within the atmosphere causes the air to warm just a bit more and the warmer the atmosphere the greater its capacity to hold more water vapor. This extra water vapor absorption further enhances the Earth’s greenhouse effect.^[28]

In the atmospheric window between approximately 8000 and 14000 nm, in the far-infrared spectrum, carbon dioxide and water absorption is weak.^[29] This window allows most of the thermal radiation in this band to be radiated out to space directly from the Earth's surface. This band is also used for remote sensing of the Earth from space, for example with thermal Infrared imaging.

As well as absorbing radiation, water vapour occasionally emits radiation in all directions, according to the Black Body Emission curve for its current temperature overlaid on the water absorption spectrum. Much of this energy will be recaptured by other water molecules, but at higher altitudes, radiation sent towards space is less likely to be recaptured, as there is less water available to recapture radiation of water-specific absorbing wavelengths. By the top of the troposphere, about 12 km above sea level, most water vapor condenses to liquid water or ice as it releases its heat of vapourisation. Once changed state, liquid water and ice fall away to lower altitudes. This will be balanced by incoming water vapour rising via convection currents.

Liquid water and ice emit radiation at a higher rate than water vapour (see graph above). Water at the top of the troposphere, particularly in liquid and solid states, cools as it emits net photons to space. Neighboring gas molecules other than water (e.g. Nitrogen) are cooled by passing their heat kinetically to the water. This is why temperatures at the top of the troposphere (known as the tropopause) are about -50 degrees Celsius

Black body

From Wikipedia, the free encyclopedia

As the temperature of a black body decreases, its intensity also decreases and its peak moves to longer wavelengths. Shown for comparison is the classical Rayleigh–Jeans law and its ultraviolet catastrophe.

A black body is an idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. A white body is one with a "rough surface [that] reflects all incident rays completely and uniformly in all directions."^[1]

A black body in thermal equilibrium (that is, at a constant temperature) emits electromagnetic radiation called black-body radiation. The radiation is emitted according to Planck's law, meaning that it has a spectrum that is determined by the temperature alone (see figure at right), not by the body's shape or composition.

A black body in thermal equilibrium has two notable properties:^[2]

1. It is an ideal emitter: at every frequency, it emits as much energy as – or more energy than – any other body at the same temperature.
2. It is a diffuse emitter: the energy is radiated isotropically, independent of direction.

An approximate realization of a black surface is a hole in the wall of a large enclosure. Any light entering the hole is reflected indefinitely or absorbed inside and is unlikely to re-emerge, making the hole a nearly perfect absorber. The radiation confined in such an enclosure may or may not be in thermal equilibrium, depending upon the nature of the walls and the other contents of the enclosure.^[3][4]

Real materials emit energy at a fraction—called the emissivity—of black-body energy levels. By definition, a black body in thermal equilibrium has an emissivity of ε = 1.0. A source with lower emissivity independent of frequency often is referred to as a gray body.^[5][6] Construction of black bodies with emissivity as close to one as possible remains a topic of current interest.^[7]

In astronomy, the radiation from stars and planets is sometimes characterized in terms of an effective temperature, the temperature of a black body that would emit the same total flux of electromagnetic energy.

Definition

The idea of a black body originally was introduced by Gustav Kirchhoff in 1860 as follows:

...the supposition that bodies can be imagined which, for infinitely small thicknesses, completely absorb all incident rays, and neither reflect nor transmit any. I shall call such bodies perfectly black, or, more briefly, black bodies.^[8]

A more modern definition drops the reference to "infinitely small thicknesses":^[9]

An ideal body is now defined, called a blackbody. A blackbody allows all incident radiation to pass into it (no reflected energy) and internally absorbs all the incident radiation (no energy transmitted through the body). This is true for radiation of all wavelengths and for all angles of incidence. Hence the blackbody is a perfect absorber for all incident radiation.^[10]

Idealizations

This section describes some concepts developed in connection with black bodies.

An approximate realization of a black body as a tiny hole in an insulated enclosure

Cavity with a hole

A widely used model of a black surface is a small hole in a cavity with walls that are opaque to radiation.^[10] Radiation incident on the hole will pass into the cavity, and is very unlikely to be re-emitted if the cavity is large. The hole is not quite a perfect black surface — in particular, if the wavelength of the incident radiation is longer than the diameter of the hole, part will be reflected. Similarly, even in perfect thermal equilibrium, the radiation inside a finite-sized cavity will not have an ideal Planck spectrum for wavelengths comparable to or larger than the size of the cavity.^[11]

Suppose the cavity is held at a fixed temperature T and the radiation trapped inside the enclosure is at thermal equilibrium with the enclosure. The hole in the enclosure will allow some radiation to escape. If the hole is small, radiation passing in and out of the hole has negligible effect upon the equilibrium of the radiation inside the cavity. This escaping radiation will approximate black-body radiation that exhibits a distribution in energy characteristic of the temperature T and does not depend upon the properties of the cavity or the hole, at least for wavelengths smaller than the size of the hole.^[11] See the figure in the Introduction for the spectrum as a function of the frequency of the radiation, which is related to the energy of the radiation by the equation E=hf, with E = energy, h = Planck's constant, f = frequency.

At any given time the radiation in the cavity may not be in thermal equilibrium, but the second law of thermodynamics states that if left undisturbed it will eventually reach equilibrium,^[12] although the time it takes to do so may be very long.^[13] Typically, equilibrium is reached by continual absorption and emission of radiation by material in the cavity or its walls.^{[3][4][14][15]} Radiation entering the cavity will be "thermalized"; by this mechanism: the energy will be redistributed until the ensemble of photons achieves a Planck distribution. The time taken for thermalization is much faster with condensed matter present than with rarefied matter such as a dilute gas. At temperatures below billions of Kelvin, direct photon–photon interactions^[16] are usually negligible compared to interactions with matter.^[17] Photons are an example of an interacting boson gas,^[18] and as described by the H-theorem,^[19] under very general conditions any interacting boson gas will approach thermal equilibrium.

Transmission, absorption, and reflection

A body's behavior with regard to thermal radiation is characterized by its transmission τ, absorption α, and reflection ρ.

The boundary of a body forms an interface with its surroundings, and this interface may be rough or smooth. A nonreflecting interface separating regions with different refractive indices must be rough, because the laws of reflection and refraction governed by the Fresnel equations for a smooth interface require a reflected ray when the refractive indices of the material and its surroundings differ.^[20] A few idealized types of behavior are given particular names:

An opaque body is one that transmits none of the radiation that reaches it, although some may be reflected.^[21][22] That is, τ=0 and α+ρ=1

A transparent body is one that transmits all the radiation that reaches it. That is, τ=1 and α=ρ=0.
A gray body is one where α, ρ and τ are uniform for all wavelengths. This term also is used to mean a body for which α is temperature and wavelength independent.

A white body is one for which all incident radiation is reflected uniformly in all directions: τ=0, α=0, and ρ=1.

For a black body, τ=0, α=1, and ρ=0. Planck offers a theoretical model for perfectly black bodies, which he noted do not exist in nature: besides their opaque interior, they have interfaces that are perfectly transmitting and non-reflective.^[23]

Kirchhoff's perfect black bodies

Kirchhoff in 1860 introduced the theoretical concept of a perfect black body with a completely absorbing surface layer of infinitely small thickness, but Planck noted some severe restrictions upon this idea. Planck noted three requirements upon a black body: the body must (i) allow radiation to enter but not reflect; (ii) possess a minimum thickness adequate to absorb the incident radiation and prevent its re-emission; (iii) satisfy severe limitations upon scattering to prevent radiation from entering and bouncing back out. As a consequence, Kirchhoff's perfect black bodies that absorb all the radiation that falls on them cannot be realized in an infinitely thin surface layer, and impose conditions upon scattering of the light within the black body that are difficult to satisfy.^[24][25]

Realizations

A realization of a black body is a real world, physical embodiment. Here are a few.

Cavity with a hole

In 1898, Otto Lummer and Ferdinand Kurlbaum published an account of their cavity radiation source.^[26] Their design has been used largely unchanged for radiation measurements to the present day. It was a hole in the wall of a platinum box, divided by diaphragms, with its interior blackened with iron oxide. It was an important ingredient for the progressively improved measurements that led to the discovery of Planck's law.^[27][28] A version described in 1901 had its interior blackened with a mixture of chromium, nickel, and cobalt oxides.^[29] See also Hohlraum.

Near-black materials

There is interest in blackbody-like materials for camouflage and radar-absorbent materials for radar invisibility.^[30][31] They also have application as solar energy collectors, and infrared thermal detectors. As a perfect emitter of radiation, a hot material with black body behavior would create an efficient infrared heater, particularly in space or in a vacuum where convective heating is unavailable.^[32] They are also useful in telescopes and cameras as anti-reflection surfaces to reduce stray light, and to gather information about objects in high-contrast areas (for example, observation of planets in orbit around their stars), where blackbody-like materials absorb light that comes from the wrong sources.

It has long been known that a lamp-black coating will make a body nearly black. An improvement on lamp-black is found in manufactured carbon nanotubes. Nano-porous materials can achieve refractive indices nearly that of vacuum, in one case obtaining average reflectance of 0.045%.^[7][33] In 2009, a team of Japanese scientists created a material called nanoblack which is close to an ideal black body, based on vertically aligned single-walled carbon nanotubes. This absorbs between 98% and 99% of the incoming light in the spectral range from the ultra-violet to the far-infrared regions.^[32]

Other examples of nearly perfect black materials are super black, prepared by chemically etching a nickel–phosphorus alloy,^[34] and vantablack made of carbon nanotubes; both absorb 99.9% of light or more.

Stars and planets

An idealized view of the cross-section of a star. The photosphere contains photons of light nearly in thermal equilibrium, and some escape into space as near-black-body radiation.

A star or planet often is modeled as a black body, and electromagnetic radiation emitted from these bodies as black-body radiation. The figure shows a highly schematic cross-section to illustrate the idea. The photosphere of the star, where the emitted light is generated, is idealized as a layer within which the photons of light interact with the material in the photosphere and achieve a common temperature T that is maintained over a long period of time. Some photons escape and are emitted into space, but the energy they carry away is replaced by energy from within the star, so that the temperature of the photosphere is nearly steady. Changes in the core lead to changes in the supply of energy to the photosphere, but such changes are slow on the time scale of interest here. Assuming these circumstances can be realized, the outer layer of the star is somewhat analogous to the example of an enclosure with a small hole in it, with the hole replaced by the limited transmission into space at the outside of the photosphere. With all these assumptions in place, the star emits black-body radiation at the temperature of the photosphere.^[35]

Effective temperature of a black body compared with the B-V and U-B color index of main sequence and super giant stars in what is called a color-color diagram.^[36]

Using this model the effective temperature of stars is estimated, defined as the temperature of a black body that yields the same surface flux of energy as the star. If a star were a black body, the same effective temperature would result from any region of the spectrum. For example, comparisons in the B (blue) or V (visible) range lead to the so-called B-V color index, which increases the redder the star,^[37] with the Sun having an index of +0.648 ± 0.006.^[38] Combining the U (ultraviolet) and the B indices leads to the U-B index, which becomes more negative the hotter the star and the more the UV radiation. Assuming the Sun is a type G2 V star, its U-B index is +0.12.^[39] The two indices for two types of stars are compared in the figure with the effective surface temperature of the stars assuming they are black bodies. It can be seen that there is only a rough correlation. For example, for a given B-V index from the blue-visible region of the spectrum., the curves for both types of star lie below the corresponding black-body U-B index that includes the ultraviolet spectrum, showing that both types of star emit less ultraviolet light than a black body with the same B-V index. It is perhaps surprising that they fit a black body curve as well as they do, considering that stars have greatly different temperatures at different depths.^[40] For example, the Sun has an effective temperature of 5780 K,^[41] which can be compared to the temperature of the photosphere of the Sun (the region generating the light), which ranges from about 5000 K at its outer boundary with the chromosphere to about 9500 K at its inner boundary with the convection zone approximately 500 km (310 mi) deep.^[42]

Black holes

A black hole is a region of spacetime from which nothing escapes. Around a black hole there is a mathematically defined surface called an event horizon that marks the point of no return. It is called "black" because it absorbs all the light that hits the horizon, reflecting nothing, making it almost an ideal black body^[43] (radiation with a wavelength equal to or larger than the radius of the hole may not be absorbed, so black holes are not perfect black bodies).^[44] Physicists believe that to an outside observer, black holes have a non-zero temperature and emit radiation with a nearly perfect black-body spectrum, ultimately evaporating.^[45] The mechanism for this emission is related to vacuum fluctuations in which a virtual pair of particles is separated by the gravity of the hole, one member being sucked into the hole, and the other being emitted.^[46] The energy distribution of emission is described by Planck's law with a temperature T:

${\displaystyle T={\frac {\hbar c^{3}}{8\pi Gk_{B}M}}\ ,}$

where c is the speed of light, ℏ is the reduced Planck constant, k_B is Boltzmann's constant, G is the gravitational constant and M is the mass of the black hole.^[47] These predictions have not yet been tested either observationally or experimentally.^[48]

Cosmic microwave background radiation

See also: Big Bang and Cosmic microwave background radiation

The big bang theory is based upon the cosmological principle, which states that on large scales the Universe is homogeneous and isotropic. According to theory, the Universe approximately a second after its formation was a near-ideal black body in thermal equilibrium at a temperature above 10¹⁰ K. The temperature decreased as the Universe expanded and the matter and radiation in it cooled. The cosmic microwave background radiation observed today is "the most perfect black body ever measured in nature".^[49] It has a nearly ideal Planck spectrum at a temperature of about 2.7 K. It departs from the perfect isotropy of true black-body radiation by an observed anisotropy that varies with angle on the sky only to about one part in 100,000.

Radiative cooling

See also: Radiative cooling and Radiosity (heat transfer)

The integration of Planck's law over all frequencies provides the total energy per unit of time per unit of surface area radiated by a black body maintained at a temperature T, and is known as the Stefan–Boltzmann law:

${\displaystyle P/A=\sigma T^{4}\ ,}$

where σ is the Stefan–Boltzmann constant, σ ≈ 5.67 × 10⁻⁸ W/(m²K⁴).^[50] To remain in thermal equilibrium at constant temperature T, the black body must absorb or internally generate this amount of power P over the given area A.
The cooling of a body due to thermal radiation is often approximated using the Stefan–Boltzmann law supplemented with a "gray body" emissivity ε ≤ 1 (P/A = εσT⁴). The rate of decrease of the temperature of the emitting body can be estimated from the power radiated and the body's heat capacity.^[51] This approach is a simplification that ignores details of the mechanisms behind heat redistribution (which may include changing composition, phase transitions or restructuring of the body) that occur within the body while it cools, and assumes that at each moment in time the body is characterized by a single temperature. It also ignores other possible complications, such as changes in the emissivity with temperature,^[52][53] and the role of other accompanying forms of energy emission, for example, emission of particles like neutrinos.^[54]

If a hot emitting body is assumed to follow the Stefan–Boltzmann law and its power emission P and temperature T are known, this law can be used to estimate the dimensions of the emitting object, because the total emitted power is proportional to the area of the emitting surface. In this way it was found that X-ray bursts observed by astronomers originated in neutron stars with a radius of about 10 km, rather than black holes as originally conjectured.^[55] It should be noted that an accurate estimate of size requires some knowledge of the emissivity, particularly its spectral and angular dependence.^[56]