Space tether

From Wikipedia, the free encyclopedia

 

Artist's conception of satellite with a tether

Space tethers are long cables which can be used for propulsion, momentum exchange, stabilization and attitude control, or maintaining the relative positions of the components of a large dispersed satellite/spacecraft sensor system. Depending on the mission objectives and altitude, spaceflight using this form of spacecraft propulsion is theorized to be significantly less expensive than spaceflight using rocket engines.

Main techniques

Tether satellites might be used for various purposes, including research into tether propulsion, tidal stabilization and orbital plasma dynamics. Five main techniques for employing space tethers are in development:

Electrodynamic tethers

Electrodynamic tethers are primarily used for propulsion. These are conducting tethers that carry a current that can generate either thrust or drag from a planetary magnetic field, in much the same way as an electric motor does.

Momentum exchange tethers

These can be either rotating tethers, or non-rotating tethers, that capture an arriving spacecraft and then release it at a later time into a different orbit with a different velocity. Momentum exchange tethers can be used for orbital maneuvering, or as part of a planetary-surface-to-orbit / orbit-to-escape-velocity space transportation system.

Tethered formation flying

This is typically a non-conductive tether that accurately maintains a set distance between multiple space vehicles flying in formation.

Electric sail

A form of solar wind sail with electrically charged tethers that will be pushed by the momentum of solar wind ions.

Universal Orbital Support System

A concept for suspending an object from a tether orbiting in space.

Many uses for space tethers have been proposed, including deployment as space elevators, as skyhooks, and for doing propellant-free orbital transfers.

History

Konstantin Tsiolkovsky once proposed a tower so tall that it reached into space, so that it would be held there by the rotation of the Earth. However, at the time, there was no realistic way to build it.

To try to solve the problems in Komsomolskaya Pravda (July 31, 1960), another Russian, Yuri Artsutanov, wrote in greater detail about the idea of a tensile cable to be deployed from a geosynchronous satellite, downwards towards the ground, and upwards away, keeping the cable balanced. This is the space elevator idea, a type of synchronous tether that would rotate with the earth. However, given the materials technology of the time, this too was impractical on Earth.
In the 1970s, Jerome Pearson independently conceived the idea of a space elevator, sometimes referred to as a synchronous tether, and, in particular, analyzed a lunar elevator that can go through the L1 and L2 points, and this was found to be possible with materials then existing.

In 1977, Hans Moravec and later Robert L. Forward investigated the physics of non-synchronous skyhooks, also known as rotating skyhooks, and performed detailed simulations of tapered rotating tethers that could pick objects off, and place objects onto, the Moon, Mars and other planets, with little loss, or even a net gain of energy.

In 1979, NASA examined the feasibility of the idea and gave direction to the study of tethered systems, especially tethered satellites.

In 1990, E. Sarmont proposed a non-rotating Orbiting Skyhook for an Earth-to-orbit / orbit-to-escape-velocity Space Transportation System in a paper titled "An Orbiting Skyhook: Affordable Access to Space". In this concept a suborbital launch vehicle would fly to the bottom end of a Skyhook, while spacecraft bound for higher orbit, or returning from higher orbit, would use the upper end.

In 2000, NASA and Boeing considered a HASTOL concept, where a rotating tether would take payloads from a hypersonic aircraft (at half of orbital velocity) to orbit.

Missions

Graphic of the US Naval Research Laboratory's TiPS tether satellite. Only a small part of the 4 km tether is shown deployed.

A tether satellite is a satellite connected to another by a space tether. A number of satellites have been launched to test tether technologies, with varying degrees of success.

Types

There are many different (and overlapping) types of tether.

Momentum exchange tethers, rotating

Momentum Exchange Tethers are one of many applications for space tethers. Momentum Exchange Tethers come in two types; rotating and non-rotating. A rotating tether will create a controlled force on the end-masses of the system due to centrifugal acceleration. While the tether system rotates, the objects on either end of the tether will experience continuous acceleration; the magnitude of the acceleration depends on the length of the tether and the rotation rate. Momentum exchange occurs when an end body is released during the rotation. The transfer of momentum to the released object will cause the rotating tether to lose energy, and thus lose velocity and altitude. However, using electrodynamic tether thrusting, or ion propulsion the system can then re-boost itself with little or no expenditure of consumable reaction mass.

Skyhook

A rotating and a tidally stabilised skyhook in orbit

A skyhook is a theoretical class of orbiting tether propulsion intended to lift payloads to high altitudes and speeds. Proposals for skyhooks include designs that employ tethers spinning at hypersonic speed for catching high speed payloads or high altitude aircraft and placing them in orbit.

Electrodynamics

Medium close-up view, captured with a 70 mm camera, shows Tethered Satellite System deployment.

Electrodynamic tethers are long conducting wires, such as one deployed from a tether satellite, which can operate on electromagnetic principles as generators, by converting their kinetic energy to electrical energy, or as motors, converting electrical energy to kinetic energy. Electric potential is generated across a conductive tether by its motion through the earth's magnetic field. The choice of the metal conductor to be used in an electrodynamic tether is determined by a variety of factors. Primary factors usually include high electrical conductivity and low density. Secondary factors, depending on the application, include cost, strength, and melting point.

An electrodynamic tether was profiled in the documentary film Orphans of Apollo as technology that was to be used to keep the Russian space station Mir in orbit.

Formation flying

This is the use of a (typically) non-conductive tether to connect multiple spacecraft. A proposed 2011 experiment to study the technique is the Tethered Experiment for Mars inter-Planetary Operations (TEMPO³).

Universal Orbital Support System

Example of a possible layout using the Universal Orbital Support System.

A theoretical type of non-rotating tethered satellite system, it is a concept for providing space-based support to things suspended above an astronomical object. The orbital system is a coupled mass system wherein the upper supporting mass (A) is placed in an orbit around a given celestial body such that it can support a suspended mass (B) at a specific height above the surface of the celestial body, but lower than (A).

Technical difficulties

Gravitational gradient stabilization

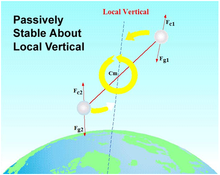
Description of the forces contributing towards maintaining a gravity gradient alignment in a tether system

Instead of rotating end for end, tethers can also be kept straight by the slight difference in the strength of gravity over their length.

A non-rotating tether system has a stable orientation that is aligned along the local vertical (of the earth or other body). This can be understood by inspection of the figure below where two spacecraft at two different altitudes have been connected by a tether. Normally, each spacecraft would have a balance of gravitational (e.g. F_g1) and centrifugal (e.g. F_c1), but when tied together by a tether, these values begin to change with respect to one another. This phenomenon occurs because, without the tether, the higher-altitude mass would travel slower than the lower mass. The system must move at a single speed, so the tether must therefore slow down the lower mass and speed up the upper one. The centrifugal force of the tethered upper body is increased, while that of the lower-altitude body is reduced. This results in the centrifugal force of the upper body and the gravitational force of the lower body being dominant. This difference in forces naturally aligns the system along the local vertical, as seen in the figure.

Atomic oxygen

Objects in low Earth orbit are subjected to noticeable erosion from atomic oxygen due to the high orbital speed with which the molecules strike as well as their high reactivity. This could quickly erode a tether.

Micrometeorites and space junk

Simple single-strand tethers are susceptible to micrometeoroids and space junk. Several systems have since been proposed and tested to improve debris resistance:

• The US Naval Research Laboratory has successfully flown a long term 6 km long, 2-3mm diameter tether with an outer layer of Spectra 1000 braid and a core of acrylic yarn. This satellite, the Tether Physics and Survivability Experiment (TiPS), was launched in June 1996 and remained in operation over 10 years, finally breaking in July 2006.
• Dr. Robert P. Hoyt patented an engineered circular net, such that a cut strand's strains would be redistributed automatically around the severed strand. This is called a Hoytether. Hoytethers have theoretical lifetimes of decades.
• Researchers with JAXA have also proposed net-based tethers for their future missions.

Large pieces of junk would still cut most tethers, including the improved versions listed here, but these are currently tracked on radar and have predictable orbits. A tether could be wiggled to dodge known pieces of junk, or thrusters used to change the orbit, avoiding a collision.

Construction

Properties of useful materials

TSS-1R tether composition [NASA].

Tether properties and materials are dependent on the application. However, there are some common properties. To achieve maximum performance and low cost, tethers would need to be made of materials with the combination of high strength or electrical conductivity and low density. All space tethers are susceptible to space debris or micrometeroids. Therefore, system designers will need to decide whether or not a protective coating is needed, including relative to UV and atomic oxygen. Research is being conducted to assess the probability of a collision that would damage the tether MAST.

For applications that exert high tensile forces on the tether, the materials need to be strong and light. Some current tether designs use crystalline plastics such as ultra high molecular weight polyethylene, aramid or carbon fiber. A possible future material would be carbon nanotubes, which have an estimated tensile strength between 140 and 177 GPa (20.3-25.6 million psi), and a proven tensile strength in the range 50-60 GPa for some individual nanotubes. (A number of other materials obtain 10 to 20 GPa in some samples on the nano scale, but translating such strengths to the macro scale has been challenging so far, with, as of 2011, CNT-based ropes being an order of magnitude less strong, not yet stronger than more conventional carbon fiber on that scale).

For some applications, the tensile force on the tether is projected to be less than 15 lbs (< 65 N) Material selection in this case depends on the purpose of the mission and design constraints. Electrodynamic tethers, such as the one used on TSS-1R, may use thin copper wires for high conductivity.

There are design equations for certain applications that may be used to aid designers in identifying typical quantities that drive material selection.

Space elevator equations typically use a "characteristic length", L_c, which is also known as its "self-support length" and is the length of untapered cable it can support in a constant 1 g gravity field.

${\displaystyle L_{c}={\frac {\sigma }{\rho g}}}$,

where σ is the stress limit (in pressure units) and ρ is the density of the material.

Hypersonic skyhook equations use the material's "specific velocity" which is equal to the maximum tangential velocity a spinning hoop can attain without breaking:

${\displaystyle V={\sqrt {\frac {\sigma }{\rho }}}}$

For rotating tethers (rotovators) the value used is the material’s ‘characteristic velocity’ which is the maximum tip velocity a rotating untapered cable can attain without breaking,

${\displaystyle V_{c}={\sqrt {\frac {2\sigma }{\rho }}}}$

The characteristic velocity equals the specific velocity multiplied by the square root of two.

These values are used in equations similar to the rocket equation and are analogous to specific impulse or exhaust velocity. The higher these values are, the more efficient and lighter the tether can be in relation to the payloads that they can carry. Eventually however, the mass of the tether propulsion system will be limited at the low end by other factors such as momentum storage.

Practical materials

Proposed materials include Kevlar, ultra high molecular weight polyethylene, carbon nanotubes and M5 fiber. M5 is a synthetic fiber that is lighter than Kevlar or Spectra. According to Pearson, Levin, Oldson, and Wykes in their article "The Lunar Space Elevator", an M5 ribbon 30 mm wide and 0.023 mm thick, would be able to support 2000 kg on the lunar surface. It would also be able to hold 100 cargo vehicles, each with a mass of 580 kg, evenly spaced along the length of the elevator. Other materials that could be used are T1000G carbon fiber, Spectra 2000, or Zylon.

Potential tether / elevator materials

Material	Density ρ (kg/m³)	Stress limit σ (GPa)	Characteristic length Lc = σ/ρg (km)	Specific velocity Vs = √σ/ρ (km/s)	Char. velocity Vc = √2σ/ρ (km/s)
Single-wall carbon nanotubes (individual molecules measured)	2266	50	2200	4.7	6.6
Aramid, polybenzoxazole (PBO) fiber ("Zylon")	1340	5.9	450	2.1	3.0
Toray carbon fiber (T1000G)	1810	6.4	360	1.9	2.7
M5 fiber (planned values)	1700	9.5	570	2.4	3.3
M5 fiber (existing)	1700	5.7	340	1.8	2.6
Honeywell extended chain polyethylene fiber (Spectra 2000)	970	3.0	316	1.8	2.5
DuPont Aramid fiber (Kevlar 49)	1440	3.6	255	1.6	2.2
Silicon carbide	3000	5.9	199	1.4	2.0

Shape

Tapering

For gravity stabilised tethers, to exceed the self-support length the tether material can be tapered so that the cross-sectional area varies with the total load at each point along the length of the cable. In practice this means that the central tether structure needs to be thicker than the tips. Correct tapering ensures that the tensile stress at every point in the cable is exactly the same. For very demanding applications, such as an Earth space elevator, the tapering can reduce the excessive ratios of cable weight to payload weight.

Thickness

For rotating tethers not significantly affected by gravity, the thickness also varies, and it can be shown that the area, A, is given as a function of r (the distance from the centre) as follows:

${\displaystyle A(r)={\frac {Mv^{2}}{TR}}\mathrm {e} ^{{\frac {\delta }{T}}{\frac {v^{2}}{2}}\left(1-{\frac {r^{2}}{R^{2}}}\right)}}$

where R is the radius of tether, v is the velocity with respect to the centre, M is the tip mass, ${\displaystyle \delta }$ is the material density, and T is the design tensile strength (Young's modulus divided by safety factor).

Mass ratio

Graph of tether mass to payload ratio versus the tip speed in multiples of the characteristic speed of the material

Integrating the area to give the volume and multiplying by the density and dividing by the payload mass gives a payload mass / tether mass ratio of:

${\displaystyle {\frac {M}{m}}={\sqrt {\pi {\frac {\delta }{T}}{\frac {V^{2}}{2}}}}\mathrm {e} ^{\left({\frac {\delta }{T}}{\frac {V^{2}}{2}}\right)}\mathrm {erf} \left({\sqrt {{\frac {\delta }{T}}{\frac {V^{2}}{2}}}}\right)}$

where erf is the normal probability error function.

Let ${\displaystyle V_{r}=V/V_{c}\,}$,

${\displaystyle V_{c}={\sqrt {\frac {2T}{\delta }}}}$

then:

${\displaystyle {\frac {M}{m}}={\sqrt {\pi }}V_{r}\mathrm {e} ^{{V_{r}}^{2}}\mathrm {erf} ({V_{r}})}$

This equation can be compared with the rocket equation, which is proportional to a simple exponent on a velocity, rather than a velocity squared. This difference effectively limits the delta-v that can be obtained from a single tether.

Redundancy

In addition the cable shape must be constructed to withstand micrometeorites and space junk. This can be achieved with the use of redundant cables, such as the Hoytether; redundancy can ensure that it is very unlikely that multiple redundant cables would be damaged near the same point on the cable, and hence a very large amount of total damage can occur over different parts of the cable before failure occurs.

Material strength

Beanstalks and rotovators are currently limited by the strengths of available materials. Although ultra-high strength plastic fibers (Kevlar and Spectra) permit rotovators to pluck masses from the surface of the Moon and Mars, a rotovator from these materials cannot lift from the surface of the Earth. In theory, high flying, supersonic (or hypersonic) aircraft could deliver a payload to a rotovator that dipped into Earth's upper atmosphere briefly at predictable locations throughout the tropic (and temperate) zone of Earth. As of May 2013, all mechanical tethers (orbital and elevators) are on hold until stronger materials are available.

Cargo capture

Cargo capture for rotovators is nontrivial, and failure to capture can cause problems. Several systems have been proposed, such as shooting nets at the cargo, but all add weight, complexity, and another failure mode. At least one lab scale demonstration of a working grapple system has been achieved however.

Life expectancy

Currently, the strongest materials in tension are plastics that require a coating for protection from UV radiation and (depending on the orbit) erosion by atomic oxygen. Disposal of waste heat is difficult in a vacuum, so overheating may cause tether failures or damage.

Control and modelling

Pendular motion instability

Electrodynamic tethers deployed along the local vertical ('hanging tethers') may suffer from dynamical instability. Pendular motion causes the tether vibration amplitude to build up under the action of electromagnetic interaction. As the mission time increases, this behavior can compromise the performance of the system. Over a few weeks, electrodynamic tethers in Earth orbit might build up vibrations in many modes, as their orbit interacts with irregularities in magnetic and gravitational fields.

One plan to control the vibrations is to actively vary the tether current to counteract the growth of the vibrations. Electrodynamic tethers can be stabilized by reducing their current when it would feed the oscillations, and increasing it when it opposes oscillations. Simulations have demonstrated that this can control tether vibration.^{[citation needed]} This approach requires sensors to measure tether vibrations, which can either be an inertial navigation system on one end of the tether, or satellite navigation systems mounted on the tether, transmitting their positions to a receiver on the end.
Another proposed method is to use spinning electrodynamic tethers instead of hanging tethers. The gyroscopic effect provides passive stabilisation, avoiding the instability.

Surges

As mentioned earlier, conductive tethers have failed from unexpected current surges. Unexpected electrostatic discharges have cut tethers (e.g. see Tethered Satellite System Reflight (TSS‑1R) on STS‑75), damaged electronics, and welded tether handling machinery. It may be that the Earth's magnetic field is not as homogeneous as some engineers have believed.

Vibrations

Computer models frequently show tethers can snap due to vibration.

Mechanical tether-handling equipment is often surprisingly heavy, with complex controls to damp vibrations. The one ton climber proposed by Dr. Brad Edwards for his Space Elevator may detect and suppress most vibrations by changing speed and direction. The climber can also repair or augment a tether by spinning more strands.

The vibration modes that may be a problem include skipping rope, transverse, longitudinal, and pendulum.

Tethers are nearly always tapered, and this can greatly amplify the movement at the thinnest tip in whip-like ways.

Other issues

A tether is not a spherical object, and has significant extent. This means that as an extended object, it is not directly modelable as a point source, and this means that the center of mass and center of gravity are not usually colocated. Thus the inverse square law does not apply except at large distances, to the overall behaviour of a tether. Hence the orbits are not completely Keplerian, and in some cases they are actually chaotic.

With bolus designs, rotation of the cable interacting with the non linear gravity fields found in elliptical orbits can cause exchange of orbital angular momentum and rotation angular momentum. This can make prediction and modelling extremely complex.

Commercial use of space

From Wikipedia, the free encyclopedia

 

A DIRECTV satellite dish on a roof

Commercial use of space is the provision of goods or services of commercial value by using equipment sent into Earth orbit or outer space. Examples of the commercial use of space include satellite navigation, satellite television and commercial satellite imagery. Operators of such services typically contract the manufacturing of satellites and their launch to private or public companies, which form an integral part of the space economy. Some commercial ventures have long-terms plans to exploit natural resources originating outside Earth, for example asteroid mining. Space tourism, currently an exceptional activity, could also be an area of future growth, as new businesses strive to reduce the costs and risks of human spaceflight.

The first commercial use of outer space occurred in 1962, when the Telstar 1 satellite was launched to transmit television signals over the Atlantic Ocean. By 2004, global investment in all space sectors was estimated to be $50.8 billion. As of 2010, 31% of all space launches were commercial.

History

The first commercial use of satellites may have been the Telstar 1 satellite, launched in 1962, which was the first privately sponsored space launch, funded by AT&T and Bell Telephone Laboratories. Telstar 1 was capable of relaying television signals across the Atlantic Ocean, and was the first satellite to transmit live television, telephone, fax, and other data signals. Two years later, the Hughes Aircraft Company developed the Syncom 3 satellite, a geosynchronous communications satellite, leased to the Department of Defense. Commercial possibilities of satellites were further realized when the Syncom 3, orbiting near the International Date Line, was used to telecast the 1964 Olympic Games from Tokyo to the United States.

Between 1960 and 1966, NASA launched a series of early weather satellites known as Television Infrared Observation Satellites (TIROS). These satellites greatly advanced meteorology worldwide, as satellite imagery was used for better forecasting, for both public and commercial interests.

On April 6, 1965, the Hughes Aircraft Company placed the Intelsat I communications satellite geosynchronous orbit over the Atlantic Ocean. Intelsat I was built for the Communications Satellite Corporation (COMSAT), and demonstrated that satellite-based communication was commercially feasible. Intelsat I allowed for near-instantaneous contact between Europe and North America by handling television, telephone and fax transmissions. Two years later, the Soviet Union launched the Orbita satellite, which provided television signals across Russia, and started the first national satellite television network. Similarly, the 1972 Anik A satellite, launched by Telesat Canada, allowed the Canadian Broadcasting Corporation to reach northern Canada for the first time.

Beginning in 1997, Iridium Communications began launching a series of satellites known as the Iridium satellite constellation, which provided the first satellites for direct satellite telephone service.

Space transportation

Delta IV Medium launch carrying DSCS III-B6

The commercial space transportation industry derives the bulk of its revenue from the launching of satellites into the Earth’s orbit. Commercial launch providers typically place private and government satellites into low Earth orbit (LEO) and geosynchronous Earth orbit (GEO). In 2002, commercial space transportation generated 6.6 billion dollars, which made up 6% of the total gross of commercial space activities.

The Federal Aviation Administration (FAA) has licensed four commercial spaceports in the United States: the Virginia Space Flight Center/Wallops Flight Facility, Kodiak Launch Complex, Spaceport Florida/Kennedy Space Center/Cape Canaveral Air Force Station, and the California Spaceport/Vandenberg AFB. Launch sites within Russia and China have added to the global commercial launch capacity. The Delta IV and Atlas V family of launch vehicles are made available for commercial ventures for the United States, while Russia promotes eight families of vehicles. The three largest Russian systems are the Proton, Soyuz, and Zenit.

Between 1996 and 2002, 245 launches were made for commercial ventures while government (non-classified) launches only total 167 for the same period. Commercial space flight has spurred investment into the development of an efficient reusable launch vehicle (RLV) which can place larger payloads into orbit. Several companies such as SpaceX and Blue Origin are currently developing new RLV designs.

In the United States, Office of Commercial Space Transportation (generally referred to as FAA/AST or simply AST) is the branch of Federal Aviation Administration (FAA) that approves any commercial rocket launch operations—that is, any launches that are not classified as model, amateur, or "by and for the government."

Satellites and equipment

Satellite manufacturing

Commercial satellite manufacturing is defined by the United States government as satellites manufactured for civilian, government, or non-profit use. Not included are satellites constructed for military use, nor for activities associated with any human space flight program. Between the years of 1996 and 2002, satellite manufacturing within the United States experienced an annual growth of 11 percent. The rest of the world experienced higher growth levels of around 13 percent.

Ground equipment manufacturing

Operating satellites communicate via receivers and transmitters on Earth. The manufacturing of satellite ground station communication terminals (including VSATs), mobile satellite telephones, and home television receivers are a part of the ground equipment manufacturing sector. This sector grew through the latter half of the 1990s as it manufactured equipment for the satellite services sector. Between the years of 1996 and 2002 this industry saw a 14 percent annual increase.

Transponder leasing

Businesses that operate satellites often lease or sell access to their satellites to data relay and telecommunication firms. This service is often referred to as transponder leasing. Between 1996 and 2002, this industry experienced a 15 percent annual growth. The United States accounts for about 32 percent of the world’s transponder market.

Subscription satellite services

In 1994, DirecTV debuted direct broadcast satellite by introducing a signal receiving dish 18inches in diameter. In 1996, Astro started in Malaysia with the launch of the MEASAT satellite. In November 1999, the Satellite Home Viewer Improvement Act became law, and local stations were then made available in satellite channel packages, fueling the industry’s growth in the years that followed. By the end of 2000, DTH subscriptions totaled over 67 million.

Satellite radio was pioneered by XM Satellite Radio and Sirius Satellite Radio. XM’s first satellite was launched on March 18, 2001 and its second on May 8, 2001. Its first broadcast occurred on September 25, 2001, nearly four months before Sirius. Sirius launched the initial phase of its service in four cities on February 14, 2002, expanding to the rest of the contiguous United States on July 1, 2002. The two companies spent over $3 billion combined to develop satellite radio technology, build and launch the satellites, and for various other business expenses.

Satellite imagery

Several operators of Earth observation satellites, such as GeoEye and Spot Image, provide images commercially.

Satellite navigation

Magellan GPS receiver in a marine application.

A satellite navigation system is a system of satellites that provide autonomous geo-spatial positioning with global coverage. It allows small electronic receivers to determine their location (longitude, latitude, and altitude/elevation) to high precision (within a few metres) using time signals transmitted along a line of sight by radio from satellites. The signals also allow the electronic receivers to calculate the current local time to high precision, which allows time synchronisation. A satellite navigation system with global coverage may be termed a global navigation satellite system (GNSS).

Space tourism

Virgin Galactic VMS Eve

Space tourism is space travel by individuals for the purpose of personal pleasure. The space tourism industry is being targeted by spaceports in numerous locations, including the Mojave Air and Space Port in California, the Clinton-Sherman Industrial Airpark near Burns Flat, Oklahoma Spaceport America in Sierra County, New Mexico, the Mid-Atlantic Regional Spaceport on the Delmarva Peninsula in Virginia, the Kodiak Launch Complex on Kodiak Island, Alaska, and the Esrange Space Center in Kiruna, Sweden.

Commercial recovery of space resources

Artist's concept of asteroid mining

Commercial recovery of space resources is the exploitation of raw materials from asteroids, comets and other space objects, including near-Earth objects. Minerals and volatiles could be mined then used in space for in-situ utilization (e.g. construction materials and rocket propellant) or taken back to Earth. These include gold, iridium, silver, osmium, palladium, platinum, rhenium, rhodium, ruthenium and tungsten for transport back to Earth; iron, cobalt, manganese, molybdenum, nickel, aluminium, and titanium for construction; water and oxygen to sustain astronauts; as well as hydrogen, ammonia, and oxygen for use as rocket propellant.

There are several commercial enterprises working in this field, including Planetary Resources and Deep Space Industries.

Regulation

Beyond the many technological factors that could make space commercialization more widespread, it has been suggested that the lack of private property, the difficulty or inability of individuals in establishing property rights in space, has been an impediment to the development of space for both human habitation and commercial development.

Since the advent of space technology in the latter half of the twentieth century, the ownership of property in space has been murky, with strong arguments both for and against. In particular, the making of national territorial claims in outer space and on celestial bodies has been specifically proscribed by the Outer Space Treaty, which had been, as of 2012, ratified by all spacefaring nations.

In November 25, 2015 President Obama signs the U.S. Commercial Space Launch Competitiveness Act (H.R. 2262) into law. The law recognizes the right of U.S. citizens to own space resources they obtain and encourages the commercial exploration and utilization of resources from asteroids. According to the article § 51303 of the law:

A United States citizen engaged in commercial recovery of an asteroid resource or a space resource under this chapter shall be entitled to any asteroid resource or space resource obtained, including to possess, own, transport, use, and sell the asteroid resource or space resource obtained in accordance with applicable law, including the international obligations of the United States

Weightlessness

From Wikipedia, the free encyclopedia

Astronauts on the International Space Station experience only microgravity and thus display an example of weightlessness. Michael Foale can be seen exercising in the foreground.

 

A block of lead in free fall on planet X. The block is said to be in a state of weightlessness although being pulled down by the planet's gravity.

 

Two bodies in free fall: the Earth and the Moon. The two bodies are GR inertial and are accelerating towards each other. They are approximately weightless.

Weightlessness is the complete or near complete absence of the sensation of weight. This is also termed zero-g, although the term is more correctly "zero g-force." It occurs in the absence of any contact forces upon objects including the human body.

The forces which support bodies at rest in a relatively strong gravitational field (such as on the surface of the Earth), is normally perceived as weight. These weight-sensations originate from contact with supporting floors, seats, beds, scales, and the like. A sensation of weight is also produced, even when the gravitational field is zero, when contact forces act upon and overcome a body's inertia by mechanical, non-gravitational forces- such as in a centrifuge, a rotating space station, or within an accelerating vehicle.

When the gravitational field is non-uniform, a body in free fall experiences tidal effects and is not stress-free. Near a black hole, such tidal effects can be very strong. In the case of the Earth, the effects are minor, especially on objects of relatively small dimension (such as the human body or a spacecraft) and the overall sensation of weightlessness in these cases is preserved. This condition is known as microgravity and it prevails in orbiting spacecraft.

Weightlessness in Newtonian mechanics

In the left half, the spring is far away from any gravity source. In the right half, it is in a uniform gravitation field. a) Zero gravity and weightless b) Zero gravity but not weightless (Spring is rocket propelled) c) Spring is in free fall and weightless d) Spring rests on a plinth and has both weight₁ and weight₂.

In Newtonian mechanics the term "weight" is given two distinct interpretations by engineers.

Weight₁: Under this interpretation, the "weight" of a body is the gravitational force exerted on the body and this is the notion of weight that prevails in engineering. Near the surface of the earth, a body whose mass is 1 kg has a weight of approximately 9.81 N, independent of its state of motion, free fall, or not. Weightlessness in this sense can be achieved by removing the body far away from the source of gravity. It can also be attained by placing the body at a neutral point between two gravitating masses.

Weight₂: Weight can also be interpreted as that quantity which is measured when one uses scales. What is being measured there is the force exerted by the body on the scales. In a standard weighing operation, the body being weighed is in a state of equilibrium as a result of a force exerted on it by the weighing machine cancelling the gravitational field. By Newton's 3rd law, there is an equal and opposite force exerted by the body on the machine. This force is called weight₂. The force is not gravitational. Typically, it is a contact force and not uniform across the mass of the body. If the body is placed on the scales in a lift (an elevator) in free fall in pure uniform gravity, the scale would read zero, and the body said to be weightless i.e. its weight₂ = 0. This describes the condition in which the body is stress free and undeformed. This is the weightlessness in free fall in a uniform gravitational field. (The situation is more complicated when the gravitational field is not uniform, or, when a body is subject to multiple forces which may, for instance, cancel each other and produce a state of stress albeit weight₂ being zero. See below.)

To sum up, we have two notions of weight of which weight₁ is dominant. Yet 'weightlessness' is typically exemplified not by absence of weight₁ but by the absence of stress associated with weight₂. This is the intended sense of weightlessness in what follows below.

A body is stress free, exerts zero weight₂, when the only force acting on it is weight₁ as when in free fall in a uniform gravitational field. Without subscripts, one ends up with the odd-sounding conclusion that a body is weightless when the only force acting on it is its weight.
 
The apocryphal apple that fell on Newton's head can be used to illustrate the issues involved. An apple weighs approximately 1 newton. This is the weight₁ of the apple and is considered to be a constant even while it is falling. During that fall, its weight₂ however is zero: ignoring air resistance, the apple is stress free. When it hits Newton, the sensation felt by Newton would depend upon the height from which the apple falls and weight₂ of the apple at the moment of impact may be many times greater than 1 N. It was great enough—in the story—to make the great man invent the theory of gravity. It is this weight₂ which distorts the apple. On its way down, the apple in its free fall does not suffer any distortion as the gravitational field is uniform.

Stress during free fall

1. In a uniform gravitational field: Consider any cross-section dividing the body into two parts. Both parts have the same acceleration and the force exerted on each is supplied by the external source of the field. There is no force exerted by one part on the other. Stress at the cross-section is zero. Weight₂ is zero.
2. In a non-uniform gravitational field: Under gravity alone, one part of the body may have a different acceleration from another part. This would tend to deform the body and generate internal stresses if the body resists deformation. Weight₂ is not 0.

Throughout this discussion on using stress as an indicator of weight, any pre-stress which may exist within a body caused by a force exerted on one part by another is not relevant. The only relevant stresses are those generated by external forces applied to the body.

The definition and use of 'weightlessness' is difficult unless it is understood that the sensation of "weight" in everyday terrestrial experience results not from gravitation acting alone (which is not felt), but instead by the mechanical forces that resist gravity. An object in a straight free fall, or in a more complex inertial trajectory of free fall (such as within a reduced gravity aircraft or inside a space station), all experience weightlessness, since they do not experience the mechanical forces that cause the sensation of weight.

Force fields other than gravity

As noted above, weightlessness occurs when

1. no resultant force acts on the object
2. uniform gravity acts solely by itself.

For the sake of completeness, a 3rd minor possibility has to be added. This is that a body may be subject to a field which is not gravitational but such that the force on the object is uniformly distributed across the object's mass. An electrically charged body, uniformly charged, in a uniform electric field is a possible example. Electric charge here replaces the usual gravitational charge. Such a body would then be stress free and be classed as weightless. Various types of levitation may fall into this category, at least approximately.

Weightlessness and proper acceleration

A body in free fall (which by definition entails no aerodynamic forces) near the surface of the earth has an acceleration approximately equal to 9.8 m s⁻² with respect to a coordinate frame tied to the earth. If the body is in a freely falling lift and subject to no pushes or pulls from the lift or its contents, the acceleration with respect to the lift would be zero. If on the other hand, the body is subject to forces exerted by other bodies within the lift, it will have an acceleration with respect to the freely falling lift. This acceleration which is not due to gravity is called "proper acceleration". On this approach, weightlessness holds when proper acceleration is zero.

How to avoid weightlessness

Weightlessness is in contrast with current human experiences in which a non-uniform force is acting, such as:

• standing on the ground, sitting in a chair on the ground, etc., where gravity is countered by the support force of the ground,
• flying in a plane, where a support force is transmitted from the lift the wings provide (special trajectories which form an exception are described below),
• during atmospheric reentry, or during the use of a parachute, when atmospheric drag decelerates a vehicle,
• during an orbital maneuver in a spacecraft, or during the launch phase, when rocket engines provide thrust.

In cases where an object is not weightless, as in the above examples, a force acts non-uniformly on the object in question. Aero-dynamic lift, drag, and thrust are all non-uniform forces (they are applied at a point or surface, rather than acting on the entire mass of an object), and thus create the phenomenon of weight. This non-uniform force may also be transmitted to an object at the point of contact with a second object, such as the contact between the surface of the Earth and one's feet, or between a parachute harness and one's body.

Tidal forces

Two rigid cubes joined by an elastic string in free fall near a black hole. The string stretches as the body falls to the right.

Tidal forces arise when the gravitational field is not uniform and gravitation gradients exist. Such indeed is the norm and strictly speaking any object of finite size even in free-fall is subject to tidal effects. These are impossible to remove by inertial motion, except at one single nominated point of the body. The Earth is in free fall but the presence of tides indicates that it is in a non-uniform gravitational field. This non-uniformity is more due to the moon than the sun. The total gravitational field due to the sun is much stronger than that of the moon but it has a minor tidal effect compared with that of the moon because of the relative distances involved. Weight₁ of the earth is essentially due to the sun's gravity. But its state of stress and deformation, represented by the tides, is more due to non uniformity in the gravitational field of the nearby moon. When the size of a region being considered is small relative to its distance from the gravitating mass the assumption of uniform gravitational field holds to a good approximation. Thus a person is small relative to the radius of Earth and the field for a person at the surface of the earth is approximately uniform. The field is strictly not uniform and is responsible for the phenomenon of microgravity. Objects near a black hole are subject to a highly non-uniform gravitational field.

Frames of reference

In all inertial reference frames, while weightlessness is experienced, Newton's first law of motion is obeyed locally within the frame. Inside the frame (for example, inside an orbiting ship or free-falling elevator), unforced objects keep their velocity relative to the frame. Objects not in contact with other objects "float" freely. If the inertial trajectory is influenced by gravity, the reference frame will be an accelerated frame as seen from a position outside the gravitational attraction, and (seen from far away) the objects in the frame (elevator, etc.) will appear to be under the influence of a force (the so-called force of gravity). As noted, objects subject solely to gravity do not feel its effects. Weightlessness can thus be realised for short periods of time in an airplane following a specific elliptic flight path, often mistakenly called a parabolic flight. It is simulated poorly, with many differences, in neutral buoyancy conditions, such as immersion in a tank of water.

Zero-g, "zero gravity", accelerometers

Zero-g is an alternative term for weightlessness and holds for instance in a freely falling lift. Zero-g is subtly different from the complete absence of gravity, something which is impossible due to the presence of gravity everywhere in the universe. "Zero-gravity" may also be used to mean effective weightlessness, neglecting tidal effects. Microgravity (or µg) is used to refer to situations that are substantially weightless but where g-force stresses within objects due to tidal effects, as discussed above, are around a millionth of that at the Earth's surface. Accelerometers can only detect g-force i.e. weight₂ (= mass × proper acceleration). They cannot detect the acceleration associated with free fall.

Sensation of weight

The force on the feet is approximately double that on the cross-section through the navel.

Humans experience their own body weight as a result of this supporting force, which results in a normal force applied to a person by the surface of a supporting object, on which the person is standing or sitting. In the absence of this force, a person would be in free-fall, and would experience weightlessness. It is the transmission of this reaction force through the human body, and the resultant compression and tension of the body's tissues, that results in the sensation of weight.

Because of the distribution of mass throughout a person's body, the magnitude of the reaction force varies between a person's feet and head. At any horizontal cross-section of a person's body (as with any column), the size of the compressive force being resisted by the tissues below the cross-section is equal to the weight of the portion of the body above the cross-section. In the pose adopted in the accompanying illustration, the shoulders carry the weight of the outstretched arms and are subject to a considerable torque.

A common misconception

A common conception about spacecraft orbiting the earth is that they are operating in a gravity free environment. Although there is a way of making sense of this within the physics of Einstein's general relativity, within Newtonian physics, this is technically inaccurate.

A geostationary satellite above a marked spot on the Equator. An observer on the marked spot will see the satellite remain directly overhead unlike the other heavenly objects which sweep across the sky.

Spacecraft are held in orbit by the gravity of the planet which they are orbiting. In Newtonian physics, the sensation of weightlessness experienced by astronauts is not the result of there being zero gravitational acceleration (as seen from the Earth), but of there being no g-force that an astronaut can feel because of the free-fall condition, and also there being zero difference between the acceleration of the spacecraft and the acceleration of the astronaut. Space journalist James Oberg explains the phenomenon this way:

The myth that satellites remain in orbit because they have "escaped Earth's gravity" is perpetuated further (and falsely) by almost universal misuse of the word "zero gravity" to describe the free-falling conditions aboard orbiting space vehicles. Of course, this isn't true; gravity still exists in space. It keeps satellites from flying straight off into interstellar emptiness. What's missing is "weight", the resistance of gravitational attraction by an anchored structure or a counterforce. Satellites stay in space because of their tremendous horizontal speed, which allows them—while being unavoidably pulled toward Earth by gravity—to fall "over the horizon." The ground's curved withdrawal along the Earth's round surface offsets the satellites' fall toward the ground. Speed, not position or lack of gravity, keeps satellites in orbit around the earth.

A geostationary satellite is of special interest in this context. Unlike other objects in the sky which rise and set, an object in a geostationary orbit appears motionless in the sky, apparently defying gravity. In fact, it is in a circular equatorial orbit with a period of one day.

Relativity

To a modern physicist working with Einstein's general theory of relativity, the situation is even more complicated than is suggested above. Einstein's theory suggests that it actually is valid to consider that objects in inertial motion (such as falling in an elevator, or in a parabola in an airplane, or orbiting a planet) can indeed be considered to experience a local loss of the gravitational field in their rest frame. Thus, in the point of view (or frame) of the astronaut or orbiting ship, there actually is nearly-zero proper acceleration (the acceleration felt locally), just as would be the case far out in space, away from any mass. It is thus valid to consider that most of the gravitational field in such situations is actually absent from the point of view of the falling observer, just as the colloquial view suggests (see equivalence principle for a fuller explanation of this point). However, this loss of gravity for the falling or orbiting observer, in Einstein's theory, is due to the falling motion itself, and (again as in Newton's theory) not due to increased distance from the Earth. However, the gravity nevertheless is considered to be absent. In fact, Einstein's realization that a pure gravitational interaction cannot be felt, if all other forces are removed, was the key insight to leading him to the view that the gravitational "force" can in some ways be viewed as non-existent. Rather, objects tend to follow geodesic paths in curved space-time, and this is "explained" as a force, by "Newtonian" observers who assume that space-time is "flat," and thus do not have a reason for curved paths (i.e., the "falling motion" of an object near a gravitational source).

In the theory of general relativity, the only gravity which remains for the observer following a falling path or "inertial" path near a gravitating body, is that which is due to non-uniformities which remain in the gravitational field, even for the falling observer. This non-uniformity, which is a simple tidal effect in Newtonian dynamics, constitutes the "microgravity" which is felt by all spacially-extended objects falling in any natural gravitational field that originates from a compact mass. The reason for these tidal effects is that such a field will have its origin in a centralized place (the compact mass), and thus will diverge, and vary slightly in strength, according to distance from the mass. It will thus vary across the width of the falling or orbiting object. Thus, the term "microgravity," an overly technical term from the Newtonian view, is a valid and descriptive term in the general relativistic (Einsteinian) view.

Microgravity

The term micro-g environment (also µg, often referred to by the term microgravity) is more or less a synonym of weightlessness and zero-G, but indicates that g-forces are not quite zero, just very small.

Weightless and reduced weight environments

Zero gravity flight maneuver

Reduced weight in aircraft

Airplanes have been used since 1959 to provide a nearly weightless environment in which to train astronauts, conduct research, and film motion pictures. Such aircraft are commonly referred by the nickname "Vomit Comet".

To create a weightless environment, the airplane flies in a six-mile long parabolic arc, first climbing, then entering a powered dive. During the arc, the propulsion and steering of the aircraft are controlled such that the drag (air resistance) on the plane is cancelled out, leaving the plane to behave as it would if it were free-falling in a vacuum. During this period, the plane's occupants experience 22 seconds of weightlessness, before experiencing about 22 seconds of 1.8 g acceleration (nearly twice their normal weight) during the pull-out from the parabola. A typical flight lasts around two hours, during which 30 parabolae are flown.

NASA's KC-135A plane ascending for a zero gravity maneuver

NASA's Reduced Gravity Aircraft

Versions of such airplanes have been operated by NASA's Reduced Gravity Research Program since 1973, where the unofficial nickname originated. NASA later adopted the official nickname 'Weightless Wonder' for publication. NASA's current Reduced Gravity Aircraft, "Weightless Wonder VI", a McDonnell Douglas C-9, is based at Ellington Field (KEFD), near Lyndon B. Johnson Space Center.

NASA's Microgravity University - Reduced Gravity Flight Opportunities Plan, also known as the Reduced Gravity Student Flight Opportunities Program, allows teams of undergraduates to submit a microgravity experiment proposal. If selected, the teams design and implement their experiment, and students are invited to fly on NASA's Vomit Comet.

European Space Agency A310 Zero-G

The European Space Agency flies parabolic flights on a specially-modified Airbus A310-300 aircraft, in order to perform research in microgravity. As well European ESA, French CNES and German DLR fly campaigns of three flights on consecutive days, each flying about 30 parabolas, for a total of about 10 minutes of weightlessness per flight. These campaigns are currently operated from Bordeaux - Mérignac Airport in France by the company Novespace, a subsidiary of French CNES, while the aircraft is flown by test pilots from DGA Essais en Vol. The first ESA Zero-G flights were in 1984, using a NASA KC-135 aircraft in Houston, Texas. As of May 2010, the ESA has flown 52 campaigns and also 9 student parabolic flight campaigns.

Other aircraft it has used include the Russian Ilyushin Il-76 MDK before founding Novespace, and using then a French Caravelle, then an Airbus A300 Zero-G and now an Airbus A310. 

Commercial flights for public passengers

Inside Zero Gravity Corporation's airplane

Novespace created Air Zero G in 2012 to share the experience of weightlessness to 40 public passengers per flight, using the same A310 ZERO-G than for scientific experiences. These flights are sold by Avico, are mainly operated from Bordeaux-Merignac, France, and intend to promote European space research, allowing public passengers to feel weighlessness. Jean-François Clervoy, Chairman of Novespace and ESA astronaut, flies with Air Zero G one-day-astronauts on board A310 Zero-G. After the flight, he explains the quest of space and talks about the 3 space travels he did along his career. The aircraft has also been used for cinema purposes, with Tom Cruise and Annabelle Wallis for the Mummy in 2017.

The Zero Gravity Corporation, founded in 1993 by Peter Diamandis, Byron Lichtenberg, and Ray Cronise, operates a modified Boeing 727 which flies parabolic arcs to create 25–30 seconds of weightlessness. Flights may be purchased for both tourism and research purposes.

Ground-based drop facilities

Zero-gravity testing at the NASA Zero Gravity Research Facility

Ground-based facilities that produce weightless conditions for research purposes are typically referred to as drop tubes or drop towers.

NASA's Zero Gravity Research Facility, located at the Glenn Research Center in Cleveland, Ohio, is a 145-meter vertical shaft, largely below the ground, with an integral vacuum drop chamber, in which an experiment vehicle can have a free fall for a duration of 5.18 seconds, falling a distance of 132 meters. The experiment vehicle is stopped in approximately 4.5 meters of pellets of expanded polystyrene and experiences a peak deceleration rate of 65g.

Also at NASA Glenn is the 2.2 Second Drop Tower, which has a drop distance of 24.1 meters. Experiments are dropped in a drag shield, in order to reduce the effects of air drag. The entire package is stopped in a 3.3 meter tall air bag, at a peak deceleration rate of approximately 20g. While the Zero Gravity Facility conducts one or two drops per day, the 2.2 Second Drop Tower can conduct up to twelve drops per day.

NASA's Marshall Space Flight Center hosts another drop tube facility that is 105 meters tall and provides a 4.6 second free fall under near-vacuum conditions.

Humans cannot utilize these gravity shafts, as the deceleration experienced by the drop chamber would likely kill or seriously injure anyone using them; 20g is about the highest deceleration that a fit and healthy human can withstand momentarily without sustaining injury.
Other drop facilities worldwide include:

• Micro-Gravity Laboratory of Japan (MGLAB) – 4.5 s free fall
• Experimental drop tube of the metallurgy department of Grenoble – 3.1 s free fall
• Fallturm Bremen University of Bremen in Bremen – 4.74 s free fall
• Queensland University of Technology Drop Tower - 2.0 s free fall

Neutral buoyancy

Weightlessness can also be simulated by creating the condition of neutral buoyancy, in which human subjects and equipment are placed in a water environment and weighted or buoyed until they hover in place. NASA uses neutral buoyancy to prepare for extra-vehicular activity (EVA) at its Neutral Buoyancy Laboratory. Neutral buoyancy is also used for EVA research at the University of Maryland's Space Systems Laboratory, which operates the only neutral buoyancy tank at a college or university.

Neutral buoyancy is not identical to weightlessness. Gravity still acts on all objects in a neutral buoyancy tank; thus, astronauts in neutral buoyancy training still feel their full body weight within their spacesuits, although the weight is well-distributed, similar to force on a human body in a water bed, or when simply floating in water. The suit and astronaut together are under no net force, as for any object that is floating, or supported in water, such as a scuba diver at neutral buoyancy. Water also produces drag, which is not present in vacuum.

Weightlessness in a spacecraft

The relationship between acceleration and velocity vectors in an orbiting spacecraft.

 

US astronaut Marsha Ivins demonstrates the effect of weightlessness on long hair during STS-98.

 

Long periods of weightlessness occur on spacecraft outside a planet's atmosphere, provided no propulsion is applied and the vehicle is not rotating. Weightlessness does not occur when a spacecraft is firing its engines or when re-entering the atmosphere, even if the resultant acceleration is constant. The thrust provided by the engines acts at the surface of the rocket nozzle rather than acting uniformly on the spacecraft, and is transmitted through the structure of the spacecraft via compressive and tensile forces to the objects or people inside.

Weightlessness in an orbiting spacecraft is physically identical to free-fall, with the difference that gravitational acceleration causes a net change in the direction, rather than the magnitude, of the spacecraft's velocity. This is because the acceleration vector is perpendicular to the velocity vector.

In typical free-fall, the acceleration of gravity acts along the direction of an object's velocity, linearly increasing its speed as it falls toward the Earth, or slowing it down if it is moving away from the Earth. In the case of an orbiting spacecraft, which has a velocity vector largely perpendicular to the force of gravity, gravitational acceleration does not produce a net change in the object's speed, but instead acts centripetally, to constantly "turn" the spacecraft's velocity as it moves around the Earth. Because the acceleration vector turns along with the velocity vector, they remain perpendicular to each other. Without this change in the direction of its velocity vector, the spacecraft would move in a straight line, leaving the Earth altogether.

Weightlessness at the center of a planet

The net gravitational force due to a spherically symmetrical planet is zero at the center. This is clear because of symmetry, and also from Newton's shell theorem which states that the net gravitational force due to a spherically symmetric shell, e.g., a hollow ball, is zero anywhere inside the hollow space. Thus the material at the center is weightless.

Human health effects

Astronaut Clayton Anderson as a large drop of water floats in front of him on the Discovery. Cohesion plays a bigger role in space.

Following the advent of space stations that can be inhabited for long periods, exposure to weightlessness has been demonstrated to have some deleterious effects on human health. Humans are well-adapted to the physical conditions at the surface of the Earth. In response to an extended period of weightlessness, various physiological systems begin to change and atrophy. Though these changes are usually temporary, long term health issues can result.

The most common problem experienced by humans in the initial hours of weightlessness is known as space adaptation syndrome or SAS, commonly referred to as space sickness. Symptoms of SAS include nausea and vomiting, vertigo, headaches, lethargy, and overall malaise. The first case of SAS was reported by cosmonaut Gherman Titov in 1961. Since then, roughly 45% of all people who have flown in space have suffered from this condition. The duration of space sickness varies, but in no case has it lasted for more than 72 hours, after which the body adjusts to the new environment. NASA jokingly measures SAS using the "Garn scale", named for United States Senator Jake Garn, whose SAS during STS-51-D was the worst on record. Accordingly, one "Garn" is equivalent to the most severe possible case of SAS.

The most significant adverse effects of long-term weightlessness are muscle atrophy (see Reduced muscle mass, strength and performance in space for more information) and deterioration of the skeleton, or spaceflight osteopenia. These effects can be minimized through a regimen of exercise such as cycling for example. Astronauts subject to long periods of weightlessness wear pants with elastic bands attached between waistband and cuffs to compress the leg bones and reduce osteopenia. Other significant effects include fluid redistribution (causing the "moon-face" appearance typical of pictures of astronauts in weightlessness), a slowing of the cardiovascular systemas blood flow decreases in response to a lack of gravity, a decreased production of red blood cells, balance disorders, and a weakening of the immune system. Lesser symptoms include loss of body mass, nasal congestion, sleep disturbance, excess flatulence, and puffiness of the face. These effects begin to reverse quickly upon return to the Earth.

In addition, after long space flight missions, astronauts may experience severe eyesight problems. Such eyesight problems may be a major concern for future deep space flight missions, including a manned mission to the planet Mars. Exposure to high levels of radiation may influence the development of atherosclerosis also.

On December 31, 2012, a NASA-supported study reported that manned spaceflight may harm the brains of astronauts and accelerate the onset of Alzheimer's disease. In October 2015, the NASA Office of Inspector General issued a health hazards report related to human spaceflight, including a human mission to Mars.

Effects on non-human organisms

Russian scientists have observed differences between cockroaches conceived in space and their terrestrial counterparts. The space-conceived cockroaches grew more quickly, and also grew up to be faster and tougher.

Chicken eggs that are put in microgravity two days after fertilization appear not to develop properly, whereas eggs put in microgravity more than a week after fertilization develop normally.

A 2006 Space Shuttle experiment found that Salmonella typhimurium, a bacterium that can cause food poisoning, became more virulent when cultivated in space. On April 29, 2013, scientists in Rensselaer Polytechnic Institute, funded by NASA, reported that, during spaceflight on the International Space Station, microbes seem to adapt to the space environment in ways "not observed on Earth" and in ways that "can lead to increases in growth and virulence".

Under certain test conditions, microbes have been observed to thrive in the near-weightlessness of space and to survive in the vacuum of outer space.

Technical adaptation in zero-gravity

Candle flame in orbital conditions (right) versus on Earth (left)

Weightlessness can cause serious problems on technical instruments, especially those consisting of many mobile parts. Physical processes that depend on the weight of a body (like convection, cooking water or burning candles) act differently in free-fall. Cohesion and advection play a bigger role in space. Everyday work like washing or going to the bathroom are not possible without adaptation. To use toilets in space, like the one on the International Space Station, astronauts have to fasten themselves to the seat. A fan creates suction so that the waste is pushed away. Drinking is aided with a straw or from tubes.