B-spline

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/B-spline

Spline curve drawn as a weighted sum of B-splines with control points/control polygon, and marked component curves

In the mathematical subfield of numerical analysis, a B-spline or basis spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. Any spline function of given degree can be expressed as a linear combination of B-splines of that degree. Cardinal B-splines have knots that are equidistant from each other. B-splines can be used for curve-fitting and numerical differentiation of experimental data.

In computer-aided design and computer graphics, spline functions are constructed as linear combinations of B-splines with a set of control points.

Introduction

The term "B-spline" was coined by Isaac Jacob Schoenberg and is short for basis spline. A spline function of order ${\displaystyle n}$ is a piecewise polynomial function of degree ${\displaystyle n-1}$ in a variable ${\displaystyle x}$. The places where the pieces meet are known as knots. The key property of spline functions is that they and their derivatives may be continuous, depending on the multiplicities of the knots.

B-splines of order ${\displaystyle n}$ are basis functions for spline functions of the same order defined over the same knots, meaning that all possible spline functions can be built from a linear combination of B-splines, and there is only one unique combination for each spline function.

Definition

Cardinal quadratic B-spline with knot vector (0, 0, 0, 1, 2, 3, 3, 3) and control points (0, 0, 1, 0, 0), and its first derivative

Cardinal cubic B-spline with knot vector (−2, −2, −2, −2, −1, 0, 1, 2, 2, 2, 2) and control points (0, 0, 0, 6, 0, 0, 0), and its first derivative

Cardinal quartic B-spline with knot vector (0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5, 5) and control points (0, 0, 0, 0, 1, 0, 0, 0, 0), and its first and second derivatives

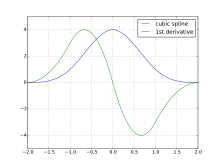
A spline of order ${\displaystyle n}$ is a piecewise polynomial function of degree ${\displaystyle n-1}$ in a variable ${\displaystyle x}$. The values of ${\displaystyle x}$ where the pieces of polynomial meet are known as knots, denoted ${\displaystyle t_0,t_1,t_2,\dots ,t_n}$ and sorted into nondecreasing order. When the knots are distinct, the first ${\displaystyle n-2}$ derivatives of the polynomial pieces are continuous across each knot. When ${\displaystyle r}$ knots are coincident, then only the first ${\displaystyle n-r-1}$ derivatives of the spline are continuous across that knot.

For a given sequence of knots, there is, up to a scaling factor, a unique spline ${\displaystyle B_{i,n}(x)}$ satisfying

${\displaystyle B_{i,n}(x)=\{\begin{array}{ll}0& \text{if }x<t_i\text{ or }x\ge t_{i+n},\\ \text{non-zero}& \text{otherwise}.\end{array}}$

If we add the additional constraint that ${\displaystyle \sum _i{B}_{i,n}(x)=1}$ for all ${\displaystyle x}$ between the first and last knot, then the scaling factor of ${\displaystyle B_{i,n}(x)}$ becomes fixed. The resulting ${\displaystyle B_{i,n}(x)}$ spline functions are called B-splines.

Alternatively, B-splines can be defined by construction by means of the Cox–de Boor recursion formula. Given a knot sequence ${\displaystyle \dots ,t_0,t_1,t_2,\dots }$, the B-splines of order 1 are defined by

${\displaystyle B_{i,1}(x):=\{\begin{array}{ll}1& \text{if }{t}_i\le x<t_{i+1},\\ 0& \text{otherwise}.\end{array}}$

These satisfy ${\displaystyle \sum _i{B}_{i,1}(x)=1}$ for all ${\displaystyle x}$ because for any ${\displaystyle x}$ exactly one of the ${\displaystyle B_{i,1}(x)=1}$, and all the others are zero.

The higher-order B-splines are defined by recursion

${\displaystyle B_{i,k+1}(x):={\omega }_{i,k}(x)B_{i,k}(x)+[1-{\omega }_{i+1,k}(x)]B_{i+1,k}(x),}$

where

${\displaystyle {\omega }_{i,k}(x):=\{\begin{array}{ll}{\displaystyle \frac{x-t_i}{t_{i+k}-t_i}},& t_{i+k}\ne t_i,\\ 0& \text{otherwise}.\end{array}}$

Properties

A B-spline function is a combination of flexible bands that is controlled by a number of points that are called control points, creating smooth curves. These functions are used to create and manage complex shapes and surfaces using a number of points. B-spline function and Bézier functions are applied extensively in shape optimization methods.

A B-spline of order ${\displaystyle n}$ is a piecewise polynomial function of degree ${\displaystyle n-1}$ in a variable ${\displaystyle x}$. It is defined over ${\displaystyle 1+n}$ locations ${\displaystyle t_j}$, called knots or breakpoints, which must be in non-descending order ${\displaystyle t_j\le t_{j+1}}$. The B-spline contributes only in the range between the first and last of these knots and is zero elsewhere. If each knot is separated by the same distance ${\displaystyle h}$ (where ${\displaystyle h=t_{j+1}-t_j}$) from its predecessor, the knot vector and the corresponding B-splines are called "uniform" (see cardinal B-spline below).

For each finite knot interval where it is non-zero, a B-spline is a polynomial of degree ${\displaystyle n-1}$. A B-spline is a continuous function at the knots. When all knots belonging to the B-spline are distinct, its derivatives are also continuous up to the derivative of degree ${\displaystyle n-2}$. If the knots are coincident at a given value of ${\displaystyle x}$, the continuity of derivative order is reduced by 1 for each additional coincident knot. B-splines may share a subset of their knots, but two B-splines defined over exactly the same knots are identical. In other words, a B-spline is uniquely defined by its knots.

One distinguishes internal knots and end points. Internal knots cover the ${\displaystyle x}$-domain one is interested in. Since a single B-spline already extends over ${\displaystyle 1+n}$ knots, it follows that the internal knots need to be extended with ${\displaystyle n-1}$ endpoints on each side, to give full support to the first and last B-spline, which affect the internal knot intervals. The values of the endpoints do not matter, usually the first or last internal knot is just repeated.

The usefulness of B-splines lies in the fact that any spline function of order ${\displaystyle n}$ on a given set of knots can be expressed as a linear combination of B-splines:

${\displaystyle S_{n,\mathbf{t}}(x)=\sum _i{\alpha }_i{B}_{i,n}(x).}$

B-splines play the role of basis functions for the spline function space, hence the name. This property follows from the fact that all pieces have the same continuity properties, within their individual range of support, at the knots.

Expressions for the polynomial pieces can be derived by means of the Cox–de Boor recursion formula

${\displaystyle B_{i,0}(x):=\{\begin{array}{ll}1& \text{if }{t}_i\le x<t_{i+1},\\ 0& \text{otherwise}.\end{array}}$

${\displaystyle B_{i,k}(x):=\frac{x-t_i}{t_{i+k}-t_i}{B}_{i,k-1}(x)+\frac{t_{i+k+1}-x}{t_{i+k+1}-t_{i+1}}{B}_{i+1,k-1}(x).}$

That is, ${\displaystyle B_{j,0}(x)}$ is piecewise constant one or zero indicating which knot span x is in (zero if knot span j is repeated). The recursion equation is in two parts:

${\displaystyle \frac{x-t_i}{t_{i+k}-t_i}}$

ramps from zero to one as x goes from ${\displaystyle t_i}$ to ${\displaystyle t_{i+k}}$, and

${\displaystyle \frac{t_{i+k+1}-x}{t_{i+k+1}-t_{i+1}}}$

ramps from one to zero as x goes from ${\displaystyle t_{i+1}}$ to ${\displaystyle t_{i+k+1}}$. The corresponding Bs are zero outside those respective ranges. For example, ${\displaystyle B_{i,1}(x)}$ is a triangular function that is zero below ${\displaystyle x=t_i}$, ramps to one at ${\displaystyle x=t_{i+1}}$ and back to zero at and beyond ${\displaystyle x=t_{i+2}}$. However, because B-spline basis functions have local support, B-splines are typically computed by algorithms that do not need to evaluate basis functions where they are zero, such as de Boor's algorithm.

This relation leads directly to the FORTRAN-coded algorithm BSPLV, which generates values of the B-splines of order n at x. The following scheme illustrates how each piece of order n is a linear combination of the pieces of B-splines of order n − 1 to its left.

${\displaystyle \begin{array}{ccc}& & 0\\ & 0& \\ 0& & B_{i-2,2}\\ & B_{i-1,1}& \\ B_{i,0}& & B_{i-1,2}\\ & B_{i,1}& \\ 0& & B_{i,2}\\ & 0& \\ & & 0\end{array}}$

Application of the recursion formula with the knots at ${\displaystyle (0,1,2,3)}$ gives the pieces of the uniform B-spline of order 3

${\displaystyle \begin{array}{rlrl}{B}_1& =x^2/2,& 0& \le x<1,\\ B_2& =(-2x^2+6x-3)/2,& 1& \le x<2,\\ B_3& =(3-x{)}^2/2,& 2& \le x<3.\end{array}}$

These pieces are shown in the diagram. The continuity property of a quadratic spline function and its first derivative at the internal knots are illustrated, as follows

${\displaystyle \begin{array}{rl}& \text{At }x=1:B_1=B_2=0.5,\frac{d{B}_1}{dx}=\frac{d{B}_2}{dx}=1.\\ & \text{At }x=2:B_2=B_3=0.5,\frac{d{B}_2}{dx}=\frac{d{B}_3}{dx}=-1.\end{array}}$

The second derivative of a B-spline of degree 2 is discontinuous at the knots:

${\displaystyle \frac{d^2{B}_1}{d{x}^2}=1,\frac{d^2{B}_2}{d{x}^2}=-2,\frac{d^2{B}_3}{d{x}^2}=-1.}$

Faster variants of the de Boor algorithm have been proposed, but they suffer from comparatively lower stability.

Cardinal B-spline

A cardinal B-spline has a constant separation h between knots. The cardinal B-splines for a given order n are just shifted copies of each other. They can be obtained from the simpler definition.

${\displaystyle B_{i,n,t}(x)=\frac{x-t_i}{h}n[0,\dots ,n](\cdot -t_i{)}_{+}^{n-1}.}$

The "placeholder" notation is used to indicate that the n-th divided difference of the function ${\displaystyle (t-x{)}_{+}^{n-1}}$ of the two variables t and x is to be taken by fixing x and considering ${\displaystyle (t-x{)}_{+}^{n-1}}$ as a function of t alone.

A cardinal B-spline has uniformly spaced knots, therefore interpolation between the knots equals convolution with a smoothing kernel.

Example, if we want to interpolate three values in between B-spline nodes (${\displaystyle \mathbf{\text{b}}}$), we can write the signal as

${\displaystyle \mathbf{x}=[{\mathbf{b}}_1,0,0,{\mathbf{b}}_2,0,0,{\mathbf{b}}_3,0,0,\dots ,{\mathbf{b}}_n,0,0].}$

Convolution of the signal ${\displaystyle \mathbf{x}}$ with a rectangle function ${\displaystyle \mathbf{h}=[1/3,1/3,1/3]}$ gives first order interpolated B-spline values. Second-order B-spline interpolation is convolution with a rectangle function twice ${\displaystyle \mathbf{y}=\mathbf{x}\ast \mathbf{h}\ast \mathbf{h}}$; by iterative filtering with a rectangle function, higher-order interpolation is obtained.

Fast B-spline interpolation on a uniform sample domain can be done by iterative mean-filtering. Alternatively, a rectangle function equals sinc in Fourier domain. Therefore, cubic spline interpolation equals multiplying the signal in Fourier domain with sinc⁴.

See Irwin–Hall distribution#Special cases for algebraic expressions for the cardinal B-splines of degree 1–4.

P-spline

The term P-spline stands for "penalized B-spline". It refers to using the B-spline representation where the coefficients are determined partly by the data to be fitted, and partly by an additional penalty function that aims to impose smoothness to avoid overfitting.

Two- and multidimensional P-spline approximations of data can use the face-splitting product of matrices to the minimization of calculation operations.

Derivative expressions

The derivative of a B-spline of degree k is simply a function of B-splines of degree k − 1:

${\displaystyle \frac{d{B}_{i,k}(x)}{dx}=k\left(\frac{B_{i,k-1}(x)}{t_{i+k}-t_i}-\frac{B_{i+1,k-1}(x)}{t_{i+k+1}-t_{i+1}}\right).}$

This implies that

${\displaystyle \frac{d}{dx}\sum _i{\alpha }_i{B}_{i,k}=\sum _{i=r-k+2}^{s-1}k\frac{{\alpha }_i-{\alpha }_{i-1}}{t_{i+k}-t_i}{B}_{i,k-1}\text{on}[t_r,t_s],}$

which shows that there is a simple relationship between the derivative of a spline function and the B-splines of degree one less.

Moments of univariate B-splines

Univariate B-splines, i.e. B-splines where the knot positions lie in a single dimension, can be used to represent 1-d probability density functions ${\displaystyle p(x)}$. An example is a weighted sum of ${\displaystyle i}$ B-spline basis functions of order ${\displaystyle n}$, which each are area-normalized to unity (i.e. not directly evaluated using the standard de-Boor algorithm)

${\displaystyle p(x)=\sum _i{c}_i\cdot B_{i,n,\mathbf{\text{norm}}}(x)}$

and with normalization constant constraint ${\displaystyle \sum _i{c}_i=1}$. The k-th raw moment ${\displaystyle {\mu }_k}$ of a normalized B-spline ${\displaystyle B_{i,n,\mathbf{\text{norm}}}}$ can be written as Carlson's Dirichlet average ${\displaystyle R_k}$, which in turn can be solved exactly via a contour integral and an iterative sum as

${\displaystyle {\mu }_k=R_k(\mathbf{m};\mathbf{t})={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{x}^k\cdot B_{i,n,\mathbf{\text{norm}}}(x\mid t_1\dots t_j)dx=\frac{\mathrm{\Gamma }(k+1)\mathrm{\Gamma }(m)}{\mathrm{\Gamma }(m+k)}\cdot D_k(\mathbf{m},\mathbf{t})}$

with

${\displaystyle D_k=\frac{1}{k}\sum _{u=1}^k\left[\left(\sum _{i=1}^j{m}_i\cdot {t_i}^u\right)D_{k-u}\right]}$

and ${\displaystyle D_0=1}$. Here, ${\displaystyle \mathbf{t}}$ represents a vector with the ${\displaystyle j}$ knot positions and ${\displaystyle \mathbf{m}}$ a vector with the respective knot multiplicities. One can therefore calculate any moment of a probability density function ${\displaystyle p(x)}$ represented by a sum of B-spline basis functions exactly, without resorting to numerical techniques.

Relationship to piecewise/composite Bézier

A Bézier curve is also a polynomial curve definable using a recursion from lower-degree curves of the same class and encoded in terms of control points, but a key difference is that all terms in the recursion for a Bézier curve segment have the same domain of definition (usually ${\displaystyle [0,1]}$), whereas the supports of the two terms in the B-spline recursion are different (the outermost subintervals are not common). This means that a Bézier curve of degree ${\displaystyle n}$ given by ${\displaystyle m\gg n}$ control points consists of about ${\displaystyle m/n}$ mostly independent segments, whereas the B-spline with the same parameters smoothly transitions from subinterval to subinterval. To get something comparable from a Bézier curve, one would need to impose a smoothness condition on transitions between segments, resulting in some manner of Bézier spline (for which many control points would be determined by the smoothness requirement).

A piecewise/composite Bézier curve is a series of Bézier curves joined with at least C0 continuity (the last point of one curve coincides with the starting point of the next curve). Depending on the application, additional smoothness requirements (such as C1 or C2 continuity) may be added. C1 continuous curves have identical tangents at the breakpoint (where the two curves meet). C2 continuous curves have identical curvature at the breakpoint.

Curve fitting

Usually in curve fitting, a set of data points is fitted with a curve defined by some mathematical function. For example, common types of curve fitting use a polynomial or a set of exponential functions. When there is no theoretical basis for choosing a fitting function, the curve may be fitted with a spline function composed of a sum of B-splines, using the method of least squares. Thus, the objective function for least-squares minimization is, for a spline function of degree k,

${\displaystyle U=\sum _{\text{all}x}{\left\{W(x)\left[y(x)-\sum _i{\alpha }_i{B}_{i,k,t}(x)\right]\right\}}^2,}$

where W(x) is a weight, and y(x) is the datum value at x. The coefficients ${\displaystyle {\alpha }_i}$ are the parameters to be determined. The knot values may be fixed or treated as parameters.

The main difficulty in applying this process is in determining the number of knots to use and where they should be placed. de Boor suggests various strategies to address this problem. For instance, the spacing between knots is decreased in proportion to the curvature (2nd derivative) of the data. A few applications have been published. For instance, the use of B-splines for fitting single Lorentzian and Gaussian curves has been investigated. Optimal spline functions of degrees 3–7 inclusive, based on symmetric arrangements of 5, 6, and 7 knots, have been computed and the method was applied for smoothing and differentiation of spectroscopic curves. In a comparable study, the two-dimensional version of the Savitzky–Golay filtering and the spline method produced better results than moving average or Chebyshev filtering.

Computer-aided design and computer graphics

In computer-aided design and computer graphics applications, a spline curve is sometimes represented as ${\displaystyle C(t)}$, a parametric curve of some real parameter ${\displaystyle t}$. In this case the curve ${\displaystyle C(t)}$ can be treated as two or three separate coordinate functions ${\displaystyle (x(t),y(t))}$, or ${\displaystyle (x(t),y(t),z(t))}$. The coordinate functions ${\displaystyle x(t)}$, ${\displaystyle y(t)}$ and ${\displaystyle z(t)}$ are each spline functions, with a common set of knot values ${\displaystyle t_1,t_2,\dots ,t_n}$.

Because a B-splines form basis functions, each of the coordinate functions can be expressed as a linear sum of B-splines, so we have

${\displaystyle \begin{array}{rl}X(t)& =\sum _i{x}_i{B}_{i,n}(t),\\ Y(t)& =\sum _i{y}_i{B}_{i,n}(t),\\ Z(t)& =\sum _i{z}_i{B}_{i,n}(t).\end{array}}$

The weights ${\displaystyle x_i}$, ${\displaystyle y_i}$ and ${\displaystyle z_i}$ can be combined to form points ${\displaystyle P_i=(x_i,y_i,z_i)}$ in 3-d space. These points ${\displaystyle P_i}$ are commonly known as control points.

Working in reverse, a sequence of control points, knot values, and order of the B-spline define a parametric curve. This representation of a curve by control points has several useful properties:

1. The control points ${\displaystyle P_i}$ define a curve. If the control points are all transformed together in some way, such as being translated, rotated, scaled, or moved by any affine transformation, then the corresponding curve is transformed in the same way.
2. Because the B-splines are non-zero for just a finite number of knot intervals, if a single control point is moved, the corresponding change to the parametric curve is just over the parameter range of a small number knot intervals.
3. Because ${\displaystyle \sum _i{B}_{i,n}(x)=1}$, and at all times each ${\displaystyle B_{i,n}(x)\ge 0}$, then the curve remains inside the bounding box of the control points. Also, in some sense, the curve broadly follows the control points.

A less desirable feature is that the parametric curve does not interpolate the control points. Usually the curve does not pass through the control points.

NURBS

Main article: Non-uniform rational B-spline

NURBS curve – polynomial curve defined in homogeneous coordinates (blue) and its projection on plane – rational curve (red)

In computer aided design, computer aided manufacturing, and computer graphics, a powerful extension of B-splines is non-uniform rational B-splines (NURBS). NURBS are essentially B-splines in homogeneous coordinates. Like B-splines, they are defined by their order, and a knot vector, and a set of control points, but unlike simple B-splines, the control points each have a weight. When the weight is equal to 1, a NURBS is simply a B-spline and as such NURBS generalizes both B-splines and Bézier curves and surfaces, the primary difference being the weighting of the control points which makes NURBS curves "rational".

By evaluating a NURBS at various values of the parameters, the curve can be traced through space; likewise, by evaluating a NURBS surface at various values of the two parameters, the surface can be represented in Cartesian space.

Like B-splines, NURBS control points determine the shape of the curve. Each point of the curve is computed by taking a weighted sum of a number of control points. The weight of each point varies according to the governing parameter. For a curve of degree d, the influence of any control point is only nonzero in d+1 intervals (knot spans) of the parameter space. Within those intervals, the weight changes according to a polynomial function (basis functions) of degree d. At the boundaries of the intervals, the basis functions go smoothly to zero, the smoothness being determined by the degree of the polynomial.

The knot vector is a sequence of parameter values that determines where and how the control points affect the NURBS curve. The number of knots is always equal to the number of control points plus curve degree plus one. Each time the parameter value enters a new knot span, a new control point becomes active, while an old control point is discarded.

A NURBS curve takes the following form:

${\displaystyle C(u)=\frac{\sum _{i=1}^k{N}_{i,n}(u)w_i{P}_i}{\sum _{i=1}^k{N}_{i,n}(u)w_i}}$

Here the notation is as follows. u is the independent variable (instead of x), k is the number of control points, N is a B-spline (used instead of B), n is the polynomial degree, P is a control point and w is a weight. The denominator is a normalizing factor that evaluates to one if all weights are one.

It is customary to write this as

${\displaystyle C(u)=\sum _{i=1}^k{R}_{i,n}(u)P_i}$

in which the functions

${\displaystyle R_{i,n}(u)=\frac{N_{i,n}(u)w_i}{\sum _{j=1}^k{N}_{j,n}(u)w_j}}$

are known as the rational basis functions.

A NURBS surface is obtained as the tensor product of two NURBS curves, thus using two independent parameters u and v (with indices i and j respectively):

${\displaystyle S(u,v)=\sum _{i=1}^k\sum _{j=1}^{\ell }{R}_{i,j}(u,v)P_{i,j}}$

with

${\displaystyle R_{i,j}(u,v)=\frac{N_{i,n}(u)N_{j,m}(v)w_{i,j}}{\sum _{p=1}^k\sum _{q=1}^{\ell }{N}_{p,n}(u)N_{q,m}(v)w_{p,q}}}$

as rational basis functions.

ExoMars

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/ExoMars

ExoMars
ЭкзоМарс

Artist's illustration of ExoMars's Trace Gas Orbiter (left), Schiaparelli lander (middle), and rover (right)
Mission type	Mars reconnaissance
Operator	ESA · SRI RAS (IKI RAN) (formerly)
Website	www.esa.int/exomars (ESA)
Mission duration	Trace Gas Orbiter: 7 years, 4 months and 24 days (in progress) Schiaparelli: 7 months
ExoMars ESA mission insignia

ExoMars (Exobiology on Mars) is an astrobiology programme of the European Space Agency (ESA).

The goals of ExoMars are to search for signs of past life on Mars, investigate how the Martian water and geochemical environment varies, investigate atmospheric trace gases and their sources and, by doing so, demonstrate the technologies for a future Mars sample-return mission.

The first part of the programme is a mission launched in 2016 that placed the Trace Gas Orbiter into Mars orbit and released the Schiaparelli EDM lander. The orbiter is operational but the lander crashed on the planet's surface. The second part of the programme was planned to launch in July 2020, when the Kazachok lander would have delivered the Rosalind Franklin rover on the surface, supporting a science mission that was expected to last into 2022 or beyond. On 12 March 2020, it was announced that the second mission was being delayed to 2022 as a result of problems with the parachutes, which could not be resolved in time for the launch window.

The Trace Gas Orbiter (TGO) and a test stationary lander called Schiaparelli were launched on 14 March 2016. TGO entered Mars orbit on 19 October 2016 and proceeded to map the sources of methane (CH₄) and other trace gases present in the Martian atmosphere that could be evidence for possible biological or geological activity. The TGO features four instruments and will also act as a communications relay satellite. The Schiaparelli experimental lander separated from TGO on 16 October and was maneuvered to land in Meridiani Planum, but it crashed on the surface of Mars. The landing was designed to test new key technologies to safely deliver the subsequent rover mission.

In June 2023, a Roscosmos lander named Kazachok ("little Cossack", referring to a folk dance), was due to deliver the ESA Rosalind Franklin rover to the Martian surface. The rover would also include some Roscosmos built instruments. The second mission operations and communications would have been led by ALTEC's Rover Control Centre in Italy.

On 17 March 2022, ESA suspended the mission due to the ongoing invasion of Ukraine by Russia. ESA expects that a restart of the mission, using a new non-Russian landing platform, is unlikely to launch before 2028.

History

Since its inception, ExoMars has gone through several phases of planning with various proposals for landers, orbiters, launch vehicles, and international cooperation planning, such as the defunct 2009 Mars Exploration Joint Initiative (MEJI) with the United States. Originally, the ExoMars concept consisted of a large robotic rover being part of ESA's Aurora Programme as a Flagship mission and was approved by the European Space Agency ministers in December 2005. Originally conceived as a rover with a stationary ground station, ExoMars was planned to launch in 2011 aboard a Russian Soyuz Fregat rocket.

ExoMars begun in 2001 as part of the ESA Aurora program for the human exploration of Mars. That initial vision called for rover in 2009 and later a Mars sample-return mission. Another mission intended to support the Aurora program is a Phobos sample return mission. In December 2005, the different nations composing the ESA gave approval to the Aurora program and to ExoMars. Aurora is an optional program and each state is allowed to decide which part of the program they want to be involved in and to what extent (e.g. how much funds they want to put into the program). The Aurora program was initiated in 2002 with support of twelve nations: Austria, Belgium, France, Germany, Italy, the Netherlands, Portugal, Spain, Sweden, Switzerland, the United Kingdom and Canada

In 2007, Canadian-based technology firm MacDonald Dettwiler and Associates Ltd. (MDA) was selected for a one-million-euro contract with EADS Astrium of Britain to design and build a prototype Mars rover chassis for the European Space Agency. Astrium was also contracted to design the final rover.

Concept of MAX-C rover

ExoMars rover at exhibit in Gasometer Oberhausen, Germany (2009)

ExoMars rover at MAKS-2021

Austrian 25 Euro, released in 2011

In July 2009 NASA and ESA signed the Mars Exploration Joint Initiative, which proposed to utilise an Atlas rocket launcher instead of a Soyuz, which significantly altered the technical and financial setting of the ExoMars mission. On 19 June, when the rover was still planned to piggyback the Mars Trace Gas Orbiter, it was reported that a prospective agreement would require that ExoMars lose enough weight to fit aboard the Atlas launch vehicle with a NASA orbiter.

Then the mission was combined with other projects to a multi-spacecraft mission divided over two Atlas V-launches: the ExoMars Trace Gas Orbiter (TGO) was merged into the project, piggybacking a stationary meteorological lander slated for launch in January 2016. It was also proposed to include a second rover, the MAX-C.

In August 2009 it was announced that the Russian Federal Space Agency (now Roscosmos) and ESA had signed a contract that included cooperation on two Mars exploration projects: Russia's Fobos-Grunt project and ESA's ExoMars. Specifically, ESA secured a Russian Proton rocket as a "backup launcher" for the ExoMars rover, which would include Russian-made parts.

On 17 December 2009, the ESA governments gave their final approval to a two-part Mars exploration mission to be conducted with NASA, confirming their commitment to spend €850 million ($1.23 billion) on missions in 2016 and 2018.

In April 2011, because of a budgeting crisis, a proposal was announced to cancel the accompanying MAX-C rover, and fly only one rover in 2018 that would be larger than either of the vehicles in the paired concept. One suggestion was that the new vehicle would be built in Europe and carry a mix of European and U.S. instruments. NASA would provide the rocket to deliver it to Mars and provide the sky crane landing system. Despite the proposed reorganisation, the goals of the 2018 mission opportunity would have stayed broadly the same.

Under the FY2013 Budget President Obama released on 13 February 2012, NASA terminated its participation in ExoMars due to budgetary cuts in order to pay for the cost overruns of the James Webb Space Telescope. With NASA's funding for this project completely cancelled, most of these plans had to be restructured.

On 14 March 2013, representatives of the ESA and the Russian space agency (Roscosmos), signed a deal in which Russia became a full partner. Roscosmos will supply both missions with Proton launch vehicles with Briz-M upper stages and launch services, as well as an additional entry, descent and landing module for the rover mission in 2018. Under the agreement, Roscosmos was granted three asking conditions:

1. Roscosmos will contribute two Proton launch vehicles as payment for the partnership.
2. The Trace Gas Orbiter payload shall include two Russian instruments that were originally developed for Fobos-Grunt.
3. All scientific results must be intellectual property of the European Space Agency and the Russian Academy of Sciences (i.e. Roscosmos will be part of all the project teams and will have full access to research data).

ESA had originally cost-capped the ExoMars projects at €1 billion, (USD 1.3 billion) but the withdrawal of the U.S. space agency (NASA) and the consequent reorganisation of the ventures will probably add several hundred million euros to the sum so far raised. So in March 2012, member states instructed the agency's executive to look at how this shortfall could be made up. One possibility is that other science activities within ESA may have to step back to make ExoMars a priority. In September 2012 it was announced that new ESA members, Poland and Romania, will be contributing up to €70 million to the ExoMars mission. ESA has not ruled out a possible partial return of NASA to the 2018 portion of ExoMars, albeit in a relatively minor role.

Russia's financing of ExoMars could be partially covered by insurance payments of 1.2 billion roubles (US$40.7 million) for the loss of Fobos-Grunt, and reassigning funds for a possible coordination between the Mars-NET and ExoMars projects. On 25 January 2013, Roscosmos fully funded the development of the scientific instruments to be flown on the first launch, the Trace Gas Orbiter (TGO).

As of March 2014, the lead builder of the ExoMars rover, the British division of Airbus Defence and Space, had started procuring critical components, but the 2018 rover mission was still short by more than 100 million euros, or $138 million. The wheels and suspension system are paid by the Canadian Space Agency and are being manufactured by MDA Corporation in Canada.

2016 first spacecraft launch

The spacecraft containing ExoMars Trace Gas Orbiter (TGO) and Schiaparelli launched on 14 March 2016 09:31 UTC (Livestream began at 08:30 GMT [03:30 AM EDT]). Four rocket burns occurred in the following 10 hours before the descent module and orbiter were released. Signals from the Orbiter were successfully received at 21:29 GMT of the same day, which confirmed that the launch was fully successful and that the spacecraft was on its way to Mars. Shortly after separation from the probes, the Briz-M upper booster stage possibly exploded a few kilometers away, however apparently without damaging the orbiter or lander. The spacecraft, which housed the Trace Gas Orbiter and the Schiaparelli lander, took its nominal orbit towards Mars and was seemingly in working order. Over the next two weeks, controllers continued to check and commission its systems, including the power, communications, startrackers, and guidance and navigation system.

Delays and suspension

A prototype of the ExoMars Rover at the 2015 Cambridge Science Festival

In January 2016 it was announced that the financial situation of the 2018 mission 'might' require a 2-year delay. Italy is the largest contributor to ExoMars, and the UK is the mission's second-largest financial backer.

The rover was scheduled to launch in 2018 and land on Mars in early 2019, but in May 2016 ESA announced that the launch would occur in 2020 due to delays in European and Russian industrial activities and deliveries of the scientific payload.

On 12 March 2020, it was announced that the second mission was being delayed to launch in 2022 due to the vehicle not being ready for launch in 2020, with delays exacerbated by travel restrictions during the COVID-19 pandemic.

On 28 February 2022, it was announced that the second mission launching in 2022 "was very unlikely" due to the sanctions on Russia in response to the invasion of Ukraine by Russia.

On 17 March 2022, the launch of ExoMars in the 2022 launch window was abandoned, with the permanent suspension of the partnership with Roscosmos. However, in November, the European Space Agency member states pledged 360 million euros towards the Rosalind Franklin rover, including covering the cost of replacing Russian components. Now planned to launch in 2028, the rover will carry a next-generation mass spectrometer, the Mars Organic Molecule Analyzer, or MOMA.

Mission objectives

The scientific objectives, in order of priority, are:

• to search for possible biosignatures of past Martian life.
• to characterise the water and geochemical distribution as a function of depth in the shallow subsurface.
• to study the surface environment and identify hazards to future human missions to Mars.
• to investigate the planet's subsurface and deep interior to better understand the evolution and habitability of Mars.
• achieve incremental steps ultimately culminating in a sample return flight.

The technological objectives to develop are:

• landing of large payloads on Mars.
• to exploit solar electric power on the surface of Mars.
• to access the subsurface with a drill able to collect samples down to a depth of 2 metres (6.6 ft)
• to develop surface exploration capability using a rover.

Mission profile

ExoMars is a joint programme of the European Space Agency (ESA) and the Russian space agency Roscosmos. According to current plans, the ExoMars project will comprise four spacecraft: two stationary landers, one orbiter and one rover. All mission elements will be sent in two launches using two heavy-lift Proton rockets.

Contributing agency	First launch in 2016	Second launch in 2022
Roscosmos	Launch by Proton rocket	Launch by Proton rocket
	Two instrument packages for the TGO	Kazachok lander, which will deliver the rover to the surface, and provide various scientific instruments for the rover.
ESA	ExoMars Trace Gas Orbiter	ExoMars's Rosalind Franklin rover, and various instruments on the Kazachok lander.
	Schiaparelli EDM lander

The two landing modules and the rover will be cleaned and sterilised to prevent contaminating Mars with Earth life forms, and also to ensure that any biomolecules detected were not carried from Earth. Cleaning will require a combination of sterilising methods, including ionising radiation, UV radiation, and chemicals such as ethyl and isopropyl alcohol.

First launch (2016)

Trace Gas Orbiter

Main article: ExoMars Trace Gas Orbiter

The Trace Gas Orbiter (TGO) is a Mars telecommunications orbiter and atmospheric gas analyzer mission that was launched on 14 March 2016 09:31 UTC. The spacecraft arrived in the Martian orbit in October 2016. It delivered the ExoMars Schiaparelli EDM lander and then proceed to map the sources of methane on Mars and other gases, and in doing so, will help select the landing site for the ExoMars rover to be launched in 2022. The presence of methane in Mars's atmosphere is intriguing because its likely origin is either present-day life or geological activity. Upon the arrival of the rover in 2023, the orbiter would be transferred into a lower orbit where it would be able to perform analytical science activities as well as provide the ExoMars rover with a telecommunication relay. NASA provided an Electra telecommunications relay and navigation instrument to ensure communications between probes and rovers on the surface of Mars and controllers on Earth. The TGO would continue serving as a telecommunication relay satellite for future landed missions until 2022.

Schiaparelli EDM lander

Main article: Schiaparelli EDM lander

Model of the ExoMars Schiaparelli EDL Demonstrator Module (EDM). During its descent it returned 600 MB of data, but it did not achieve a soft landing.

The Entry, Descent and Landing Demonstrator Module (EDM) called Schiaparelli, was intended to provide the European Space Agency (ESA) and Russia's Roscosmos with the technology for landing on the surface of Mars. It was launched together with the ExoMars Trace Gas Orbiter (TGO) on 14 March 2016, 09:31 UTC and was scheduled to land softly on 19 October 2016. No signal indicating a successful landing was received, and on 21 October 2016 NASA released a Mars Reconnaissance Orbiter image showing what appears to be the lander crash site. The lander was equipped with a non-rechargeable electric battery with enough power for four sols. The soft landing should have taken place on Meridiani Planum during the dust storm season, which would have provided a unique chance to characterise a dust-loaded atmosphere during entry and descent, and to conduct surface measurements associated with a dust-rich environment.

Once on the surface, it was to measure the wind speed and direction, humidity, pressure and surface temperature, and determine the transparency of the atmosphere. It carried a surface payload, based on the proposed meteorological DREAMS (Dust Characterisation, Risk Assessment, and Environment Analyser on the Martian Surface) package, consists of a suite of sensors to measure the wind speed and direction (MetWind), humidity (MetHumi), pressure (MetBaro), surface temperature (MarsTem), the transparency of the atmosphere (Optical Depth Sensor; ODS), and atmospheric electrification (Atmospheric Radiation and Electricity Sensor; MicroARES). The DREAMS payload was to function for 2 or 3 days as an environmental station for the duration of the EDM surface mission after landing.

Second launch (2028)

The ExoMars 2022 mission was planned for launch during a twelve-day launch window starting on 20 September 2022, and scheduled to land on Mars on 10 June 2023. It would have included a German-built cruise stage and Russian descent module. On 28 February 2022, the ESA announced that, as a result of sanctions related to the 2021–2022 Russo-Ukrainian crisis, a 2022 launch is "very unlikely." On 28 March 2022, the ExoMars rover was confirmed to be technically ready for launch, but the 2022 launch window for the mission is no longer possible due to the Russian invasion of Ukraine. The launch of a revised version of the mission, using a new non-Russian landing platform, is expected to occur no earlier than 2028.

Cruise stage

The Kazachok lander and Rosalind Franklin rover will be sent Mars inside the descent module. The descent module will be attached to the carrier module, which will provide power, propulsion, and navigation. The carrier module has 16 hydrazine powered thrusters, 6 solar arrays that will provide electricity, and sun sensors and star trackers for navigation. It was developed and built by OHB System in Bremen, Germany. The carrier module will separate from the descent module right before the rest of the spacecraft arrives at Mars.

Kazachok lander and descent stage

Main article: Kazachok

Kazachok is an 1800 lbs (827.9 kg) Russian-built lander that is derived from the 2016 Schiaparelli EDM lander. It will place the Rosalind Franklin rover on the surface of Mars. Kazachok lander will be built 80% by the Russian company Lavochkin, and 20% by ESA. Lavochkin will produce most of the landing system's hardware, while ESA will handle elements such as the guidance, radar and navigation systems. Lavochkin's current landing strategy is to use two parachutes; one will open while the module is still moving at supersonic speed, and another will deploy once the probe has been slowed down to subsonic velocity. The heat shield will eventually fall away from the entry capsule to allow the ExoMars rover, riding its retro-rocket-equipped lander, to come for a soft landing on legs or struts. The lander will then deploy ramps for the rover to drive down.

Critics have stated that while Russian expertise may be sufficient to provide a launch vehicle, it does not currently extend to the critical requirement of a landing system for Mars.

After landing on Mars in June 2023, the rover was intended to descend from the Kazachok lander via a ramp. The lander was expected to image the landing site, monitor the climate, investigate the atmosphere, analyse the radiation environment, study the distribution of any subsurface water at the landing site, and perform geophysical investigations of the internal structure of Mars. Following a March 2015 request for the contribution of scientific instruments for the landing system, there will be 13 instruments. Examples of the instruments on the lander include the HABIT (HabitAbility: Brine, Irradiation and Temperature) package, the METEO meteorological package, the MAIGRET magnetometer, and the LaRa (Lander Radioscience) experiment.

The stationary lander was expected to operate for at least one Earth year, and its instruments would have been powered by solar arrays.

Rosalind Franklin rover

Main article: Rosalind Franklin (rover)

 

An early ExoMars rover design model at the ILA 2006 in Berlin

 

Another early design model of the rover at the Paris Air Show 2007

ExoMars's Rosalind Franklin rover was due to land in June 2023 and to navigate autonomously across the Martian surface. However, the partnership with Russian scientists was cancelled in 2022 as a response to the Russian invasion of Ukraine that began that year. Rosalind Franklin is now projected to launch in 2028.

Instrumentation would consist of the exobiology laboratory suite, known as "Pasteur analytical laboratory" to look for signs of biomolecules and biosignatures from past life. Among other instruments, the rover will also carry a 2-metre (6.6 ft) sub-surface core drill to pull up samples for its on-board laboratory. They will have a mass of about 207 kg (456 lb).

The Rosalind Franklin rover includes the Pasteur instrument suite, including the Mars Organic Molecule Analyzer (MOMA), MicrOmega-IR, and the Raman Laser Spectrometer (RLS). Examples of external instruments on the rover include:

• Mars Multispectral Imager for Subsurface Studies
• Infrared Spectrometer for ExoMars
• ADRON-RM

Landing site selection

Oxia Planum, near the equator, is the selected landing site for its potential to preserve biosignatures and smooth surface

A primary goal when selecting the rover's landing site is to identify a particular geologic environment, or set of environments, that would support —now or in the past— microbial life. The scientists prefer a landing site with both morphologic and mineralogical evidence for past water. Furthermore, a site with spectra indicating multiple hydrated minerals such as clay minerals is preferred, but it will come down to a balance between engineering constraints and scientific goals.

Engineering constraints call for a flat landing site in a latitude band straddling the equator that is only 30° latitude from top to bottom because the rover is solar-powered and will need best sunlight exposure. The landing module carrying the rover will have a landing ellipse that measures about 105 km by 15 km. Scientific requirements include landing in an area with 3.6 billion years old sedimentary rocks that are a record of the past wet habitable environment. The year before launch, the European Space Agency will make the final decision. By March 2014, the long list was:

• Aram Dorsum
• Coogoon Valles
• Hypanis Vallis
• Mawrth Vallis
• Oxia Planum
• Simud Valles
• Southern Isidis

Following additional review by an ESA-appointed panel, four sites, all of which are located relatively near the equator, were formally recommended in October 2014 for further detailed analysis:

• Aram Dorsum
• Hypanis Vallis
• Mawrth Vallis
• Oxia Planum

On 21 October 2015, Oxia Planum was reported to be the preferred landing site for the ExoMars rover.

The delay of the rover mission to 2020 from 2018 meant that Oxia Planum was no longer the only favourable landing site due to changes in the possible landing ellipse. Both Mawrth Vallis and Aram Dorsum, surviving candidates from the previous selection, could be reconsidered. ESA convened further workshops to re-evaluate the three remaining options and in March 2017 selected two sites to study in detail.

• Mawrth Vallis
• Oxia Planum

On 9 November 2018, ESA announced that Oxia Planum was favoured by the Landing Site Selection Working Group. The favored Oxia Planum landing ellipse is situated at 18.20°N, 335.45°E. In 2019, Oxia Planum was confirmed by ESA as the landing site for the planned 2020 mission. Later that year, a flyover video of the landing site was released, created using high-accuracy 3D models of the terrain obtained from HiRISE.

As of July 2020, it has not been stated by ESA if the choice of landing site will be affected by the delay of the mission beyond 2022, similar to the re-evaluation prompted by the first delay in 2018.