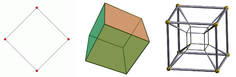
Vector addition and scalar multiplication: a vector v (blue) is added to another vector w (red, upper illustration). Below, w is stretched by a factor of 2, yielding the sum v + 2w.
A vector space (also called a linear space) is a collection of objects called vectors, which may be added together and multiplied ("scaled") by numbers, called scalars. Scalars are often taken to be real numbers, but there are also vector spaces with scalar multiplication by complex numbers, rational numbers, or generally any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called axioms, listed below.
Euclidean vectors are an example of a vector space. They represent physical quantities such as forces: any two forces (of the same type) can be added to yield a third, and the multiplication of a force vector by a real multiplier is another force vector. In the same vein, but in a more geometric sense, vectors representing displacements in the plane or in three-dimensional space also form vector spaces. Vectors in vector spaces do not necessarily have to be arrow-like objects as they appear in the mentioned examples: vectors are regarded as abstract mathematical objects with particular properties, which in some cases can be visualized as arrows.
Vector spaces are the subject of linear algebra and are well characterized by their dimension, which, roughly speaking, specifies the number of independent directions in the space. Infinite-dimensional vector spaces arise naturally in mathematical analysis, as function spaces, whose vectors are functions. These vector spaces are generally endowed with additional structure, which may be a topology, allowing the consideration of issues of proximity and continuity. Among these topologies, those that are defined by a norm or inner product are more commonly used, as having a notion of distance between two vectors. This is particularly the case of Banach spaces and Hilbert spaces, which are fundamental in mathematical analysis.
Historically, the first ideas leading to vector spaces can be traced back as far as the 17th century's analytic geometry, matrices, systems of linear equations, and Euclidean vectors. The modern, more abstract treatment, first formulated by Giuseppe Peano in 1888, encompasses more general objects than Euclidean space, but much of the theory can be seen as an extension of classical geometric ideas like lines, planes and their higher-dimensional analogs.
Today, vector spaces are applied throughout mathematics, science and engineering. They are the appropriate linear-algebraic notion to deal with systems of linear equations. They offer a framework for Fourier expansion, which is employed in image compression routines, and they provide an environment that can be used for solution techniques for partial differential equations. Furthermore, vector spaces furnish an abstract, coordinate-free way of dealing with geometrical and physical objects such as tensors. This in turn allows the examination of local properties of manifolds by linearization techniques. Vector spaces may be generalized in several ways, leading to more advanced notions in geometry and abstract algebra.
Introduction and definition
The concept of vector space will first be explained by describing two particular examples:First example: arrows in the plane
The first example of a vector space consists of arrows in a fixed plane, starting at one fixed point. This is used in physics to describe forces or velocities. Given any two such arrows, v and w, the parallelogram spanned by these two arrows contains one diagonal arrow that starts at the origin, too. This new arrow is called the sum of the two arrows and is denoted v + w. In the special case of two arrows on the same line, their sum is the arrow on this line whose length is the sum or the difference of the lengths, depending on whether the arrows have the same direction. Another operation that can be done with arrows is scaling: given any positive real number a, the arrow that has the same direction as v, but is dilated or shrunk by multiplying its length by a, is called multiplication of v by a. It is denoted av. When a is negative, av is defined as the arrow pointing in the opposite direction, instead.The following shows a few examples: if a = 2, the resulting vector aw has the same direction as w, but is stretched to the double length of w (right image below). Equivalently, 2w is the sum w + w. Moreover, (−1)v = −v has the opposite direction and the same length as v (blue vector pointing down in the right image).
 |
 |
Second example: ordered pairs of numbers
A second key example of a vector space is provided by pairs of real numbers x and y. (The order of the components x and y is significant, so such a pair is also called an ordered pair.) Such a pair is written as (x, y). The sum of two such pairs and multiplication of a pair with a number is defined as follows:- (x1, y1) + (x2, y2) = (x1 + x2, y1 + y2)
- a (x, y) = (ax, ay).
Definition
In this article, vectors are represented in boldface to distinguish them from scalars.[nb 1]A vector space over a field F is a set V together with two operations that satisfy the eight axioms listed below.
- The first operation, called vector addition or simply addition + : V × V → V, takes any two vectors v and w and assigns to them a third vector which is commonly written as v + w, and called the sum of these two vectors. (Note that the resultant vector is also an element of the set V ).
- The second operation, called scalar multiplication · : F × V → V, takes any scalar a and any vector v and gives another vector av. (Similarly, the vector av is an element of the set V ).
In the two examples above, the field is the field of the real numbers and the set of the vectors consists of the planar arrows with fixed starting point and of pairs of real numbers, respectively.
To qualify as a vector space, the set V and the operations of addition and multiplication must adhere to a number of requirements called axioms.[1] In the list below, let u, v and w be arbitrary vectors in V, and a and b scalars in F.
| Axiom | Meaning |
|---|---|
| Associativity of addition | u + (v + w) = (u + v) + w |
| Commutativity of addition | u + v = v + u |
| Identity element of addition | There exists an element 0 ∈ V, called the zero vector, such that v + 0 = v for all v ∈ V. |
| Inverse elements of addition | For every v ∈ V, there exists an element −v ∈ V, called the additive inverse of v, such that v + (−v) = 0. |
| Compatibility of scalar multiplication with field multiplication | a(bv) = (ab)v [nb 2] |
| Identity element of scalar multiplication | 1v = v, where 1 denotes the multiplicative identity in F. |
| Distributivity of scalar multiplication with respect to vector addition | a(u + v) = au + av |
| Distributivity of scalar multiplication with respect to field addition | (a + b)v = av + bv |
These axioms generalize properties of the vectors introduced in the above examples. Indeed, the result of addition of two ordered pairs (as in the second example above) does not depend on the order of the summands:
- (xv, yv) + (xw, yw) = (xw, yw) + (xv, yv).
Subtraction of two vectors and division by a (non-zero) scalar can be defined as
- v − w = v + (−w),
- v/a = (1/a)v.
In contrast to the intuition stemming from vectors in the plane and higher-dimensional cases, there is, in general vector spaces, no notion of nearness, angles or distances. To deal with such matters, particular types of vector spaces are introduced; see below.
Alternative formulations and elementary consequences
Vector addition and scalar multiplication are operations, satisfying the closure property: u + v and av are in V for all a in F, and u, v in V. Some older sources mention these properties as separate axioms.[2]In the parlance of abstract algebra, the first four axioms are equivalent to requiring the set of vectors to be an abelian group under addition. The remaining axioms give this group an F-module structure. In other words, there is a ring homomorphism f from the field F into the endomorphism ring of the group of vectors. Then scalar multiplication av is defined as (f(a))(v).[3]
There are a number of direct consequences of the vector space axioms. Some of them derive from elementary group theory, applied to the additive group of vectors: for example the zero vector 0 of V and the additive inverse −v of any vector v are unique. Other properties follow from the distributive law, for example av equals 0 if and only if a equals 0 or v equals 0.
History
Vector spaces stem from affine geometry via the introduction of coordinates in the plane or three-dimensional space. Around 1636, Descartes and Fermat founded analytic geometry by equating solutions to an equation of two variables with points on a plane curve.[4] In 1804, to achieve geometric solutions without using coordinates, Bolzano introduced certain operations on points, lines and planes, which are predecessors of vectors.[5] His work was then used in the conception of barycentric coordinates by Möbius in 1827.[6] In 1828 C. V. Mourey suggested the existence of an algebra surpassing not only ordinary algebra but also two-dimensional algebra created by him searching a geometrical interpretation of complex numbers.[7]The definition of vectors was founded on Bellavitis' notion of the bipoint, an oriented segment of which one end is the origin and the other a target, then further elaborated with the presentation of complex numbers by Argand and Hamilton and the introduction of quaternions and biquaternions by the latter.[8] They are elements in R2, R4, and R8; their treatment as linear combinations can be traced back to Laguerre in 1867, who also defined systems of linear equations.
In 1857, Cayley introduced matrix notation, which allows for a harmonization and simplification of linear maps. Around the same time, Grassmann studied the barycentric calculus initiated by Möbius. He envisaged sets of abstract objects endowed with operations.[9] In his work, the concepts of linear independence and dimension, as well as scalar products, are present. In fact, Grassmann's 1844 work extended a vector space of n dimensions to one of 2n dimensions by consideration of 2-vectors
 and 3-vectors
and 3-vectors  called multivectors. This extension, called multilinear algebra, is governed by the rules of exterior algebra. Peano was the first to give the modern definition of vector spaces and linear maps in 1888.[10]
called multivectors. This extension, called multilinear algebra, is governed by the rules of exterior algebra. Peano was the first to give the modern definition of vector spaces and linear maps in 1888.[10]An important development of vector spaces is due to the construction of function spaces by Lebesgue. This was later formalized by Banach and Hilbert, around 1920.[11] At that time, algebra and the new field of functional analysis began to interact, notably with key concepts such as spaces of p-integrable functions and Hilbert spaces.[12] Vector spaces, including infinite-dimensional ones, then became a firmly established notion, and many mathematical branches started making use of this concept.
Examples
Coordinate spaces
The simplest example of a vector space over a field F is the field itself, equipped with its standard addition and multiplication. More generally, a vector space can be composed of n-tuples (sequences of length n) of elements of F, such as- (a1, a2, ..., an), where each ai is an element of F.[13]
Complex numbers and other field extensions
The set of complex numbers C, i.e., numbers that can be written in the form x + iy for real numbers x and y where i is the imaginary unit, form a vector space over the reals with the usual addition and multiplication: (x + iy) + (a + ib) = (x + a) + i(y + b) and c ⋅ (x + iy) = (c ⋅ x) + i(c ⋅ y) for real numbers x, y, a, b and c. The various axioms of a vector space follow from the fact that the same rules hold for complex number arithmetic.In fact, the example of complex numbers is essentially the same (i.e., it is isomorphic) to the vector space of ordered pairs of real numbers mentioned above: if we think of the complex number x + i y as representing the ordered pair (x, y) in the complex plane then we see that the rules for sum and scalar product correspond exactly to those in the earlier example.
More generally, field extensions provide another class of examples of vector spaces, particularly in algebra and algebraic number theory: a field F containing a smaller field E is an E-vector space, by the given multiplication and addition operations of F.[14] For example, the complex numbers are a vector space over R, and the field extension
 is a vector space over Q.
is a vector space over Q.Function spaces
Functions from any fixed set Ω to a field F also form vector spaces, by performing addition and scalar multiplication pointwise. That is, the sum of two functions f and g is the function (f + g) given by- (f + g)(w) = f(w) + g(w),
- f(x) = r0 + r1x + ... + rn−1xn−1 + rnxn, where the coefficients r0, ..., rn are in F.[16]
Linear equations
Systems of homogeneous linear equations are closely tied to vector spaces.[17] For example, the solutions ofa + 3b + c = 0 4a + 2b + 2c = 0
- Ax = 0,
 is the matrix containing the coefficients of the given equations, x is the vector (a, b, c), Ax denotes the matrix product, and 0 = (0, 0) is the zero vector. In a similar vein, the solutions of homogeneous linear differential equations form vector spaces. For example,
is the matrix containing the coefficients of the given equations, x is the vector (a, b, c), Ax denotes the matrix product, and 0 = (0, 0) is the zero vector. In a similar vein, the solutions of homogeneous linear differential equations form vector spaces. For example,- f′′(x) + 2f′(x) + f(x) = 0
Basis and dimension
A vector v in R2 (blue) expressed in terms of different bases: using the standard basis of R2 v = xe1 + ye2 (black), and using a different, non-orthogonal basis: v = f1 + f2 (red).
Bases allow one to represent vectors by a sequence of scalars called coordinates or components. A basis is a (finite or infinite) set B = {bi}i ∈ I of vectors bi, for convenience often indexed by some index set I, that spans the whole space and is linearly independent. "Spanning the whole space" means that any vector v can be expressed as a finite sum (called a linear combination) of the basis elements:
- (1)
For example, the coordinate vectors e1 = (1, 0, ..., 0), e2 = (0, 1, 0, ..., 0), to en = (0, 0, ..., 0, 1), form a basis of Fn, called the standard basis, since any vector (x1, x2, ..., xn) can be uniquely expressed as a linear combination of these vectors:
- (x1, x2, ..., xn) = x1(1, 0, ..., 0) + x2(0, 1, 0, ..., 0) + ... + xn(0, ..., 0, 1) = x1e1 + x2e2 + ... + xnen.
Every vector space has a basis. This follows from Zorn's lemma, an equivalent formulation of the Axiom of Choice.[18] Given the other axioms of Zermelo–Fraenkel set theory, the existence of bases is equivalent to the axiom of choice.[19] The ultrafilter lemma, which is weaker than the axiom of choice, implies that all bases of a given vector space have the same number of elements, or cardinality (cf. Dimension theorem for vector spaces).[20] It is called the dimension of the vector space, denoted by dim V. If the space is spanned by finitely many vectors, the above statements can be proven without such fundamental input from set theory.[21]
The dimension of the coordinate space Fn is n, by the basis exhibited above. The dimension of the polynomial ring F[x] introduced above is countably infinite, a basis is given by 1, x, x2, ... A fortiori, the dimension of more general function spaces, such as the space of functions on some (bounded or unbounded) interval, is infinite.[nb 4] Under suitable regularity assumptions on the coefficients involved, the dimension of the solution space of a homogeneous ordinary differential equation equals the degree of the equation.[22] For example, the solution space for the above equation is generated by e−x and xe−x. These two functions are linearly independent over R, so the dimension of this space is two, as is the degree of the equation.
A field extension over the rationals Q can be thought of as a vector space over Q (by defining vector addition as field addition, defining scalar multiplication as field multiplication by elements of Q, and otherwise ignoring the field multiplication). The dimension (or degree) of the field extension Q(α) over Q depends on α. If α satisfies some polynomial equation

with rational coefficients qn, ..., q0 (in other words, if α is algebraic), the dimension is finite. More precisely, it equals the degree of the minimal polynomial having α as a root.[23] For example, the complex numbers C are a two-dimensional real vector space, generated by 1 and the imaginary unit i.
The latter satisfies i2 + 1 = 0, an equation of degree two. Thus, C is a two-dimensional R-vector space (and, as any field, one-dimensional as a vector space over itself, C). If α is not algebraic, the dimension of Q(α) over Q is infinite. For instance, for α = π there is no such equation, in other words π is transcendental.[24]
Linear maps and matrices
The relation of two vector spaces can be expressed by linear map or linear transformation. They are functions that reflect the vector space structure—i.e., they preserve sums and scalar multiplication:- f(x + y) = f(x) + f(y) and f(a · x) = a · f(x) for all x and y in V, all a in F.[25]
Describing an arrow vector v by its coordinates x and y yields an isomorphism of vector spaces.
For example, the "arrows in the plane" and "ordered pairs of numbers" vector spaces in the introduction are isomorphic: a planar arrow v departing at the origin of some (fixed) coordinate system can be expressed as an ordered pair by considering the x- and y-component of the arrow, as shown in the image at the right. Conversely, given a pair (x, y), the arrow going by x to the right (or to the left, if x is negative), and y up (down, if y is negative) turns back the arrow v.
Linear maps V → W between two vector spaces form a vector space HomF(V, W), also denoted L(V, W).[27] The space of linear maps from V to F is called the dual vector space, denoted V∗.[28] Via the injective natural map V → V∗∗, any vector space can be embedded into its bidual; the map is an isomorphism if and only if the space is finite-dimensional.[29]
Once a basis of V is chosen, linear maps f : V → W are completely determined by specifying the images of the basis vectors, because any element of V is expressed uniquely as a linear combination of them.[30] If dim V = dim W, a 1-to-1 correspondence between fixed bases of V and W gives rise to a linear map that maps any basis element of V to the corresponding basis element of W. It is an isomorphism, by its very definition.[31] Therefore, two vector spaces are isomorphic if their dimensions agree and vice versa. Another way to express this is that any vector space is completely classified (up to isomorphism) by its dimension, a single number. In particular, any n-dimensional F-vector space V is isomorphic to Fn. There is, however, no "canonical" or preferred isomorphism; actually an isomorphism φ : Fn → V is equivalent to the choice of a basis of V, by mapping the standard basis of Fn to V, via φ. The freedom of choosing a convenient basis is particularly useful in the infinite-dimensional context, see below.
Matrices

A typical matrix
Matrices are a useful notion to encode linear maps.[32] They are written as a rectangular array of scalars as in the image at the right. Any m-by-n matrix A gives rise to a linear map from Fn to Fm, by the following
, where
denotes summation,
- x ↦ Ax.
The volume of this parallelepiped is the absolute value of the determinant of the 3-by-3 matrix formed by the vectors r1, r2, and r3.
The determinant det (A) of a square matrix A is a scalar that tells whether the associated map is an isomorphism or not: to be so it is sufficient and necessary that the determinant is nonzero.[34] The linear transformation of Rn corresponding to a real n-by-n matrix is orientation preserving if and only if its determinant is positive.
Eigenvalues and eigenvectors
Endomorphisms, linear maps f : V → V, are particularly important since in this case vectors v can be compared with their image under f, f(v). Any nonzero vector v satisfying λv = f(v), where λ is a scalar, is called an eigenvector of f with eigenvalue λ.[nb 5][35] Equivalently, v is an element of the kernel of the difference f − λ · Id (where Id is the identity map V → V). If V is finite-dimensional, this can be rephrased using determinants: f having eigenvalue λ is equivalent to- det(f − λ · Id) = 0.
Basic constructions
In addition to the above concrete examples, there are a number of standard linear algebraic constructions that yield vector spaces related to given ones. In addition to the definitions given below, they are also characterized by universal properties, which determine an object X by specifying the linear maps from X to any other vector space.Subspaces and quotient spaces
A nonempty subset W of a vector space V that is closed under addition and scalar multiplication (and therefore contains the 0-vector of V) is called a linear subspace of V, or simply a subspace of V, when the ambient space is unambiguously a vector space.[38][nb 7] Subspaces of V are vector spaces (over the same field) in their own right. The intersection of all subspaces containing a given set S of vectors is called its span, and it is the smallest subspace of V containing the set S. Expressed in terms of elements, the span is the subspace consisting of all the linear combinations of elements of S.[39]
A linear subspace of dimension 1 is a vector line. A linear subspace of dimension 2 is a vector plane. A linear subspace that contains all elements but one of a basis of the ambient space is a vector hyperplane. In a vector space of finite dimension n, a vector hyperplane is thus a subspace of dimension n – 1.
The counterpart to subspaces are quotient vector spaces.[40] Given any subspace W ⊂ V, the quotient space V/W ("V modulo W") is defined as follows: as a set, it consists of v + W = {v + w : w ∈ W}, where v is an arbitrary vector in V. The sum of two such elements v1 + W and v2 + W is (v1 + v2) + W, and scalar multiplication is given by a · (v + W) = (a · v) + W. The key point in this definition is that v1 + W = v2 + W if and only if the difference of v1 and v2 lies in W.[nb 8] This way, the quotient space "forgets" information that is contained in the subspace W.
The kernel ker(f) of a linear map f : V → W consists of vectors v that are mapped to 0 in W.[41] Both kernel and image im(f) = {f(v) : v ∈ V} are subspaces of V and W, respectively.[42] The existence of kernels and images is part of the statement that the category of vector spaces (over a fixed field F) is an abelian category, i.e. a corpus of mathematical objects and structure-preserving maps between them (a category) that behaves much like the category of abelian groups.[43] Because of this, many statements such as the first isomorphism theorem (also called rank–nullity theorem in matrix-related terms)
- V / ker(f) ≡ im(f).
An important example is the kernel of a linear map x ↦ Ax for some fixed matrix A, as above. The kernel of this map is the subspace of vectors x such that Ax = 0, which is precisely the set of solutions to the system of homogeneous linear equations belonging to A. This concept also extends to linear differential equations
, where the coefficients ai are functions in x, too.
,
Direct product and direct sum
The direct product of vector spaces and the direct sum of vector spaces are two ways of combining an indexed family of vector spaces into a new vector space.The direct product
 of a family of vector spaces Vi consists of the set of all tuples (vi)i ∈ I, which specify for each index i in some index set I an element vi of Vi.[44] Addition and scalar multiplication is performed componentwise. A variant of this construction is the direct sum
of a family of vector spaces Vi consists of the set of all tuples (vi)i ∈ I, which specify for each index i in some index set I an element vi of Vi.[44] Addition and scalar multiplication is performed componentwise. A variant of this construction is the direct sum  (also called coproduct and denoted
(also called coproduct and denoted  ), where only tuples with finitely many nonzero vectors are allowed. If the index set I is finite, the two constructions agree, but in general they are different.
), where only tuples with finitely many nonzero vectors are allowed. If the index set I is finite, the two constructions agree, but in general they are different.Tensor product
The tensor product V ⊗F W, or simply V ⊗ W, of two vector spaces V and W is one of the central notions of multilinear algebra which deals with extending notions such as linear maps to several variables. A map g : V × W → X is called bilinear if g is linear in both variables v and w. That is to say, for fixed w the map v ↦ g(v, w) is linear in the sense above and likewise for fixed v.The tensor product is a particular vector space that is a universal recipient of bilinear maps g, as follows. It is defined as the vector space consisting of finite (formal) sums of symbols called tensors
- v1 ⊗ w1 + v2 ⊗ w2 + ... + vn ⊗ wn,
- a · (v ⊗ w) = (a · v) ⊗ w = v ⊗ (a · w), where a is a scalar,
- (v1 + v2) ⊗ w = v1 ⊗ w + v2 ⊗ w, and
- v ⊗ (w1 + w2) = v ⊗ w1 + v ⊗ w2.[45]
Commutative diagram depicting the universal property of the tensor product.
These rules ensure that the map f from the V × W to V ⊗ W that maps a tuple (v, w) to v ⊗ w is bilinear. The universality states that given any vector space X and any bilinear map g : V × W → X, there exists a unique map u, shown in the diagram with a dotted arrow, whose composition with f equals g: u(v ⊗ w) = g(v, w).[46] This is called the universal property of the tensor product, an instance of the method—much used in advanced abstract algebra—to indirectly define objects by specifying maps from or to this object.
Vector spaces with additional structure
From the point of view of linear algebra, vector spaces are completely understood insofar as any vector space is characterized, up to isomorphism, by its dimension. However, vector spaces per se do not offer a framework to deal with the question—crucial to analysis—whether a sequence of functions converges to another function. Likewise, linear algebra is not adapted to deal with infinite series, since the addition operation allows only finitely many terms to be added. Therefore, the needs of functional analysis require considering additional structures.A vector space may be given a partial order ≤, under which some vectors can be compared.[47] For example, n-dimensional real space Rn can be ordered by comparing its vectors componentwise. Ordered vector spaces, for example Riesz spaces, are fundamental to Lebesgue integration, which relies on the ability to express a function as a difference of two positive functions
- f = f+ − f−,
Normed vector spaces and inner product spaces
"Measuring" vectors is done by specifying a norm, a datum which measures lengths of vectors, or by an inner product, which measures angles between vectors. Norms and inner products are denoted and
and  ,
respectively. The datum of an inner product entails that lengths of
vectors can be defined too, by defining the associated norm
,
respectively. The datum of an inner product entails that lengths of
vectors can be defined too, by defining the associated norm  . Vector spaces endowed with such data are known as normed vector spaces and inner product spaces, respectively.[49]
. Vector spaces endowed with such data are known as normed vector spaces and inner product spaces, respectively.[49]
Coordinate space Fn can be equipped with the standard dot product:
 are called orthogonal. An important variant of the standard dot product is used in Minkowski space: R4 endowed with the Lorentz product
are called orthogonal. An important variant of the standard dot product is used in Minkowski space: R4 endowed with the Lorentz productIn contrast to the standard dot product, it is not positive definite:
 also takes negative values, for example for
also takes negative values, for example for  . Singling out the fourth coordinate—corresponding to time, as opposed to three space-dimensions—makes it useful for the mathematical treatment of special relativity.
. Singling out the fourth coordinate—corresponding to time, as opposed to three space-dimensions—makes it useful for the mathematical treatment of special relativity.Topological vector spaces
Convergence questions are treated by considering vector spaces V carrying a compatible topology, a structure that allows one to talk about elements being close to each other.[51][52] Compatible here means that addition and scalar multiplication have to be continuous maps. Roughly, if x and y in V, and a in F vary by a bounded amount, then so do x + y and ax.[nb 9] To make sense of specifying the amount a scalar changes, the field F also has to carry a topology in this context; a common choice are the reals or the complex numbers.In such topological vector spaces one can consider series of vectors. The infinite sum
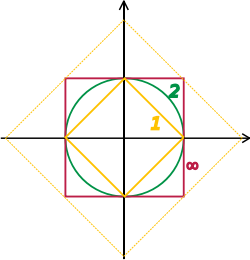
Unit "spheres" in R2 consist of plane vectors of norm 1. Depicted are the unit spheres in different p-norms, for p = 1, 2, and ∞. The bigger diamond depicts points of 1-norm equal to 2.
A way to ensure the existence of limits of certain infinite series is to restrict attention to spaces where any Cauchy sequence has a limit; such a vector space is called complete. Roughly, a vector space is complete provided that it contains all necessary limits. For example, the vector space of polynomials on the unit interval [0,1], equipped with the topology of uniform convergence is not complete because any continuous function on [0,1] can be uniformly approximated by a sequence of polynomials, by the Weierstrass approximation theorem.[53] In contrast, the space of all continuous functions on [0,1] with the same topology is complete.[54] A norm gives rise to a topology by defining that a sequence of vectors vn converges to v if and only if
From a conceptual point of view, all notions related to topological vector spaces should match the topology. For example, instead of considering all linear maps (also called functionals) V → W, maps between topological vector spaces are required to be continuous.[56] In particular, the (topological) dual space V∗ consists of continuous functionals V → R (or to C). The fundamental Hahn–Banach theorem is concerned with separating subspaces of appropriate topological vector spaces by continuous functionals.[57]
Banach spaces
Banach spaces, introduced by Stefan Banach, are complete normed vector spaces.[58] A first example is the vector space ℓ p consisting of infinite vectors with real entries x = (x1, x2, ...) whose p-norm (1 ≤ p ≤ ∞) given byfor p < ∞ and
, but
Hilbert spaces
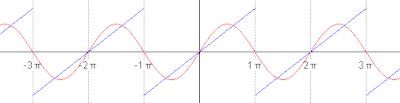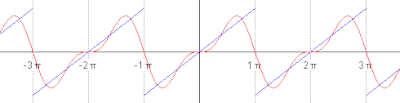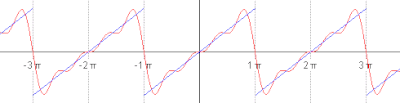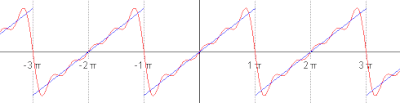
The succeeding snapshots show summation of 1 to 5 terms in approximating
a periodic function (blue) by finite sum of sine functions (red).
Complete inner product spaces are known as Hilbert spaces, in honor of David Hilbert.[61] The Hilbert space L2(Ω), with inner product given by
 denotes the complex conjugate of g(x),[62][nb 12] is a key case.
denotes the complex conjugate of g(x),[62][nb 12] is a key case.By definition, in a Hilbert space any Cauchy sequence converges to a limit. Conversely, finding a sequence of functions fn with desirable properties that approximates a given limit function, is equally crucial. Early analysis, in the guise of the Taylor approximation, established an approximation of differentiable functions f by polynomials.[63] By the Stone–Weierstrass theorem, every continuous function on [a, b] can be approximated as closely as desired by a polynomial.[64] A similar approximation technique by trigonometric functions is commonly called Fourier expansion, and is much applied in engineering, see below. More generally, and more conceptually, the theorem yields a simple description of what "basic functions", or, in abstract Hilbert spaces, what basic vectors suffice to generate a Hilbert space H, in the sense that the closure of their span (i.e., finite linear combinations and limits of those) is the whole space. Such a set of functions is called a basis of H, its cardinality is known as the Hilbert space dimension.[nb 13] Not only does the theorem exhibit suitable basis functions as sufficient for approximation purposes, but together with the Gram–Schmidt process, it enables one to construct a basis of orthogonal vectors.[65] Such orthogonal bases are the Hilbert space generalization of the coordinate axes in finite-dimensional Euclidean space.
The solutions to various differential equations can be interpreted in terms of Hilbert spaces. For example, a great many fields in physics and engineering lead to such equations and frequently solutions with particular physical properties are used as basis functions, often orthogonal.[66] As an example from physics, the time-dependent Schrödinger equation in quantum mechanics describes the change of physical properties in time by means of a partial differential equation, whose solutions are called wavefunctions.[67] Definite values for physical properties such as energy, or momentum, correspond to eigenvalues of a certain (linear) differential operator and the associated wavefunctions are called eigenstates. The spectral theorem decomposes a linear compact operator acting on functions in terms of these eigenfunctions and their eigenvalues.[68]
Algebras over fields

A hyperbola, given by the equation x ⋅ y = 1. The coordinate ring of functions on this hyperbola is given by R[x, y] / (x · y − 1), an infinite-dimensional vector space over R.
General vector spaces do not possess a multiplication between vectors. A vector space equipped with an additional bilinear operator defining the multiplication of two vectors is an algebra over a field.[69] Many algebras stem from functions on some geometrical object: since functions with values in a given field can be multiplied pointwise, these entities form algebras. The Stone–Weierstrass theorem mentioned above, for example, relies on Banach algebras which are both Banach spaces and algebras.
Commutative algebra makes great use of rings of polynomials in one or several variables, introduced above. Their multiplication is both commutative and associative. These rings and their quotients form the basis of algebraic geometry, because they are rings of functions of algebraic geometric objects.[70]
Another crucial example are Lie algebras, which are neither commutative nor associative, but the failure to be so is limited by the constraints ([x, y] denotes the product of x and y):
- [x, y] = −[y, x] (anticommutativity), and
- [x, [y, z]] + [y, [z, x]] + [z, [x, y]] = 0 (Jacobi identity).[71]
The tensor algebra T(V) is a formal way of adding products to any vector space V to obtain an algebra.[72] As a vector space, it is spanned by symbols, called simple tensors
- v1 ⊗ v2 ⊗ ... ⊗ vn, where the degree n varies.
When a field, F is explicitly stated, a common term used is F-algebra.
Applications
Vector spaces have many applications as they occur frequently in common circumstances, namely wherever functions with values in some field are involved. They provide a framework to deal with analytical and geometrical problems, or are used in the Fourier transform. This list is not exhaustive: many more applications exist, for example in optimization. The minimax theorem of game theory stating the existence of a unique payoff when all players play optimally can be formulated and proven using vector spaces methods.[74] Representation theory fruitfully transfers the good understanding of linear algebra and vector spaces to other mathematical domains such as group theory.[75]Distributions
A distribution (or generalized function) is a linear map assigning a number to each "test" function, typically a smooth function with compact support, in a continuous way: in the above terminology the space of distributions is the (continuous) dual of the test function space.[76] The latter space is endowed with a topology that takes into account not only f itself, but also all its higher derivatives. A standard example is the result of integrating a test function f over some domain Ω:Fourier analysis
The heat equation describes the dissipation of physical properties over
time, such as the decline of the temperature of a hot body placed in a
colder environment (yellow depicts colder regions than red).
Resolving a periodic function into a sum of trigonometric functions forms a Fourier series, a technique much used in physics and engineering.[nb 14][78] The underlying vector space is usually the Hilbert space L2(0, 2π), for which the functions sin mx and cos mx (m an integer) form an orthogonal basis.[79] The Fourier expansion of an L2 function f is
,
Fourier series are used to solve boundary value problems in partial differential equations.[84] In 1822, Fourier first used this technique to solve the heat equation.[85] A discrete version of the Fourier series can be used in sampling applications where the function value is known only at a finite number of equally spaced points. In this case the Fourier series is finite and its value is equal to the sampled values at all points.[86] The set of coefficients is known as the discrete Fourier transform (DFT) of the given sample sequence. The DFT is one of the key tools of digital signal processing, a field whose applications include radar, speech encoding, image compression.[87] The JPEG image format is an application of the closely related discrete cosine transform.[88]
The fast Fourier transform is an algorithm for rapidly computing the discrete Fourier transform.[89] It is used not only for calculating the Fourier coefficients but, using the convolution theorem, also for computing the convolution of two finite sequences.[90] They in turn are applied in digital filters[91] and as a rapid multiplication algorithm for polynomials and large integers (Schönhage–Strassen algorithm).[92][93]
Differential geometry

The tangent space to the 2-sphere at some point is the infinite plane touching the sphere in this point.
The tangent plane to a surface at a point is naturally a vector space whose origin is identified with the point of contact. The tangent plane is the best linear approximation, or linearization, of a surface at a point.[nb 15] Even in a three-dimensional Euclidean space, there is typically no natural way to prescribe a basis of the tangent plane, and so it is conceived of as an abstract vector space rather than a real coordinate space. The tangent space is the generalization to higher-dimensional differentiable manifolds.[94]
Riemannian manifolds are manifolds whose tangent spaces are endowed with a suitable inner product.[95] Derived therefrom, the Riemann curvature tensor encodes all curvatures of a manifold in one object, which finds applications in general relativity, for example, where the Einstein curvature tensor describes the matter and energy content of space-time.[96][97] The tangent space of a Lie group can be given naturally the structure of a Lie algebra and can be used to classify compact Lie groups.[98]
Generalizations
Vector bundles

A Möbius strip. Locally, it looks like U × R.
A vector bundle is a family of vector spaces parametrized continuously by a topological space X.[94] More precisely, a vector bundle over X is a topological space E equipped with a continuous map
- π : E → X
Properties of certain vector bundles provide information about the underlying topological space. For example, the tangent bundle consists of the collection of tangent spaces parametrized by the points of a differentiable manifold. The tangent bundle of the circle S1 is globally isomorphic to S1 × R, since there is a global nonzero vector field on S1.[nb 17] In contrast, by the hairy ball theorem, there is no (tangent) vector field on the 2-sphere S2 which is everywhere nonzero.[100] K-theory studies the isomorphism classes of all vector bundles over some topological space.[101] In addition to deepening topological and geometrical insight, it has purely algebraic consequences, such as the classification of finite-dimensional real division algebras: R, C, the quaternions H and the octonions O.
The cotangent bundle of a differentiable manifold consists, at every point of the manifold, of the dual of the tangent space, the cotangent space. Sections of that bundle are known as differential one-forms.
Modules
Modules are to rings what vector spaces are to fields: the same axioms, applied to a ring R instead of a field F, yield modules.[102] The theory of modules, compared to that of vector spaces, is complicated by the presence of ring elements that do not have multiplicative inverses. For example, modules need not have bases, as the Z-module (i.e., abelian group) Z/2Z shows; those modules that do (including all vector spaces) are known as free modules. Nevertheless, a vector space can be compactly defined as a module over a ring which is a field with the elements being called vectors. Some authors use the term vector space to mean modules over a division ring.[103] The algebro-geometric interpretation of commutative rings via their spectrum allows the development of concepts such as locally free modules, the algebraic counterpart to vector bundles.Affine and projective spaces
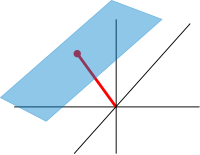
An affine plane (light blue) in R3. It is a two-dimensional subspace shifted by a vector x (red).
Roughly, affine spaces are vector spaces whose origins are not specified.[104] More precisely, an affine space is a set with a free transitive vector space action. In particular, a vector space is an affine space over itself, by the map
- V × V → V, (v, a) ↦ a + v.
- Ax = b
The set of one-dimensional subspaces of a fixed finite-dimensional vector space V is known as projective space; it may be used to formalize the idea of parallel lines intersecting at infinity.[106] Grassmannians and flag manifolds generalize this by parametrizing linear subspaces of fixed dimension k and flags of subspaces, respectively.


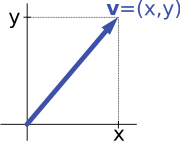
















![{\frac {a_{0}}{2}}+\sum _{m=1}^{\infty }\left[a_{m}\cos \left(mx\right)+b_{m}\sin \left(mx\right)\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/b02fb26ebada4babaa1d88e20bb63e3b370c13b3)