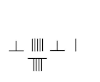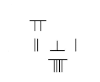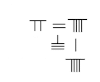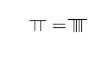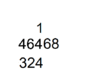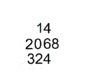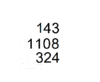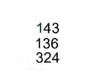Chinese mathematics

From Wikipedia, the free encyclopedia

Mathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry.

 

In the Han Dynasty, the Chinese made substantial progress on root extraction and linear algebra. The major texts from the period,The Nine Chapters on the Mathematical Art and the Writings on Reckoning gave detailed processes to solving mathematical problems in daily life. All procedures were computed using a counting board in both texts, and they included negative numbers as well as fractions. The texts provide procedures similar to that Gaussian elimination and Horner's method for linear algebra and solving quadratic equations, respectively. While the Greek mathematics declined in the west during the mediaeval times, the achievement of Chinese algebra reached its zenith in the 13th century, when Zhu Shijie invented the method of four unknowns.

As a result of obvious linguistic and geographic barriers, as well as content, Chinese mathematics and the mathematics of the ancient Mediterranean world are presumed to have developed more or less independently up to the time when The Nine Chapters on the Mathematical Art reached its final form, while the Writings on Reckoning and Huainanzi are roughly contemporary with classical Greek mathematics. Some exchange of ideas across Asia through known cultural exchanges from at least Roman times is likely. Frequently, elements of the mathematics of early societies correspond to rudimentary results found later in branches of modern mathematics such as geometry or number theory. The Pythagorean theorem for example, has been attested to the time of the Duke of Zhou. Knowledge of Pascal's triangle has also been shown to have existed in China centuries before Pascal, such as the Song dynasty Chinese polymath Shen Kuo.

Early Chinese mathematics

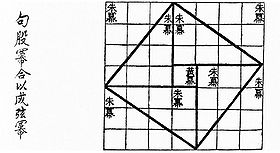
Visual proof for the (3, 4, 5) triangle as in the Zhoubi Suanjing 500–200 BC.

 

Oracle bone script numeral system

 

counting rod place value decimal

Simple mathematics on Oracle bone script date back to the Shang Dynasty (1600–1050 BC). One of the oldest surviving mathematical works is the Yi Jing, which greatly influenced written literature during the Zhou Dynasty (1050–256 BC). For mathematics, the book included a sophisticated use of hexagrams. Leibniz pointed out, the I Ching (Yi Jing) contained elements of binary numbers.

Since the Shang period, the Chinese had already fully developed a decimal system. Since early times, Chinese understood basic arithmetic (which dominated far eastern history), algebra, equations, and negative numbers with counting rods. Although the Chinese were more focused on arithmetic and advanced algebra for astronomical uses, they were also the first to develop negative numbers, algebraic geometry (only Chinese geometry) and the usage of decimals.

Math was one of the Liù Yì (六艺) or Six Arts, students were required to master during the Zhou Dynasty (1122–256 BC). Learning them all perfectly was required to be a perfect gentleman, or in the Chinese sense, a "Renaissance Man". Six Arts have their roots in the Confucian philosophy.

The oldest existent work on geometry in China comes from the philosophical Mohist canon of c. 330 BC, compiled by the followers of Mozi (470–390 BC). The Mo Jing described various aspects of many fields associated with physical science, and provided a small wealth of information on mathematics as well. It provided an 'atomic' definition of the geometric point, stating that a line is separated into parts, and the part which has no remaining parts (i.e. cannot be divided into smaller parts) and thus forms the extreme end of a line is a point. Much like Euclid's first and third definitions and Plato's 'beginning of a line', the Mo Jing stated that "a point may stand at the end (of a line) or at its beginning like a head-presentation in childbirth. (As to its invisibility) there is nothing similar to it." Similar to the atomists of Democritus, the Mo Jing stated that a point is the smallest unit, and cannot be cut in half, since 'nothing' cannot be halved. It stated that two lines of equal length will always finish at the same place, while providing definitions for the comparison of lengths and for parallels, along with principles of space and bounded space. It also described the fact that planes without the quality of thickness cannot be piled up since they cannot mutually touch. The book provided word recognition for circumference, diameter, and radius, along with the definition of volume.

The history of mathematical development lacks some evidence. There are still debates about certain mathematical classics. For example, the Zhoubi Suanjing dates around 1200–1000 BC, yet many scholars believed it was written between 300–250 BC. The Zhoubi Suanjing contains an in-depth proof of the Gougu Theorem (a special case of the Pythagorean Theorem) but focuses more on astronomical calculations. However, the recent archaeological discovery of the Tsinghua Bamboo Slips, dated c. 305 BC, has revealed some aspects of pre-Qin mathematics, such as the first known decimal multiplication table.

The abacus was first mentioned in the second century BC, alongside 'calculation with rods' (suan zi) in which small bamboo sticks are placed in successive squares of a checkerboard.

Qin mathematics

Not much is known about Qin dynasty mathematics, or before, due to the burning of books and burying of scholars, circa 213–210 BCE. Knowledge of this period can be determined from civil projects and historical evidence. The Qin dynasty created a standard system of weights. Civil projects of the Qin dynasty were significant feats of human engineering. Emperor Qin Shihuang （秦始皇） ordered many men to build large, lifesize statues for the palace tomb along with other temples and shrines, and the shape of the tomb was designed with geometric skills of architecture. It is certain that one of the greatest feats of human history, the Great Wall of China, required many mathematical techniques. All Qin dynasty buildings and grand projects used advanced computation formulas for volume, area and proportion.

Qin bamboo cash purchased at the antiquarian market of Hong Kong by the Yuelu Academy, according to the preliminary reports, contains the earliest epigraphic sample of a mathematical treatise.

Han mathematics

The Nine Chapters on the Mathematical Art.

In the Han Dynasty, numbers were developed into a place value decimal system and used on a counting board with a set of counting rods called chousuan, consisting of only nine symbols with a blank space on the counting board representing zero. Negative numbers and fractions were also incorporated into solutions of the great mathematical texts of the period. The mathematical texts of the time, the Suàn shù shū and the Jiuzhang suanshu solved basic arithmetic problems such as addition, subtraction, multiplication and division. Furthermore, they gave the processes for square and cubed root extraction, which eventually was applied to solving quadratic equations up to the third order. Both texts also made substantial progress in Linear Algebra, namely solving systems of equations with multiple unkowns. The value of pi is taken to be equal to three in both texts. However, the mathematicians Liu Xin (d. 23) and Zhang Heng (78–139) gave more accurate approximations for pi than Chinese of previous centuries had used. Mathematics was developed to solve practical problems in the time such as division of land or problems related to division of payment. The Chinese did not focus on theoretical proofs based on geometry or algebra in the modern sense of proving equations to find area or volume. The Book of Computations and The Nine Chapters on the Mathematical Art provide numerous practical examples that would be used in daily life.

Suan shu shu

The Suàn shù shū (Writings on Reckoning or The Book of Computations) is an ancient Chinese text on mathematics approximately seven thousand characters in length, written on 190 bamboo strips. It was discovered together with other writings in 1984 when archaeologists opened a tomb at Zhangjiashan in Hubei province. From documentary evidence this tomb is known to have been closed in 186 BC, early in the Western Han dynasty. While its relationship to the Nine Chapters is still under discussion by scholars, some of its contents are clearly paralleled there. The text of the Suan shu shu is however much less systematic than the Nine Chapters, and appears to consist of a number of more or less independent short sections of text drawn from a number of sources.

The Book of Computations contains many perquisites to problems that would be expanded upon in The Nine Chapters on the Mathematical Art. An example of the elementary mathematics in the Suàn shù shū, the square root is approximated by using an "excess and deficiency" method which says to "combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend." Furthermore, The Book of Computations solves systems of two equations and two unknowns using the same excess and deficiency method.

The Nine Chapters on the Mathematical Art

The Nine Chapters on the Mathematical Art is a Chinese mathematics book, its oldest archeological date being 179 AD (traditionally dated 1000 BC), but perhaps as early as 300–200 BC. Although the author(s) are unknown, they made a huge contribution in the eastern world. Problems are set up with questions immediately followed by answers and procedure. There are no formal mathematical proofs within the text, just a step by step procedure. The commentary of Liu Hui provided geometrical and algebraic proofs to the problems given within the text.

The Nine Chapters on the Mathematical Art was one of the most influential of all Chinese mathematical books and it is composed of some 246 problems. It would later be incorporated into The Ten Computational Cannons which would become the core of mathematical education in later centuries. This book includes 246 problems on surveying, agriculture, partnerships, engineering, taxation, calculation, the solution of equations, and the properties of right triangles. The Nine Chapters made significant additions to solving quadratic equations in a way similar to Horner's Method. It also made advanced contributions to "fangcheng" or what is now known as linear algebra. Chapter seven solves system of linear equations with two unknowns using the excess and deficit method, similar to The Book of Computations. Chapter eight deals with solving determinate and indeterminate simultaneous linear equations using positive and negative numbers, with one problem dealing with solving four equations in five unknowns. The Nine Chapters solves systems of equations using methods similar to the modern methods of Gaussian elimination and back substitution.

Calculation of pi

The calculation of pi is often used to gauge the mathematical capabilities of a society. Problems in The Nine Chapters on the Mathematical Art take pi to be equal to three in calculating problems related to circles and spheres, such as spherical surface area. There is no explicit formula given within the text for the calculation of pi to be three, but it is used throughout the problems of both The Nine Chapters on the Mathematical Art and the Artificer's Record, which was produced in the same time period. Historians believe that this figure of pi was calculated using the 3:1 relationship between the circumference and diameter of a circle. Some Han mathematicians attempted to improve this number, such as Liu Xin, who is believed to have estimated pi to be 3.154. There is no explicit method or record of how he calculated this estimate.

Division and root extraction

Basic arithmetic processes such as addition, subtraction, multiplication and division were present before the Han Dynasty. The Nine Chapters on the Mathematical Art take these basic operations for granted and simply instruct the reader to perform them. Han mathematicians calculated square and cubed roots in a similar manner as division, and problems on division and root extraction both occur in Chapter Four of The Nine Chapters on the Mathematical Art. Calculating the squared and cubed roots of numbers is done through successive approximation, the same as division, and often uses similar terms such as dividend (shi) and divisor (fa) throughout the process. This process of successive approximation was then extended to solving quadratics of the second and third order, such as ${\displaystyle x^{2}+a=b}$, using a method similar to Horner's Method. The method was not extended to solve quadratics of the nth order during the Han Dynasty, however, this method would eventually be used to solve these equations.

Fangcheng on a Counting Board

Linear algebra

The Book of Computations is the first known text to solve systems of equations with two unknowns. There are a total of three sets problems within The Book of Computations involving solving systems of equations with the excess and deficit method, and again are put into practical terms. Chapter Seven of The Nine Chapters on the Mathematical Art also deals with solving a system of two equations with two unknown with the excess and deficit method. To solve for the greater of the two unknowns, the excess and deficit method instructs the reader to cross multiply the minor terms or "zi" (which are the values given for the excess and deficit) with the major terms "mu". To solve for the lesser of the two unknowns, simply add the minor terms together.

Chapter Eight of The Nine Chapters on the Mathematical Art deals with solving infinite equations with infinite unknowns. This process is referred to as the "fangcheng procedure" throughout out the chapter. Many Historians chose to leave the term fangcheng untranslated due to conflicting evidence of what the term means. Many historians refer translate the word to Linear Algebra today. In this chapter, the process of Gaussian Elimination and back substitution are used to solve systems of equations with many unknowns. Problems were done on a counting board and included the use of negative numbers as well as fractions. The counting board was effectively a matrix, where the top line is the first variable of one equation and the bottom was the last.

Liu Hui's Commentary on The Nine Chapters on the Mathematical Art

Liu Hui's Exhaustion Method

Liu Hui's commentary on The Nine Chapters on the Mathematical Art is the earliest edition of the original text available. Hui is believed by most to be a mathematician shortly after the Han dynasty. Within his commentary, Hui qualified and proved some of the problems from either and algebraic or geometrical standpoint. For instance, throughout The Nine Chapters on the Mathematical Art the value of pi is taken to be equal to three in problems regarding circles or spheres. In his commentary, Liu Hui finds a more accurate estimation of pi using the exhaustion method. The exhaustion method involves creating successive polynomials within a circle so that eventually the area of a higher order polygon will be identical to the circle. From this method, Liu Hui asserted that the value of pi is about 3.14. Liu Hui also presented a geometric proof of square and cubed root extraction similar to the Greek Method, which involved cutting a square or cube in any line or section and determining the square root through symmetry of the remaining rectangles.

Mathematics in the period of disunity

Liu Hui's Survey of sea island

 

Sunzi algorithm for division 400 AD

 

al Khwarizmi division in the 9th century

 

Statue of Zu Chongzhi.

In the third century Liu Hui wrote his commentary on the Nine Chapters and also wrote Haidao Suanjing which dealt with using Pythagorean theorem (already known by the 9 chapters), and triple, quadruple triangulation for surveying; his accomplishment in the mathematical surveying exceeded those accomplished in the west by a millennium. He was the first Chinese mathematician to calculate π = 3.1416 with his π algorithm. He discovered the usage of Cavalieri's principle to find an accurate formula for the volume of a cylinder, and also developed elements of the integral and the differential calculus during the 3rd century CE.

Fraction interpolation for pi

In the fourth century, another influential mathematician named Zu Chongzhi, introduced the Da Ming Li. This calendar was specifically calculated to predict many cosmological cycles that will occur in a period of time. Very little is really known about his life. Today, the only sources are found in Book of Sui, we now know that Zu Chongzhi was one of the generations of mathematicians. He used Liu Hui's pi-algorithm applied to a 12288-gon and obtained a value of pi to 7 accurate decimal places (between 3.1415926 and 3.1415927), which would remain the most accurate approximation of π available for the next 900 years. He also used He Chengtian's interpolation method for approximating irrational number with fraction in his astronomy and mathematical works, he obtained ${\displaystyle {\tfrac {355}{113}}}$ as a good fraction approximate for pi; Yoshio Mikami commented that neither the Greeks, nor the Hindus nor Arabs knew about this fraction approximation to pi, not until the Dutch mathematician Adrian Anthoniszoom rediscovered it in 1585, "the Chinese had therefore been possessed of this the most extraordinary of all fractional values over a whole millennium earlier than Europe"

Along with his son, Zu Geng, Zu Chongzhi used the Cavalieri Method to find an accurate solution for calculating the volume of the sphere. Besides containing formulas for the volume of the sphere, his book also included formulas of cubic equations and the accurate value of pi. His work, Zhui Shu was discarded out of the syllabus of mathematics during the Song dynasty and lost. Many believed that Zhui Shu contains the formulas and methods for linear, matrix algebra, algorithm for calculating the value of π, formula for the volume of the sphere. The text should also associate with his astronomical methods of interpolation, which would contain knowledge, similar to our modern mathematics.

A mathematical manual called "Sunzi mathematical classic" dated between 200—400 CE contained the most detailed step by step description of multiplication and division algorithm with counting rods. The earliest record of multiplication and division algorithm using the Hindu-Arabic numeral system was in writing by Al Khwarizmi in the early 9th century. Khwarizmi's step by step division algorithm was completely identical to Sunzi division algorithm described in Sunzi mathematical classic four centuries earlier. Khwarizmi's work was translated into Latin in the 13th century and spread to the west, the division algorithm later evolved into Galley division. The route of transmission of Chinese place value decimal arithmetic know how to the west is unclear, how Sunzi's division and multiplication algorithm with rod calculus ended up in Hindu Arabic numeral form in Khwarizmi's work is unclear, as Al Khwarizmi never given any Sanskrit source nor quoted any Sanskrit stanza. However, the influence of rod calculus on Hindu division is evident, for example in the division example, 324 should be 32400, only rod calculus used blanks for zeros.

In the fifth century the manual called "Zhang Qiujian suanjing" discussed linear and quadratic equations. By this point the Chinese had the concept of negative numbers.

Tang mathematics

By the Tang Dynasty study of mathematics was fairly standard in the great schools. The Ten Computational Canons was a collection of ten Chinese mathematical works, compiled by early Tang dynasty mathematician Li Chunfeng (李淳风 602－670），as the official mathematical texts for imperial examinations in mathematics. The Sui dynasty and Tang dynasty ran the "School of Computations".

Wang Xiaotong was a great mathematician in the beginning of the Tang Dynasty, and he wrote a book: Jigu Suanjing (Continuation of Ancient Mathematics), where numerical solutions which general cubic equations appear for the first time.

The Tibetans obtained their first knowledge of mathematics (arithmetic) from China during the reign of Nam-ri srong btsan, who died in 630.

The table of sines by the Indian mathematician, Aryabhata, were translated into the Chinese mathematical book of the Kaiyuan Zhanjing, compiled in 718 AD during the Tang Dynasty. Although the Chinese excelled in other fields of mathematics such as solid geometry, binomial theorem, and complex algebraic formulas,early forms of trigonometry were not as widely appreciated as in the contemporary Indian and Islamic mathematics.

Yi Xing, the mathematician and Buddhist monk was credited for calculating the tangent table. Instead, the early Chinese used an empirical substitute known as chong cha, while practical use of plane trigonometry in using the sine, the tangent, and the secant were known. Yi Xing was famed for his genius, and was known to have calculated the number of possible positions on a go board game (though without a symbol for zero he had difficulties expressing the number).

Song and Yuan mathematics

Northern Song Dynasty mathematician Jia Xian developed an additive multiplicative method for extraction of square root and cubic root which implemented the "Horner" rule.

Yang Hui triangle (Pascal's triangle) using rod numerals, as depicted in a publication of Zhu Shijie in 1303 AD

Four outstanding mathematicians arose during the Song Dynasty and Yuan Dynasty, particularly in the twelfth and thirteenth centuries: Yang Hui, Qin Jiushao, Li Zhi (Li Ye), and Zhu Shijie. Yang Hui, Qin Jiushao, Zhu Shijie all used the Horner-Ruffini method six hundred years earlier to solve certain types of simultaneous equations, roots, quadratic, cubic, and quartic equations. Yang Hui was also the first person in history to discover and prove "Pascal's Triangle", along with its binomial proof (although the earliest mention of the Pascal's triangle in China exists before the eleventh century AD). Li Zhi on the other hand, investigated on a form of algebraic geometry based on Tian yuan shu. His book; Ceyuan haijing revolutionized the idea of inscribing a circle into triangles, by turning this geometry problem by algebra instead of the traditional method of using Pythagorean theorem. Guo Shoujing of this era also worked on spherical trigonometry for precise astronomical calculations. At this point of mathematical history, a lot of modern western mathematics were already discovered by Chinese mathematicians. Things grew quiet for a time until the thirteenth century Renaissance of Chinese math. This saw Chinese mathematicians solving equations with methods Europe would not know until the eighteenth century. The high point of this era came with Zhu Shijie's two books Suanxue qimeng and the Siyuan yujian. In one case he reportedly gave a method equivalent to Gauss's pivotal condensation.

Qin Jiushao (c. 1202–1261) was the first to introduce the zero symbol into Chinese mathematics. Before this innovation, blank spaces were used instead of zeros in the system of counting rods. One of the most important contribution of Qin Jiushao was his method of solving high order numerical equations. Referring to Qin's solution of a 4th order equation, Yoshio Mikami put it: "Who can deny the fact of Horner's illustrious process being used in China at least nearly six long centuries earlier than in Europe?" Qin also solved a 10th order equation.

Pascal's triangle was first illustrated in China by Yang Hui in his book Xiangjie Jiuzhang Suanfa (详解九章算法), although it was described earlier around 1100 by Jia Xian. Although the Introduction to Computational Studies (算学启蒙) written by Zhu Shijie (fl. 13th century) in 1299 contained nothing new in Chinese algebra, it had a great impact on the development of Japanese mathematics.

Algebra

Ceyuan haijing

Li Ye's inscribed circle in triangle:Diagram of a round town

 

Yang Hui's magic concentric circles – numbers on each circle and diameter (ignoring the middle 9) sum to 138

Ceyuan haijing (pinyin: Cèyuán Hǎijìng) (Chinese characters:測圓海鏡), or Sea-Mirror of the Circle Measurements, is a collection of 692 formula and 170 problems related to inscribed circle in a triangle, written by Li Zhi (or Li Ye) (1192–1272 AD). He used Tian yuan shu to convert intricated geometry problems into pure algebra problems. He then used fan fa, or Horner's method, to solve equations of degree as high as six, although he did not describe his method of solving equations. "Li Chih (or Li Yeh, 1192–1279), a mathematician of Peking who was offered a government post by Khublai Khan in 1206, but politely found an excuse to decline it. His Ts'e-yuan hai-ching (Sea-Mirror of the Circle Measurements) includes 170 problems dealing with[...]some of the problems leading to polynomial equations of sixth degree. Although he did not describe his method of solution of equations, it appears that it was not very different from that used by Chu Shih-chieh and Horner. Others who used the Horner method were Ch'in Chiu-shao (ca. 1202 – ca.1261) and Yang Hui (fl. ca. 1261–1275).

Jade Mirror of the Four Unknowns

Facsimile of Zhu Shijie's Jade Mirror of Four Unknowns

Si-yüan yü-jian (四元玉鑒), or Jade Mirror of the Four Unknowns, was written by Zhu Shijie in 1303 AD and marks the peak in the development of Chinese algebra. The four elements, called heaven, earth, man and matter, represented the four unknown quantities in his algebraic equations. It deals with simultaneous equations and with equations of degrees as high as fourteen. The author uses the method of fan fa, today called Horner's method, to solve these equations.

There are many summation series equations given without proof in the Mirror. A few of the summation series are:

${\displaystyle 1^{2}+2^{2}+3^{2}+\cdots +n^{2}={n(n+1)(2n+1) \over 3!}}$

${\displaystyle 1+8+30+80+\cdots +{n^{2}(n+1)(n+2) \over 3!}={n(n+1)(n+2)(n+3)(4n+1) \over 5!}}$

Mathematical Treatise in Nine Sections

Shu-shu chiu-chang, or Mathematical Treatise in Nine Sections, was written by the wealthy governor and minister Ch'in Chiu-shao (ca. 1202 – ca. 1261 AD) and with the invention of a method of solving simultaneous congruences, it marks the high point in Chinese indeterminate analysis.

Magic squares and magic circles

The earliest known magic squares of order greater than three are attributed to Yang Hui (fl. ca. 1261–1275), who worked with magic squares of order as high as ten. He also worked with magic circle.

Trigonometry

The embryonic state of trigonometry in China slowly began to change and advance during the Song Dynasty (960–1279), where Chinese mathematicians began to express greater emphasis for the need of spherical trigonometry in calendarical science and astronomical calculations. The polymath Chinese scientist, mathematician and official Shen Kuo (1031–1095) used trigonometric functions to solve mathematical problems of chords and arcs. Victor J. Katz writes that in Shen's formula "technique of intersecting circles", he created an approximation of the arc of a circle s by s = c + 2v²/d, where d is the diameter, v is the versine, c is the length of the chord c subtending the arc. Sal Restivo writes that Shen's work in the lengths of arcs of circles provided the basis for spherical trigonometry developed in the 13th century by the mathematician and astronomer Guo Shoujing (1231–1316). As the historians L. Gauchet and Joseph Needham state, Guo Shoujing used spherical trigonometry in his calculations to improve the calendar system and Chinese astronomy. Along with a later 17th-century Chinese illustration of Guo's mathematical proofs, Needham states that:

Guo used a quadrangular spherical pyramid, the basal quadrilateral of which consisted of one equatorial and one ecliptic arc, together with two meridian arcs, one of which passed through the summer solstice point...By such methods he was able to obtain the du lü (degrees of equator corresponding to degrees of ecliptic), the ji cha (values of chords for given ecliptic arcs), and the cha lü (difference between chords of arcs differing by 1 degree).

Ming mathematics

Ming dynasty selected intellectuals by eight-legged essays in the imperial examinations which neglected and marginalized the development of mathematics. Due to the restriction on new ideologies, especially those confronting Confucianism, the scholars in the Ming dynasty paid less attention to mathematics. Gu Yingxiang and Tang Shunzhi were the leading figures of Chinese mathematics in the Ming dynasty but they knew little about Tian yuan shu or Increase multiply method. In 1450, the Ming mathematician Wu Jing wrote The Annotations of Calculations in the Nine Chapters on the Mathematical Art by collecting and compiling the mathematical calculation problems from the previous dynasties and discarding Tian yuan shu and the increase multiply method.

However, zhusuan, the arithmetic calculation through abacus, gained popularity during the Ming dynasty which was credited with a group of relevant texts. Suanfa Tongzong (General Source of Computational Methods), written by Cheng Dawei (1533-1606) in 1592, stood out and was widely adopted to the development of commerce. This text comprised 17 volumes and 595 entries, presenting a detailed and explicit picture of abacus calculation. Suanfa Tongzong has been reprinted and adapted for over 300 years, enjoying a widespread prestige in the Chinese mathematics society. In the late 16th century, the European missionaries such as Matteo Ricci came to China and translated Euclid's Elements to Chinese with Xu Guangqi. Afterwards, missionaries introduced some elementary mathematical knowledge such as trigonometry and logarithm to China. From then Chinese mathematics started to clash with the west, which contributed to the exchange and collision of mathematical study between China and western countries.

Qing mathematics

There are many prestigious mathematicians during this period. Mei Wending (1633-1721) devoted himself to the cross-cultural mathematical study and delivered many treaties. His works were compiled by his grandson Mei Goucheng to Meishi Congshu Jiyang (The Compiled works of Mei). Among the 60 volumes of this book, mathematical research takes up 40 volumes, covering nearly all schools of Chinese mathematics at that time and having a profound impact on the further development of Qing mathematics. The Kangxi Emperor had a great interest in mathematics. Under his command, Mei Goucheng and three other outstanding mathematicians complied a 53-volume Shuli Jingyun (The Essence of Mathematical Study) which gave a systematic introduction of the introduced western mathematical knowledge. This book was officially printed in 1723. The Yongzheng Emperor acceded to the throne in 1723. He believed that the missionary from western countries would endanger his reign and delude his subjects. Therefore, he chased all western missionaries to Macao except some holding office in the royal court. Afterwards, the introduction of western mathematics became stagnant. During this period, Chinese mathematicians were reflecting on the study that they learned from western mathematics on one hand and compiling the classical Chinese mathematical works on another.

A turning point in Qing mathematics

In 1773, the Qianlong Emperor decided to compile Siku Quanshu (The Complete Library of the Four Treasuries). Dai Zhen (1724-1777) selected and proofread The Nine Chapters on the Mathematical Art from Yongle Encyclopedia and several other mathematical works from Han and Tang dynasties. The long-missing mathematical works from Song and Yuan dynasties such as Si-yüan yü-jian and Ceyuan haijing were also found and printed, which directly led to the wave of investigating and collecting Chinese classical mathematics during the reign of Qianlong Emperor and Jiaqing Emperor. The most annotated work were Jiuzhang suanshu xicaotushuo (The Illustrations of Calculation Process forThe Nine Chapters on the Mathematical Art ) contributed by Li Huang and Siyuan yujian xicao (The Detailed Explanation of Si-yuan yu-jian) by Luo Shilin. They were two extraordinary scholars in Chinese mathematics of that time.

Late Imperial developments

The word "abacus" was first mentioned by Xu Yue(160–220) in his book suanshu jiyi (算数记遗), or Notes on Traditions of Arithmetic Methods, in Hang Dynasty. As it described, the original abacus had five beads (suan zhu) bunched by a stick in each column, separated by a transverse rod, and arrayed in a wooden rectangle box. One in the upper part represents five and each of four in the lower part represents one. People move the beads to do the calculation.

After the overthrow of the Yuan Dynasty, China became suspicious of knowledge it used. The Ming Dynasty turned away from math and physics in favor of botany and pharmacology.

In 15 century, abacus came into its suan pan form and overtook the counting rods and became the preferred computing device, spreading among merchants to the other countries. It is easy to use and carry, which also provides fast and accurate operation. Zhu Zaiyu, Prince of Zheng who invented the equal temperament used 81 position abacus to calculate the square root and cubic root of 2 to 25 figure accuracy.

Although this switch from counting rods to the abacus allowed for reduced computation times, it may have also led to the stagnation and decline of Chinese mathematics. The pattern rich layout of counting rod numerals on counting boards inspired many Chinese inventions in mathematics, such as the cross multiplication principle of fractions and methods for solving linear equations. Similarly, Japanese mathematicians were influenced by the counting rod numeral layout in their definition of the concept of a matrix. However, during the Ming dynasty, mathematicians were fascinated with perfecting algorithms for the abacus. As such, many works devoted to abacus mathematics appeared in this period; at the expense of new idea creation.

Despite the achievements of Shen and Guo's work in trigonometry, another substantial work in Chinese trigonometry would not be published again until 1607, with the dual publication of Euclid's Elements by Chinese official and astronomer Xu Guangqi (1562–1633) and the Italian Jesuit Matteo Ricci (1552–1610).

A revival of mathematics in China began in the late nineteenth century, when Joseph Edkins, Alexander Wylie and Li Shanlan translated works on astronomy, algebra and differential-integral calculus into Chinese, published by London Missionary Press in Shanghai.

Post-Imperial Chinese mathematics

In 1840, the First Opium War forced China to open its door and looked at the outside world, which also led to an influx of western mathematical studies at a rate unrivaled in the previous centuries. In 1852, the Chinese mathematician Li Shanlan and the British missionary Alexander Wylie co-translated the later nine volumes of Elements, 13-volume Algebra and many other western mathematical works. Li Shanlan is the first Chinese mathematician who initiated the modern Chinese mathematical study. However, the post-imperial China witnessed economic intrusion from western countries and domestic social instability, which did not provide a good external environment for Chinese mathematicians to develop their research. The conventional Confucian scholars also had bias against and refused to delve in the western study. Due to the political chaos such as Hundred Days' Reform and New Culture Movement, the research on classical Chinese mathematics was abruptly broken off, and the following Chinese mathematical study was incorporated into the mainstream modern mathematics.

Modern Chinese mathematics

Chinese mathematics experienced a great surge of revival following the establishment of a modern Chinese republic in 1912. Ever since then, modern Chinese mathematicians have made numerous achievements in various mathematical fields.

Some famous modern ethnic Chinese mathematicians include:

• Shiing-Shen Chern was widely regarded as a leader in geometry and one of the greatest mathematicians of the twentieth century and was awarded the Wolf prize for his immense number of mathematical contributions.
• Ky Fan, made a tremendous number of fundamental contributions to many different fields of mathematics. His work in fixed point theory, in addition to influencing nonlinear functional analysis, has found wide application in mathematical economics and game theory, potential theory, calculus of variations, and differential equations.
• Shing-Tung Yau, his contributions have influenced both physics and mathematics, and he has been active at the interface between geometry and theoretical physics and subsequently awarded the Fields medal for his contributions.
• Terence Tao, an ethnic Chinese child prodigy who received his master's degree at just the age of 16, was the youngest participant in the International Mathematical Olympiad's entire history, first competing at the age of ten, winning a bronze, silver, and gold medal. He remains the youngest winner of each of the three medals in the Olympiad's history. He would go on to receive the Fields medal.
• Yitang Zhang, a number theorist who established the first finite bound on gaps between prime numbers.
• Chen Jingrun, a number theorist who proved that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime (the product of two primes) which is now called Chen's theorem .^[70] His work was known as a milestone in the research of Goldbach's conjecture.

Performance at the IMO

In comparison to other participating countries at the International Mathematical Olympiad, China has highest team scores and the won the all-members-gold IMO with a full team the most number of times.

Abacus-based Mental Calculation

By learning how to calculate with abacus, one can improve his mental calculation which becomes faster and more accurate in doing large number calculations. Abacus‐based mental calculation (AMC) was derived from the abacus which means doing calculation, including addition, subtraction, multiplication, and division, in mind with an imaged abacus. It is a high-level cognitive skill that run through calculations with an effective algorithm. People doing long-term AMC training shows higher numerical memory capacity and has more effectively connected neural pathways. They are able to retrieve memory to deal with complex processes to calculate. The processing of AMC involves both the visuospatial and visuomotor processing which generate the visual abacus and perform the movement of the imagery bead. Since the only thing needed to be remembered is the finial position of beads, it takes less memory and less computation time.

Mathematical texts

Zhou Dynasty
 
Zhoubi Suanjing c. 1000 BCE-100 CE

• Astronomical theories, and computation techniques
• Proof of the Pythagorean theorem (Shang Gao Theorem)
• Fractional computations
• Pythagorean theorem for astronomical purposes

Nine Chapters on the Mathematical Art 1000 BCE? – 50 CE

• ch.1, computational algorithm, area of plane figures, GCF, LCD
• ch.2, proportions
• ch.3, proportions
• ch.4, square, cube roots, finding unknowns
• ch.5, volume and usage of pi as 3
• ch.6, proportions
• ch,7, interdeterminate equations
• ch.8, Gaussian elimination and matrices
• ch.9, Pythagorean theorem (Gougu Theorem)

Han Dynasty
 
Book on Numbers and Computation 202 BC-186 BC

• Calculation of the volume of various 3-dimensional shapes
• Calculation of unknown side of rectangle, given area and one side
• Using the false position method for finding roots and the extraction of approximate square roots
• Conversion between different units

Mathematics in education

The first reference to a book being used in learning mathematics in China is dated to the second century CE (Hou Hanshu: 24, 862; 35,1207). We are told that Ma Xu (a youth ca 110) and Zheng Xuan (127-200) both studied the Nine Chapters on Mathematical procedures. C.Cullen claims that mathematics, in a manner akin to medicine, was taught orally. The stylistics of the Suàn shù shū from Zhangjiashan suggest that the text was assembled from various sources and then underwent codification.

Chinese astronomy

From Wikipedia, the free encyclopedia

The Dunhuang map from the Tang Dynasty (North Polar region). This map is thought to date from the reign of Emperor Zhongzong of Tang (705–710). Founded in Dunhuang, Gansu. Constellations of the three schools were distinguished with different colors: white, black and yellow for stars of Wu Xian, Gan De and Shi Shen respectively. The whole set of star maps contained 1,300 stars.

Astronomy in China has a long history, beginning from the Shang Dynasty (Chinese Bronze Age). Star names later categorized in the twenty-eight mansions have been found on oracle bones unearthed at Anyang, dating back to the middle Shang Dynasty, and the mansion (xiù:宿) system's nucleus seems to have taken shape by the time of the ruler Wu Ding (1339-1281 BCE).

Detailed records of astronomical observations began during the Warring States period (fourth century BCE) and flourished from the Han period onward. Chinese astronomy was equatorial, centered as it was on close observation of circumpolar stars, and was based on different principles from those prevailing in traditional Western astronomy, where heliacal risings and settings of zodiac constellations formed the basic ecliptic framework. Needham has described the ancient Chinese as the most persistent and accurate observers of celestial phenomena anywhere in the world before the Islamic astronomers.

Some elements of Indian astronomy reached China with the expansion of Buddhism after the Eastern Han Dynasty (25–220 CE), but the most detailed incorporation of Indian astronomical thought occurred during the Tang Dynasty (618-907 CE), when numerous Indian astronomers took up residence in the Chinese capital, and Chinese scholars, such as the Tantric Buddhist monk and mathematician Yi Xing, mastered its system. Islamic astronomers collaborated closely with their Chinese colleagues during the Yuan Dynasty, and, after a period of relative decline during the Ming Dynasty, astronomy was revitalized under the stimulus of Western cosmology and technology after the Jesuits established their missions. The telescope was introduced in the seventeenth century. In 1669, the Peking observatory was completely redesigned and refitted under the direction of Ferdinand Verbiest. Today, China continues to be active in astronomy, with many observatories and its own space program.

Early history

Purpose of astronomical observations in the past

Wide view of the Crab Nebula.

One of the main functions was for the purpose of timekeeping. The Chinese used a lunisolar calendar, but, because the cycles of the sun and the moon are different, intercalation had to be done.
The Chinese calendar was considered to be a symbol of a dynasty. As dynasties would rise and fall, astronomers and astrologers of each period would often prepare a new calendar to be made, with observations for that purpose.

Astrological divination was also an important part of astronomy. Astronomers took careful note of guest stars, which suddenly appeared among the fixed stars. The supernova that created the Crab Nebula observed in 1054, now known as the SN 1054, is an example of a guest star observed by Chinese astronomers, recorded also by the Arab astronomers, although it was not recorded by their European contemporaries. Ancient astronomical records of phenomena like comets and supernovae are sometimes used in modern astronomical studies.

Indian influence

Indian astronomy reached China with the expansion of Buddhism during the Later Han (25–220 CE). Further translation of Indian works on astronomy was completed in China by the Three Kingdoms era (220–265 CE).^[5] However, the most detailed incorporation of Indian astronomy occurred only during the Tang Dynasty (618–907 CE) when a number of Chinese scholars—such as Yi Xing— were versed both in Indian and Chinese astronomy. A system of Indian astronomy was recorded in China as Jiuzhi-li (718 CE), the author of which was an Indian by the name of Qutan Xida—a translation of Devanagari Gotama Siddha—the director of the Tang dynasty's national astronomical observatory.During the 8th century, the astronomical table of sines by the Indian astronomer and mathematician, Aryabhatta (476-550), were translated into the Chinese astronomical and mathematical book of the Treatise on Astrology of the Kaiyuan Era (Kaiyuan Zhanjing), compiled in 718 CE during the Tang Dynasty. The Kaiyuan Zhanjing was compiled by Gautama Siddha, an astronomer and astrologer born in Chang'an, and whose family was originally from India. He was also notable for his translation of the Navagraha calendar into Chinese. Gautama Siddha introduced Indian numerals with zero (〇) in 718 in China as a replacement of counting rods. In 3rd-century C.E, the Matanaga avadha was translated into Chinese.although the original is believed to date earlier. It gives the lengths of monthly shadows of a 12-inch gnomon, which is the standard parameter of Indian astronomy.The work also mentions the 28 Indian nakshatras. In the beginning of the second century, Sardulakarnavadana was translated into Chinese several times, This work contains the usual Sanskrit names of the 28 nakshatras. starting with krttika. From the 1st century onward Lalitavistara was translated into Chinese several times. It is in this work that the famous Buddhist centesimal-scale counting occurs during the dialogue between Prince Gautamaand and the mathematician Arjuna. The first series of counts ends with tallaksana (= 10⁵³), beyond which eight more ganana series are mentioned.Atomic-scale counting is also mentioned.The Mahaprajnaparamita Sastra (of Nagarjuna, second century) was translated into Chinese by Kumarajiva in the early fifth century.16 The astronomical parameters mentioned in this translation are comparable to those given in the Vedanga Jyotisha.Indian system of numeration appeared in the Chinese work Ta PaoChi Ching (Maharatnakuta Sutra), translated by Upasunya (in 541 c.e.) The Chinese translations of the following works are mentioned in the Sui Shu, or Official History of the Sui Dynasty (seventh century):

• Po-lo-men Thien Wen Ching (Brahminical Astronomical Classic) in 21 books.
• Po-lo-men Chieh-Chhieh Hsien-jen Thien Wen Shuo (Astronomical Theories of

Brahman.a Chieh-Chhieh Hsienjen) in 30 books.

• Po-lo-men Thien Ching (Brahminical Heavenly Theory) in one book.
• Mo-teng-Chia Ching Huang-thu (Map of Heaven and Earth in the Matangi Sutra) in one

book.

• Po-lo-men Suan Ching (Brahminical Arithmetical Classic) in three books.
• Po-lo-men Suan Fa (Brahminical Arithmetical Rules) in one book.
• Po-lo-men Ying Yang Suan Ching (Brahminical Method of Calculating Time)

Although these translations are lost, they were also mentioned in other sources.

Cosmology

The Chinese developed three cosmological models:

• The Gai Tian, or hemispherical dome, model conceived the heavens as a hemisphere lying over a dome-shaped earth.
• The second cosmological model, associated with the Hun Tian school, saw the heavens as a celestial sphere not unlike the spherical models developed in the Greek and Hellenistic traditions.
• The third cosmology, associated with the Xuan Ye school, viewed the heavens as infinite in extent and the celestial bodies as floating about at rare intervals, and "the speed of the luminaries depends on their individual natures, which shows they are not attached to anything."

Constellations

The divisions of the sky began with the Northern Dipper and the 28 mansions.

In 1977, a lacquer box was excavated from the tomb of Yi, the marquis of Zeng, in Suixian, Hubei Province. Names of the 28 lunar mansions were found on the cover of the box, proving that the use of this classification system was made before 433 BCE.

As lunar mansions have such an ancient origin, the meanings of most of their names have become obscure. Even worse, the name of each lunar mansion consists of only one Chinese word, the meaning of which could vary at different times in history. The meanings of the names are still under discussion.

Besides the 28 lunar mansions, most constellations are based on the works of Shi Shen-fu and Gan De, who were astrologists during the period of Warring States (481 BCE - 221 BCE) in China.

In the late period of the Ming Dynasty, the agricultural scientist and mathematician Xu Guangqi (1562 - 1633 CE) introduced 23 additional constellations near to the Celestial South Pole, which are based on star catalogues from the West.

Star catalogues and maps

Star catalogues

In the fourth century BCE, the two Chinese astronomers responsible for the earliest information going into the star catalogues were Shi Shen and Gan De of the Warring States period.

Author	Translated name	Chinese catalogue name	Pinyin
Shi Shen	Shi Shen astronomy	石申天文	Shi Shen tianwen
Gan De	Astronomic star observation	天文星占	Tianwen xingzhan

These books appeared to have lasted until the sixth century, but were lost after that. A number of books share similar names, often quoted and named after them. These texts should not be confused with the original catalogues written by them. Notable works that helped preserve the contents include:

Author	Translated name	Chinese name	Pinyin	Comments
Sima Qian	Book of Celestial Offices	天官書	Tianguan shu	This is the astronomical chapter of the Records of the Grand Historian, a massive history compiled during the late 2nd century BCE by the Han-era scholar and official Sima Qian. This chapter provides a star catalogue and discusses the schools of Gan De and Shi Shen.
Ma Xian (馬顯)	Star Manual of the Masters Gan and Shi	甘石星經	Gan Shi Xingjing	Despite having the name credited to Shi and Gan, it was lost and later compiled circa 579 CE as an appendix to the Treatise on Astrology of the Kaiyuan Era, and summarized in the book 郡齋讀書志.
	Book of Jin	晉書	Jin shu	In the astronomical chapters of the text
	Book of Sui	隋書	Sui shu
Gautama Siddha	Treatise on Astrology of the Kaiyuan Era	開元占經	Kaiyuan Zhanjing	During the reign of Emperor Xuanzong of Tang (712-756 CE). After analyzing and providing a summary on the work of Gan De and Shi Shen, Tang era astronomers mentioned the names of more than 800 stars that were found, 121 of them marked with positions. The astronomical table of sines by the Indian astronomer and mathematician Aryabhata were also translated into the Kaiyuan Zhanjing.
	The Great Firmament Star Manual Common to Astrology	通占大象曆星經	Tongzhan taxiangli xingjing	This renamed star manual is incorporated in the Taoist book Daozang.

Wu Xian (巫咸) has been one of the astronomers in debate. He is often represented as one of the "Three Schools Astronomical tradition" along with Gan and Shi. The Chinese classic text Star Manual of Master Wu Xian (巫咸星經) and its authorship is still in dispute, because it mentioned names of twelve countries that did not exist in the Shang Dynasty, the era of which it was supposed to have been written. Moreover, it was customary in the past for the Chinese to forge works of notable scholars, as this could lead to a possible explanation for the inconsistencies found. Wu Xian is generally mentioned as the astronomer who lived many years before Gan and Shi.

The Han Dynasty astronomer and inventor Zhang Heng (78-139 CE) not only catalogued some 2500 different stars, but also recognized more than 100 different constellations. Zhang Heng also published his work Ling Xian, a summary of different astronomical theories in China at the time. In the subsequent period of the Three Kingdoms (220-280 CE), Chen Zhuo (陳卓) combined the work of his predecessors, forming another star catalogue. This time, 283 constellations and 1464 stars were listed. The astronomer Guo Shoujin of the Yuan Dynasty (1279-1368 CE) created a new catalogue, which was believed to contain thousands of stars. Unfortunately, many of the documents of that period were destroyed, including that of Shoujin. Imperial Astronomical Instruments (儀象考成) was published in 1757 and contains 3083 stars exactly.

Star maps

A star map with a cylindrical projection. Su Song's star maps represent the oldest existent ones in printed form.

The Chinese drew many maps of stars in the past centuries. It is debatable as to which counts as the oldest star maps, since pottery and old artifacts can also be considered star maps. One of the oldest existent star maps in printed form is from Su Song's (1020-1101 CE) celestial atlas of 1092 CE, which was included in the horological treatise on his clocktower. The most famous one is perhaps the Dunhuang map found in Dunhuang, Gansu. Uncovered by the British archaeologist Marc Aurel Stein in 1907, the star map was brought to the British Museum in London. The map was drawn on paper and represents the complete sky, with more than 1,350 stars. Although ancient Babylonians and Greeks also observed the sky and catalogued stars, no such complete record of the stars may exist or survive. Hence, this is the oldest chart of the skies at present.

According to recent studies, the map may date the manuscript to as early as the seventh century CE (Tang Dynasty). Scholars believe the star map dating from 705 to 710 CE, which is the reign of Emperor Zhongzong of Tang. There are some texts (Monthly Ordinances, 月令) describing the movement of the sun among the sky each month, which was not based on the observation at that time.

Solar and lunar eclipses

Chinese astronomers recorded 1,600 observations of solar and lunar eclipses from 750 BCE. The ancient Chinese astronomer Shi Shen (fl. fourth century BCE) was aware of the relation of the moon in a solar eclipse, as he provided instructions in his writing to predict them by using the relative positions of the moon and the sun. The radiating-influence theory, where the moon's light was nothing but a reflection of the sun's, was supported by the mathematician and music theorist Jing Fang (78–37 BCE), yet opposed by the Chinese philosopher Wang Chong (27–97 CE), who made clear in his writing that this theory was nothing new. Jing Fang wrote:

The moon and the planets are Yin; they have shape but no light. This they receive only when the sun illuminates them. The former masters regarded the sun as round like a crossbow bullet, and they thought the moon had the nature of a mirror. Some of them recognized the moon as a ball too. Those parts of the moon which the sun illuminates look bright, those parts which it does not, remain dark.

The ancient Greeks had known this as well, since Parmenides and Aristotle supported the theory of the moon shining because of reflected light. The Chinese astronomer and inventor Zhang Heng (78–139 CE) wrote of both solar eclipse and lunar eclipse in the publication of Ling Xian (靈憲), 120 CE:

The sun is like fire and the moon like water. The fire gives out light and the water reflects it. Thus the moon's brightness is produced from the radiance of the sun, and the moon's darkness (pho) is due to (the light of) the sun being obstructed (pi). The side which faces the sun is fully lit, and the side which is away from it is dark. The planets (as well as the moon) have the nature of water and reflect light. The light pouring forth from the sun (tang jih chih chhung kuang) does not always reach the moon owing to the obstruction (pi) of the earth itself—this is called 'an-hsü', a lunar eclipse. When (a similar effect) happens with a planet (we call it) an occulation (hsing wei); when the moon passes across (kuo) (the sun's path) then there is a solar eclipse (shih).

The later Song Dynasty scientist Shen Kuo (1031–1095 CE) used the models of lunar eclipse and solar eclipse in order to prove that the celestial bodies were round, not flat. This was an extension of the reasoning of Jing Fang and other theorists as early as the Han Dynasty. In his Dream Pool Essays of 1088  CE, Shen related a conversation he had with the director of the Astronomical Observatory, who had asked Shen if the shapes of the sun and the moon were round like balls or flat like fans. Shen Kuo explained his reasoning for the former:

If they were like balls they would surely obstruct each other when they met. I replied that these celestial bodies were certainly like balls. How do we know this? By the waxing and waning of the moon. The moon itself gives forth no light, but is like a ball of silver; the light is the light of the sun (reflected). When the brightness is first seen, the sun (-light passes almost) alongside, so the side only is illuminated and looks like a crescent. When the sun gradually gets further away, the light shines slanting, and the moon is full, round like a bullet. If half of a sphere is covered with (white) powder and looked at from the side, the covered part will look like a crescent; if looked at from the front, it will appear round. Thus we know that the celestial bodies are spherical.

When he asked Shen Kuo why eclipses occurred only on an occasional basis while in conjunction and opposition once a day, Shen Kuo wrote:

I answered that the ecliptic and the moon's path are like two rings, lying one over the other, but distant by a small amount. (If this obliquity did not exist), the sun would be eclipsed whenever the two bodies were in conjunction, and the moon would be eclipsed whenever they were exactly in opposition. But (in fact) though they may occupy the same degree, the two paths are not (always) near (each other), and so naturally the bodies do not (intrude) upon one another.

Equipment and innovation

Armillary sphere (渾儀)

A method of making observation instruments at the times of Qing Dynasty

The earliest development of the armillary sphere in China goes back to the 1st century BCE,^[28] as they were equipped with a primitive single-ring armillary instrument. This would have allowed them to measure the north polar distance (去極度, the Chinese form of declination) and measurement that gave the position in a hsiu (入宿度, the Chinese form of right ascension).

During the Western Han Dynasty (202 BC-9 CE), additional developments made by the astronomers Luo Xiahong (落下閎), Xiangyu Wangren, and Geng Shouchang (耿壽昌) advanced the use of the armillary in its early stage of evolution. In 52 BCE, it was the astronomer Geng Shou-chang who introduced the fixed equatorial ring to the armillary sphere. In the subsequent Eastern Han Dynasty (23-220  CE) period, the astronomers Fu An and Jia Kui added the elliptical ring by 84 CE. With the famous statesman, astronomer, and inventor Zhang Heng (78-139 CE), the sphere was totally completed in 125 CE, with horizon and meridian rings.^[29] It is of great importance to note that the world's first hydraulic (i.e., water-powered) armillary sphere was created by Zhang Heng, who operated his by use of an inflow clepsydra clock.

Abridged armilla (簡儀)

Designed by famous astronomer Guo Shoujing in 1276 AD, it solved most problems found in armillary spheres at that time.

The primary structure of abridged armilla contains two large rings that are perpendicular to each other, of which one is parallel with the equatorial plane and is accordingly called "equatorial ring", and the other is a double ring that is perpendicular to the center of the equatorial ring, revolving around a metallic shaft, and is called "right ascension double ring".

The double ring holds within itself a sighting tube with crosshairs. When observing, astronomers would aim at the star with the sighting tube, whereupon the star's position could be deciphered by observing the dials of the equatorial ring and the right ascension double ring.

A foreign missionary melted the instrument in 1715 CE. The surviving one was built in 1437 CE and was taken to what is now Germany. It was then stored in a French Embassy in 1900, during the Eight-Nation Alliance. Under the pressure of international public discontent, Germany returned the instrument to China. In 1933, it was placed in Purple Mountain Observatory, which prevented it from being destroyed in the Japanese invasion of China. In the 1980s, it had become seriously eroded and rusted down and was nearly destroyed. In order to restore the device, the Nanjing government spent 11 months to repair it.

Celestial globe (渾象) before Qing Dynasty

Celestial globe from Qing Dynasty

Besides star maps, the Chinese also made celestial globes, which show stars' positions like a star map and can present the sky at a specific time. Because of its Chinese name, it is often confused with the armillary sphere, which is just one word different in Chinese (渾象 vs. 渾儀).

According to records, the first celestial globe was made by Geng Shou-chang (耿壽昌) between 70 BC and 50 BCE. In the Ming Dynasty, the celestial globe at that time was a huge globe, showing the 28 mansions, celestial equator and ecliptic. None of them have survived.

Celestial globe (天體儀) in the Qing Dynasty

Celestial globes were named 天體儀 ("Miriam celestial bodies") in the Qing Dynasty. The one in Beijing Ancient Observatory was made by Belgian missionary Ferdinand Verbiest (南懷仁) in 1673 CE. Unlike other Chinese celestial globes, it employs 360 degrees rather than the 365.24 degrees (which is a standard in ancient China). It is also the first Chinese globe that shows constellations near to the Celestial South Pole.

The water-powered armillary sphere and celestial globe tower (水運儀象台)

The inventor of the hydraulic-powered armillary sphere was Zhang Heng (78-139 CE) of the Han Dynasty. Zhang was well known for his brilliant applications of mechanical gears, as this was one of his most impressive inventions (alongside his seismograph to detect the cardinal direction of earthquakes that struck hundreds of miles away).

Started by Su Song (蘇頌) and his colleagues in 1086 CE and finished in 1092 CE, his large astronomical clock tower featured an armillary sphere (渾儀), a celestial globe (渾象) and a mechanical chronograph. It was operated by an escapement mechanism and the earliest known chain drive. However, 35 years later, the invading Jurchen army dismantled the tower in 1127 CE upon taking the capital of Kaifeng. The armillary sphere part was brought to Beijing, yet the tower was never successfully reinstated, not even by Su Song's son.

Fortunately, two versions of Su Song's treatise written on his clock tower have survived the ages, so that studying his astronomical clock tower is made possible through medieval texts.

True north and planetary motion

The polymath Chinese scientist Shen Kuo (1031–1095 CE) was not only the first in history to describe the magnetic-needle compass, but also made a more accurate measurement of the distance between the pole star and true north that could be used for navigation. Shen achieved this by making nightly astronomical observations along with his colleague Wei Pu, using Shen's improved design of a wider sighting tube that could be fixed to observe the pole star indefinitely. Along with the pole star, Shen Kuo and Wei Pu also established a project of nightly astronomical observation over a period of five successive years, an intensive work that even would rival the later work of Tycho Brahe in Europe. Shen Kuo and Wei Pu charted the exact coordinates of the planets on a star map for this project and created theories of planetary motion, including retrograde motion.

Foreign influences

Indian astronomy

Buddhism first reached China during the Eastern Han Dynasty, and translation of Indian works on astronomy came to China by the Three Kingdoms era (220–265 CE). However, the most detailed incorporation of Indian astronomy occurred only during the Tang Dynasty (618-907), when a number of Chinese scholars—such as Yi Xing—were versed both in Indian and Chinese astronomy. A system of Indian astronomy was recorded in China as Jiuzhi-li (718 CE), the author of which was an Indian by the name of Qutan Xida—a translation of Devanagari Gotama Siddha—the director of the Tang dynasty's national astronomical observatory.

The astronomical table of sines by the Indian astronomer and mathematician Aryabhatan was translated into the Chinese astronomical and mathematical book Treatise on Astrology of the Kaiyuan Era (Kaiyuan Zhanjing), compiled in 718 CE during the Tang Dynasty. The Kaiyuan Zhanjing was compiled by Gautama Siddha, an astronomer and astrologer born in Chang'an, and whose family was originally from India. He was also notable for his translation of the Navagraha calendar into Chinese.

Islamic astronomy in East Asia

Early European drawing of the Beijing Ancient Observatory.

 

Gaocheng Astronomical Observatory. It was built in 1276.

 

Islamic influence on Chinese astronomy was first recorded during the Song dynasty when a Hui Muslim astronomer named Ma Yize introduced the concept of 7 days in a week and made other contributions.

Islamic astronomers were brought to China in order to work on calendar making and astronomy during the Mongol Empire and the succeeding Yuan Dynasty. The Chinese scholar Yelü Chucai accompanied Genghis Khan to Persia in 1210 and studied their calendar for use in the Mongol Empire. Kublai Khan brought Iranians to Beijing to construct an observatory and an institution for astronomical studies.

Several Chinese astronomers worked at the Maragheh observatory, founded by Nasir al-Din al-Tusi in 1259 under the patronage of Hulagu Khan in Persia. One of these Chinese astronomers was Fu Mengchi, or Fu Mezhai.

In 1267, the Persian astronomer Jamal ad-Din, who previously worked at Maragha observatory, presented Kublai Khan with seven Persian astronomical instruments, including a terrestrial globe and an armillary sphere, as well as an astronomical almanac, which was later known in China as the Wannian Li ("Ten Thousand Year Calendar" or "Eternal Calendar"). He was known as "Zhama Luding" in China, where, in 1271, he was appointed by Khan as the first director of the Islamic observatory in Beijing, known as the Islamic Astronomical Bureau, which operated alongside the Chinese Astronomical Bureau for four centuries. Islamic astronomy gained a good reputation in China for its theory of planetary latitudes, which did not exist in Chinese astronomy at the time, and for its accurate prediction of eclipses.

Some of the astronomical instruments constructed by the famous Chinese astronomer Guo Shoujing shortly afterwards resemble the style of instrumentation built at Maragheh. In particular, the "simplified instrument" (jianyi) and the large gnomon at the Gaocheng Astronomical Observatory show traces of Islamic influence. While formulating the Shoushili calendar in 1281, Shoujing's work in spherical trigonometry may have also been partially influenced by Islamic mathematics, which was largely accepted at Kublai's court. These possible influences include a pseudo-geometrical method for converting between equatorial and ecliptic coordinates, the systematic use of decimals in the underlying parameters, and the application of cubic interpolation in the calculation of the irregularity in the planetary motions.

Emperor Taizu (r. 1368-1398) of the Ming Dynasty (1328–1398), in the first year of his reign (1368), conscripted Han and non-Han astrology specialists from the astronomical institutions in Beijing of the former Mongolian Yuan to Nanjing to become officials of the newly established national observatory.

That year, the Ming government summoned for the first time the astronomical officials to come south from the upper capital of Yuan. There were fourteen of them. In order to enhance accuracy in methods of observation and computation, Emperor Taizu reinforced the adoption of parallel calendar systems, the Han and the Hui. In the following years, the Ming Court appointed several Hui astrologers to hold high positions in the Imperial Observatory. They wrote many books on Islamic astronomy and also manufactured astronomical equipment based on the Islamic system.

The translation of two important works into Chinese was completed in 1383: Zij (1366) and al-Madkhal fi Sina'at Ahkam al-Nujum, Introduction to Astrology (1004).

In 1384, a Chinese astrolabe was made for observing stars based on the instructions for making multi-purposed Islamic equipment. In 1385, the apparatus was installed on a hill in northern Nanjing.

Around 1384, during the Ming Dynasty, Emperor Zhu Yuanzhang ordered the Chinese translation and compilation of Islamic astronomical tables, a task that was carried out by the scholars Mashayihei, a Muslim astronomer, and Wu Bozong, a Chinese scholar-official. These tables came to be known as the Huihui Lifa (Muslim System of Calendrical Astronomy), which was published in China a number of times until the early 18th century, though the Qing Dynasty had officially abandoned the tradition of Chinese-Islamic astronomy in 1659. The Muslim astronomer Yang Guangxian was known for his attacks on the Jesuit's astronomical sciences.

Jesuit activity in China

The introduction of Western science to China by Jesuit priest astronomers was a mixed blessing during the late sixteenth century and early seventeenth century.

The telescope was introduced to China in the early seventeenth century. The telescope was first mentioned in Chinese writing by Manuel Dias the Younger (Yang Manuo), who wrote his Tian Wen Lüe in 1615. In 1626, Johann Adam Schall von Bell (Tang Ruowang) published the Chinese treatise on the telescope known as the Yuan Jing Shuo (The Far-Seeing Optic Glass). The Chongzhen Emperor (r 1627–1644) of the Ming dynasty acquired the telescope of Johannes Terrentius (or Johann Schreck; Deng Yu-han) in 1634, ten years before the collapse of the Ming Dynasty.^[40] However, the impact on Chinese astronomy was limited.

The Jesuit China missions of the sixteenth and seventeenth centuries brought Western astronomy, then undergoing its own revolution, to China and—via João Rodrigues's gifts to Jeong Duwon—to Joseon Korea. After the Galileo affair early in the seventeenth century, the Roman Catholic Jesuit order was required to adhere to geocentrism and ignore the heliocentric teachings of Copernicus and his followers, even though they were becoming standard in European astronomy. Thus, the Jesuits initially shared an Earth-centered and largely pre-Copernican astronomy with their Chinese hosts (i.e., the Ptolemaic-Aristotelian views from Hellenistic times). The Jesuits (such as Giacomo Rho) later introduced Tycho's geoheliocentric model as the standard cosmological model. The Chinese often were fundamentally opposed to this as well, since the Chinese had long believed (from the ancient doctrine of Xuan Ye) that the celestial bodies floated in a void of infinite space. This contradicted the Aristotelian view of solid concentric crystalline spheres, where there was not a void, but a mass of air between the heavenly bodies.

Of course, the views of Copernicus, Galileo, and Tycho Brahe would eventually triumph in European science, and these ideas slowly leaked into China despite Jesuit efforts to curb them in the beginning. In 1627, the Polish Jesuit Michael Boym (Bu Mige) introduced Johannes Kepler's Copernican Rudolphine Tables with much enthusiasm to the Ming court at Beijing. In Adam Schall von Bell's Chinese-written treatise of Western astronomy in 1640, the names of Copernicus (Ge-Bai-Ni), Galileo (Jia-li-lüe), and Tycho Brahe (Di-gu) were formally introduced to China. There were also Jesuits in China who were in favor of the Copernican theory, such as Nicholas Smogulecki and Wenceslaus Kirwitzer. However, Copernican views were not widespread or wholly accepted in China during this time.

Ferdinand Augustin Hallerstein (Liu Songling) created the first spherical astrolabe as the Head of the Imperial Astronomical Bureau from 1739 until 1774. The former Beijing Astronomical observatory, now a museum, still hosts the armillary sphere with rotating rings, which was made under Hallerstein’s leadership and is considered the most prominent astronomical instrument.

While in Edo Japan, the Dutch aided the Japanese with the first modern observatory of Japan in 1725, headed by Nakane Genkei, whose observatory of astronomers wholly accepted the Copernican view. In contrast, the Copernican view was not accepted in mainstream China until the early nineteenth century, with the Protestant missionaries such as Joseph Edkins, Alex Wylie, and John Fryer.