Mathematical model

From Wikipedia, the free encyclopedia

A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in the social sciences (such as economics, psychology, sociology, political science).

A model may help to explain a system and to study the effects of different components, and to make predictions about behavior.

Elements of a mathematical model

Mathematical models can take many forms, including dynamical systems, statistical models, differential equations, or game theoretic models. These and other types of models can overlap, with a given model involving a variety of abstract structures. In general, mathematical models may include logical models. In many cases, the quality of a scientific field depends on how well the mathematical models developed on the theoretical side agree with results of repeatable experiments. Lack of agreement between theoretical mathematical models and experimental measurements often leads to important advances as better theories are developed.

In the physical sciences, a traditional mathematical model contains most of the following elements:

1. Governing equations
2. Supplementary sub-models
   1. Defining equations
   2. Constitutive equations
3. Assumptions and constraints
   1. Initial and boundary conditions
   2. Classical constraints and kinematic equations

Classifications

Mathematical models are usually composed of relationships and variables. Relationships can be described by operators, such as algebraic operators, functions, differential operators, etc. Variables are abstractions of system parameters of interest, that can be quantified. Several classification criteria can be used for mathematical models according to their structure:

• Linear vs. nonlinear: If all the operators in a mathematical model exhibit linearity, the resulting mathematical model is defined as linear. A model is considered to be nonlinear otherwise. The definition of linearity and nonlinearity is dependent on context, and linear models may have nonlinear expressions in them. For example, in a statistical linear model, it is assumed that a relationship is linear in the parameters, but it may be nonlinear in the predictor variables. Similarly, a differential equation is said to be linear if it can be written with linear differential operators, but it can still have nonlinear expressions in it. In a mathematical programming model, if the objective functions and constraints are represented entirely by linear equations, then the model is regarded as a linear model. If one or more of the objective functions or constraints are represented with a nonlinear equation, then the model is known as a nonlinear model.
  Nonlinearity, even in fairly simple systems, is often associated with phenomena such as chaos and irreversibility. Although there are exceptions, nonlinear systems and models tend to be more difficult to study than linear ones. A common approach to nonlinear problems is linearization, but this can be problematic if one is trying to study aspects such as irreversibility, which are strongly tied to nonlinearity.
• Static vs. dynamic: A dynamic model accounts for time-dependent changes in the state of the system, while a static (or steady-state) model calculates the system in equilibrium, and thus is time-invariant. Dynamic models typically are represented by differential equations or difference equations.
• Explicit vs. implicit: If all of the input parameters of the overall model are known, and the output parameters can be calculated by a finite series of computations, the model is said to be explicit. But sometimes it is the output parameters which are known, and the corresponding inputs must be solved for by an iterative procedure, such as Newton's method (if the model is linear) or Broyden's method (if non-linear). In such a case the model is said to be implicit. For example, a jet engine's physical properties such as turbine and nozzle throat areas can be explicitly calculated given a design thermodynamic cycle (air and fuel flow rates, pressures, and temperatures) at a specific flight condition and power setting, but the engine's operating cycles at other flight conditions and power settings cannot be explicitly calculated from the constant physical properties.
• Discrete vs. continuous: A discrete model treats objects as discrete, such as the particles in a molecular model or the states in a statistical model; while a continuous model represents the objects in a continuous manner, such as the velocity field of fluid in pipe flows, temperatures and stresses in a solid, and electric field that applies continuously over the entire model due to a point charge.
• Deterministic vs. probabilistic (stochastic): A deterministic model is one in which every set of variable states is uniquely determined by parameters in the model and by sets of previous states of these variables; therefore, a deterministic model always performs the same way for a given set of initial conditions. Conversely, in a stochastic model—usually called a "statistical model"—randomness is present, and variable states are not described by unique values, but rather by probability distributions.
• Deductive, inductive, or floating: A deductive model is a logical structure based on a theory. An inductive model arises from empirical findings and generalization from them. The floating model rests on neither theory nor observation, but is merely the invocation of expected structure. Application of mathematics in social sciences outside of economics has been criticized for unfounded models. Application of catastrophe theory in science has been characterized as a floating model.

Significance in the natural sciences

Mathematical models are of great importance in the natural sciences, particularly in physics. Physical theories are almost invariably expressed using mathematical models.

Throughout history, more and more accurate mathematical models have been developed. Newton's laws accurately describe many everyday phenomena, but at certain limits relativity theory and quantum mechanics must be used; even these do not apply to all situations and need further refinement. It is possible to obtain the less accurate models in appropriate limits, for example relativistic mechanics reduces to Newtonian mechanics at speeds much less than the speed of light. Quantum mechanics reduces to classical physics when the quantum numbers are high. For example, the de Broglie wavelength of a tennis ball is insignificantly small, so classical physics is a good approximation to use in this case.

It is common to use idealized models in physics to simplify things. Massless ropes, point particles, ideal gases and the particle in a box are among the many simplified models used in physics. The laws of physics are represented with simple equations such as Newton's laws, Maxwell's equations and the Schrödinger equation. These laws are such as a basis for making mathematical models of real situations. Many real situations are very complex and thus modeled approximate on a computer, a model that is computationally feasible to compute is made from the basic laws or from approximate models made from the basic laws. For example, molecules can be modeled by molecular orbital models that are approximate solutions to the Schrödinger equation. In engineering, physics models are often made by mathematical methods such as finite element analysis.

Different mathematical models use different geometries that are not necessarily accurate descriptions of the geometry of the universe. Euclidean geometry is much used in classical physics, while special relativity and general relativity are examples of theories that use geometries which are not Euclidean.

Some applications

Since prehistorical times simple models such as maps and diagrams have been used.

Often when engineers analyze a system to be controlled or optimized, they use a mathematical model. In analysis, engineers can build a descriptive model of the system as a hypothesis of how the system could work, or try to estimate how an unforeseeable event could affect the system. Similarly, in control of a system, engineers can try out different control approaches in simulations.

A mathematical model usually describes a system by a set of variables and a set of equations that establish relationships between the variables. Variables may be of many types; real or integer numbers, boolean values or strings, for example. The variables represent some properties of the system, for example, measured system outputs often in the form of signals, timing data, counters, and event occurrence (yes/no). The actual model is the set of functions that describe the relations between the different variables.

Building blocks

In business and engineering, mathematical models may be used to maximize a certain output. The system under consideration will require certain inputs. The system relating inputs to outputs depends on other variables too: decision variables, state variables, exogenous variables, and random variables.

Decision variables are sometimes known as independent variables. Exogenous variables are sometimes known as parameters or constants. The variables are not independent of each other as the state variables are dependent on the decision, input, random, and exogenous variables. Furthermore, the output variables are dependent on the state of the system (represented by the state variables).

Objectives and constraints of the system and its users can be represented as functions of the output variables or state variables. The objective functions will depend on the perspective of the model's user. Depending on the context, an objective function is also known as an index of performance, as it is some measure of interest to the user. Although there is no limit to the number of objective functions and constraints a model can have, using or optimizing the model becomes more involved (computationally) as the number increases.

For example, economists often apply linear algebra when using input-output models. Complicated mathematical models that have many variables may be consolidated by use of vectors where one symbol represents several variables.

A priori information

To analyse something with a typical "black box approach",

only the behavior of the stimulus/response will be accounted

for, to infer the (unknown) box. The usual representation of

this black box system is a data flow diagram centered in the box.

Mathematical modeling problems are often classified into black box or white box models, according to how much a priori information on the system is available. A black-box model is a system of which there is no a priori information available. A white-box model (also called glass box or clear box) is a system where all necessary information is available. Practically all systems are somewhere between the black-box and white-box models, so this concept is useful only as an intuitive guide for deciding which approach to take.

Usually it is preferable to use as much a priori information as possible to make the model more accurate. Therefore, the white-box models are usually considered easier, because if you have used the information correctly, then the model will behave correctly. Often the a priori information comes in forms of knowing the type of functions relating different variables. For example, if we make a model of how a medicine works in a human system, we know that usually the amount of medicine in the blood is an exponentially decaying function. But we are still left with several unknown parameters; how rapidly does the medicine amount decay, and what is the initial amount of medicine in blood? This example is therefore not a completely white-box model. These parameters have to be estimated through some means before one can use the model.

In black-box models one tries to estimate both the functional form of relations between variables and the numerical parameters in those functions. Using a priori information we could end up, for example, with a set of functions that probably could describe the system adequately. If there is no a priori information we would try to use functions as general as possible to cover all different models. An often used approach for black-box models are neural networks which usually do not make assumptions about incoming data. Alternatively the NARMAX (Nonlinear AutoRegressive Moving Average model with eXogenous inputs) algorithms which were developed as part of nonlinear system identification  can be used to select the model terms, determine the model structure, and estimate the unknown parameters in the presence of correlated and nonlinear noise. The advantage of NARMAX models compared to neural networks is that NARMAX produces models that can be written down and related to the underlying process, whereas neural networks produce an approximation that is opaque.

Subjective information

Sometimes it is useful to incorporate subjective information into a mathematical model. This can be done based on intuition, experience, or expert opinion, or based on convenience of mathematical form. Bayesian statistics provides a theoretical framework for incorporating such subjectivity into a rigorous analysis: we specify a prior probability distribution (which can be subjective), and then update this distribution based on empirical data.

An example of when such approach would be necessary is a situation in which an experimenter bends a coin slightly and tosses it once, recording whether it comes up heads, and is then given the task of predicting the probability that the next flip comes up heads. After bending the coin, the true probability that the coin will come up heads is unknown; so the experimenter would need to make a decision (perhaps by looking at the shape of the coin) about what prior distribution to use. Incorporation of such subjective information might be important to get an accurate estimate of the probability.

Complexity

In general, model complexity involves a trade-off between simplicity and accuracy of the model. Occam's razor is a principle particularly relevant to modeling, its essential idea being that among models with roughly equal predictive power, the simplest one is the most desirable. While added complexity usually improves the realism of a model, it can make the model difficult to understand and analyze, and can also pose computational problems, including numerical instability. Thomas Kuhn argues that as science progresses, explanations tend to become more complex before a paradigm shift offers radical simplification
.
For example, when modeling the flight of an aircraft, we could embed each mechanical part of the aircraft into our model and would thus acquire an almost white-box model of the system. However, the computational cost of adding such a huge amount of detail would effectively inhibit the usage of such a model. Additionally, the uncertainty would increase due to an overly complex system, because each separate part induces some amount of variance into the model. It is therefore usually appropriate to make some approximations to reduce the model to a sensible size. Engineers often can accept some approximations in order to get a more robust and simple model. For example, Newton's classical mechanics is an approximated model of the real world. Still, Newton's model is quite sufficient for most ordinary-life situations, that is, as long as particle speeds are well below the speed of light, and we study macro-particles only.

Training and tuning

Any model which is not pure white-box contains some parameters that can be used to fit the model to the system it is intended to describe. If the modeling is done by an artificial neural network or other machine learning, the optimization of parameters is called training, while the optimization of model hyperparameters is called tuning and often uses cross-validation. In more conventional modeling through explicitly given mathematical functions, parameters are often determined by curve fitting.

Model evaluation

A crucial part of the modeling process is the evaluation of whether or not a given mathematical model describes a system accurately. This question can be difficult to answer as it involves several different types of evaluation.

Fit to empirical data

Usually the easiest part of model evaluation is checking whether a model fits experimental measurements or other empirical data. In models with parameters, a common approach to test this fit is to split the data into two disjoint subsets: training data and verification data. The training data are used to estimate the model parameters. An accurate model will closely match the verification data even though these data were not used to set the model's parameters. This practice is referred to as cross-validation in statistics.

Defining a metric to measure distances between observed and predicted data is a useful tool of assessing model fit. In statistics, decision theory, and some economic models, a loss function plays a similar role.

While it is rather straightforward to test the appropriateness of parameters, it can be more difficult to test the validity of the general mathematical form of a model. In general, more mathematical tools have been developed to test the fit of statistical models than models involving differential equations. Tools from non-parametric statistics can sometimes be used to evaluate how well the data fit a known distribution or to come up with a general model that makes only minimal assumptions about the model's mathematical form.

Scope of the model

Assessing the scope of a model, that is, determining what situations the model is applicable to, can be less straightforward. If the model was constructed based on a set of data, one must determine for which systems or situations the known data is a "typical" set of data.

The question of whether the model describes well the properties of the system between data points is called interpolation, and the same question for events or data points outside the observed data is called extrapolation.

As an example of the typical limitations of the scope of a model, in evaluating Newtonian classical mechanics, we can note that Newton made his measurements without advanced equipment, so he could not measure properties of particles travelling at speeds close to the speed of light. Likewise, he did not measure the movements of molecules and other small particles, but macro particles only. It is then not surprising that his model does not extrapolate well into these domains, even though his model is quite sufficient for ordinary life physics.

Philosophical considerations

Many types of modeling implicitly involve claims about causality. This is usually (but not always) true of models involving differential equations. As the purpose of modeling is to increase our understanding of the world, the validity of a model rests not only on its fit to empirical observations, but also on its ability to extrapolate to situations or data beyond those originally described in the model. One can think of this as the differentiation between qualitative and quantitative predictions. One can also argue that a model is worthless unless it provides some insight which goes beyond what is already known from direct investigation of the phenomenon being studied.

An example of such criticism is the argument that the mathematical models of optimal foraging theory do not offer insight that goes beyond the common-sense conclusions of evolution and other basic principles of ecology.

Examples

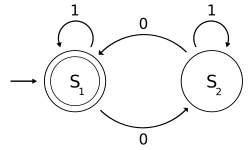
• One of the popular examples in computer science is the mathematical models of various machines, an example is the deterministic finite automaton (DFA) which is defined as an abstract mathematical concept, but due to the deterministic nature of a DFA, it is implementable in hardware and software for solving various specific problems. For example, the following is a DFA M with a binary alphabet, which requires that the input contains an even number of 0s.

The state diagram for M

M = (Q, Σ, δ, q₀, F) where

• Q = {S₁, S₂},
• Σ = {0, 1},
• q₀ = S₁,
• F = {S₁}, and
• δ is defined by the following state transition table:

	0	1
S1	S2	S1
S2	S1	S2

The state S₁ represents that there has been an even number of 0s in the input so far, while S₂ signifies an odd number. A 1 in the input does not change the state of the automaton. When the input ends, the state will show whether the input contained an even number of 0s or not. If the input did contain an even number of 0s, M will finish in state S₁, an accepting state, so the input string will be accepted.

The language recognized by M is the regular language given by the regular expression 1*( 0 (1*) 0 (1*) )*, where "*" is the Kleene star, e.g., 1* denotes any non-negative number (possibly zero) of symbols "1".

• Many everyday activities carried out without a thought are uses of mathematical models. A geographical map projection of a region of the earth onto a small, plane surface is a model which can be used for many purposes such as planning travel.
• Another simple activity is predicting the position of a vehicle from its initial position, direction and speed of travel, using the equation that distance traveled is the product of time and speed. This is known as dead reckoning when used more formally. Mathematical modeling in this way does not necessarily require formal mathematics; animals have been shown to use dead reckoning.
• Population Growth. A simple (though approximate) model of population growth is the Malthusian growth model. A slightly more realistic and largely used population growth model is the logistic function, and its extensions.
• Model of a particle in a potential-field. In this model we consider a particle as being a point of mass which describes a trajectory in space which is modeled by a function giving its coordinates in space as a function of time. The potential field is given by a function ${\displaystyle V\!:\mathbb {R} ^{3}\!\rightarrow \mathbb {R} }$ and the trajectory, that is a function ${\displaystyle \mathbf {r} \!:\mathbb {R} \rightarrow \mathbb {R} ^{3}}$, is the solution of the differential equation:

${\displaystyle -{\frac {\mathrm {d} ^{2}\mathbf {r} (t)}{\mathrm {d} t^{2}}}m={\frac {\partial V[\mathbf {r} (t)]}{\partial x}}\mathbf {\hat {x}} +{\frac {\partial V[\mathbf {r} (t)]}{\partial y}}\mathbf {\hat {y}} +{\frac {\partial V[\mathbf {r} (t)]}{\partial z}}\mathbf {\hat {z}} ,}$

that can be written also as:

${\displaystyle m{\frac {\mathrm {d} ^{2}\mathbf {r} (t)}{\mathrm {d} t^{2}}}=-\nabla V[\mathbf {r} (t)].}$

Note this model assumes the particle is a point mass, which is certainly known to be false in many cases in which we use this model; for example, as a model of planetary motion.

• Model of rational behavior for a consumer. In this model we assume a consumer faces a choice of n commodities labeled 1,2,...,n each with a market price p₁, p₂,..., p_n. The consumer is assumed to have an ordinal utility function U (ordinal in the sense that only the sign of the differences between two utilities, and not the level of each utility, is meaningful), depending on the amounts of commodities x₁, x₂,..., x_n consumed. The model further assumes that the consumer has a budget M which is used to purchase a vector x₁, x₂,..., x_n in such a way as to maximize U(x₁, x₂,..., x_n). The problem of rational behavior in this model then becomes an optimization problem, that is:

${\displaystyle \max U(x_{1},x_{2},\ldots ,x_{n})}$

 

subject to:

 

${\displaystyle \sum _{i=1}^{n}p_{i}x_{i}\leq M.}$

${\displaystyle x_{i}\geq 0\;\;\;\forall i\in \{1,2,\ldots ,n\}}$

This model has been used in a wide variety of economic contexts, such as in general equilibrium theory to show existence and Pareto efficiency of economic equilibria.

• Neighbour-sensing model explains the mushroom formation from the initially chaotic fungal network.
• Computer science: models in Computer Networks, data models, surface model,...
• Mechanics: movement of rocket model,...

Research

From Wikipedia, the free encyclopedia

Basrelief sculpture "Research holding the torch of knowledge" (1896) by Olin Levi Warner. Library of Congress, Thomas Jefferson Building, Washington, D.C.

Research comprises "creative and systematic work undertaken to increase the stock of knowledge, including knowledge of humans, culture and society, and the use of this stock of knowledge to devise new applications." It is used to establish or confirm facts, reaffirm the results of previous work, solve new or existing problems, support theorems, or develop new theories. A research project may also be an expansion on past work in the field. Research projects can be used to develop further knowledge on a topic, or in the example of a school research project, they can be used to further a student's research prowess to prepare them for future jobs or reports. To test the validity of instruments, procedures, or experiments, research may replicate elements of prior projects or the project as a whole. The primary purposes of basic research (as opposed to applied research) are documentation, discovery, interpretation, or the research and development (R&D) of methods and systems for the advancement of human knowledge. Approaches to research depend on epistemologies, which vary considerably both within and between humanities and sciences. There are several forms of research: scientific, humanities, artistic, economic, social, business, marketing, practitioner research, life, technological, etc.

Etymology

Aristotle, (384–322 BC), one of the early figures in the development of the scientific method.

 

The word research is derived from the Middle French "recherche", which means "to go about seeking", the term itself being derived from the Old French term "recerchier" a compound word from "re-" + "cerchier", or "sercher", meaning 'search'. The earliest recorded use of the term was in 1577.

Definitions

Research has been defined in a number of different ways, and while there are similarities, there does not appear to be a single, all-encompassing definition that is embraced by all who engage in it.

One definition of research is used by the OECD, "Any creative systematic activity undertaken in order to increase the stock of knowledge, including knowledge of man, culture and society, and the use of this knowledge to devise new applications."

Another definition of research is given by John W. Creswell, who states that "research is a process of steps used to collect and analyze information to increase our understanding of a topic or issue". It consists of three steps: pose a question, collect data to answer the question, and present an answer to the question.

The Merriam-Webster Online Dictionary defines research in more detail as "studious inquiry or examination; especially : investigation or experimentation aimed at the discovery and interpretation of facts, revision of accepted theories or laws in the light of new facts, or practical application of such new or revised theories or laws"

Forms of research

Original research is research that is not exclusively based on a summary, review or synthesis of earlier publications on the subject of research. This material is of a primary source character. The purpose of the original research is to produce new knowledge, rather than to present the existing knowledge in a new form (e.g., summarized or classified).
Original research can take a number of forms, depending on the discipline it pertains to. In experimental work, it typically involves direct or indirect observation of the researched subject(s), e.g., in the laboratory or in the field, documents the methodology, results, and conclusions of an experiment or set of experiments, or offers a novel interpretation of previous results. In analytical work, there are typically some new (for example) mathematical results produced, or a new way of approaching an existing problem. In some subjects which do not typically carry out experimentation or analysis of this kind, the originality is in the particular way existing understanding is changed or re-interpreted based on the outcome of the work of the researcher.

The degree of originality of the research is among major criteria for articles to be published in academic journals and usually established by means of peer review. Graduate students are commonly required to perform original research as part of a dissertation.

Scientific research is a systematic way of gathering data and harnessing curiosity. This research provides scientific information and theories for the explanation of the nature and the properties of the world. It makes practical applications possible. Scientific research is funded by public authorities, by charitable organizations and by private groups, including many companies. Scientific research can be subdivided into different classifications according to their academic and application disciplines. Scientific research is a widely used criterion for judging the standing of an academic institution, but some argue that such is an inaccurate assessment of the institution, because the quality of research does not tell about the quality of teaching (these do not necessarily correlate).

Research in the humanities involves different methods such as for example hermeneutics and semiotics. Humanities scholars usually do not search for the ultimate correct answer to a question, but instead, explore the issues and details that surround it. Context is always important, and context can be social, historical, political, cultural, or ethnic. An example of research in the humanities is historical research, which is embodied in historical method. Historians use primary sources and other evidence to systematically investigate a topic, and then to write histories in the form of accounts of the past. Other studies aim to merely examine the occurrence of behaviours in societies and communities, without particularly looking for reasons or motivations to explain these. These studies may be qualitative or quantitative, and can use a variety of approaches, such as queer theory or feminist theory.

Artistic research, also seen as 'practice-based research', can take form when creative works are considered both the research and the object of research itself. It is the debatable body of thought which offers an alternative to purely scientific methods in research in its search for knowledge and truth.

Scientific research

Primary scientific research being carried out at the Microscopy Laboratory of the Idaho National Laboratory.

 

Scientific research equipment at MIT.

 

German maritime research vessel Sonne

Generally, research is understood to follow a certain structural process. Though step order may vary depending on the subject matter and researcher, the following steps are usually part of most formal research, both basic and applied:

1. Observations and formation of the topic: Consists of the subject area of one's interest and following that subject area to conduct subject related research. The subject area should not be randomly chosen since it requires reading a vast amount of literature on the topic to determine the gap in the literature the researcher intends to narrow. A keen interest in the chosen subject area is advisable. The research will have to be justified by linking its importance to already existing knowledge about the topic.
2. Hypothesis: A testable prediction which designates the relationship between two or more variables.
3. Conceptual definition: Description of a concept by relating it to other concepts.
4. Operational definition: Details in regards to defining the variables and how they will be measured/assessed in the study.
5. Gathering of data: Consists of identifying a population and selecting samples, gathering information from or about these samples by using specific research instruments. The instruments used for data collection must be valid and reliable.
6. Analysis of data: Involves breaking down the individual pieces of data to draw conclusions about it.
7. Data Interpretation: This can be represented through tables, figures, and pictures, and then described in words.
8. Test, revising of hypothesis
9. Conclusion, reiteration if necessary

A common misconception is that a hypothesis will be proven. Generally, a hypothesis is used to make predictions that can be tested by observing the outcome of an experiment. If the outcome is inconsistent with the hypothesis, then the hypothesis is rejected. However, if the outcome is consistent with the hypothesis, the experiment is said to support the hypothesis. This careful language is used because researchers recognize that alternative hypotheses may also be consistent with the observations. In this sense, a hypothesis can never be proven, but rather only supported by surviving rounds of scientific testing and, eventually, becoming widely thought of as true.

A useful hypothesis allows prediction and within the accuracy of observation of the time, the prediction will be verified. As the accuracy of observation improves with time, the hypothesis may no longer provide an accurate prediction. In this case, a new hypothesis will arise to challenge the old, and to the extent that the new hypothesis makes more accurate predictions than the old, the new will supplant it. Researchers can also use a null hypothesis, which states no relationship or difference between the independent or dependent variables.

Historical research

German historian Leopold von Ranke (1795–1886), considered to be one of the founders of modern source-based history.

The historical method comprises the techniques and guidelines by which historians use historical sources and other evidence to research and then to write history. There are various history guidelines that are commonly used by historians in their work, under the headings of external criticism, internal criticism, and synthesis. This includes lower criticism and sensual criticism. Though items may vary depending on the subject matter and researcher, the following concepts are part of most formal historical research:

• Identification of origin date
• Evidence of localization
• Recognition of authorship
• Analysis of data
• Identification of integrity
• Attribution of credibility

Artistic research

The controversial trend of artistic teaching becoming more academics-oriented is leading to artistic research being accepted as the primary mode of enquiry in art as in the case of other disciplines. One of the characteristics of artistic research is that it must accept subjectivity as opposed to the classical scientific methods. As such, it is similar to the social sciences in using qualitative research and intersubjectivity as tools to apply measurement and critical analysis.

Artistic research has been defined by the University of Dance and Circus (Dans och Cirkushögskolan, DOCH), Stockholm in the following manner - "Artistic research is to investigate and test with the purpose of gaining knowledge within and for our artistic disciplines. It is based on artistic practices, methods, and criticality. Through presented documentation, the insights gained shall be placed in a context." Artistic research aims to enhance knowledge and understanding with presentation of the arts. A more simple understanding by Julian Klein defines Artistic Research as any kind of research employing the artistic mode of perception.

According to artist Hakan Topal, in artistic research, "perhaps more so than other disciplines, intuition is utilized as a method to identify a wide range of new and unexpected productive modalities". Most writers, whether of fiction or non-fiction books, also have to do research to support their creative work. This may be factual, historical, or background research. Background research could include, for example, geographical or procedural research.

The Society for Artistic Research (SAR) publishes the triannual Journal for Artistic Research (JAR), an international, online, open access, and peer-reviewed journal for the identification, publication, and dissemination of artistic research and its methodologies, from all arts disciplines and it runs the Research Catalogue (RC), a searchable, documentary database of artistic research, to which anyone can contribute.

Patricia Leavy addresses eight arts-based research (ABR) genres: narrative inquiry, fiction-based research, poetry, music, dance, theatre, film, and visual art.

In 2016 ELIA (European League of the Institutes of the Arts) launched The Florence Principles' on the Doctorate in the Arts. The Florence Principles relating to the Salzburg Principles and the Salzburg Recommendations of EUA (European University Association) name seven points of attention to specify the Doctorate / PhD in the Arts compared to a scientific doctorate / PhD The Florence Principles have been endorsed and are supported also by AEC, CILECT, CUMULUS and SAR.

Documentary research

Steps in conducting research

Research is often conducted using the hourglass model structure of research. The hourglass model starts with a broad spectrum for research, focusing in on the required information through the method of the project (like the neck of the hourglass), then expands the research in the form of discussion and results. The major steps in conducting research are:

• Identification of research problem
• Literature review
• Specifying the purpose of research
• Determining specific research questions
• Specification of a conceptual framework, sometimes including a set of hypotheses
• Choice of a methodology (for data collection)
• Data collection
• Verifying data
• Analyzing and interpreting the data
• Reporting and evaluating research
• Communicating the research findings and, possibly, recommendations

The steps generally represent the overall process; however, they should be viewed as an ever-changing iterative process rather than a fixed set of steps. Most research begins with a general statement of the problem, or rather, the purpose for engaging in the study. The literature review identifies flaws or holes in previous research which provides justification for the study. Often, a literature review is conducted in a given subject area before a research question is identified. A gap in the current literature, as identified by a researcher, then engenders a research question. The research question may be parallel to the hypothesis. The hypothesis is the supposition to be tested. The researcher(s) collects data to test the hypothesis. The researcher(s) then analyzes and interprets the data via a variety of statistical methods, engaging in what is known as empirical research. The results of the data analysis in rejecting or failing to reject the null hypothesis are then reported and evaluated. At the end, the researcher may discuss avenues for further research. However, some researchers advocate for the reverse approach: starting with articulating findings and discussion of them, moving "up" to identification of a research problem that emerges in the findings and literature review. The reverse approach is justified by the transactional nature of the research endeavor where research inquiry, research questions, research method, relevant research literature, and so on are not fully known until the findings have fully emerged and been interpreted.

Rudolph Rummel says, "... no researcher should accept any one or two tests as definitive. It is only when a range of tests are consistent over many kinds of data, researchers, and methods can one have confidence in the results."

Plato in Meno talks about an inherent difficulty, if not a paradox, of doing research that can be paraphrased in the following way, "If you know what you're searching for, why do you search for it?! [i.e., you have already found it] If you don't know what you're searching for, what are you searching for?!"

Research methods

The research room at the New York Public Library, an example of secondary research in progress.

 

Maurice Hilleman is credited with saving more lives than any other scientist of the 20th century.

 

The goal of the research process is to produce new knowledge or deepen understanding of a topic or issue. This process takes three main forms (although, as previously discussed, the boundaries between them may be obscure):

• Exploratory research, which helps to identify and define a problem or question.
• Constructive research, which tests theories and proposes solutions to a problem or question.
• Empirical research, which tests the feasibility of a solution using empirical evidence.

There are two major types of empirical research design: qualitative research and quantitative research. Researchers choose qualitative or quantitative methods according to the nature of the research topic they want to investigate and the research questions they aim to answer:

Qualitative research

This involves understanding human behavior and the reasons that govern such behavior, by asking a broad question, collecting data in the form of words, images, video etc that is analyzed, and searching for themes. This type of research aims to investigate a question without attempting to quantifiably measure variables or look to potential relationships between variables. It is viewed as more restrictive in testing hypotheses because it can be expensive and time-consuming and typically limited to a single set of research subjects. Qualitative research is often used as a method of exploratory research as a basis for later quantitative research hypotheses. Qualitative research is linked with the philosophical and theoretical stance of social constructionism.

Social media posts are used for qualitative research.

Quantitative research

This involves systematic empirical investigation of quantitative properties and phenomena and their relationships, by asking a narrow question and collecting numerical data to analyze it utilizing statistical methods. The quantitative research designs are experimental, correlational, and survey (or descriptive). Statistics derived from quantitative research can be used to establish the existence of associative or causal relationships between variables. Quantitative research is linked with the philosophical and theoretical stance of positivism.

The quantitative data collection methods rely on random sampling and structured data collection instruments that fit diverse experiences into predetermined response categories. These methods produce results that are easy to summarize, compare, and generalize. Quantitative research is concerned with testing hypotheses derived from theory or being able to estimate the size of a phenomenon of interest.

If the research question is about people, participants may be randomly assigned to different treatments (this is the only way that a quantitative study can be considered a true experiment). If this is not feasible, the researcher may collect data on participant and situational characteristics to statistically control for their influence on the dependent, or outcome, variable. If the intent is to generalize from the research participants to a larger population, the researcher will employ probability sampling to select participants.

In either qualitative or quantitative research, the researcher(s) may collect primary or secondary data. Primary data is data collected specifically for the research, such as through interviews or questionnaires. Secondary data is data that already exists, such as census data, which can be re-used for the research. It is good ethical research practice to use secondary data wherever possible.

Mixed-method research, i.e. research that includes qualitative and quantitative elements, using both primary and secondary data, is becoming more common. This method has benefits that using one method alone cannot offer. For example, a researcher may choose to conduct a qualitative study and follow it up with a quantitative study to gain additional insights.

Big data has brought big impacts on research methods so that now many researchers do not put much effort into data collection; furthermore, methods to analyze easily available huge amounts of data have also been developed.

Non-empirical research

Non-empirical (theoretical) research is an approach that involves the development of theory as opposed to using observation and experimentation. As such, non-empirical research seeks solutions to problems using existing knowledge as its source. This, however, does not mean that new ideas and innovations cannot be found within the pool of existing and established knowledge. Non-empirical research is not an absolute alternative to empirical research because they may be used together to strengthen a research approach. Neither one is less effective than the other since they have their particular purpose in science. Typically empirical research produces observations that need to be explained; then theoretical research tries to explain them, and in so doing generates empirically testable hypotheses; these hypotheses are then tested empirically, giving more observations that may need further explanation; and so on.

A simple example of a non-empirical task is the prototyping of a new drug using a differentiated application of existing knowledge; another is the development of a business process in the form of a flow chart and texts where all the ingredients are from established knowledge. Much of cosmological research is theoretical in nature. Mathematics research does not rely on externally available data; rather, it seeks to prove theorems about mathematical objects.

Research ethics

Research ethics involves the application of fundamental ethical principles to a variety of topics involving research, including scientific research. These principles include deontology, consequentialism, virtue ethics and value (ethics). Ethical issues may arise in the design and implementation of research involving human experimentation or animal experimentation, such as: various aspects of academic scandal, including scientific misconduct (such as fraud, fabrication of data and plagiarism), whistleblowing; regulation of research, etc. Research ethics is most developed as a concept in medical research. The key agreement here is the 1964 Declaration of Helsinki. The Nuremberg Code is a former agreement, but with many still important notes. Research in the social sciences presents a different set of issues than those in medical research and can involve issues of researcher and participant safety, empowerment and access to justice.

When research involves human subjects, obtaining informed consent from them is essential.

Problems in research

Methods of research

In many disciplines, Western methods of conducting research are predominant. Researchers are overwhelmingly taught Western methods of data collection and study. The increasing participation of indigenous peoples as researchers has brought increased attention to the lacuna in culturally-sensitive methods of data collection. Non-Western methods of data collection may not be the most accurate or relevant for research on non-Western societies. For example, "Hua Oranga" was created as a criterion for psychological evaluation in Māori populations, and is based on dimensions of mental health important to the Māori people – "taha wairua (the spiritual dimension), taha hinengaro (the mental dimension), taha tinana (the physical dimension), and taha whanau (the family dimension)".

Linguicism

Periphery scholars face the challenges of exclusion and linguicism in research and academic publication. As the great majority of mainstream academic journals are written in English, multilingual periphery scholars often must translate their work to be accepted to elite Western-dominated journals. Multilingual scholars' influences from their native communicative styles can be assumed to be incompetence instead of difference.

Publication Peer Review

Peer review is a form of self-regulation by qualified members of a profession within the relevant field. Peer review methods are employed to maintain standards of quality, improve performance, and provide credibility. In academia, scholarly peer review is often used to determine an academic paper's suitability for publication. Usually, the peer review process involves experts in the same field who are consulted by editors to give a review of the scholarly works produced by a colleague of theirs from an unbiased and impartial point of view, and this is usually done free of charge. The tradition of peer reviews being done for free has however brought many pitfalls which are also indicative of why most peer reviewers decline many invitations to review. It was observed that publications from periphery countries rarely rise to the same elite status as those of North America and Europe, because limitations on the availability of resources including high-quality paper and sophisticated image-rendering software and printing tools render these publications less able to satisfy standards currently carrying formal or informal authority in the publishing industry. These limitations in turn result in the under-representation of scholars from periphery nations among the set of publications holding prestige status relative to the quantity and quality of those scholars' research efforts, and this under-representation in turn results in disproportionately reduced acceptance of the results of their efforts as contributions to the body of knowledge available worldwide.

Influence of the open-access movement

The open access movement assumes that all information generally deemed useful should be free and belongs to a "public domain", that of "humanity". This idea gained prevalence as a result of Western colonial history and ignores alternative conceptions of knowledge circulation. For instance, most indigenous communities consider that access to certain information proper to the group should be determined by relationships.

There is alleged to be a double standard in the Western knowledge system. On the one hand, "digital right management" used to restrict access to personal information on social networking platforms is celebrated as a protection of privacy, while simultaneously when similar functions are used by cultural groups (i.e. indigenous communities) this is denounced as "access control" and reprehended as censorship.

Future perspectives

Even though Western dominance seems to be prominent in research, some scholars, such as Simon Marginson, argue for "the need [for] a plural university world". Marginson argues that the East Asian Confucian model could take over the Western model.

This could be due to changes in funding for research both in the East and the West. Focussed on emphasizing educational achievement, East Asian cultures, mainly in China and South Korea, have encouraged the increase of funding for research expansion. In contrast, in the Western academic world, notably in the United Kingdom as well as in some state governments in the United States, funding cuts for university research have occurred, which some say may lead to the future decline of Western dominance in research.

Professionalisation

In several national and private academic systems, the professionalisation of research has resulted in formal job titles.

In Russia

In present-day Russia, the former Soviet Union and in some post-Soviet states the term researcher (Russian: Научный сотрудник, nauchny sotrudnik) is both a generic term for a person who carried out scientific research, as well as a job position within the frameworks of the USSR Academy of Sciences, Soviet universities, and in other research-oriented establishments. The term is also sometimes translated as research fellow, research associate, etc.

The following ranks are known:

• Junior Researcher (Junior Research Associate)
• Researcher (Research Associate)
• Senior Researcher (Senior Research Associate)
• Leading Researcher (Leading Research Associate)
• Chief Researcher (Chief Research Associate)

Publishing

Cover of the first issue of Nature, 4 November 1869.

Academic publishing is a system that is necessary for academic scholars to peer review the work and make it available for a wider audience. The system varies widely by field and is also always changing, if often slowly. Most academic work is published in journal article or book form. There is also a large body of research that exists in either a thesis or dissertation form. These forms of research can be found in databases explicitly for theses and dissertations. In publishing, STM publishing is an abbreviation for academic publications in science, technology, and medicine. research paper guides Most established academic fields have their own scientific journals and other outlets for publication, though many academic journals are somewhat interdisciplinary, and publish work from several distinct fields or subfields. The kinds of publications that are accepted as contributions of knowledge or research vary greatly between fields, from the print to the electronic format. A study suggests that researchers should not give great consideration to findings that are not replicated frequently. It has also been suggested that all published studies should be subjected to some measure for assessing the validity or reliability of its procedures to prevent the publication of unproven findings. Business models are different in the electronic environment. Since about the early 1990s, licensing of electronic resources, particularly journals, has been very common. Presently, a major trend, particularly with respect to scholarly journals, is open access. There are two main forms of open access: open access publishing, in which the articles or the whole journal is freely available from the time of publication, and self-archiving, where the author makes a copy of their own work freely available on the web.

Research funding

Most funding for scientific research comes from three major sources: corporate research and development departments; private foundations, for example, the Bill and Melinda Gates Foundation; and government research councils such as the National Institutes of Health in the USA and the Medical Research Council in the UK. These are managed primarily through universities and in some cases through military contractors. Many senior researchers (such as group leaders) spend a significant amount of their time applying for grants for research funds. These grants are necessary not only for researchers to carry out their research but also as a source of merit.

The Social Psychology Network provides a comprehensive list of U.S. Government and private foundation funding sources.